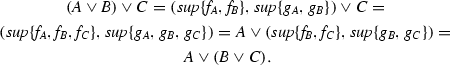Two Approaches to Fuzzy Implication

Abstract

We discuss construction of fuzzy implication and also correlation between negation and implication operators defined on fuzzy values. Two structures for fuzzy implications are studied: the lattice of Step-Ordered Fuzzy Numbers (SOFNs) and the Boolean algebra $\mathfrak {B}$ of membership degrees for metasets. Even though these two approaches stem from completely different areas it turned out that they lead to similar applications and results. Both of them emerged from research conducted by W. Kosiński and can be applied not only in the most popular application field which is approximate reasoning but also for designing decision-support systems, enriching methods and techniques of opinion mining, or modeling fuzzy beliefs in multiagent systems.

1 Introduction

In his recent research Kosiński focused on new fields for applications of Ordered Fuzzy Numbers (OFNs) [24,25,26]. One of the promising domains was approximate reasoning involving fuzzy implication. Among the results of this development one has to mention Prokopowicz’s dissertation dealing with definition of engineering implications. Another branch of this development, fuzzy implication on Step-Ordered Fuzzy Numbers (SOFNs), which emerged as the result of cooperation with Kacprzak, is presented in the following. At that time Kosiński, as the Starosta’s PhD supervisor, also took part in the development of metaset theory. The metaset concept is an alternative approach to fuzzy membership, which has many interesting properties. Some of them are related to fuzzy implication and many-valued logics and are presented in the following. In this chapter we confront two approaches to fuzzy implication: OFN based and metaset based.

Fuzzy implication is an operation computing the fulfillment degree of a rule expressed by IF X THEN Y, where the antecedent and the consequent are fuzzy. These functions must comply with certain basic properties and the most typical is the Kleene-Dienes implication, based on the classical implication definition $(x \rightarrow y \equiv \lnot x \vee y)$, using the Zadeh negation and the maximum S-norm, but other fuzzy implication functions exist. On the other hand, fuzzy implication is an extension of the classical implication operator in which the two values involved and the result are not necessarily true or false (1 or 0), but can belong to the set [0,1]. Thus, it is a function $f: [0,1] \rightarrow [0,1]$.

Kosiński’s effort was aimed at proposing an implication operation on OFNs analogous to classical implication, which preserves its main properties. One of them says that for any two formulas $\alpha$ and $\beta$, formula if $\alpha$ then $\beta$, that is, $\alpha \rightarrow \beta$ is equivalent to formula $\lnot \alpha \vee \beta$. We want to obtain a similar equality for OFNs. The problem is with operation of negation. Because the set of all OFNs is not a complete lattice, the way of defining the implication is not straightforward. In 2011 Kacprzak and Kosiński proposed a new binary operator on the set $\mathscr {N}$ called 2K-fuzzy implication that satisfies conditions of fuzzy implication, classically formulated in the theory of fuzzy sets [6] for two-value operations on a complete lattice (in the particular case on the interval [0, 1]) requiring it to be decreasing with respect to the first variable and increasing with respect to the second variable. It is an open question how to define negation and implication on the set of all OFNs $\mathscr {R}$.

During fruitful discussions with Kosiński it turned out that metaset theory has all the capabilities necessary for defining fuzzy implication as well as for its applications. Metasets admit partial membership of its members. Consequently, they allow formalization of properties satisfied with degrees other than complete truth or falsity. Metaset sentences express vague properties and they are evaluated in a Boolean algebra. Therefore, defining implication on their certainty values is straightforward. As opposed to the original Kosiński idea based on OFNs, the implication developed for metasets operates on crisp values, not fuzzy ones. Collection of all these values, however, forms a structure (the Boolean algebra) that enables expressing imprecision with the help of sentences of the metaset language.

In this chapter we examine two approaches. Therefore, it is divided into two main sections: Sect. 7.2 summarizes Step-Ordered Fuzzy Numbers and gives the construction of fuzzy implications defined on these numbers; next, Sect. 7.3 discusses the Boolean algebra of membership degrees for metasets and introduces metaset-based implication. Finally, in Sect. 7.4 we provide a summary of both approaches and outline directions for future research.

2 Lattice Structure and Implications on SOFNs

Orthodox Ordered Fuzzy Number A is defined as an ordered pair of continuous real functions specified on the interval [0, 1]; that is,

$$A = (f,g)$$

with

$$f, g : [0,1] \rightarrow \mathbf{R }.$$

In this chapter, the set of all OFNs is denoted by $\mathscr {R}$. The continuity of both functions implies that their images are bounded intervals, say UP and DOWN, respectively. The following symbols are used to mark boundaries for $UP = [l_{A}, 1_{A}^{-}]$ and for $DOWN = [1_{A}^{+}, p_{A}]$. If we further assume that f and g are monotone (and consequently invertible), and add the constant function on the interval $[1_{A}^{-}, 1_{A}^{+}]$ with its value equal to 1, we might define the membership function

$$\begin{aligned} \mu (x)= \left\{ \begin{array}{lll} \mu _{up}(x) &{} \text {if} &{} x\in [l_{A}, 1_{A}^{-}]=[f(0), f(1)], \\ \mu _{down}(x) \;\;\;\;&{} \text {if} \;\;\;\; &{} x\in [1_{A}^{+}, p_{A}]=[g(1), g(0)], \\ 1 &{} \text {if} &{} x\in [1_{A}^{-}, 1_{A}^{+}]. \end{array} \right. \end{aligned}$$

(7.1)

where

• 1. $\mu _{up}(x)=:f^{-1}(x)$ and $\mu _{down}(x)=:g^{-1}(x)$.

• 2. f is increasing; g is decreasing.

• 3. $f\le g$ (pointwise).

Obtained in this way the membership function $\mu (x), x\in \mathbf{R }$ represents a mathematical object that refers to a convex fuzzy number in the classical sense [10, 34]. However, we can observe here some limitations. This is because some membership functions already known in the classical theory of fuzzy numbers (cf. [10, 18, 46]) cannot be obtained by taking inverses of continuous functions f and g in the process described above. These are the functions that are piecewise constant; that is, $\mu _{up}$ and $\mu _{down}$ are not strictly monotone. The lack of strict monotonicity implies that functions inverse to $\mu _{up}$ and $\mu _{down}$ do not exist in the classical sense. To cope with this problem Kosiński offered to accept some limitations assuming that for both functions $\mu _{up}$ and $\mu _{down}$ there exist a finite (or at most countable) number of such constancy subintervals, and then the inverse functions are piecewise continuous and monotone with a finite (or at most countable) number of discontinuity points [36]. In this way we can employ a class of functions larger than continuous ones. This is the class of real-valued functions of bounded (finite) variation, BV [41].

2.1 Step-Ordered Fuzzy Numbers

In 2006 Kosiński introduced a generalization of the original definition of OFNs to make the algebra a more efficient tool in dealing with imprecise, fuzzy quantitative terms [36].

Definition 1

By an OFN A (in the generalized form) we mean an ordered pair (f, g) of functions such that $f,g:[0,1] \rightarrow \mathbf{R }$ are of bounded variation, that is, $f,g \in BV$.

Let $\mathscr {R}_{BV}$ denote the set of all generalized OFNs, that is, those that meet Definition 1. Notice that all convex fuzzy numbers are contained in this new space, $\mathscr {R}\subset \mathscr {R}_{BV}$. Operations for generalized OFNs are defined in a similar way to operations for orthodox OFNs, the norm, however, will change into the norm of the Cartesian product of the space of functions of bounded variations.

An important consequence of this generalization is the possibility of introducing a subspace of an OFN composed of pairs of step functions [37]. First, a natural number K is fixed and [0, 1) is split into $K - 1$ subintervals $[a_{i}, a_{i+1})$; that is,

$$ \bigcup \limits _{i=1}^{K-1}[a_{i}, a_{i+1})=[0,1), $$

where

$$0 = a_1< a_2< \cdots < a_{K} = 1. $$

Now, define a step function f of resolution K by putting value $u_i \in \mathbf{R }$ on each subinterval $[a_{i}, a_{i + 1})$. Each such function f is identified with a K-dimensional vector; that is,

$$f \sim {{\varvec{u}}} = (u_1, u_2, \ldots ,u_K)\in \mathbf{R }^K,$$

where the Kth value $u_K$ corresponds to $y = 1$; that is, $f(1) = u_K$. Taking a pair of such functions we have an OFN from $\mathscr {R}_{BV}$.

Definition 2

By a Step-Ordered Fuzzy Number A of resolution K we mean an ordered pair (f, g) of functions such that $f, g : [0,1] {\rightarrow } \mathbf{R }$ are step functions of resolution K.

We use $\mathscr {R}_K$ for denotation of the set of elements satisfying the above definition. The example of an SOFN (also called Step Kosiński’s fuzzy number, SKFN) and its membership relation (represented by a curve) are shown in Figs. 7.1 and 7.2. The set $\mathscr {R}_K \subset \mathscr {R}_{BV}$ has been extensively elaborated in [22, 35].

We can identify $\mathscr {R}_K$ with the Cartesian product of $\mathbf{R }^K \times \mathbf{R }^K$ because each K-step function is represented by its K values. It is obvious that each element of the space $\mathscr {R}_K$ may be regarded as an approximation of elements from $\mathscr {R}_{BV}$; by increasing the number K of steps we are getting a better approximation. The norm of $\mathscr {R}_K$ is assumed to be the Euclidean one of $\mathbf{R }^{2K}$, thus we have an inner-product structure at our disposal.

Fig. 7.1

Example of a Step-Ordered Fuzzy Number $A = (f,g) \in \mathscr {R}_K$, a function f, b function g

Fig. 7.2

Membership relation of the Step-Ordered Fuzzy Number $A = (f,g) \in \mathscr {R}_K$ depicted in Fig. 7.1

Now let $\mathscr {B}$ be the set of two binary values: 0, 1 and let us introduce the particular subset $\mathscr {N}$ of $\mathscr {R}_K$

$$\begin{aligned} {\mathscr {N}} = \{A =(\underline{u},\underline{v}) \in \mathscr {R}_K : \underline{u}\in {\mathscr {B}}^K\, , \underline{v}\in {\mathscr {B}}^K \}. \end{aligned}$$

(7.2)

It means that each such component of the vector $\underline{u}$ as well as of $\underline{v}$ has value 1 or 0. Because each element of $\mathscr {N}$ is represented by a 2K-dimensional binary vector the cardinality of the set $\mathscr {N}$ is $2^{2K}$. The set ${\mathscr {N}}$ consists of all binary SOFN, also called Binary Step Kosiński’s Fuzzy Numbers (BSKFN).

Definition 3

By a BSKFN A of resolution K we mean an ordered pair (f, g) of functions such that $f, g : [0,1] {\rightarrow } {\mathscr {B}}$ are step functions of resolution K.

2.2 Lattice on $\mathscr {R}_K$

Let us consider the set $\mathscr {R}_K$ of SOFNs with operations

$$A \wedge B =:F \;\;\;and\;\;\;A \vee B =:G$$

defined for each two fuzzy numbers $A = (f_A,g_A), B = (f_B,g_B)$ by the relations:

$$\begin{aligned} F=(f_F,g_F), \, {\text {if }} \, f_F=\sup \{f_A, f_B\}\, , g_F=\sup \{g_A, g_B\}\, , \end{aligned}$$

(7.3)

$$\begin{aligned} F=(f_F,g_F), \, {\text {if }} \, f_F=\inf \{f_A, f_B\}\, , g_F=\inf \{g_A, g_B\}\, . \end{aligned}$$

(7.4)

Notice that $\vee$ and $\wedge$ are actually operations in $\mathscr {R}_K$; that is, they are defined for all A, $B \in {\mathscr {R}_K}$ and the result of the operations is in ${\mathscr {R}_K}$. Next, let us observe that operation $\vee$ is

• Idempotent: Whenever it is applied to two equal values, it gives that value as the result:

  $$\begin{aligned} A \vee A = (sup\{f_A,f_A\},sup\{g_A,g_A\})=(f_A,g_A)=A, \end{aligned}$$

• Commutative:

  $$\begin{aligned} A\vee B=(sup\{f_A,f_B\},sup\{g_A,g_B\})=(sup\{f_B,f_A\},sup\{g_B,g_A\})=B\vee A, \end{aligned}$$

• Associative:

  

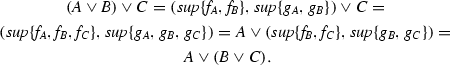
The same properties characterize the operation $\wedge$. Moreover, these two operations are connected by the absorption law:

$$\begin{aligned}&A \wedge (A \vee B) = A\wedge (sup\{f_A,f_B\},sup\{g_A,g_B\})=\\&(inf\{f_A,sup\{f_A,f_B\}\},inf\{g_A,sup\{g_A,g_B\}\})=(f_A,g_A) =A \end{aligned}$$

and similarly for

$$ A \vee (A \wedge B) = A. $$

The absorption laws ensure that the set ${\mathscr {R}_K}$ with an order $\le$ defined as

$$\begin{aligned} A \le B \;\;\; \text {iff} \;\;\; B=A \vee B \end{aligned}$$

(7.5)

is a partial order within which meets and joins are given through the operations $\vee$ and $\wedge$. It is easy to show that for every $A,B\in \mathscr {R}_K$ it holds that $A \vee B = B$ iff $B - A\ge 0$. Moreover, joints and meets exist for every two elements of $\mathscr {R}$. The following theorem is the consequence of the above reasoning.

Theorem 1

The algebra $({\mathscr {R}_K},\vee ,\wedge )$ is a lattice.

2.3 Complements and Negation on $\mathscr {N}$

Now let us consider the subset $\mathscr {N}$ of $\mathscr {R}_K$ defined in Sect. 7.2.1. As we have already noted above, every element of $\mathscr {N}$ can be represented by a binary vector and thereby $\mathscr {N}$ is isomorphic to the space of Boolean vectors. Below, we use the notation $A_{(a_1,a_2,\ldots ,a_{2K})}$ for a number A represented by vector $(a_1,a_2,\dots ,a_{2K})$ and we show that $\mathscr {N}$ is a Boolean algebra.

It is easy to observe that all subsets of $\mathscr {N}$ have both a join and a meet in $\mathscr {N}$. In fact, for every pair of numbers from the set $\{0,1\}$ we can determine max and min and it is always 0 or 1. Therefore $\mathscr {N}$ creates a complete lattice. In such a lattice we can distinguish the greatest element $\underline{1} = A_{(1,1,\ldots ,1)}$ and the least element $\underline{0} = A_{(0,0,\ldots ,0)}$.

Theorem 2

The algebra $({\mathscr {N}},\vee ,\wedge )$ is a complete lattice.

In a lattice in which the greatest and the least elements exist it is possible to define complements. We say that two elements A and B are complements of each other if and only if

$$A \vee B = \underline{1} \; \;\; \text {and} \;\;\; A \wedge B = \underline{0}. $$

The complement of a number A is marked with $\lnot A$ and is defined as follows.

Definition 4

Let $A_{(a_1,a_2,\dots ,a_{2K})} \in {\mathscr {N}}$ be a SOFN. Then the complement of $A_{(a_1,a_2,\dots ,a_{2K})}$ equals

$$\lnot A_{(a_1,a_2,\dots ,a_{2K})} = A_{(1 - a_1,1 - a_2,\dots ,1 -a_{2K})}.$$

A bounded lattice for which every element has a complement is called a complemented lattice. The structure of Step-Ordered Fuzzy Numbers $({\mathscr {N}},\vee ,\wedge )$ forms complete and complemented lattices in which complements are unique. In fact it is a Boolean algebra. An example of such an algebra is depicted in Fig. 7.3. A set of universe is created by numbers

$$ {\mathscr {N}}=\{A_{(a_1,a_2,a_3,a_4)} : a_i \in \{0,1\} \;\;\; \text {for} \;\;\; i=1,2,3,4\}. $$

The complements of elements are:

$$\begin{aligned} \lnot A_{(0,0,0,0)}=A_{(1,1,1,1)}, \lnot A_{(0,1,0,0)}=A_{(1,0,1,1)}, \lnot A_{(1,1,0,0)}=A_{(0,0,1,1)} \mathrm{etc.}. \end{aligned}$$

Fig. 7.3

A complete and complemented lattice defined on the set ${\mathscr {N}} \subset \mathbf{R }^4$

Now we can rewrite the definition of the complement in terms of a new mapping.

Definition 5

For any $A \in {\mathscr {N}}$ we define its negation as

$$ N(A):= (1 - a_1,1 - a_2,\dots ,1 - a_{2K})\,\;\;\; {\text {for}} \, \;\;\; A = (a_1,a_2,\dots ,a_{2K}) . $$

It is obvious, from Definitions 4 and 5, that the negation of a given number A is its complement. Moreover, the operator N is a strong negation, because it is involutive:

$$ N(N(A)) = A \, {\text { for any }}\, A\in {\mathscr {N}}\, .$$

One can refer here to known facts from the theory of fuzzy implications (cf. [6, 7, 21]) and write the strong negation N in terms of the standard strong negation $N_I$ on the unit interval $I = [0, 1]$ defined by $N_I(x) = 1 - x\, , x\in I$, namely $N((a_1,a_2,\dots ,a_{2K})) = ((N_I(a_1), N_I(a_2),\dots ,N_I(a_{2K}))$.

2.4 Fuzzy Implication on BSOFN

The implication operator holds center stage in the inference mechanisms of any logic. Thus, the obvious question is whether and how one can define an implication on an OFN. Studies on this issue were initiated in the works by Kacprzak and Kosiński in 2011 [28, 38]. The aim was to propose an implication operation on Ordered Fuzzy Numbers analogous to classical implication that preserves its main properties. In the literature we can find several different definitions of fuzzy implications. Some of them are built from basic fuzzy logic connectives. In Sect. 7.2.2 conjunction and disjunction operations for any two-order fuzzy numbers are defined. However, the main problem is the negation operation. In Sect. 7.2.3 complements for SOFNs from the set $\mathscr {N}$ are constructed. Thus given disjunction and complement, implication can be defined in the standard way. Such a new operator on the set $\mathscr {N}$ was introduced by Kacprzak and Kosiński and is called 2K-fuzzy implication [28, 29, 38]. The set of all OFNs is not a complete lattice, therefore the way of defining implication is still an open question.

In the classical Zadeh fuzzy logic the definition of a fuzzy implication on an abstract lattice ${\mathscr {L}} = (L,\le _{L})$ is based on the notation from fuzzy set theory introduced in [21].

Definition 6

Let ${\mathscr {L}} = (L,\le _{L}, 0_L, 1_L)$ be a complete lattice. A mapping ${\mathscr {I}}:L^2\rightarrow L$ is called a fuzzy implication on $\mathscr {L}$ if it is decreasing with respect to the first variable, increasing with respect to the second variable, and fulfills the border conditions

$$\begin{aligned} {\mathscr {I}}(0_L, 0_L)={\mathscr {I}}(1_L,1_L) = 1_L\, , {\mathscr {I}}(1_L,0_L) =0_L\, . \end{aligned}$$

(7.6)

Now, possessing the lattice structure of ${\mathscr {R}_{\mathscr {K}}}$ and the Boolean structure of our lattice $\mathscr {N}$, we can repeat most of the definitions known in Zadeh’s fuzzy set theory. The first one is the Kleene-Dienes operation, called 2K-fuzzy implication [28]

$$\begin{aligned} {\mathscr {I}}_{b}(A, B) = N(A)\vee B\, , {\text { for any}} \;\;\; A , B\in {\mathscr {N}}\, . \, \end{aligned}$$

(7.7)

In other words, the result of the binary implication ${\mathscr {I}}_{b}(A, B)$, denoted in [28] by $A \rightarrow B$, is equal to the result of operation sup for the number B and the complement of A:

$$ A \rightarrow B = sup\{\lnot A, B \}. $$

For illustration, let us assume two numbers $A_{(0,1,1,0)}$ and $A_{(0,1,0,1)}$. The implication

$$ A_{(0,1,1,0)} \rightarrow A_{(0,1,0,1)} $$

equals

$$ N(A_{(0,1,1,0)}) \vee A_{(0,1,0,1)} = A_{(1,0,0,1)} \vee A_{(0,1,0,1)}= A_{(1,1,0,1)}. $$

Examples of other implications are given in Table 7.1.

Table 7.1 Examples of implications for SOFN

2K-fuzzy implication satisfies the basic property of logical implication: it returns false if and only if the first term is true, and the second term is false.

Proposition 1

Let us consider the Boolean algebra $({\mathscr {N}}, \vee , \wedge , \lnot , \underline{1}, \underline{0})$. The values of the 2K-fuzzy implication on the greatest and the least elements of this algebra are given in Table 7.2.

Table 7.2 Table of values of implications for the least element and the greatest elements of $\mathscr {N}$

In fact, because $\lnot \;\underline{0} = \underline{1}$ and $\lnot \;\underline{1} = \underline{0}$ it holds that:

• $\underline{0} \rightarrow \underline{0} = N(\underline{0}) \vee \underline{0} = \underline{1}\vee \underline{0} = \underline{1}$.

• $\underline{0} \rightarrow \underline{1} = N(\underline{0}) \vee \underline{1} = \underline{1}\vee \underline{1} = \underline{1}$.

• $\underline{1} \rightarrow \underline{0} = N(\underline{1}) \vee \underline{0} = \underline{0}\vee \underline{0} = \underline{0}$.

• $\underline{1} \rightarrow \underline{1} = N(\underline{1}) \vee \underline{1} = \underline{0}\vee \underline{1} = \underline{1}$.

Next we may introduce the Zadeh implication by

$$\begin{aligned} {\mathscr {I}}_{Z}(A, B) = (A \wedge B)\vee N(A)\, , {\text { for any }} A , B\in {\mathscr {N}}\, . \end{aligned}$$

(7.8)

In our lattice $\mathscr {R}_K$ the arithmetic operations are well defined, therefore we may introduce the counterpart of the Łukasiewicz implication by

$$\begin{aligned} {\mathscr {I}}_{L}(A, B) = C\, , {\text {where }} \, C=1 \wedge (1-A+B) \, . \end{aligned}$$

(7.9)

When calculating the right-hand side of (7.9) we have to regard all numbers as elements of $\mathscr {R}_K$, because by adding step fuzzy number A from $\mathscr {N}$ to the crisp number 1 we may leave the subset $\mathscr {N}\subset \mathscr {R}_K$. However, the operation $\wedge$ takes us back to the lattice $\mathscr {N}$. It is obvious that in our notation $1_N = 1$. The explicit calculation is: if $C = (c_1, c_2,\dots , c_{2K)}), A = (a_1,a_2,\dots ,a_{2K}), B = (b_1,b_2,\dots ,b_{2K})$, then $c_i = min\{1, 1 - a_i + b_i\}$, where $1\le i \le 2K$.

It is obvious that all implications ${\mathscr {I}}_{b}, {\mathscr {I}}_{Z}$, and ${\mathscr {I}}_{L}$ satisfy the border conditions (7.6) as well as the fourth condition of the classical binary implication, namely ${\mathscr {I}}(0_N, 1_N) = 1_N$.

2.5 Applications

Initially, OFNs were designed to deal with optimization problems when data are fuzzy [14, 15, 17, 20]. When Kacprzak and Kosiński observed that a subspace of OFNs, called SOFN, may be equipped with a lattice structure, it turned out that OFNs have a much wider field of application. The ability to define Boolean operations such as conjunction, disjunction, and, more important, diverse types of implications, has become the basis for creating a new logical system. In consequence, it turned out that SOFNs can be used not only for evaluation of linguistic statements such as, “A patient is fat” or “A car is fast,” but also for approximate reasoning on such imprecise notions.

One of the important applications is employing SOFNs in multiagent systems for modeling agents’ beliefs about fuzzy expressions [27]. This can be helpful in evaluating features of multiagent systems concerning agents’ fuzzy beliefs. If some sentence is expressed by an agent in a multiagent system then we could try to evaluate the level of truth for an agent’s belief about another agent’s belief. This is the first step in the application of the fuzzy logic that stands behind the SOFN.

Just before his death, Kosiński with his coworkers Kacprzak and Wȩgrzyn-Wolska showed another application of SOFNs in specification and automatic verification of diversity of opinion [30]. As a consequence, SOFN can also be used in reasoning about communicating software agents or boots that are decision-support systems. For example, we can analyze activity of agents that assists clients with their decisions in e-shops, that is, agents which support users of a system in making decisions and choosing the right product.

3 Metasets

The metaset is the new concept of a set with a partial membership relation. It was inspired by the method of forcing [11, 47] in the classical Zermelo-Fraenkel set theory (ZFC) [23, 39]. Nonetheless it is directed towards artificial intelligence applications and efficient computer implementations. Its scope of practical usage is similar to fuzzy sets [57], intuitionistic fuzzy sets [5], or rough sets [45]. There are close relationships between fuzzy set and metaset approaches, described in [50, 55].

Metasets admit standard set-theoretic relations that are valued in a nontrivial Boolean algebra, and therefore enable expressing fractional degrees of membership, equality, subset, and their negations. Algebraic operations for metasets are defined and they satisfy Boolean algebra axioms [54].

Metasets enable the representation and processing of vague imprecise notions and data. Recent development in applications of metasets is focused on decision systems [31,32,33]. There have been successful attempts to utilize metasets in character recognition problems [49, 51].

Before we discuss the definition of a metaset we review some necessary basic notions and establish a notation.

3.1 The Binary Tree $\mathbf{T}$ and the Boolean Algebra $\mathfrak {B}$

The binary tree $\mathbf{T}$ is the set of all finite binary sequences, that is, functions whose domains are finite ordinals, valued in 2 ($\omega$ is the set of all finite ordinals)¹:

$$\begin{aligned} \mathbf{T}= \bigcup _{n \in \omega } 2^n \; . \end{aligned}$$

(7.10)

The ordering $\le$ in the tree $\mathbf{T}$ (see Fig. 7.4) is the reverse inclusion of functions: for $p,q \in \mathbf{T}$ such that $p :n \mapsto 2$ and $q :m \mapsto 2$, we have $p \le q$ whenever $p \supseteq q$; that is, $n \ge m$ and $p_{\upharpoonright m} = q$. The root $\mathbf{1}$, being the empty function, is the largest element of $\mathbf{T}$ in this ordering.

Fig. 7.4

The levels $\mathbf{T}_{0}$–$\mathbf{T}_{2}$ of the binary tree $\mathbf{T}$ and the ordering of nodes. Arrows point at the larger element

Nodes of $\mathbf{T}$ are sometimes called conditions. We denote binary sequences that are elements of $\mathbf{T}$ using square brackets, for example: [00], [101]. A level in $\mathbf{T}$ is the set of all finite binary sequences with the same length. The set $2^{n}$ consisting of all sequences of the same length n is the level n, denoted by $\mathbf{T}_{n}$. The level 0 consists of the empty sequence $\mathbf{1}$ only. A branch $C$ in $\mathbf{T}$ is an infinite binary sequence, that is, a function $\omega \mapsto 2$. We write $p \in C$ to mark that the binary sequence $p \in \mathbf{T}$ is a prefix of the branch $C$.

For the given $p \in \mathbf{T}$ the set of all infinite branches containing p determines a closed-open set $\bar{p} = \left\{ \, C \in 2^\omega :p \in C \,\right\}$ in the Cantor space $2^\omega$. The family of all such sets is the closed-open topological basis of this space. Because every clopen set is regular open² and the family of regular open sets of any topological space forms a complete Boolean algebra, we get the complete algebra $\mathfrak {B}$ of clopen sets in $2^\omega$. The operations of join, meet, and complement correspond to standard set-theoretic operations in this case: union, intersection, and complement. Top and bottom elements are $2^\omega$ and $\emptyset$, respectively.

We use the algebra $\mathfrak {B}$ to evaluate metaset sentences, particularly to evaluate membership degrees.

3.2 General Definition of Metaset

A metaset is a classical set with a specific structure coding membership degrees of metaset members. The degrees, by construction, are expressed as nodes of the tree $\mathbf{T}$ but they represent elements of the algebra $\mathfrak {B}$.

Definition 7

A set that is either the empty set $\emptyset$ or has the form:

$$\begin{aligned} \tau = \left\{ \,\left\langle \sigma , p \right\rangle :\sigma \text { is a metaset, } p \in \mathbf{T}\,\right\} \end{aligned}$$

is called a metaset.

Thus the structure we use to encode the degrees of membership is based on ordered pairs. The first element of each pair is the member and the second element is a node of the binary tree that contributes to the membership degree of the first element.

Formally, this is a definition by induction on the well-founded relation $\in$. By the axiom of foundation in Zermelo-Fraenkel set theory there are no infinite branches in the recursion as well as there are no cycles. Therefore, no metaset is a member of itself. From the point of view of ZFC a metaset is a particular case of a $\mathrm {P}$-name (see also [39, Chap. VII, Sect. 2] for justification of such type of definition).

For the given metaset $\tau$, the sets:

$$\begin{aligned} \mathrm {dom}(\tau )= & {} \left\{ \,\sigma :\exists _{p \in \mathbf{T}} \; \left\langle \sigma , p \right\rangle \in \tau \,\right\} \; ,\end{aligned}$$

(7.11)

$$\begin{aligned} \mathrm {ran}(\tau )= & {} \left\{ \,p:\exists _{\sigma \in \mathrm {dom}(\tau )} \; \left\langle \sigma , p \right\rangle \in \tau \,\right\} \end{aligned}$$

(7.12)

are called the domain and the range of the metaset $\tau$, respectively.

3.3 Interpretations of Metasets

An interpretation of a metaset is a classical crisp set. It is produced from the given metaset with a branch of the binary tree. Different branches determine different interpretations of the given metaset. All of them taken together make up a collection of sets with specific internal dependencies, which represents the source metaset by means of its crisp views.

Properties of sets that are interpretations of the given metaset determine the properties of the metaset itself. In particular we use interpretations to define set-theoretic relations for metasets.

Definition 8

Let $\tau$ be a metaset and let $C \subset \mathbf{T}$ be a branch. The set

$$\begin{aligned} \tau _ C = \left\{ \,\sigma _ C :\left\langle \sigma , p \right\rangle \in \tau \wedge p \in C \,\right\} \end{aligned}$$

is called the interpretation of the metaset $\tau$ given by the branch $C$.

The process of producing an interpretation of a metaset consists of two stages, repeated recursively. In the first stage we remove all the ordered pairs whose second elements are nodes that do not belong to the branch $C$. The second stage replaces the remaining pairs – whose second elements lie on the branch $C$ – with interpretations of first elements. As the result we obtain a classical set.

Example 1

Let $p \in \mathbf{T}$ and let $\tau = \left\{ \, \left\langle \emptyset , p \right\rangle \,\right\}$. If $C$ is a branch, then

$$\begin{aligned} p \in C\rightarrow & {} \tau _{ C } = \left\{ \, \emptyset \,\right\} \; , \\ p \not \in C\rightarrow & {} \tau _{ C } = \emptyset \; . \end{aligned}$$

Depending on the branch the metaset $\tau$ acquires one of two different interpretations: $\left\{ \, \emptyset \,\right\}$ or $\emptyset$. Note that $\mathrm {dom}(\tau ) = \left\{ \, \emptyset \,\right\}$.

As we see, a metaset may have multiple different interpretations: each branch in the tree determines one of them. Usually, most of them are pairwise equal, thus the number of different interpretations is much less than the number of branches.

3.4 Forcing

We define and investigate a relation between a condition and a sentence. This relation, called the forcing relation, is designed to describe the level of confidence or certainty assigned to the sentence. The level is evaluated by means of conditions in $\mathbf{T}$ that determine elements of the Boolean algebra $\mathfrak {B}$. The root condition $\mathbf{1}$ specifies the absolute certainty, whereas its descendants represent less certain degrees. The sentences are classical set theory formulas, where free variables are substituted by metasets and bound variables range over the class of metasets.

Given a branch $C$, we may substitute particular metasets in the sample sentence $\sigma \in \tau$ with their interpretations that are ordinary sets: $\sigma _ C \in \tau _ C$. The resulting sentence is a ZFC sentence expressing some property of the sets $\tau _ C$ and $\sigma _ C$, the membership relation in this case. Such a sentence may be either true or false, depending on $\tau _ C$ and $\sigma _ C$.

For the given metaset $\tau$ each condition $p \in \mathbf{T}$ specifies a family of interpretations of $\tau$: they are determined by all the branches $C$ containing this particular condition p. If for each such branch the resulting sentence (after substituting metasets with their interpretations) has constant logical value, then we may think of a conditional truth or falsity of the given sentence, which is qualified by the condition p. Therefore, we may consider p as the certainty degree for the sentence.

Let $\varPhi$ be a formula built using the following symbols: variables ($x^{1}, x^{2},\ldots$), the constant symbol ($\emptyset$), the relational symbols ($\in , =, \subset$), logical connectives ($\wedge , \vee$, $\lnot , \rightarrow$), quantifiers ($\forall , \exists$), and parentheses. If we substitute each free variable $x^{i}$ $(i = 1 \dots n)$ with some metaset $\nu ^{i}$, and restrict the range of each quantifier to the class of metasets $\mathfrak {M}$, then we get as the result the sentence $\varPhi (\nu ^{1},\ldots , \nu ^{n})$ of the metaset language that states some property of the metasets $\nu ^{1},\ldots , \nu ^{n}$. It is called a metaset sentence. By the interpretation of this sentence, determined by the branch $C$, we understand the sentence $\varPhi (\nu ^{1}_{ C },\ldots , \nu ^{n}_{ C })$ denoted in brief by $\varPhi _{ C }$. The sentence $\varPhi _{ C }$ is the result of substituting free variables of the formula $\varPhi$ with the interpretations $\nu ^{i}_{ C }$ of the metasets $\nu ^{i}$, and restricting the range of bound variables to the universe of all sets $\mathbf V$. In other words, we replace the metasets in the sentence $\varPhi$ with their interpretations. The only admissible constant $\emptyset$ in $\varPhi$ as well as in $\varPhi _{ C }$ denotes the empty set which is the same set in both cases.

Definition 9

Let $x^{1}, x^{2},\ldots x^{n}$ all be free variables of the formula $\varPhi$ and let $\nu ^{1}, \ldots \nu ^{n}$ be metasets. We say that the condition $p \in \mathbf{T}$ forces the sentence $\varPhi (\nu ^{1}, \nu ^{2},\ldots \nu ^{n})$, whenever for each branch $C \subset \mathbf{T}$ containing p, the sentence $\varPhi (\nu ^{1}_{ C }, \ldots \nu ^{n}_{ C })$ is true. We denote the forcing relation with $\Vdash$. Thus,

$$\begin{aligned} p \Vdash \varPhi (\nu ^{1}, \ldots \nu ^{n}) \quad \text { iff } \quad \forall _{ C \subset \mathbf{T}} \, \left( C \text { is a branch } \wedge p \in C \; \rightarrow \; \varPhi (\nu ^{1}_{ C },\ldots \nu ^{n}_{ C })\right) \;. \end{aligned}$$

The key idea behind the forcing relation lies in transferring classical properties from sets onto metasets. Let a property described by a formula $\varPhi (x)$ be satisfied by all sets of form $\nu _{ C }$, where $\nu$ is a metaset and $C$ is a branch in $\mathbf{T}$. In other words, $\varPhi (\nu _{ C })$ holds for all the sets that are interpretations of the metaset $\nu$ given by all branches $C$ in $\mathbf{T}$. Then we might suppose that this property also “holds” for the metaset $\nu$, and we formulate this fact by saying that $\mathbf{1}$ forces $\varPhi (\nu )$. If $\varPhi (\nu _{ C })$ holds only for branches $C$ containing some condition p, then we might suppose that it “holds to the degree p” for the metaset $\nu$; we say that p forces $\varPhi (\nu )$ in such a case. Because we try to transfer, or force, satisfiability of some property from classical sets onto metasets, we call this mechanism forcing.³ The next example shows how to transfer the property of being equal onto two specific metasets.

Example 2

Let $\tau = \left\{ \, \left\langle \emptyset , p \right\rangle \,\right\}$ and $\sigma = \left\{ \, \left\langle \emptyset , p \mathop {\cdot } 0\right\rangle , \left\langle \emptyset , p \mathop {\cdot } 1\right\rangle \,\right\}$, where $p \in \mathbf{T}$ and $p \mathop {\cdot } 0$, $p \mathop {\cdot } 1$ denote its children. Let $C$ be a branch.

$$\begin{aligned} p \mathop {\cdot } 0\in C \quad\rightarrow & {} \quad \tau _ C = \left\{ \, \emptyset \,\right\} \,&\wedge \, \sigma _ C = \left\{ \, \emptyset \,\right\} \quad&\rightarrow \quad \tau _ C = \sigma _ C \;, \\ p \mathop {\cdot } 1\in C \quad\rightarrow & {} \quad \tau _ C = \left\{ \, \emptyset \,\right\} \,&\wedge \, \sigma _ C = \left\{ \, \emptyset \,\right\} \quad&\rightarrow \quad \tau _ C = \sigma _ C \;, \\ p \not \in C \quad\rightarrow & {} \quad \tau _ C = \emptyset \,&\wedge \, \sigma _ C = \emptyset \quad\rightarrow & {} \quad \tau _ C = \sigma _ C \;. \end{aligned}$$

Of course, the last case is possible only when $p \ne \mathbf{1}$, because the root of $\mathbf{T}$ is contained in each branch. As we can see, the interpretations of $\tau$ and $\sigma$ are always pairwise equal, although they are different sets depending on the chosen branch $C$. Analyzing only the structure of $\tau$ and $\sigma$ we may easily conclude that $p \Vdash \tau = \sigma$. However, because for any branch $C$ that does not contain p the interpretations of $\tau$ and $\sigma$ are both empty, then also $\mathbf{1} \Vdash \tau = \sigma$.

Thus, for the given metaset sentence $\varPhi$, the set of all conditions that force it, $\left\{ \,p \in \mathbf{T}:p \Vdash \varPhi \,\right\}$, determines an element of the Boolean algebra $\mathfrak {B}$. We interpret it as the certainty degree for $\varPhi$ (cf. [55, 56])

Definition 10

Let $\varPhi$ be a metaset sentence. The following element of algebra $\mathfrak {B}$ is called the certainty degree for $\varPhi$.

$$\begin{aligned} \mathopen \vert \varPhi \mathclose \vert \; = \; \bigcup \left\{ \,\mathfrak {b}_p \in \mathfrak {B}: p \Vdash \varPhi \,\right\} \; , \end{aligned}$$

(7.13)

where $\mathfrak {b}_p$ is the set of all branches containing p.

In other words $\mathfrak {b}_p$ is the set of infinite binary sequences sharing the common prefix p.

3.5 Set-Theoretic Relations for Metasets

We briefly sketch the methodology behind the definitions of standard set-theoretic relations for metasets. For a detailed discussion of the relations or their evaluation the reader is referred to [54, 55].

Definition 11

We say that the metaset $\sigma$ belongs to the metaset $\tau$ under the condition $p \in \mathbf{T}$, whenever $p \Vdash \sigma \in \tau$. We use the notation $\sigma \mathrel {\varepsilon }_{p} \tau$.

In other words, $\sigma \mathrel {\varepsilon }_{p} \tau$ whenever for each branch $C$ containing p, it holds $\sigma _ C \in \tau _ C$. Formally, we define an infinite number of membership relations: each $p \in \mathbf{T}$ specifies another relation $\mathrel {\varepsilon }_{p}$. Any two metasets may simultaneously be in multiple membership relations qualified by different conditions: $\sigma \mathrel {\varepsilon }_{p} \tau \wedge \sigma \mathrel {\varepsilon }_{q} \tau$. Membership under the root condition $\mathbf{1}$ resembles the full unconditional membership of crisp sets, inasmuch as it is independent of interpretations. By the Definition 10, the membership degree of $\sigma$ in $\tau$ is $\mathopen \vert \sigma \in \tau \mathclose \vert$. This degree encompasses all the p that force the membership; it is the union of elements of $\mathfrak {B}$ corresponding to these p.

The metaset membership admits a hesitancy degree known from the intuitionistic fuzzy sets’ field. It is possible that degrees of membership and nonmembership do not sum up to unity. The remaining part is called the hesitancy degree of membership (see [55, 56]). This property has important consequences mentioned in Sect. 7.3.7.

Conditional equality and subset relations for metasets are defined similarly as for a membership.

3.6 Applications of Metasets

The conditional membership reflects the idea that a metaset $\mu$ belongs to a metaset $\tau$ whenever some conditions are fulfilled. The conditions are represented by nodes of $\mathbf{T}$ but they relate to elements of algebra $\mathfrak {B}$. In applications they refer to a modeled reality and denote some real conditions that justify the statement. Let $\mu$ be some individual and let $\tau$ be the family of those individuals who are nice: they satisfy the property of being nice. The sentence $\mu \mathrel {\varepsilon }_{p} \tau$ says that $\mu$ is nice under the condition p, or, in other words, to the degree p. The condition p itself might be expressed using human language terms, for example: pretty face (thus $\sigma$ is nice because of pretty face). Labeling conditions with human language terms requires imposing partial ordering on these terms, which is generally rather subjective and not straightforward. We investigated such orderings in a series of papers discussing a new decision-support system based on this idea (see [31,32,33]).

3.7 Classical and Fuzzy Implication

We may easily define classical implication on the algebra $\mathfrak {B}$ as follows.

$$\begin{aligned} \mathfrak {b} \Rightarrow \mathfrak {c} \; \equiv \; \lnot \mathfrak {b} \cup \mathfrak {c}, \quad \mathfrak {b}, \mathfrak {c} \in \mathfrak {B}\; . \end{aligned}$$

(7.14)

Clearly, it is a fuzzy implication. We may define other fuzzy implications on $\mathfrak {B}$ too, however, from the point of view of metaset theory we are interested in those that satisfy the following.

$$\begin{aligned} \mathopen \vert \varPhi \mathclose \vert \Rightarrow \mathopen \vert \varPsi \mathclose \vert \; = \; \mathopen \vert \varPhi \rightarrow \varPsi \mathclose \vert \; . \end{aligned}$$

(7.15)

Here, $\varPhi$ and $\varPsi$ are metaset sentences and $\mathopen \vert \varPhi \mathclose \vert$, $\mathopen \vert \varPsi \mathclose \vert$ are their corresponding certainty degrees, which are members of $\mathfrak {B}$. We would like the implication to commute with the forcing relation that determines certainty degrees for sentences. In other words, we want to have certainty degree of implication $\varPhi \rightarrow \varPsi$ to be equal to the implication of certainty degrees for sentences $\varPhi$ and $\varPsi$.

Unfortunately, in the general case (7.15) does not hold. In other words, generally $\lnot \mathopen \vert \varPhi \mathclose \vert \cup \mathopen \vert \varPsi \mathclose \vert$ does not have to be equal $\mathopen \vert \lnot \varPhi \vee \varPsi \mathclose \vert$ and also the border condition ${\mathscr {I}}(0_L, 0_L) = 1_L$ of definition (6) might not be satisfied. The reason for this is metasets’ capability of expressing uncertainty. The value of $\mathopen \vert \varPhi \mathclose \vert$ is the measure of certainty, that is, our knowledge about $\varPhi$. However, in general, $\lnot \mathopen \vert \varPhi \mathclose \vert$ is not equal to the certainty degree of $\lnot \varPhi$, but it is not less and it might also include the hesitancy degree of $\varPhi$, just as in intuitionistic fuzzy sets.⁴ To exclude the uncertainty issues one has to limit the scope to the class of hereditarily finite metasets. A metaset $\sigma$ is hereditarily finite when it is a hereditarily finite set: $\mathrm {ran}(\sigma )$ is finite and $\mathrm {dom}(\sigma )$ consists of hereditarily finite metasets only. For such metasets uncertainty vanishes, $\lnot \mathopen \vert \varPhi \mathclose \vert = \mathopen \vert \lnot \varPhi \mathclose \vert$, and (7.15) holds (see [55]).⁵ The class of hereditarily finite metasets includes metasets representable in machines and it is sufficient for applications. Investigating implication (7.14), which satisfies (7.15), is one of the next goals in the development of metaset theory and related logic of metaset sentences.

4 Conclusions and Further Research

The purpose of this chapter was to present new operators that satisfy the conditions for fuzzy implication in the classical sense [6]. These results emerged from the research conducted by Kosiński, undertaken in his last years of life. They were initiated by investigation of applications of Ordered Fuzzy Numbers, alternatively called Kosiński’s fuzzy numbers. Even though the described approaches stem from completely different areas, it turned out that they lead to similar applications and results. Furthermore, they launched a new stream of research that has continued by his coworkers Kacprzak, Starosta, and Wȩgrzyn-Wolska after Kosiński’s death. The applications of the research on OFNs and metasets concern not only approximate reasoning but also decision-support systems and opinion mining [31,32,33].

In this chapter we discussed two structures for fuzzy implication: the lattice of Step-Ordered Fuzzy Numbers and the Boolean algebra $\mathfrak {B}$ of membership degrees for metasets. In both of them a fuzzy implication operator (FI) is defined. The implication operator holds center stage in the inference mechanisms of any logic. We can find several different definitions of fuzzy implications in the literature. They play a similar role to Boolean implications that are employed in inference schemes such as modus ponens and modus tollens. However, now reasoning is done with fuzzy statements whose truth values lie in [0, 1] instead of $\{0, 1\}$. The most exploited area of applications of fuzzy implications is approximate reasoning, wherein from imprecise inputs and fuzzy premises or rules we can obtain imprecise conclusions.

In the the first part of the chapter the binary Step-Ordered Fuzzy Numbers are explored. As mentioned earlier, Kosiński was looking for new inference schemas and thereby implications based on the orthodox Ordered Fuzzy Numbers (f, g), where functions f and g are assumed to be continuous. This question still remains unanswered and studies are in progress. The biggest challenge was to define a negation operator. During the research Kacprzak and Kosiński observed that BSOFN (f, g), in which functions f and g are step functions that can return binary values 1 or 0, form a lattice. This property allows us to define the fuzzy implications similar to those proposed by Kleene-Dienes, Zadeh, or Łukasiewicz.

The second part of the chapter focuses on the results obtained by Starosta and Kosiński in the field of metasets. In the algebra $\mathfrak {B}$ we can also define some fuzzy implication operators analogous to those from classical fuzzy set theory. However, the most important property that we are interested in is the equality of the certainty degree of the sentence $\varPhi \rightarrow \varPsi$ and the result of applying the operator $\Rightarrow$ to the certainty degrees of sentences $\varPhi$ and $\varPsi$. Unfortunately, in the general case, this equality does not hold. Only when we make certain restrictions and limit the scope to the class of hereditarily finite metasets, we get the desired behavior of the operator.

We dedicate future research on fuzzy implications aimed at developing theories and searching for the answers to the questions that are still open to the memory of Professor Kosiński.