Fast One-Way Cellular Automata with Reversible Mealy Cells

Abstract

We investigate cellular automata that are composed of reversible components with regard to the recognition of formal languages. In particular, real-time one-way cellular automata ($\text {OCA}$) are considered which are composed of reversible Mealy automata. Moreover, we differentiate between three notions of reversibility in the Mealy automata, namely, between weak and strong reversibility as well as reversible partitioned $\text {OCA}$ which have been introduced by Morita in [14]. Here, it turns out that every real-time $\text {OCA}$ can be transformed into an equivalent real-time $\text {OCA}$ with weakly reversible automata in its cells, whereas the remaining two notions seem to be weaker. However, a non-semilinear language is provided that can be accepted by a real-time $\text {OCA}$ with strongly reversible cells. On the other hand, we present a context-free, non-regular language that is accepted by some real-time reversible partitioned $\text {OCA}$.

1 Introduction

The study of computational devices performing reversible computations is mostly motivated by the physical observation that a loss of information yields heat dissipation [12]. To avoid such situations computations are of interest in which every configuration has a unique successor configuration as well as a unique predecessor configuration so that at every point of the computation no information gets lost. Reversibility has been studied for many computational devices starting with Bennett’s investigations for Turing machines in [3] where it is shown that for every (possibly irreversible) Turing machine an equivalent reversible Turing machine can be constructed. A similar result has been obtained for deterministic space-bounded Turing machines, in particular, deterministic linear bounded automata by Lange, McKenzie, and Tapp in [13]. For deterministic pushdown automata and deterministic queue automata the situation is different: in both cases it is possible to show (see, for example, [8, 11]) that the reversible variant is weaker than the general model, that is, there are languages which can be accepted by the general model, but not by its reversible variant. In these cases, the loss of information in computations is inevitable. For deterministic multi-head finite automata the picture is split: for two-way multi-head finite automata Morita has shown in [17] that the general model and the reversible model coincide. On the other hand, in case of one-way motion it is shown in [9] that the reversible model is weaker than the general model. Reversible computations in deterministic finite automata have been introduced in [2] and it is shown in [20] that there are regular languages which cannot be accepted by any (one-way) reversible deterministic finite automaton. However, if two-way motion of the input head is allowed, it is known due to [5] that the general model and the reversible model coincide. A structural approach to reversible computing not depending on specific computational models has been proposed in [1].

For cellular automata (CA), the notion of reversibility has been investigated from several points of view. One fundamental result is that the reversibility of a cellular automaton is equivalent to the injectivity of the global transition function. Moreover, the injectivity of the global transition function is decidable for one-dimensional CAs, but becomes undecidable in higher dimensions. Details and literature for these results may be found in the survey paper [4]. The question whether every cellular automaton can be made reversible has been answered in the affirmative first by Toffoli who shows in [21] that every k-dimensional CA can be simulated by a $(k+1)$-dimensional reversible CA. This result has been improved by Morita and Harao in [19] where it is shown that every reversible Turing machine can be simulated by a one-dimensional reversible CA. By introducing the notion of partitioned cellular automata further improvements are given by Morita in [14, 15] where, for example, the latter result is shown to hold also for one-dimensional one-way reversible CAs. More results on reversible CAs may be found in the survey paper [16].

In the context of language recognition, cellular automata are working on finite configurations with fixed boundary conditions. With regard to reversible computations, it is clear that reversibility in such devices cannot be defined on the injectivity of the global transition function. Thus, one considers computations that are reversible on the core of computation, namely, starting in the initial configuration and ending in the configuration given by the time complexity. From this point of view, language recognition by reversible devices has been studied for real-time two-way CAs [6], for real-time iterative arrays [7], and more recently for real-time one-way CAs [10]. Another recent result is provided by Morita in [18] where it is shown that every deterministic linear bounded automaton can be simulated by a reversible CA working on finite configurations with fixed boundary conditions.

In this paper, we consider another aspect of reversibility. In all cellular models studied so far the reversibility concerns configurations, that is, from every configuration the successor as well as the predecessor configuration can be computed in a unique way. Since CAs are basically arrays of interacting deterministic finite automata, one can also consider the reversibility of the single deterministic finite automata, that is, of the local transition function, and we will speak in this context of locally reversible CAs. For partitioned cellular automata and unbounded computations it is known [15, 19] that such automata are globally reversible if and only if they are locally reversible if and only if they are locally injective. Apart from a theoretical interest in locally reversible computations, there is also a practical interest to investigate such CAs, since in this case the devices are composed of reversible components. Here, we will study local reversibility with regard to language recognition for weak cellular devices, namely, we will focus on real-time computations in one-way CAs (OCAs). Moreover, we consider OCAs having Mealy automata in their cells instead of deterministic finite automata. This generalization allows in particular a comparison with the notion of partitioned cellular automata. The paper is organized as follows. In Sect. 2 we summarize basic notions and introduce weakly and strongly reversible Mealy automata which are subsequently used to define one-way Mealy cellular automata with weakly or strongly reversible cells. Moreover, we provide an example of a non-semilinear language that is accepted by some real-time $\text {OCA}$ with strongly reversible cells. Section 3 is devoted to investigating real-time $\text {OCA}$s with weakly reversible cells and it turns out that every real-time $\text {OCA}$ can be converted to the former model. This means that every real-time $\text {OCA}$ computation can be simulated by a real-time $\text {OCA}$ with weakly reversible cells. In Sect. 4 we study reversible one-way partitioned CAs working in contrast to [14] on finite configurations with fixed boundary conditions. We first discuss how this notion is related to our concept of Mealy cellular automata. Then, it is shown that every regular language (reversible or not) is accepted by such automata. Moreover, it is possible to accept a certain context-free, non-regular language. Finally, we give a short conclusion. We would like to note that some proofs are omitted due to space considerations.

2 Preliminaries and Definitions

We denote the set of non-negative integers by $\mathbb {N}$. The reversal of a word w is denoted by $w^R$. For the length of w we write |w|. We write $\subseteq$ for set inclusion, and $\subset$ for strict set inclusion. In order to avoid technical overloading in writing, two languages L and $L'$ are considered to be equal, if they differ at most by the empty word. Throughout the article two devices are said to be equivalent if and only if they accept the same language.

A deterministic finite Mealy automaton ($\text {DFMA}$) is a deterministic finite automaton that emits a symbol during each transition performed. So, it is particularly composed of a finite state set S, a finite input alphabet A, a finite output alphabet B, and a partial transition function $\delta$ that maps from $S\times A$ to $S\times B$. In this way, the new state and the symbol emitted during a transition are given. Let $\pi _S$ denote the projection on the first component and $\pi _B$ denote the projection on the second component of pairs from $S\times B$. A state in a $\text {DFMA}$ is called a sink state, if the state can never be left once entered.

A $\text {DFMA}$ is said to be weakly reversible ($\text {WREV-DFMA}$) if every pair (a, b) from $A\times B$ induces an injective partial mapping from the state set S to itself via the mapping $\delta _{(a,b)}:S\rightarrow S$ where $\delta _{(a,b)}(s)=s'$ if and only if $b=\pi _B(\delta (s,a))$ and $s'=\pi _S(\delta (s,a))$. In this case, the reverse transition function $\delta ^{\scriptscriptstyle \leftarrow }:S \times A \times B \rightarrow S$ defined by $\delta ^{\scriptscriptstyle \leftarrow }(s',a,b)=s$ if and only if $\delta (s,a,b)=s'$ induces for every pair (a, b) from $A\times B$ a (partial) injective function $\delta ^{\scriptscriptstyle \leftarrow }_{(a,b)}:S \rightarrow S$ (see Fig. 1). A $\text {WREV-DFMA}$ can also be considered as a (partial) permutation automaton.

A $\text {DFMA}$ is said to be strongly reversible ($\text {SREV-DFMA}$) if every letter a from A induces an injective partial mapping from the state set S to itself via the mapping $\delta _{a}:S\rightarrow S$ where $\delta _{a}(s)=s'$ if and only if $s'=\pi _S(\delta (s,a))$. In this case, the reverse transition function $\delta ^{\scriptscriptstyle \leftarrow }$ induces for every letter a from A a (partial) injective function $\delta ^{\scriptscriptstyle \leftarrow }_a:S \rightarrow S$. The property of being strongly reversible is also known as being codeterministic.

Fig. 1.

A weakly reversible deterministic finite Mealy automaton, where an edge from p to q labeled by a, b means $\delta (p,a)=(q,b)$. Example transitions are $\delta (s_1,1)=(\bar{s}_0,1)$, $\delta _{(1,1)}(s_1)=\bar{s}_0$, $\delta ^{\scriptscriptstyle \leftarrow }(\bar{s}_0,1,1)=s_1$ and $\delta ^{\scriptscriptstyle \leftarrow }_{(1,1)}(\bar{s}_0)=s_1$.

Next, we consider one-way cellular automata whose cells are $\text {DFMA}$s. A one-way cellular automaton with Mealy cells (one-way Mealy cellular automaton) is a linear array of identical deterministic finite Mealy machines, called cells. Except for the rightmost cell each one is connected to its nearest neighbor to the right. The state transition of a cell depends on its current state and the latest output that has been emitted by its neighbor. We say that this output is the message sent to the neighbor. Initially, a distinguished initial message is sent. The rightmost cell receives information associated with a boundary symbol on its free input line. The state changes take place simultaneously at discrete time steps. The input mode for cellular automata is called parallel. One can suppose that all cells fetch their input symbol during a pre-initial step.

Formally, a one-way Mealy cellular automaton $(\text {OMCA})$ is a system given as $\langle S,F,A,B,\bot ,\texttt {\#},\delta \rangle$, where S is the finite, nonempty set of cell states, $F\subseteq S$ is the set of accepting states, $A\subseteq S$ is the nonempty set of input symbols, B is the finite, nonempty set of messages, $\bot \in B$ is the initial message, $\texttt {\#}\in B$ is the boundary message, and $\delta :S\times B \rightarrow S\times B$ is the local transition function.

A configuration of a one-way Mealy cellular automaton $\langle S,F,A,B,\bot ,\texttt {\#},\delta \rangle$ is a mapping $c :\{1,2,\dots ,n\} \rightarrow (S\times B)$, for $n\ge 1$, that assigns a state and a message to each cell, where it is understood that the state is the current state of the cell and the message is the latest message sent by its neighbor. As before, given some $c(i)=(s,m)$, the projection on its state part s is denoted by $\pi _S(c(i))$ and the projection on its message part m is denoted by $\pi _B(c(i))$. The operation starts in a so-called initial configuration, which is defined by the given input $w=a_1a_2\cdots a_n\in A^+$. We set $c_0(i)=(a_i,\bot )$, for $1\le i\le n-1$, and $c_0(n)=(a_n,\texttt {\#})$. Successor configurations are computed according to the global transition function $\varDelta$. Let c be a configuration with $n\ge 1$, then the successor configuration $c'$ is

$$ c' = \varDelta (c) \iff \left\{ \begin{array}{l} \pi _S(c'(i)) = \pi _S(\delta (c(i))), i\in \{1,2,\dots ,n\}\\ \pi _B(c'(i)) = \pi _B(\delta (c(i+1))), i\in \{1,2,\dots ,n-1\}\\ \pi _B(c'(n)) = \texttt {\#}\\ \end{array} \right. . $$

An input w is accepted by a one-way Mealy cellular automaton M if at some time step during the course of its computation the leftmost cell enters an accepting state. The language accepted by M is denoted by L(M). If all $w\in L(M)$ are accepted with at most $|w|+1$ time steps, then M is said to operate in real-time. The family of languages accepted by some device $\mathrm {X}$ operating in real-time is denoted by $\mathscr {L}_{rt}(\mathrm {X})$.

Note that the state transitions of cells in an $\text {OMCA}$ depend on the current state and the latest output symbol emitted by the neighbor. So, taking a single cell as $\text {DFMA}$, its input alphabet is equal to its output alphabet B.

Now the structural restriction of one-way Mealy cellular automata we are interested in is that the single cells have to be reversible deterministic finite Mealy automata. These cellular automata are referred to by one-way Mealy cellular automata with strongly or weakly reversible cells and are denoted by $\text {SRC-OMCA}$ and $\text {WRC-OMCA}$. In general, the transition functions for reversible deterministic finite Mealy automata may be partial in order to cope with situations that would drive the automaton into a rejecting sink state. Instead of entering the sink state, now the $\text {DFMA}$ simply stops and rejects since it could not process the input entirely. However, since the concept of cellular automata does not allow single cells to stop, here, a rejecting sink state of the cells cannot be avoided in general. So, we slightly soften the notion of reversibility by disregarding rejecting sink states and say that an $\text {OMCA}$ is an $\text {RC-OMCA}$ if its cells are deterministic finite automata that are reversible with the exception of a possible rejecting sink state. However, it turns out in the next section that the disregarding of rejecting sink states is no restriction at least for $\text {WRC-OMCA}$s.

These definitions are justified and compared with related concepts after the following example that should clarify the notation.

Example 1

The non-semilinear language $\{a^nb^{k\cdot 2^n}\mid k,n\ge 1\}$ is accepted by the following one-way Mealy cellular automaton with strongly reversible cells $M=\langle S,F,\{a,b\},B ,\bot ,\texttt {\#},\delta \rangle$ in real time. We set $S=\{a,a_1,b,s_-,s_+\}$, where $B= \{1,0,s,s_-,s_+,\bot ,\texttt {\#}\}$, $F=\{s_+\}$, is the sole accepting state, and $s_-$ is a rejecting sink state. The transition function $\delta$ is defined through:

and $\delta (s_-,x)=(s_-,s_-)$ and $\delta (s_+,x)=(s_-,s_-)$, for all $x\in B$.

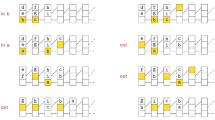
By inspecting the transition function, it is verified that the cells are in fact $\text {SREV-DFMA}$s. An example computation on input $a^3b^8$ is depicted in Fig. 2. Basically, the consecutive b-cells stay in their state, where message 1 is transmitted in every step. Additionally, a message s is sent by the rightmost cell upon receiving the border message. This message moves through the b-cells one cell per time step.

The consecutive a-cells set up a binary counter with the least significant bit in the rightmost a-cell. To this end, state a is used to represent digit zero and state $a_1$ is used to represent digit one. A message 1 indicates a carry-over and a message 0 indicates no carry-over. Finally, when the signal s meets the a-cells, it becomes signal $s_+$ as long as it only sees digits one, that is, states $a_1$. Otherwise, it turns to signal $s_-$ which is rejecting.

So, in order to accept an input, the leftmost cell has to enter state $s_+$. This is only possible if message $s_+$ has moved through a counter that represents a binary number of the form $1^n$, that is, $2^n-1$. Since due to the initial step, the counter starts to increase at time step one, this is only possible if message s has passed through a sequence of b-cells whose length is a multiple of $2^n$.    $\blacksquare$

Fig. 2.

Space-time diagram of a real-time computation of a one-way Mealy cellular automaton with strongly reversible cells on input $a^3b^8$.

Another related concept has been studied in [10]. Based on the observation, that in reversible one-way cellular automata information flow is from right to left in a forward computation and from left to right in a backward computation, a one-way cellular automaton is said to be reversible if there exists a reverse local transition function that computes the predecessor states. Due to the domain $S^2$ and the range S, obviously, the local transition function cannot be injective in general. However, since for reverse computation steps the flow of information is reversed as well, for the reverse transition function, each cell receives the state of its left neighbor. For example, let $s_1s_1s_2s_1$ be the states of four adjacent cells, and $\delta (s_1,s_1)=s_1$, $\delta (s_1,s_2)=s_2$, and $\delta (s_2,s_1)=s_1$, then the successor states of the three left cells are $s_1s_2s_1$. So, for the reverse transition function $\delta ^R$ we obtain $\delta ^R(s_1,s_2)=s_1$ and $\delta ^R(s_2,s_1)=s_2$ and, thus, such a behavior is possible in reversible one-way cellular automata. However, the single cell is not a reversible finite automaton, since $\delta ^{\scriptscriptstyle \leftarrow }(s_1,s_1)=s_1$ and $\delta ^{\scriptscriptstyle \leftarrow }(s_1,s_1)=s_2$. On the other hand, let $s_1s_2s_2$ as well as $s_2s_3s_3$ be the states of three adjacent cells, and $\delta (s_1,s_2)=s_1$, $\delta (s_2,s_2)=s_2'$, $\delta (s_2,s_3)=s_1$, and $\delta (s_3,s_3)=s_2'$. Then the successor states of the two left cells are $s_1s_2'$ in both cases. So, a reverse transition function $\delta ^R$ cannot exist since it must map $(s_1,s_2')$ to $s_2$ and to $s_3$. However, the transitions $\delta ^{\scriptscriptstyle \leftarrow }(s_1,s_2)=s_1$, $\delta ^{\scriptscriptstyle \leftarrow }(s_2',s_2)=s_2$, $\delta ^{\scriptscriptstyle \leftarrow }(s_1,s_3)=s_2$, and $\delta ^{\scriptscriptstyle \leftarrow }(s_2',s_3)=s_3$ do not violate the reversibility of the finite automaton used as single cell.

3 The Computational Capacity of One-Way Mealy Cellular Automata with Weakly Reversible Cells

Here, we explore the computational capacity of $\text {WRC-OMCA}$. To this end, we start to shed light on the role played by the sink states in such devices.

Lemma 2

Let M be a $\text {WRC-OMCA}$ whose cells are reversible disregarding sink states. Then an equivalent $\text {WRC-OMCA}$ where all cells are reversible including sink states can effectively be constructed.

Proof

Let $M=\langle S,F,A,B,\bot ,\texttt {\#},\delta \rangle$ be a $\text {WRC-OMCA}$ whose cells are reversible except for sink states (see Fig. 3).

We consider the state graph of a cell of M. For every sink state s the following steps are repeated. Let G be the part of the graph that does neither include s nor any edge to s. The first step is to remove irreversibility for the edges that enter the sink state from some states in G. To this end, state s is copied as many times as there are incoming edges from states in G. Now these edges are directed to different copies of s.

The next step is to remove the irreversibility caused by the looping edges and the incoming edge from a state in G. To this end, a new copy $\bar{B}=\{\bar{b}\mid b\in B\}$ of B is used. Each edge from a copy of a sink state to itself labeled a, b is relabeled by $a,\bar{b}$. The state graph obtained so far is weakly reversible. However, by providing a copy of B the number of messages that may be sent to neighboring cells is increased. Since $A=B$, additional edges have to be included. To overcome this problem, for every edge in G labeled a, b, an additional edge between the same states labeled $\bar{a}, b$ is included in $G'$. Again, this step preserves weak reversibility. Altogether, we have constructed an equivalent $\text {WRC-OMCA}$, since every pair (a, b) from $B\times B$ induces an injective partial mapping from the state set S to itself.    $\square$

Fig. 3.

How to make an automaton with sink state reversible. Automaton G is reversible except for the sink state s, where $0\le i,j\le |B|-1$ (left). Automaton $G'$ is reversible including the two sink states $s_1$ and $s_2$ (right). Every edge in G labeled a, b is labeled a, b and $\bar{a},b$ in $G'$ which preserves weak reversibility.

The idea used to prove Lemma 2 can in fact be generalized. So, it turns out that even $\text {WRC-OMCA}$s have the full computational capacity of $\text {OMCA}$s.

Theorem 3

Let M be an $\text {OMCA}$. Then an equivalent $\text {WRC-OMCA}$ with all cells reversible including sink states can effectively be constructed.

4 Reversible One-Way Partitioned Cellular Automata

Now we turn to discuss the details of the definitions in comparison with another related model. In [18] reversible two-way partitioned cellular automata are studied in terms of language recognition. The important concept of partitioned cellular automata is well-suited to define the notion of reversibility of cellular automata computations. In detail, the cells of a one-way partitioned cellular automaton have partitioned states that is, a state consists of a state part that represents the actual state and a message part the represents the message to be sent to the left neighbor. This message is created by the transition function during a transition. So, as for Mealy cellular automata the transition depends on the current state part and the current message part of its neighbor, and gives the new state part and the message part to be sent to the left, where initially each cell sends a message corresponding to its input symbol and the rightmost cell receives information associated with a boundary symbol on its free input line. So far, Mealy and partitioned cellular automata formalize similar concepts, but in partitioned cellular automata the message to be sent is a part of the state, while in Mealy cellular automata it is not. This makes a difference for reversibility considerations.

Formally, a one-way partitioned cellular automaton $(\text {OPCA})$ is a system $\langle S,F,A,\texttt {\#},\delta \rangle$, where $S=T\times C$ is the finite, nonempty set of cell states, where T is the message part and C is the state part, $F\subseteq S$ is the set of accepting states, $\texttt {\#}\in T$ is the distinguished boundary message, A is the nonempty set of input symbols with $A\subseteq C$ and $A\subseteq T$, and $\delta : C\times T \rightarrow T\times C$ is the local transition function.

Given some cell state $s=(t, c)$, the projection on its message part t is denoted by $\pi _T(s)$ and the projection on its state part c is denoted by $\pi _C(s)$.

A configuration of a one-way partitioned cellular automaton $\langle S,F,A,\texttt {\#},\delta \rangle$ is a mapping $c:\{1,2,\dots ,n\} \rightarrow S$, for $n\ge 1$, that assigns a state to each cell. The operation starts in a so-called initial configuration, which is defined by the given input $w=a_1a_2\cdots a_n\in A^+$. We set $c_0(i)=(a_i,a_i)$, for $1\le i\le n$. Successor configurations are computed according to the global transition function $\varDelta$. Let c be a configuration with $n\ge 1$, then the successor configuration $c'$ is

$$ c' = \varDelta (c) \iff \left\{ \begin{array}{l} c'(i) = \delta (\pi _C(c(i)),\pi _T(c(i+1))), i\in \{1,2,\dots ,n-1\}\\ c'(n) = \delta (\pi _C(c(n)),\texttt {\#})\\ \end{array} \right. . $$

A partitioned cellular automaton is said to be (locally) reversible $(\text {REV-OPCA})$ if and only if its local transition function is injective. So, given a state (s, m) and a transition $\delta (s,\ell )= (m',s')$, by the injectivity, from $(m',s')$ the predecessor state s of the cell and the message $\ell$ received in the previous step are uniquely determined. The latter is part of the predecessor state of the right neighbor. In particular, the message part m of the cell cannot be determined. Instead, it is uniquely determined from the left neighbor. So, looking at the whole configuration, the predecessor configuration can be computed. However, the single cell is not necessarily a reversible finite automaton.

In $\text {RC-OMCA}$s the single cells have to be reversible $\text {OMCA}$s. So, for example, transitions $\delta (s_1,a_1)=(s,b)$ and $\delta (s_2,a_2)=(s,b)$ are allowed, where $\delta ^{\scriptscriptstyle \leftarrow }(s,a_1,b)=s_1$ and $\delta ^{\scriptscriptstyle \leftarrow }(s,a_2,b)=s_2$. These transitions are forbidden in reversible partitioned cellular automata since they violate the injectivity of $\delta$.

The next theorem marks a lower bound for the computational capacity of real-time $\text {OPCA}$s. It says that a real-time $\text {OPCA}$ is at least as powerful as a deterministic finite automaton ($\text {DFA}$), where a $\text {DFA}$ is a $\text {DFMA}$ with a singleton output alphabet, thus, the output is omitted from the transition function. Since it is well known that there are regular languages that are not accepted by reversible $\text {DFA}$s [2, 20], the next theorem provides a construction of a reversible cellular device that simulates any possibly irreversible regular language.

Theorem 4

Let L be a regular language. Then L is accepted by a real-time $\text {REV-OPCA}$.

Proof

Since the regular languages are closed under reversal, we may assume that language $L^R$ is accepted by some $\text {DFA}$ M with state set S, input alphabet A, initial state $s_0$, set of accepting states F, and transition function $\delta : S \times A \rightarrow S$. Moreover, we may assume that the initial state $s_0$ is left with the very first transition and never reentered.

The idea for the simulation of M by a real-time $\text {OPCA}$ $M'$ is straightforward. The cells of $M'$ run through a loop that keeps their initial states, while at the right end a signal is set up that moves through the array with maximum speed and computes and sends the states of the simulated $\text {REV-DFA}$ M. A little extra attention has to be paid for implementing the local transition function of $M'=\langle S',F',A,\texttt {\#},\delta '\rangle$ injectively. Depending on M we identify the boundary symbol $\texttt {\#}$ of $M'$ with the initial state $s_0$ of M and define $\texttt {\#}=s_0$, $T=S\cup A$, $C=A \cup (S \times A)$, $F'=\{ (s,a) \in S\times A \mid \delta (s,a) \in F\}$, and $\delta '(a,b)=(b, a)$, for all $a,b\in A$, $\delta '(a,\texttt {\#})=(\delta (s_0,a),(s_0,a))$, for all $a \in A$, $\delta '(a,s)=(\delta (s,a),(s,a))$, for all $a \in A$ and $s \in S {\setminus } \{s_0\}$, and $\delta '((s,a),\texttt {\#})=(\texttt {\#},(s,a))$, for all $(s,a) \in S \times A$ (see Fig. 4).

Fig. 4.

A real-time $\text {REV-OPCA}$ accepting a regular language, where $s_{i+1}=\delta (s_i,a_{5-i})$, for $0\le i\le 4$. The input is accepted if $\delta (s_4,a_1)=s_5$ is an accepting state in M.

An inspection of the transition function $\delta '$ and taking into account that the initial state of M is left in the very first transition and never reentered shows the injectivity of $\delta '$. Let the input be $a_1a_2\cdots a_n$. At time step 1, the rightmost cell n initiates the signal by calculating and sending $s_1=\delta (s_0, a_n)$. In general, for $0 \le i \le n-1$, the signal reaches cell $n-i$ at time $i+1$ and calculates and sends state $s_{i+1}=\delta (s_i,a_{n-i})$. The accepting states of $M'$ are defined as those states sending an accepting state of M. So, $M'$ accepts $L(M)^R=(L^R)^R=L$.    $\square$

The next construction shows that real-time $\text {REV-OPCA}$s are also able to accept non-regular context-free languages.

Lemma 5

There is a non-regular context-free language that is accepted by some real-time $\text {REV-OPCA}$.

Proof

We use a language L over alphabet $\{a,b\}^*$ as witness that has the property $L\cap a^*b^* = \{a^m b^n\mid n\ge m \ge 1\}$. Since the regular languages are closed under intersection and $\{a^m b^n\mid n\ge m \ge 1\}$ is not regular, L is not regular either.

First, we partially construct a real-time $\text {REV-OPCA}$ $M=\langle S,F,A,\texttt {\#},\delta \rangle$ that accepts inputs from $\{a^m b^n\mid n\ge m \ge 1\}$. The basic idea is to send a signal with half speed from the rightmost a-cell to the left and a second signal that moves with maximum speed from the rightmost b-cell to the left. Whenever the second signal reaches a cell that already has seen the first signal, the cell enters the accepting state. The crucial point is to implement this behavior with an injective transition function. To this end, we set $A=\{a,b\}$, $T=\{\texttt {\#}\}\cup A$, $C=A\cup \{1,2\}$, and $F= \{(\texttt {\#}, 1)\}$.

General transitions and transitions that implement the half-speed signal are

The second signal is identified with the message $\texttt {\#}$. It is implemented by

By inspection of the right-hand sides of the transition function it is evident that $\delta$ is injective so far.

In order to provide further transition rules for inputs not of the form $a^mb^n$, we extend $\delta$ injectively by

Now inputs of the form $b^ma^n$ are treated similarly as inputs of the form $a^mb^n$. However, in the b-cells now state parts 2 are used that are not part of accepting states.

Since the $\texttt {\#}$-signal is transmitted further to the left, one may obtain further accepting computations if the inputs are appropriately extended to the left. However, every input of the form $b^ma^n$, for $m,n\ge 1$, is rejected, and every input of the form $a^mb^n$, for $n\ge m \ge 1$, is accepted. In particular, we derive that $L(M)\cap a^*b^*= \{a^m b^n\mid n\ge m \ge 1\}$, which shows the lemma.    $\square$

5 Conclusions

We have introduced and discussed several notions of local reversibility for real-time $\text {OCA}$s. We have shown that weak reversibility can always be achieved, that is, every possibly irreversible real-time $\text {OCA}$ computation can be realized by a real-time $\text {OCA}$ composed of weakly reversible components. Concerning the other two notions, namely, strong reversibility and reversible partitioned $\text {OCA}$s we have the conjecture that both models are less powerful. However, both models are still able to accept complex languages such as the non-semilinear language given in Example 1 and the context-free, non-regular language used in Lemma 5. Apart from the question of whether both language classes can be separated from the general model, it would clearly be of interest to identify further language classes which can be accepted by these models. Finally, the strength of a model is to some extent documented by the undecidability of the usually investigated decidability questions such as emptiness, finiteness, inclusion, or equivalence. While all such questions are undecidable for real-time $\text {OCA}$s and hence also for real-time $\text {OCA}$s with weakly reversible cells, nothing is known yet on the status of the decidability questions for real-time $\text {OCA}$s with strongly reversible cells and real-time reversible partitioned $\text {OCA}$s.