A Universal 3D Gait Planning Based on Comprehensive Motion Constraints

Abstract

To realize stable walking and complex motion in the 3D unstructured environment, a parametric universal gait planning is proposed with the consideration of boundary constraints, physical constraints and ZMP stability constraints of locomotion. This approach adopts a spline-based parametric method to simplify the complicated joint trajectory planning problem, and converts it to a constrained optimization problem of the parametric vector. With different gait parameters and boundary constraints, this approach was extended to more complex gait planning. As examples, three different gaits were generated, including start walking, stop walking and kicking a ball.

1 Introduction

Living in human life and coexisting harmoniously with human being is the final goal of humanoid robot research. How to realize stable walking and complex motion in the 3D unstructured living environment is one of the important topics. Because of the essentially unstable characteristic of biped walking, rigorous walking constraints should be considered with 3D gait planning, which requires perfect coordination of joint actuating torques, together with accurate control of ground reaction forces in order to ensure the dynamic balance of the biped walking [1].

ZMP (Zero Moment Point), as the most common dynamic stability criterion, firstly introduced by Vukubratovic [2, 3], was widely used to synthesize and control a stable locomotion [4,5,6,7]. In general, ZMP based approach uses one or several high order polynomials to describe the joint motion or ZMP trajectory, along with the optimization of one or several important parameters, for example, energy consumption [8], joint torque [1, 9] and stability margin [10].

In the early 1970s, Chow and Jacobson [11] firstly mentioned the most import factor for a stable biped locomotion was hip motion. The hip motion synthesis should be prior to the synthesis of joint trajectory. Channon et al. [12] accepted this idea and realized a stable walking in seven-link plane robot. It adopts cubic splines to describe the motion of hip and foot, and minimized the energy consumption of biped walking. Park et al. [13] also use a three-order polynomial to describe the trajectory of the hip. With the simplified ZMP, this approach achieved online gait planning on humanoid robot KHR-3. Chevallereau and Aoustin [14] adopt four-order polynomial to describe joint motions. They hypothesized that the transition between single-support phase and double-support phase was instantaneous, which was modeled as a passive impact. With the constraint of ZMP, several sets of energy optimized walking and running gait were realized in a five DoF (Degrees of freedom) planar biped robot. Huang et al. [10] used two cubic splines to describe hip and ankle motion of swing leg. According to adjustment of the translation distance of body in single-support phase, a biped walking gait with maximum stability region was generated. But this approach didn’t include motion constraints in transition. The generated gait was not smooth, and jerk motion may appear when transiting from single-support phase to double-support phase. In [1, 9], Bessonnet and Seguin developed an efficient method with the consideration of four points boundary constrains in gait transition, but their approach didn’t count the effect of lateral motion. Based on Bessonnet’s method, the stability constrain was introduced in [15], and a biped walking gait of energy optimization was generated. But this research still focuses on the sagittal plane. Tlalolini et al. [16] divided single-support phase to two sub-phases, rotating around the toe and freely swinging in the air. They adopt three-order polynomials to describe joint trajectory. With the analysis of feasible gait constraints, a group of torque-optimized joint trajectory in the 3D environment was synthesized. Furthermore, compared energy consumption with and without rotation motion around toe was studied. But this method only considers the single-support phase, it can not be used for the whole cyclic motion of biped robot.

In this paper, we present a 3D universal parametric gait optimization method, which is firstly introduced by Bessonnet et al. [1]. But we aim at achieving the numerical synthesis of gait steps in the 3D environment [19] and extending it to a universal complicated gait planning. To avoid jerk motion, multi four-order splines were used to describe each joint. In Sect. 2, the comprehensive cyclic gait constraints in the 3D environment were introduced, including six-point boundary constraints, physical constraints, and stability constraints. In Sect. 3, a 13-mass-block constrained dynamic model in the 3D environment was presented. With the spline-based parametric approach, the problem of complex joint trajectory planning in 3D environment became to a constrained optimization problem of the parametric vector in Sect. 4. Section 5 shows the synthetic results of cyclic walking gait. With different gait parameters and boundary constraints, Sect. 6 extended this approach to more complex gait planning, including start gait, stop gait and kicking a ball. The simulated and experimental results demonstrated the effectiveness of this approach. Section 7 shows the conclusions.

2 Comprehensive Gait Constraints in 3D Environment

Biped walking is a periodic phenomenon. A complete cyclic motion can be divided into two phases: a single-support phase (SSP) and a double-support phase (DSP). During the single-support phase, only one foot is in touch with the ground, the other foot swings from the rear to the front. The locomotion system moves as an open tree-like kinematic chain. During the double-support phase, both feet are in contact with the ground. This phase begins with the heel of the forward foot touching the ground, and ends with the toe of the rear foot leaving the ground. The locomotion system is kinematic closed and over-actuated.

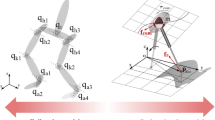
Figure 1 shows the basic stick figures of transition between SSP and DSP in both forward and lateral views. Where $H_{\text{foot}}$ denotes the distance from the sole to the ankle. $L_{\text{foot}}$ denotes the length of foot. $L_{\text{calf}}$ and $L_{\text{thigh}}$ separately denotes the length of calf and thigh. $L_{\text{width}}$ denotes the distance between two hip joints. $[q_{1}^{\text{si}} ,q_{2}^{\text{si}} , \ldots ,q_{13}^{\text{si}} ]^{\text{T}}$, $[q_{1}^{\text{sf}} ,q_{2}^{\text{sf}} , \ldots ,q_{13}^{\text{sf}} ]^{\text{T}}$, $[q_{1}^{\text{di}} ,q_{2}^{\text{fi}} , \ldots ,q_{13}^{\text{di}} ]^{\text{T}}$ and $[q_{1}^{\text{df}} ,q_{2}^{\text{df}} , \ldots ,q_{13}^{\text{df}} ]^{\text{T}}$ are joint angle vectors, used to describe the start and stop postures of SSP and DSP.

Fig. 1.

Stick figures of biped walking

2.1 Boundary Constraints of Cyclic Gait

As stated in above paragraph, a cyclic step is the sequence of two main events, SSP and DSP. In more detail, to crossing over a certain obstacle, the walking step should reach to a specific height. Thus, we divided SSP to two sub-phases. The first phase begins at toeing off, ends at the highest position. The second phase runs from highest position to heel touching. To generate a rolling gait, the DSP was divided to three sub-phases. The first phase describes the rotation around the heel of the front foot. The second phase is the process when both feet fully touching the ground. The third phase describes the rotation around the toe of the rear foot. Thus, to meet the above conditions, a whole cyclic locomotion is described by six-point boundary constraints.

Initial Time of SSP $t_{\text{si}}$.

Referring to Fig. 1, the distance between two feet is constant. The swing leg is leaving the ground. To avoid jerk motion, we suppose the toe’s speed equals to 0.

$$ \left\{ {\begin{array}{*{20}c} {{\mathbf{p}}_{{o_{ 2}^{\text{si}} }} ({\mathbf{q}}(t_{\text{si}} )) - {\mathbf{p}}_{{o_{ 2}^{\text{si}} }} ({\mathbf{q}}(t_{\text{si}} )) = [\begin{array}{*{20}c} {L_{\text{step}} - L_{\text{foot}} } & {L_{\text{width}} } & 0 \\ \end{array} ]^{\text{T}} } \\ {v_{{o_{2}^{\text{si}} }} ({\mathbf{q}}(t_{\text{si}} ),{\dot{\mathbf{q}}}(t_{\text{si}} )) = \frac{{\partial {\mathbf{p}}_{{o_{ 2}^{\text{si}} }} ({\mathbf{q}}(t_{\text{si}} ))}}{{\partial {\mathbf{q}}}}{\dot{\mathbf{q}}}(t_{\text{si}} ) = {\mathbf{0}}^{3x1} } \\ {q_{11} (t_{\text{si}} ) = - q_{\text{b}} } \\ \end{array} } \right. $$

(1)

Where $L_{\text{step}}$ the length of step, $L_{\text{foot}}$ is the length of the foot, $L_{\text{width}}$ is the lateral distance between two feet, $\varvec{p}_{{o_{ 1}^{\text{si}} }} ,\varvec{p}_{{o_{ 4}^{\text{si}} }}$ is the position of point $O_{1}$ and point $O_{4}$ at $t_{\text{si}}$, $q_{\text{b}}$ is the angle between foot and ground, $\varvec{0}^{3 \times 1}$ is zero vector.

Middle Time of SSP $t_{\text{sm}}$.

Swing leg goes to the highest position, the speed of ankle joint is 0.

$$ \left\{{\begin{array}{*{20}c} {{\varvec{p}_{{{\text{ankle}}\_{\text{sm}}}}}^{\text{T}} (\varvec{q}(t_{\text{sm}} )) \cdot \varvec{e}_{z} = H_{\text{foot}} + H_{\text{step}} } \\ {{v_{{{\text{ankle}}\_{\text{sm}}}}}^{\text{T}} (\varvec{q}(t_{\text{sm}}),\dot{\varvec{q}}(t_{\text{sm}} )) \cdot \varvec{e}_{z} = [\frac{{\partial \varvec{p}_{\text{ankle}} (\varvec{q}(t_{\text{sm}} ))}}{{\partial \varvec{q}}}\dot{\varvec{q}}(t_{\text{sm}} )]^{\text{T}} \cdot \varvec{e}_{z} = 0} \\ \end{array} } \right. $$

(2)

Where $\varvec{e}_{x} ,\varvec{e}_{y} ,\varvec{e}_{z}$ denotes the unit vector of x, y and z-axis. $H_{\text{step}}$ is step height. $\varvec{p}_{{{\text{ankle}}\_{\text{sm}}}}$, $v_{{{\text{ankle}}\_{\text{sm}}}}$ is ankle position and speed at $t_{\text{sm}}$.

Transition Time from SSP to DSP $t_{\text{t}}$.

The distance between support foot and heel of swing foot is constant. To avoid jerk motion when transition, we suppose the speed of swing heel equals to 0.

$$ \left\{ {\begin{array}{*{20}c} {\varvec{p}_{{o_{ 2}^{\text{t}} }} (\varvec{q}(t_{\text{t}} )) - \varvec{p}_{{o_{ 2}^{\text{t}} }} (\varvec{q}(t_{\text{t}} )) = [\begin{array}{*{20}c} {L_{\text{step}} - L_{\text{foot}} } & {L_{\text{width}} } & 0 \\ \end{array} ]^{\text{T}} } \\ {v_{{o_{2}^{\text{t}} }} (\varvec{q}(t_{\text{t}} ),\dot{\varvec{q}}(t_{\text{t}} )) = \frac{{\partial \varvec{p}_{{o_{ 2}^{\text{t}} }} (\varvec{q}(t_{t} ))}}{{\partial \varvec{q}}}\dot{\varvec{q}}(t_{\text{t}} ) = {\varvec{0}}^{3x1} } \\ {q_{11} (t_{\text{t}} ) = q_{\text{f}} } \\ \end{array} } \right. $$

(3)

Where $q_{\text{f}}$ is the angle between the swing foot and the ground.

Finish Time of First Sub-phase in DSP $t_{\text{d1}}$.

Swing leg fully touches the ground. The angle speed of ankle joint equals to 0.

$$ \left\{ {\begin{array}{*{20}c} {q_{11} (t_{\text{d1}} ) = 0} \\ {\dot{q}_{11} (t_{\text{d1}} ) = 0} \\ \end{array} } \right. $$

(4)

Finish Time of Second Sub-phase in DSP $t_{\text{d2}}$.

The rear feet starts to rotate around its toe. To avoid jerk motion, the angle speed of ankle joint is supposed to 0.

$$ \left\{ {\begin{array}{*{20}c} {q_{5} (t_{\text{d2}} )= 0} \\ {\dot{q}_{5} (t_{\text{d2}} ) = 0} \\ \end{array} } \right. $$

(5)

Finish Time of DSP $t_{\text{df}}$.

The constraints at the finish time of DSP $t_{\text{df}}$ are similar to initial time $t_{\text{si}}$, but mirroring joint rotations and velocities with the consideration of cyclic characteristics.

$$ \left\{ {\begin{array}{*{20}c} {q_{i} (t_{\text{df}} )= {\text{q}}_{{{\text{i}} + 6}} (t_{\text{si}} ),q_{{{\text{i}} + 6}} (t_{\text{df}} ) = q_{i} (t_{\text{si}} ),i = 1, \ldots ,6} \\ {\dot{q}_{i} (t_{\text{df}} )= {\dot{\text{q}}}_{{{\text{i}} + 6}} (t_{\text{si}} ),\dot{q}_{{{\text{i}} + 6}} (t_{\text{df}} ) = \dot{q}_{i} (t_{\text{si}} ),i = 1, \ldots ,6} \\ \end{array} } \right. $$

(6)

2.2 Physical Constraints

Except the six-point boundary constraints of cyclic motion, to realize stable walking, it must meet the physical constraints, which include singular posture forgiveness, no ground touching of swing leg, coordination of lateral motion, limitation of joint angle and limitation of joint torque.

Singular Posture Forgiveness.

Singular posture is defined as the posture when the inverse Jacobian matrix of the robot does not exist. Literature [17] presents three different singular postures in biped walking. To avoid that, the robot should act in a slight squat when walking.

$$ \varvec{p}_{13} (\varvec{q}(t)) \cdot \varvec{e}_{z} + \varDelta_{z} \le H_{\text{foot}} + L_{\text{calf}} + L_{\text{thigh}} $$

(7)

Where $\varvec{p}_{13}$ denotes the position of torso, $\varDelta_{z}$ is the minimum value of squat.

No Ground Touching in SSP.

When walking, the swing leg can not go under the ground. That means the position of bottom surface of swing foot must higher than ground.

$$ {\varvec{S}_{\text{foot}}}^{\text{T}} (\varvec{q}(t)) \cdot \varvec{e}_{z} > {\mathbf{0}}^{{n_{\text{p}} \times 1}} ,t \in (t_{\text{si}} ,t_{\text{t}} ) $$

(8)

Where $\varvec{S}_{\text{foot}}$ denotes the bottom surface of swing foot, $n_{\text{p}}$ is vertices of the polygon. When the foot shape of the robot is a rectangle, $n_{\text{p}}$ equals to 4.

Coordination of Lateral Motion.

The hip joint and ankle joint in lateral motion should have the same value to keep the swing foot be parallel to the support foot.

$$ q_{2} (t) = q_{6} (t) = - q_{8} (t) = - q_{12} (t),\,\,t \in (t_{\text{si}} ,t_{\text{t}} ) $$

(9)

Limitation of Joint Angle.

Every joint has a mechanical limitation, the relative rotation angle of each joint should meet the followings constraints.

$$ \left\{ {\begin{array}{*{20}c} {\theta_{{i\_{ \hbox{min} }}} \le \theta_{i} (\varvec{q}(t)) \le \theta_{{i\_{ \hbox{max} }}} } \\ {\dot{\theta }_{{i\_{ \hbox{min} }}} \le \dot{\theta }_{i} (\varvec{q}(t),\dot{\varvec{q}}(t)) \le \dot{\theta }_{{i\_{ \hbox{max} }}} } \\ \end{array} } \right. $$

(10)

Limitation of Joint Torque.

The output torque of each driving motor has a limitation. The constraints are given as followings.

$$ \left| {u_{i} (t)} \right| < u_{i\_\hbox{max} } ,\,\,i < 13 $$

(11)

2.3 ZMP Stability Constraints

The keep the stability of biped walking, the ZMP must be located within the convex hull of all contact points (stable region).

$$ \varvec{p}_{\text{zmp}} = [\begin{array}{*{20}c} {x_{\text{zmp}} } & {y_{\text{zmp}} } & {z_{\text{zmp}} } \\ \end{array} ] \in \varvec{S}^{r} $$

(12)

Where $S^{r}$ denotes the convex hull of all contact points. Because the foot shape of the real robot in this paper is a rectangle, and the locomotion is only on the flat surface. The constraints of stability can be simply written as the following inequalities.

$$ ZMP_{{x{\text{Lmax}}}} (t) \le {\varvec{p}_{\text{zmp}}}^{\text{T}} (\varvec{q}(t),\dot{\varvec{q}}(t),\ddot{\textit{\textbf{q}}}(t)) \cdot \varvec{e}_{x} \le ZMP_{{x{\text{Rmax}}}} (t) $$

(13)

$$ ZMP_{{y{\text{Lmax}}}} (t) \le {\varvec{p}_{\text{zmp}}}^{\text{T}} (\varvec{q}(t),\dot{\varvec{q}}(t),\ddot{\textit{\textbf{q}}}(t)) \cdot \varvec{e}_{y} \le ZMP_{{y{\text{Rmax}}}} (t) $$

(14)

3 Constrained Dynamic Model in 3D Environment

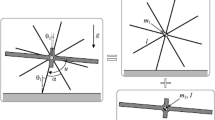
As stated in Sect. 2, the biped system is assumed to be an open kinematic chain in SSP, but close kinematic and over-actuated in DSP. To realize 3D motion, a 13-mass-block dynamic model was present. Figure 2 shows the configuration and definition of mass blocks in the biped robot, where R1-R13 represent the rotation matrix for each mass block. Setting torso as the base of the robot, the joint motion for both legs can be derived with Denavit-Hartenberg parameters.

Fig. 2.

13-mass-block robot model

Considering the coupling effect between the forward and lateral movement, a 13-mass-block dynamic model was created. The Lagrange Equation with close-chain constraints shows in the (15).

$$ \begin{aligned} \varvec{M}(\varvec{q}(t))\dot{\varvec{q}}(t) + \varvec{C}(\varvec{q}(t),\dot{\varvec{q}}(t))\dot{q}(t) + \varvec{G}(\varvec{q}(t)) \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \varvec{ = A}_{\tau } (\varvec{q}(t))\varvec{\tau}(t) +\varvec{\lambda}^{\text{T}} (\varvec{q}(t))\varvec{u}(t) \hfill \\ \end{aligned} $$

(15)

Where $\varvec{M} \in \varvec{R}^{{ 1 3 {\text{x13}}}}$ denotes the mass matrix, $\varvec{C} \in \varvec{R}^{{ 1 3 {\text{x13}}}}$ is the centrifugal and Coriolis inertia matrix. $\varvec{G} \in \varvec{R}^{ 1 3}$ is the gravity term. $\varvec{\tau}\in \varvec{R}^{ 1 3}$ is the actuating joint torques. $\varvec{u}$ is a six-dimensional vector, which denotes the 3D reacting forces $\varvec{F}_{\text{r}}$ and reacting torques $\varvec{\tau}_{\text{r}}$ in DSP, $\varvec{u}(t) \in \varvec{0}^{{ 6 {\text{x1}}}}$ in SSP. $\varvec{A} \in \varvec{R}^{13x13}$ is the constant matrix, $\lambda \in \varvec{R}^{6x13}$ the Jacobian matrix of the robot, it is defined as $\lambda (\varvec{q}(t)) = \partial C^{d} /\partial \varvec{q}$, where $C^{d}$ is the constraints of the close chain in DSP (shown in Fig. 3). As stated in Sect. 2, the DSP can be divided to three sub-phases. In the first phase, the front foot touches the ground, and rotate around its heel, $C^{d} \equiv \varvec{L}_{s} (\varvec{q}(t))$. In the second phase, both feet touch the ground completely, $C^{d} \equiv \varvec{L}_{m} (\varvec{q}(t))$. In the third phase, the rear foot starts rotating around its toe, $C^{d} \equiv \varvec{L}_{f} (\varvec{q}(t))$.

Fig. 3.

Constraints of closed chain in DSP

4 Spline-Based Parametrization

Because energy based optimization method easily presents some disadvantages, including discontinuous motion and backlashes on the joints. Thus a performance criterion, defined as the integral quadratic amount of driving torque is adopted. The objective function shows in Eq. (16). Where $\varvec{\tau}$ denotes torque vector of joints, $\varvec{u}$ denotes the interacting forces in double-support phase.

$$ J(\varvec{q},\dot{\varvec{q}}) = \int\limits_{{t_{\text{si}} }}^{{t_{t} }} {\varvec{\tau}^{T} } (t)\varvec{\tau}(t) + \int\limits_{{t_{t} }}^{{t_{\text{df}} }} {(\varvec{\tau}^{\text{T}} } (t)\varvec{\tau}(t) + \varvec{u}^{\text{T}} (t)\varvec{u}(t)) $$

(16)

To generate jerk-less motion, several sections of four-order interpolating polynomials are built to describe the joint trajectory. The number of sections is decided by the points of boundary constraints. Suppose the number of sections is N, the $k_{th}$ four-order polynomial is shown in formula (17).

$$ \left\{ {\begin{array}{*{20}c} {\tau_{t} = (t - t_{k} )/(t_{k + 1} - t_{k} )} \\ {q_{i} (t) \cong \varphi_{ik} (\tau_{t} ) = \sum\nolimits_{j = 0}^{4} {c_{ikj} \tau_{t}^{j} } } \\ \end{array} } \right.,\,\,t \in [t_{k} ,t_{k + 1} ] $$

(17)

Set $\varvec{X}_{i} = \left[{{\varvec{x}_{i1}}^{\text{T}},{\varvec{x}_{i2}}^{\text{T}}, \ldots,{\varvec{x}_{ik}}^{\text{T}}, \ldots,{\varvec{x}_{iN}}^{\text{T}}} \right]^{\text{T}}$, where $\varvec{x}_{ik} = [c_{ik0} ,c_{ik1} ,c_{ik2} ,c_{ik3} ,c_{ik4} ]^{\text{T}}$, the trajectory of $i_{th}$ joint can be expressed as formula (18).

$$ q_{i} (t) \cong \phi_{i} (\varvec{X}_{i} ,t) $$

(18)

Type (18) substitute in (15) and (16), the problem of complicated joint trajectory planning in the 3D environment becomes to a constrained optimization problem of the parametric vector.

$$ \hbox{min} \,J(\varvec{X}) = { \hbox{min} }(\sum\limits_{i = 1}^{\text{N}} {\int\limits_{{t_{i} }} {[\varvec{\tau}^{\text{T}} (\varvec{X}_{i} )}\varvec{\tau}(\varvec{X}_{i} ) + \varvec{u}^{\text{T}} (\varvec{X}_{i} )\varvec{u}(\varvec{X}_{i} )]} ) $$

(19)

Subjects to the following inequality and equality constraints,

$$ \left\{ {\begin{array}{*{20}c} {c(c_{\text{b}} (\varvec{X}),c_{\text{p}} (\varvec{X}),c_{\text{zmp}} (\varvec{X})) \le \varvec{0}} \\ {cep(c_{\text{b}} (\varvec{X}),c_{\text{p}} (\varvec{X}),c_{\text{zmp}} (\varvec{X})) = \varvec{0}} \\ \end{array} } \right. $$

(20)

Where $c_{\text{b}} (\varvec{X})$, $c_{\text{p}} (\varvec{X})$ and $c_{\text{zmp}} (\varvec{X})$ separately denotes boundary constraints of transition between SSP and DSP, physical constraints of feasible gait and ZMP stability constraints.

Typically, constrained and nonlinear minimization problem can be solved by sequential quadratic programming [1, 9]. In this paper, fimincon in Matlab Optimization Toolbox was used to obtain the optimal joint trajectory.

5 Cyclic Walking Gait

With different walking parameters, two types of walking gait were generated. The walking speed was 0.15 m/s and 0.4 m/s, representing static and dynamic walking separately. The robot physical model was a kid-size humanoid robot THBIP-II. More details about THBIP-II can be found in the paper [18].

Figure 4 shows the stick figures for both static and dynamic cyclic walking gait. Firstly, we can found that the dynamic walking has a bigger body angle and step size. That means, walking speed can be controlled through the adjustment of body angle. Secondly, the body’s movement in vertical direction shows the lateral motion takes more effects in static walking than dynamic walking, especially in double support phase. Thirdly, from the foot trajectory, we can found that the swing foot moves to the highest point and holds a while before moving back ground in static walking, but it just sharply moves back ground in dynamic walking. It shows that the static walking gives more benefits for stepping over a certain obstacle.

Fig. 4.

Stick figures of static and dynamic cyclic walking

Figure 5 shows the joint torque. The torque for each joint is successive and smooth. In static walking, the maximum torque happens in the keen joint of the support leg. Different with static walking, it happens in heel lateral joint and heel forward joint of support leg in dynamic walking. That because the dynamic walking need overcomes the inertia force and Coriolis force generated from acceleration. Moreover, the hip rotation joint in both static and dynamic walking is not zero. It even reaches to 12 Nm when transiting from SSP to DSP in dynamic walking. It should be noticed that it can not be obtained from 7-link or 9-link plane robot model. Thus, 13-mass-block model, in a certain condition, can be used for the analysis of coupling problems between lateral motion and front motion.

Fig. 5.

Joint torque of cyclic walking

Figure 6 shows the real ZMP and CoG (center of Gravity) in THBIP-II. In static walking, ZMP overlaps with CoG. In dynamic walking, CoG deviates from the stable region, but ZMP still keeps inside there. Furthermore, fluctuations of ZMP curve occurs when the transition from SSP to DSP because of the lateral motions.

Fig. 6.

ZMP and COG of cyclic walking

6 Complicate Gait Planning

From the analysis of Sect. 2, we can find that the six-point boundary constraints can completely describe the whole 3D cyclic motion, and the synthetic gait is continuous and smooth. When giving different gait parameters and boundary constraints, different gait motion can be obtained. Thus, in this section, we extended this approach to complicated gait planning by using different boundary constraints, but the same physical constraints and stability constraints.

6.1 Start Gait and Stop Gait Planning

In addition to cyclic gait, the robot should start from stationary posture to stable walking and stop from stable walking to stationary posture in the real environment. We defined these two transition process as start gait and stop gait. As shown in Fig. 7, start gait is consists of two single steps, start step and transition step. Stop gait also consists of two single steps, transition step and stop step.

Fig. 7.

Stick frame of the whole biped motion including start, cycle and stop gait

Different with boundary constraints of cyclic gait, there are no constraints of periodicity. The two-point boundary constraints for the start gait and the stop gait are shown in (21), (22) and (23), (24). Where $\varvec{q}_{0}$ is stationary posture, $\varvec{q}_{cyc}$ is the initial posture of cyclic gait, which is also described in formula (1) as $\varvec{q}(t_{\text{si}} )$.

$$ \varvec{q}(t) = \varvec{q}_{0} ,\dot{\varvec{q}}(t) = \varvec{0}^{13x1} ,\,\,t = t_{\text{si}}^{\text{s}} $$

(21)

$$ \varvec{q}(t) = \varvec{q}_{cyc} ,\dot{\varvec{q}}(t) = \dot{\varvec{q}}_{cyc} ,\,\,t = t_{\text{tf}}^{\text{s}} $$

(22)

$$ \varvec{q}(t) = \varvec{q}_{cyc} ,\dot{\varvec{q}}(t) = \dot{\varvec{q}}_{cyc} ,\,\,t = t_{\text{ti}}^{\text{s}} $$

(23)

$$ \varvec{q}(t) = \varvec{q}_{0} ,\dot{\varvec{q}}(t) = \varvec{0}^{13x1} ,\,\,t = t_{\text{sf}}^{\text{s}} $$

(24)

Giving the walking speed as 0.15 m/s, the step in start and stop gait as 0.15 m, the step in transition phase as 0.3 m, the swing height as 4 cm, the percentage of support phase in walking period as 30%, an optimized walking gait which includes start gait, cycle gait and stop gait was generated with the consideration of boundary constraints, physical constraints, and ZMP stable constraints. Figure 7 shows the stick figures of whole biped motion. Figure 8 shows the planned joints curves. Figure 9 is the video frames implemented in THBIP-II biped robot [18]. Figure 10 presents the real ZMP and CoG curves. From these results, we can find the generated gait is smooth and stable.

Fig. 8.

Joint angles of the whole biped motion including start, cycle and stop gait

Fig. 9.

Video frames of the whole biped motion including start, cycle and stop gait

Fig. 10.

ZMP and CoG curves of the whole biped motion including start, cycle and stop gait

6.2 Kicking Ball Gait Planning

As an example, a much more complicated gait, kicking a ball was studied in this chapter. The gait of kicking a ball starts from stationary posture, it consists of 6 sub-phases. The first phase is a double-support phase, the main movement in this phase is lateral motion which is used to keep robot stable when kicking the ball. The second sub-phase begins at single leg supporting. During this phase, the swing leg moves to the highest position. In the third phase, a forward motion with acceleration is generated. During this phase, the swing leg moves to the ball’s location and touches the ball. After kicking the ball, the speed of swing leg decelerates to zero in the fourth phase. The fifth phase is a recovery process. The swing leg moves from the farthest position to the initial position and goes back to double support phase. The sixth phase is the inverse process of the first phase, the robot goes back to stationary posture. The seven-point boundary constraints for kicking a ball are shown in (25)–(31).

$$ \varvec{q}(t) = \varvec{q}_{0} ,\,\,\dot{\varvec{q}}(t) = \varvec{0}^{{ 1 3 {\text{x1}}}} ,\,\,t = t_{1}^{k} $$

(25)

$$ \varvec{q}(t) = \varvec{q}_{\text{stable}} ,\,\,\dot{\varvec{q}}(t) = \varvec{0}^{{ 1 3 {\text{x1}}}} ,\,\,t = t_{2}^{k} $$

(26)

$$ \left\{ {\begin{array}{*{20}c} {p_{\text{z}}^{\text{sfoot}} (\varvec{q}(t)) = H_{ \hbox{max} } } \\ {\dot{\varvec{q}}(t) = \varvec{0}^{13x1} } \\ \end{array} } \right.,\,\,t = t_{3}^{k} $$

(27)

$$ \left\{ {\begin{array}{*{20}c} {p_{x}^{\text{sfoot}} ({\mathbf{q}}(t)) = x_{ball} } \\ {v_{x}^{{s{\text{foot}}}} ({\mathbf{q}}(t)) = v_{\hbox{max} } } \\ \end{array} } \right.,\,\,t = t_{4}^{k} $$

(28)

$$ \left\{ {\begin{array}{*{20}c} {p_{x}^{\text{sfoot}} (\varvec{q}(t)) = x_{\hbox{max} } } \\ {v_{x}^{{s{\text{foot}}}} (\varvec{q}(t)) = 0} \\ \end{array} } \right.,\,\,t = t_{5}^{k} $$

(29)

$$ \left\{ {\begin{array}{*{20}c} {\varvec{v}^{{s{\text{foot}}}} (\varvec{q}(t)) = \varvec{0}^{{ 3 {\text{x1}}}} } \\ {\varvec{q}(t) = \varvec{q}_{\text{stable}} } \\ {\dot{\varvec{q}}(t) = \varvec{0}^{{ 1 3 {\text{x1}}}} } \\ \end{array} } \right.,\,\,t = t_{6}^{k} $$

(30)

$$ \varvec{q}(t) = \varvec{q}_{0} ,\,\,\dot{\varvec{q}}(t) = \varvec{0}^{{ 1 3 {\text{x1}}}} ,\,\,\,t = t_{7}^{k} $$

(31)

Setting the position of ball as $\left[ {\begin{array}{*{20}c} {0.02} & {0.065} & 0 \\ \end{array} } \right]^{\text{T}}$ m, the maximum speed when kicking the ball as 2 m/s, a stable ball kicking gait was generated. Figure 11 shows the joint curve of swing leg, Fig. 12 shows the video frames and real ZMP curve of THBIP-II. From these results, we can find the joint curves are smooth and ZMP always locates in the stable region.

Fig. 11.

Joint curve of swing leg

Fig. 12.

Video frames and ZMP curve

7 Conclusions

A universal 3D parametric gait planning is proposed with the consideration of comprehensive biped walking constraints. With the analysis of periodic biped walking of robot, six-point boundary constraints of successive and impact-less steps including single-support phase and double-support phase are present. By adopting the parametric gait optimization approach, the complicated joint trajectory planning problem was transformed into the constrained optimization problem of the parametric vector. To solve it, the sequential quadratic programming method was used. With different gait parameters and boundary constraints, this approach was extended to more complex gait planning. As examples, a start gait, a stop gait and a gait of kicking ball were planned and implemented in biped robot THBIP-II. The simulated and experimental results demonstrated the effectiveness of this approach.