Abstract
Climate warming has been and will continue to be faster in the Arctic compared to the other domains of the world, which generates major challenges for human adaptation. Among others, the development of socio-economic infrastructure and strategic planning requires long-term projections of water availability and extreme hydrological events. In this context, it is preferable that the projections of river runoff should be performed statistically, allowing the evaluation of economical risks and costs for hydraulic structures, which are connected to changes in hydrological extremes. In this study, the hydrological model MARCS (MARcov Chan System) is suggested as a tool to simulate the parameters of probability density functions (PDFs) of maximal runoff or peak flow, based on climate projections of the Representative Concentration Pathways. Following that, the PDFs of the maximal runoff were constructed within the Pearson Type III distributions to estimate the runoff values of a small exceedance probability. To evaluate the risks and costs of a long-term investment based on the future projections of river maximal discharge of 1 % probability, simple calculations were performed for the new bridge over the Nadym River as an example.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- Hydrological Model
- Couple Model Intercomparison Project Phase
- Climate Projection
- Exceedance Probability
- Total Investment
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Floods are among most dangerous natural hazards. Flood extremes cause substantial economic losses due to damage an infrastructure, such as bridges, roads, pipelines, dams, houses etc. Floods are commonly required in risk analysis of hydraulic structures (Scott 2011; Bowles 2001). Traditional methods of hydrological engineering use two main approaches to evaluate floods in given location at stream (Calver et al. 2009). The deterministic approach (or design storm method) combines a synthetic storm rainfall with physically-based hydrological model to evaluate the flood hydrograph (Pilgrim and Cordery 1975). The precipitation input is usually calculated from the intensity duration frequency curve of rainfall using observations in this case. However, the meteorological forcing can also be obtained from the climate projections, and then used to simulate the future river runoff hydrographs for a single or set of catchments (Archeimer and Lindström 2015; Lawrence and Haddeland 2011). The maximal discharges of particular exceedance probability are then evaluated from the modeled time series. The main short comings of this approach are that (i) the resulting flood estimations are sensitive to the algorithms of calculation of the projected meteorological values (Verzano 2009); (ii) the uncertainty produced by model parameters and algorithms can be significant (Butts et al. 2004); (iii) the calculations by the physically-based hydrological models are extremely costly computationally, especially in the case of ensembles of climate scenarios or regional scale assessment.
The statistical approach (or frequency analysis) considering multi-year runoff time series as realizations of stationary ergodic process, that can be performed statistically with distributions from the Pearson System (Andreev et al. 2005) fitted to the observations (Bulletin 17B 1982; SP33-101-2003 2004). The parameters of these distributions are evaluated from the observed runoff time series with different methods (van Gender and Vrijing 1997), and then the runoff quantiles of a small exceedance probability are estimated to support a design of the hydraulic structures. The greatest limitation of this method is that the runoff records should be representative for evaluation of the tailed values of fitted distributions (Katz et al. 2002). Also, the standard flood frequency analysis is based on the hypothesis of stationarity: it is assumed that the runoff statistics do not change over time, and past observations are representative for the future. However, the assumption of stationarity might not be applicable in changing climate, and advanced methods to evaluate flood frequency are required (Madsen et al. 2013).
To extend the statistical approach in the evaluation of flood and drought extreme quantiles under the expected climate change, the concept of quasi-stationarity of future hydrological regime is proposed by Kovalenko (1993). This idea allows evaluating the parameters of distributions of multi-year runoff for a future time period based on the sampled runoff statistics from past time period, and the distributions’ parameters are different for the past (reference) and the future (projected) period. The climate projections are usually presented as the multi-year means of the meteorological values for the period of 20–30 years (Pachauri and Reisinger 2007), i.e. under the same assumption of quasi-stationarity. To simulate the future parameters of distributions of multi-year runoff based on quasi-stationary climate projections, the Kolmogorov Backward Equation (KBE) is simplified due to the specific of hydrological data and stationarity/quasi-stationarity concepts of engineering hydrology (Kovalenko 1993, Dominges and Rivera 2010, Viktorova and Gromova 2008).
In this study, the simplification of the KBE suggested by Kovalenko et al. (2010) was used, and a probabilistic hydrological model MARCS (MARcov Chan System) was developed as a tool using the Python capabilities. Recently, the MARCS model contains the following blocks for the preliminary analysis of runoff/meteorological time series, the model’s parameterization and hindcasts, the forecasting based on the future climatology, the visualization and analysis of the modeling results.
The aims of this study were to describe the MARCS model structure and basic principles, and to provide an example of the model output in form of probabilistic projections of the maximal runoff for the Russian Arctic. Also, a method to utilize the projections of flood extremes to evaluate the economical investment to construct new bridges is suggested.
2 Method and Data
The probabilistic hydrological model, MARCS, includes five blocks. Each block contains the tools for (i) the data analysis and generalization (ii) the statistical methods for the data screening (both meteorological and hydrological), (iii) the schemes of the model parametrization (including regional oriented) and hindcasts, (vi) the forecasting, (v) the methods to perform statistical analyses and visualization of the modeling results (Table 8.1).
To simulate the probability density functions of multi-year maximal runoff over the territory of the Russian Arctic, the following data were used: the reference climatology was calculated from the meteorological time series, which were obtained from the catalogs of climatology for 209 weather stations (Radionov and Fetterer 2003, Catalogue 1989). The observed daily time series of river discharges for the period from early 1930s to 2002 from the R-ArcticNET database (www.r-arcticnet.sr.unh.edu/v4.0/) as well as the dataset of the Russian State Hydrological Institute (www.hydrology.ru/) were collected for 108 river gauges located over the northern Russia. The daily discharges were used to calculate the annual time series of the spring flood depth of the runoff (SFDR, mm/(time period)) as the volume of spring flood (m3) from the drainage basin divided by its area (m2). The volume of spring flood (m3) was evaluated using flood beginning and ending dates (Shevnina 2013). The SFDR time series were used as the predicting value in the further analysis and modeling. The reason why the SFDR was chosen instead of the maximal discharge, is that it allows the regionalization and mapping, since the discharges depend on the watershed area. The river maximal discharge (m3s-1) with the required exceedance probability is calculated as described in Shevnina et al. (2016).
The core of the MARCS hydrological model is the Pearson System, which allows to model the PDFs within 12 types depending on the values of the parameters. The four parameters of the Pearson system could be estimated from the sampled initial moments (Stuard and Ord 1994). On the other hand, the parameters of the Pearson system can be evaluated from the parameters of KBE (see details in Kovalenko 2014, Domínguez and Rivera 2010, Pugachev et al. 1974). In our study, the Pearson Type III distribution were used to model PDF of SFDR and to evaluate the maximal discharges with required exceedance probability, thus the parameter denoted as b 2 in Andreev et al. (2005) was equal to 0.
The future climatology can be evaluated from the historical and projected runs of any Atmosphere-Ocean General Circulation Model (AOCGM) from the collection of the Coupled Model Intercomparison Project Phase 5 (CMIP5, http://cmip-pcmdi.llnl.gov/cmip5). In the present study, the HadGEM2-ES climate model (Jones et al. 2011) was considered as an example. The projected mean values of the precipitation and air temperature for the period of 2010–2039 were used to force the MARCS model, and to simulate the probabilistic projections of the peak flow expressed though the PDF parameters of the spring flood depth of runoff. The model also allows calculating the maximal discharge of required exceedance probability at chosen site. In the present study the calculations was done for the Nadym River as described in Shevnina (2014).
In providing the practical example how the probabilistic projections of the peak flow can be applied in the economic, the evaluation of the total investments required for a new bridge was provided. In design of the hydraulic constructions the bridge height, type and costs are usually estimated using the peak flow discharges with particular exceedance probability (Megahan 1977, Guideline 1974). In this study the method to calculate the total investment to a bridge (P, ₽) from the Guideline (1974) was modified by including two components; the possible losses due to flooding during operational period (α, ₽) and the additional investment to a bridge allowing decreasing risks of damaging due to flooding during operational period (β, ₽) were added:

where K is the total building cost (₽); Э t is the cost during the operational period (₽); t is the duration of the operational period equal to 35 years; E is the coefficient of inflation (₽ per year). Both additional components (α and β) are connected to the risk of accident due to extreme flooding during the period of operation of a bridge (i.e. 2010–2039). In present study, extreme flooding was considered as increasing the river flow the maximal discharge of 1% exceedance probability evaluated from the observed time series (namely reference 100-year discharge, Q 1R ). In this study, the river maximal discharge of 1% exceedance probability (namely projected 100-year discharge, Q 1P ) was also evaluated from the MARCS model based on the RCP4.5 climate projection. Thus, there are two options to estimate the total investment to the bridge depending of the height of structure based on the reference or projected 100-year discharges.
Considering the case when the Q 1P is equal to Q 1R or less then Q 1R , the total investment (P 1 in Fig. 8.1) contains only two components (the building and operational costs, K 1 and Э t in Fig. 8.1). It is expected that the risks to get any losses connected to flooding during operational period are low (α=0) and there is no need for additional investments connected to the flood protection (β=0). In case when the Q 1P is larger then Q 1R, the risks to get temporal breaks in traffic or damage accident during a bridge operational period are also larger. In this case, the investment includes the expenses connected to an accident (P 2 in Fig. 8.1 in assumption that K, E and Э t are the same as in the previous case), and these losses are not equal to zero (α in Fig. 8.1). In this case, it is suggested to use the Q 1P to design of a bridge structure, then the additional costs (β in Fig. 8.1) are required. However these expenses may be less than losses due to the extreme flooding event. In this study, the total investments to the new bridge over the Nadym River at the Nadym City were calculated using reference and projected 100-year discharges. The total investments to the bridge (P 1 in Fig. 8.1) is equal to 14 milliards of rubles (see, www.finmarket.ru/news/4107593); in this study the additional components take amount of 10% and 2 % of K 1 for loses α and cost β respectively. The projected values of 100-year discharge were calculated based on the outputs of four climate models under RCP 4.5 for the period of 2010–2039.
The estimation of the total investment to a bridge construction by the Eq. (8.1)
3 Results and Discussion
To evaluate the long-term projections of floods over the Russian Arctic, the MARCS model were developed as the tool, and it now contained four blocks. The Data Preparation Block (DPB) implemented the tools to evaluate the reference climatology from the observations at weather stations or gridded datasets, and the projected climatology from climate model outputs using the delta correction method (Hamlet et al. 2010). To map the reference/projected climatology, the regularized spline with tension interpolation technique by Hofierka et al. (2002) was implemented. The DBP also included the procedures to calculate the SFDR using the observed daily river discharges (Shevnina 2013).
The Data Screening Block (DSB) contained the tools implementing the statistical screening for the absence of trends and the stability of variance and mean (Dahmen and Hall 1990). In the screening procedures, the time series were divided into two sub-series by known year, when a distortion of a natural regime is expected (i.e. due to building a reservoir, starting a water regulation, water withdrawals, etc). However, the year of subdivision is usually not known, thus two algorithms were implemented into the model. In the “floating point” technique, the yearly time series were divided into two sub-series, and the lengths of the sub-series were usually different. Therefore, the method suggested by Fagerland and Sandvik (2009) was implemented to evaluate the values of Fisher and Student Test for sub-samples with unequal sizes. The “floating period” technique of the time series division uses two sub-series with equal size and is described in details in Shevnina et al. (2016). The significance of trend and the stability of variance and mean were checked on the statistical level equal to 0.05 in both algorithms. The procedures to calculate the sampled initial statistical moments based homogeneous runoff/meteorological time series were also implemented into the DSB.
The Parametrization and Hindcasts Block (PHB) included the procedure to evaluate the MARCS model hindcasts based on the runoff PDF parameters for two time periods using a cross-validation technique (see details in Shevnina et al. 2016). Two parameterization schemes were implemented into the MPHB: the general parameterization scheme and the regional parameterization scheme. In general scheme, the model parameters are constant for the reference and projected time periods (Kovalenko 1993). The regional parameterization scheme incorporates the projected climatology into the model parameters (Shevnina 2011).
The Model Core Block (MCB) contained the procedures to calculate the parameters of runoff PDFs based on the projected climatology (see details in Kovalenko et al. 2010). The forcing variables are the projected mean values of the precipitation and air temperature, and the output variables are mean value, the coefficients of variation and skewness of the runoff. The procedure to calculate the peak flow discharges with required exceedance probability using the Pearson Type III distribution was also implemented in this block.
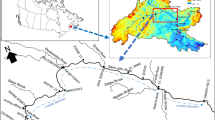
The Visualization and Analysis Block (VAB) contained the tools to map the projected the mean value and coefficient of variation, and the regions with substantial changes in the runoff statistics (and extremes) compared with the reference period. Figure 8.2 shows the regions with changes in the SFDR means (top) and in the coefficient of variation (bottom) for the territory of the Russian Arctic under RCP4.5 climate scenario. These regions were obtained by applying the thresholds of the simulation uncertainties (see Shevnina et al. 2016 for details). The yellow and red areas in Fig. 8.2 (top) indicate the regions, where the risk to get flooding increases in the future compared to the reference period. Thus, correcting for the maximal river discharges of small exceedance probability for the expected climate changes was suggested here to evaluate the total investment to the hydraulic structures. The Nadym River is located in the region with increase of the mean values of SPDR up to 15–30 %, according to RCP4.5 climate scenario (Fig. 8.2), and the projected value of 100 year maximal discharge is larger than the reference.
The regions with substantial changes in the future mean values of the spring flood depth of runoff (top) and coefficients of variation (bottom) of the spring flood depth of runoff over the Russian Arctic (red line outlines its boundary) according to RCP 4.5 climate scenario: HadGEM2-ES model (2010–2039)
The Economic Application Block (EAB) should be developed in the future and included the procedures to evaluate the economical values based on the runoff probabilistic projections. In this study, the algorithm to calculate the total investment to a new bridge was implemented (see section Data and Method) and was tested an example of the bridge over the Nadym River at the Nadym City (Shevnina 2014). The results show that the total investment to the Nadym River bridge could be less about 13 % in case of using the projected 100-year maximal discharges of 1% exceedance probability under the given assumption about the costs and losses in the Eq. 8.1. Using the climate-based projection of maximal runoff of the 1 % exceedance probability during the designing stage may lead to decrease of the total investment to the bridge construction over the Nadym River, which was already damaged by extremal flooding during the spring of 2016.
4 Conclusions
The main features of the MARCS model are (i) low numbers of the forcing and simulated variables (only the basic statistics of meteorological and hydrological variables are used); (ii) low numbers of the model parameters (the physical processes described integrally by the lumped model); (iii) the projected climatology is depicted by the model parameters, and it provides the way for developmet of the advanced regional-oriented parameterization schemes.
In this study, the MARCS model with the regional parameterization scheme was used to calculate the parameters of the SFDR PDFs over the Russian Arctic. However, the additional algorithms should be implemented to the model before developing regional-oriented schemes for the catchments located in the mid-latitudes. As the role of evaporation is more important in the general water balance on the south regions, this variable has to be considered (Kovalenko and Gaidukova 2011).
In this study, the MARCS model was forced by the outputs from the climate model with big spatial resolution, which is usually cause the challenges in the physically-based spatially distributed hydrological models. However, it seems to not be a big issue for the hydrological models such as the MARCS model. The physical core of the model is a lumped model in form of a linear filter with stochastic components (see Kovalenko 1993 for details). The role of spatial resolution in the datasets used to force the MARCS model and the options connected with the regional climate projections can be issues for future studies.
The vision for the future is changing continuously, and the set of climate change scenarios is renewed almost every 5 years since the meteorological models are improving unceasingly. The feature of the MARCS model is its general simplicity (only the projected statistics are evaluated instead of a time series), and is easy to perform for a regional scale assessment of the future water availability not only for an mean runoff value, but also for outliers (i.e for extreme hydrological events) under any chosen climate projection. These outliers are important for economists since they are usually the ones dealing with risks associated with weather/runoff extremes. The methods to evaluate the economic values from the outputs of the MARCS hydrological models are the topic of the future studies.
References
Andreev A, Kanto A, Malo P (2005) Simple approach for distribution selection in the Pearson System. Working paper of Helsinki School W-388. Helsinki
Archeimer B, Lindström G (2015) Climate impact on floods: changes in high flow in Sweden in the past and the future (1911–2100). Hydrol Earth Syst Sci 19(2):771–784
Bowles D (2001) Evaluation and use of risk estimates in Dam safety decision making. In: Risk-based decision making in water resources, IX. American Society of Civil Engineers, Reston, pp 17–32
Bulletin 17–B Guideline for determining flood flow frequency (1982) U.S. Geological Survey, Virginia, 72p
Butts MB, Payne JT, Kristensen M, Madsen H (2004) An evaluation of the impact of model structure on hydrological modeling uncertainty for streamflow simulation. J Hydrol 298(1–4):242–266
Calver A, Stewart E, Goodsel G (2009) Comparative analysis of statistical and catchment modeling approaches to river flood frequency estimation. J Flood Risk Manag 2:23–31
Catalogue of climatology of USSR Serie 3: multi-year data (1989) Gidrometeoizdat, Leningrad. (In Russian)
Dahmen ER, Hall MJ (1990) Screening of hydrological data: tests for stationarity and relative consistency. International Institute for Land Reclamation and Improvement, Dordrecht, 58p
Domínguez EK, Rivera H (2010) A Fokker–Planck–Kolmogorov equation approach for the monthly affluence forecast of Betania hydropower reservoir. J Hydroinf 12(4):486–501
Fagerland MW, Sandvik L (2009) Performance of five two-sample location tests for skewed distributions with unequal variances. Control Clin Trials 30:490–496
van Gender PHAJM, Vrijing JK (1997) A comparative study of different parameter estimation methods for statistical distribution functions in civil engineering applications. Struct Safety Reliability 1:665–668
Guideline on the economic calculations in construction and reconstruction of bridges VSN 2–73 (1974) The standards in building constraction, [online]. Available at: http://standartov.ru/norma_info/48/48033.htm. Accessed 1 Feb 2017. (in Russian)
Hamlet AF, Salathé EP, Carrasco P (2010) Statistical downscaling techniques for global climate model simulations of temperature and precipitation with application to water resources planning studies. Final Report for the Columbia Basin Climate Change Scenarios Project [online], 27 p. Available at: www.hydro.washington.edu/2860/products/sites/r7climate/study_report/ CBCCSP_chap4_gcm_final.pdf. Accessed 1 Feb 2017
Hofierka J, Parajka J, Mitasova H, Mitas L (2002) Multivariate interpolation of precipitation using regularized spline with tension. Trans GIS 6(2):135–150
Jones C, Hughes J, Bellouin N, Hardiman S, Jones G, Knight J, Liddicoat S, O’onnor F, Andres R, Bell C, Boo K, Bozzo A, Butchart N, Cadule P, Corbin K, Doutriaux-Boucher M, Friedlingstein P, Gornall J, Gray L, Halloran P, Hurtt G, Ingram W, Lamarque J, Law R, Meinshausen M, Osprey S, Palin E, Chini L, Raddatz T, Sanderson M, Sellar A, Schurer A, Valdes P, Wood N, Woodward S, Yoshioka M, Zerroukat M (2011) The HadGEM2-ES implementation of CMIP5 centennial simulations. Geosci Model Dev 4:543–570
Katz RW, Parlange MB, Naveau P (2002) Statistic of extremes in hydrology. Adv Water Resour 25(8-12):1287–1304
Kovalenko VV (1993) Modeling of hydrological processes. Gidrometizdat, Sankt-Peterburg, 178p. (in Russian)
Kovalenko VV (2014) Using a probability model for steady long-term estimation of modal values of long-term river runoff characteristics. Russ Meteorol Hydrol 39(1):57–62
Kovalenko VV, Gaidukova EV (2011) Influence of climatological norms of the surface air temperature on the fractal dimensionality of the series of long-term river discharge. Dokl Earth Sci 439(2):1183–1185
Kovalenko V, Victorova N, Gaydukova E, Gromova M, Khaustov V, Shevnina E (2010) Guidelines on robust runoff estimation for projected hydraulic structures under non-steady climate. RSHU Publishing Co, St. Petersburg, 51 p. (in Russian)
Lawrence D, Haddeland I (2011) Uncertainty in hydrological modeling of climate change impacts in four Norwegian catchments. Hydrol Res 42(6):457–471
Madsen H, Lawrence D, Lang M, Martinkova M, Kjeldsen TR (2013) A review of applied methods in Europe for flood-frequency analysis in a changing environment. NERC/Centre for Ecology & Hydrology on behalf of COST, [online]. Available at: http://nora.nerc.ac.uk/501751/. Accessed 2 Feb 2017
Megahan WF (1977) Reducing erosional impacts of roads. In: Guidelines for watershed management. Food and Agriculture Organization, United Nations, Rome, pp 237–261
Pachauri RK, Reisinger A (eds) (2007) Synthesis report, contribution of working groups I, II and III to the fourth assessment report of the Intergovernmental Panel on Climate Change. IPCC, Geneva https://www.ipcc.ch/publications_and_data_publications_ipcc_fourth_assessment_report_synthesis_report.htm. Accessed 2 Feb 2017
Pilgrim DH, Cordery I (1975) Rainfal temporal patterns design floods. J Hydraul Div 101(1):81–95
Pugachev VS, Kazakov IE, Evlanov LG (1974) Basics of statistical theory of automatic system. Mashinostroenie, Moscow, 400 p
Radionov VF, Fetterer F (2003) Meteorological data from the Russian Arctic 1961–2000. National Snow and Ice Data Center, Boulder, [online]. Available at: http://nsidc.org/data/docs/noaa/g02141_esdimmet/. Accessed 2 Feb 2017
Scott G (2011) The practical application of risk assessment to dam safety. Geo-Risk 2011:129–168
Shevnina E (2011) Parametrization of the probabilistic model to evaluate multi-year statistics of spring flow depth of runoff over the territory of the Russian Arctic. Scient Notes Russian State Hydrometeorol Univ 21:38–46. (in Russian)
Shevnina E (2013) Algorithm to calculate spring flood characteristics from daily discharges. Probl Arctic Antarctic 1(95):44–50. (in Russian)
Shevnina E (2014) Changes of maximal runoff regime in the Arctic. Const Unique Build Struct 7(22):128–141. (in Russian)
Shevnina E, Kourzeneva E, Kovalenko V, Vihma T (2016) Assessment of extreme flood events in changing climate for a long-term planning of socio-economic infrastructure in the Russian Arctic. Hydrological Earth System Science,doi: 10.5194/hess-2015-504, discussion paper (in review)
SP 33-101-2003 Guideline to estimate basic hydrological characteristics (2004) Gosstroy, Moscow, 234 p. (in Russian)
Stuart A, Ord J (1994) Kendall’s advance theory of statistics, Distribution theory, vol 1. Edward Arnold, London
Verzano K (2009) Climate change impacts on flood related hydrological processes: further development and application of a global scale hydrological model, Reports on Earth system science 71. Max Planck Institute for Meteorology, Hamburg, 198 p
Viktorova NV, Gromova MN (2008) Long-term forecasting of characteristics of minimal river runoff discharges in Russia in case of possible climate change. Russ Meteorol Hydrol 33(6):388–393
Willmott CJ, Matsuura K (2001) Terrestrial air temperature and precipitation: monthly and annual time series, [online]. Available at: http://climate.geog.udel.edu/~climate/html_pages/README.ghcn_ts2.html. Accessed 2 Feb 2017
Zwillinger D, Kokoska S (2000) CRC standard probability and statistics tables and formulas. Chapman & Hall, New York
Acknowledgments
The study was supported by the Academy of Finland (contract 283101, project TWASE) and by the Ministry of Science and Education of the Russian Federation (contract 01 2014 58678).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2017 The Author(s)
About this chapter
Cite this chapter
Shevnina, E., Gaidukova, E. (2017). Hydrological Probabilistic Model MARCS and Its Application to Simulate the Probability Density Functions of Multi-year Maximal Runoff: The Russian Arctic as a Case of Study. In: Latola, K., Savela, H. (eds) The Interconnected Arctic — UArctic Congress 2016. Springer Polar Sciences. Springer, Cham. https://doi.org/10.1007/978-3-319-57532-2_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-57532-2_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-57531-5
Online ISBN: 978-3-319-57532-2
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)