Keywords

Introduction

Like roads, railroads affect wildlife through direct mortality, habitat loss and habitat fragmentation (van der Grift 1999; Forman et al. 2003; Davenport and Davenport 2006). Direct mortalities result when trains strike wildlife. Strikes can be a significant source of mortality for some wildlife populations and have been reported for decades (Child 1983; Gundersen et al. 1998; Bertch and Gibeau 2010a). Studies have reported strike rates for large mammals such as grizzly bears (Ursus arctos) (Bertch and Gibeau 2010a, b) and moose (Alces alces) (Child 1983, 1991; Modafferi 1991).

In Canada’s Rocky Mountain National Parks, train strikes are a leading source of mortality for grizzly bears (0.35 year−1) and black bears (1.95 year−1), and the second largest source of mortality for deer (Odocoileus spp.), elk (Cervus elaphus) and moose (Bertch and Gibeau 2010a, b) in the Banff and Yoho National Parks. It is likely that true mortality rates due to train strikes are higher than reported. For example, as few as 50% of strikes with large mammals were reported by standard observers (train engineers) along the Canadian Pacific Railroad (CPR) during a six-year period (Wells et al. 1999). In other cases, strikes may not be reported except when large groups (>450) of wildlife are killed (Chaney 2011) or when strikes occur within protected areas (Waller and Servheen 2005). Long-term data of train strikes along the CPR exist because strikes have been reported to Parks Canada for at least 30 years. However, other railroads may not report or record strikes with such consistency.

Studies on roads have analyzed the spatial pattern of road-kills, which showed that these occurred in clusters (Finder et al. 1999; Clevenger et al. 2003; Malo et al. 2004). The spatial pattern of road-kills has been explained by landscape, environmental and infrastructure variables (Finder et al. 1999; Hubbard and Danielson 2000; Gunson et al. 2006; Kassar 2005). These studies have helped inform management actions targeted at reducing road-kills (Clevenger et al. 2001; Grilo et al. 2009). At least five general factors are thought to affect the spatial pattern of road-kills and train strikes (Seiler and Helldin 2006). Along railroads, these include: animal (e.g., wildlife abundance and behavior); train (e.g., train speed and frequency); railroad design (e.g., curvature or alignment); and landscape (e.g., vegetation type) variables (Huber et al. 1998; Bashore et al. 1985; Finder et al. 1999; Seiler and Helldin 2006). Driver behavior variables are largely removed from train strike analyses because trains generally cannot stop or swerve to avoid animals.

Landscape variables derived from land cover data have been found to be the best predictors of road-kill rates (Bashore et al. 1985; Finder et al. 1999; Roger and Ramp 2009). We suggest that estimates of relative abundance be used to assess the spatial pattern of road-kills and train strikes. The importance of including wildlife abundance in the analysis of factors contributing to wildlife strikes was demonstrated for moose: strikes coincided with locations of high moose abundance in wintering areas and on migration routes (Gundersen et al. 1998; Ito et al. 2008). Train variables and railroad design, as well as animal abundance, vary along the CPR and may also affect strike rates. If train or railroad variables altered the probability of a strike, the rate of strikes would vary spatially along with differences in these variables, even if wildlife abundance were constant. There are at least three theoretical mechanisms that could alter the spatial probability of strike occurrence. These mechanisms, based on wildlife behavior are: (1) constrained flight paths—some design features, such as bridges, may restrict wildlife movements on the rail bed surface instead of out of the path of oncoming trains; (2) reduced detectability—some design features may impede the sight and/or sound of oncoming trains, so that wildlife are less likely to detect trains resulting in increased strike rates; and (3) reduced reaction time—higher train speeds may reduce the time available to wildlife to successfully cross or flee before being struck. These mechanisms likely interact. For example, with increasing train speeds both the time to detect and flee may be reduced.

There is evidence that these mechanisms affect the rate of train strikes with ungulates and bears along railroads. Previous studies have shown that bears were struck at bridges and rock cuts (constrained flight paths) and in locations where the sound of oncoming trains was reduced (reduced detectability) (Van Why and Chamberlain 2003; Kaczensky et al. 2003). Moose have been observed to not flee off the railroad tracks in Alaska, with the suggestion that deep snow alongside the railroad restricted their ability to flee down the track (Andersen et al. 1991; Modafferi 1991). Similarly for bears, engine-mounted video footage suggested that some bears were struck while fleeing from trains where track-side slopes or other design variables appeared to obligate flight paths on the tracks instead of off and out of danger. Other associations are unclear, for example bighorn sheep (Ovis canadensis) strikes have been associated with rock cuts and may be a result of fine-scale habitat selection or multiple design mechanisms acting concurrently (Van Tighem 1981). As a result, it may be difficult to determine the exact mechanism(s) driving strike rates. However, identifying the animal, train or railroad variables associated with strikes and the direction of the effect (e.g., increased mortality at a particular design feature) may be a more tractable approach and could indicate ways to reduce strikes along the CPR and railways more broadly.

The purpose of this research was to identify locations where species-specific mitigation solutions are needed, and to identify the variables associated with those locations along the CPR. Four ungulate species (elk, mule deer [Odocoileus hemionus], white-tailed deer [O. virginianus] and two bear species (grizzly and black bear) were used for this analysis). We tested whether strike rates were correlated with the relative abundance and nine railway variables that could alter the flight path, detectability or reaction time of animals present.

Methods

Study Area

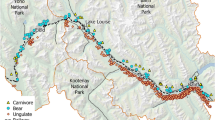
The study was conducted along a 134 km section of the CPR running from the western boundary of Yoho National Park, British Columbia (116° 39′W, 51° 14′N) to the eastern boundary of Banff National Park, Alberta (115° 25′W, 51° 8′N) (Fig. 9.1). An average of 19 trains a day−1 pass through the study area at an average speed of 60 km h−1. The Trans-Canada Highway runs parallel to the CPR throughout the study area, on average 416 m (±325 m) away. To prevent wildlife-vehicle collisions, there is a 2.4 m high wildlife exclusion fence along the highway for 48 km, starting at the eastern border of the study area (Clevenger et al. 2001). There were 27 wildlife crossing structures over or under the highway at the time of this study, one of the structures was a shared wildlife crossing and railroad underpass. An additional section of fencing (28 km) was completed in 2010 along with wildlife crossing structures and a shared wildlife railroad underpass (Clevenger et al. 2009).

Fig. 9.1
figure 1

Map of the 134 km of the Canadian Pacific Railroad study area that traverses the Banff and Yoho National Parks in the Canadian Rocky Mountains. Each analysis segment (4.86 km) is shown denoted by a small perpendicular bar along the railroad. Segments with high strike risk are labeled for (E) elk, (D) deer, and (B) bears during the 21-year period (1989–2009) along the Canadian Pacific Railroad through the Banff and Yoho National Parks

Full size image

The CPR crosses the Western Continental Divide at 1670 m above sea level 9.0 km west of Lake Louise, Alberta. The CPR consists of one track except for an 8.3 km long section near Lake Louise, where two tracks diverge to a maximum of 500 m. Due to large elevation gradients in the area (>2,000 m), a number of different vegetation types exist, and the average annual rainfall decreases from west to east. Approximately 39% of the land area in Banff and Yoho National Parks is at or above tree line (~2,300 m). Where vegetation was present, it consisted of closed and open canopy forest, dominated by lodgepole pine (Pinus contorta), white spruce (Picea glauca), and subalpine fir (Abies lasiocarpa) (Holland and Coen 1983). Vegetation within the CPR right-of-way (ROW) was kept in an early successional stage by mechanical treatments and consisted primarily of herbaceous vegetation (grasses, sedges and rushes), dandelions (Taraxacum spp.), bearberry (Arctostaphylos uva-ursi) and horsetail (Equisetum spp.). Numerous species of shrub including buffaloberry (Sheperdia canadensis) and tree species including lodgepole pine and white fir were present at reduced heights (<2 m). Vegetation between the rails was almost non-existent due to herbicide treatments and the rocky substrate. Where there was vegetation between the rails there was small herbaceous growth of native and non-native grasses or young sprouts of train-spilled agricultural products (cereal grains).

Data Collected

Wildlife Strike Records

Counts of train-struck ungulates and bears were obtained from Parks Canada for a 21-year period (1989–2009) (Parks Canada, unpublished data, 2010). These records included all strikes reported by CPR and Parks Canada personnel. Strikes were visited and removed only by Parks Canada personnel to avoid double counting. Records after 2001 were spatially referenced with a Garmin® global positioning system (GPS), but before 2001, records were referenced to permanent mile-marker posts or to geographic features along the CPR. As a result some strike records were spatially inaccurate by as much as 1.6 km (1.0 mile); thus, an error of plus or minus 1.6 km was assumed for all records. A spatial data layer representing the railroad was acquired from CPR and then imported into a geographic information system (GIS). The spatial layer was separated into 30 roughly equal segments 4.86 km (3 miles) in long. The segment length was based on a conservative estimate of the minimum mapping accuracy of the wildlife strike records, which were tallied to the appropriate 4.86 km (3 mile) segment in a GIS.

Relative Abundance Data

Relative abundance data were collected by sampling transects oriented parallel and perpendicular to the CPR (hereinafter called “rail bed transects” and “perpendicular transects,” respectively). Both methods were binned to 4.86 km long rail segments, ensuring that data were analyzed at the same spatial scale. Sampling was carried during the summers of 2008–2009 by the same observer. A total of 313 km of rail bed transects and 129 perpendicular transects were surveyed in 2008 and 2009.

The relative abundance of bears was sampled using both methods. However, ungulates were sampled only using perpendicular transects that allowed for an accurate representation of ungulate distribution throughout the year.

Parallel transects were centered directly on the rail bed. Segments were treated as a strip transect 3 m wide and 4.86 km long. Locations of bear scats were recorded using a GPS unit (Trimble Navigation Ltd., Sunnyvale, USA). Black and grizzly bear scats were classified as “bear” because they could not be differentiated in the field. When the diameter, age and contents were visibly similar for scats found within 5 m, only one scat was recorded. All scats detected were removed from the CPR to avoid double counting. Where multiple tracks were encountered, e.g., sidings, all tracks were surveyed and the mean number of scats detected per track was used in the analysis.

Perpendicular transects were used to estimate relative abundance for bears and ungulates within the railroad corridor (<250 m). Two random points were generated within each rail segment in a GIS for each sampling year. Each point was used as the starting location for a perpendicular transect. At each point, a transect extended out perpendicularly away from the CPR in both directions for 250 m; the transects were 3 m wide. Pellet groups and scat found more than 1.5 m from the transect center were not recorded. Perpendicular transects were truncated at the edge of impassable features such as rock cliffs, rivers and open water. Along each transect ungulate pellet groups were classified into those of elk or deer based on differences in size and shaped as described by Elbroch (2003). White-tailed deer and mule deer pellets were combined into one class of “deer” because they could not be reliably differentiated in the field. The number of pellet groups was counted for each transect. Bear scats were recorded using the same criteria as the rail bed transects. Pellets and scat that appeared to be more than a year old-based on visible signs of decay (bleached color or unconsolidated) were excluded as were amorphous ungulate or bear feces (Elbroch 2003).

The count of bear scats were weighted based on the date they were detected, as they are detectable throughout the short summer season (Dorsey 2011). The first day that bears have been historically sighted in the study area is April 15; although the date of bears’ emergence varies each year, it was used as a starting date for when bears could have been foraging on grain and left scats. As each day passed after April 15, there were cumulatively more days when bears could have visited and left scats. Therefore, each scat was given a weight inversely proportional to the day of year it was detected after April 15, which is the 105th Julian calendar day of the year. For example, the weighted value of one scat detected on September 13th, (day 273 of the year) would be ((273–105)−1 = 0.006). The final value was the sum of all weighted scats detected for each track segment stored as RArail bed.

The relative abundance for each species was defined as the number of pellet groups or weighted value km−1 within each 4.86 km long segment (i) (Eq. 1). For example, the relative abundance of elk, RArail corridor (i) was the number of elk pellet groups km−1 averaged over n transects (t) within each rail segment (i).

$$RA_{rail\,corridor} \left( i \right) = \frac{{\sum {\left( {\frac{{pellet\,groups_{t} }}{{transect\,length_{t} }}} \right)} *1000}}{{\mathop \sum \nolimits_{t = 1}^{n} t}}$$
(1)

Railroad Design and Train Spill Grain Data

Three additional variables were measured at the starting location of each perpendicular transect. The mean right-of-way width (ROWmean) was measured using a Bushnell® Yardage Pro® 1,000 range finder (Bushnell Corporation, Denver, CO), which extended to the forest edge or open water. A maximum distance of 500 m was imposed in locations where open habitat and level ground resulted in an unidentifiable ROW corridor. Topography adjacent to the railroad was classified into three categories similar to those used to assess wildlife-vehicle collisions on the parallel Trans-Canada Highway (Clevenger et al. 2003; Gunson et al. 2006) (VERGESLOPE): (0) flat; (1) raised and partly raised; and (2) buried, buried-raised, and partly buried. Train-spilled grain was also measured at each transect starting location on the rail bed. Grain density was estimated visually by counting the wheat and barley seeds inside a frame (10 cm2) placed randomly on the rail bed three times within a 5 m segment of track (Fig. 9.2). The sampling process was repeated for each track where sidings were present. Grain density was calculated as the average of all subsamples within a rail segment (GRAINmean); the density was affected by the date it was measured because grain spill decreased over the course of a summer (Dorsey 2011). Therefore, grain density was weighted by the week of year it was measured. For both years, the weighted value was calculated as the mean seed count multiplied by the average rate of decrease (3%) for each additional week after April 15th (data not shown). For example, a weighted seed count of 80 wheat and barley seeds measured on June 20th (4 weeks after April 15th) was [80 × (0.97 × 4) = 310.4]. The grain density data were binned to the appropriate 4.86 km long segment in a GIS.

Fig. 9.2
figure 2

Grain spill sampling method used on the rail bed. The sampling frame (10 × 10 cm2), was randomly thrown three times to estimate the mean density of wheat and barley seeds within a 5 m zone

Full size image

The GIS layer representing the railroad contained additional information on train speed limits, bridges, sidings and track grades. The highest posted train speed limit (SPEEDmax) and mean track grade (GRADEmean) were calculated for each segment. The variable SINUOSITY was calculated using the “sinuosity” function in Hawth’s analysis tools extension for ArcGIS 9 (ESRI Redlands, CA 2004). The number of bridges were counted and summed for the variable, hereinafter termed “BRIDGEc”. A count of vehicle overpasses, tunnels, snow sheds or rock cuts occurring along each segment were each given a value of “1” and summed for the variable hereinafter called “BARRIERc”. The lengths of track inside two tunnels and one secondary track west of Lake Louise were omitted from analyses; in all, 28 segments were used in the analysis.

Data Analysis

Analyses were conducted independently for elk, deer and bears. Strikes that occurred over the 21-year period were compared to relative abundance estimated using data covering a 2-year period (2008 and 2009). This comparison assumes that relative abundance across the study area remained relatively stable during the preceding years. To assess this assumption, we looked for changes in the distribution of strikes over time. A better approach would be to assess changes in relative abundance over time, but these data were not available for enough of the study area or species. Changes in the distribution of strikes over time were assessed by conducting ANOVA on year and rail segments. More variability in year than rail segment may mean that substantial shifts occurred in the relative abundance, therby invalidating further analysis. Next, to determine if strikes and/or wildlife abundance were evenly distributed along the CPR, chi-squared tests were used. To identify hotspots the upper 95% confidence interval of strikes per segment was used, which assumed that the counts followed a Poisson distribution (Bivand et al. 2008; Malo et al. 2004).

Risk estimates for each rail segment were developed through three steps. First, the RArail corridor or RArail bed estimates for each segment (i) were converted to a percentage of the total from all rail segments. Next, the expected number of strikes for each rail segment (Expected(i)) was calculated by multiplying the percent of total scat on that segment by the overall mortality rate for that species (Eq. 2).

$$Expected_{i} = \frac{{\sum {STRIKES_{i} } }}{{\sum {RA_{{rail\,corridor_{i} }} } }}*RA_{{rail\,corridor_{i} }}$$
(2)

Risk was estimated by assessing the ratio of the number of strikes to the expected number of strikes for each segment (Eq. 3). Both values were assumed to equal at least 1.0 for all rail segments because all species are included in the study area. In cases where no strikes or no pellets were detected the risk estimate was set to 1.0 without confidence intervals. Otherwise the risk estimate would have equaled zero or infinity in these cases.

$$Risk_{i} = \frac{{Strikes_{i} }}{{Expected_{i} }}$$
(3)

The risk estimate, evaluates relative risk between segments. It has been widely used in spatial epidemiology studies and is referred to as a standardized mortality ratio where the ratio is expected to equal 1.0 because internal standardization was used (Mantel and Haenszel 2004; Banerjee et al. 2004; Bivand et al. 2008). In these data, the average risk (risk = 1.0) meant that the number of strikes was proportional to the relative abundance for that species. When the estimated ratio was above 1.0 it indicated relatively high risk (more strikes occurred than expected). Internal standardization reduced the number of degrees of freedom to n − 1 which was used in chi-squared tests (Kim and Wakefield 2010).

To test for non-constant risk, the number of strikes observed was compared to the number expected using χ 2 tests (Bivand et al. 2008) and the relationship between observed and expected was evaluated with generalized linear models assuming a Poisson count distribution and a log link function. To determine which sections had an unusually high risk, a bootstrap function was used to resample the wildlife abundance estimates from scat counts for each rail segment. A new relative risk estimate was computed for each of 1,000 resampled abundance estimates; then confidence intervals were assessed from the distribution of the 1,000 estimates. High-risk segments were defined as those where 95% of bootstrapped estimates of risk were above 1.0. All analyses were performed in R (R Development Core Team 2009).

A set of variables hypothesized to affect train strikes were tested using generalized linear mixed models with a log link function (Table 9.1). Models were evaluated for each species by fitting the count of strikes per segment (summed over the 21-year period) to 10 predictors, including the appropriate wildlife abundance estimate (which included two for bears, due to evaluation at the rail bed and landscape scales). Initial fits used restricted maximum likelihood estimation and likelihood ratio tests to assess whether a negative binomial distribution was needed (Zuur et al. 2009). Each model was subjected to a “drop one approach,” where the least significant parameter was dropped until all remaining parameters were significant. If models were reduced to a single predictor, the model with the minimal residual deviance was selected as the final model. Final models were refit with maximum likelihood and inspected using standard diagnostic plots. Semivariograms and residuals from the final model were plotted to assess the remaining spatial trends. Prior to performing the analysis, co-variates were tested for collinearity (Menard 1995). When correlated variables (r > 0.6) were found, the one with a higher correlation to the response remained in the analysis (Guisan and Zimmermann 2000). Based on this cut-off, track grade was significantly correlated with train speed and was removed from the analysis.

Table 9.1 Description of field-collected and GIS-derived spatially varying train and railroad design variables and the hypothesized correlation to strike rates
Full size table

Results

Strike Rates

Over the 21-year period (1989–2009), 862 strikes were recorded along 134 km of the CPR, consisting of 579 elk, 185 deer, 69 black bears, 9 grizzly bears, and 1 unidentified bear species. The bear data were combined into one class for further analysis. The spatial distribution of strikes per rail segment were non-uniform for elk χ 2(1, 27) = 834.4, p < 0.001, deer χ 2(1, 27) = 252.5, p < 0.001, and bears χ 2(1, 27) = 37.1, p = 0.03 (Fig. 9.3).

Fig. 9.3
figure 3

The number of train strikes (white bars) for a elk; b deer; and c bear, compared to the expected number of strikes (gray bars, a positive value) based on the abundance of wildlife signs along each 4.86 km segment using perpendicular transects; d compares on-track relative abundance for bears to number of strikes. Hotspots are segments with a strike count above the 95% confidence interval (gray dashed line) and high-risk segments are those with a risk estimate significantly above 1.0 (black points and error bars). Gray points are risk estimates not significantly different from 1.0 (the number killed was close to the number expected based on wildlife abundance). Segments proceed west to east, where 0 is the first 4.86 km inside the western boundary of Yoho National Park. The field town site is located at segment 6, the Lake Louise town site corresponds to segment 13, and the Banff town site segment 24

Full size image

The strike rates also varied temporally for elk, deer, and bears (Fig. 9.4). A decreasing trend was detected for elk strikes [βelk = −1.04, t(19) = −2.29, p = 0.03], and conversely an increasing trend for deer [βdeer = 1.13, t(19) = 8.18, p < 0.001] and bears [βbear = 1.12, t(19) = 4.58, p < 0.001] over the 21-year period. Although annual mortality rates fluctuated for all three species, the spatial distribution of strikes accounted for more of the variability in strikes for both elk and bear, but not for deer (Table 9.2).

Fig. 9.4
figure 4

Annual train strikes for a elk, b deer and c bears along 134 km of the Canadian Pacific Railroad through the Banff and Yoho National Parks, 1989–2009

Full size image
Table 9.2 Variation between years and railroad segments for (a) elk, (b) deer, and (c) bears along the Canadian Pacific Railroad within the Banff and Yoho National Parks, 1989–2009
Full size table

Relative Abundance

A total of 341 bear scats were detected on the CPR, resulting in a detection rate of 0.46 km−1 year−1. On perpendicular transects, 599 elk pellet groups (5.98 km−1 year−1), 212 deer pellet groups (2.23 km−1 year−1), and 39 bear scats (0.33 km−1 year−1) were detected. Relative abundance varied for elk [χ 2(27) = 940.12, p < 0.001] and deer [χ 2(27) = 294.2, p < 0.001]. Bear scats were unevenly distributed both on the rail bed [χ 2(27) = 263.3, p < 0.001] and on perpendicular transects [χ 2(27) = 125.4, p < 0.001] (Fig. 9.3c, d). The rail bed transects likely better represented relative risk for bears, because few bear scats were detected along the perpendicular transects (n = 39) relative to the 341 scats detected directly on the rail bed (Fig. 9.3d). Therefore, further analyses for bears were based on rail bed scats.

Hotspots and Relative Risk

Six elk hotspots were identified (21% of the CPR segments), which were segments with 29 or more strikes (Fig. 9.3a). Likewise, five deer hotspots (17% of the CPR segments) were identified, which averaged 6.54 ± 1.73 per segment (Fig. 9.3b). Bears were struck on average 2.86 ± 0.44 per segment, but no segment was identified as a hotspot because no single segment incurred more than seven strikes.

After estimating the ratio of strikes to wildlife abundance for each segment, overall non-constant risk was apparent for elk (χ 2 = 286.1, df = 27; p < 0.0001), deer (χ 2 = 182.0, df = 27; p < 0.0001), and bears (χ 2 = 7.4 × 106, df = 27; p < 0.0001). High-risk segments were identified for each species (Figs. 9.1 and 9.3). Five, two and six high-risk segments were determined for elk, deer and bears, respectively, and hotspots and high-risk segments differed in number and location (Fig. 9.3).

Variables Associated with Strikes

The variability in train strikes to relative abundance and nine train or railroad design variables (Table 9.1) indicated a negative binomial distribution for all species models. Initial models did not indicate that autocorrelation was present between rail segments and the most parsimonious models are reported (Table 9.3).

Table 9.3 Significant (p < 0.05) parameter estimates explaining train strike rates with elk, deer, and bears
Full size table

Elk

Train speed and relative abundance explained the variability in elk strikes (Log likelihood = −113.0 with 2 df, χ 2 = 26.3, p < 0.001). Elk strikes increased on average e0.07 = 1.07 per segment, with each 1.0 mph increase in maximum posted train speed when elk relative abundance was held constant (Table 9.3). Likewise when the SPEEDmax was held constant strikes increased e0.03 = 1.03 for each one unit increase in elk RArail corridor. The variable SPEEDmax averaged 37.5 ± 1.85 mph (60.3 kmph) and ranged from 20 to 50 mph.

Deer

The variables deer relative abundance (RArail corridor), SPEEDmax and ROWmean best explained the variability in deer strikes using the model selection process (Log likelihood = −78.46 with 5 df, χ 2 = 48.89, p < 0.001). The parameter coefficients from a maximum likelihood fit indicated that e0.06 = 1.06 additional deer strikes were observed on average with an 1.0 mph increase in the posted train speed limit when deer abundance and ROW width were held constant. Likewise, e0.009 = 1.009 additional deer strikes were observed for each 1.0 m increase in ROW width when speed and deer abundance were held constant. The variable ROWmean was on average 79.78 ± 7.68 m across all segments.

Bears

A single predictor model, including the variable BARRIERc, best explained bear strikes (Log likelihood = −57.233 on 4 df, χ 2 = 14.686, p < 0.001). The parameter estimated for BARRIERc (βbarrier = e0.458 = 1.58) revealed that for each additional barrier feature per segment bear strikes increased on average 1.58 (95% CI 1.13 to 2.20) (Table 9.3). A second single predictor model has almost equal explanatory power. This model included the variable BRIDGEc. However, BRIDGEc and BARRIERc were not correlated (r = 0.23, t = 1.1968, df = 26, p = 0.24). The variable BRIDGEc was positively correlated to bear strikes (r = 0.44, p < 0.02).

For bears, neither estimate of relative abundance was significant; therefore, the final model did not include either variable describing bears relative abundance. This changes the modeling results from assessing risk to incidence rate. For this reason, the model selection procedure was repeated with the variable RArail bed log transformed and held in the model as an offset to assess relative risk (Zuur et al. 2009). This model selection procedure resulted in a single predictor model that included SPEEDmax, indicating that as posted train speed increased, so did the “risk” of bear strikes (β = e0.053 = 1.054). However, train speed explained only 17% of the deviance, compared to 82% explained by the BARRIERc model (Table 9.3).

Discussion

This study is the first attempt to account for unevenly distributed wildlife populations when assessing strikes along a railroad; its information was used to help understand the spatial pattern of train strikes along the CPR. Hotspots were segments of the CPR that had strike rates significantly higher than the overall mean, and were identified for elk and deer, but not bears. Hotspots were generally associated with higher relative abundance for elk and deer at the analysis scale (3 miles). Although there was disagreement between bears’ relative abundance and strike rates at this scale (Fig. 9.3c, d), general correlation was apparent at a larger scale. For example, bear strikes and relative abundance were relatively higher in the western half of the study area (Fig. 9.3d segments 0–3), compared to the eastern half (Fig. 9.3d segments 14–27). High-risk segments had significantly higher kill rates than expected, based on estimates of relative wildlife abundance, and they indicated potential problem areas that may have been overlooked using strike data alone.

There was a significant relationship for elk, deer and bears with at least one train or railroad design variable. These relationships indicated higher abundance and train speeds (elk and deer), and larger right-of-way widths (deer) were associated with increased strike rates. For bears, the number of barriers and presence of bridges was also positively correlated with strike rates. These results supported the hypothesis that there are at least three general variables that affect the spatial pattern of train strikes: 1) the relative abundance of wildlife either on the rail bed or on the adjacent landscape; 2) train speed; and 3) railroad designs such as highway overpasses, rock-cuts, tunnels, snow sheds and bridges. Other railroad studies have shown similar associations with bears. In Slovenia, Eurasian brown bears (U. arctos) were struck at rock cuts and on bridges (Kaczensky et al. 2003). At least one road study has noted the effect of bridges on strikes with bears (Van Why and Chamberlain 2003). Huber et al. (1998) studied locations where brown bears were struck by trains in Croatia, and used variables similar to those of this study. They found no difference in verge slope or longitudinal or perpendicular visibility but did detect a difference in the presence of bear foods at strike locations compared to random locations. They noted a slight difference in the distance at which trains were first audible at strike locations (Huber et al. 1998). Data on train noise was not collected in this study, but field observations suggested that train volume varied depending on train direction within the study area, and the direction in which the trains were moving when each animal was struck was not recorded.

There are at least four possible explanations for the lack of correlation between bear strikes and relative abundance found in this study. The first is based on the strength of non-constant risk phenomena, and three others deal with limitations of the methods and analysis. First, railroad design or other variables may have strongly affected strike probabilities. If these variables had strong causal or probabilistic effects, the spatial pattern of strikes would be a function of the spatial pattern of these variables and not the bears’ relative abundance. However, it is unclear whether this is the case because the sample size is relatively low (n = 80) and no validation of these results has been attempted. Therefore, other explanations for the lack of agreement between strikes and bears’ relative abundance could be due to the field and/or analysis methods used. The survey design has been shown to affect the estimation of roadkill hotspots for small-bodied species (Santos et al. 2015).

The field data collected may have failed to adequately represent the true distribution of bears along the CPR, since bears may have been moving or utilizing the railroad without leaving scat, which would have been undetectable using these methods. Additionally, scat sampling methods may have only represented animals that regularly encountered the CPR and have learned to coexist, to some degree, with the railroad. Bears that utilized grain as a food item in this study area may have developed behaviors that allowed them to forage on grain with reduced strike risk (learned behavior). Lastly, the analysis scale may have been too small or too large. Bears have been documented to have large home ranges thus a larger analysis scale may have been more appropriate. General large-scale agreement between relative abundance and strikes are apparent in Fig. 9.3d. However, it may be difficult to implement management solutions at this scale other than those generally aimed at population distribution, size, or health.

Similarly, the data collected may have failed to fully describe the deer distribution. This may have been why right-of-way width (ROW-width) was positively correlated to strikes for deer. The hypothesized influence of ROW width was that narrower ROW’s (a negative relationship) would increase strike risk to wildlife. This variable may have accounted for spatial or temporal variability in deer abundance that the transect data failed to capture.

An animal’s behavior when a strike occurs is only partially influenced by location-specific variables. Other variables that are likely to affect an animal’s behavior are difficult to measure over long periods of time and large geographic areas. These variables include: fine-scale temporal variables and behavioral heterogeneity between individual animals. For this study, strikes spanning 21 years was used to provide adequate sample sizes for comparison to railroad variables that have not changed during that time; however, it is clear that strikes have changed over this period (Fig. 9.4), and thus relative abundance may have also changed during this period. To address this concern, analyses were repeated using a 10 year period. Results showed some shifts in the locations of hotspots and high-risk segments, but they these did not alter the general conclusions. The longer term 21-year analysis was likely better because of the larger sample size, which provided more information for hotspots, multivariate modeling, and more stable risk estimates.

Management Implications

This study found the wildlife abundance, train speed, barriers, bridges, and right-of-way widths affect strike rates for ungulates and/or bears. Based on these results, a variety of approaches could be used to reduce strike rates. These include those that affect wildlife abundance near railroads, reduced train speeds, or modified railway designs. Much of the CPR is co-aligned with a productive montane habitat, hence altering the abundance of deer or other species near the CPR may not be feasible. A two- step approach may be needed that both reduces forage quality and availability along the CPR and increases habitat quality away from it.

Two studies have documented a decrease in strike rates for moose (Jaren et al. 1991; Andreassen et al. 2005). One developed ungulate habitat away from a railroad (Jaren et al. 1991), and the other both modified habitat and provided supplemental forage away from the railroad (Andreassen et al. 2005). The feasibility of such an approach will be site-specific, but is likely to be beneficial to large mammal populations.

Train speed was also clearly important. Reduced train speeds may be an effective measure to reduce strike risk, particularly in problem areas. Train speed is a spatially and temporally explicit management solution, and likely interacts with the other mechanisms described above; thus, it could be implemented where or when strikes are most likely to occur. However, reduced speeds may be ineffective if other mechanisms are the primary driver in strike occurrences. For example, a study in Alaska observed a possible mechanism (constrained flight paths) resulting in strikes with moose (Becker and Grauvogel 1991). The study then evaluated reduced train speeds (reaction time mechanism) on reducing moose strike rates. The authors found reduced train speeds to be ineffective in this case but suggested that at some levels of speed reduction, the approach may have been effective; since these speeds are surely economically cost-prohibitive (Becker and Grauvogel 1991), and so variables (such as snow removal) enabling moose to move off the railroad, vegetative or other terrain modifications should be evaluated. Although moose were not analyzed in this study, speed was positively associated with increasing strike risks for elk and deer along the CPR. Speed reduction in hotspots and high-risk areas should be empirically evaluated in the future.

For bears, it may be most important to evaluate design modifications or mitigation solutions targeted at barriers including: highway vehicle overpasses, tunnels, snow sheds, rock cuts and bridges. However, multiple approaches are likely warranted in high-risk segments, including those that decrease the probability the bears will be exposed to strikes, increase the detectability of trains, increase the opportunities for safe flight paths off-track, and increase the time bears have to successfully avoid trains.