Keywords

1 Introduction

In order to perform numerical simulations of vapour explosion, a phenomenum resulting from the violent interaction between a hot liquid metal and a coolant (usually liquid water and its vapour), flow models with at least three phases are mandatory. Owing to the high velocity and high pressure levels arising in these situations, and also due to the occurence of strong shock waves, models should at least enable highly unsteady simulations, and should be such that unique and well defined jump conditions hold through discontinuities. However, only few contributions arise from the literature on that topic. Among these, one may at least mention [6,7,8, 10, 11]. Actually, we will focus here on the barotropic class defined in [8], and will present a possible fractional step method in order to compute approximate solutions of the latter model. Some among identified difficulties concern the way to cope with pressure relaxation effects and to preserve positive values of densities and statistical fractions; moreover, schemes should be such that they provide convergent and consistant approximations of shock patterns. Possible extensions to the non barotropic framework and problems arising with mass transfer terms are not addressed here.

2 Three-Phase Flow Model

Governing equations

In the sequel, \(\alpha _k \in [0,1]\), \(\rho _k\), \(m_k=\alpha _k \rho _k\), \(U_k\), respectively denote the mean statistical fraction, the mean density, the partial mass and the mean velocity of phase k (phase 1 denotes liquid metal). The mean pressure \(P_k(\rho _k)\) is an increasing function with:

$$ \lim _{x \rightarrow \infty } P_k(x) = + \infty \qquad ; \qquad \lim _{x \rightarrow 0} P_k(x) = 0 $$

and we note as usual \(c_k^2 = P_k'(\rho _k)\). The set of PDEs that is considered is (see [8]):

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \alpha _k}{\partial t} + {\mathscr {V}_i(W)} \frac{\partial \alpha _k}{\partial x} = \phi _k(W) \ ; \\ \frac{\partial m_k}{\partial t} + \frac{\partial m_k U_k}{\partial x} = 0 \ ; \\ \frac{\partial m_k U_k}{\partial t} + \frac{\partial m_k U_k^2 + \alpha _k P_k}{\partial x} + \varSigma _{l=1, l \ne k}^3 \varPi _{kl}(W) \frac{\partial \alpha _l}{\partial x} = m_k S_k(W) \ . \\ \end{array} \right. \end{aligned}$$
(1)

It may be alternatively rewritten in a more condensed form:

$$\begin{aligned} \frac{\partial W}{\partial t} + \frac{\partial F(W)}{\partial x} + G(W) \frac{\partial H(W)}{\partial x} = S(W) \end{aligned}$$
(2)

where the main variable W and fluxes F(W), H(W) are defined as:

$$ W = (\alpha _2,\alpha _3,m_1,m_2,m_3,m_1 U_1, m_2 U_2,m_3 U_3)^t $$
$$ F(W)= (0,0,m_1 U_1, m_2 U_2,m_3 U_3,m_1 U_1^2 + \alpha _1 P_1, m_2 U_2^2 + \alpha _2 P_2,m_3 U_3^2 + \alpha _3 P_3 )^t $$
$$ H(W) = (\alpha _2,\alpha _3,0,0,0,0,0,0)^t $$

G(W) being implicitly defined by (1). The statistical fraction \(\alpha _1\) complies with: \(\alpha _1=1-\alpha _2-\alpha _3\). We restrict herein to the case where: \(\mathscr {V}_i(W)=U_1\), with (see [8]):

$$\begin{aligned} \left\{ \begin{array}{l} \varPi _{12}(W) = \varPi _{21}(W) = \varPi _{23}(W) = P_2 \ ; \\ \varPi _{13}(W)= \varPi _{31}(W) = \varPi _{32}(W) = P_3 \ . \\ \end{array} \right. \end{aligned}$$
(3)

Closure laws for \(\phi _k(W), S_k(W)\) take the form:

$$\begin{aligned} \left\{ \begin{array}{l} \phi _k(W) = d(W) \varSigma _{l=1}^{3} \left( (P_k - P_l) \right) \ ; \\ m_k S_k(W) = \varSigma _{l=1}^{3} \left( e_{kl}(W) (U_l - U_k) \right) \end{array} \right. \end{aligned}$$
(4)

where d(W) and \(e_{kl}(W)=e_{lk}(W)\) are positive bounded functions. Meaningful pressure relaxation time scales d(W) arise from [5]. Other relaxation time scales \(e_{kl}(W)\) embedded in momentum transfer terms may be found in the standard literature. We also define: \(\psi _k'(\rho _k) =\frac{P_k(\rho _k)}{\rho _k^2}\), and the entropy of the mixture:

$$ \eta = \varSigma _{k=1}^3 \left( m_k U_k^2/2 + \psi _k(\rho _k) \right) , $$

together with the entropy flux: \(f_{\eta } (W) = \varSigma _{k=1}^3 \left( \frac{U_k^2}{2} + \psi _k(\rho _k) +\frac{P_k}{\rho _k} \right) m_k U_k \). Actually this three-phase flow model inherits from similar properties as the Baer Nunziato two-phase flow model [1] (see [2, 3] for a slightly broader class).

Main properties

We recall first the main properties of the latter system (see [8]):

Property 1

  • Structure of the convective subset:

    The homogeneous convective subset (left hand side of (2)) is hyperbolic unless \(|U_1-U_k|=c_k\). Its eigenvalues are:

    $$ \lambda _{0,1} (W)= U_1 \quad ; \quad \lambda _{2,3} (W)= U_1 \pm c_1 \quad ; \quad \lambda _{4,5} (W)= U_2 \pm c_2 \quad ; \quad \lambda _{6,7} (W)= U_3 \pm c_3 $$

    The \({0-1}\)-wave is linearly degenerate, while other fields are genuinely non linear.

  • Entropy inequality:

    Smooth solutions of (2) comply with the entropy inequality:

    $$\begin{aligned} \frac{\partial \eta (W)}{\partial t} + \frac{\partial f_{\eta }(W)}{\partial x} \le 0. \end{aligned}$$
    (5)

  • Jump conditions:

    Within each isolated wave, system (2) admits unique jump conditions.

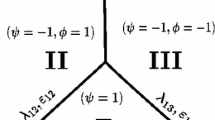
We may now consider the \({0-1}\) coupling wave, which is the key point of the homogeneous model. Actually, six independent Riemann invariants arise which are given below. These will be used in order to construct exact solutions of the one-dimensional Riemann problem associated with (2) when neglecting source terms.

Proposition 1

Riemann invariants of the \({0-1}\) coupling wave are:

$$ I_{0,1}^{1} (W) = U_1 \quad ; \quad I_{0,1}^2 (W) = m_2 (U_2-U_1) \quad ; \quad I_{0,1}^3 (W) = m_3 (U_3-U_1) ; $$
$$ I_{0,1}^4 (W) = \frac{(U_1-U_2)^2}{2} + \int _0^{\rho _2} (\frac{c_2^2(x)}{x} dx) \quad ; \quad I_{0,1}^5 (W) = \frac{(U_1-U_3)^2}{2} + \int _0^{\rho _3} (\frac{c_3^2(x)}{x} dx) ; $$
$$ I_{0,1}^6 (W) = m_2 (U_2-U_1)^2 + m_3 (U_3-U_1)^2 + \varSigma _{k=1}^3 (\alpha _k P_k) . $$

The proof is straightforward though cumbersome.

3 Numerical Scheme

A fractional step method is introduced in order to compute approximate solutions of (2). The latter method complies with the entropy inequality (5). A Finite Volume scheme is built, considering a classical one-dimensional mesh, where \(\varDelta x_i\) denotes the size of cell \(\varOmega _i\). The first step involves an explicit scheme, whereas the scheme in the second -relaxation- step is implicit.

Time scheme

  • Step 1. A first evolution step computes approximations of solutions of the convective subset; for given \(W_i^n\), the state variable is updated following:

    $$\begin{aligned} \left\{ \begin{array}{l} \varDelta x_i (W_i^{n+1,-} - W_i^n) + \varDelta t^n \left( \mathscr {F}_{i+1/2}(W_i^n,W_{i+1}^n) - \mathscr {F}_{i-1/2}(W_{i-1}^n,W_{i}^n) \right) \\ \quad \quad \quad + \varDelta t^n G(W_i^n) \left( \mathscr {H}_{i+1/2}(W_i^n,W_{i+1}^n) - \mathscr {H}_{i-1/2}(W_{i-1}^n,W_{i}^n) \right) = 0. \end{array} \right. \end{aligned}$$
    (6)

  • Step 2. The second step takes all source terms into account, for given \(W_i^{n+1,-}\), and computes \(W_i^{n+1}\) solution of:

    $$\begin{aligned} (W_i^{n+1} - W_i^{n+1,-}) - \varDelta t^n \mathscr {S} (W_i^{n+1,-},W_i^{n+1}) = 0 \end{aligned}$$
    (7)

    where: \(\mathscr {S} (W_i^{n+1,-},W_i^{n+1})= (\phi _{i,2},\phi _{i,3},0,0,0,S_{i,1},S_{i,2},S_{i,3})^t\), with:

    $$ \phi _{i,k}= \varSigma _{l=1}^{3} \left( d(W_i^{n+1,-}) (P_k(W_i^{n+1}) - P_l(W_i^{n+1}) \right) $$

    and:

    $$ S_{i,k}= \varSigma _{l=1}^{3} \left( e_{kl}(W_i^{n+1,-}) (U_l(W_i^{n+1}) - U_k(W_i^{n+1}) \right) $$

    for \(k=1,2,3\).

Numerical fluxes in the evolution step

We restrict herein to simple first-order Rusanov-type fluxes defined as follows:

$$ \mathscr {F}_{ij}(W_i,W_j) = \left( F(W_i) + F(W_j) - R_{ij}(W_j - W_i) \right) / 2 \ , $$

together with:

$$ \mathscr {H}_{ij}(W_{i},W_{j}) = \left( H(W_i) + H(W_j) \right) / 2 $$

\(R_{ij}\) is defined as : \(max_{i,j} (r(W_i),r(W_j))\), where r(W) denotes the spectral radius of the whole jacobian matrix \((\frac{\partial F(W)}{\partial W} + G(W) \frac{\partial H(W)}{\partial W} )\).

Property 2

  • For given strictly positive values \((\alpha _k)_i^n\) and \((m_k)_i^n\), the evolution step computes positive values \((\alpha _k)_i^{n+1,-}\) and \((m_k)_i^{n+1,-}\) if and only if the time step complies with the classical CFL-like condition:

    $$\begin{aligned} \varDelta t^n max_{j=1 \rightarrow N_{cell}} (R_{j-1/2}+R_{j+1/2}) / (2 \varDelta x_j) = CFL < 1 \end{aligned}$$
    (8)

  • Assume that \((\alpha _k)_i^{n+1,-}\) and \((m_k)_i^{n+1,-}\) are positive. Then the discrete relaxation Step 2 computes a unique set of positive values \((\alpha _k)_i^{n+1}\) and \((m_k)_i^{n+1}\), and a unique set \((U_1,U_2,U_3)_i^{n+1}\) without any restriction on the time step.

The proof for the first part involving the evolution Step 1 is classical. Actually, \((m_k)_i^{n+1,-}\) is a convex combination of partial masses \((m_k)_i^{n}\) and \((m_k)_{i \pm 1}^{n}\), as soon as condition (8) holds. A similar result holds for \((\alpha _k)_i^{n+1,-}\). Moreover, when turning to Step 2, it may be easily checked that the linear system that provides \((U_1,U_2,U_3)^{n+1}\) admits a unique solution, since the determinant \(\delta \) of the local discrete system:

$$\begin{aligned} \begin{array}{l} \delta _i= m_1 m_2 m_3 + (\hat{e}_{13} + \hat{e}_{23}) m_1 m_2 + (\hat{e}_{12} + \hat{e}_{23}) m_1 m_3 + (\hat{e}_{12} + \hat{e}_{13}) m_2 m_3 \\ \qquad \qquad \qquad \qquad \qquad \quad + (\hat{e}_{12} \hat{e}_{13} + \hat{e}_{12} \hat{e}_{23} + \hat{e}_{13} \hat{e}_{23}) (m_1+m_2+m_3) \ , \\ \end{array} \end{aligned}$$
(9)

where \(\hat{e}_{kl}\) and \(m_k\) respectively stand for \( \varDelta t^n e_{kl}(W_i^{n+1,-})\) and \((m_k)_i^{n+1,-}\), is strictly positive. Moreover, the relation \((m_k)_i^{n+1}=(m_k)_i^{n+1,-}\) guarantees positive values of partial masses. Eventually, the proof of existence and uniqueness of positive values of \((\alpha _k)_i^{n+1}\) is more intricate; it requires solving a non linear system with respect to \((x,y)=((\alpha _2)_i^{n+1},(\alpha _3)_i^{n+1})\) under the constraints: \(x>0\), \(y>0\), \(1-x-y>0\). We emphasize that similar schemes have been used for two-phase flow models [9].

Fig. 1
figure 1

Riemann problem 1. Pressure profiles on the finest mesh: \(P_1\) (green), \(P_2\) (black), \(P_3\) (red)

Full size image

4 Numerical Results

We focus here on simple EOS that read: \(P_k(\rho _k)=P_k^0 (\rho _k)^{\gamma _k}\). Two distinct Riemann problems are investigated, these being representative of what happens in water-vapour explosion. The time step complies with the CFL-like condition (8). We have set in all cases: \(CFL=1/2\). The initial discontinuity separating states \(W_L\) and \(W_R\) is located at \(x=1/2\). We restrict here to uniform meshes, and we consider very large relaxation time scales, setting \(d(W)=0\) and \(e_{kl}(W)=0\).

Fig. 2
figure 2

Riemann problem 1. Pressure profiles on the finest mesh: \(\mathscr {P} = I_{0,1}^6 (W)\) (black), \(P_{wall}\) (red)

Full size image
Fig. 3
figure 3

Riemann problem 1. Velocity profiles on the finest mesh: \(U_1\) (green), \(U_2\) (black), \(U_3\) (red)

Full size image
Fig. 4
figure 4

Riemann problem 2. Pressure profiles for \(\mathscr {P} = I_{0,1}^6 (W)\) on three distinct meshes: 8000 cells (black), 2000 cells (red), 800 cells (green)

Full size image
Fig. 5
figure 5

Riemann problem 2. \(L^1\) norm of the error for \(\mathscr {P} = I_{0,1}^6 (W)\) vs the mesh size h, using log/log scale. Coarsest and finest meshes contain 100 and 6400 regular cells respectively

Full size image

Riemann problem 1: The first test case is a classical shock tube problem, where the initial data are such that velocities are null everywhere at the beginning of the computation, whatever the phase is. More precisely, we define \(W_L\) and \(W_R\) such that:

$$ (\alpha _2)_L= 0.4 \quad ;\quad (\alpha _3)_L= 0.5 \quad ;\quad (\alpha _2)_R= 0.2 \quad ;\quad (\alpha _2)_R= 0.3; $$
$$ (U_k)_L= (U_k)_R= 0. \quad ;\quad (\rho _k)_L= 1. \quad ;\quad (\rho _k)_R= 1/8. $$

where EOS are such that: \(\gamma _1=7/5\), \(\gamma _2=1.005\), \(\gamma _3=1.001\) and \(P_k^0=1.10^5\). Phasic pressures are plotted on Fig. 1, while \(\mathscr {P} = I_{0,1}^6 (W)\) and the effective pressure of the mixture acting on wall boundaries \(P_{wall}=\varSigma _{k=1 \rightarrow 3} \alpha _k P_k\) are given on Fig. 2. \(\mathscr {P}\) is clearly well preserved through the right-going \(0-1\)-wave -which is located around \(=0.702\)- unlike \(P_{wall}\), which was expected. Velocity profiles have been added on Fig. 3. The finest mesh contains 80000 regular cells.

Riemann problem 2: The second test case is a simple Riemann problem where the initial data \(W_L\) and \(W_R\) are chosen such that:

$$ I_{0,1}^m (W_L) = I_{0,1}^m (W_R) $$

for \(m =1 \rightarrow 6\), see property (3). EOS are such that: \(\gamma _1=3/2\), \(\gamma _2=2\), \(\gamma _3=5/2\), and we still set: \(P_k^0=1.10^5\). Actually, this is a very tough test case, which is much more discriminating than most of other Riemann problems that involve all waves. A simple though efficient way to measure errors in this particular case consists in computing the \(L^1\) norm of independent variables \(I_{0,1}^m(W)\). Obviously, and as expected, the rough Rusanov scheme yields rather high levels of error (close to 0.1% on the coarsest mesh, see Fig. 4). Nonetheless, and as expected, the error in \(L^1\) norm varies as \(h^{1/2}\), since the \(0-1\)-wave is LD (see Fig. 5).