Keywords

1 Introduction

Bilevel optimization problems occur in various applications, e.g. in locomotion and biomechanics, see [1, 2, 15, 20], in optimal control under safety constraints, see [12, 18, 19], or in Stackelberg dynamic games, compare [10, 24]. An abstract bilevel optimization problem (BOP) reads as follows:

Minimize F(x, y) with respect to \((x,y)\in X\times Y\) subject to the constraints

$$\begin{aligned} G(x,y) \in K, \qquad H(x,y)=0,\qquad y\in M(x), \end{aligned}$$

where M(x) is the set of minimizers of the lower level optimization problem

$$\begin{aligned} {Minimize} \quad f(x,y) \quad {w.r.t.} \quad y\in Y\quad {s.t.} \quad g(x,y)\in C,\quad h(x,y) = 0. \end{aligned}$$

Herein, X, Y are (finite or infinite) Banach spaces, \(F,f: X\times Y \rightarrow {\mathbb R}\), \(H:X\times Y\rightarrow V^u\), \(h:X\times Y\rightarrow V^\ell \), \(G:X\times Y\rightarrow W^u\), \(g:X\times Y\rightarrow W^\ell \) are sufficiently smooth functions into Banach spaces \(V^u,V^\ell ,W^u,W^\ell \), and \(K\subset W^u\), \(C\subset W^\ell \) are convex and closed cones.

Bilevel optimization problems turn out to be very challenging with regard to both, the investigation of theoretical properties and numerical methods, compare [8]. Necessary conditions have been investigated, e.g., in [9, 25]. Typical solution approaches aim at reducing the bilevel structure into a single stage optimization problem. In the MPCC approach a single level optimization problem subject to complementarity constraints (MPCC) is obtained by replacing the lower level problem by its first order necessary conditions, compare [1]. However, if the lower level problem is non-convex, the MPCC is not equivalent in general to the original bilevel problem since non-optimal stationary points or non-global solutions may satisfy the necessary conditions as well. Still, the approach is often used owing to a well-established theory and the availability of numerical methods for MPCCs, especially for finite dimensional problems.

In this paper we focus on an equivalent transformation of the bilevel problem to a single level problem (see [7] for an alternative way). The equivalence can be guaranteed by exploitation of the value function \(V:X \rightarrow {\mathbb R}\) of the lower level problem, which is defined as

$$\begin{aligned} V(x) := \inf _{y\in Y} \{ f(x,y) \;|\; g(x,y)\in C, h(x,y)=0\}. \end{aligned}$$

An equivalent reformulation of the bilevel optimization problem is then given by the following single level problem, compare [22, 25, 26]:

Minimize F(x, y) w.r.t. \((x,y)\in X\times Y\) subject to the constraints

$$\begin{aligned} G(x,y)\in K, \ H(x,y) = 0, \ g(x,y)\in C,\ h(x,y)=0, \ f(x,y) \le V(x). \end{aligned}$$

The advantage of the value function approach is its equivalence with the bilevel problem. On the downside one has to be able to compute the value function, which in general might be intractable. Moreover, the value function is non-smooth in general (often Lipschitz continuous) and hence suitable methods from non-smooth optimization are required to solve the resulting single level problem. In Sect. 2 we discuss a class of bilevel optimal control problems that fit into the problem class BOP. In Sect. 3 we we are able to derive an analytical expression for the value function for an example and present numerical results. The new contribution of this paper is the discussion of a particular example, which combines the analytical expression of the value function of the lower level problem and a direct discretization method for the reformulated single level problem. This problem may serve as a test problem for theoretical and numerical investigations. The problem exhibits already most features of more challenging problems such as non-convexity, pure state constraints on the upper level problem as well as control constraints on both levels.

2 A Class of Bilevel Optimal Control Problems

Let \(T>0\), be the fixed final time, \(X := W^{1,\infty }([0,T],{\mathbb R}^{n_x})\times L^\infty ([0,T],{\mathbb R}^{n_u})\times {\mathbb R}^{n_p}\), \(n_x,n_u,n_p\in {\mathbb N}_0\), \(Y := W^{1,\infty }([0,T],{\mathbb R}^{n_y})\times L^\infty ([0,T],{\mathbb R}^{n_v})\times {\mathbb R}^{n_q}\), \(n_y,n_v,n_q\in {\mathbb N}_0\), where \(L^\infty ([0,T],{\mathbb R}^n)\) denotes the Banach space of essentially bounded vector-valued functions from [0, T] into \({\mathbb R}^{n}\) and \(W^{1,\infty }([0,T],{\mathbb R}^n)\) is the Banach space of absolutely continuous vector-valued functions from [0, T] into \({\mathbb R}^n\) with essentially bounded first derivatives. Moreover, let the Banach spaces \(V^u := L^\infty ([0,T],{\mathbb R}^{n_x})\times {\mathbb R}^{n_H}\), \(V^\ell := L^\infty ([0,T],{\mathbb R}^{n_y})\times {\mathbb R}^{n_h}\), \(n_H,n_h\in {\mathbb N}_0\), and the closed convex cones \(W^u := \{ k \in L^\infty ([0,T],{\mathbb R}^{n_G}) \;|\; k(t) \le 0\text { a.e. in }[0,T]\}\), \(W^\ell := \{ k \in L^\infty ([0,T],{\mathbb R}^{n_g}) \;|\; k(t) \le 0\text { a.e. in }[0,T]\}\), \(n_G,n_g\in {\mathbb N}_0\), be given. Let

$$\begin{aligned} J,j :\,&{\mathbb R}^{n_x} \times {\mathbb R}^{n_y} \times {\mathbb R}^{n_p}\times {\mathbb R}^{n_q} \rightarrow {\mathbb R},\\ F : \,&{\mathbb R}^{n_x}\times {\mathbb R}^{n_y}\times {\mathbb R}^{n_u} \times {\mathbb R}^{n_v} \times {\mathbb R}^{n_p} \times {\mathbb R}^{n_q} \rightarrow {\mathbb R}^{n_x}, \\ f : \,&{\mathbb R}^{n_y}\times {\mathbb R}^{n_v} \times {\mathbb R}^{n_p} \times {\mathbb R}^{n_q} \rightarrow {\mathbb R}^{n_y}, \\ \varPsi :\,&{\mathbb R}^{n_x} \times {\mathbb R}^{n_y} \times {\mathbb R}^{n_x} \times {\mathbb R}^{n_y} \times {\mathbb R}^{n_p}\times {\mathbb R}^{n_q} \rightarrow {\mathbb R}^{n_H},\\ \psi :\,&{\mathbb R}^{n_x} \times {\mathbb R}^{n_y} \times {\mathbb R}^{n_x} \times {\mathbb R}^{n_y} \times {\mathbb R}^{n_p}\times {\mathbb R}^{n_q} \rightarrow {\mathbb R}^{n_h},\\ S :\,&{\mathbb R}^{n_x}\times {\mathbb R}^{n_y}\times {\mathbb R}^{n_u} \times {\mathbb R}^{n_v} \times {\mathbb R}^{n_p} \times {\mathbb R}^{n_q} \rightarrow {\mathbb R}^{n_G}, \\ s :\,&{\mathbb R}^{n_y}\times {\mathbb R}^{n_v} \times {\mathbb R}^{n_p} \times {\mathbb R}^{n_q} \rightarrow {\mathbb R}^{n_g}. \end{aligned}$$

be sufficiently smooth mappings. With these definitions the following class of bilevel optimal control problems (BOCP) subject to control-state constraints and boundary conditions fits into the general bilevel optimization problem BOP.

Minimize J(x(T), y(T), p, q) w.r.t. \((x,u,p,y,v,q)\in X\times Y\) subject to the constraints

$$\begin{aligned} x'(t)= & {} F(x(t),y(t),u(t),v(t),p,q), \end{aligned}$$
(1)
$$\begin{aligned} 0= & {} \varPsi (x(0),y(0),x(T),y(T),p,q), \end{aligned}$$
(2)
$$\begin{aligned} 0\ge & {} S(x(t),y(t),u(t),v(t),p,q), \\ (y,v,q)\in & {} M(x(0),x(T),p) \nonumber \end{aligned}$$
(3)

where M(x(0), x(T), p) is the set of minimizers of the lower level problem \({OCP}_L(x(0),x(T),p)\) :

Minimize j(x(T), y(T), p, q) w.r.t. \((y,v,q)\in Y\) subject to the constraints

$$\begin{aligned} y'(t)= & {} f(y(t),v(t),p,q), \end{aligned}$$
(4)
$$\begin{aligned} 0= & {} \psi (x(0),y(0),x(T),y(T),p,q), \end{aligned}$$
(5)
$$\begin{aligned} 0\ge & {} s(y(t),v(t),p,q). \end{aligned}$$
(6)

Herein, \((x,u,p)\in X\) are the state, the control, and the parameter vector of the upper level problem and \((y,v,q)\in Y\) are the state, the control, and the parameter vector of the lower level problem. Please note that the lower level problem only depends on the initial and terminal states x(0), x(T) and the parameter vector p of the upper level problem. The value function V is then a mapping from \({\mathbb R}^{n_x}\times {\mathbb R}^{n_x}\times {\mathbb R}^{n_p}\) into \({\mathbb R}\) defined by

$$\begin{aligned} V(x_0,x_T,p) := \inf _{(y,v,q)\in Y} \left\{ j(x_T,y(T),p,q) \;\Bigg |\; \begin{array}{rcl} y'(t) &{} = &{} f(y(t),v(t),p,q), \\ 0 &{} = &{} \psi (x_0,y(0),x_T,y(T),p,q), \\ 0 &{} \ge &{} s(y(t),v(t),p,q) \end{array}\right\} . \end{aligned}$$

Remark 1

In a formal way the problem class can be easily extended in such a way that the lower level dynamics f and the lower level control-state constraints s depend on x, u as well. However, in the latter case the value function of the lower level problem would then be a functional \(V: X \rightarrow {\mathbb R}\), i.e. a functional defined on the Banach space X rather than a functional defined on the finite dimensional space \({\mathbb R}^{n_x}\times {\mathbb R}^{n_x}\times {\mathbb R}^{n_p}\). Computing the mapping \(V : X\rightarrow {\mathbb R}\) numerically would be computationally intractable in most cases.

Using the value function V we arrive at the following equivalent single level optimal control problem subject to control-state constraints, smooth boundary conditions, and an in general non-smooth boundary condition with the value function.

Minimize J(x(T), y(T), p, q) w.r.t. \((x,u,p,y,v,q)\in X\times Y\) subject to the constraints ( 1 )-( 3 ), ( 4 )-( 6 ), and

$$\begin{aligned} j(x(T),y(T),p,q)\le & {} V(x(0),x(T),p). \end{aligned}$$
(7)

It remains to compute the value function V and to solve the potentially non-smooth single level optimal control problem. Both are challenging tasks owing to non-smoothness and non-convexity. The value function sometimes can be derived analytically as we shall demonstrate in Sect. 3. Otherwise, if Bellman’s optimality principle applies, the value function satisfies a Hamilton-Jacobi-Bellman (HJB) equation, see [3]. Various methods exist for its numerical solution, compare [4, 11, 14, 17, 21]. The HJB approach is feasible if the state dimension \(n_y\) does not exceed 5 or 6. If no analytical formula is available and if the HJB approach is not feasible, then a pointwise evaluation of V at (x(0), x(T), p) can be realized by using suitable optimal control software, e.g. [13]. However, if the lower level problem is non-convex, then it is usually not possible to guarantee global optimality by such an approach. The single level problem can be approached by the non-smooth necessary conditions in [5, 6]. Alternatively, direct discretization methods may be applied. The non-smoothness in V in (7) has to be taken into account by, e.g., using bundle type methods, see [23], or by smoothing the value function and applying standard software. Finally, the HJB approach could also be applied to the single level problem again.

3 A Follow-the-leader Application

We consider a pursuit-evasion dynamic Stackelberg game of two vehicles moving in the plane. Throughout we assume that the evader knows the optimal strategy of the pursuer and can optimize its own’s strategy accordingly. This gives rise to a bilevel optimal control problem. The lower level player (=pursuer P) aims to capture the upper level player (=evader E) in minimum time T. The evader aims to minimize a linear combination of the negative capture time \(-T\) and its control effort. The players have individual dynamics and constraints. The coupling occurs through capture conditions at the final time.

3.1 The Bilevel Optimal Control Problem

The evader E aims to solve the following optimal control problem, called the upper level problem (\(\text {OCP}_U\)):

Minimize

$$\begin{aligned} -T + \int _{0}^{T} \frac{\alpha _1}{2} w(t)^2 + \frac{\alpha _2}{2} a(t)^2 dt \end{aligned}$$
(8)

subject to the constraints

$$\begin{aligned}&x_E'(t) = v_E(t) \cos \psi (t), \quad x_E(0) = x_{E,0}, \ x_E(T) = x_P(T), \end{aligned}$$
(9)
$$\begin{aligned}&y_E'(t) = v_E(t) \sin \psi (t), \quad y_E(0) = y_{E,0}, \ y_E(T) = y_P(T), \end{aligned}$$
(10)
$$\begin{aligned}&\psi '(t) = \frac{v_E(t)}{\ell } \tan \delta (t), \quad \psi (0) = \psi _0,\end{aligned}$$
(11)
$$\begin{aligned}&\delta '(t) = w(t),\quad \delta (0) = \delta _0,\end{aligned}$$
(12)
$$\begin{aligned}&v_E'(t) = a(t), \quad v_E(0) = v_{E,0}, \end{aligned}$$
(13)
$$\begin{aligned}&v_E(t) \in [0,v_{E,max}], \quad w(t) \in [-w_{max},w_{max}], \quad a(t) \in [a_{min},a_{max}], \\&(x_P,y_P,T) \in M(x_E(T),y_E(T)), \nonumber \end{aligned}$$
(14)

where \(M(x_E(T),y_E(T))\) denotes the set of minimizers of the lower level problem \({OCP}_L(x_E(T),y_E(T))\) below.

The equations of motion of E describe a simplified car model of length \(\ell >0\) moving in the plane. The controls are the steering angle velocity w and the acceleration a with given bounds \(\pm w_{max}\), \(a_{min}\), and \(a_{max}\), respectively. The velocity \(v_E\) is bounded by the state constraint \(v_E(t) \in [0,v_{E,max}]\) with a given bound \(v_{E,max}>0\). The position of the car’s rear axle is given by \(z_E = (x_E,y_E)^\top \) and its velocity by \(v_E\). \(\psi \) denotes the yaw angle and \(\alpha _1,\alpha _2\ge 0\) are weights in the objective function. The initial state is fixed by the values \(x_{E,0},y_{E,0},\psi _0,\delta _0,v_{E,0}\). The final time T is determined by the lower level player P, who aims to solve the following optimal control problem, called the lower level problem \(\text {OCP}_L(x_{E,T},y_{E,T})\) with its set of minimizers denoted by \(M(x_{E,T},y_{E,T})\):

Minimize \(T= \int _0^{T} 1 dt\) subject to the constraints

$$\begin{aligned} z_P'(t)= & {} v_P(t), \quad z_P(0) = z_{P,0}, \; z_P(T) = (x_{E,T},y_{E,T})^\top , \end{aligned}$$
(15)
$$\begin{aligned} v_P'(t)= & {} u_P(t), \quad v_P(0) = v_P(T) = 0, \end{aligned}$$
(16)
$$\begin{aligned} u_{P,i}(t)\in & {} [-u_{max},u_{max}], \quad i=1,2. \end{aligned}$$
(17)

Herein, \(z_P = (x_P,y_P)^\top \), \(v_P=(v_{P,1},v_{P,2})^\top \), and \(u_P=(u_{P,1},u_{P,2})^\top \) denote the position vector, the velocity vector, and the acceleration vector, respectively, of P in the two-dimensional plane. \(z_{P,0} = (x_{P,0},y_{P,0})^\top \in {\mathbb R}^2\) is a given initial position. \(u_{max}>0\) is a given control bound for the acceleration. The dynamics of the pursuer allow to move in x and y direction independently, which models, e.g., a robot with omnidirectional wheels.

3.2 The Lower-Level Problem and Its Value Function

The lower level problem admits an analytical solution. To this end, the Hamilton function (regular case only) reads as

$$\begin{aligned} \mathcal {H}(z_P,v_P,u_P,\lambda _z,\lambda _v) = 1 + \lambda _z^\top v_P + \lambda _v^\top u_P. \end{aligned}$$

The first order necessary optimality conditions for a minimum \((\hat{z}_P,\hat{v}_P,\hat{u}_P,\hat{T})\) are given by the minimum principle, compare [16]. There exist adjoint multipliers \(\lambda _z,\lambda _v\) with

$$\begin{aligned} \lambda _z'(t) = -\nabla _{z_P} \mathcal {H}[t] = 0,\qquad \lambda _v'(t) = -\nabla _{v_P} \mathcal {H}[t] = -\lambda _z(t), \end{aligned}$$

and

$$\begin{aligned} \mathcal {H}(\hat{z}_P(t),\hat{v}_P(t),\hat{u}_P(t),\lambda _z(t),\lambda _v(t))\le & {} \mathcal {H}(\hat{z}_P(t),\hat{v}_P(t),u_P,\lambda _z(t),\lambda _v(t)) \end{aligned}$$

for all \(u_P \in [-u_{max},u_{max}]^2\) for almost every \(t\in [0,\hat{T}]\). The latter implies

$$\begin{aligned} \hat{u}_{P,i}(t)= & {} \left\{ \begin{array}{rl} u_{max}, &{} \text { if } \lambda _{v,i}(t) < 0\\ -u_{max}, &{} \text { if } \lambda _{v,i}(t) > 0\\ \text {singular}, &{} \text { if } \lambda _{v,i}(t) = 0 \text { on some interval}, \end{array}\right. \qquad i=1,2. \end{aligned}$$

The adjoint equations yield \(\lambda _z(t) = c_z\) and \(\lambda _v(t) = -c_z t + c_v\) with constants \(c_z,c_v\in {\mathbb R}^2\). A singular control component \(\hat{u}_{P,i}\) with \(i\in \{1,2\}\) can only occur if \(c_{z,i} = c_{v,i} = 0\). In this case, the minimum principle provides no information on the singular control except feasibility. Notice furthermore that not all control components can be singular since this would lead to trivial multipliers in contradiction to the minimum principle. Hence, there is at least one index i for which the control component \(\hat{u}_{P,i}\) is non-singular. In the non-singular case there can be at most one switch of each component \(\hat{u}_{P,i}\), \(i\in \{1,2\}\), in the time interval \([0,\hat{T}]\), since \(\lambda _{v,i}\) is linear in time. The switching time \(\hat{t}_{s,i}\) for the i-th control component computes to \(\hat{t}_{s,i} = c_{v,i}/c_{z,i}\) if \(c_{z,i}\not =0\). We discuss several cases for non-singular controls.

  • Case 1: No switching occurs in \(\hat{u}_{P,i}\), i.e. \(\hat{u}_{P,i}(t) \equiv \pm u_{max}\) for \(i\in \{1,2\}\). By integration we obtain \(\hat{v}_{P,i}(t) = \pm u_{max} t \) and thus \(\hat{v}_{P,i}(\hat{T}) \not = 0\) in contradiction to the boundary conditions. Consequently, each non-singular control component switches exactly once in \([0,\hat{T}]\).

  • Case 2: The switching structure for control component \(i\in \{1,2\}\) is

    $$\begin{aligned} \hat{u}_{P,i}(t) = \left\{ \begin{array}{rl} u_{max}, &{} \text {if } 0\le t < \hat{t}_{s,i},\\ -u_{max}, &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

    By integration and the boundary conditions we find

    $$\begin{aligned} \hat{v}_{P,i}(t)= & {} \left\{ \begin{array}{cl} u_{max} t , &{} \text {if } 0\le t<\hat{t}_{s,i}\\ u_{max} (2\hat{t}_{s,i}-t), &{} \text {otherwise} \end{array}\right. \\ \hat{z}_{P,i}(t)= & {} \left\{ \begin{array}{cl} \hat{z}_{P,i}(0) + \frac{1}{2} u_{max} t^2, &{} \text {if } 0\le t<\hat{t}_{s,i}\\ \hat{z}_{P,i}(0) + u_{max} \left( \hat{t}_{s,i}^2 - \frac{1}{2} (2\hat{t}_{s,i} - t)^2 \right) , &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

    The boundary conditions for \(\hat{v}_{P,i}(\hat{T})\) and \(\hat{z}_{P,i}(\hat{T})\) yield

    $$\begin{aligned} \hat{T}_i = 2 \hat{t}_{s,i} \quad \text {and} \quad \hat{t}_{s,i} = \sqrt{\frac{\hat{z}_{P,i}(\hat{T})-\hat{z}_{P,i}(0)}{u_{max}}}\text { if}\ \hat{z}_{P,i}(\hat{T})-\hat{z}_{P,i}(0)\ge 0. \end{aligned}$$

  • Case 3: The switching structure for control component \(i\in \{1,2\}\) is

    $$\begin{aligned} \hat{u}_{P,i}(t) = \left\{ \begin{array}{rl} -u_{max}, &{} \text {if } 0\le t < \hat{t}_{s,i},\\ u_{max}, &{} \text {otherwise}. \end{array}\right. \end{aligned}$$

This case can be handled analogously to Case 2 and we obtain

$$\begin{aligned} \hat{T}_i = 2 \hat{t}_{s,i} \quad \text {and} \quad \hat{t}_{s,i} = \sqrt{\frac{\hat{z}_{P,i}(0)-\hat{z}_{P,i}(\hat{T})}{u_{max}}}\text { if}\ \hat{z}_{P,i}(0)-\hat{z}_{P,i}(\hat{T})\ge 0. \end{aligned}$$

The above analysis reveals the shortest times \(\hat{T}_i\), \(i\in \{1,2\}\), in which the i-th state can reach its terminal boundary condition. The minimum time \(\hat{T}\) for a given terminal position is thus given by the value function V of \(\text {OCP}_L(x_{E,T},y_{E,T})\) (=minimum time function) with

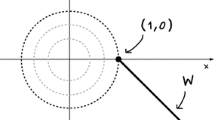
$$\begin{aligned} V(x_{E,T},y_{E,T}) = \max \{ \hat{T}_1,\hat{T}_2\} = 2\max \left\{ \sqrt{ \frac{| x_{P,0} - x_{E,T} |}{u_{max}}}, \sqrt{ \frac{| y_{P,0} - y_{E,T}|}{u_{max}}}\right\} . \end{aligned}$$
(18)

That is, the final time is defined by the component i with the largest distance \(|\hat{z}_{P,i}(\hat{T})-\hat{z}_{P,i}(0)|\). For this component, the control is of bang-bang type with one switch at the midpoint of the time interval. The remaining control can be singular and it is not uniquely defined. The value function is locally Lipschitz continuous except at the point \((x_{E,T},y_{E,T}) = (x_{P,0},y_{P,0})\), compare Fig. 1. This point, however, is of minor interest because interception takes place immediately.

Fig. 1.
figure 1

Value function of lower level problem with data \(x_{P,0} = y_{P,0} = 0\), \(u_{max}=1\).

Full size image
Fig. 2.
figure 2

Numerical results for the bilevel optimal control problem: Trajectories of pursuer (lines with ‘+’) and evader (lines with boxes, top), controls of the pursuer (middle), controls of the evader (bottom).

Full size image
Fig. 3.
figure 3

Left picture: Trajectories of pursuer (lines with ‘+’) and evader (lines with boxes) for \(\psi _E(0)=\pi /4\). Right picture: Trajectories of the pursuer (lines with ‘+’) and the evader (lines with boxes) for different initial yaw angles of the evader.

Full size image

The equivalent single level problem (SL-OCP) reads as follows:

Minimize ( 8 ) subject to the constraints ( 9 )-( 14 ), ( 15 )-( 17 ) with \((x_{E,T},y_{E,T})^\top = (x_E(T),y_E(T))^\top \) and the non-smooth constraint

$$\begin{aligned} T \le V(x_E(T),y_E(T)). \end{aligned}$$
(19)

3.3 Numerical Results

For the numerical solution of the single level problem SL-OCP we applied the direct shooting method OCPID-DAE1, [13]. The non-smooth constraint \(T\le V(x_E(T),y_E(T))\) with V from (18) was replaced by a continuously differentiable constraint which was obtained by smoothing the maximum function and the absolute value function in (18). Figure 2 shows a numerical solution of the pursuit-evasion Stackelberg bilevel optimal control problem for the data \(v_{E,0}=10\), \(\psi _E(0)=\pi /4\), \(\alpha _1=10\), \(\alpha _2=0\), \(w_{max}=0.5\), \(v_{E,max}=20\), \(a_{min}=-5\), \(a_{max}=1\), \(u_{max}=5\), \(N=50\), \(T\approx 18.01\). Figure 3 shows several trajectories for the pursuer and the evader for different initial yaw angles covering the interval \([0,2\pi )\).

Remark 2

The constraint (19) may become infeasible under discretization. Instead, the value function \(V_h\) of the discretized lower level optimal control problem should be used. However, since \(V_h\) is hardly available for all kinds of discretizations, we use instead the relaxed constraint \(T \le V(x_{E}(T),y_E(T)) + \varepsilon \) with some \(\varepsilon > 0\).

4 Conclusions and Outlook

The paper discusses a specific bilevel optimal control problem and its reformulation as an equivalent single level problem using the value function of the lower level problem. For a sample problem it is possible to compute the value function analytically and to solve the overall bilevel problem numerically using a direct discretization method. This first numerical study leaves many issues open that have to be investigated in future research for the general problem setting. Amongst them are smoothness properties of the value function, representation of subdifferentials, the development of appropriate solution methods for non-smooth problems, and the derivation of necessary (and sufficient) conditions of optimality for the class of bilevel optimal control problems.