Abstract
Vibration problems lead to differential equations with solutions that oscillate in time, typically in a damped or undamped sinusoidal fashion. Such solutions put certain demands on the numerical methods compared to other phenomena whose solutions are monotone or very smooth. Both the frequency and amplitude of the oscillations need to be accurately handled by the numerical schemes. The forthcoming text presents a range of different methods, from classical ones (Runge-Kutta and midpoint/Crank-Nicolson methods), to more modern and popular symplectic (geometric) integration schemes (Leapfrog, Euler-Cromer, and Störmer-Verlet methods), but with a clear emphasis on the latter. Vibration problems occur throughout mechanics and physics, but the methods discussed in this text are also fundamental for constructing successful algorithms for partial differential equations of wave nature in multiple spatial dimensions.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Vibration problems lead to differential equations with solutions that oscillate in time, typically in a damped or undamped sinusoidal fashion. Such solutions put certain demands on the numerical methods compared to other phenomena whose solutions are monotone or very smooth. Both the frequency and amplitude of the oscillations need to be accurately handled by the numerical schemes. The forthcoming text presents a range of different methods, from classical ones (Runge-Kutta and midpoint/Crank-Nicolson methods), to more modern and popular symplectic (geometric) integration schemes (Leapfrog, Euler-Cromer, and Störmer-Verlet methods), but with a clear emphasis on the latter. Vibration problems occur throughout mechanics and physics, but the methods discussed in this text are also fundamental for constructing successful algorithms for partial differential equations of wave nature in multiple spatial dimensions.
1.1 Finite Difference Discretization
Many of the numerical challenges faced when computing oscillatory solutions to ODEs and PDEs can be captured by the very simple ODE \(u^{\prime\prime}+u=0\). This ODE is thus chosen as our starting point for method development, implementation, and analysis.
1.1.1 A Basic Model for Vibrations
The simplest model of a vibrating mechanical system has the following form:
Here, ω and I are given constants. Section 1.12.1 derives (1.1 ) from physical principles and explains what the constants mean.
The exact solution of (1.1) is
That is, u oscillates with constant amplitude I and angular frequency ω. The corresponding period of oscillations (i.e., the time between two neighboring peaks in the cosine function) is \(P=2\pi/\omega\). The number of periods per second is \(f=\omega/(2\pi)\) and measured in the unit Hz. Both f and ω are referred to as frequency, but ω is more precisely named angular frequency, measured in rad/s.
In vibrating mechanical systems modeled by (1.1), u(t) very often represents a position or a displacement of a particular point in the system. The derivative \(u^{\prime}(t)\) then has the interpretation of velocity, and \(u^{\prime\prime}(t)\) is the associated acceleration. The model (1.1) is not only applicable to vibrating mechanical systems, but also to oscillations in electrical circuits.
1.1.2 A Centered Finite Difference Scheme
To formulate a finite difference method for the model problem (1.1 ), we follow the four steps explained in Section 1.1.2 in [9].
Step 1: Discretizing the domain
The domain is discretized by introducing a uniformly partitioned time mesh. The points in the mesh are \(t_{n}=n\Delta t\), \(n=0,1,\ldots,N_{t}\), where \(\Delta t=T/N_{t}\) is the constant length of the time steps. We introduce a mesh function u n for \(n=0,1,\ldots,N_{t}\), which approximates the exact solution at the mesh points. (Note that n = 0 is the known initial condition, so u n is identical to the mathematical u at this point.) The mesh function u n will be computed from algebraic equations derived from the differential equation problem.
Step 2: Fulfilling the equation at discrete time points
The ODE is to be satisfied at each mesh point where the solution must be found:
Step 3: Replacing derivatives by finite differences
The derivative \(u^{\prime\prime}(t_{n})\) is to be replaced by a finite difference approximation. A common second-order accurate approximation to the second-order derivative is
Inserting (1.4) in (1.3) yields
We also need to replace the derivative in the initial condition by a finite difference. Here we choose a centered difference, whose accuracy is similar to the centered difference we used for \(u^{\prime\prime}\):
Step 4: Formulating a recursive algorithm
To formulate the computational algorithm, we assume that we have already computed \(u^{n-1}\) and u n, such that \(u^{n+1}\) is the unknown value to be solved for:
The computational algorithm is simply to apply (1.7 ) successively for \(n=1,2,\ldots,N_{t}-1\). This numerical scheme sometimes goes under the name Störmer’s method, Verlet integration Footnote 1, or the Leapfrog method (one should note that Leapfrog is used for many quite different methods for quite different differential equations!).
Computing the first step
We observe that (1.7) cannot be used for n = 0 since the computation of u 1 then involves the undefined value u −1 at \(t=-\Delta t\). The discretization of the initial condition then comes to our rescue: (1.6) implies \(u^{-1}=u^{1}\) and this relation can be combined with (1.7) for n = 0 to yield a value for u 1:
which reduces to
Exercise 1.5 asks you to perform an alternative derivation and also to generalize the initial condition to \(u^{\prime}(0)=V\neq 0\).
The computational algorithm
The steps for solving (1.1) become
-
1.
\(u^{0}=I\)
-
2.
compute u 1 from (1.8)
-
3.
for \(n=1,2,\ldots,N_{t}-1\): compute \(u^{n+1}\) from (1.7)
The algorithm is more precisely expressed directly in Python:

Remark on using w for ω in computer code
In the code, we use w as the symbol for ω. The reason is that the authors prefer w for readability and comparison with the mathematical ω instead of the full word omega as variable name.
Operator notation
We may write the scheme using a compact difference notation listed in Appendix A.1 (see also Section 1.1.8 in [9]). The difference (1.4) has the operator notation \([D_{t}D_{t}u]^{n}\) such that we can write:
Note that \([D_{t}D_{t}u]^{n}\) means applying a central difference with step \(\Delta t/2\) twice:
which is written out as
The discretization of initial conditions can in the operator notation be expressed as
where the operator \([D_{2t}u]^{n}\) is defined as
1.2 Implementation
1.2.1 Making a Solver Function
The algorithm from the previous section is readily translated to a complete Python function for computing and returning \(u^{0},u^{1},\ldots,u^{N_{t}}\) and \(t_{0},t_{1},\ldots,t_{N_{t}}\), given the input I, ω, \(\Delta t\), and T:

We have imported numpy and matplotlib under the names np and plt, respectively, as this is very common in the Python scientific computing community and a good programming habit (since we explicitly see where the different functions come from). An alternative is to do from numpy import * and a similar ‘‘import all’’ for Matplotlib to avoid the np and plt prefixes and make the code as close as possible to MATLAB. (See Section 5.1.4 in [9] for a discussion of the two types of import in Python.)
A function for plotting the numerical and the exact solution is also convenient to have:

A corresponding main program calling these functions to simulate a given number of periods (num_periods) may take the form

Adjusting some of the input parameters via the command line can be handy. Here is a code segment using the ArgumentParser tool in the argparse module to define option value (--option value) pairs on the command line:

Such parsing of the command line is explained in more detail in Section 5.2.3 in [9].
A typical execution goes like

Computing \(u^{\prime}\)
In mechanical vibration applications one is often interested in computing the velocity \(v(t)=u^{\prime}(t)\) after u(t) has been computed. This can be done by a central difference,
This formula applies for all inner mesh points, \(n=1,\ldots,N_{t}-1\). For n = 0, \(v(0)\) is given by the initial condition on \(u^{\prime}(0)\), and for \(n=N_{t}\) we can use a one-sided, backward difference:
Typical (scalar) code is

Since the loop is slow for large N t , we can get rid of the loop by vectorizing the central difference. The above code segment goes as follows in its vectorized version (see Problem 1.2 in [9] for explanation of details):

1.2.2 Verification
Manual calculation
The simplest type of verification, which is also instructive for understanding the algorithm, is to compute u 1, u 2, and u 3 with the aid of a calculator and make a function for comparing these results with those from the solver function. The test_three_steps function in the file vib_undamped.py shows the details of how we use the hand calculations to test the code:

This function is a proper test function, compliant with the pytest and nose testing framework for Python code, because
-
the function name begins with test_
-
the function takes no arguments
-
the test is formulated as a boolean condition and executed by assert
We shall in this book implement all software verification via such proper test functions, also known as unit testing. See Section 5.3.2 in [9] for more details on how to construct test functions and utilize nose or pytest for automatic execution of tests. Our recommendation is to use pytest. With this choice, you can run all test functions in vib_undamped.py by

Testing very simple polynomial solutions
Constructing test problems where the exact solution is constant or linear helps initial debugging and verification as one expects any reasonable numerical method to reproduce such solutions to machine precision. Second-order accurate methods will often also reproduce a quadratic solution. Here \([D_{t}D_{t}t^{2}]^{n}=2\), which is the exact result. A solution \(u=t^{2}\) leads to \(u^{\prime\prime}+\omega^{2}u=2+(\omega t)^{2}\neq 0\). We must therefore add a source in the equation: \(u^{\prime\prime}+\omega^{2}u=f\) to allow a solution \(u=t^{2}\) for \(f=2+(\omega t)^{2}\). By simple insertion we can show that the mesh function \(u^{n}=t_{n}^{2}\) is also a solution of the discrete equations. Problem 1.1 asks you to carry out all details to show that linear and quadratic solutions are solutions of the discrete equations. Such results are very useful for debugging and verification. You are strongly encouraged to do this problem now!
Checking convergence rates
Empirical computation of convergence rates yields a good method for verification. The method and its computational details are explained in detail in Section 3.1.6 in [9]. Readers not familiar with the concept should look up this reference before proceeding.
In the present problem, computing convergence rates means that we must
-
perform m simulations, halving the time steps as: \(\Delta t_{i}=2^{-i}\Delta t_{0}\), \(i=1,\ldots,m-1\), and \(\Delta t_{i}\) is the time step used in simulation i;
-
compute the L 2 norm of the error, \(E_{i}=\sqrt{\Delta t_{i}\sum_{n=0}^{N_{t}-1}(u^{n}-u_{\mbox{\footnotesize e}}(t_{n}))^{2}}\) in each case;
-
estimate the convergence rates r i based on two consecutive experiments \((\Delta t_{i-1},E_{i-1})\) and \((\Delta t_{i},E_{i})\), assuming \(E_{i}=C(\Delta t_{i})^{r}\) and \(E_{i-1}=C(\Delta t_{i-1})^{r}\), where C is a constant. From these equations it follows that \(r=\ln(E_{i-1}/E_{i})/\ln(\Delta t_{i-1}/\Delta t_{i})\). Since this r will vary with i, we equip it with an index and call it \(r_{i-1}\), where i runs from 1 to m − 1.
The computed rates \(r_{0},r_{1},\ldots,r_{m-2}\) hopefully converge to the number 2 in the present problem, because theory (from Sect. 1.4) shows that the error of the numerical method we use behaves like \(\Delta t^{2}\). The convergence of the sequence \(r_{0},r_{1},\ldots,r_{m-2}\) demands that the time steps \(\Delta t_{i}\) are sufficiently small for the error model \(E_{i}=C(\Delta t_{i})^{r}\) to be valid.
All the implementational details of computing the sequence \(r_{0},r_{1},\ldots,r_{m-2}\) appear below.

The error analysis in Sect. 1.4 is quite detailed and suggests that r = 2. It is also a intuitively reasonable result, since we used a second-order accurate finite difference approximation \([D_{t}D_{t}u]^{n}\) to the ODE and a second-order accurate finite difference formula for the initial condition for \(u^{\prime}\).
In the present problem, when \(\Delta t_{0}\) corresponds to 30 time steps per period, the returned r list has all its values equal to 2.00 (if rounded to two decimals). This amazingly accurate result means that all \(\Delta t_{i}\) values are well into the asymptotic regime where the error model \(E_{i}=C(\Delta t_{i})^{r}\) is valid.
We can now construct a proper test function that computes convergence rates and checks that the final (and usually the best) estimate is sufficiently close to 2. Here, a rough tolerance of 0.1 is enough. Later, we will argue for an improvement by adjusting omega and include also that case in our test function here. The unit test goes like

The complete code appears in the file vib_undamped.py.
Visualizing convergence rates with slope markers
Tony S. Yu has written a script plotslopes.py Footnote that is very useful to indicate the slope of a graph, especially a graph like \(\ln E=r\ln\Delta t+\ln C\) arising from the model \(E=C\Delta t^{r}\). A copy of the script resides in the src/vib Footnote directory. Let us use it to compare the original method for \(u^{\prime\prime}+\omega^{2}u=0\) with the same method applied to the equation with a modified ω. We make log-log plots of the error versus \(\Delta t\). For each curve we attach a slope marker using the slope_marker((x,y), r) function from plotslopes.py, where (x,y) is the position of the marker and r and the slope (\((r,1)\)), here (2,1) and (4,1).

Figure 1.1 displays the two curves with the markers. The match of the curve slope and the marker slope is excellent.
1.2.3 Scaled Model
It is advantageous to use dimensionless variables in simulations, because fewer parameters need to be set. The present problem is made dimensionless by introducing dimensionless variables \(\bar{t}=t/t_{c}\) and \(\bar{u}=u/u_{c}\), where t c and u c are characteristic scales for t and u, respectively. We refer to Section 2.2.1 in [11] for all details about this scaling.
The scaled ODE problem reads
A common choice is to take t c as one period of the oscillations, \(t_{c}=2\pi/w\), and \(u_{c}=I\). This gives the dimensionless model
Observe that there are no physical parameters in (1.13)! We can therefore perform a single numerical simulation \(\bar{u}(\bar{t})\) and afterwards recover any \(u(t;\omega,I)\) by
We can easily check this assertion: the solution of the scaled problem is \(\bar{u}(\bar{t})=\cos(2\pi\bar{t})\). The formula for u in terms of \(\bar{u}\) gives \(u=I\cos(\omega t)\), which is nothing but the solution of the original problem with dimensions.
The scaled model can be run by calling solver(I=1, w=2*pi, dt, T). Each period is now 1 and T simply counts the number of periods. Choosing dt as 1./M gives M time steps per period.
1.3 Visualization of Long Time Simulations
Figure 1.2 shows a comparison of the exact and numerical solution for the scaled model (1.13) with \(\Delta t=0.1,0.05\). From the plot we make the following observations:
-
The numerical solution seems to have correct amplitude.
-
There is an angular frequency error which is reduced by decreasing the time step.
-
The total angular frequency error grows with time.
By angular frequency error we mean that the numerical angular frequency differs from the exact ω. This is evident by looking at the peaks of the numerical solution: these have incorrect positions compared with the peaks of the exact cosine solution. The effect can be mathematically expressed by writing the numerical solution as \(I\cos\tilde{\omega}t\), where \(\tilde{\omega}\) is not exactly equal to ω. Later, we shall mathematically quantify this numerical angular frequency \(\tilde{\omega}\).
1.3.1 Using a Moving Plot Window
In vibration problems it is often of interest to investigate the system’s behavior over long time intervals. Errors in the angular frequency accumulate and become more visible as time grows. We can investigate long time series by introducing a moving plot window that can move along with the p most recently computed periods of the solution. The SciTools Footnote 4 package contains a convenient tool for this: MovingPlotWindow. Typing pydoc scitools.MovingPlotWindow shows a demo and a description of its use. The function below utilizes the moving plot window and is in fact called by the main function in the vib_undamped module if the number of periods in the simulation exceeds 10.

We run the scaled problem (the default values for the command-line arguments --I and --w correspond to the scaled problem) for 40 periods with 20 time steps per period:

The moving plot window is invoked, and we can follow the numerical and exact solutions as time progresses. From this demo we see that the angular frequency error is small in the beginning, and that it becomes more prominent with time. A new run with \(\Delta t=0.1\) (i.e., only 10 time steps per period) clearly shows that the phase errors become significant even earlier in the time series, deteriorating the solution further.
1.3.2 Making Animations
Producing standard video formats
The visualize_front function stores all the plots in files whose names are numbered: tmp_0000.png, tmp_0001.png, tmp_0002.png, and so on. From these files we may make a movie. The Flash format is popular,

The ffmpeg program can be replaced by the avconv program in the above command if desired (but at the time of this writing it seems to be more momentum in the ffmpeg project). The -r option should come first and describes the number of frames per second in the movie (even if we would like to have slow movies, keep this number as large as 25, otherwise files are skipped from the movie). The -i option describes the name of the plot files. Other formats can be generated by changing the video codec and equipping the video file with the right extension:
Format | Codec and filename |
|---|---|
Flash | -c:v flv movie.flv |
MP4 | -c:v libx264 movie.mp4 |
WebM | -c:v libvpx movie.webm |
Ogg | -c:v libtheora movie.ogg |
The video file can be played by some video player like vlc, mplayer, gxine, or totem, e.g.,

A web page can also be used to play the movie. Today’s standard is to use the HTML5 video tag:

Modern browsers do not support all of the video formats. MP4 is needed to successfully play the videos on Apple devices that use the Safari browser. WebM is the preferred format for Chrome, Opera, Firefox, and Internet Explorer v9+. Flash was a popular format, but older browsers that required Flash can play MP4. All browsers that work with Ogg can also work with WebM. This means that to have a video work in all browsers, the video should be available in the MP4 and WebM formats. The proper HTML code reads

The MP4 format should appear first to ensure that Apple devices will load the video correctly.
Caution: number the plot files correctly
To ensure that the individual plot frames are shown in correct order, it is important to number the files with zero-padded numbers (0000, 0001, 0002, etc.). The printf format %04d specifies an integer in a field of width 4, padded with zeros from the left. A simple Unix wildcard file specification like tmp_*.png will then list the frames in the right order. If the numbers in the filenames were not zero-padded, the frame tmp_11.png would appear before tmp_2.png in the movie.
Playing PNG files in a web browser
The scitools movie command can create a movie player for a set of PNG files such that a web browser can be used to watch the movie. This interface has the advantage that the speed of the movie can easily be controlled, a feature that scientists often appreciate. The command for creating an HTML with a player for a set of PNG files tmp_*.png goes like

The fps argument controls the speed of the movie (‘‘frames per second’’).
To watch the movie, load the video file vib.html into some browser, e.g.,

Click on Start movie to see the result. Moving this movie to some other place requires moving vib.html and all the PNG files tmp_*.png:

Making animated GIF files
The convert program from the ImageMagick software suite can be used to produce animated GIF files from a set of PNG files:

The -delay option needs an argument of the delay between each frame, measured in 1/100 s, so 4 frames/s here gives 25/100 s delay. Note, however, that in this particular example with \(\Delta t=0.05\) and 40 periods, making an animated GIF file out of the large number of PNG files is a very heavy process and not considered feasible. Animated GIFs are best suited for animations with not so many frames and where you want to see each frame and play them slowly.
1.3.3 Using Bokeh to Compare Graphs
Instead of a moving plot frame, one can use tools that allow panning by the mouse. For example, we can show four periods of several signals in several plots and then scroll with the mouse through the rest of the simulation simultaneously in all the plot windows. The Bokeh Footnote 5 plotting library offers such tools, but the plots must be displayed in a web browser. The documentation of Bokeh is excellent, so here we just show how the library can be used to compare a set of u curves corresponding to long time simulations. (By the way, the guidance to correct pronunciation of Bokeh in the documentation Footnote 6 and on Wikipedia Footnote 7 is not directly compatible with a YouTube video Footnote 8 …).
Imagine we have performed experiments for a set of \(\Delta t\) values. We want each curve, together with the exact solution, to appear in a plot, and then arrange all plots in a grid-like fashion:

Furthermore, we want the axes to couple such that if we move into the future in one plot, all the other plots follows (note the displaced t axes!):

A function for creating a Bokeh plot, given a list of u arrays and corresponding t arrays, is implemented below. The code combines data from different simulations, described compactly in a list of strings legends.

A particular example using the bokeh_plot function appears below.

1.3.4 Using a Line-by-Line Ascii Plotter
Plotting functions vertically, line by line, in the terminal window using ascii characters only is a simple, fast, and convenient visualization technique for long time series. Note that the time axis then is positive downwards on the screen, so we can let the solution be visualized ‘‘forever’’. The tool scitools.avplotter.Plotter makes it easy to create such plots:

The call p.plot returns a line of text, with the t axis marked and a symbol + for the first function (u) and o for the second function (the exact solution). Here we append to this text a time counter reflecting how many periods the current time point corresponds to. A typical output (\(\omega=2\pi\), \(\Delta t=0.05\)) looks like this:

1.3.5 Empirical Analysis of the Solution
For oscillating functions like those in Fig. 1.2 we may compute the amplitude and frequency (or period) empirically. That is, we run through the discrete solution points \((t_{n},u_{n})\) and find all maxima and minima points. The distance between two consecutive maxima (or minima) points can be used as estimate of the local period, while half the difference between the u value at a maximum and a nearby minimum gives an estimate of the local amplitude.
The local maxima are the points where
and the local minima are recognized by
In computer code this becomes

Note that the two returned objects are lists of tuples.
Let \((t_{i},e_{i})\), \(i=0,\ldots,M-1\), be the sequence of all the M maxima points, where t i is the time value and e i the corresponding u value. The local period can be defined as \(p_{i}=t_{i+1}-t_{i}\). With Python syntax this reads

The list p created by a list comprehension is converted to an array since we probably want to compute with it, e.g., find the corresponding frequencies 2*pi/p.
Having the minima and the maxima, the local amplitude can be calculated as the difference between two neighboring minimum and maximum points:

The code segments are found in the file vib_empirical_analysis.py .
Since a[i] and p[i] correspond to the i-th amplitude estimate and the i-th period estimate, respectively, it is most convenient to visualize the a and p values with the index i on the horizontal axis. (There is no unique time point associated with either of these estimate since values at two different time points were used in the computations.)
In the analysis of very long time series, it is advantageous to compute and plot p and a instead of u to get an impression of the development of the oscillations. Let us do this for the scaled problem and \(\Delta t=0.1,0.05,0.01\). A ready-made function

computes the empirical amplitudes and periods, and creates a plot where the amplitudes and angular frequencies are visualized together with the exact amplitude I and the exact angular frequency w. We can make a little program for creating the plot:

Figure 1.3 shows the result: we clearly see that lowering \(\Delta t\) improves the angular frequency significantly, while the amplitude seems to be more accurate. The lines with \(\Delta t=0.01\), corresponding to 100 steps per period, can hardly be distinguished from the exact values. The next section shows how we can get mathematical insight into why amplitudes are good while frequencies are more inaccurate.
1.4 Analysis of the Numerical Scheme
1.4.1 Deriving a Solution of the Numerical Scheme
After having seen the phase error grow with time in the previous section, we shall now quantify this error through mathematical analysis. The key tool in the analysis will be to establish an exact solution of the discrete equations. The difference equation (1.7) has constant coefficients and is homogeneous. Such equations are known to have solutions on the form \(u^{n}=CA^{n}\), where A is some number to be determined from the difference equation and C is found as the initial condition (C = I). Recall that n in u n is a superscript labeling the time level, while n in A n is an exponent.
With oscillating functions as solutions, the algebra will be considerably simplified if we seek an A on the form
and solve for the numerical frequency \(\tilde{\omega}\) rather than A. Note that \(i=\sqrt{-1}\) is the imaginary unit. (Using a complex exponential function gives simpler arithmetics than working with a sine or cosine function.) We have
The physically relevant numerical solution can be taken as the real part of this complex expression.
The calculations go as
The last line follows from the relation \(\cos x-1=-2\sin^{2}(x/2)\) (try cos(x)-1 in wolframalpha.com Footnote 9 to see the formula).
The scheme (1.7) with \(u^{n}=Ie^{i\tilde{\omega}\Delta t\,n}\) inserted now gives
which after dividing by \(Ie^{i\tilde{\omega}t_{n}}\) results in
The first step in solving for the unknown \(\tilde{\omega}\) is
Then, taking the square root, applying the inverse sine function, and multiplying by \(2/\Delta t\), results in
1.4.2 The Error in the Numerical Frequency
The first observation following (1.18) tells that there is a phase error since the numerical frequency \(\tilde{\omega}\) never equals the exact frequency ω. But how good is the approximation (1.18)? That is, what is the error \(\omega-\tilde{\omega}\) or \(\tilde{\omega}/\omega\)? Taylor series expansion for small \(\Delta t\) may give an expression that is easier to understand than the complicated function in (1.18):

This means that
The error in the numerical frequency is of second-order in \(\Delta t\), and the error vanishes as \(\Delta t\rightarrow 0\). We see that \(\tilde{\omega}> \omega\) since the term \(\omega^{3}\Delta t^{2}/24> 0\) and this is by far the biggest term in the series expansion for small \(\omega\Delta t\). A numerical frequency that is too large gives an oscillating curve that oscillates too fast and therefore ‘‘lags behind’’ the exact oscillations, a feature that can be seen in the left plot in Fig. 1.2.
Figure 1.4 plots the discrete frequency (1.18) and its approximation (1.19) for ω = 1 (based on the program vib_plot_freq.py ). Although \(\tilde{\omega}\) is a function of \(\Delta t\) in (1.19), it is misleading to think of \(\Delta t\) as the important discretization parameter. It is the product \(\omega\Delta t\) that is the key discretization parameter. This quantity reflects the number of time steps per period of the oscillations. To see this, we set \(P=N_{P}\Delta t\), where P is the length of a period, and N P is the number of time steps during a period. Since P and ω are related by \(P=2\pi/\omega\), we get that \(\omega\Delta t=2\pi/N_{P}\), which shows that \(\omega\Delta t\) is directly related to N P .
The plot shows that at least \(N_{P}\sim 25-30\) points per period are necessary for reasonable accuracy, but this depends on the length of the simulation (T) as the total phase error due to the frequency error grows linearly with time (see Exercise 1.2).
1.4.3 Empirical Convergence Rates and Adjusted ω
The expression (1.19) suggests that adjusting omega to
could have effect on the convergence rate of the global error in u (cf. Sect. 1.2.2). With the convergence_rates function in vib_undamped.py we can easily check this. A special solver, with adjusted w, is available as the function solver_adjust_w. A call to convergence_rates with this solver reveals that the rate is 4.0! With the original, physical ω the rate is 2.0 – as expected from using second-order finite difference approximations, as expected from the forthcoming derivation of the global error, and as expected from truncation error analysis analysis as explained in Appendix B.4.1.
Adjusting ω is an ideal trick for this simple problem, but when adding damping and nonlinear terms, we have no simple formula for the impact on ω, and therefore we cannot use the trick.
1.4.4 Exact Discrete Solution
Perhaps more important than the \(\tilde{\omega}=\omega+{\cal O}(\Delta t^{2})\) result found above is the fact that we have an exact discrete solution of the problem:
We can then compute the error mesh function
From the formula \(\cos 2x-\cos 2y=-2\sin(x-y)\sin(x+y)\) we can rewrite e n so the expression is easier to interpret:
The error mesh function is ideal for verification purposes and you are strongly encouraged to make a test based on (1.20) by doing Exercise 1.11.
1.4.5 Convergence
We can use (1.19) and (1.21), or (1.22), to show convergence of the numerical scheme, i.e., \(e^{n}\rightarrow 0\) as \(\Delta t\rightarrow 0\), which implies that the numerical solution approaches the exact solution as \(\Delta t\) approaches to zero. We have that
by L’Hopital’s rule. This result could also been computed WolframAlpha Footnote 10, or we could use the limit functionality in sympy:

Also (1.19) can be used to establish that \(\tilde{\omega}\rightarrow\omega\) when \(\Delta t\rightarrow 0\). It then follows from the expression(s) for e n that \(e^{n}\rightarrow 0\).
1.4.6 The Global Error
To achieve more analytical insight into the nature of the global error, we can Taylor expand the error mesh function (1.21). Since \(\tilde{\omega}\) in (1.18) contains \(\Delta t\) in the denominator we use the series expansion for \(\tilde{\omega}\) inside the cosine function. A relevant sympy session is

Series expansions in sympy have the inconvenient O() term that prevents further calculations with the series. We can use the removeO() command to get rid of the O() term:

Using this w_tilde_series expression for \(\tilde{w}\) in (1.21), dropping I (which is a common factor), and performing a series expansion of the error yields

Since we are mainly interested in the leading-order term in such expansions (the term with lowest power in \(\Delta t\), which goes most slowly to zero), we use the .as_leading_term(dt) construction to pick out this term:

The last result means that the leading order global (true) error at a point t is proportional to \(\omega^{3}t\Delta t^{2}\). Considering only the discrete t n values for t, t n is related to \(\Delta t\) through \(t_{n}=n\Delta t\). The factor \(\sin(\omega t)\) can at most be 1, so we use this value to bound the leading-order expression to its maximum value
This is the dominating term of the error at a point.
We are interested in the accumulated global error, which can be taken as the \(\ell^{2}\) norm of e n. The norm is simply computed by summing contributions from all mesh points:
The sum \(\sum_{n=0}^{N_{t}}n^{2}\) is approximately equal to \(\frac{1}{3}N_{t}^{3}\). Replacing N t by \(T/\Delta t\) and taking the square root gives the expression
This is our expression for the global (or integrated) error. A primary result from this expression is that the global error is proportional to \(\Delta t^{2}\).
1.4.7 Stability
Looking at (1.20), it appears that the numerical solution has constant and correct amplitude, but an error in the angular frequency. A constant amplitude is not necessarily the case, however! To see this, note that if only \(\Delta t\) is large enough, the magnitude of the argument to \(\sin^{-1}\) in (1.18) may be larger than 1, i.e., \(\omega\Delta t/2> 1\). In this case, \(\sin^{-1}(\omega\Delta t/2)\) has a complex value and therefore \(\tilde{\omega}\) becomes complex. Type, for example, asin(x) in wolframalpha.com Footnote 11 to see basic properties of \(\sin^{-1}(x)\).
A complex \(\tilde{\omega}\) can be written \(\tilde{\omega}=\tilde{\omega}_{r}+i\tilde{\omega}_{i}\). Since \(\sin^{-1}(x)\) has a negative imaginary part for x > 1, \(\tilde{\omega}_{i}<0\), which means that \(e^{i\tilde{\omega}t}=e^{-\tilde{\omega}_{i}t}e^{i\tilde{\omega}_{r}t}\) will lead to exponential growth in time because \(e^{-\tilde{\omega}_{i}t}\) with \(\tilde{\omega}_{i}<0\) has a positive exponent.
Stability criterion
We do not tolerate growth in the amplitude since such growth is not present in the exact solution. Therefore, we must impose a stability criterion so that the argument in the inverse sine function leads to real and not complex values of \(\tilde{\omega}\). The stability criterion reads
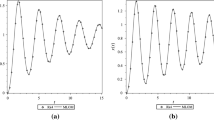
With \(\omega=2\pi\), \(\Delta t> \pi^{-1}=0.3183098861837907\) will give growing solutions. Figure 1.5 displays what happens when \(\Delta t=0.3184\), which is slightly above the critical value: \(\Delta t=\pi^{-1}+9.01\cdot 10^{-5}\).
1.4.8 About the Accuracy at the Stability Limit
An interesting question is whether the stability condition \(\Delta t<2/\omega\) is unfortunate, or more precisely: would it be meaningful to take larger time steps to speed up computations? The answer is a clear no. At the stability limit, we have that \(\sin^{-1}\omega\Delta t/2=\sin^{-1}1=\pi/2\), and therefore \(\tilde{\omega}=\pi/\Delta t\). (Note that the approximate formula (1.19) is very inaccurate for this value of \(\Delta t\) as it predicts \(\tilde{\omega}=2.34/pi\), which is a 25 percent reduction.) The corresponding period of the numerical solution is \(\tilde{P}=2\pi/\tilde{\omega}=2\Delta t\), which means that there is just one time step \(\Delta t\) between a peak (maximum) and a through Footnote 12 (minimum) in the numerical solution. This is the shortest possible wave that can be represented in the mesh! In other words, it is not meaningful to use a larger time step than the stability limit.
Also, the error in angular frequency when \(\Delta t=2/\omega\) is severe: Figure 1.6 shows a comparison of the numerical and analytical solution with \(\omega=2\pi\) and \(\Delta t=2/\omega=\pi^{-1}\). Already after one period, the numerical solution has a through while the exact solution has a peak (!). The error in frequency when \(\Delta t\) is at the stability limit becomes \(\omega-\tilde{\omega}=\omega(1-\pi/2)\approx-0.57\omega\). The corresponding error in the period is \(P-\tilde{P}\approx 0.36P\). The error after m periods is then 0.36mP. This error has reached half a period when \(m=1/(2\cdot 0.36)\approx 1.38\), which theoretically confirms the observations in Fig. 1.6 that the numerical solution is a through ahead of a peak already after one and a half period. Consequently, \(\Delta t\) should be chosen much less than the stability limit to achieve meaningful numerical computations.
Summary
From the accuracy and stability analysis we can draw three important conclusions:
-
1.
The key parameter in the formulas is \(p=\omega\Delta t\). The period of oscillations is \(P=2\pi/\omega\), and the number of time steps per period is \(N_{P}=P/\Delta t\). Therefore, \(p=\omega\Delta t=2\pi/N_{P}\), showing that the critical parameter is the number of time steps per period. The smallest possible N P is 2, showing that \(p\in(0,\pi]\).
-
2.
Provided p ≤ 2, the amplitude of the numerical solution is constant.
-
3.
The ratio of the numerical angular frequency and the exact one is \(\tilde{\omega}/\omega\approx 1+\frac{1}{24}p^{2}\). The error \(\frac{1}{24}p^{2}\) leads to wrongly displaced peaks of the numerical solution, and the error in peak location grows linearly with time (see Exercise 1.2).
1.5 Alternative Schemes Based on 1st-Order Equations
A standard technique for solving second-order ODEs is to rewrite them as a system of first-order ODEs and then choose a solution strategy from the vast collection of methods for first-order ODE systems. Given the second-order ODE problem
we introduce the auxiliary variable \(v=u^{\prime}\) and express the ODE problem in terms of first-order derivatives of u and v:
The initial conditions become \(u(0)=I\) and \(v(0)=0\).
1.5.1 The Forward Euler Scheme
A Forward Euler approximation to our 2 × 2 system of ODEs (1.24)–(1.25) becomes
or written out,
Let us briefly compare this Forward Euler method with the centered difference scheme for the second-order differential equation. We have from (1.28) and (1.29) applied at levels n and n − 1 that
Since from (1.28)
it follows that
which is very close to the centered difference scheme, but the last term is evaluated at \(t_{n-1}\) instead of t n . Rewriting, so that \(\Delta t^{2}\omega^{2}u^{n-1}\) appears alone on the right-hand side, and then dividing by \(\Delta t^{2}\), the new left-hand side is an approximation to \(u^{\prime\prime}\) at t n , while the right-hand side is sampled at \(t_{n-1}\). All terms should be sampled at the same mesh point, so using \(\omega^{2}u^{n-1}\) instead of \(\omega^{2}u^{n}\) points to a kind of mathematical error in the derivation of the scheme. This error turns out to be rather crucial for the accuracy of the Forward Euler method applied to vibration problems (Sect. 1.5.4 has examples).
The reasoning above does not imply that the Forward Euler scheme is not correct, but more that it is almost equivalent to a second-order accurate scheme for the second-order ODE formulation, and that the error committed has to do with a wrong sampling point.
1.5.2 The Backward Euler Scheme
A Backward Euler approximation to the ODE system is equally easy to write up in the operator notation:
This becomes a coupled system for \(u^{n+1}\) and \(v^{n+1}\):
We can compare (1.32)–(1.33) with the centered scheme (1.7) for the second-order differential equation. To this end, we eliminate \(v^{n+1}\) in (1.32) using (1.33) solved with respect to \(v^{n+1}\). Thereafter, we eliminate v n using (1.32) solved with respect to \(v^{n+1}\) and also replacing n + 1 by n and n by n − 1. The resulting equation involving only \(u^{n+1}\), u n, and \(u^{n-1}\) can be ordered as
which has almost the same form as the centered scheme for the second-order differential equation, but the right-hand side is evaluated at \(u^{n+1}\) and not u n. This inconsistent sampling of terms has a dramatic effect on the numerical solution, as we demonstrate in Sect. 1.5.4.
1.5.3 The Crank-Nicolson Scheme
The Crank-Nicolson scheme takes this form in the operator notation:
Writing the equations out and rearranging terms, shows that this is also a coupled system of two linear equations at each time level:
We may compare also this scheme to the centered discretization of the second-order ODE. It turns out that the Crank-Nicolson scheme is equivalent to the discretization
That is, the Crank-Nicolson is equivalent to (1.7) for the second-order ODE, apart from an extra term of size \(\Delta t^{2}\), but this is an error of the same order as in the finite difference approximation on the left-hand side of the equation anyway. The fact that the Crank-Nicolson scheme is so close to (1.7) makes it a much better method than the Forward or Backward Euler methods for vibration problems, as will be illustrated in Sect. 1.5.4.
Deriving (1.38) is a bit tricky. We start with rewriting the Crank-Nicolson equations as follows
and add the latter at the previous time level as well:
We can also rewrite (1.39) at the previous time level as
Inserting (1.40) for \(v^{n+1}\) in (1.39) and (1.41) for v n in (1.39) yields after some reordering:
Now, \(v^{n}+v^{n-1}\) can be eliminated by means of (1.42). The result becomes
It can be shown that
meaning that (1.43) is an approximation to the centered scheme (1.7) for the second-order ODE where the sampling error in the term \(\Delta t^{2}\omega^{2}u^{n}\) is of the same order as the approximation errors in the finite differences, i.e., \(\mathcal{O}(\Delta t^{2})\). The Crank-Nicolson scheme written as (1.43) therefore has consistent sampling of all terms at the same time point t n .
1.5.4 Comparison of Schemes
We can easily compare methods like the ones above (and many more!) with the aid of the Odespy Footnote 13 package. Below is a sketch of the code.

There is quite some more code dealing with plots also, and we refer to the source file vib_undamped_odespy.py for details. Observe that keyword arguments in f(u,t,w=1) can be supplied through a solver parameter f_kwargs (dictionary of additional keyword arguments to f).
Specification of the Forward Euler, Backward Euler, and Crank-Nicolson schemes is done like this:

The vib_undamped_odespy.py program makes two plots of the computed solutions with the various methods in the solvers list: one plot with u(t) versus t, and one phase plane plot where v is plotted against u. That is, the phase plane plot is the curve \((u(t),v(t))\) parameterized by t. Analytically, \(u=I\cos(\omega t)\) and \(v=u^{\prime}=-\omega I\sin(\omega t)\). The exact curve \((u(t),v(t))\) is therefore an ellipse, which often looks like a circle in a plot if the axes are automatically scaled. The important feature, however, is that the exact curve \((u(t),v(t))\) is closed and repeats itself for every period. Not all numerical schemes are capable of doing that, meaning that the amplitude instead shrinks or grows with time.
Figure 1.7 show the results. Note that Odespy applies the label MidpointImplicit for what we have specified as CrankNicolson in the code (CrankNicolson is just a synonym for class MidpointImplicit in the Odespy code). The Forward Euler scheme in Fig. 1.7 has a pronounced spiral curve, pointing to the fact that the amplitude steadily grows, which is also evident in Fig. 1.8. The Backward Euler scheme has a similar feature, except that the spriral goes inward and the amplitude is significantly damped. The changing amplitude and the spiral form decreases with decreasing time step. The Crank-Nicolson scheme looks much more accurate. In fact, these plots tell that the Forward and Backward Euler schemes are not suitable for solving our ODEs with oscillating solutions.
1.5.5 Runge-Kutta Methods
We may run two other popular standard methods for first-order ODEs, the 2nd- and 4th-order Runge-Kutta methods, to see how they perform. Figures 1.9 and 1.10 show the solutions with larger \(\Delta t\) values than what was used in the previous two plots.
The visual impression is that the 4th-order Runge-Kutta method is very accurate, under all circumstances in these tests, while the 2nd-order scheme suffers from amplitude errors unless the time step is very small.
The corresponding results for the Crank-Nicolson scheme are shown in Fig. 1.11. It is clear that the Crank-Nicolson scheme outperforms the 2nd-order Runge-Kutta method. Both schemes have the same order of accuracy \(\mathcal{O}(\Delta t^{2})\), but their differences in the accuracy that matters in a real physical application is very clearly pronounced in this example. Exercise 1.13 invites you to investigate how the amplitude is computed by a series of famous methods for first-order ODEs.
1.5.6 Analysis of the Forward Euler Scheme
We may try to find exact solutions of the discrete equations (1.28)–(1.29) in the Forward Euler method to better understand why this otherwise useful method has so bad performance for vibration ODEs. An ‘‘ansatz’’ for the solution of the discrete equations is
where q and A are scalars to be determined. We could have used a complex exponential form \(e^{i\tilde{\omega}n\Delta t}\) since we get oscillatory solutions, but the oscillations grow in the Forward Euler method, so the numerical frequency \(\tilde{\omega}\) will be complex anyway (producing an exponentially growing amplitude). Therefore, it is easier to just work with potentially complex A and q as introduced above.
The Forward Euler scheme leads to
We can easily eliminate A, get \(q^{2}+\omega^{2}=0\), and solve for
which gives
We shall take the real part of A n as the solution. The two values of A are complex conjugates, and the real part of A n will be the same for both roots. This is easy to realize if we rewrite the complex numbers in polar form, which is also convenient for further analysis and understanding. The polar form \(re^{i\theta}\) of a complex number x + iy has \(r=\sqrt{x^{2}+y^{2}}\) and \(\theta=\tan^{-1}(y/x)\). Hence, the polar form of the two values for A becomes
Now it is very easy to compute A n:
Since \(\cos(\theta n)=\cos(-\theta n)\), the real parts of the two numbers become the same. We therefore continue with the solution that has the plus sign.
The general solution is \(u^{n}=CA^{n}\), where C is a constant determined from the initial condition: \(u^{0}=C=I\). We have \(u^{n}=IA^{n}\) and \(v^{n}=qIA^{n}\). The final solutions are just the real part of the expressions in polar form:
The expression \((1+\omega^{2}\Delta t^{2})^{n/2}\) causes growth of the amplitude, since a number greater than one is raised to a positive exponent n ∕ 2. We can develop a series expression to better understand the formula for the amplitude. Introducing \(p=\omega\Delta t\) as the key variable and using sympy gives

The amplitude goes like \(1+\frac{1}{2}n\omega^{2}\Delta t^{2}\), clearly growing linearly in time (with n).
We can also investigate the error in the angular frequency by a series expansion:

This means that the solution for u n can be written as
The error in the angular frequency is of the same order as in the scheme (1.7) for the second-order ODE, but the error in the amplitude is severe.
1.6 Energy Considerations
The observations of various methods in the previous section can be better interpreted if we compute a quantity reflecting the total energy of the system. It turns out that this quantity,
is constant for all t. Checking that E(t) really remains constant brings evidence that the numerical computations are sound. It turns out that E is proportional to the mechanical energy in the system. Conservation of energy is much used to check numerical simulations, so it is well invested time to dive into this subject.
1.6.1 Derivation of the Energy Expression
We start out with multiplying
by \(u^{\prime}\) and integrating from 0 to T:
Observing that
we get
where we have introduced
The important result from this derivation is that the total energy is constant:
E(t) is closely related to the system’s energy
The quantity E(t) derived above is physically not the mechanical energy of a vibrating mechanical system, but the energy per unit mass. To see this, we start with Newton’s second law F = ma (F is the sum of forces, m is the mass of the system, and a is the acceleration). The displacement u is related to a through \(a=u^{\prime\prime}\). With a spring force as the only force we have F = −ku, where k is a spring constant measuring the stiffness of the spring. Newton’s second law then implies the differential equation
This equation of motion can be turned into an energy balance equation by finding the work done by each term during a time interval \([0,T]\). To this end, we multiply the equation by \(du=u^{\prime}dt\) and integrate:
The result is
where
is the kinetic energy of the system, and
is the potential energy. The sum \(\tilde{E}(t)\) is the total mechanical energy. The derivation demonstrates the famous energy principle that, under the right physical circumstances, any change in the kinetic energy is due to a change in potential energy and vice versa. (This principle breaks down when we introduce damping in the system, as we do in Sect. 1.10.)
The equation \(mu^{\prime\prime}+ku=0\) can be divided by m and written as \(u^{\prime\prime}+\omega^{2}u=0\) for \(\omega=\sqrt{k/m}\). The energy expression \(E(t)=\frac{1}{2}(u^{\prime})^{2}+\frac{1}{2}\omega^{2}u^{2}\) derived earlier is then \(\tilde{E}(t)/m\), i.e., mechanical energy per unit mass.
Energy of the exact solution
Analytically, we have \(u(t)=I\cos\omega t\), if \(u(0)=I\) and \(u^{\prime}(0)=0\), so we can easily check the energy evolution and confirm that E(t) is constant:
Growth of energy in the Forward Euler scheme
It is easy to show that the energy in the Forward Euler scheme increases when stepping from time level n to n + 1.
1.6.2 An Error Measure Based on Energy
The constant energy is well expressed by its initial value \(E(0)\), so that the error in mechanical energy can be computed as a mesh function by
where
if \(u(0)=I\) and \(u^{\prime}(0)=V\). Note that we have used a centered approximation to \(u^{\prime}\): \(u^{\prime}(t_{n})\approx[D_{2t}u]^{n}\).
A useful norm of the mesh function \(e_{E}^{n}\) for the discrete mechanical energy can be the maximum absolute value of \(e_{E}^{n}\):
Alternatively, we can compute other norms involving integration over all mesh points, but we are often interested in worst case deviation of the energy, and then the maximum value is of particular relevance.
A vectorized Python implementation of \(e_{E}^{n}\) takes the form

The convergence rates of the quantity e_E_norm can be used for verification. The value of e_E_norm is also useful for comparing schemes through their ability to preserve energy. Below is a table demonstrating the relative error in total energy for various schemes (computed by the vib_undamped_odespy.py program). The test problem is \(u^{\prime\prime}+4\pi^{2}u=0\) with \(u(0)=1\) and \(u^{\prime}(0)=0\), so the period is 1 and \(E(t)\approx 4.93\). We clearly see that the Crank-Nicolson and the Runge-Kutta schemes are superior to the Forward and Backward Euler schemes already after one period.
Method | T | \(\Delta t\) | \(\max\left|e_{E}^{n}\right|/e_{E}^{0}\) |
|---|---|---|---|
Forward Euler | 1 | 0.025 | \(1.678\cdot 10^{0}\) |
Backward Euler | 1 | 0.025 | \(6.235\cdot 10^{-1}\) |
Crank-Nicolson | 1 | 0.025 | \(1.221\cdot 10^{-2}\) |
Runge-Kutta 2nd-order | 1 | 0.025 | \(6.076\cdot 10^{-3}\) |
Runge-Kutta 4th-order | 1 | 0.025 | \(8.214\cdot 10^{-3}\) |
However, after 10 periods, the picture is much more dramatic:
Method | T | \(\Delta t\) | \(\max\left|e_{E}^{n}\right|/e_{E}^{0}\) |
|---|---|---|---|
Forward Euler | 10 | 0.025 | \(1.788\cdot 10^{4}\) |
Backward Euler | 10 | 0.025 | \(1.000\cdot 10^{0}\) |
Crank-Nicolson | 10 | 0.025 | \(1.221\cdot 10^{-2}\) |
Runge-Kutta 2nd-order | 10 | 0.025 | \(6.250\cdot 10^{-2}\) |
Runge-Kutta 4th-order | 10 | 0.025 | \(8.288\cdot 10^{-3}\) |
The Runge-Kutta and Crank-Nicolson methods hardly change their energy error with T, while the error in the Forward Euler method grows to huge levels and a relative error of 1 in the Backward Euler method points to \(E(t)\rightarrow 0\) as t grows large.
Running multiple values of \(\Delta t\), we can get some insight into the convergence of the energy error:
Method | T | \(\Delta t\) | \(\max\left|e_{E}^{n}\right|/e_{E}^{0}\) |
|---|---|---|---|
Forward Euler | 10 | 0.05 | \(1.120\cdot 10^{8}\) |
Forward Euler | 10 | 0.025 | \(1.788\cdot 10^{4}\) |
Forward Euler | 10 | 0.0125 | \(1.374\cdot 10^{2}\) |
Backward Euler | 10 | 0.05 | \(1.000\cdot 10^{0}\) |
Backward Euler | 10 | 0.025 | \(1.000\cdot 10^{0}\) |
Backward Euler | 10 | 0.0125 | \(9.928\cdot 10^{-1}\) |
Crank-Nicolson | 10 | 0.05 | \(4.756\cdot 10^{-2}\) |
Crank-Nicolson | 10 | 0.025 | \(1.221\cdot 10^{-2}\) |
Crank-Nicolson | 10 | 0.0125 | \(3.125\cdot 10^{-3}\) |
Runge-Kutta 2nd-order | 10 | 0.05 | \(6.152\cdot 10^{-1}\) |
Runge-Kutta 2nd-order | 10 | 0.025 | \(6.250\cdot 10^{-2}\) |
Runge-Kutta 2nd-order | 10 | 0.0125 | \(7.631\cdot 10^{-3}\) |
Runge-Kutta 4th-order | 10 | 0.05 | \(3.510\cdot 10^{-2}\) |
Runge-Kutta 4th-order | 10 | 0.025 | \(8.288\cdot 10^{-3}\) |
Runge-Kutta 4th-order | 10 | 0.0125 | \(2.058\cdot 10^{-3}\) |
A striking fact from this table is that the error of the Forward Euler method is reduced by the same factor as \(\Delta t\) is reduced by, while the error in the Crank-Nicolson method has a reduction proportional to \(\Delta t^{2}\) (we cannot say anything for the Backward Euler method). However, for the RK2 method, halving \(\Delta t\) reduces the error by almost a factor of 10 (!), and for the RK4 method the reduction seems proportional to \(\Delta t^{2}\) only (and the trend is confirmed by running smaller time steps, so for \(\Delta t=3.9\cdot 10^{-4}\) the relative error of RK2 is a factor 10 smaller than that of RK4!).
1.7 The Euler-Cromer Method
While the Runge-Kutta methods and the Crank-Nicolson scheme work well for the vibration equation modeled as a first-order ODE system, both were inferior to the straightforward centered difference scheme for the second-order equation \(u^{\prime\prime}+\omega^{2}u=0\). However, there is a similarly successful scheme available for the first-order system \(u^{\prime}=v\), \(v^{\prime}=-\omega^{2}u\), to be presented below. The ideas of the scheme and their further developments have become very popular in particle and rigid body dynamics and hence are widely used by physicists.
1.7.1 Forward-Backward Discretization
The idea is to apply a Forward Euler discretization to the first equation and a Backward Euler discretization to the second. In operator notation this is stated as
We can write out the formulas and collect the unknowns on the left-hand side:
We realize that after \(u^{n+1}\) has been computed from (1.52), it may be used directly in (1.53) to compute \(v^{n+1}\).
In physics, it is more common to update the v equation first, with a forward difference, and thereafter the u equation, with a backward difference that applies the most recently computed v value:
The advantage of ordering the ODEs as in (1.54)–(1.55) becomes evident when considering complicated models. Such models are included if we write our vibration ODE more generally as
We can rewrite this second-order ODE as two first-order ODEs,
This rewrite allows the following scheme to be used:
We realize that the first update works well with any g since old values u n and v n are used. Switching the equations would demand \(u^{n+1}\) and \(v^{n+1}\) values in g and result in nonlinear algebraic equations to be solved at each time level.
The scheme (1.54)–(1.55) goes under several names: forward-backward scheme, semi-implicit Euler method Footnote 14, semi-explicit Euler, symplectic Euler, Newton-Störmer-Verlet, and Euler-Cromer. We shall stick to the latter name.
How does the Euler-Cromer method preserve the total energy? We may run the example from Sect. 1.6.2:
Method | T | \(\Delta t\) | \(\max\left|e_{E}^{n}\right|/e_{E}^{0}\) |
|---|---|---|---|
Euler-Cromer | 10 | 0.05 | \(2.530\cdot 10^{-2}\) |
Euler-Cromer | 10 | 0.025 | \(6.206\cdot 10^{-3}\) |
Euler-Cromer | 10 | 0.0125 | \(1.544\cdot 10^{-3}\) |
The relative error in the total energy decreases as \(\Delta t^{2}\), and the error level is slightly lower than for the Crank-Nicolson and Runge-Kutta methods.
1.7.2 Equivalence with the Scheme for the Second-Order ODE
We shall now show that the Euler-Cromer scheme for the system of first-order equations is equivalent to the centered finite difference method for the second-order vibration ODE (!).
We may eliminate the v n variable from (1.52)–(1.53) or (1.54)–(1.55). The \(v^{n+1}\) term in (1.54) can be eliminated from (1.55):
The v n quantity can be expressed by u n and \(u^{n-1}\) using (1.55):
and when this is inserted in (1.56) we get
which is nothing but the centered scheme (1.7)! The two seemingly different numerical methods are mathematically equivalent. Consequently, the previous analysis of (1.7) also applies to the Euler-Cromer method. In particular, the amplitude is constant, given that the stability criterion is fulfilled, but there is always an angular frequency error (1.19). Exercise 1.18 gives guidance on how to derive the exact discrete solution of the two equations in the Euler-Cromer method.
Although the Euler-Cromer scheme and the method (1.7) are equivalent, there could be differences in the way they handle the initial conditions. Let us look into this topic. The initial condition \(u^{\prime}=0\) means \(u^{\prime}=v=0\). From (1.54) we get
and from (1.55) it follows that
When we previously used a centered approximation of \(u^{\prime}(0)=0\) combined with the discretization (1.7) of the second-order ODE, we got a slightly different result: \(u^{1}=u^{0}-\frac{1}{2}\omega^{2}\Delta t^{2}u^{0}\). The difference is \(\frac{1}{2}\omega^{2}\Delta t^{2}u^{0}\), which is of second order in \(\Delta t\), seemingly consistent with the overall error in the scheme for the differential equation model.
A different view can also be taken. If we approximate \(u^{\prime}(0)=0\) by a backward difference, \((u^{0}-u^{-1})/\Delta t=0\), we get \(u^{-1}=u^{0}\), and when combined with (1.7), it results in \(u^{1}=u^{0}-\omega^{2}\Delta t^{2}u^{0}\). This means that the Euler-Cromer method based on (1.55)–(1.54) corresponds to using only a first-order approximation to the initial condition in the method from Sect. 1.1.2.
Correspondingly, using the formulation (1.52)–(1.53) with \(v^{n}=0\) leads to \(u^{1}=u^{0}\), which can be interpreted as using a forward difference approximation for the initial condition \(u^{\prime}(0)=0\). Both Euler-Cromer formulations lead to slightly different values for u 1 compared to the method in Sect. 1.1.2. The error is \(\frac{1}{2}\omega^{2}\Delta t^{2}u^{0}\).
1.7.3 Implementation
Solver function
The function below, found in vib_undamped_EulerCromer.py , implements the Euler-Cromer scheme (1.54)–(1.55):

Verification
Since the Euler-Cromer scheme is equivalent to the finite difference method for the second-order ODE \(u^{\prime\prime}+\omega^{2}u=0\) (see Sect. 1.7.2), the performance of the above solver function is the same as for the solver function in Sect. 1.2. The only difference is the formula for the first time step, as discussed above. This deviation in the Euler-Cromer scheme means that the discrete solution listed in Sect. 1.4.4 is not a solution of the Euler-Cromer scheme!
To verify the implementation of the Euler-Cromer method we can adjust v[1] so that the computer-generated values can be compared with the formula (1.20) from in Sect. 1.4.4. This adjustment is done in an alternative solver function, solver_ic_fix in vib_EulerCromer.py. Since we now have an exact solution of the discrete equations available, we can write a test function test_solver for checking the equality of computed values with the formula (1.20):

Another function, demo, visualizes the difference between the Euler-Cromer scheme and the scheme (1.7) for the second-oder ODE, arising from the mismatch in the first time level.
Using Odespy
The Euler-Cromer method is also available in the Odespy package. The important thing to remember, when using this implementation, is that we must order the unknowns as v and u, so the u vector at each time level consists of the velocity v as first component and the displacement u as second component:

Convergence rates
We may use the convergence_rates function in the file vib_undamped.py to investigate the convergence rate of the Euler-Cromer method, see the convergence_rate function in the file vib_undamped_EulerCromer.py. Since we could eliminate v to get a scheme for u that is equivalent to the finite difference method for the second-order equation in u, we would expect the convergence rates to be the same, i.e., r = 2. However, measuring the convergence rate of u in the Euler-Cromer scheme shows that r = 1 only! Adjusting the initial condition does not change the rate. Adjusting ω, as outlined in Sect. 1.4.2, gives a 4th-order method there, while there is no increase in the measured rate in the Euler-Cromer scheme. It is obvious that the Euler-Cromer scheme is dramatically much better than the two other first-order methods, Forward Euler and Backward Euler, but this is not reflected in the convergence rate of u.
1.7.4 The Störmer-Verlet Algorithm
Another very popular algorithm for vibration problems, especially for long time simulations, is the Störmer-Verlet algorithm. It has become the method among physicists for molecular simulations as well as particle and rigid body dynamics.
The method can be derived by applying the Euler-Cromer idea twice, in a symmetric fashion, during the interval \([t_{n},t_{n+1}]\):
-
1.
solve \(v^{\prime}=-\omega u\) by a Forward Euler step in \([t_{n},t_{n+\frac{1}{2}}]\)
-
2.
solve \(u^{\prime}=v\) by a Backward Euler step in \([t_{n},t_{n+\frac{1}{2}}]\)
-
3.
solve \(u^{\prime}=v\) by a Forward Euler step in \([t_{n+\frac{1}{2}},t_{n+1}]\)
-
4.
solve \(v^{\prime}=-\omega u\) by a Backward Euler step in \([t_{n+\frac{1}{2}},t_{n+1}]\)
With mathematics,
The two steps in the middle can be combined to
and consequently
Writing the last equation as \(v^{n}=v^{n-\frac{1}{2}}-\frac{1}{2}\Delta t\omega^{2}u^{n}\) and using this v n in the first equation gives \(v^{n+\frac{1}{2}}=v^{n-\frac{1}{2}}-\Delta t\omega^{2}u^{n}\), and the scheme can be written as two steps:
which is nothing but straightforward centered differences for the 2 × 2 ODE system on a staggered mesh, see Sect. 1.8.1. We have thus seen that four different reasonings (discretizing \(u^{\prime\prime}+\omega^{2}u\) directly, using Euler-Cromer, using Stömer-Verlet, and using centered differences for the 2 × 2 system on a staggered mesh) all end up with the same equations! The main difference is that the traditional Euler-Cromer displays first-order convergence in \(\Delta t\) (due to less symmetry in the way u and v are treated) while the others are \(\mathcal{O}(\Delta t^{2})\) schemes.
The most numerically stable scheme, with respect to accumulation of rounding errors, is (1.61)–(1.62). It has, according to [6], better properties in this regard than the direct scheme for the second-order ODE.
1.8 Staggered Mesh
A more intuitive discretization than the Euler-Cromer method, yet equivalent, employs solely centered differences in a natural way for the 2 × 2 first-order ODE system. The scheme is in fact fully equivalent to the second-order scheme for \(u^{\prime\prime}+\omega u=0\), also for the first time step. Such a scheme needs to operate on a staggered mesh in time. Staggered meshes are very popular in many physical application, maybe foremost fluid dynamics and electromagnetics, so the topic is important to learn.
1.8.1 The Euler-Cromer Scheme on a Staggered Mesh
In a staggered mesh, the unknowns are sought at different points in the mesh. Specifically, u is sought at integer time points t n and v is sought at \(t_{n+1/2}\) between two u points. The unknowns are then \(u^{1},v^{3/2},u^{2},v^{5/2}\), and so on. We typically use the notation u n and \(v^{n+\frac{1}{2}}\) for the two unknown mesh functions. Figure 1.12 presents a graphical sketch of two mesh functions u and v on a staggered mesh.
On a staggered mesh it is natural to use centered difference approximations, expressed in operator notation as
or if we switch the sequence of the equations:
Writing out the formulas gives
We can eliminate the v values and get back the centered scheme based on the second-order differential equation \(u^{\prime\prime}+\omega^{2}u=0\), so all these three schemes are equivalent. However, they differ somewhat in the treatment of the initial conditions.
Suppose we have \(u(0)=I\) and \(u^{\prime}(0)=v(0)=0\) as mathematical initial conditions. This means \(u^{0}=I\) and
Using the discretized equation (1.67) for n = 0 yields
and eliminating \(v^{-\frac{1}{2}}=-v^{\frac{1}{2}}\) results in
and
which is exactly the same equation for u 1 as we had in the centered scheme based on the second-order differential equation (and hence corresponds to a centered difference approximation of the initial condition for \(u^{\prime}(0)\)). The conclusion is that a staggered mesh is fully equivalent with that scheme, while the forward-backward version gives a slight deviation in the computation of u 1.
We can redo the derivation of the initial conditions when \(u^{\prime}(0)=V\):
Using this \(v^{-\frac{1}{2}}\) in
then gives \(v^{\frac{1}{2}}=V-\frac{1}{2}\Delta t\omega^{2}I\). The general initial conditions are therefore
1.8.2 Implementation of the Scheme on a Staggered Mesh
The algorithm goes like this:
- 1.
-
2.
For \(n=1,2,\ldots\):
Implementation with integer indices
Translating the schemes (1.68) and (1.67) to computer code faces the problem of how to store and access \(v^{n+\frac{1}{2}}\), since arrays only allow integer indices with base 0. We must then introduce a convention: \(v^{1+\frac{1}{2}}\) is stored in v[n] while \(v^{1-\frac{1}{2}}\) is stored in v[n-1]. We can then write the algorithm in Python as

Note that u and v are returned together with the mesh points such that the complete mesh function for u is described by u and t, while v and t_v represent the mesh function for v.
Implementation with half-integer indices
Some prefer to see a closer relationship between the code and the mathematics for the quantities with half-integer indices. For example, we would like to replace the updating equation for v[n] by

This is easy to do if we could be sure that n+half means n and n-half means n-1. A possible solution is to define half as a special object such that an integer plus half results in the integer, while an integer minus half equals the integer minus 1. A simple Python class may realize the half object:

The __radd__ function is invoked for all expressions n+half (″right add″ with self as half and other as n). Similarly, the __rsub__ function is invoked for n-half and results in n-1.
Using the half object, we can implement the algorithms in an even more readable way:

Verification of this code is easy as we can just compare the computed u with the u produced by the solver function in vib_undamped.py (which solves \(u^{\prime\prime}+\omega^{2}u=0\) directly). The values should coincide to machine precision since the two numerical methods are mathematically equivalent. We refer to the file vib_undamped_staggered.py for the details of a unit test (test_staggered) that checks this property.
1.9 Exercises and Problems
Problem 1.1 (Use linear/quadratic functions for verification)
Consider the ODE problem
-
a)
Discretize this equation according to \([D_{t}D_{t}u+\omega^{2}u=f]^{n}\) and derive the equation for the first time step (u 1).
-
b)
For verification purposes, we use the method of manufactured solutions (MMS) with the choice of \(u_{\mbox{\footnotesize e}}(t)=ct+d\). Find restrictions on c and d from the initial conditions. Compute the corresponding source term f. Show that \([D_{t}D_{t}t]^{n}=0\) and use the fact that the \(D_{t}D_{t}\) operator is linear, \([D_{t}D_{t}(ct+d)]^{n}=c[D_{t}D_{t}t]^{n}+[D_{t}D_{t}d]^{n}=0\), to show that \(u_{\mbox{\footnotesize e}}\) is also a perfect solution of the discrete equations.
-
c)
Use sympy to do the symbolic calculations above. Here is a sketch of the program vib_undamped_verify_mms.py:

Fill in the various functions such that the calls in the main function works.
-
d)
The purpose now is to choose a quadratic function \(u_{\mbox{\footnotesize e}}=bt^{2}+ct+d\) as exact solution. Extend the sympy code above with a function quadratic for fitting f and checking if the discrete equations are fulfilled. (The function is very similar to linear.)
-
e)
Will a polynomial of degree three fulfill the discrete equations?
-
f)
Implement a solver function for computing the numerical solution of this problem.
-
g)
Write a test function for checking that the quadratic solution is computed correctly (to machine precision, but the round-off errors accumulate and increase with T) by the solver function.
Filename: vib_undamped_verify_mms.
Exercise 1.2 (Show linear growth of the phase with time)
Consider an exact solution \(I\cos(\omega t)\) and an approximation \(I\cos(\tilde{\omega}t)\). Define the phase error as the time lag between the peak I in the exact solution and the corresponding peak in the approximation after m periods of oscillations. Show that this phase error is linear in m.
Filename: vib_phase_error_growth.
Exercise 1.3 (Improve the accuracy by adjusting the frequency)
According to (1.19), the numerical frequency deviates from the exact frequency by a (dominating) amount \(\omega^{3}\Delta t^{2}/24> 0\). Replace the w parameter in the algorithm in the solver function in vib_undamped.py by w*(1 - (1./24)*w**2*dt**2 and test how this adjustment in the numerical algorithm improves the accuracy (use \(\Delta t=0.1\) and simulate for 80 periods, with and without adjustment of ω).
Filename: vib_adjust_w.
Exercise 1.4 (See if adaptive methods improve the phase error)
Adaptive methods for solving ODEs aim at adjusting \(\Delta t\) such that the error is within a user-prescribed tolerance. Implement the equation \(u^{\prime\prime}+u=0\) in the Odespy Footnote 15 software. Use the example from Section 3.2.11 in [9]. Run the scheme with a very low tolerance (say 10−14) and for a long time, check the number of time points in the solver’s mesh (len(solver.t_all)), and compare the phase error with that produced by the simple finite difference method from Sect. 1.1.2 with the same number of (equally spaced) mesh points. The question is whether it pays off to use an adaptive solver or if equally many points with a simple method gives about the same accuracy.
Filename: vib_undamped_adaptive.
Exercise 1.5 (Use a Taylor polynomial to compute u 1)
As an alternative to computing u 1 by (1.8), one can use a Taylor polynomial with three terms:
With \(u^{\prime\prime}=-\omega^{2}u\) and \(u^{\prime}(0)=0\), show that this method also leads to (1.8). Generalize the condition on \(u^{\prime}(0)\) to be \(u^{\prime}(0)=V\) and compute u 1 in this case with both methods.
Filename: vib_first_step.
Problem 1.6 (Derive and investigate the velocity Verlet method)
The velocity Verlet method for \(u^{\prime\prime}+\omega^{2}u=0\) is based on the following ideas:
-
1.
step u forward from t n to \(t_{n+1}\) using a three-term Taylor series,
-
2.
replace \(u^{\prime\prime}\) by \(-\omega^{2}u\)
-
3.
discretize \(v^{\prime}=-\omega^{2}u\) by a Crank-Nicolson method.
Derive the scheme, implement it, and determine empirically the convergence rate.
Problem 1.7 (Find the minimal resolution of an oscillatory function)
Sketch the function on a given mesh which has the highest possible frequency. That is, this oscillatory ‘‘cos-like’’ function has its maxima and minima at every two grid points. Find an expression for the frequency of this function, and use the result to find the largest relevant value of \(\omega\Delta t\) when ω is the frequency of an oscillating function and \(\Delta t\) is the mesh spacing.
Filename: vib_largest_wdt.
Exercise 1.8 (Visualize the accuracy of finite differences for a cosine function)
We introduce the error fraction
to measure the error in the finite difference approximation \(D_{t}D_{t}u\) to \(u^{\prime\prime}\). Compute E for the specific choice of a cosine/sine function of the form \(u=\exp{(i\omega t)}\) and show that
Plot E as a function of \(p=\omega\Delta t\). The relevant values of p are \([0,\pi]\) (see Exercise 1.7 for why p > π does not make sense). The deviation of the curve from unity visualizes the error in the approximation. Also expand E as a Taylor polynomial in p up to fourth degree (use, e.g., sympy).
Filename: vib_plot_fd_exp_error.
Exercise 1.9 (Verify convergence rates of the error in energy)
We consider the ODE problem \(u^{\prime\prime}+\omega^{2}u=0\), \(u(0)=I\), \(u^{\prime}(0)=V\), for \(t\in(0,T]\). The total energy of the solution \(E(t)=\frac{1}{2}(u^{\prime})^{2}+\frac{1}{2}\omega^{2}u^{2}\) should stay constant. The error in energy can be computed as explained in Sect. 1.6.
Make a test function in a separate file, where code from vib_undamped.py is imported, but the convergence_rates and test_convergence_rates functions are copied and modified to also incorporate computations of the error in energy and the convergence rate of this error. The expected rate is 2, just as for the solution itself.
Filename: test_error_conv.
Exercise 1.10 (Use linear/quadratic functions for verification)
This exercise is a generalization of Problem 1.1 to the extended model problem (1.71) where the damping term is either linear or quadratic. Solve the various subproblems and see how the results and problem settings change with the generalized ODE in case of linear or quadratic damping. By modifying the code from Problem 1.1, sympy will do most of the work required to analyze the generalized problem.
Filename: vib_verify_mms.
Exercise 1.11 (Use an exact discrete solution for verification)
Write a test function in a separate file that employs the exact discrete solution (1.20) to verify the implementation of the solver function in the file vib_undamped.py.
Filename: test_vib_undamped_exact_discrete_sol.
Exercise 1.12 (Use analytical solution for convergence rate tests)
The purpose of this exercise is to perform convergence tests of the problem (1.71) when \(s(u)=cu\), \(F(t)=A\sin\phi t\) and there is no damping. Find the complete analytical solution to the problem in this case (most textbooks on mechanics or ordinary differential equations list the various elements you need to write down the exact solution, or you can use symbolic tools like sympy or wolframalpha.com). Modify the convergence_rate function from the vib_undamped.py program to perform experiments with the extended model. Verify that the error is of order \(\Delta t^{2}\).
Filename: vib_conv_rate.
Exercise 1.13 (Investigate the amplitude errors of many solvers)
Use the program vib_undamped_odespy.py from Sect. 1.5.4 (utilize the function amplitudes) to investigate how well famous methods for 1st-order ODEs can preserve the amplitude of u in undamped oscillations. Test, for example, the 3rd- and 4th-order Runge-Kutta methods (RK3, RK4), the Crank-Nicolson method (CrankNicolson), the 2nd- and 3rd-order Adams-Bashforth methods (AdamsBashforth2, AdamsBashforth3), and a 2nd-order Backwards scheme (Backward2Step). The relevant governing equations are listed in the beginning of Sect. 1.5.
Running the code, we get the plots seen in Fig. 1.13, 1.14, and 1.15. They show that RK4 is superior to the others, but that also CrankNicolson performs well. In fact, with RK4 the amplitude changes by less than 0.1 per cent over the interval.
Filename: vib_amplitude_errors.
Problem 1.14 (Minimize memory usage of a simple vibration solver)
We consider the model problem \(u^{\prime\prime}+\omega^{2}u=0\), \(u(0)=I\), \(u^{\prime}(0)=V\), solved by a second-order finite difference scheme. A standard implementation typically employs an array u for storing all the u n values. However, at some time level n+1 where we want to compute u[n+1], all we need of previous u values are from level n and n-1. We can therefore avoid storing the entire array u, and instead work with u[n+1], u[n], and u[n-1], named as u, u_n, u_nmp1, for instance. Another possible naming convention is u, u_n[0], u_n[-1]. Store the solution in a file for later visualization. Make a test function that verifies the implementation by comparing with the another code for the same problem.
Filename: vib_memsave0.
Problem 1.15 (Minimize memory usage of a general vibration solver)
The program vib.py stores the complete solution \(u^{0},u^{1},\ldots,u^{N_{t}}\) in memory, which is convenient for later plotting. Make a memory minimizing version of this program where only the last three \(u^{n+1}\), u n, and \(u^{n-1}\) values are stored in memory under the names u, u_n, and u_nm1 (this is the naming convention used in this book). Write each computed \((t_{n+1},u^{n+1})\) pair to file. Visualize the data in the file (a cool solution is to read one line at a time and plot the u value using the line-by-line plotter in the visualize_front_ascii function - this technique makes it trivial to visualize very long time simulations).
Filename: vib_memsave.
Exercise 1.16 (Implement the Euler-Cromer scheme for the generalized model)
We consider the generalized model problem
-
a)
Implement the Euler-Cromer method from Sect. 1.10.8.
-
b)
We expect the Euler-Cromer method to have first-order convergence rate. Make a unit test based on this expectation.
-
c)
Consider a system with m = 4, \(f(v)=b|v|v\), b = 0.2, s = 2u, F = 0. Compute the solution using the centered difference scheme from Sect. 1.10.1 and the Euler-Cromer scheme for the longest possible time step \(\Delta t\). We can use the result from the case without damping, i.e., the largest \(\Delta t=2/\omega\), \(\omega\approx\sqrt{0.5}\) in this case, but since b will modify the frequency, we take the longest possible time step as a safety factor 0.9 times 2 ∕ ω. Refine \(\Delta t\) three times by a factor of two and compare the two curves.
Filename: vib_EulerCromer.
Problem 1.17 (Interpret \([D_{t}D_{t}u]^{n}\) as a forward-backward difference)
Show that the difference \([D_{t}D_{t}u]^{n}\) is equal to \([D_{t}^{+}D_{t}^{-}u]^{n}\) and \(D_{t}^{-}D_{t}^{+}u]^{n}\). That is, instead of applying a centered difference twice one can alternatively apply a mixture of forward and backward differences.
Filename: vib_DtDt_fw_bw.
Exercise 1.18 (Analysis of the Euler-Cromer scheme)
The Euler-Cromer scheme for the model problem \(u^{\prime\prime}+\omega^{2}u=0\), \(u(0)=I\), \(u^{\prime}(0)=0\), is given in (1.55)–(1.54). Find the exact discrete solutions of this scheme and show that the solution for u n coincides with that found in Sect. 1.4.
Hint
Use an ‘‘ansatz’’ \(u^{n}=I\exp{(i\tilde{\omega}\Delta t\,n)}\) and \(v^{n}=qu^{n}\), where \(\tilde{\omega}\) and q are unknown parameters. The following formula is handy:
1.10 Generalization: Damping, Nonlinearities, and Excitation
We shall now generalize the simple model problem from Sect. 1.1 to include a possibly nonlinear damping term \(f(u^{\prime})\), a possibly nonlinear spring (or restoring) force s(u), and some external excitation F(t):
We have also included a possibly nonzero initial value for \(u^{\prime}(0)\). The parameters m, \(f(u^{\prime})\), s(u), F(t), I, V, and T are input data.
There are two main types of damping (friction) forces: linear \(f(u^{\prime})=bu\), or quadratic \(f(u^{\prime})=bu^{\prime}|u^{\prime}|\). Spring systems often feature linear damping, while air resistance usually gives rise to quadratic damping. Spring forces are often linear: \(s(u)=cu\), but nonlinear versions are also common, the most famous is the gravity force on a pendulum that acts as a spring with \(s(u)\sim\sin(u)\).
1.10.1 A Centered Scheme for Linear Damping
Sampling (1.71) at a mesh point t n , replacing \(u^{\prime\prime}(t_{n})\) by \([D_{t}D_{t}u]^{n}\), and \(u^{\prime}(t_{n})\) by \([D_{2t}u]^{n}\) results in the discretization
which written out means
where F n as usual means F(t) evaluated at \(t=t_{n}\). Solving (1.73) with respect to the unknown \(u^{n+1}\) gives a problem: the \(u^{n+1}\) inside the f function makes the equation nonlinear unless \(f(u^{\prime})\) is a linear function, \(f(u^{\prime})=bu^{\prime}\). For now we shall assume that f is linear in \(u^{\prime}\). Then
which gives an explicit formula for u at each new time level:
For the first time step we need to discretize \(u^{\prime}(0)=V\) as \([D_{2t}u=V]^{0}\) and combine with (1.75) for n = 0. The discretized initial condition leads to
which inserted in (1.75) for n = 0 gives an equation that can be solved for u 1:
1.10.2 A Centered Scheme for Quadratic Damping
When \(f(u^{\prime})=bu^{\prime}|u^{\prime}|\), we get a quadratic equation for \(u^{n+1}\) in (1.73 ). This equation can be straightforwardly solved by the well-known formula for the roots of a quadratic equation. However, we can also avoid the nonlinearity by introducing an approximation with an error of order no higher than what we already have from replacing derivatives with finite differences.
We start with (1.71) and only replace \(u^{\prime\prime}\) by \(D_{t}D_{t}u\), resulting in
Here, \(u^{\prime}|u^{\prime}|\) is to be computed at time t n . The idea is now to introduce a geometric mean, defined by
for some quantity w depending on time. The error in the geometric mean approximation is \(\mathcal{O}(\Delta t^{2})\), the same as in the approximation \(u^{\prime\prime}\approx D_{t}D_{t}u\). With \(w=u^{\prime}\) it follows that
The next step is to approximate \(u^{\prime}\) at \(t_{n\pm 1/2}\), and fortunately a centered difference fits perfectly into the formulas since it involves u values at the mesh points only. With the approximations
we get
The counterpart to (1.73) is then
which is linear in the unknown \(u^{n+1}\). Therefore, we can easily solve (1.81) with respect to \(u^{n+1}\) and achieve the explicit updating formula
In the derivation of a special equation for the first time step we run into some trouble: inserting (1.76) in (1.82) for n = 0 results in a complicated nonlinear equation for u 1. By thinking differently about the problem we can easily get away with the nonlinearity again. We have for n = 0 that \(b[u^{\prime}|u^{\prime}|]^{0}=bV|V|\). Using this value in (1.78) gives
Writing this equation out and using (1.76) results in the special equation for the first time step:
1.10.3 A Forward-Backward Discretization of the Quadratic Damping Term
The previous section first proposed to discretize the quadratic damping term \(|u^{\prime}|u^{\prime}\) using centered differences: \([|D_{2t}|D_{2t}u]^{n}\). As this gives rise to a nonlinearity in \(u^{n+1}\), it was instead proposed to use a geometric mean combined with centered differences. But there are other alternatives. To get rid of the nonlinearity in \([|D_{2t}|D_{2t}u]^{n}\), one can think differently: apply a backward difference to \(|u^{\prime}|\), such that the term involves known values, and apply a forward difference to \(u^{\prime}\) to make the term linear in the unknown \(u^{n+1}\). With mathematics,
The forward and backward differences both have an error proportional to \(\Delta t\) so one may think the discretization above leads to a first-order scheme. However, by looking at the formulas, we realize that the forward-backward differences in (1.85) result in exactly the same scheme as in (1.81) where we used a geometric mean and centered differences and committed errors of size \(\mathcal{O}(\Delta t^{2})\). Therefore, the forward-backward differences in (1.85) act in a symmetric way and actually produce a second-order accurate discretization of the quadratic damping term.
1.10.4 Implementation
The algorithm arising from the methods in Sect.s 1.10.1 and 1.10.2 is very similar to the undamped case in Sect. 1.1.2. The difference is basically a question of different formulas for u 1 and \(u^{n+1}\). This is actually quite remarkable. The equation (1.71) is normally impossible to solve by pen and paper, but possible for some special choices of F, s, and f. On the contrary, the complexity of the nonlinear generalized model (1.71) versus the simple undamped model is not a big deal when we solve the problem numerically!
The computational algorithm takes the form
-
1.
\(u^{0}=I\)
-
2.
compute u 1 from (1.77) if linear damping or (1.84) if quadratic damping
-
3.
for \(n=1,2,\ldots,N_{t}-1\):
Modifying the solver function for the undamped case is fairly easy, the big difference being many more terms and if tests on the type of damping:

The complete code resides in the file vib.py .
1.10.5 Verification
Constant solution
For debugging and initial verification, a constant solution is often very useful. We choose \(u_{\mbox{\footnotesize e}}(t)=I\), which implies V = 0. Inserted in the ODE, we get \(F(t)=s(I)\) for any choice of f. Since the discrete derivative of a constant vanishes (in particular, \([D_{2t}I]^{n}=0\), \([D_{t}I]^{n}=0\), and \([D_{t}D_{t}I]^{n}=0\)), the constant solution also fulfills the discrete equations. The constant should therefore be reproduced to machine precision. The function test_constant in vib.py implements this test.
Linear solution
Now we choose a linear solution: \(u_{\mbox{\footnotesize e}}=ct+d\). The initial condition \(u(0)=I\) implies d = I, and \(u^{\prime}(0)=V\) forces c to be V. Inserting \(u_{\mbox{\footnotesize e}}=Vt+I\) in the ODE with linear damping results in
while quadratic damping requires the source term
Since the finite difference approximations used to compute \(u^{\prime}\) all are exact for a linear function, it turns out that the linear \(u_{\mbox{\footnotesize e}}\) is also a solution of the discrete equations. Exercise 1.10 asks you to carry out all the details.
Quadratic solution
Choosing \(u_{\mbox{\footnotesize e}}=bt^{2}+Vt+I\), with b arbitrary, fulfills the initial conditions and fits the ODE if F is adjusted properly. The solution also solves the discrete equations with linear damping. However, this quadratic polynomial in t does not fulfill the discrete equations in case of quadratic damping, because the geometric mean used in the approximation of this term introduces an error. Doing Exercise 1.10 will reveal the details. One can fit F n in the discrete equations such that the quadratic polynomial is reproduced by the numerical method (to machine precision).
Catching bugs
How good are the constant and quadratic solutions at catching bugs in the implementation? Let us check that by introducing some bugs.
-
Use m instead of 2*m in the denominator of u[1]: code works for constant solution, but fails (as it should) for a quadratic one.
-
Use b*dt instead of b*dt/2 in the updating formula for u[n+1] in case of linear damping: constant and quadratic both fail.
-
Use F[n+1] instead of F[n] in case of linear or quadratic damping: constant solution works, quadratic fails.
We realize that the constant solution is very useful for catching certain bugs because of its simplicity (easy to predict what the different terms in the formula should evaluate to), while the quadratic solution seems capable of detecting all (?) other kinds of typos in the scheme. These results demonstrate why we focus so much on exact, simple polynomial solutions of the numerical schemes in these writings.
1.10.6 Visualization
The functions for visualizations differ significantly from those in the undamped case in the vib_undamped.py program because, in the present general case, we do not have an exact solution to include in the plots. Moreover, we have no good estimate of the periods of the oscillations as there will be one period determined by the system parameters, essentially the approximate frequency \(\sqrt{s^{\prime}(0)/m}\) for linear s and small damping, and one period dictated by F(t) in case the excitation is periodic. This is, however, nothing that the program can depend on or make use of. Therefore, the user has to specify T and the window width to get a plot that moves with the graph and shows the most recent parts of it in long time simulations.
The vib.py code contains several functions for analyzing the time series signal and for visualizing the solutions.
1.10.7 User Interface
The main function is changed substantially from the vib_undamped.py code, since we need to specify the new data c, s(u), and F(t). In addition, we must set T and the plot window width (instead of the number of periods we want to simulate as in vib_undamped.py). To figure out whether we can use one plot for the whole time series or if we should follow the most recent part of u, we can use the plot_empricial_freq_and_amplitude function’s estimate of the number of local maxima. This number is now returned from the function and used in main to decide on the visualization technique.

The program vib.py contains the above code snippets and can solve the model problem (1.71). As a demo of vib.py, we consider the case I = 1, V = 0, m = 1, c = 0.03, \(s(u)=\sin(u)\), \(F(t)=3\cos(4t)\), \(\Delta t=0.05\), and T = 140. The relevant command to run is

This results in a moving window following the function Footnote 16 on the screen. Figure 1.16 shows a part of the time series.
1.10.8 The Euler-Cromer Scheme for the Generalized Model
The ideas of the Euler-Cromer method from Sect. 1.7 carry over to the generalized model. We write (1.71) as two equations for u and \(v=u^{\prime}\). The first equation is taken as the one with \(v^{\prime}\) on the left-hand side:
Again, the idea is to step (1.86) forward using a standard Forward Euler method, while we update u from (1.87) with a Backward Euler method, utilizing the recent, computed \(v^{n+1}\) value. In detail,
resulting in the explicit scheme
We immediately note one very favorable feature of this scheme: all the nonlinearities in s(u) and f(v) are evaluated at a previous time level. This makes the Euler-Cromer method easier to apply and hence much more convenient than the centered scheme for the second-order ODE (1.71).
The initial conditions are trivially set as
1.10.9 The Störmer-Verlet Algorithm for the Generalized Model
We can easily apply the ideas from Sect. 1.7.4 to extend that method to the generalized model
However, since the scheme is essentially centered differences for the ODE system on a staggered mesh, we do not go into detail here, but refer to Sect. 1.10.10.
1.10.10 A Staggered Euler-Cromer Scheme for a Generalized Model
The more general model for vibration problems,
can be rewritten as a first-order ODE system
It is natural to introduce a staggered mesh (see Sect. 1.8.1) and seek u at mesh points t n (the numerical value is denoted by u n) and v between mesh points at \(t_{n+1/2}\) (the numerical value is denoted by \(v^{n+\frac{1}{2}}\)). A centered difference approximation to (1.96)–(1.95) can then be written in operator notation as
Written out,
With linear damping, \(f(v)=bv\), we can use an arithmetic mean for \(f(v^{n})\): \(f(v^{n})\approx=\frac{1}{2}(f(v^{n-\frac{1}{2}})+f(v^{n+\frac{1}{2}}))\). The system (1.99)–(1.100) can then be solved with respect to the unknowns u n and \(v^{n+\frac{1}{2}}\):
In case of quadratic damping, \(f(v)=b|v|v\), we can use a geometric mean: \(f(v^{n})\approx b|v^{n-\frac{1}{2}}|v^{n+\frac{1}{2}}\). Inserting this approximation in (1.99)–(1.100) and solving for the unknowns u n and \(v^{n+\frac{1}{2}}\) results in
The initial conditions are derived at the end of Sect. 1.8.1:
1.10.11 The PEFRL 4th-Order Accurate Algorithm
A variant of the Euler-Cromer type of algorithm, which provides an error \(\mathcal{O}(\Delta t^{4})\) if \(f(v)=0\), is called PEFRL [14]. This algorithm is very well suited for integrating dynamic systems (especially those without damping) over very long time periods. Define
The algorithm is explicit and features these steps:
The parameters ξ, λ, and ξ have the values
1.11 Exercises and Problems
Exercise 1.19 (Implement the solver via classes)
Reimplement the vib.py program using a class Problem to hold all the physical parameters of the problem, a class Solver to hold the numerical parameters and compute the solution, and a class Visualizer to display the solution.
Hint
Use the ideas and examples from Sections 5.5.1 and 5.5.2 in [9]. More specifically, make a superclass Problem for holding the scalar physical parameters of a problem and let subclasses implement the s(u) and F(t) functions as methods. Try to call up as much existing functionality in vib.py as possible.
Filename: vib_class.
Problem 1.20 (Use a backward difference for the damping term)
As an alternative to discretizing the damping terms \(\beta u^{\prime}\) and \(\beta|u^{\prime}|u^{\prime}\) by centered differences, we may apply backward differences:
The advantage of the backward difference is that the damping term is evaluated using known values u n and \(u^{n-1}\) only. Extend the vib.py code with a scheme based on using backward differences in the damping terms. Add statements to compare the original approach with centered difference and the new idea launched in this exercise. Perform numerical experiments to investigate how much accuracy that is lost by using the backward differences.
Filename: vib_gen_bwdamping.
Exercise 1.21 (Use the forward-backward scheme with quadratic damping)
We consider the generalized model with quadratic damping, expressed as a system of two first-order equations as in Sect. 1.10.10:
However, contrary to what is done in Sect. 1.10.10, we want to apply the idea of a forward-backward discretization: u is marched forward by a one-sided Forward Euler scheme applied to the first equation, and thereafter v can be marched forward by a Backward Euler scheme in the second equation, see in Sect. 1.7. Express the idea in operator notation and write out the scheme. Unfortunately, the backward difference for the v equation creates a nonlinearity \(|v^{n+1}|v^{n+1}\). To linearize this nonlinearity, use the known value v n inside the absolute value factor, i.e., \(|v^{n+1}|v^{n+1}\approx|v^{n}|v^{n+1}\). Show that the resulting scheme is equivalent to the one in Sect. 1.10.10 for some time level n ≥ 1.
What we learn from this exercise is that the first-order differences and the linearization trick play together in ‘‘the right way’’ such that the scheme is as good as when we (in Sect. 1.10.10) carefully apply centered differences and a geometric mean on a staggered mesh to achieve second-order accuracy. There is a difference in the handling of the initial conditions, though, as explained at the end of Sect. 1.7.
Filename: vib_gen_bwdamping.
1.12 Applications of Vibration Models
The following text derives some of the most well-known physical problems that lead to second-order ODE models of the type addressed in this book. We consider a simple spring-mass system; thereafter extended with nonlinear spring, damping, and external excitation; a spring-mass system with sliding friction; a simple and a physical (classical) pendulum; and an elastic pendulum.
1.12.1 Oscillating Mass Attached to a Spring
The most fundamental mechanical vibration system is depicted in Fig. 1.17. A body with mass m is attached to a spring and can move horizontally without friction (in the wheels). The position of the body is given by the vector \(\boldsymbol{r}(t)=u(t)\boldsymbol{i}\), where i is a unit vector in x direction. There is only one force acting on the body: a spring force \(\boldsymbol{F}_{s}=-ku\boldsymbol{i}\), where k is a constant. The point x = 0, where u = 0, must therefore correspond to the body’s position where the spring is neither extended nor compressed, so the force vanishes.
The basic physical principle that governs the motion of the body is Newton’s second law of motion: \(\boldsymbol{F}=m\boldsymbol{a}\), where F is the sum of forces on the body, m is its mass, and \(\boldsymbol{a}=\ddot{\boldsymbol{r}}\) is the acceleration. We use the dot for differentiation with respect to time, which is usual in mechanics. Newton’s second law simplifies here to \(-\boldsymbol{F}_{s}=m\ddot{u}\boldsymbol{i}\), which translates to
Two initial conditions are needed: \(u(0)=I\), \(\dot{u}(0)=V\). The ODE problem is normally written as
It is not uncommon to divide by m and introduce the frequency \(\omega=\sqrt{k/m}\):
This is the model problem in the first part of this chapter, with the small difference that we write the time derivative of u with a dot above, while we used \(u^{\prime}\) and \(u^{\prime\prime}\) in previous parts of the book.
Since only one scalar mathematical quantity, u(t), describes the complete motion, we say that the mechanical system has one degree of freedom (DOF).
Scaling
For numerical simulations it is very convenient to scale (1.120) and thereby get rid of the problem of finding relevant values for all the parameters m, k, I, and V. Since the amplitude of the oscillations are dictated by I and V (or more precisely, V ∕ ω), we scale u by I (or V ∕ ω if I = 0):
The time scale t c is normally chosen as the inverse period \(2\pi/\omega\) or angular frequency 1 ∕ ω, most often as \(t_{c}=1/\omega\). Inserting the dimensionless quantities \(\bar{u}\) and \(\bar{t}\) in (1.120) results in the scaled problem
where β is a dimensionless number. Any motion that starts from rest (V = 0) is free of parameters in the scaled model!
The physics
The typical physics of the system in Fig. 1.17 can be described as follows. Initially, we displace the body to some position I, say at rest (V = 0). After releasing the body, the spring, which is extended, will act with a force \(-kI\boldsymbol{i}\) and pull the body to the left. This force causes an acceleration and therefore increases velocity. The body passes the point x = 0, where u = 0, and the spring will then be compressed and act with a force \(kx\boldsymbol{i}\) against the motion and cause retardation. At some point, the motion stops and the velocity is zero, before the spring force \(kx\boldsymbol{i}\) has worked long enough to push the body in positive direction. The result is that the body accelerates back and forth. As long as there is no friction forces to damp the motion, the oscillations will continue forever.
1.12.2 General Mechanical Vibrating System
The mechanical system in Fig. 1.17 can easily be extended to the more general system in Fig. 1.18, where the body is attached to a spring and a dashpot, and also subject to an environmental force \(F(t)\boldsymbol{i}\). The system has still only one degree of freedom since the body can only move back and forth parallel to the x axis. The spring force was linear, \(\boldsymbol{F}_{s}=-ku\boldsymbol{i}\), in Sect. 1.12.1, but in more general cases it can depend nonlinearly on the position. We therefore set \(\boldsymbol{F}_{s}=s(u)\boldsymbol{i}\). The dashpot, which acts as a damper, results in a force F d that depends on the body’s velocity \(\dot{u}\) and that always acts against the motion. The mathematical model of the force is written \(\boldsymbol{F}_{d}=f(\dot{u})\boldsymbol{i}\). A positive \(\dot{u}\) must result in a force acting in the positive x direction. Finally, we have the external environmental force \(\boldsymbol{F}_{e}=F(t)\boldsymbol{i}\).
Newton’s second law of motion now involves three forces:
The common mathematical form of the ODE problem is
This is the generalized problem treated in the last part of the present chapter, but with prime denoting the derivative instead of the dot.
The most common models for the spring and dashpot are linear: \(f(\dot{u})=b\dot{u}\) with a constant b ≥ 0, and \(s(u)=ku\) for a constant k.
Scaling
A specific scaling requires specific choices of f, s, and F. Suppose we have
We introduce dimensionless variables as usual, \(\bar{u}=u/u_{c}\) and \(\bar{t}=t/t_{c}\). The scale u c depends both on the initial conditions and F, but as time grows, the effect of the initial conditions die out and F will drive the motion. Inserting \(\bar{u}\) and \(\bar{t}\) in the ODE gives
We divide by \(u_{c}/t_{c}^{2}\) and demand the coefficients of the \(\bar{u}\) and the forcing term from F(t) to have unit coefficients. This leads to the scales
The scaled ODE becomes
where there are two dimensionless numbers:
The β number measures the size of the damping term (relative to unity) and is assumed to be small, basically because b is small. The ϕ number is the ratio of the time scale of free vibrations and the time scale of the forcing. The scaled initial conditions have two other dimensionless numbers as values:
1.12.3 A Sliding Mass Attached to a Spring
Consider a variant of the oscillating body in Sect. 1.12.1 and Fig. 1.17: the body rests on a flat surface, and there is sliding friction between the body and the surface. Figure 1.19 depicts the problem.
The body is attached to a spring with spring force \(-s(u)\boldsymbol{i}\). The friction force is proportional to the normal force on the surface, \(-mg\boldsymbol{j}\), and given by \(-f(\dot{u})\boldsymbol{i}\), where
Here, μ is a friction coefficient. With the signum function
we can simply write \(f(\dot{u})=\mu mg\,\hbox{sign}(\dot{u})\) (the sign function is implemented by numpy.sign).
The equation of motion becomes
1.12.4 A Jumping Washing Machine
A washing machine is placed on four springs with efficient dampers. If the machine contains just a few clothes, the circular motion of the machine induces a sinusoidal external force from the floor and the machine will jump up and down if the frequency of the external force is close to the natural frequency of the machine and its spring-damper system.
1.12.5 Motion of a Pendulum
Simple pendulum
A classical problem in mechanics is the motion of a pendulum. We first consider a simplified pendulum Footnote 17 (sometimes also called a mathematical pendulum): a small body of mass m is attached to a massless wire and can oscillate back and forth in the gravity field. Figure 1.20 shows a sketch of the problem.
The motion is governed by Newton’s 2nd law, so we need to find expressions for the forces and the acceleration. Three forces on the body are considered: an unknown force S from the wire, the gravity force mg, and an air resistance force, \(\frac{1}{2}C_{D}\varrho A|v|v\), hereafter called the drag force, directed against the velocity of the body. Here, C D is a drag coefficient, \(\varrho\) is the density of air, A is the cross section area of the body, and v is the magnitude of the velocity.
We introduce a coordinate system with polar coordinates and unit vectors i r and i θ as shown in Fig. 1.21. The position of the center of mass of the body is
where i and j are unit vectors in the corresponding Cartesian coordinate system in the x and y directions, respectively. We have that \(\boldsymbol{i}_{r}=\cos\theta\boldsymbol{i}+\sin\theta\boldsymbol{j}\).
The forces are now expressed as follows.
-
Wire force: \(-S\boldsymbol{i}_{r}\)
-
Gravity force: \(-mg\boldsymbol{j}=mg(-\sin\theta\,\boldsymbol{i}_{\theta}+\cos\theta\,\boldsymbol{i}_{r})\)
-
Drag force: \(-\frac{1}{2}C_{D}\varrho A|v|v\,\boldsymbol{i}_{\theta}\)
Since a positive velocity means movement in the direction of i θ, the drag force must be directed along −i θ so it works against the motion. We assume motion in air so that the added mass effect can be neglected (for a spherical body, the added mass is \(\frac{1}{2}\varrho V\), where V is the volume of the body). Also the buoyancy effect can be neglected for motion in the air when the density difference between the fluid and the body is so significant.
The velocity of the body is found from r:
since \(\frac{d}{d\theta}\boldsymbol{i}_{r}=\boldsymbol{i}_{\theta}\). It follows that \(v=|\boldsymbol{v}|=L\dot{\theta}\). The acceleration is
since \(\frac{d}{d\theta}\boldsymbol{i}_{\theta}=-\boldsymbol{i}_{r}\).
Newton’s 2nd law of motion becomes
leading to two component equations
From (1.124) we get an expression for \(S=mg\cos\theta+L\dot{\theta}^{2}\), and from (1.125) we get a differential equation for the angle \(\theta(t)\). This latter equation is ordered as
Two initial conditions are needed: θ = Θ and \(\dot{\theta}=\Omega\). Normally, the pendulum motion is started from rest, which means Ω = 0.
Equation (1.126) fits the general model used in (1.71) in Sect. 1.10 if we define u = θ, \(f(u^{\prime})=\frac{1}{2}C_{D}\varrho AL|\dot{u}|\dot{u}\), \(s(u)=L^{-1}mg\sin u\), and F = 0. If the body is a sphere with radius R, we can take \(C_{D}=0.4\) and \(A=\pi R^{2}\). Exercise 1.25 asks you to scale the equations and carry out specific simulations with this model.
Physical pendulum
The motion of a compound or physical pendulum where the wire is a rod with mass, can be modeled very similarly. The governing equation is \(I\boldsymbol{a}=\boldsymbol{T}\) where I is the moment of inertia of the entire body about the point \((x_{0},y_{0})\), and T is the sum of moments of the forces with respect to \((x_{0},y_{0})\). The vector equation reads
The component equation in i θ direction gives the equation of motion for \(\theta(t)\):
1.12.6 Dynamic Free Body Diagram During Pendulum Motion
Usually one plots the mathematical quantities as functions of time to visualize the solution of ODE models. Exercise 1.25 asks you to do this for the motion of a pendulum in the previous section. However, sometimes it is more instructive to look at other types of visualizations. For example, we have the pendulum and the free body diagram in Fig. 1.20 and 1.21. We may think of these figures as animations in time instead. Especially the free body diagram will show both the motion of the pendulum and the size of the forces during the motion. The present section exemplifies how to make such a dynamic body diagram. Two typical snapshots of free body diagrams are displayed below (the drag force is magnified 5 times to become more visual!).

Dynamic physical sketches, coupled to the numerical solution of differential equations, requires a program to produce a sketch for the situation at each time level. Pysketcher Footnote 18 is such a tool. In fact (and not surprising!) Fig. 1.20 and 1.21 were drawn using Pysketcher. The details of the drawings are explained in the Pysketcher tutorial Footnote 19. Here, we outline how this type of sketch can be used to create an animated free body diagram during the motion of a pendulum.
Pysketcher is actually a layer of useful abstractions on top of standard plotting packages. This means that we in fact apply Matplotlib to make the animated free body diagram, but instead of dealing with a wealth of detailed Matplotlib commands, we can express the drawing in terms of more high-level objects, e.g., objects for the wire, angle θ, body with mass m, arrows for forces, etc. When the position of these objects are given through variables, we can just couple those variables to the dynamic solution of our ODE and thereby make a unique drawing for each θ value in a simulation.
Writing the solver
Let us start with the most familiar part of the current problem: writing the solver function. We use Odespy for this purpose. We also work with dimensionless equations. Since θ can be viewed as dimensionless, we only need to introduce a dimensionless time, here taken as \(\bar{t}=t/\sqrt{L/g}\). The resulting dimensionless mathematical model for θ, the dimensionless angular velocity ω, the dimensionless wire force \(\bar{S}\), and the dimensionless drag force \(\bar{D}\) is then
with
as a dimensionless parameter expressing the ratio of the drag force and the gravity force. The dimensionless ω is made non-dimensional by the time, so \(\omega\sqrt{L/g}\) is the corresponding angular frequency with dimensions.
A suitable function for computing (1.128)–(1.131) is listed below.

Drawing the free body diagram
The sketch function below applies Pysketcher objects to build a diagram like that in Fig. 1.21, except that we have removed the rotation point \((x_{0},y_{0})\) and the unit vectors in polar coordinates as these objects are not important for an animated free body diagram.


Making the animated free body diagram
It now remains to couple the simulate and sketch functions. We first run simulate:

The next step is to run through the time levels in the simulation and make a sketch at each level:

The individual sketches are (by the sketch function) saved in files with names tmp_%04d.png. These can be combined to videos using (e.g.) ffmpeg. A complete function animate for running the simulation and creating video files is listed below.

1.12.7 Motion of an Elastic Pendulum
Consider a pendulum as in Fig. 1.20, but this time the wire is elastic. The length of the wire when it is not stretched is L 0, while L(t) is the stretched length at time t during the motion.
Stretching the elastic wire a distance \(\Delta L\) gives rise to a spring force \(k\Delta L\) in the opposite direction of the stretching. Let n be a unit normal vector along the wire from the point \(\boldsymbol{r}_{0}=(x_{0},y_{0})\) and in the direction of i θ, see Fig. 1.21 for definition of \((x_{0},y_{0})\) and i θ. Obviously, we have \(\boldsymbol{n}=\boldsymbol{i}_{\theta}\), but in this modeling of an elastic pendulum we do not need polar coordinates. Instead, it is more straightforward to develop the equation in Cartesian coordinates.
A mathematical expression for n is
where \(L(t)=||\boldsymbol{r}-\boldsymbol{r}_{0}||\) is the current length of the elastic wire. The position vector r in Cartesian coordinates reads \(\boldsymbol{r}(t)=x(t)\boldsymbol{i}+y(t)\boldsymbol{j}\), where i and j are unit vectors in the x and y directions, respectively. It is convenient to introduce the Cartesian components n x and n y of the normal vector:
The stretch \(\Delta L\) in the wire is
The force in the wire is then \(-S\boldsymbol{n}=-k\Delta L\boldsymbol{n}\).
The other forces are the gravity and the air resistance, just as in Fig. 1.21. For motion in air we can neglect the added mass and buoyancy effects. The main difference is that we have a model for S in terms of the motion (as soon as we have expressed \(\Delta L\) by r). For simplicity, we drop the air resistance term (but Exercise 1.27 asks you to include it).
Newton’s second law of motion applied to the body now results in
The two components of (1.132) are
Remarks about an elastic vs a non-elastic pendulum
Note that the derivation of the ODEs for an elastic pendulum is more straightforward than for a classical, non-elastic pendulum, since we avoid the details with polar coordinates, but instead work with Newton’s second law directly in Cartesian coordinates. The reason why we can do this is that the elastic pendulum undergoes a general two-dimensional motion where all the forces are known or expressed as functions of x(t) and y(t), such that we get two ordinary differential equations. The motion of the non-elastic pendulum, on the other hand, is constrained: the body has to move along a circular path, and the force S in the wire is unknown.
The non-elastic pendulum therefore leads to a differential-algebraic equation, i.e., ODEs for x(t) and y(t) combined with an extra constraint \((x-x_{0})^{2}+(y-y_{0})^{2}=L^{2}\) ensuring that the motion takes place along a circular path. The extra constraint (equation) is compensated by an extra unknown force \(-S\boldsymbol{n}\). Differential-algebraic equations are normally hard to solve, especially with pen and paper. Fortunately, for the non-elastic pendulum we can do a trick: in polar coordinates the unknown force S appears only in the radial component of Newton’s second law, while the unknown degree of freedom for describing the motion, the angle \(\theta(t)\), is completely governed by the asimuthal component. This allows us to decouple the unknowns S and θ. But this is a kind of trick and not a widely applicable method. With an elastic pendulum we use straightforward reasoning with Newton’s 2nd law and arrive at a standard ODE problem that (after scaling) is easy to solve on a computer.
Initial conditions
What is the initial position of the body? We imagine that first the pendulum hangs in equilibrium in its vertical position, and then it is displaced an angle Θ. The equilibrium position is governed by the ODEs with the accelerations set to zero. The x component leads to \(x(t)=x_{0}\), while the y component gives
since \(n_{y}=-11\) in this position. The corresponding y value is then from \(n_{y}=-1\):
Let us now choose \((x_{0},y_{0})\) such that the body is at the origin in the equilibrium position:
Displacing the body an angle Θ to the right leads to the initial position
The initial velocities can be set to zero: \(x^{\prime}(0)=y^{\prime}(0)=0\).
The complete ODE problem
We can summarize all the equations as follows:
We insert n x and n y in the ODEs:
Scaling
The elastic pendulum model can be used to study both an elastic pendulum and a classic, non-elastic pendulum. The latter problem is obtained by letting \(k\rightarrow\infty\). Unfortunately, a serious problem with the ODEs (1.135)–(1.136) is that for large k, we have a very large factor k ∕ m multiplied by a very small number \(1-L_{0}/L\), since for large k, \(L\approx L_{0}\) (very small deformations of the wire). The product is subject to significant round-off errors for many relevant physical values of the parameters. To circumvent the problem, we introduce a scaling. This will also remove physical parameters from the problem such that we end up with only one dimensionless parameter, closely related to the elasticity of the wire. Simulations can then be done by setting just this dimensionless parameter.
The characteristic length can be taken such that in equilibrium, the scaled length is unity, i.e., the characteristic length is \(L_{0}+mg/k\):
We must then also work with the scaled length \(\bar{L}=L/(L_{0}+mg/k)\).
Introducing \(\bar{t}=t/t_{c}\), where t c is a characteristic time we have to decide upon later, one gets
For a non-elastic pendulum with small angles, we know that the frequency of the oscillations are \(\omega=\sqrt{L/g}\). It is therefore natural to choose a similar expression here, either the length in the equilibrium position,
or simply the unstretched length,
These quantities are not very different (since the elastic model is valid only for quite small elongations), so we take the latter as it is the simplest one.
The ODEs become
We can now identify a dimensionless number
which is the ratio of the unstretched length and the stretched length in equilibrium. The non-elastic pendulum will have β = 1 (\(k\rightarrow\infty\)). With β the ODEs read
We have here added a parameter ϵ, which is an additional downward stretch of the wire at t = 0. This parameter makes it possible to do a desired test: vertical oscillations of the pendulum. Without ϵ, starting the motion from \((0,0)\) with zero velocity will result in x = y = 0 for all times (also a good test!), but with an initial stretch so the body’s position is \((0,\epsilon)\), we will have oscillatory vertical motion with amplitude ϵ (see Exercise 1.26).
Remark on the non-elastic limit
We immediately see that as \(k\rightarrow\infty\) (i.e., we obtain a non-elastic pendulum), \(\beta\rightarrow 1\), \(\bar{L}\rightarrow 1\), and we have very small values \(1-\beta\bar{L}^{-1}\) divided by very small values 1 − β in the ODEs. However, it turns out that we can set β very close to one and obtain a path of the body that within the visual accuracy of a plot does not show any elastic oscillations. (Should the division of very small values become a problem, one can study the limit by L’Hospital’s rule:
and use the limit \(\bar{L}^{-1}\) in the ODEs for β values very close to 1.)
1.12.8 Vehicle on a Bumpy Road
We consider a very simplistic vehicle, on one wheel, rolling along a bumpy road. The oscillatory nature of the road will induce an external forcing on the spring system in the vehicle and cause vibrations. Figure 1.22 outlines the situation.
To derive the equation that governs the motion, we must first establish the position vector of the black mass at the top of the spring. Suppose the spring has length L without any elongation or compression, suppose the radius of the wheel is R, and suppose the height of the black mass at the top is H. With the aid of the r 0 vector in Fig. 1.22, the position r of the center point of the mass is
where u is the elongation or compression in the spring according to the (unknown and to be computed) vertical displacement u relative to the road. If the vehicle travels with constant horizontal velocity v and h(x) is the shape of the road, then the vector r 0 is
if the motion starts from x = 0 at time t = 0.
The forces on the mass is the gravity, the spring force, and an optional damping force that is proportional to the vertical velocity \(\dot{u}\). Newton’s second law of motion then tells that
This leads to
To simplify a little bit, we omit the gravity force mg in comparison with the other terms. Introducing \(u^{\prime}\) for \(\dot{u}\) then gives a standard damped, vibration equation with external forcing:
Since the road is normally known just as a set of array values, \(h^{\prime\prime}\) must be computed by finite differences. Let \(\Delta x\) be the spacing between measured values \(h_{i}=h(i\Delta x)\) on the road. The discrete second-order derivative \(h^{\prime\prime}\) reads
We may for maximum simplicity set the end points as \(q_{0}=q_{1}\) and \(q_{N_{x}}=q_{N_{x}-1}\). The term \(-mh^{\prime\prime}(vt)v^{2}\) corresponds to a force with discrete time values
This force can be directly used in a numerical model
Software for computing u and also making an animated sketch of the motion like we did in Sect. 1.12.6 is found in a separate project on the web: https://github.com/hplgit/bumpy . You may start looking at the tutorial Footnote 20.
1.12.9 Bouncing Ball
A bouncing ball is a ball in free vertically fall until it impacts the ground, but during the impact, some kinetic energy is lost, and a new motion upwards with reduced velocity starts. After the motion is retarded, a new free fall starts, and the process is repeated. At some point the velocity close to the ground is so small that the ball is considered to be finally at rest.
The motion of the ball falling in air is governed by Newton’s second law F = ma, where a is the acceleration of the body, m is the mass, and F is the sum of all forces. Here, we neglect the air resistance so that gravity −mg is the only force. The height of the ball is denoted by h and v is the velocity. The relations between h, v, and a,
combined with Newton’s second law gives the ODE model
or expressed alternatively as a system of first-order equations:
These equations govern the motion as long as the ball is away from the ground by a small distance \(\epsilon_{h}> 0\). When \(h<\epsilon_{h}\), we have two cases.
-
1.
The ball impacts the ground, recognized by a sufficiently large negative velocity (\(v<-\epsilon_{v}\)). The velocity then changes sign and is reduced by a factor C R , known as the coefficient of restitution Footnote 21. For plotting purposes, one may set h = 0.
-
2.
The motion stops, recognized by a sufficiently small velocity (\(|v|<\epsilon_{v}\)) close to the ground.
1.12.10 Two-Body Gravitational Problem
Consider two astronomical objects A and B that attract each other by gravitational forces. A and B could be two stars in a binary system, a planet orbiting a star, or a moon orbiting a planet. Each object is acted upon by the gravitational force due to the other object. Consider motion in a plane (for simplicity) and let \((x_{A},y_{A})\) and \((x_{B},y_{B})\) be the positions of object A and B, respectively.
The governing equations
Newton’s second law of motion applied to each object is all we need to set up a mathematical model for this physical problem:
where F is the gravitational force
where
and G is the gravitational constant: \(G=6.674\cdot 10^{-11}\,\hbox{Nm}^{2}/\hbox{kg}^{2}\).
Scaling
A problem with these equations is that the parameters are very large (m A , m B , \(||\boldsymbol{r}||\)) or very small (G). The rotation time for binary stars can be very small and large as well. It is therefore advantageous to scale the equations. A natural length scale could be the initial distance between the objects: \(L=\boldsymbol{r}(0)\). We write the dimensionless quantities as
The gravity force is transformed to
so the first ODE for x A becomes
Assuming that quantities with a bar and their derivatives are around unity in size, it is natural to choose t c such that the fraction \(Gm_{B}t_{c}/L^{2}=1\):
From the other equation for x B we get another candidate for t c with m A instead of m B . Which mass we choose play a role if \(m_{A}\ll m_{B}\) or \(m_{B}\ll m_{A}\). One solution is to use the sum of the masses:
Taking a look at Kepler’s laws Footnote 22 of planetary motion, the orbital period for a planet around the star is given by the t c above, except for a missing factor of \(2\pi\), but that means that \(t_{c}^{-1}\) is just the angular frequency of the motion. Our characteristic time t c is therefore highly relevant. Introducing the dimensionless number
we can write the dimensionless ODE as
In the limit \(m_{A}\ll m_{B}\), i.e., \(\alpha\ll 1\), object B stands still, say \(\bar{\boldsymbol{x}}_{B}=0\), and object A orbits according to
Solution in a special case: planet orbiting a star
To better see the motion, and that our scaling is reasonable, we introduce polar coordinates r and θ:
which means \(\bar{\boldsymbol{x}}_{A}\) can be written as \(\bar{\boldsymbol{x}}_{A}=r\boldsymbol{i}_{r}\). Since
we have
The equation of motion for mass A is then
The special case of circular motion, r = 1, fulfills the equations, since the latter equation then gives \(\dot{\theta}=\hbox{const}\) and the former then gives \(\dot{\theta}=1\), i.e., the motion is \(r(t)=1\), \(\theta(t)=t\), with unit angular frequency as expected and period \(2\pi\) as expected.
1.12.11 Electric Circuits
Although the term ‘‘mechanical vibrations’’ is used in the present book, we must mention that the same type of equations arise when modeling electric circuits. The current I(t) in a circuit with an inductor with inductance L, a capacitor with capacitance C, and overall resistance R, is governed by
where V(t) is the voltage source powering the circuit. This equation has the same form as the general model considered in Sect. 1.10 if we set u = I, \(f(u^{\prime})=bu^{\prime}\) and define b = R ∕ L, \(s(u)=L^{-1}C^{-1}u\), and \(F(t)=\dot{V}(t)\).
1.13 Exercises
Exercise 1.22 (Simulate resonance)
We consider the scaled ODE model (1.122) from Sect. 1.12.2. After scaling, the amplitude of u will have a size about unity as time grows and the effect of the initial conditions die out due to damping. However, as \(\gamma\rightarrow 1\), the amplitude of u increases, especially if β is small. This effect is called resonance. The purpose of this exercise is to explore resonance.
-
a)
Figure out how the solver function in vib.py can be called for the scaled ODE (1.122).
-
b)
Run γ = 5,1.5,1.1,1 for β = 0.005,0.05,0.2. For each β value, present an image with plots of u(t) for the four γ values.
Filename: resonance.
Exercise 1.23 (Simulate oscillations of a sliding box)
Consider a sliding box on a flat surface as modeled in Sect. 1.12.3. As spring force we choose the nonlinear formula
-
a)
Plot \(g(u)=\alpha^{-1}\tanh(\alpha u)\) for various values of α. Assume \(u\in[-1,1]\).
-
b)
Scale the equations using I as scale for u and \(\sqrt{m/k}\) as time scale.
-
c)
Implement the scaled model in b). Run it for some values of the dimensionless parameters.
Filename: sliding_box.
Exercise 1.24 (Simulate a bouncing ball)
Section 1.12.9 presents a model for a bouncing ball. Choose one of the two ODE formulation, (1.151) or (1.152)–(1.153), and simulate the motion of a bouncing ball. Plot h(t). Think about how to plot v(t).
Hint
A naive implementation may get stuck in repeated impacts for large time step sizes. To avoid this situation, one can introduce a state variable that holds the mode of the motion: free fall, impact, or rest. Two consecutive impacts imply that the motion has stopped.
Filename: bouncing_ball.
Exercise 1.25 (Simulate a simple pendulum)
Simulation of simple pendulum can be carried out by using the mathematical model derived in Sect. 1.12.5 and calling up functionality in the vib.py file (i.e., solve the second-order ODE by centered finite differences).
-
a)
Scale the model. Set up the dimensionless governing equation for θ and expressions for dimensionless drag and wire forces.
-
b)
Write a function for computing θ and the dimensionless drag force and the force in the wire, using the solver function in the vib.py file. Plot these three quantities below each other (in subplots) so the graphs can be compared. Run two cases, first one in the limit of Θ small and no drag, and then a second one with Θ = 40 degrees and α = 0.8.
Filename: simple_pendulum.
Exercise 1.26 (Simulate an elastic pendulum)
Section 1.12.7 describes a model for an elastic pendulum, resulting in a system of two ODEs. The purpose of this exercise is to implement the scaled model, test the software, and generalize the model.
-
a)
Write a function simulate that can simulate an elastic pendulum using the scaled model. The function should have the following arguments:

To set the total simulation time and the time step, we use our knowledge of the scaled, classical, non-elastic pendulum: \(u^{\prime\prime}+u=0\), with solution \(u=\Theta\cos\bar{t}\). The period of these oscillations is \(P=2\pi\) and the frequency is unity. The time for simulation is taken as num_periods times P. The time step is set as P divided by time_steps_per_period.
The simulate function should return the arrays of x, y, θ, and t, where \(\theta=\tan^{-1}(x/(1-y))\) is the angular displacement of the elastic pendulum corresponding to the position \((x,y)\).
If plot is True, make a plot of \(\bar{y}(\bar{t})\) versus \(\bar{x}(\bar{t})\), i.e., the physical motion of the mass at \((\bar{x},\bar{y})\). Use the equal aspect ratio on the axis such that we get a physically correct picture of the motion. Also make a plot of \(\theta(\bar{t})\), where θ is measured in degrees. If Θ < 10 degrees, add a plot that compares the solutions of the scaled, classical, non-elastic pendulum and the elastic pendulum (\(\theta(t)\)).
Although the mathematics here employs a bar over scaled quantities, the code should feature plain names x for \(\bar{x}\), y for \(\bar{y}\), and t for \(\bar{t}\) (rather than x_bar, etc.). These variable names make the code easier to read and compare with the mathematics.
Hint 1
Equal aspect ratio is set by plt.gca().set_aspect(’equal’) in Matplotlib (import matplotlib.pyplot as plt) and in SciTools by the command plt.plot(..., daspect=[1,1,1], daspectmode=’equal’) (provided you have done import scitools.std as plt).
Hint 2
If you want to use Odespy to solve the equations, order the ODEs like \(\dot{\bar{x}},\bar{x},\dot{\bar{y}},\bar{y}\) such that odespy.EulerCromer can be applied.
-
a)
Write a test function for testing that Θ = 0 and ϵ = 0 gives x = y = 0 for all times.
-
b)
Write another test function for checking that the pure vertical motion of the elastic pendulum is correct. Start with simplifying the ODEs for pure vertical motion and show that \(\bar{y}(\bar{t})\) fulfills a vibration equation with frequency \(\sqrt{\beta/(1-\beta)}\). Set up the exact solution.
Write a test function that uses this special case to verify the simulate function. There will be numerical approximation errors present in the results from simulate so you have to believe in correct results and set a (low) tolerance that corresponds to the computed maximum error. Use a small \(\Delta t\) to obtain a small numerical approximation error.
-
c)
Make a function demo(beta, Theta) for simulating an elastic pendulum with a given β parameter and initial angle Θ. Use 600 time steps per period to get every accurate results, and simulate for 3 periods.
Filename: elastic_pendulum.
Exercise 1.27 (Simulate an elastic pendulum with air resistance)
This is a continuation Exercise 1.26. Air resistance on the body with mass m can be modeled by the force \(-\frac{1}{2}\varrho C_{D}A|\boldsymbol{v}|\boldsymbol{v}\), where C D is a drag coefficient (0.2 for a sphere), \(\varrho\) is the density of air (1.2 \(\hbox{kg}\,{\hbox{m}}^{-3}\)), A is the cross section area (\(A=\pi R^{2}\) for a sphere, where R is the radius), and v is the velocity of the body. Include air resistance in the original model, scale the model, write a function simulate_drag that is a copy of the simulate function from Exercise 1.26, but with the new ODEs included, and show plots of how air resistance influences the motion.
Filename: elastic_pendulum_drag.
Remarks
Test functions are challenging to construct for the problem with air resistance. You can reuse the tests from Exercise 1.27 for simulate_drag, but these tests does not verify the new terms arising from air resistance.
Exercise 1.28 (Implement the PEFRL algorithm)
We consider the motion of a planet around a star (Sect. 1.12.10). The simplified case where one mass is very much bigger than the other and one object is at rest, results in the scaled ODE model
-
a)
It is easy to show that x(t) and y(t) go like sine and cosine functions. Use this idea to derive the exact solution.
-
b)
One believes that a planet may orbit a star for billions of years. We are now interested in how accurate methods we actually need for such calculations. A first task is to determine what the time interval of interest is in scaled units. Take the earth and sun as typical objects and find the characteristic time used in the scaling of the equations (\(t_{c}=\sqrt{L^{3}/(mG)}\)), where m is the mass of the sun, L is the distance between the sun and the earth, and G is the gravitational constant. Find the scaled time interval corresponding to one billion years.
-
c)
Solve the equations using 4th-order Runge-Kutta and the Euler-Cromer methods. You may benefit from applying Odespy for this purpose. With each solver, simulate 10,000 orbits and print the maximum position error and CPU time as a function of time step. Note that the maximum position error does not necessarily occur at the end of the simulation. The position error achieved with each solver will depend heavily on the size of the time step. Let the time step correspond to 200, 400, 800 and 1600 steps per orbit, respectively. Are the results as expected? Explain briefly. When you develop your program, have in mind that it will be extended with an implementation of the other algorithms (as requested in d) and e) later) and experiments with this algorithm as well.
-
d)
Implement a solver based on the PEFRL method from Sect. 1.10.11. Verify its 4th-order convergence using an equation \(u^{\prime\prime}+u=0\).
-
e)
The simulations done previously with the 4th-order Runge-Kutta and Euler-Cromer are now to be repeated with the PEFRL solver, so the code must be extended accordingly. Then run the simulations and comment on the performance of PEFRL compared to the other two.
-
f)
Use the PEFRL solver to simulate 100,000 orbits with a fixed time step corresponding to 1600 steps per period. Record the maximum error within each subsequent group of 1000 orbits. Plot these errors and fit (least squares) a mathematical function to the data. Print also the total CPU time spent for all 100,000 orbits.
Now, predict the error and required CPU time for a simulation of 1 billion years (orbits). Is it feasible on today’s computers to simulate the planetary motion for one billion years?
Filename: vib_PEFRL.
Remarks
This exercise investigates whether it is feasible to predict planetary motion for the life time of a solar system.
Notes
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
Author information
Authors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this chapter are included in the chapter’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2017 The Author(s)
About this chapter
Cite this chapter
Linge, S., Langtangen, H.P. (2017). Vibration ODEs. In: Finite Difference Computing with PDEs. Texts in Computational Science and Engineering, vol 16. Springer, Cham. https://doi.org/10.1007/978-3-319-55456-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-55456-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-55455-6
Online ISBN: 978-3-319-55456-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)