Abstract
The importance of cost-effectively prioritizing test cases is undeniable in automated testing practice in industry. This paper focuses on prioritizing test cases developed to test product lines of Video Conferencing Systems (VCSs) at Cisco Systems, Norway. Each test case requires setting up configurations of a set of VCSs, invoking a set of test APIs with specific inputs, and checking statuses of the VCSs under test. Based on these characteristics and available information related with test case execution (e.g., number of faults detected), we identified that the test case prioritization problem in our particular context should focus on achieving high coverage of configurations, test APIs, statuses, and high fault detection capability as quickly as possible. To solve this problem, we propose a search-based test case prioritization approach (named STIPI) by defining a fitness function with four objectives and integrating it with a widely applied multi-objective optimization algorithm (named Non-dominated Sorting Genetic Algorithm II). We compared STIPI with random search (RS), Greedy algorithm, and three approaches adapted from literature, using three real sets of test cases from Cisco with four time budgets (25 %, 50 %, 75 % and 100 %). Results show that STIPI significantly outperformed the selected approaches and managed to achieve better performance than RS for on average 39.9 %, 18.6 %, 32.7 % and 43.9 % for the coverage of configurations, test APIs, statuses and fault detection capability, respectively.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Testing is a critical activity for system or software development, through which system/software quality is ensured [1]. To improve the testing efficiency, a large number of researchers have been focusing on prioritizing test cases into an optimal execution order to achieve maximum effectiveness (e.g., fault detection capability) as quickly as possible [2–4]. In the industrial practice of automated testing, test case prioritization is even more critical because usually there is a limited budget (e.g., time) to execute test cases, and thus executing all available test cases at a given context is infeasible [1, 5].
Our industrial partner for this work is Cisco System, Norway, who develops product lines of Video Conferencing Systems (VCSs), which enable high quality conference meetings [4, 5]. To ensure the delivery of high quality VCSs to the market, test engineers of Cisco continually develop test cases to test software of VCSs under various hardware or software configurations, statuses (i.e., states) of VCSs with dedicated test APIs. A test case is typically composed of the following parts: (1) setting up test configurations of a set of VCSs under test; (2) invoking a set of test APIs of the VCSs; and (3) checking the statuses of the VCSs after invoking the test APIs to determine the success or failure of an execution of the test case. When executing test cases, several objectives need to be achieved, i.e., covering the maximum number of possible configurations, test APIs, statuses and detecting as many faults as possible. However, given a number of available test cases, it is often infeasible to execute all of them in practice due to a limited budget of execution time (e.g., 10 h), and it is therefore important to seek an approach for prioritizing the given test cases to cover maximum number of configurations, test APIs, statuses and detect faults as quickly as possible.
To address the above-mentioned challenge, we propose a search-based test case prioritization approach named Search-based Test case prioritization based on Incremental unique coverage and Position Impact (STIPI). STIPI defines a fitness function with four objectives to evaluate the quality of test case prioritization solutions, i.e., Configuration Coverage (CC), test API Coverage (APIC), Status Coverage (SC) and Fault Detection Capability (FDC), and integrates the fitness function with a widely-applied multi-objective search algorithm (i.e., Non-dominated Sorting Genetic Algorithm II) [6]. Moreover, we propose two prioritization strategies when defining the fitness function in STIPI: (1) Incremental Unique Coverage, i.e., for a specific test case, we only consider the incremental unique elements (e.g., test APIs) covered by the test case as compared with the elements covered by the already prioritized test cases; and (2) Position Impact, i.e., a test case with a higher execution position (i.e., scheduled to be executed earlier) has more impact on the quality of a prioritization solution. Notice that both of these strategies are defined to help search to achieve high criteria (i.e., CC, APIC, SC and FDC) as quickly as possible.
To evaluate STIPI, we chose five approaches for the comparison: (1) Random Search (RS) to assess the complexity of the problem; (2) Greedy approach; (3) One existing approach [7] and two modified approaches from the existing literature [8, 9]. The evaluation uses in total 211 test cases from Cisco, which are divided into three sets with varying complexity. Moreover, four different time budgets are used for our evaluation, i.e., 25 %, 50 %, 75 % and 100 % (100 % refers to the total execution time of all the test cases in a given set). Notice that 12 comparisons were performed (i.e., three sets of test cases*four time budgets) for comparing STIPI with each approach, and thus in total 60 comparisons were conducted for the five approaches. Results show that STIPI significantly outperformed the selected approaches for 54 out of 60 comparisons (90 %). In addition, STIPI managed to achieve higher performance than RS for on average 39.9 % (configuration coverage), 18.6 % (test API coverage), 32.7 % (status coverage), and 43.9 % (fault detection capability).
The remainder of the paper is organized as follows: Sect. 2 presents the context, a running example and motivation. STIPI is presented in Sect. 3 followed by experiment design (Sect. 4). Section 5 presents experiment results and overall discussion. Related work is discussed in Sect. 6, and we conclude the work in Sect. 7.
2 Context, Running Example and Motivation
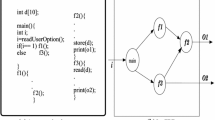
Figure 1 presents a simplified context of testing VCSs (Systems Under Test (SUTs)), and Fig. 2 illustrates (partial) configuration, test API and status information for testing a VCS. First, one VCS consists of one or more configuration variables (e.g., attribute protocol of class VCS in Fig. 2), each of which can take two or more configuration variable values (e.g., literal SIP of enumeration Protocol). Second, a VCS holds one or more status variables defining the statuses of the VCS (e.g., NumberofActiveCalls), and each status variable can have two or more status variable values (e.g., NumberofActiveCalls taking values of 0, 1, 2, 3 and 4). Third, testing a VCS requires employing one or more test API commands (e.g., dial), each of which includes zero or more test API parameters (e.g., callType for dial). Each test API parameter can take two or more test API parameter values (e.g., Video and Audio for CallType).
Figure 3 illustrates the key steps of a test case for testing VCSs. First, a test case configures one or more VCSs by assigning values to configuration variables. For example, the test case shown in Fig. 3 configures the configuration variable protocol with SIP (Line 1). Second, a test API command is invoked with appropriate values assigned to its input parameters, if any. For example, the test case in Fig. 3 invokes the test API command dial consisting of the two test API parameter values: Video for callType and SIP for protocol) (Line 2). Third, the test case checks the actual statuses of VCSs. For example, the test case in Fig. 3 checks the status of the VCS to see if NumberOfActiveCalls equals to 1 (Line 4).
In the context of testing VCSs, test case prioritization is a critical task since it is practically infeasible to execute all the available test cases within a given time budget (e.g., 5 h). Therefore, it is essential to cover maximum configurations (i.e., configuration variables and their values), test APIs (i.e., test API commands, parameters and their values) and statuses (i.e., status variables and their values), and detect faults as quickly as possible. For instance, Table 1 lists five test cases \( (T_{1} \ldots T_{5} ) \) with the information about configurations, test APIs and statuses. The test case in Fig. 3 is represented as T 1 in Table 1, which (1) sets the configuration variable protocol as SIP; (2) uses three test API commands: dial with two parameters (callType, protocol), accept and disconnect; and (3) checks values of three status variables (e.g., MaxVideoCalls).
Notice that the five test cases in Table 1 can be executed in 325 orders (i.e., \( C\left( {5,1} \right) \times 1! + C\left( {5,2} \right) \times 2! + \ldots + C(5,5) \times 5! \)). When there is a time budget, each particular order can be considered as a prioritization solution. Given two prioritization solutions \( s_{1} = \left\{ {T_{5} , T_{1} , T_{4} , T_{2} , T_{3} } \right\} \), \( s_{2} = \left\{ {T_{1} , T_{3} , T_{5} ,T_{2} ,T_{4} } \right\} \), one can observe that \( s_{1} \) is better than \( s_{2} \) since the first three test cases in \( s_{1} \) can cover all the configuration variables and their values, test API commands, test API parameters, test API parameter values, status variables and status variable values, while \( s_{2} \) needs to execute all the five test cases to achieve the same coverage as \( s_{1} \). Therefore, it is important to seek an efficient approach to find an optimal order for executing a given number of test cases to achieve high coverage of configurations, test APIs and statuses, and detect faults as quickly as possible, which forms the motivation of this work.
3 STIPI: Search-Based Test Case Prioritization Based on Incremental Unique Coverage and Position Impact
This section presents the problem representation (Sect. 3.1), four defined objectives, fitness function (Sect. 3.2) and solution encoding (Sect. 3.3).
3.1 Basic Notations and Problem Representation
Basic Notations.
We provide the basic notations as below used throughout the paper.
\( T = \left\{ {T_{1} ,T_{2} \ldots T_{n} } \right\} \) represents a set of n test cases to be prioritized.
\( ET = \left\{ {et_{1} , et_{2} \ldots et_{n} } \right\} \) refers to the execution time for each test case in T.
\( CV = \left\{ {cv_{1} , cv_{2} \ldots cv_{mcv} } \right\} \) represents the configuration variables covered by T. For each \( cv_{i} \), \( CVV_{i} \) refers to the configuration variable values: \( CVV_{i} = \left\{ {cvv_{i1} \ldots cvv_{icvv} } \right\} \). mcvv is the total number of unique values for all the configuration variables, which can be calculated as: \( mcvv = \left| {\left( {\mathop {\bigcup }\limits_{i = 1}^{mcv} CVV_{i} } \right)} \right| \).
\( AC = \left\{ {ac_{1} , ac_{2} \ldots ac_{mac} } \right\} \) represents a set of test API commands covered by T. For each \( ac_{i} \), \( AP_{i} \) denotes the test API parameters: \( AP_{i} = \left\{ {ap_{i1} \ldots ap_{iap} } \right\} \). map is the total number of unique test API parameters, calculated as: \( map = |\left( {\mathop {\bigcup }\limits_{i = 1}^{mac} AP_{i} } \right)| \). For each \( ap_{i} \), \( AV_{i} \) refers to the test API parameter values: \( AV_{i} = \left\{ {av_{i1} \ldots av_{iav} } \right\} \). mav is the total number of unique test API parameter values, i.e., \( mav = |\left( {\mathop {\bigcup }\limits_{i = 1}^{map} AV_{i} } \right)| \).
\( SV = \left\{ {sv_{1} , sv_{2} \ldots sv_{msv} } \right\} \) represents a set of status variables covered by T. For each \( sv_{i} \), \( SVV_{i} \) refers to the status variable values: \( SVV_{i} = \left\{ {svv_{i1} \ldots svv_{isvv} } \right\} \). msvv is the total number of unique status variable values, calculated as: \( msvv = \left| {\left( {\mathop {\bigcup }\limits_{i = 1}^{msv} SVV_{i} } \right)} \right|. \)
\( Effect = \left\{ {effect_{1} \ldots effect_{neffect} } \right\} \) defines a set of effectiveness measures.
\( S = \left\{ {s_{1} , s_{2 } \ldots s_{ns} } \right\} \) represents a set of potential solutions, such that \( ns = C\left( {n,1} \right) \times 1! + C\left( {n,2} \right) \times 2! + \ldots + C(n,n) \times n! \). Each solution \( s_{j} \) consists of a set of prioritized test cases in T: \( s_{j} = \left\{ {T_{j1} \ldots T_{jn} } \right\} \), where \( T_{ji} \in T \) refers to the test case with the execution position i in the prioritized solution \( s_{j} \). Note that it is possible for the maximum number of test cases in \( s_{j} \) (i.e., jn) to be less than the total number of test cases in T, since only a subset of T is prioritized during limited budget (e.g., time).
Problem Representation.
We aim to prioritize the test cases in T in two contexts: (1) 100 % time budget and (2) less than 100 % time budget (i.e., time-aware [1]). Therefore, we formulate the test case prioritization problem as follows: (a) search a solution \( s_{k} \) with nk test cases from the total number of ns solutions in S to obtain the highest effectiveness; and (b) a test case \( T_{jr} \) in a particular solution (e.g.,\( s_{j} \)) with a higher position p has more influence for Effect than the test case with a lower position q.
-
(1)
With 100 % time budget:
$$ \begin{aligned} & \forall_{i = 1\,to\,n\,effect} \forall_{j = 1\,to\,ns} \,Effect\,(s_{k} ,\,effect_{i} ) \ge Effect\left( {s_{j} ,effect_{i} } \right) \\ & \vee effect_{i} \left( {T_{jr} ,p} \right) > \forall_{q \ge (p + 1)} effect_{i} (T_{jr} ,q). \\ \end{aligned} $$where \( effect_{i} \left( {T_{jr} , p} \right) \) and \( effect_{i} \left( {T_{jr} , q} \right) \) refer to the effectiveness measure i for a test case \( T_{jr} \) at position p and q, respectively for a particular solution \( s_{j} \). \( Effect(s_{k} , effect_{i} ) \) and \( Effect(s_{j} , effect_{i} ) \) returns the effectiveness measure i for solutions \( s_{k} \), \( s_{j} \) respectively.
-
(2)
With a time budget tb less than 100 % time budget:
$$ \begin{aligned} & \forall_{i = 1\,to\,neffect} \forall_{j = 1\,to\,ns} \,Effect\,(s_{k} ,\,effect_{i} ) \ge Effect\,\left( {s_{j} ,\,effect_{i} } \right) \\ & \vee \sum\nolimits_{l = 1}^{nk} {ET_{l} \le tb} ,effect_{i} \left( {T_{jr} ,p} \right) > \forall_{q \ge (p + 1)} effect_{i} (T_{jr} ,q). \\ \end{aligned} $$
3.2 Fitness Function
Recall that we aim at maximizing the overall coverage for configuration, test API and status, and detect faults as quickly as possible (Sect. 2). Therefore, we define four objective functions for the fitness function to guide the search towards finding optimal solutions, which are presented in details as below.
Maximize Configuration Coverage (CC).
CC measures the overall configuration coverage of a solution \( s_{j} \) with jn number of test cases, which is composed of Configuration Variable Coverage (CVC) and Configuration Variable Values Coverage (CVVC). We can calculate CVC and CVVC for \( s_{j} \) as: \( CVC_{{ s_{j} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{jn} UCV_{{T_{ji } }} \times \frac{n - i + 1}{n}}}{mcv},\,CVVC_{{ s_{j} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{jn} UCVV_{{T_{ji } }} \times \frac{n - i + 1}{n}}}{mcvv} \), where mcv and mcvv represent the total number of unique Configuration Variables (CV) and Configuration Variable Values (CVV) respectively covered by the total test cases in T (e.g., in Table 1 \( mcvv = 3 \)). Moreover, we propose two prioritization strategies for calculating CVC and CVVC. The first one is Incremental Unique Coverage, i.e., \( UCV_{{ T_{ji} }} \) and \( UCVV_{{ T_{ji} }} \) representing the number of incremental unique CV and CVV covered by \( T_{ji} \) (Sect. 3.1). For example, in Table 1, for one test case prioritization solution \( s_{1} = \left\{ {T_{5} , T_{1} , T_{4} , T_{2} , T_{3} } \right\}, UCVV_{{ T_{5} }} \) is 1 since \( T_{5} \) is in the first execution position and covers one CVV (i.e., H320). \( UCVV_{{ T_{1} }} \) and \( UCVV_{{ T_{4} }} \) are at the second and third position, and cover one CVV each (i.e., SIP, H323). However, \( UCVV_{{ T_{2} }} \) and \( UCVV_{{ T_{3} }} \) are 0, since they are already covered by \( UCVV_{{ T_{1} }} \). This strategy is defined since test case prioritization in our case concerns how many configurations, test APIs, and statuses can be covered rather than how many times they can be covered. The second prioritization strategy is Position Impact, which is calculated as \( \frac{n - i + 1}{n} \), where n is the total number of test cases, and i is a specific execution position in a prioritization solution. Thus, test cases with higher execution positions have higher impact on the quality of a prioritization solution, which fits the scope of test case prioritization that aims at achieving higher criteria as quickly as possible. For instance, using this strategy, CVVC for \( s_{1} \) is: \( CVVC_{{ s_{1} }} = \frac{{1 \times \frac{5}{5} + 1 \times \frac{4}{5} + 1 \times \frac{3}{5} + 0 \times \frac{2}{5} + 0 \times \frac{1}{5}}}{3} = 0.8. \) Moreover, CC for \( s_{j} \) is represented as: \( CC_{{ s_{j} }} = \frac{{CVC _{{s_{j} }} + CVVC _{{s_{j} }} }}{2} \). A higher value of CC shows a higher coverage of configuration.
Maximize Test API Coverage (APIC).
APIC measures the overall test API coverage of a solution \( s_{j} \) with jn number of test cases. It consists of three sub measures: Test API Command Coverage (ACC), Test API Parameter Coverage (APC), and Test API parameter Value Coverage (AVC). ACC, APC and AVC can be calculated as below:
Similarly, the same two strategies (i.e., Incremental Unique Coverage and Position Impact) are applied for calculating ACC, APC and AVC, where \( UAC_{{ T_{ji} }} \), \( UAP_{{ T_{ji} }} \) and \( UAV_{{ T_{ji} }} \) denotes the number of unique test API commands (AC), test API parameters (AP), and test API parameter values (AV) respectively covered by \( T_{ji} \) (Sect. 3.1). They are measured similar as for \( UCVV_{ T} \) in CVVC. mac, map, and mav refer to the total number of unique AC, AP, and AV covered by the total number of test cases as explained for mcvv in CVVC. The APIC for \( s_{j} \) is represented as: \( APIC_{{ s_{j} }} = \frac{{ACC _{{s_{j} }} + APC _{{s_{j} }} + AVC _{{s_{j} }} }}{3} \). A higher value of APIC shows a higher coverage of test APIs.
Maximize Status Coverage (SC).
SC measures the total status coverage of a solution \( s_{j} \). It consists of two sub measures: Status Variable Coverage (SVC) and Status Variable Value Coverage (SVVC), calculated as follow: \( SVC_{{ s_{j} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{jn} USV_{{T_{ji } }} \times \frac{n - i + 1}{n}}}{msv} \), \( SVVC_{{ s_{j} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{jn} USVV_{{T_{ji } }} \times \frac{n - i + 1}{n}}}{msvv} \). Similarly, \( USV_{{ T_{ji} }} \) and \( USVV_{{ T_{ji} }} \) are the number of unique Status Variables (SV) and Status Variable Values (SVV) respectively covered by \( T_{ji} \) (Sect. 3.1), which are measured similar as \( UCVV_{ T} \) in CVVC. msv and msvv represent the total number of unique SV and SVV respectively measured similar as for mcvv in CVVC. The SC for \( s_{j} \) is represented as: \( SC_{{ s_{j} }} = \frac{{{\text{SVC}} _{{s_{j} }} + SVVC _{{s_{j} }} }}{2} \), with a higher value indicating a higher status coverage, and therefore representing a better solution.
Maximize Fault Detection Capability (FDC).
In the context of Cisco, FDC is defined as the detected number of faults for test cases in a solution \( s_{j} \) [4, 5, 10–12]. The FDC for a test case \( T_{ji} \) is calculated as: \( FDC_{{ T_{ji} }} = \frac{{Number\,of\,times\,that\,T_{ji} \,found\,a\,fault}}{{Number\,of\,times\,that\,T_{ji} \,was\,executed}} \). Notice that the FDC of \( T_{ji} \) is calculated based on the historical information of executing \( T_{ji} \). For example, if \( tc_{i} \) was executed 10 times, and it detected fault 4 times, the FDC for \( tc_{i} \) is 0.4. We calculate FDC for a solution \( s_{j} \) as: \( FDC_{{ s_{j} }} = \frac{{\mathop \sum \nolimits_{i = 1}^{jn} FDC_{{T_{ji } }} \times \frac{n - i + 1}{n}}}{mfdc} \). \( FDC_{{ T_{ji} }} \) denotes the FDC for a \( T_{ji} \), mfdc represents the sum of all FDC of test cases, and a higher value of FDC implies a better solution. Notice that we cannot apply the incremental unique coverage strategy for calculating \( FDC_{{ s_{j} }} \) since the relations between faults and test cases are not known in our case (i.e., we only know whether the test cases can detect faults after executing it for a certain number of times rather than having access to the detailed faults detected).
3.3 Solution Representation
The test cases in T are encoded as an array \( A = \left\{ {v_{1} ,v_{2} \ldots v_{n} } \right\} \), where each variable \( v_{i} \) represents one test case in T, and holds a unique value from 0 to 1. We prioritize the test cases in TS by sorting the variables in A in a descending order from higher to lower, such that 1 is the highest, and 0 is the lowest order. Initially, each variable in A is assigned a random value between 0 and 1, and during search our approach returns solutions with optimal values for A guided by the fitness function defined in Sect. 3.2. In terms of time-aware test case prioritization (i.e., with a time budget less than 100 %), we pick the maximum number of test cases that fit the given time budget. For example, in Table 1 for \( TS = \left\{ {T_{1} \ldots T_{5} } \right\} \) with A as \( \left\{ {0.6, 0.2, 0.4, 0.9, 0.3} \right\} \) and the execution time (recorded as minutes) as \( ET = \left\{ {4, 5, 6, 4, 3} \right\} \), the prioritized test cases are \( \left\{ {T_{4} , T_{1} ,T_{3} ,T_{5} ,T_{2} } \right\} \) based on our encoding way for test case prioritization. If we have a time budget of 11 min, the first two test cases (in total 8 min for execution) are first added to the prioritized solution \( s_{j} \), and there are 3 min left, which is not sufficient for executing \( T_{3} \) (6 min). Thus, \( T_{3} \) is not added into \( s_{j} \), and the next test case is evaluated to see if the total execution time can fit the given time budget. \( T_{5} \) with 3 min will be added into \( s_{j} \), since the inclusion of \( T_{5} \) will not make the total execution time exceed the time budget. Therefore, the new prioritized solution will be \( \left\{ {T_{4} , T_{1} , T_{5} } \right\} \).
Moreover, we integrate our fitness function with a widely applied multi-objective search algorithm named Non-dominated Sorting Genetic Algorithm (NSGA-II) [6, 13, 14]. The tournament selection operator [6] is applied to select individual solutions with the best fitness for inclusion into the next generation. The crossover operator is used to produce offspring solutions from the parent solutions by swapping some of the parts (e.g., test cases in our context) of the parent solutions. The mutation operator is applied to randomly change the values of one or more variables (e.g., in our context, each variable represents a test case) based on the pre-defined mutation probability, e.g., 1/(total number of test cases) in our context.
4 Empirical Study Design
4.1 Research Questions
-
RQ1: Is STIPI effective for test case prioritization as compared with RS (i.e., random prioritization)? We compare STIPI with RS for four time budgets: 100 % (i.e., total execution time of all the test cases in a given set), 75 %, 50 % and 25 %, to assess the complexity of the problem such that the use of search algorithms is justified.
-
RQ2: Is STIPI effective for test case prioritization as compared with four selected approaches, in the contexts of four time budgets: 100 %, 75 %, 50 % and 25 %?
-
RQ2.1: Is STIPI effective as compared with the Greedy approach (a local search approach)?
-
RQ2.2: Is STIPI effective as compared with the approach used in [7] (named as A1 in this paper)? Notice that we chose A1 since it also proposed a strategy to give higher importance to test cases with higher execution positions.
-
RQ2.3: Is STIPI effective as compared with the modified version of the approach proposed in [8] (named as A2 in this paper)? We chose A2 since it combines the Average Percentage of Faults Detected (APFD) metric and NSGA-II for test case prioritization without considering time budget. We modified it by defining Average Percentage of Configuration Coverage (APCC), Average Percentage of test API Coverage (APAC) and Average Percentage of Status Coverage (APSC) (Sect. 4.3) for assessing the quality of prioritization solutions for configurations, test APIs and statuses.
-
RQ2.4: Is STIPI effective as compared with the modified version of the approach in [9] (named as A3 in this paper)? We chose A3 since (1) it combines the ADFD with cost (APFD c ) metric and NSGA-II for addressing time-aware test case prioritization problem. We revised A3 by defining Average Percentage of Configuration Coverage with cost (APCC c ), Average Percentage of test API Coverage with cost (APAC c ) and Average Percentage of Status Coverage with cost (APSC c ). For illustration, we provide a formula for Average Percentage of Configuration Variable Value Coverage with cost (APCVVC c ) that is a sub-metric for APCC c as: \( APCVVC_{c} = \frac{{\mathop \sum \nolimits_{i = 1}^{mcvv} (\mathop \sum \nolimits_{{k = TCVV_{i} }}^{jn} et_{k} - \frac{1}{2}et_{{TCVV_{i} }} )}}{{\mathop \sum \nolimits_{k = 1}^{jn} et_{k} \times mcvv}} \). For a solution \( s_{j} \) with jn test cases, \( TCVV_{\text{i}} \) is the first test case from \( s_{j} \) that covers \( CVV_{\text{i}} \) (i.e., the i th configuration variable value), mcvv is the total number of unique configuration variable value, and \( et_{k} \) is the execution time for k th test case. Notice that the detailed formulas for APCC c , APAC c and APSC c can be consulted in our technical report in [15].
We also compare the running time of STIPI with all the five chosen approaches, since STIPI is invoked very frequently (e.g., more than 50 times per day) in our context, i.e., the test cases require to be prioritized and executed often. Therefore, it would be practically infeasible if it takes too much time to apply STIPI.
4.2 Experiment Tasks
As shown in Table 2 (Experiment Task column), we designed two tasks (T 1 , T 2 ) for addressing RQ1–RQ2. The task T 1 is designed to compare STIPI with RS for the four time budgets (i.e., 100 %, 75 %, 50 % and 25 %) and three sets of test cases (i.e., 100, 150 and 211). Similarly, the task T 2 is designed to compare STIPI with the other four test case prioritization approaches, which is divided into four sub-tasks for comparing Greedy, A1, A2 and A3, respectively.
Moreover, we employed 211 real test cases from Cisco for evaluation by dividing it into three sets with varying complexity (#Test Cases column in Table 2). For the first set, we used all the 211 test cases. For the second set, we used 100 random test cases from the 211 test cases. Finally, for the third set, we used the 150 test cases by choosing 111 test cases not selected in the second set (i.e., 100) and 39 random test cases from the second set. Notice that the goal for using three test case sets is to evaluate our approach with test datasets with different complexity.
4.3 Evaluation Metrics
To answer the RQs, we defined in total seven EMs (Table 3). Six are used to assess how fast the configurations, test APIs and statuses can be covered: (1) Average Percentage Configuration Coverage (APCC), (2) Average Percentage test API Coverage (APAC), (3) Average Percentage Status Coverage (APSC), (4) Average Percentage Configuration Coverage that penalizes missing configuration (APCC p ), (5) Average Percentage test API Coverage that penalizes missing test API (APAC p ) and (6) Average Percentage Status Coverage with penalization for missing status (APSC p ). We defined APCC, APAC and APSC for test case prioritization with 100 % time budget based on the APFD metric [8, 16]. For example, for a solution \( s_{j} \) with jn test cases and total number of test cases n from T (a given number of test cases), \( TCV_{1} \) is the first test case from \( s_{j} \) that covers \( CV_{1} \) for the sub metric APCVC in Table 3 (Sect. 3.1). Notice that n and jn are equal when there is 100 % time budget.
When there is a limited time budget, it is possible that not all the configurations, test APIs and statuses can be covered. Therefore, we defined APCC p , APAC p , and APAC p to give penalty to missing configurations, test APIs, and statuses for time-aware prioritization (i.e., 25 %, 50 % and 75 % time budget) based on the variant of APFD metric used for time-aware prioritization [1, 16]. For example, for a solution \( s_{j} \) with jn test cases \( reveal\left( {cv,s_{j} } \right) \) gives the test case from \( s_{j} \) that covers cv for APCVC p in Table 3. If \( s_{j} \) does not contain a test case that covers cv, \( reveal\left( {cv,s_{j} } \right) = jn + 1 \). Notice that in our context, we only have information about how many times in a given period (e.g., a week) a test case was successful in finding faults. Therefore, it is not possible to use the APFD metric to evaluate FDC. Hence, we defined a metric: Measured Fault Detection Capability (MFDC) to measure the percentage of fault detected for time budget of 25 %, 50 % and 75 %.
4.4 Quality Indicator, Statistical Tests and Parameter Settings
When comparing the overall performance of multi-objective search algorithms (e.g., NSGA-II [6]), it is common to apply quality indicators such as hypervolume (HV). Following the guideline in [10], we employ HV based on the defined EMs to address RQ2.2–RQ2.4 (i.e., tasks T 2.2 –T 2.4 in Table 2). HV calculates the volume in the objective space covered by members of a non-dominated set of solutions (i.e., Pareto front) produced by search algorithms for measuring both convergence and diversity [17]. A higher value of HV indicates a better performance of the algorithm.
The Vargha and Delaney \( \hat{A}_{12} \) statistics [18] and Mann-Whitney U test are used to compare the EMs (T 1 and T 2 ), and HV (T 2.2 –T 2.4 ), as shown in Table 2 by following the guidelines in [19]. The Vargha and Delaney \( \hat{A}_{12} \) statistics is a non-parametric effect size measure, and Mann-Whitney U test tells if results are statistically significant [20]. For two algorithms A and B, A has better performance than B if \( \hat{A}_{12} \) is greater than 0.5, and the difference is significant if p-value is less than 0.05.
Notice that STIPI, A1, A2 and A3 are all combined with NSGA-II. Since tuning parameters to different settings might result in different performance of search algorithms, standard settings are recommended [19]. We used standard settings (i.e., population size = 100, crossover rate = 0.9, mutation rate = 1/(number of test cases)) as implemented in jMetal [21]. The search process is terminated when the fitness function has been evaluated for 50,000 times. Since A2 does not support prioritization with a time budget, we collect the maximum number of test cases that can fit a given time budget.
5 Results, Analyses and Discussion
5.1 RQ1: Sanity Check (STIPI vs. RS)
Results in Tables 4 and 5 show that on average STIPI is higher than RS for all the EMs across the three sets of test cases. Moreover, for the three test sets using four time budgets, STIPI managed to achieve higher performance than RS for on average 39.9 % (configuration coverage), 18.6 % (test API coverage), 32.7 % (status coverage), and 43.9 % (FDC). In addition, results of the Vargha and Delaney statistics and the Mann Whitney U test show that STIPI significantly outperformed RS for all the Ems since all the values of \( \hat{A}_{12} \) are greater than 0.5 and all the p-values are less than 0.05.
5.2 RQ2: Comparison with the Selected Approaches
We compared STIPI with Greedy, A1, A2 and A3 using the statistical tests (Vargha and Delaney statistics and Mann Whitney U test) for the four time budgets (25 %, 50 %, 75 % and 100 %), and the three sets of test cases (i.e., 100, 150, 211). Results are summarized in Fig. 4. For example, the first bar (i.e., Gr) in Fig. 4 refers to the comparison between STIPI and Greedy for the 100 % time budget where A = STIPI and B = Greedy. A > B means the percentage of EMs for which STIPI has significantly better performance than Greedy \( (\hat{A}_{12} > 0. 5\,\& \& \,p < 0.0 5),A < B \) means the opposite \( (\hat{A}_{12} < 0.5\,\& \& \,p < 0.0 5) \), and A = B implies there is no significant difference in performance (\( p \ge 0.05 \)).
RQ2.1 (STIPI vs. Greedy).
From Tables 4 and 5, we can observe that the average values of STIPI are higher than Greedy for 93.3 % (42/45)Footnote 1 EMs across the three sets of test cases with the four time budgets. Moreover, from Fig. 4, we can observe STIPI performed significantly better than Greedy for an average of 93.1 % for the four time budgets (i.e., 88.9 % for 100 %, 91.7 % for 75 %, 91.7 % for 50 %, and 100 % for 25 % time budget). Detailed results are available in [15].
RQ2.2 (STIPI vs. A1).
Based on Tables 4 and 5, we can see that STIPI has a higher average value than A1 for 82.2 % (37/45) EMs, and STIPI performed significantly better than A1 for an average of 76.4 % EMs across the four time budgets, while there was no difference in performance for 14.6 % from Fig. 4. Figure 5 shows that for HV, STIPI outperformed A1 for all the three sets of test cases with the four time budgets, and such better results are statistically significant. Detailed results are in [15].
RQ2.3 (STIPI vs. A2).
RQ2.3 is designed to compare STIPI with the approach A2 (Sect. 4.1). Table 4 shows that the two approaches had similar average for EMs with 100 % time budget. Moreover, for 100 % time budget, there was no significant difference in the performance between STIPI and A2 in terms of EMs and HV (Figs. 4 and 5). However, when considering the time budgets of 25 %, 50 % and 75 %, STIPI had a higher performance for 96.3 % (26/27) EMs (Tables 4 and 5). Furthermore, the statistical tests in Figs. 4 and 5 show that STIPI significantly outperformed A2 for an average of 88.9 % EMs and HV values across the three time budgets (25 %, 50 %, 75 %), while there was no significant difference for 11.1 %.
RQ2.4 (STIPI vs. A3).
Based on the results (Tables 4 and 5), STIPI held a higher average values for 75 % (27/36) EM values for the four time budgets and three sets of test cases. For 100 %, 75 %, and 50 %, we can observe from Fig. 4 that STIPI performed significantly better than A3 for an average of 74.1 % EMs, while there was no significant difference for 22.2 %. For the 25 % time budget, there was no statistically significant difference in terms of EMs for STIPI and A3. However, when comparing the HV values, STIPI significantly outperformed A3 for an average of 91.7 % across the four time budgets and three sets of test cases.
Notice that 12 comparisons were performed when comparing STIPI with each of the five selected approaches (i.e., three test case sets * four time budgets), and thus in total 60 comparisons were conducted. Based on the results, we can observe that STIPI significantly outperformed the five selected approaches for 54 out of 60 comparisons (90 %), which indicate that STIPI has a good capability for solving our test case prioritization problem. In addition, STIPI took an average time of 36.5, 51.6 and 82 s (secs) for the three sets of test cases. The average running time for the five chosen approaches are: (1) RS: 18, 24.7 and 33.2 s; (2) Greedy: 42, 48 and 54 ms; (3) A1: 35.7, 42.8 and 65.5 s; (4) A2: 35.2, 42.2 and 55.4 s; and (5) A3: 8.9, 33.4 and 41.2 s. Notice that there is no practical difference in terms of the running time for the approaches except Greedy, however the performance of Greedy is significantly worse than STIPI (Sect. 5.2), and thus Greedy cannot be employed to solve our test case prioritization problem. In addition, based on the domain knowledge of VCS testing, the running time in seconds is acceptable when deployed in practice.
5.3 Overall Discussion
For RQ1, we observed that STIPI performed significantly better than RS for all the EMs with the three sets of test cases under the four time budgets. Such an observation reveals that solving our test case prioritization problem is not trivial, which requires an efficient approach. As for RQ2, we compared STIPI with Greedy, A1, A2 and A3 (Sect. 4.1). Results show that STIPI performed significantly better than Greedy. This can be explained that Greedy is a local search algorithm that may get stuck in a local space during the search process, while STIPI employs mutation operator (Sect. 4.4) to explore the whole search space towards finding optimal solutions. In addition, Greedy converted our multi-objective optimization problem into a single-objective optimization problem by assigning weights to each objective, which may lose many other optimal solutions that hold the same quality [22], while STIPI (integrating NSGA-II) produces a set of non-dominated solutions (i.e., solutions with equivalent quality).
When comparing STIPI with A1, A2 and A3, the results of RQ2 showed that STIPI performed significantly better than A1, A2 and A3 by 83.3 % (30/36). Overall STIPI outperformed the five selected approaches for 90 % (54/60) comparisons. That might be due to two main reasons: (1) STIPI considers the coverage of incremental unique elements (e.g., test API commands) when evaluating the prioritization solutions, i.e., only the incremental unique elements covered by a certain test case are taken into account as compared with the already prioritized test cases; and (2) STIPI provides the test cases with higher execution positions more influence on the quality of a given prioritization solution. Furthermore, A2 and A3 usually work under the assumption that the relations between detected faults and test cases are known beforehand, which is sometimes not the situation in practice, e.g., in our case, we are only aware how many execution times a test case can detect faults rather than having access to the detailed faults detected. However, STIPI defined FDC to measure the fault detection capability (Sect. 3.2) without knowing the detailed relations between faults and test cases, which may be applicable to the similar other contexts when the detailed faults cannot be accessed. It is worth mentioning that the current practice of Cisco do not have an efficient approach for test case prioritization, and thus we are working on deploying our approach in their current practice for further strengthening STIPI.
5.4 Threats to Validity
The internal validity threat arises due to using search algorithms with only one configuration setting for its parameters as we did in our experiment [23]. However, we used the default parameter setting from the literature [24], and based on our previous experience [5, 10], good performance can be achieved for various search algorithms with the default setting. To mitigate the construct validity threat, we used the same stopping criteria (50,000 fitness evaluations) for finding the optimal solutions. To avoid conclusion validity threat due to the random variations in the search algorithms, we repeated the experiments 10 times to reduce the possibility that the results were obtained by chance. Following the guidelines of reporting the results for randomized algorithms [19], we employed the Vargha and Delaney test as the effect size measure and Mann-Whitney test to determine the statistical significance of results. First external validity threat is that one may argue the comparison performed only included RS, Greedy, one existing approach and two modified versions of the existing approaches, which may not be sufficient. Notice that we discussed and justified why we chose these approaches in Sect. 4.1, and it is also possible to compare our approach with other existing approaches, which requires further investigation as the next step. Second external validity threat is due to the fact that we only performed the evaluation using one industrial case study. We need to mention that we conducted the experiment using three sets of test cases with four distinct time budgets based on the domain knowledge of VCS testing.
6 Related Work
In the last several decades, test case prioritization has attracted a lot of attention and considerable amount of work has been done [1–3, 8]. Several survey papers [25, 26] present results that compare existing test case prioritization techniques from different aspects, e.g., based on coverage criteria. Followed by the aspects presented in [25], we summarize the related work close to our approach and highlight the key differences from the following three aspects: coverage criteria, search-based prioritization techniques (which is related with our approach) and evaluation metrics.
Coverage Criteria.
Existing works defined a number of coverage criteria for evaluating the quality of prioritization solutions [2, 3, 26] such as branch coverage and statement coverage, function coverage and function-level fault exposing potential, block coverage, modified condition/decision coverage, transition coverage and round trip coverage. As compared with the state-of-the-art, we proposed three new coverage criteria driven by the industrial problem (Sect. 3.2): (1) Configuration coverage (CC); (2) Test API coverage (APIC) and (3) Status coverage (SC).
Search-Based Prioritization Techniques.
Search-based techniques have been widely applied for addressing test case prioritization problem [3–5, 10]. For instance, Li et al. [3] defined a fitness function with three objectives (i.e., Block, Decision and Statement Coverage) and integrated the fitness function with hill climbing and GA for test case prioritization. Arrieta et al. [7] proposed to prioritize test cases by defining a two-objective fitness function (i.e., test case execution time and fault detection capability) and evaluated the performance of several search algorithms. The authors of [7] also proposed a strategy to give higher importance to test cases with higher positions (to be executed earlier). A number of research papers have focused on addressing the test case prioritization problem within a limited budget (e.g., time and test resource) using search-based approaches. For instance, Walcott et al. [1] proposed to combine selection (of a subset of test cases) and prioritization (of the selected test cases) for prioritizing test cases within a limited time budget. Different weights are assigned to the selection part and prioritization part when defining the fitness function followed by solving the problem with GA. Wang et al. [5] focused on the test case prioritization within a given limited test resource budget (i.e., hardware, which is different as compared with the time budget used in this work) and defined four cost-effectiveness measures (e.g., test resource usage), and evaluated several search algorithms (e.g., NSGA-II).
As compared with the existing works, our approach (i.e., STIPI) defines a fitness function that considers configurations, test APIs and statuses, which were not addressed in the current literature. When defining the fitness function, STIPI proposed two strategies, which include (1) only considering the unique elements (e.g., configurations) achieved; and (2) taking the impact of test case execution orders on the quality of prioritization solutions into account, which is not the case in the existing works.
Evaluation Metrics (EMs).
APFD is widely used in the literature as an EM [2, 3, 8, 16]. Moreover, the modified version of APFD (i.e., APFD p ) using time penalty [1, 16] is usually applied for test case prioritization with a time budget. Other metrics were also defined and applied as EMs [9, 26] such as Average Severity of Faults Detected, Total Percentage of Faults Detected and Average Percentage of Faults Detected per Cost (APFD c ). As compared with the existing EMs, we defined in total six new EMs driven by our industrial problem for configurations, test APIs and statuses (Table 3), which include: (1) APCC, APAC, and APSC, inspired by APFD, when there is 100 % time budget; and (2) APCC p , APAC p , and APSC p inspired by APFD p , when there is a limited time budget (e.g., 25 % time budget). Furthermore, we defined the seventh EM (MFDC) to assess to what extent faults can be detected when the time budget is less than 100 % (Table 3). To the best of our knowledge, there is no existing work that applies these seven EMs for assessing the quality of test case prioritization solutions.
7 Conclusion and Future Work
Driven by our industrial problem, we proposed a multi-objective search-based test case prioritization approach named STIPI for covering maximum number of configurations, test APIs, statuses, and achieving high fault detection capability as quickly as possible. We compared STIPI with five test case prioritization approaches using three sets of test cases with four time budgets. The results show that STIPI performed significantly better than the chosen approaches for 90 % of the cases. STIPI managed to achieve a higher performance than random search for on average 39.9 % (configuration coverage), 18.6 % (test API coverage), 32.7 % (status coverage) and 43.9 % (FDC). In the future, we plan to compare STIPI with more prioritization approaches from the literature using additional case studies with larger scale to further generalize the results.
References
Walcott, K.R., Soffa, M.L., Kapfhammer, G.M., Roos, R.S.: Timeaware test suite prioritization. In: Proceedings of 2006 International Symposium on Software Testing and Analysis, pp. 1–12 (2006)
Rothermel, G., Untch, R.H., Chu, C., Harrold, M.J.: Test case prioritization: an empirical study. In: Proceedings of International Conference on Software Maintenance (ICSM 1999), pp. 179–188 (1999)
Li, Z., Harman, M., Hierons, R.M.: Search algorithms for regression test case prioritization. IEEE Trans. Softw. Eng. (TSE) 33, 225–237 (2007)
Wang, S., Buchmann, D., Ali, S., Gotlieb, A., Pradhan, D., Liaaen, M.: Multi-objective test prioritization in software product line testing: an industrial case study. In: International Software Product Line Conference, pp. 32–41 (2014)
Wang, S., Ali, S., Yue, T., Bakkeli, Ø., Liaaen, M.: Enhancing test case prioritization in an industrial setting with resource awareness and multi-objective search. In: ICSE, pp. 182–191 (2016)
Deb, K., Pratap, A., Agarwal, S., Meyarivan, T.: A fast and elitist multiobjective genetic algorithm: NSGA-II. TSE 6, 182–197 (2002)
Arrieta, A., Wang, S., Sagardui, G., Etxeberria, L.: Test case prioritization of configurable cyber-physical systems with weight-based search algorithms. In: Genetic and Evolutionary Computation (GECCO), pp. 1053–1060 (2016)
Rothermel, G., Untch, R.H., Chu, C., Harrold, M.J.: Prioritizing test cases for regression testing. TSE 27, 929–948 (2001)
Elbaum, S., Malishevsky, A., Rothermel, G.: Incorporating varying test costs and fault severities into test case prioritization. In: Proceedings of International Conference on Software Engineering (ICSE), pp. 329–338 (2001)
Wang, S., Ali, S., Yue, T., Li, Y., Liaaen, M.: A practical guide to select quality indicators for assessing pareto-based search algorithms in search-based software engineering. In: ICSE, pp. 631–642 (2016)
Wang, S., Ali, S., Gotlieb, A.: Cost-effective test suite minimization in product lines using search techniques. J. Syst. Softw. 103, 370–391 (2015)
Wang, S., Ali, S., Gotlieb, A.: Minimizing test suites in software product lines using weight-based genetic algorithms. In: Proceedings of 15th Annual Conference on Genetic and Evolutionary Computation, pp. 1493–1500 (2013)
Sarro, F., Petrozziello, A., Harman, M.: Multi-objective software effort estimation. In: ICSE, pp. 619–630 (2016)
Wang, S., Ali, S., Yue, T., Liaaen, M.: UPMOA: an improved search algorithm to support user-preference multi-objective optimization. In: International Symposium on Software Reliability Engineering (ISSRE), pp. 393–404 (2015)
Technical report (2016-06): https://www.simula.no/publications/stipi-using-search-prioritize-test-cases-based-multi-objectives-derived-industrial
Lu, Y., Lou, Y., Cheng, S., Zhang, L., Hao, D., Zhou, Y., Zhang, L.: How does regression test prioritization perform in real-world software evolution? In: Proceedings of 38th ICSE, pp. 535–546 (2016)
Nebro, A.J., Luna, F., Alba, E., Dorronsoro, B., Durillo, J.J., Beham, A.: AbYSS: adapting scatter search to multiobjective optimization. IEEE Trans. Evol. Comput. 12, 439–457 (2008)
Vargha, A., Delaney, H.D.: A critique and improvement of the CL common language effect size statistics of McGraw and Wong. J. Educ. Behav. Stat. 25, 101–132 (2000)
Arcuri, A., Briand, L.: A practical guide for using statistical tests to assess randomized algorithms in software engineering. In: 33rd International Conference on Software Engineering (ICSE), pp. 1–10 (2011)
Mann, H.B., Whitney, D.R.: On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 18, 50–60 (1947)
Durillo, J.J., Nebro, A.J.: jMetal: a Java framework for multi-objective optimization. Adv. Eng. Softw. 42, 760–771 (2011)
Konak, A., Coit, D.W., Smith, A.E.: Multi-objective optimization using genetic algorithms: a tutorial. Reliab. Eng. Syst. Safety 91, 992–1007 (2006)
De Oliveira Barros, M., Neto, A.: Threats to validity in search-based software engineering empirical studies. Technical report 6, UNIRIO-Universidade Federal do Estado do Rio de Janeiro (2011)
Arcuri, A., Fraser, G.: On parameter tuning in search based software engineering. In: Cohen, M.B., Ó Cinnéide, M. (eds.) SSBSE 2011. LNCS, vol. 6956, pp. 33–47. Springer, Heidelberg (2011)
Yoo, S., Harman, M.: Regression testing minimization, selection and prioritization: a survey. Softw. Test. Verif. Reliab. 22, 67–120 (2012)
Catal, C., Mishra, D.: Test case prioritization: a systematic mapping study. Softw. Qual. J. 21, 445–478 (2013)
Acknowledgements
This research is supported by the Research Council of Norway (RCN) funded Certus SFI. Shuai Wang is also supported by the RFF Hovedstaden funded MBE-CR project. Shaukat Ali and Tao Yue are also supported by the RCN funded Zen-Configurator project, the EU Horizon 2020 project funded U-Test, the RFF Hovedstaden funded MBE-CR project and the RCN funded MBT4CPS project.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 IFIP International Federation for Information Processing
About this paper
Cite this paper
Pradhan, D., Wang, S., Ali, S., Yue, T., Liaaen, M. (2016). STIPI: Using Search to Prioritize Test Cases Based on Multi-objectives Derived from Industrial Practice. In: Wotawa, F., Nica, M., Kushik, N. (eds) Testing Software and Systems. ICTSS 2016. Lecture Notes in Computer Science(), vol 9976. Springer, Cham. https://doi.org/10.1007/978-3-319-47443-4_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-47443-4_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-47442-7
Online ISBN: 978-3-319-47443-4
eBook Packages: Computer ScienceComputer Science (R0)