Abstract
We introduce a smooth non-convex approach in a novel geometric framework which complements established convex and non-convex approaches to image labeling. The major underlying concept is a smooth manifold of probabilistic assignments of a prespecified set of prior data (the “labels”) to given image data. The Riemannian gradient flow with respect to a corresponding objective function evolves on the manifold and terminates, for any \(\delta > 0\), within a \(\delta \)-neighborhood of an unique assignment (labeling). As a consequence, unlike with convex outer relaxation approaches to (non-submodular) image labeling problems, no post-processing step is needed for the rounding of fractional solutions. Our approach is numerically implemented with sparse, highly-parallel interior-point updates that efficiently converge, largely independent from the number of labels. Experiments with noisy labeling and inpainting problems demonstrate competitive performance.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Image labeling is the process of assigning a finite set of labels to given image data and constitutes a key problem of low-level computer vision. This task is typically formulated as Maximum A-Posterior (MAP) problem based on a discrete Markov Random Field (MRF) model. We refer to [1] for a recent survey and to [2] for a comprehensive evaluation of various inference methods. Because the labeling problem is NP-hard (ignoring a subset of problems which can be reformulated as a maximum-flow problem), problem relaxations are necessary in order to compute efficiently approximate solutions. The prevailing convex approach is based on the linear programming relaxation [3] with the so-called local polytope as feasible set [4]. A major obstacle to speeding up the convergence rate is the inherent non-smoothness of the polyhedral relaxation, e.g. in terms of a dual objective function after a problem decomposition into exactly solvable subproblems. Because the convex approach constitutes an outer relaxation, fractional solutions are obtained in general, and a subsequent rounding step is needed to obtain a unique label assignment. Non-convex relaxations are e.g. based on the mean-field approach [4, Sect. 5]. They constitute inner relaxations of the combinatorially complex feasible set (the so-called marginal polytope) and hence do not require a post-processing step for rounding. However, as for non-convex optimization problems in general, inference suffers from the local-minima problem, and auxiliary parameters introduced for alleviating this difficulty, e.g. by deterministic annealing, can only be heuristically tuned. Variational methods in connection with the labeling problem have been addressed before e.g. [5, 6].
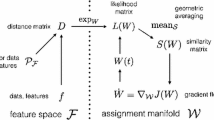
Contribution. We introduce a novel approach to the image labeling problem based on a geometric formulation. Figure 1 illustrates the major components of the approach and their interplay. Labeling denotes the tasks to assign prior features, which are elements of the prior set \(\mathcal {P_F}\), to given features f in any metric space (raw data just constitute a basic specific example). The mapping \(\exp _W\) lifts the distance matrix D to the assignment manifold \(\mathcal {W}\). The assignment is determined by solving a Riemannian gradient flow with respect to an appropriate objective function J(W), where W is called the assignment matrix, which evolves on the assignment manifold. The latter key concept encompasses the set of all strictly positive stochastic matrices equipped with a Fisher-Rao product metric. This furnishes a proper geometry for computing local Riemannian means, described by the similarity matrix S(W) of the likelihood matrix L(W). This achieves spatially coherent labelings and suppress the influence of noise. The Riemannian metric also determines the gradient flow and leads to efficient, sparse interior-point updates that converge in few dozens of outer iterations. Even larger numbers of labels do not significantly slow down the convergence rate. We show that the local Riemannien means can be accurately approximated by closed-form expressions which eliminates inner iterations and hence further speeds up the numerical implementation. For any specified \(\delta > 0\), the iterates terminate within a \(\delta \)-neighborhood of unique assignments, which finally determines the labeling.
Geometric labeling approach and its components. The feature space \(\mathcal {F}\) with a distance function \(d_{\mathcal {F}}\), along with observed data and prior data to be assigned, constitute the application specific part. A labeling of the data is determined by a Riemannian gradient flow on the manifold of probabilistic assignments, which terminates at a unique assignment, i.e. a labeling of the given data. Sections 2–5 detail all depicted components of the approach and their interplay.
Our approach is non-convex and smooth. Regarding the non-convexity, no parameter tuning is needed to escape from poor local minima: For any problem instance, the flow is naturally initialized at the barycenter of the assignment manifold, from which it smoothly evolves and terminates at a labeling.
Organization. We formally detail the components of our approach in Sects. 2 and 3. The objective function and the optimization approach are described in Sects. 4 and 5. Few academical experiments are reported in Sect. 6 which illustrate properties of our approach and contrast it with the prevailing convex relaxation approach.
Our main objective is to introduce and announce a novel approach to the image labeling problem of computer vision. Elaboration of any specific application is beyond the scope of this paper. Due to lack of space, we omitted all proofs and refer the reader to the report [7] which also provides a more comprehensive discussion of the literature.
Basic Notation. We set \([n]=\{1,2,\ldots ,n\}\) and \(\mathbbm {1}=(1,1,\ldots ,1)^{\top }\). \(\langle u,v \rangle = \sum _{i \in [n]} u_{i} v_{i}\) denotes the Euclidean inner product and for matrices \(\langle A, B \rangle := \mathrm {tr}(A^{\top } B)\). For strictly positive vectors we often write pointwise operations more efficiently in vector form. For example, for \(0 < p \in \mathbb {R}^{n}\) and \(u \in \mathbb {R}^{n}\), the expression \(\frac{u}{\sqrt{p}}\) denotes the vector \((u_{1}/\sqrt{p_{1}},\ldots ,u_{n}/\sqrt{p_{n}})^{\top }\).
2 The Assignment Manifold
In this section, we define the feasible set for representing and computating image labelings in terms of assignment matrices \(W \in \mathcal {W}\), the assignment manifold \(\mathcal {W}\). The basic building block is the open probability simplex \(\mathcal {S}\) equipped with the Fisher-Rao metric. We refer to [8, 9] for background reading.
2.1 Geometry of the Probability Simplex
The relative interior \(\mathcal {S}=\mathring{\varDelta }_{n-1}\) of the probability simplex \(\varDelta _{n-1} = \{p \in \mathbb {R}_{+}^{n} :\langle \mathbbm {1}, p \rangle = 1\}\) becomes a differentiable Riemannian manifold when endowed with the Fisher-Rao metric, which in this particular case reads
with tangent spaces denotes by \(T_{p}\mathcal {S}\). The Riemannian gradient \(\nabla _{\mathcal {S}} f(p) \in T_{p}\mathcal {S}\) of a smooth function \(f :\mathcal {S} \rightarrow \mathbb {R}\) at \(p \in \mathcal {S}\) is the tangent vector given by
We also regard the scaled sphere \(\mathcal {N}=2\mathbb {S}^{n-1}\) as manifold with Riemannian metric induced by the Euclidean inner product of \(\mathbb {R}^{n}\). The following diffeomorphism \(\psi \) between \(\mathcal {S}\) and the open subset \(\psi (\mathcal {S}) \subset \mathcal {N}\), henceforth called sphere-map, was suggested e.g. by [10, Sect. 2.1] and [8, Sect. 2.5]
The sphere-map enables to compute the geometry of \(\mathcal {S}\) from the geometry of the 2-sphere. The sphere-map \(\psi \) (3) is an isometry, i.e. the Riemannian metric is preserved. Consequently, lenghts of tangent vectors and curves are preserved as well. In particular, geodesics as critical points of length functionals are mapped by \(\psi \) to geodesics. We denote by
respectively, the Riemannian distance on \(\mathcal {S}\) between two points \(p, q \in \mathcal {S}\), and the geodesic on \(\mathcal {S}\) emanating from \(p=\gamma _v(0)\) in the direction \(v =\dot{\gamma }_v(0) \in T_{p}\mathcal {S}\). The exponential mapping for \(\mathcal {S}\) is denoted by
The Riemannian mean \(\mathrm {mean}_{\mathcal {S}}(\mathcal {P})\) of a set of points \(\mathcal {P}=\{p^{i}\}_{i \in [N]} \subset \mathcal {S}\) with corresponding weights \(w \in \varDelta _{N-1}\) minimizes the objective function
We use uniform weights \(w = \frac{1}{N} \mathbbm {1}_{N}\) in this paper. The following fact is not obvious due to the non-negative curvature of the manifold \(\mathcal {S}\). It follows from [11, Theorem 1.2] and the radius of the geodesic ball containing \(\psi (\mathcal {S}) \subset \mathcal {N}\).
Lemma 1
The Riemannian mean (6) is unique for any data \(\mathcal {P} = \{p^{i}\}_{i \in [n]} \subset \mathcal {S}\) and weights \(w \in \varDelta _{n-1}\).
We call the computation of Riemannian means geometric averaging (cf. Fig. 1).
2.2 Assignment Matrices and Manifold
A natural question is how to extend the geometry of \(\mathcal {S}\) to the stochastic assignment matrices \(W \in \mathbb {R}^{m \times n}\), with rows \(W_{i} \in \mathcal {S},\,i \in [m]\) consisting of discrete probability distributions where m is the number of features and n is the number of labels, so as to preserve the information-theoretic properties induced by this metric (that we do not discuss here – cf. [8, 12]).
This problem was recently studied by [13]. The authors suggested three natural definitions of manifolds. It turned out that all of them are slight variations of taking the product of \(\mathcal {S}\), differing only by the scaling of the resulting product metric. As a consequence, we make the following
Definition 1
(Assignment Manifold). The manifold of assignment matrices, called assignment manifold, is the set
According to this product structure and based on (1), the Riemannian metric is given by
Note that \(V \in T_{W}\mathcal {W}\) means \(V_{i} \in T_{W_{i}} \mathcal {S},\,i \in [m]\).
Remark 1
We call stochastic matrices contained in \(\mathcal {W}\) assignment matrices, due to their role in the variational approach described next.
3 Features, Distance Function, Assignment
We refer the reader to Fig. 1 for an overview of the following definitions. Let \(f :\mathcal {V} \rightarrow \mathcal {F}\), \(i \mapsto f_{i}\) and \(i \in \mathcal {V}=[m]\) denote any given data, either raw image data or features extracted from the data in a preprocessing step. In any case, we call f feature. At this point, we do not make any assumption about the feature space \(\mathcal {F}\) except that a distance function \( d_{\mathcal {F}} :\mathcal {F} \times \mathcal {F} \rightarrow \mathbb {R}, \) is specified. We assume that a finite subset of \(\mathcal {F}\)
additionally is given, called prior set. We are interested in the assignment of the prior set to the data in terms of an assignment matrix \( W \in \mathcal {W} \subset \mathbb {R}^{m \times n}, \) with the manifold \(\mathcal {W}\) defined by (7). Thus, by definition, every row vector \(0 < W_{i} \in \mathcal {S}\) is a discrete distribution with full support \({{\mathrm{supp}}}(W_{i})=[n]\). The element
quantifies the assignment of prior item \(f^{*}_{j}\) to the observed data point \(f_{i}\). We may think of this number as the posterior probability that \(f^{*}_{j}\) generated the observation \(f_{i}\).
The assignment task asks for determining an optimal assignment \(W^{*}\), considered as “explanation” of the data based on the prior data \(\mathcal {P}_{\mathcal {F}}\). We discuss next the ingredients of the objective function that will be used to solve assignment tasks (see also Fig. 1).
Distance Matrix. Given \(\mathcal {F}, d_{\mathcal {F}}\) and \(\mathcal {P}_{\mathcal {F}}\), we compute the distance matrix
where \(\rho \) is the first (from two) user parameters to be set. This parameter serves two purposes. It accounts for the unknown scale of the data f that depends on the application and hence cannot be known beforehand. Furthermore, its value determines what subset of the prior features \(f^{*}_{j},\,j \in [n]\) effectively affects the process of determining the assignment matrix W. We call \(\rho \) selectivity parameter.
Furthermore, we set
That is, W is initialized with the uninformative uniform assignment that is not biased towards a solution in any way.
Likelihood Matrix. The next processing step is based on the following
Definition 2
(Lifting Map (Manifolds \(\mathcal {S}, \mathcal {W}\) )). The lifting mapping is defined by
where \(U_{i}, W_{i}, i \in [m]\) index the row vectors of the matrices U, W, and where the argument decides which of the two mappings \(\exp \) applies.
Remark 2
The lifting mapping generalizes the well-known softmax function through the dependency on the base point p. In addition, it approximates geodesics and accordingly the exponential mapping \({{\mathrm{Exp}}}\), as stated next. We therefore use the symbol \(\exp \) as mnemomic. Unlike \({{\mathrm{Exp}}}_{p}\) in (5), the mapping \(\exp _{p}\) is defined on the entire tangent space, which is convenient for numerical computations.
Proposition 1
Let
Then \(\exp _{p}(u t)\) given by (13a) solves
and provides a first-order approximation of the geodesic \(\gamma _{v}(t)\) from (4), (5).
Given D and W, we lift the vector field D to the manifold \(\mathcal {W}\) by
with \(\exp _{W}\) defined by (13b). We call L likelihood matrix because the row vectors are discrete probability distributions which separately represent the similarity of each observation \(f_{i}\) to the prior data \(\mathcal {P}_{\mathcal {F}}\), as measured by the distance \(d_{\mathcal {F}}\) in (11). Note that the operation (17) depends on the assignment matrix \(W \in \mathcal {W}\).
Similarity Matrix. Based on the likelihood matrix L, we define the similarity matrix
where each row is the Riemannian mean (6) of the likelihood vectors, indexed by the neighborhoods as specified by the underying graph \(\mathcal {G}=(\mathcal {V},\mathcal {E})\), such that the local neighborhood \(\tilde{\mathcal {N}}_{\mathcal {E}}(i) = \{i\} \cup \mathcal {N}_{\mathcal {E}}(i)\) with \(\mathcal {N}_{\mathcal {E}}(i) = \{j \in \mathcal {V} :ij \in \mathcal {E}\}\) is augmented by the center pixel. Note that S depends on W because L does so by (17). The size of the neighbourhoods \(|\tilde{\mathcal {N}}_{\mathcal {E}}(i)|\) is the second user parameter, besides the selectivity parameter \(\rho \) for scaling the distance matrix (11). Typically, each \(\tilde{\mathcal {N}}_{\mathcal {E}}(i)\) indexes the same local “window” around pixel location i. We then call the window size \(|\tilde{\mathcal {N}}_{\mathcal {E}}(i)|\) scale parameter. In basic applications, the distance matrix D will not change once the features and the feature distance \(d_{\mathcal {F}}\) are determined. On the other hand, the likelihood matrix L(W) and the similarity matrix S(W) have to be recomputed as the assignment W evolves, as part of any numerical algorithm used to compute an optimal assignment \(W^{*}\). We point out, however, that more general scenarios are conceivable – without essentially changing the overall approach – where \(D = D(W)\) depends on the assignment as well and hence has to be updated too, as part of the optimization process.
4 Objective Function, Optimization
We specify next the objective function as criterion for assignments and the gradient flow on the assignment manifold, to compute an optimal assignment \(W^{*}\). Finally, based on \(W^{*}\), the so-called assignment mapping is defined.
Objective Function. Getting back to the interpretation from Sect. 3 of the assignment matrix \(W \in \mathcal {W}\) as posterior probabilities,
of assigning prior feature \(f^{*}_{j}\) to the observed feature \(f_{i}\), a natural objective function to be maximized is
The functional J together with the feasible set \(\mathcal {W}\) formalizes the following objectives:
-
1.
Assignments W should maximally correlate with the feature-induced similarities \(S = S(W)\), as measured by the inner product which defines the objective function J(W).
-
2.
Assignments of prior data to observations should be done in a spatially coherent way. This is accomplished by geometric averaging of likelihood vectors over local spatial neighborhoods, which turns the likelihood matrix L(W) into the similarity matrix S(W), depending on W.
-
3.
Maximizers \(W^{*}\) should define image labelings in terms of rows \(\overline{W}_{i}^{*} = e^{k_{i}} \in \{0,1\}^{n},\; i, k_{i} \in [m]\), that are indicator vectors. While the latter matrices are not contained in the assignment manifold \(\mathcal {W}\), which we notationally indicate by the overbar, we compute in practice assignments \(W^{*} \approx \overline{W}^{*}\) arbitrarily close to such points. It will turn out below that the geometry enforces this approximation.
As a consequence of 3 and in view of (19), such points \(W^{*}\) maximize posterior probabilities akin to the interpretation of MAP-inference with discrete graphical models by minimizing corresponding energy functionals. The mathematical structure of the optimization task of our approach, however, and the way of fusing data and prior information, are quite different. The following Lemma states point 3 above more precisely.
Lemma 2
Let \(\overline{\mathcal {W}}\) denote the closure of \(\mathcal {W}\). We have
and the supremum is attained at the extreme points
corresponding to matrices with unit vectors as row vectors.
Assignment Mapping. Regarding the feature space \(\mathcal {F}\), no assumptions were made so far, except for specifying a distance function \(d_{\mathcal {F}}\). We have to be more specific about \(\mathcal {F}\) only if we wish to synthesize the approximation to the given data f, in terms of an assignment \(W^{*}\) that optimizes (20) and the prior data \(\mathcal {P}_{\mathcal {F}}\). We denote the corresponding approximation by
and call it assignment mapping.
A simple example of such a mapping concerns cases where prototypical feature vectors \(f^{*j},\, j\in [n]\) are assigned to data vectors \(f^{i},\, i \in [m]\): the mapping \(u(W^{*})\) then simply replaces each data vector by the convex combination of prior vectors assigned to it,
And if \(W^{*}\) approximates a global maximum \(\overline{W}^{*}\) as characterized by Lemma 2, then each \(f_{i}\) is uniquely replaced (“labelled”) by some \(u^{*k_{i}} = f^{*k_{i}}\).
Optimization Approach. The optimization task (20) does not admit a closed-form solution. We therefore compute the assignment by the Riemannian gradient ascent flow on the manifold \(\mathcal {W}\),
using the initialization (12) with
which results from applying (2) to the objective (20). The flows 25a, b for \(i \in [m]\), are not independent as the product structure of \(\mathcal {W}\) (cf. Sect. 2.2) might suggest. Rather, they are coupled through the gradient \(\nabla J(W)\) which reflects the interaction of the distributions \(W_{i},\,i \in [m]\), due to the geometric averaging which results in the similarity matrix (18).
5 Algorithm, Implementation
We discuss in this section specific aspects of the implementation of the variational approach.
Assignment Normalization. Because each vector \(W_{i}\) approaches some vertex \(\overline{W}^{*} \in \overline{\mathcal {W}}^{*}\) by construction, and because the numerical computations are designed to evolve on \(\mathcal {W}\), we avoid numerical issues by checking for each \(i \in [m]\) every entry \(W_{ij},\, j \in [n]\), after each iteration of the algorithm (30) below. Whenever an entry drops below \(\eta =10^{-10}\), we rectify \(W_{i}\) by
In other words, the number \(\eta \) plays the role of 0 in our impementation. Our numerical experiments show that this operation removes any numerical issues without affecting convergence in terms of the termination criterion specified at the end of this section.
Computing Riemannian Means. Computation of the similarity matrix S(W) due to Eq. (18) involves the computation of Riemannian means. Although a corresponding fixed-point iteration (that we omit here) converges quickly, carrying out such iterations as a subroutine, at each pixel and iterative step of the outer iteration (30) below, increases runtime (of non-parallel implementations) noticeably. In view of the approximation of the exponential map \({{\mathrm{Exp}}}_{p}(v) = \gamma _{v}(1)\) by (16), it is natural to approximate the Riemannian mean as well.
Lemma 3
Replacing in the optimality condition of the Riemannian mean (6) (see, e.g. [9, Lemma 4.8.4]) the inverse exponential mapping \({{\mathrm{Exp}}}_{p}^{-1}\) by the inverse \(\exp _{p}^{-1}\) of the lifting map (13a), yields the closed-form expression
as approximation of the Riemannian mean \(\mathrm {mean}_{\mathcal {S}}(\mathcal {P})\), with the geometric mean \(\mathrm {mean}_{g}(\mathcal {P})\) applied componentwise to the vectors in \(\mathcal {P}\).
Optimization Algorithm. A thorough analysis of various discrete schemes for numerically integrating the gradient flow 25a, b, including stability estimates, is beyond the scope of this paper. Here, we merely adopt the following basic strategy from [14], that has been widely applied in the literature (in different contexts) and performed remarkably well in our experiments. Approximating the flow 25a, b for each vector \(W_{i},\, i \in [m]\), and \(W_{i}^{(k)} := W_{i}(t_{i}^{(k)})\), by the time-discrete scheme
and choosing the adaptive step-sizes \(t_{i}^{(k+1)}-t_{i}^{(k)} = \frac{1}{\langle W_{i}^{(k)}, \nabla _{i} J(W^{(k)})\rangle }\), yields the multiplicative updates
We further simplify this update in view of the explicit expression of the gradient of the objective function with components \(\partial _{W_{ij}} J(W)= \langle T^{ij}(W), W \rangle + S_{ij}(W)\), that comprise two terms. The first one in terms of a matrix \(T^{ij}\) (that we do not further specify here) contributes the derivative of S(W) with respect to \(W_{i}\), which is significantly smaller than the second term \(S_{ij}(W)\), because \(S_{i}(W)\) results from averaging (18) the likelihood vectors \(L_{j}(W_{j})\) over spatial neighborhoods and hence changes slowly, consequently, we simply drop this first term.
Thus, for computing the numerical results reported in this paper, we used the fixed-point iteration
together with the approximation due to Lemma 3 for computing Riemannian means, which define by (18) the similarity matrices \(S(W^{(k)})\). Note that this requires to recompute the likelihood matrices (17) as well, at each iteration k.
Termination Criterion. Algorithm (30) was terminated if the average entropy
dropped below a threshold. For example, a threshold value \(10^{-4}\) means in practice that, up to a tiny fraction of indices \(i \subset [m]\) that should not matter for a subsequent further analysis, all vectors \(W_{i}\) are very close to unit vectors, thus indicating an almost unique assignment of prior items \(f_{j}^{*},\,j \in [n]\) to the data \(f_{i},\,i \in [m]\). This termination criterion was adopted for all experiments.
Parameter influence on labeling. Panels (a) and (b) show a ground-truth image and noisy input data. Panels (c)–(k) show the assignments \(u(W^{*})\) for various parameter values where \(W^{*}\) maximizes the objective function (20). The spatial scale \(|\mathcal {N}_{\mathcal {E}}|\) increases from left to right. The results illustrate the compromise between sensitivity to noise and to the geometry of signal transitions.
6 Experiments
In this section, we show results on empirical convergence rate and the influence of the fix-point iteration (30). Additionally, we show results on a multi-class labeling problem of inpainting by labeling.
6.1 Parameters, Empirical Convergence Rate
The color images in Fig. 2 comprise of 31 color vectors forming the prior data set \(\mathcal {P}_{\mathcal {F}} = \{f^{1*},\ldots ,f^{31*}\}\) and are used to illustrate the labeling problem. The labeling task is to assign these vectors in a spatially coherent way to the input data so as to recover the ground truth image. Every color vector was encoded by the vertices of the simplex \(\varDelta _{30}\), that is by the unit vectors \(\{e^{1},\ldots ,e^{31}\} \subset \{0,1\}^{31}\). Choosing the distance \(d_{\mathcal {F}}(f^{i},f^{j}) := \Vert f^{i}-f^{j}\Vert _{1}\), this results in unit distances between all pairs of data points and hence enables to assess most clearly the impact of geometric spatial averaging and the influence of the two parameters \(\rho \) and \(|\mathcal {N}_{\varepsilon }|\), introduced in Sect. 3. All results were computed using the assignment mapping (24) without rounding. This shows that the termination criterion of Sect. 5, illustrated by Fig. 3 leads to (almost) unique assignments.
In Fig. 2, the selectivity parameter \(\rho \) increases from top to bottom. If \(\rho \) is chosen too small, then there is a tendency to noise-induced oversegmentation, in particular at small spatial scales \(|\mathcal {N}_{\mathcal {E}}|\). The reader familiar with total variation based denoising [15], where a single parameter is only used to control the influence of regularization, may ask why two parameters are used in the present approach and if they are necessary. Note, however, that depending on the application, the ability to separate the physical and the spatial scale in order to recognize outliers with small spatial support, while performing diffusion at a larger spatial scale as in panels (c),(d),(f),(i), may be beneficial. We point out that this separation of the physical and spatial scales (image range vs. image domain) is not possible with total variation based regularization where these scales are coupled through the co-area formula. As a consequence, a single parameter is only needed in total variation. On the other hand, larger values of the total variation regularization parameter lead to the well-known loss-of-contrast effect, which in the present approach can be avoided by properly choosing the parameters \(\rho , |\mathcal {N}_{\varepsilon }|\) corresponding to these two scales.
Parameter values and convergence rate. Average entropy of the assignment vectors \(W_{i}^{(k)}\) as a function of the iteration counter k and the two parameters \(\rho \) and \(|\mathcal {N}_{\varepsilon }|\), for the labeling task illustrated by Fig. 2. The left panel shows that despite high selectivity in terms of a small value of \(\rho \), small spatial scales necessitate to resolve more conflicting assignments through propagating information by geometric spatial averaging. As a consequence, more iterations are needed to achieve convergence and a labeling. The right panel, shows that at a fixed spatial scale \(|\mathcal {N}_{\varepsilon }|\) higher selectivity leads to faster convergence, because outliers are simply removed from the averaging process, low selectivity leads to an assignment (labeling) taking all data into account.
6.2 Inpainting by Labeling
Inpainting represents the problem of filling in a known region with the missing data. We set the feature metric as in the previous example, but with the difference of defining the distance between the unknown feature vectors to priors to be large, i.e., we do not bias the final assignment to any of the prior features.
Note that our geometrical approach is significantly different from traditional graphical models where unitary and pair-wise terms are used for labeling. Therefore, the evaluation of an objective function’s “energy”, as done in [2], is not an applicable criteria. We instead report the more objective ratio of correctly assigned labels. Terminology and abbreviations are adopted from [2] and all competing methods were evaluated using OpenGM 2 [16]. The methods we include in this study are TRWS, a polyhedral method stemming from linear programming and block-coordinate-ascent [17]. The popular message passing algorithms BPS (sequential) and LBP (parallel) of loopy belief propagation [18]. We also include iterative refinement by partitioning the label space via the \(\alpha \)-\(\beta \)-SWAP algorithm and the \(\alpha \) expansion algorithm \(\alpha \)-Exp algorithms, see [19, 20]. For reference, we include the fast primal-dual algorithm FastPD [21]. We refer to the respective works for additional details.
Synthetic example. In the synthetic example in Fig. 4, we show the region to be inpainted in black color. This is a labeling problem consisting of 3 uniformly distributed color vectors and 1 label representing the background (white). From the result images in the same figure, it is clear that LBP performs better than TRWS. However, in LBP there are discretization artifacts and the intersection point is not center symmetric as for our Geometric approach. A center symmetric intersection of the geometric filter is natural due to the filters isotropic interaction with the neighborhood and lack of prior assumptions. Although, our approach still shows few artifacts on the diagonal borders, computing the ratio of correctly assigned labels, we achieve near perfect reconstruction, 99 %, of the missing data with \(120^\circ \) intersection at the circle center.
Synthetic inpainting example. Here TRWS (truncated linear) shows the worst performance with only 78 % correctly assigned labels. The values show ratio of correctly assigned labels and higher is better. LBP performs better than TRWS, but does not produce an interception of \(120^\circ \) in the circle’s center. The update scheme of our geometric filter was terminated at entropy \(10^{-4}\), with a neighborhood \(3\times 3\) and selectivity parameter \(\rho =0.1\) and produces the most accurate labeling.
Recovery of missing and noisy data. This example is from the mrf-inpainting dataset in [2]. The selectivity parameter was set to \(\rho =1\) and the neighborhood size was \(3\times 3\). The ratio of correctly assigned labels are shown in Fig. 6. It is evident our geometric filter adopts better to the underlying image data, while producing a plausible labeling of the inpainting area.
Ratio of correctly assigned labels for the penguin in Fig. 5 is displayed on the y-axis and the number of labels from the original image are iterated on the x-axis. For label distances 1–6 inference with TRWS shows better agreement with the original image labeling. However, considering larger label distances, our geometric filter shows the most accurate ratio. (TL stands for truncated linear functions and we refer to [2] and respective works for additional details.)
Inpainting. In this second inpainting problem, where each variable can attain 256 labels, is more challenging for established graphical models with respect to numerical implementation. Measured in energy of objective function TRWS obtained the lowest energy value in the evaluation of [2]. However, as inpainting results, TRWS, SWAP and BPS all show poor performance as much of the image details are not represented by the labeling. In our geometric approach, the labeling retains more image details. In Fig. 6 we show the ratio of correctly assigned labels for the penguin (size \(122\times 179\) pixels) in Fig. 5. We again refer to [2] for details on the methods implementations. All methods shows similar accuracy in labeling, and our geometric filter is only challenged by TRWS for label distances smaller than 6 from the original image. Considering label distances larger than 6, our approach shows the best ratio. We further remark that our framework is computationally efficient as it only require few dozens of massively parallel outer iterations. Our non-optimized Matlab implementation reaches the termination criteria \((\delta = 10^{-4})\) after 194 iterations in 2 min and 59 s on an Intel i5 CPU at 3.5 GHz.
7 Conclusion
We presented a novel approach to image labeling, formulated in a smooth geometric setting. The approach contrasts with etablished convex and non-convex relaxations of the image labeling problem through smoothness and geometric averaging. The numerics boil down to parallel sparse updates, that maximize the objective along an interior path in the feasible set of assignments and finally return a labeling. Although an elementary first-order approximation of the gradient flow was only used, the convergence rate seems competitive. In particular, a large number of labels does not slow down convergence as is the case of convex relaxations. All aspects specific to an application domain are represented by a distance matrix D and a user parameter \(\rho \). This flexibility and the absence of ad-hoc tuning parameters should promote applications of the approach to various image labeling problems.
References
Wang, C., Komodakis, N., Paragios, N.: Markov random field modeling, inference & learning in computer vision & image understanding: a survey. Comput. Vis. Image Underst. 117(11), 1610–1627 (2013)
Kappes, J., Andres, B., Hamprecht, F., Schnörr, C., Nowozin, S., Batra, D., Kim, S., Kausler, B., Kröger, T., Lellmann, J., Komodakis, N., Savchynskyy, B., Rother, C.: A comparative study of modern inference techniques for structured discrete energy minimization problems. Int. J. Comp. Vis. 115(2), 155–184 (2015)
Werner, T.: A linear programming approach to max-sum problem: a review. IEEE Trans. Patt. Anal. Mach. Intell. 29(7), 1165–1179 (2007)
Wainwright, M., Jordan, M.: Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 1(1–2), 1–305 (2008)
Sundaramoorthi, G., Hong, B.W.: Fast label: easy and efficient solution of joint multi-label and estimation problems. In: 2014 CVPR, pp. 3126–3133, June 2014
Jung, M., Chung, G., Sundaramoorthi, G., Vese, L.A., Yuille, A.L.: Sobolev gradients and joint variational image segmentation, denoising, and deblurring. In: Proceedings of the SPIE, vol. 7246, pp. 72460I–72460I-13 (2009)
Åström, F., Petra, S., Schmitzer, B., Schnörr, C.: Image Labeling by Assignment 16 March 2016, preprint: http://arxiv.org/abs/1603.05285
Amari, S.I., Nagaoka, H.: Methods of Information Geometry. Amer. Math. Soc. and Oxford University Press (2000)
Jost, J.: Riemannian Geometry and Geometric Analysis, 4th edn. Springer, Heidelberg (2005)
Kass, R.: The geometry of asymptotic inference. Statist. Sci. 4(3), 188–234 (1989)
Karcher, H.: Riemannian center of mass and mollifier smoothing. Comm. Pure Appl. Math. 30, 509–541 (1977)
C̆encov, N.: Statistical Decision Rules and Optimal Inference. Amer. Math. Soc. (1982)
Montúfar, G., Rauh, J., Ay, N.: On the fisher metric of conditional probability polytopes. Entropy 16(6), 3207–3233 (2014)
Losert, V., Alin, E.: Dynamics of games and genes: discrete versus continuous time. J. Math. Biol. 17(2), 241–251 (1983)
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Phys. D 60(1–4), 259–268 (1992)
Andres, B., Beier, T., Kappes, J.: OpenGM: A C++ library for discrete graphical models. CoRR abs/1206.0111 (2012)
Kolmogorov, V.: Convergent tree-reweighted message passing for energy minimization. IEEE Trans. Pattern Anal. Mach. Intell. 28(10), 1568–1583 (2006)
Szeliski, R., Zabih, R., Scharstein, D., Veksler, O., Kolmogorov, V., Agarwala, A., Tappen, M., Rother, C.: A comparative study of energy minimization methods for markov random fields with smoothness-based priors. IEEE Trans. Pattern Anal. Mach. Intell. 30(6), 1068–1080 (2008)
Boykov, Y., Veksler, O., Zabih, R.: Fast approximate energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 23(11), 1222–1239 (2001)
Kolmogorov, V., Zabin, R.: What energy functions can be minimized via graph cuts? IEEE PAMI 26(2), 147–159 (2004)
Komodakis, N., Tziritas, G.: Approximate labeling via graph cuts based on linear programming. IEEE Trans. Pattern Anal. Mach. Intell. 29(8), 1436–1453 (2007)
Acknowledgments
FÅ, SP and CS thank the German Research Foundation (DFG) for support via grant GRK 1653. BS was supported by the European Research Council (project SIGMA-Vision).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Åström, F., Petra, S., Schmitzer, B., Schnörr, C. (2016). A Geometric Approach to Image Labeling. In: Leibe, B., Matas, J., Sebe, N., Welling, M. (eds) Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science(), vol 9909. Springer, Cham. https://doi.org/10.1007/978-3-319-46454-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-319-46454-1_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46453-4
Online ISBN: 978-3-319-46454-1
eBook Packages: Computer ScienceComputer Science (R0)