Interactive Visual Data Exploration with Subjective Feedback

Abstract

Data visualization and iterative/interactive data mining are growing rapidly in attention, both in research as well as in industry. However, integrated methods and tools that combine advanced visualization and data mining techniques are rare, and those that exist are often specialized to a single problem or domain. In this paper, we introduce a novel generic method for interactive visual exploration of high-dimensional data. In contrast to most visualization tools, it is not based on the traditional dogma of manually zooming and rotating data. Instead, the tool initially presents the user with an ‘interesting’ projection of the data and then employs data randomization with constraints to allow users to flexibly and intuitively express their interests or beliefs using visual interactions that correspond to exactly defined constraints. These constraints expressed by the user are then taken into account by a projection-finding algorithm to compute a new ‘interesting’ projection, a process that can be iterated until the user runs out of time or finds that constraints explain everything she needs to find from the data. We present the tool by means of two case studies, one controlled study on synthetic data and another on real census data. The data and software related to this paper are available at http://www.interesting-patterns.net/forsied/interactive-visual-data-exploration-with-subjective-feedback/.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Data visualization and iterative/interactive data mining are both mature, actively researched topics of great practical importance. However, while progress in both fields is abundant (see Sect. 4), methods that combine iterative data mining with visualization and interaction are rare, except for a number of tools designed for specific problem domains.

Yet, tools that combine state-of-the-art data mining with visualization and interaction are highly desirable as they would maximally exploit the strengths of both human data analysts and computer algorithms. While humans are unmatched in spotting interesting relations in low-dimensional visual representations but poor at handling high-dimensional data, computers excel in manipulating high-dimensional data but are weaker at identifying patterns that are truly relevant to the user. A symbiosis of the human data analyst and a well-designed computer system thus promises to provide the most efficient way of navigating the complex information space hidden in high-dimensional data [17].

Fig. 1.

This three-step cycle illustrates our tool’s flow of action.

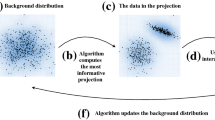
Contributions in This Paper. In this paper we introduce a generically applicable methodology and a tool that demonstrates the proposed approach for interactive visual exploration of (high-dimensional) data. The tool iteratively cycles through three steps, as indicated in Fig. 1. Throughout these cycles, the user builds up an increasingly accurate understanding of the aspects of the data. Our tool maintains a model for this understanding—to which we refer as the background model.

Step 1. The tool initially presents the user with an ‘interesting’ projection of the data, visualized as a scatter plot (Fig. 1 step 1). Here, interesting is formalized with respect to the initial background model; more details follow below.

Step 2. On investigating this scatter plot, the user may take note of some features of the data that contrast with, or add to, their beliefs about the data. We will refer to such features as patterns. In step 2, the user is offered the opportunity to tell the tool what patterns they have noted and assimilated.

Step 3. In step 3, the tool updates the background model to reflect this newly assimilated information embodied by the patterns highlighted by the user. Then the most interesting projection with respect to this updated background model can be computed, and the cycle can be reiterated until the user runs out of time or finds that patterns explain everything the user needs at the moment.

Formalizing the Background Model. A crucial challenge in realizing such a tool is the formalization of the background model. One way to do this is by specifying a randomization procedure that, when applied to the data, does not affect how plausible the user would deem it to be [7, 13]. Access to such a randomized version of the data can be sufficient for determining interesting remaining structure in the data that is not yet known to the user. New patterns are then incorporated by adding corresponding constraints to the randomization procedure, ensuring that the patterns remain present after randomization. We will refer to this approach as the CORAND approach (for Constrained Randomization).

An Illustrative Example. As an example, consider a synthetic data set consisting of 1000 10-dimensional data vectors of which dimensions 1–4 can be clustered into five clusters, dimensions 5–6 into four clusters involving different subsets of data points, and of which dimensions 7–10 are Gaussian noise. All dimensions have equal variance. Figure 2 shows the scatter plots for all pairs of dimensions.

We designed this example to illustrate the two pattern types that a user can specify in the current implementation of our tool. Additionally, it shows how the tool succeeds in finding interesting projections given previously identified patterns. Thirdly, it also demonstrates how the user interactions meaningfully affect subsequent visualizations.

Fig. 2.

Subsample of the toy data.

The first projection projects the data onto a two-dimensional subspace of the first four dimensions of the data (Fig. 3a), i.e., in a subspace of the space in which the data is clustered into 5 clusters. This is indeed sensible, as the structure within this four-dimensional subspace is arguably the strongest.

We then consider two possible user actions (step 2, shown in Fig. 3b). In the first possibility, the user marks all points within each cluster (cluster by cluster), indicating they have taken note of the positions of these groups of points within this particular projection. In the second possibility, the user additionally concludes that these points appear to be clustered, possibly also in other dimensions. (Details on how these two pattern types are formalized will follow.)

Both these pattern types lead to additional constraints on the randomization procedure. The effect of these constraints is identical within the two-dimensional projection of the current visualization (Fig. 3c): the projections of the randomized points onto this plane are identical to the projections of the original points onto this plane. Not visible though, is that in the second possibility the randomization is restricted also in orthogonal dimensions (possibly different ones for different clusters), to account for the additional clustering assumption.

The most interesting subsequent projection, following the user interaction, is different in the two cases (see Fig. 3d). In the first case, the remaining cluster structure within dimensions 1–4 is shown. However, in the second case this cluster structure is fully explained by the constraints, and as a result, the cluster structure in dimensions 5–6 being is shown instead.

Fig. 3.

Two user interaction scenarios for the toy data set. The smaller filled points represent actual data vectors, whereas the unfilled circles represent randomized data vectors. Row (a) shows the first visualization, which is the starting point for both scenarios. Row (b) shows the sets of data points marked by the user, (c) shows the randomized data and original data projected onto the same plane as (a), and (d) shows the most interesting visualization given these specified patterns. The left column shows the scenario when the user assumes nothing beyond the values of the data points in the projection in row (a), whereas the right column shows the scenario when the user assumes each of these sets of points may be clustered in other dimensions as well. (Color figure online)

Outline of This Paper. To use the CORAND approach, three main challenges had to be addressed, as discussed in Sect. 2: (1) defining intuitive pattern types that can be observed and specified based on a scatter plot of a two-dimensional projection of the data; (2) defining a suitable randomization scheme, that can be constrained to take account of such patterns; and (3) a way to identify the most interesting projections given the background model. The resulting system is evaluated in Sect. 3 for usefulness as well as computational properties, on the the synthetic data from the above example as well as on a census dataset. Finally, related work is discussed in Sect. 4, before concluding the paper in Sect. 5.

2 Methodology

We will use the notational convention that bold face upper case symbols represent matrices, bold face lower case symbols represent column vectors, and standard face lower case symbols represent scalars. We assume that our data set consists of n d-dimensional data vectors $\mathbf {x}_i$. The data set is represented by a real matrix $\mathbf {X}=\left( \begin{array}{cccc}\mathbf {x}_1^T&\mathbf {x}_2^T&\cdots&\mathbf {x}_n^T\end{array}\right) ^T\in {\mathbb {R}}^{n\times d}$. More generally, we will denote the transpose of the ith row of any matrix $\mathbf {A}$ as $\mathbf {a}_i$ (i.e., $\mathbf {a}_i$ is a column vector). Finally, we will use the shorthand notation $[n]=\{1,\ldots ,n\}$.

2.1 Projection Tile Patterns in Two Flavours

In the interaction step, the proposed system allows users to declare that they have become aware of (and thus are no longer interested in seeing) the value of the projections of a set of points onto a specific subspace of the data space. We call such information a projection tile pattern for reasons that will become clear later. A projection tile parametrizes a set of constraints to the randomization.

Formally, a projection tile pattern, denoted $\tau$, is defined by a k-dimensional (with $k\le d$ and $k=2$ in the simplest case) subspace of $\mathbb {R}^d$, and a subset of data points $\mathcal {I}_\tau \subseteq [n]$. We will formalize the k-dimensional subspace as the column space of an orthonormal matrix $\mathbf {W}_\tau \in \mathbb {R}^{d\times k}$ with $\mathbf {W}_\tau ^T\mathbf {W}_\tau =\mathbf {I}$, and can thus denote the projection tile as $\tau =(\mathbf {W}_\tau ,\mathcal {I}_\tau )$. The proposed tool provides two ways in which the user can define the projection vectors $\mathbf {W}_\tau$ for a projection tile $\tau$.

2D Tiles. The first approach simply chooses $\mathbf {W}_\tau$ as the (two) weight vectors defining the projection within which the data vectors belonging to $\mathcal {I}_\tau$ were marked. This approach allows the user to simply specify that they have taken note of the positions of that set of data points within this projection. The user makes no further assumptions – they assimilate solely what they see without drawing conclusions not supported by direct evidence, see Fig. 3b (left).

Clustering Tiles. It seems plausible, however, that when the marked points are tightly clustered, the user concludes that these points are clustered not just within the two dimensions shown in the scatter plot. To allow the user to express such belief, the second approach takes $\mathbf {W}_\tau$ to additionally include a basis for other dimensions along which these data points are strongly clustered, see Fig. 3b (right). This is achieved as follows.

Let $\mathbf {X}(\mathcal {I}_\tau ,:)$ represent a matrix containing the rows indexed by elements from $\mathcal {I}_\tau$ from $\mathbf {X}$. Let $\mathbf {W}\in \mathbb {R}^{d\times 2}$ contain the two weight vectors onto which the data was projected for the current scatter plot. In addition to $\mathbf {W}$, we want to find any other dimensions along which these data vectors are clustered. These dimensions can be found as those along which the variance of these data points is not much larger than the variance of the projection $\mathbf {X}(\mathcal {I}_\tau ,:)\mathbf {W}$.

To find these dimensions, we first project the data onto the subspace orthogonal to $\mathbf {W}$. Let us represent this subspace by a matrix with orthonormal columns, further denoted as $\mathbf {W}^{\perp }$. Thus, ${\mathbf {W}^{\perp }}^T\mathbf {W}^{\perp }=\mathbf {I}$ and $\mathbf {W}^T\mathbf {W}^{\perp }=\mathbf {0}$. Then, Principal Component Analysis (PCA) is applied to the resulting matrix $\mathbf {X}(\mathcal {I}_\tau ,:)\mathbf {W}^{\perp }$. The principal directions corresponding to a variance smaller than a threshold are then selected and stored as columns in a matrix $\mathbf {V}$. In other words, the variance of each of the columns of $\mathbf {X}(\mathcal {I}_\tau ,:)\mathbf {W}^{\perp }\mathbf {V}$ is below the threshold.

The matrix $\mathbf {W}_\tau$ associated to the projection tile pattern is then taken to be:

$$\begin{aligned} \mathbf {W}_\tau =\left( \begin{array}{cc}\mathbf {W}&\,\,\mathbf {W}^\perp \mathbf {V}\end{array}\right) . \end{aligned}$$

The threshold on the variance used could be a tunable parameter, but was set here to twice the average of the variance of the two dimensions of $\mathbf {X}(\mathcal {I}_\tau ,:)\mathbf {W}$.

2.2 The Randomization Procedure

Here we describe the approach to randomizing the data. The randomized data should represent a sample from an implicitly defined background model that represents the user’s belief state about the data.

Initially, our approach assumes the user merely has an idea about the overall scale of the data. However, throughout the interactive exploration, the patterns in data described by the projection tiles will be maintained in the randomization.

Initial Randomization. The proposed randomization procedure is parametrized by n orthogonal rotation matrices $\mathbf {U}_i\in {\mathbb {R}}^{d\times d}$, where $i\in [n]$, and the matrices satisfy $(\mathbf {U}_i)^T=(\mathbf {U}_i)^{-1}$. We further assume that we have a bijective mapping $f: [n]\times [d]\mapsto [n]\times [d]$ that can be used to permute the indices of the data matrix. The randomization proceeds in three steps:  

Random rotation of the rows.:

Each data vector $\mathbf {x}_i$ is rotated by multiplication with its corresponding random rotation matrix $\mathbf {U}_i$, leading to a randomised matrix $\mathbf {Y}$ with rows $\mathbf {y}_i^T$ that are defined by:

$$\begin{aligned} \forall i:\ \mathbf {y}_i = \mathbf {U}_i\mathbf {x}_i. \end{aligned}$$

Global permutation.:

The matrix $\mathbf {Y}$ is further randomized by randomly permuting all its elements, leading to the matrix $\mathbf {Z}$ defined as:

$$\begin{aligned} \forall i,j:\ \mathbf {Z}_{i,j}=\mathbf {Y}_{f(i,j)}. \end{aligned}$$

Inverse rotation of the rows.:

Each randomised data vector in $\mathbf {Z}$ is rotated with the inverse rotation applied in step 1, leading to the fully randomised matrix $\mathbf {X}^{*}$ with rows $\mathbf {x}_i^{*}$ defined as follows in terms of the rows $\mathbf {z}_i^T$ of $\mathbf {Z}$:

$$\begin{aligned} \forall i:\ \mathbf {x}^{*}_i = {\mathbf {U}_i}^T\mathbf {z}_i. \end{aligned}$$

The random rotations $\mathbf {U}_i$ and the permutation f are sampled uniformly at random from all possible rotation matrices and permutations, respectively.

Intuitively, this randomization scheme preserves the scale of the data points. Indeed, the random rotations leave their lengths unchanged, and the global permutation subsequently shuffles the values of the d components of the rotated data points. Note that without the permutation step, the two rotation steps would undo each other such that $\mathbf {X}^{*}=\mathbf {X}$. Thus, it is the combined effect that results in a randomization of the data set.¹

Accounting for One Projection Tile. Once the user has assimilated the information in a projection tile $\tau =(\mathbf {W}_\tau ,\mathcal {I}_\tau )$, the randomization scheme should incorporate this information by ensuring that it is present also in all randomized versions of the data. This ensures that it continues to be a sample from a distribution representing the user’s belief state about the data.

This is achieved by imposing the following constraints on the parameters defining the randomization:  

Constraints on the rotation matrices.:

For each $i\in \mathcal {I}_\tau$, the component of $\mathbf {x}_i$ that is within the column space of $\mathbf {W}_\tau$ must be mapped onto the first k dimensions of $\mathbf {y}_i=\mathbf {U}_i\mathbf {x}_i$ by the rotation matrix $\mathbf {U}_i$. This can be achieved by ensuring that:²

$$\begin{aligned} \forall i \in \mathcal {I}_\tau :\ \mathbf {W}_\tau ^T\mathbf {U}_i=\left( \begin{array}{cc}\mathbf {I}&\ \mathbf {0}\end{array}\right) . \end{aligned}$$

(1)

Constraints on the permutation.:

The permutation should not affect any matrix cells with row indices $i\in \mathcal {I}_\tau$ and columns indices $j\in [k]$:

$$\begin{aligned} \forall i\in \mathcal {I}_\tau ,j\in [k]:\ f(i,j)=(i,j). \end{aligned}$$

(2)

 

Proposition 1

Using the above constraints on the rotation matrices $\mathbf {U}_i$ and the permutation f, it holds that:

$$\begin{aligned} \forall i\in \mathcal {I}_\tau , \mathbf {x}_i^T\mathbf {W}_\tau = {\mathbf {x}_i^{*}}^T\mathbf {W}_\tau . \end{aligned}$$

(3)

Thus, the values of the projections of the points in the projection tile remain unaltered by the constrained randomization. We omit the proof as the more general Proposition 2 is provided with proof further below.

Accounting for Multiple Projection Tiles. Throughout subsequent iterations, additional projection tile patterns will be specified by the user. A set of tiles $\tau _i$ for which $\mathcal {I}_{\tau _i}\cap \mathcal {I}_{\tau _j}=\emptyset$ if $i\ne j$ is straightforwardly combined simply by applying the relevant constraints on the rotation matrices to the respective rows. When the sets of data points affected by the projection tiles overlap though, the constraints on the rotation matrices need to be combined. The aim of such a combined constraint should be to preserve the values of the projections onto the projection directions for each of the projection tiles a data vector was part of.

The combined effect of a set of tiles will thus be that the constraint on the rotation matrix $\mathbf {U}_i$ will vary per data vector, and depends on the set of projections $\mathbf {W}_\tau$ for which $i\in \mathcal {I}_\tau$. More specifically, we propose to use the following constraint on the rotation matrices:  

Constraints on the rotation matrices.:

Let $\mathbf {W}_i\in \mathbb {R}^{d\times d_i}$ denote a matrix of which the columns are an orthonormal basis for space spanned by the union of the columns of the matrices $\mathbf {W}_\tau$ for $\tau$ with $i\in \mathcal {I}_\tau$. Thus, for any i and $\tau :i\in \mathcal {I}_\tau$, it holds that $\mathbf {W}_\tau =\mathbf {W}_i\mathbf {v}_\tau$ for some $\mathbf {v}_\tau \in \mathbb {R}^{d_i\times \dim (\mathbf {W}_\tau )}$. Then, for each data vector i, the rotation matrix $\mathbf {U}_i$ must satisfy:

$$\begin{aligned} \forall i \in \mathcal {I}_\tau :\ \mathbf {W}_i^T\mathbf {U}_i=\left( \begin{array}{cc}\mathbf {I}&\ \mathbf {0}\end{array}\right) . \end{aligned}$$

(4)

Constraints on the permutation.:

Then the permutation should not affect any matrix cells in row i and columns $[d_i]$:

$$\begin{aligned} \forall i\in [n],j\in [d_i]:\ f(i,j)=(i,j). \end{aligned}$$

 

Proposition 2

Using the above constraints on the rotation matrices $\mathbf {U}_i$ and the permutation f, it holds that:

$$\begin{aligned} \forall \tau ,\forall i\in \mathcal {I}_\tau , \mathbf {x}_i^T\mathbf {W}_\tau = {\mathbf {x}_i^{*}}^T\mathbf {W}_\tau . \end{aligned}$$

Proof

We first show that ${\mathbf {x}_i^{*}}^T\mathbf {W}_i=\mathbf {x}_i^T\mathbf {W}_i$:

$$\begin{aligned} {\mathbf {x}_i^{*}}^T\mathbf {W}_i&= \mathbf {z}_i^T\mathbf {U}_i^T\mathbf {W}_i=\mathbf {z}_i^T\left( \begin{array}{c}\mathbf {I}\\ \mathbf {0}\end{array}\right) =\mathbf {z}_i(1:d_i)^T=\mathbf {y}_i(1:d_i)^T =\mathbf {y}_i^T\left( \begin{array}{c}\mathbf {I}\\ \mathbf {0}\end{array}\right) =\mathbf {x}_i^T\mathbf {W}_i. \end{aligned}$$

The result follows from the fact that $\mathbf {W}_\tau =\mathbf {W}_i\mathbf {v}_\tau$ for some $\mathbf {v}_\tau \in \mathbb {R}^{d_i\times \dim (\mathbf {W}_\tau )}$.   $\square$

Technical Implementation of the Randomization Procedure. To ensure the randomization can be carried out efficiently throughout the process, note that the matrix $\mathbf {W}_i$ for the $i\in \mathcal {I}_\tau$ for a new projection tile $\tau$ can be updated by computing an orthonormal basis for $\left( \begin{array}{cc}\mathbf {W}_i&\ \mathbf {W}\end{array}\right)$.³

Additionally, note that the tiles define an equivalence relation over the row indices, in which i and j are equivalent if they were included in the same set of projection tiles so far. Within each equivalence class, the matrix $\mathbf {W}_i$ will be constant, such that it suffices to compute it only once, simply keeping track of which points belong to which equivalence class.

2.3 Visualization: Finding the Most Interesting Two-Dimensional Projection

Given the data set $\mathbf {X}$ and the randomized data set $\mathbf {X}^{*}$, it is now possible to quantify the extent to which the empirical distribution of a projection $\mathbf {X}\mathbf {w}$ and $\mathbf {X}^{*}\mathbf {w}$ onto a weight vector $\mathbf {w}$ differ. There are various ways in which this difference can be quantified. We investigated a number of possibilities and found that the $L_1$-distance between the cumulative distribution functions works particularly well in practice. Thus, with $F_\mathbf {x}$ the empirical cumulative distribution function for the set of values in $\mathbf {x}$, the optimal projection is found by solving:

$$\begin{aligned} \max _{\mathbf {w}}&\left\| F_{\mathbf {X}\mathbf {w}}-F_{\mathbf {X}^{*}\mathbf {w}}\right\| _1. \end{aligned}$$

The second dimension of the scatter plot can be sought by optimizing the same objective while requiring it to be orthogonal to the first dimension.

We are unaware of any special structure of this optimization problem that makes solving it particularly efficient. Yet, using the standard quasi-Newton solver in R [18]⁴ already yields satisfactory result. Note that runs of the method may produce different local optimum due to random initialization.

3 Experiments

We present two case studies to illustrate the framework and its utility. The case studies are completed by using a JavaScript version of our tool, made freely available along with the data used for maximum reproducibility.⁵

Table 1. Weight vectors of projections for the synthetic data.

3.1 Synthetic Data Case Study

This section gives an extended discussion of the illustrative example from the introduction, namely the synthetic data case study. The data is described in Sect. 1 and shown in Fig. 2. The first projection shows that the projected data (blue dots in Fig. 3a) differs strongly from the randomized data (gray circles). The weight vectors defining the projection, shown in the 1st row of Table 1, contain large weights in dimensions 1–4. Therefore, the cluster structure seen here mainly corresponds to dimensions 1–4 of the data. A user can indicate this insight by means of a clustering tile for each of the clustered sets of data points (Fig. 3b, right). Encoding this into the background model, results in a randomization shown in Fig. 3c (right), where in the projection the randomized points perfectly align with data points. The new projection that differs most from this updated random background model is given by Fig. 3d (right), revealing the four clusters in dimensions 5–6 that the user was not aware of before.

If the user does not want to draw conclusions about the points being clustered in dimensions other than those shown, she can use 2D tiles instead of clustering tiles (Fig. 3b, left). The updated background model then results in a randomization shown in Fig. 3c (left). In the given projection, this randomization is indistinguishable from the one with a clustering tile, but it results in a different subsequent projection. Indeed, now it shows just another view of the five clusters in dimensions 1–4 (Fig. 3d, left), as confirmed by the large weights for dimensions 1–4 in the 2nd row of Table 1.

Thus, by these simple interactions the user can choose whether she will explore more the cluster structure in dimensions 1–4 or if she already is aware of the cluster structure or does not find it interesting, in which case the system would direct her to the structure occurring in dimensions 5–6.

3.2 UCI Adult Dataset Case Study

In this case study, we demonstrate the utility of our method by exploring a real world dataset. The data is compiled from UCI Adult dataset⁶. To ensure the real time interactivity, we sub-sampled 218 data points and selected six features: “Age” ($17-90$), “Education” ($1-16$), “HoursPerWeek” ($1-99$), “Ethnic Group” (White, AsianPacIlander, Black, Other), “Gender” (Female, Male), “Income” ($\ge 50k$). Among the selected features, “Ethnic Group” is a categorical feature with five categories, “Gender” and “Income” are binary features, the rest are all numeric. To make our method applicable to this dataset, we further binarized the “Ethnic Group” feature (yielded four binary features) and the final dataset consists of 218 points and 9 features.

Fig. 4.

Projections of UCI Adult dataset: (a) projection in the 1st iteration, (b) clusters marked by user in the 1st iteration, (c) projection in the 2nd iteration, and (d) projection in the 3rd iteration.

Table 2. Weight vectors of projections for the UCI Adult dataset.

Table 3. Mean vectors of user marked clusters for the UCI Adult data set.

We assume the user uses clustering tiles throughout her exploration. Each of the patterns discovered during the exploration process thus corresponds to certain demographic clustering pattern. To illustrate how our tool helps the user rapidly gain an understanding of the data, we discuss the first three iterations of the exploration process below.

The first projection (Fig. 4a) visually consists of four clusters. The user notes that the weight vectors corresponding to the axes of the plot assign large weights to the “Ethnic Group” attributes (1st row, Table 2). As mentioned, we assume the user marks these points as part of the same clustering tile. When marking the clusters (Fig. 4b), the tool informs the user of the mean vectors of the points within each clustering tile. The 1st row of Table 3 shows that each cluster completely represents one out of four ethnic groups, which corroborates the user’s understanding.

Taking the user’s feedback into consideration, a new projection is generated by the tool. The new scatter plot (Fig. 4c) shows two large clusters, each consisting of some points from the previous four-cluster structure (points from these four clusters are colored differently). Thus, the new scatter plot elucidates structure not shown in the previous one. Indeed, the weight vectors (2nd row of Table 2) show that the clusters are separated mainly according to the “Gender” attribute. After marking the two clusters separately, the mean vector of each cluster (2nd row of Table 3) again confirms this: the cluster on the left represents male group, and the female group is on the right.

The projection in the third iteration (Fig. 4d) consists of three clusters, separated only along the X-axis. Interestingly, the corresponding weight vector (3rd row of Table 2) has strongly negative weights for the attributes “Income” and “Ethnic Group - White”. This indicates the left cluster mainly represents the people with high income and whose ethnic group is also “White”. As this cluster has relatively low Y-value, according to the weight vector, they are also generally older and more highly educated. These observations are corroborated by the cluster mean (3rd row of Table 3).

This case study shows that the proposed tool facilitates human data exploration iteratively presenting an information projection considering what the user has already learned about the data.

3.3 Performance on Synthetic Data

Ideally interactive data exploration tools should work in close to real time. This section contains an empirical analysis of an (unoptimized) R implementation of our tool, as a function of the size, dimensionality, and complexity of the data. Note that limits on screen resolution as well as on human visual perception render it useless to display more than of the order of a few hundred data vectors, such that larger data sets can be down sampled without noticeably affecting the data exploration experience.

We evaluated the scalability on synthetic data with $d\in \{16,32,64,128\}$ dimensions and $n\in \{64,128,256,512\}$ data points scattered around $k\in \{2,4,8,16\}$ randomly drawn cluster centroids (Table 4). The randomization is done here with the initial background model. The most costly part in randomization is the multiplication of orthogonal matrices. Indeed, the running time of the randomization scales roughly as $nd^{2-3}$. The results suggests the running time of the optimization is roughly proportional to the size of the data matrix nd and the complexity of data k has here only a minimal effect in the running time of the optimization.

Furthermore, in 69 % of the cases, the $L_1$ on the first axis is within $1\,\%$ of the best $L_1$ norm out of ten restarts. The optimization algorithm is thus quite stable, and in practical applications it may well be be sufficient to run the optimization algorithm only once. These results have been obtained with unoptimized and single-threaded R implementation on a 2.3 GHz Intel Xeon E5 processor.⁷ The performance could probably be significantly boosted, e.g., by carefully optimizing the code and the implementation. Yet, even with this unoptimized code, response times are already of the order of 1 s to 1 min.

Table 4. Median wall clock running times for randomization (“rand.”) and for optimization (“optim.”) over ten iterations of the optimization algorithm that finds the two-dimensional projection using the $L_1$ loss function for datasets of n data items and d dimensions with k clusters and its randomized version. We also show the number of iterations in which the $L_1$ norm first component ended up within $1\,\%$ of the result with the largest $L_1$ norm out of 10 tries; 10 means that the $L_1$ of the first component was within $1\,\%$ for all ten optimization runs.

4 Related Work

Dimensionality Reduction. Dimensionality reduction for exploratory data analysis has been studied for decades. Early research into visual exploration of data led to approaches such as multidimensional scaling [11, 21] and projection pursuit [6, 9]. Most recent research on this topic (also referred to as manifold learning) is still inspired by the aim of multi-dimensional scaling; find a low-dimensional embedding of points such that their distances in the high-dimensional space are well represented. In contrast to Principal Component Analysis [16], one usually does not treat all distances equal. Rather, the idea is to preserve small distances well, while large distances are irrelevant, as long as they remain large; examples are Local Linear and (t-)Stochastic Neighbor Embedding [8, 14, 19]. Typically, it is not even possible to achieve this perfectly, and a trade-off between precision and recall arises [22]. Recent works are mostly spectral methods along this line.

Iterative Data Mining and Machine Learning. There are two general frameworks for iterative data mining: FORSIED [3, 4] is based on modeling the belief state of the user as an evolving probability distribution in order to formalize subjective interestingness of patterns. This distribution is chosen as the Maximum Entropy distribution subject to the user beliefs as constraints, at that moment in time. Given a pattern syntax, one then aims to find the pattern that provides the most information, quantified as the pattern’s ‘subjective information content’. The other framework, which we here named CORAND [7, 13], is similar, but the evolving distribution does not need to have an explicit form. Instead, it relies on sampling (randomization) of the data, using the user beliefs as constraints.

Both these frameworks are general in the sense that it has been shown they can be applied in various data mining settings; local pattern mining, clustering, dimensionality reduction, etc. The main difference is that in FORSIED, the background model is expressed analytically, while in CORAND it may be defined implicitly. This leads to differences in how they are deployed and when they are effective. Randomization schemes are easier to propose, or at least they require little mathematical skills. Explicit models have the advantage that they often enable faster search of the best pattern, and the models may be more transparent. Also, randomization schemes are computationally demanding when many randomizations are required. Yet, in cases like the current paper, a single randomization suffices, and the approach scales well. For both frameworks, the pattern syntax ultimately determines their relative tractability.

Many special-purpose methods have been developed for active learning, a form of iterative mining/learning, in diverse settings: classification, ranking, etc., as well as explicit models for user preferences. However, since these approaches do not target data exploration, we do not review them here. Finally, several special-purpose methods have been developed for visual iterative data exploration in specific contexts, for example for itemset mining and subgroup discovery [1, 5, 12, 15], information retrieval [20], and network analysis [2].

Visually Controllable Data Mining. This work was motivated by and can be considered an instance of visually controllable data mining [17], where the objective is to implement advanced data analysis method so that they are understandable and efficiently controllable by the user. Our proposed method satisfies the properties of a visually controllable data mining method (see [17], Sect. II B): (VC1) the data and model space are presented visually, (VC2) there are intuitive visual interactions that allow the user to modify the model space, and (VC3) the method is fast enough to allow for visual interaction.

Information Visualization and Visual Analytics. Many new interactive visualization methods are presented yearly at the IEEE Conference on Visual Analytics Science and Technology (VAST). The focus in these communities is less on the use or development of advanced data mining or machine learning techniques, and more on efficient use of displays and human cognition, as well as efficient exploration via selection of data objects and features, but the need to merge with the data mining community has been long recognized [10].

5 Conclusions

There is a growing need for generic tools that integrate advanced visualization with data mining techniques to facilitate visual data analysis by a human user. Our aim with this paper was to present a proof of concept for how this need can be addressed: a tool that initially presents the user with an ‘interesting’ projection of the data and then employs data randomization with constraints to allow users to flexibly express their interests or beliefs. These constraints expressed by the user are then taken into account by a projection-finding algorithm to compute a new ‘interesting’ projection, a process that can be iterated until the user runs out of time or finds that constraints explain everything the user needs to know about the data.

In our example, the user can associate two types of constraints on a chosen subset of data points: the appearance of the points in the particular projection or the fact that the points can be nearby also in other projections. We also tested the tool on two data sets, one controlled experiment on synthetic data and another on real census data. We found that the tool performs according to our expectations; it manages to find interesting projections, although interesting can be case specific and relies on the definition of an appropriate interestingness measure, here $L_1$ norm. More research into that is warranted. Nonetheless, we think this approach is useful in constructing new tools and methods for visually controllable interactive data analysis in variety of settings. In further work we intend to investigate the use of the FORSIED approach to formalizing the background model [3, 4], as well as its use for computing the most informative data projections. Additionally, alternative types of constraints will be investigated.