Secondary Analysis of Electronic Health Records pp 285-294 | Cite as
Instrumental Variable Analysis of Electronic Health Records
Abstract
Sources of variation in treatments received that are exogenous to patients can be used to estimate causal effects from observational data. We present an example of this methodology that estimates the effect of critically ill patients being cared for in “non-target ICUs” due to capacity constraints—a process known as boarding.
Keywords
Instrumental variables Spillovers Boarding Causal effectsLearning Objectives
-
Estimate causal effects of a potential intervention when there is an instrumental variable available.
-
Identify appropriate model classes with which to estimate effects using instrumental variables.
-
Examine potential sources of treatment effect heterogeneity.
19.1 Introduction
The goal of observational research is to identify the causal effects of exposures or treatments on clinical outcomes of interest. The availability of data derived from electronic health records (EHRs) has improved the feasibility of large-scale observational studies. However, both treatments and patient characteristics (covariates) affect outcomes. Since in general the two are dependent, it is not accurate to simply compare the outcomes of those receiving different treatments to decide which treatment is more effective. While regression analysis can account for the variation in those covariates that can be observed, estimates remain biased if there are unobservable covariates that affect treatment propensity and outcomes.
Idealized randomized controlled experiments overcome the problem of unobserved covariates by virtue of them being randomly distributed in a balanced manner between the treatment and control groups as the sample size becomes large. In practice, however, such experiments are affected by participant non-compliance. Instrumental variable techniques, which use treatment assignment as the instrument and actual treatment taken as the endogenous variables (those that result from choices that may be affected by unobservables), are useful in this setting.
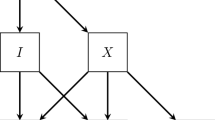
Instrumental variable analyses employ instruments that affect the likelihood of the exposure but do not otherwise affect the outcome
- 1.
Control variables should be pre-treatment characteristics of the patients or providers: One should not control for outcomes or decisions that occur after the treatment, even if they are not the outcome of interest, as this would bias results. Drawing the causal model and analyzing the paths provides a principled way of understanding the underlying assumptions that are being made. Web-based software [1] is available to facilitate this.
- 2.
The instrument must be correlated with the treatment and explain a substantial portion of the variation in the treatment: The less variation in the treatment that the instrument explains (the “weaker” the instrument), the higher the variance of the estimates obtained. This higher variance may deny any benefits from bias reduction.
- 3.
The instrument must be independent of the outcome through any mechanism other than the treatment: This remains one of the greatest challenges of employing IVAs accurately in medical data, as identifying instruments that have no relationship with any unobservable clinical variation beyond the treatment is difficult.
To illustrate these concepts we propose using an IVA to estimate the effect on intensive care unit (ICU) mortality of receiving care in a “non-target” ICU, defined as a unit that has a different specialty focus than the ICU to which patients would have been assigned in the absence of capacity constraints. For example, patients being cared for by a medical ICU team ideally care for their patients in a defined geographic area designated as the medical ICU (MICU), but when no beds are available in that unit a patient may instead be assigned to an unoccupied bed in a non-target ICU such as a surgical ICU (SICU). In this study, we define those patients assigned beds in non-target ICUs as boarders.
Although the physicians of the MICU team retain responsibility for the care of boarders, most other staff involved in the patient’s care (e.g. nurses, respiratory therapists, physical therapists) will change as a result of boarding status. This is because these staff are assigned to a specific geographically-defined ICU such as the SICU. As a result, boarders are typically cared for by nurses and other staff who possess expertise more appropriate for managing surgical patients than medical patients. Additionally, since physicians and nurses who work in different ICUs may not be as familiar with each other’s clinical practices, communication difficulties can arise. Lastly, there are also greater geographic distances between boarders and their physicians compared to non-boarders. This can contribute to delays in care and impairment of a physician’s level of situational awareness. It therefore seems reasonable to hypothesize that boarding may negatively impact upon clinical outcomes, including survival.
19.2 Methods
19.2.1 Dataset
The Medical Information Mart for Intensive Care (MIMIC-III) database contains clinical and administrative data on over 60,000 ICU stays at Beth Israel Deaconess Medical Center (BIDMC) between 2001 and 2012. It includes operational-level data on bed assignments and service transfers, as well as ICD-9-CM diagnoses and several mortality measures (ICU stay mortality, hospital mortality, and survival duration up to one year).
19.2.2 Methodology
Cohort Selection
We included all adult subjects, aged 18 years or older, cared for by the MICU at any point during their admission. The study period was defined as June, 2002 through December, 2012. In order to ensure independence of observations only the last ICU admission for each subject was included in the analysis.
Exclusion criteria included subjects whose primary hospital team at any point during their admission was non-medical (i.e. surgical or cardiac), as this might imply a specific reason aside from capacity constraints for a patient to be a boarder in a non-medical ICU (for example, a postoperative subject in the surgical ICU being transferred from the surgical ICU team to the medical ICU team for persistent respiratory failure).
The final study population included 8442 subjects, of whom 1881 (22 %) were exposed to the effects of boarding.
Statistical Approach
A naive estimate of the effect of boarding on mortality would compare the outcomes of patients who were boarders to those who were not. However, the decision to board a patient is not random. It takes into account the level of severity of a given patient’s condition, as well as how that compares with the severity levels of other incoming patients also in need of an ICU bed. It is likely that much of the information that informs this decision is unobservable. As a consequence, if we conducted this study as a simple regression analysis we would obtain biased estimates of the effect of boarding.
For example, assume that boarding increases mortality, but also that ICU staff preferentially select less severely ill patients to be boarders. In this hypothetical scenario, the observed association between boarding and mortality could appear protective if the negative effect of boarding on mortality is smaller than the positive effect on observed mortality of selecting healthier patients. While one may, and should, control for patients’ severity of illness and pre-existing health levels, it is not usually possible to observe these with the same granularity and accuracy as the hospital staff who decide whether the patient will become a boarder. As a result, boarders may still be healthier than non-boarders even after conditioning on a measure of severity of illness.
Simplified causal diagram illustrating confounding of the relationship between boarding and mortality due to unobservable heterogeneity in patient risk, and potential conditional instrument west_initial_remaining_beds. The diagram can be manipulated at http://dagitty.net/dags.html?id=AVKMi0
The Oxford Acute Severity of Illness Score (OASIS) is employed to help account for residual differences between the health status of boarders and non-boarders at the time of their intake into the ICU. OASIS is an ICU scoring system that has been shown to have non-inferior performance characteristics relative to APACHE (Acute Physiology and Chronic Health Evaluation), MPM (Mortality Probability Model), and SAPS (Simplified Acute Physiology Score) [2]. We preferentially use OASIS for severity of illness adjustment because its scores can be more accurately reconstructed in MIMIC-III in a retrospective manner than the aforementioned alternatives.
At times when hospital load is high, the total number of patients being cared for by the ICU team (west_initial_team_census) is likely to be high, and west_initial_remaining_beds is likely to be low. Furthermore, it is plausible that higher values of west_initial_team_census might affect mortality as a relatively fixed quantity of ICU resources (e.g. physicians) is stretched across a greater number of patients.
At first it may be unclear why there is imperfect correlation between west_initial_team_census and west_initial_remaining_beds, as one might anticipate that the number of remaining beds is simply inversely proportional to the total number of patients being cared for by the ICU team. The source of variation between these variables is two-fold. The primary driver is the stochastic pattern of ICU discharges. It is improbable that all boarders will be discharged prior to any of the non-boarders. Discharging a non-boarder while other patients remain as boarders creates a situation where the total team census may continue to be higher than the bed capacity of the MICU, yet the number of available beds in the MICU becomes non-zero. The second, smaller source of variation is occupancy of MICU beds by patients being cared for by other ICU teams (e.g a SICU patient boarding in the MICU).
Using west_initial_remaining_beds as an instrument is therefore valid, but we must control for west_initial_team_census. To check that west_initial_remaining_beds is correlated to the propensity of patients to board, we fit a generalized additive model with a logistic link function.
Once a natural experiment has been identified and the validity of the instrumental variable confirmed, an IVA can be conducted to estimate the causal effect of the treatment. The standard in the econometrics literature has been to use a two-step ordinary least squares (OLS) regression. There are two important limitations to this approach in biomedical settings. Firstly, it requires continuous treatment and outcome variables, both of which tend to be discrete or binary in medical applications. Secondly, it requires knowledge of the functional form of the underlying relationships such that the data can be transformed to make the relationships linear in the parameters of the estimated model. This is often beyond what is known in the biomedical field.
Several approaches have been developed to address these limitations. Probit models are part of a family of generalized linear models (GLM) that is well suited to working with discrete data, thereby addressing the first aforementioned limitation. Furthermore, use of a basis expansion may allow the functional form to be approximated flexibly using penalized splines, substantially relaxing the second limitation related to knowledge of functional forms. At least one statistical package, SemiParBIVProbit for R, combines these two approaches in an accessible implementation.
In addition to the probit model, we used the survival package for R to estimate a non-instrumental Cox proportional hazards model as a robustness check. In order to minimize selection bias in this non-instrumental model, we used a subset of the dataset in which it is intuitive that selective pressures would be reduced or non-existent: west_initial_remaining_beds equal to zero (all patients must board irrespective of their severity of illness) or west_initial_remaining_beds greater than or equal to three (no imminent capacity constraint exerting pressure on physicians to board patients). The linear assumptions of the Cox models are strong and not justified a priori, therefore in order to test for potential nonlinearities in the instrumental model we used the Vuong and Clarke tests of the SemiParBIVProbit package.
All of our models included controls for patient age, gender, OASIS and Elixhauser comorbidity scores, length of hospital stay prior to ICU admission, and calendar year. In addition to controlling for the west_initial_team_census, we also controlled for the total number of boarders under the care of the MICU team.
19.2.3 Pre-processing
We used a software package called Chatto-Transform [3] that connects to a local PostgreSQL instance of MIMIC-III and simplifies the process of importing table data into an interactive Jupyter notebook [4]. Python 3 and the Pandas library [5] were used for data extraction and analysis (see code supplement).
The publicly available version of MIMIC-III applies random time-shifts to records to help prevent subjects from being identified. After institutional review board approval, we obtained the exact dates and bed assignments for each subject’s ICU stay and used this to reconstruct the entire hospital ICU census.
The services table in MIMIC-III documents the specific service (e.g. medicine, general surgery, cardiology) responsible for a patient at a given moment in time. The service providing MICU care is classified as ‘medicine’. Therefore general medicine patients who are initially admitted to a ward and later require a MICU bed will still only have one entry per admission in this table, provided that they are not transferred to the care of a different service. We consider a refined copy of the services table (‘med_service_only’) that retains only those rows pertaining to patients cared for exclusively by the medicine service during their stay. The resulting table therefore has only one row per hospital admission.
The transfers table documents every change in a patient’s location during their hospital admission, including exact bed assignments and timestamp data. A new table df can be created by performing a left join between transfers and med_service_only. In the resulting table, rows pertaining to the population of interest (i.e. medicine patients who incurred a MICU stay at some point during their admission) will have data corresponding to both the left (transfers) and right (med_service_only) tables. Rows pertaining to all other patients will only have data from the transfers table. We further subdivide this table into inboarders (which contains rows pertaining to non-MICU patients occupying beds in the MICU) and df5 (which contains rows pertaining to our population of interest).
Death during ICU stay was determined a priori to be our primary outcome of interest. We identified a number of instances in the dataset where death occurred within minutes or hours of discharge from the ICU. This was most likely due to combination of expected deaths (subjects transitioned to comfort-focused care who were transferred out of the ICU shortly prior to death), unexpected deaths, and minor time discrepancies inherent to large datasets that include administrative details. Prior to data analysis it was decided that our preferred definition of death during ICU stay would include those within 24 h of leaving the ICU.
19.3 Results
Looking at the fitted models, we observe an increase in mortality from boarding across the different specifications. In the semiparametric bivariate probit model, using the west_initial_remaining_beds as an instrument, the estimated causal [6] average risk ratio is 1.44 (95 % interval: 1.17, 1.79). In the non-instrumental Cox proportional hazards model we observe a similar estimate of 1.34 (1.06, 1.70).
Often treatments result in different effects of different patients, thus it is sensible to think of average treatment effects (ATE). Instrumental variable analyses, however, restrict the estimation to the variation in the data that is attributable to the instrument. That is, the effect they estimate is the local effect on those patients whose treatment is affected by the instrument. This is termed the Local Average Treatment Effect (LATE), and is what is estimated by an IVA when there is heterogeneity in treatment effects.
19.4 Next Steps
Much of the existing medical literature utilizing IVAs has addressed policy questions as opposed to the effect of medical treatments. This has been driven by the interest in such questions by health care economists, as well as the greater availability and suitability of administrative—rather than clinical—data within the medical field. In contrast, the growing adoption and increasing sophistication of EHRs now presents us with an opportunity to investigate the effects of medical treatments through their provision of a rich source of observable variables and potential instruments. Examples include measurable variation in the number and characteristics of hospital staff, as well as load levels that cause spillover between units and thus are exogenous to a particular patient in a given unit. There is also a large body of literature that has explored Mendelian randomization as a source of instruments, however these usually create limited variation therefore instrument weakness is a substantial concern.
Aside from serving as candidate instruments or controls, some variables easily extracted from EHRs may be useful for checking the plausibility of a proposed pseudo-randomization process: if an instrument is truly randomizing patients with respect to a treatment then we would expect a balanced distribution of a wide range of observable variables (e.g. patient demographics). This is akin to tables that compare the baseline characteristics between groups in the results of randomized controlled trial. Estimating causal effects from natural experiments is an important part of the econometrics literature. For an influential practitioners reference, see Mostly Harmless Econometrics [7]. A excellent counterpoint can be found in part III of Shalizi [8].
Instrumental variables are powerful tools in the identification of causal relationships, but it is critical to remain mindful of potential sources of confounding. Garabedian et al. reviewed the studies published in the medical literature using IVAs and found that the four most commonly used instrument categories—distance to facility, regional variation, facility variation, and physician variation—all suffered from “potential unadjusted instrument–outcome confounders … including patient race, socioeconomic status, clinical risk factors, health status, and urban or rural residency; facility and procedure volume; and co-occurring treatments” [9].
19.5 Conclusions
This case study demonstrates the steps involved in the identification and validation of an instrumental variable. It also illustrates the process of conducting an IVA to estimate effect sizes and infer causal relationships from observational data.
The results of our study support the hypothesis that boarding of critically ill patients has deleterious effects on ICU survival. We recommend that institutions take steps to minimize boarding among ICU patients and that further studies be undertaken to more precisely characterize the effect size. Better understanding of the mediators through which boarding influences mortality is also important, and may help to identify groups of patients who are able to board without detrimental effects, and those for whom boarding should be particularly avoided.
References
- 1.Textor J, Hardt J, Knüppel S (2011) DAGitty: a graphical tool for analyzing causal diagrams. Epidemiology 22(5):745CrossRefPubMedGoogle Scholar
- 2.Johnson AEW, Kramer AA, Clifford GD (2013) A new severity of illness scale using a subset of acute physiology and chronic health evaluation data elements shows comparable predictive accuracy. Crit Care Med 41(7):1711–1718CrossRefPubMedGoogle Scholar
- 3.Spitz D, Spencer D (2015) Chatto-transformGoogle Scholar
- 4.Jupyter Team, “Project Jupyter.”Google Scholar
- 5.PyData Development Team (2015) Pandas data analysis libraryGoogle Scholar
- 6.Marra G, Giampiero M, Rosalba R (2011) Estimation of a semiparametric recursive bivariate probit model in the presence of endogeneity. Can J Stat 39(2):259–279CrossRefGoogle Scholar
- 7.Angrist JD, Pischke J-S (2008) Mostly harmless econometrics: an empiricist’s companion. Princeton University Press, PrincetonGoogle Scholar
- 8.Shalizi CR (2016) Advanced data analysis from an elementary point of view, 18 Jan 2016Google Scholar
- 9.Garabedian LF, Chu P, Toh S, Zaslavsky AM, Soumerai SB (2014) Potential bias of instrumental variable analyses for observational comparative effectiveness research. Ann Intern Med 161(2):131–138CrossRefPubMedGoogle Scholar
Copyright information
Open Access This chapter is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.
The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.