Abstract
As well as being free from viscosity, the Bose–Einstein condensate has another striking property—it is constrained to circulate only through the presence of whirlpools of fixed size and quantized circulation. In contrast, in conventional fluids, the eddies can have arbitrary size and circulation. Here we establish the form of these quantum vortices, their key properties, and how they are formed and modelled.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
We recall that in cylindrical coordinates, the curl of the vector \(\mathbf{A}=(A_r,A_{\theta },A_z)\) is
$$\begin{aligned} \nabla \times \mathbf{A}=\left( \frac{1}{r} \frac{\partial A_z}{\partial \theta } -\frac{\partial A_{\theta }}{\partial z}, \frac{\partial A_r}{\partial z} - \frac{\partial A_z}{\partial r}, \frac{1}{r}\frac{\partial (r A_{\theta })}{\partial r} -\frac{1}{r}\frac{\partial A_r}{\partial \theta } \right) . \end{aligned}$$.
- 2.
We have expressed the Laplacian in its cylindrically symmetric form,
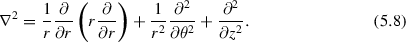
- 3.
Stokes Theorem states that
$$\begin{aligned} \oint _C \mathbf{A} \cdot \mathrm{d}{\varvec{\ell }}=\int _S (\nabla \times \mathbf{A}) \cdot \mathrm{d}{} \mathbf{S}, \end{aligned}$$where the surface S enclosed by the oriented curve C is simply-connected, i.e. any closed curve on S can be shrunk continuously to a point within S.
- 4.
Often this cutoff is taken instead as the healing length \(\xi \).
- 5.
An exception is through the technique of phase imprinting, in which the condensate phase can be directly and almost instantaneously imprinted with a desired distribution. In this manner vortices can be suddenly formed within the condensate.
References
Y. Shin et al., Phys. Rev. Lett. 93, 160406 (2004)
T. Winiecki, Numerical Studies of Superfluids and Superconductors, Ph.D. thesis, University of Durham (2001)
E.J. Yarmchuck, M.J.V. Gordon, R.E. Packard, Phys. Rev. Lett. 43, 214 (1979)
J.R. Abo-Shaeer, C. Raman, J.M. Vogels, W. Ketterle, Science 292, 476 (2001)
C. Raman, J.R. Abo-Shaeer, J.M. Vogels, K. Xu, W. Ketterle, Phys. Rev. Lett. 87, 210402 (2001)
A. Recati, F. Zambelli, S. Stringari, Phys. Rev. Lett. 86, 377 (2001)
S. Sinha, Y. Castin, Phys. Rev. Lett. 87, 190402 (2001)
K.W. Madison, F. Chevy, V. Bretin, J. Dalibard, Phys. Rev. Lett. 86, 4443 (2001)
N.G. Parker, R.M.W. van Bijnen, A.M. Martin, Phys. Rev. A 73, 061603(R) (2006)
T.P. Simula, P.B. Blakie, Phys. Rev. Lett. 96, 020404 (2006)
G.W. Stagg, A.J. Allen, C.F. Barenghi, N.G. Parker, J. Phys.: Conf. Ser. 594, 012044 (2015)
C.F. Barenghi, R. Hänninen, M. Tsubota, Phys. Rev. E 74, 046303 (2006)
P. Nozieres, D. Pines, The Theory of Quantum Liquids (Perseus Books, Cambridge, 1999)
T.W. Neely, E.C. Samson, A.S. Bradley, M.J. Davis, B.P. Anderson, Phys. Rev. Lett. 104, 160401 (2010)
W.J. Kwon, S.W. Seo, S. W., Y. Shin. Phys. Rev. A 92, 033613 (2015)
T. Winiecki, C.S. Adams, Europhys. Lett. 52, 257 (2000)
B. Jackson, J.F. McCann, C.S. Adams, Phys. Rev. A 61, 013604 (1999)
D.V. Freilich, D.M. Bianchi, A.M. Kaufman, T.K. Langin, D.S. Hall, Science 329, 1182 (2010)
H. Salman, Phys. Rev. Lett. 16, 165301 (2013)
G.P. Bewley, M.S. Paoletti, K.R. Sreenivasan, D.P. Lathrop, Proc. Nat. Acad. Sci. USA 105, 13707 (2008)
S. Serafini, M. Barbiero, M. Debortoli, S. Donadello, F. Larcher, F. Dalfovo, G. Lamporesi, G. Ferrari, Phys. Rev. Lett. 115, 170402 (2015)
A.L. Fetter, Rev. Mod. Phys. 81, 647 (2009)
M. Tsubota, K. Kasamatsu, M. Ueda, Phys. Rev. A 65, 023603 (2002)
S. Zuccher, M. Caliari, A.W. Baggaley, C.F. Barenghi, Phys. Fluids 24, 125108 (2012)
G.W. Stagg, A.J. Allen, N.G. Parker, C.F. Barenghi, Phys. Rev. A 91, 013612 (2015)
A.J. Groszek, T.P. Simula, D.M. Paganin, K. Helmerson, Phys. Rev. A 93, 043614 (2016)
A. Cidrim, F.E.A. dos Santos, L. Galantucci, V.S. Bagnato, C.F. Barenghi, Phys. Rev. A 93, 033651 (2016)
N.G. Parker, Numerical studies of vortices and dark solitons in atomic Bose-Einstein condensates, Ph.D. thesis, University of Durham (2004)
N.G. Berloff, C.F. Barenghi, Phys. Rev. Lett. 93, 090401 (2004)
A. Aftalion, I. Danaila, Phys. Rev. A 68, 023603 (2003)
D. Proment, M. Onorato, C.F. Barenghi, Phys. Rev. E 85, 036306 (2012)
R.P. Feynman, Applications of quantum mechanics to liquid helium, in Progress in Low Temperature Physics, vol. 1, ed. by C.J. Gorter (North-Holland, Amsterdam, 1955)
C.F. Barenghi, L. Skrbek, K.R. Sreenivasan, Proc. Nat. Acad. Sci. USA suppl.1 111, 4647 (2014)
M.C. Tsatsos, P.E.S. Tavares, A. Cidrim, A.R. Fritsch, M.A. Caracanhas, F.E.A. dos Santos, C.F. Barenghi, V.S. Bagnato, Phys. Reports 622, 1 (2016)
A.C. White, C.F. Barenghi, N.P. Proukakis, A.J. Youd, D.H. Wacks, Phys. Rev. Lett. 104, 075301 (2010)
P.M. Walmsley, A.I. Golov, Phys. Rev. Lett. 100, 245301 (2008)
J. Maurer, P. Tabeling, Europhys. Lett. 43, 29 (1998)
C. Nore, M. Abid, M.E. Brachet, Phys. Rev. Lett. 78, 3896 (1997)
T. Araki, M. Tsubota, S.K. Nemirovskii, Phys. Rev. Lett. 89, 145301 (2002)
A.W. Baggaley, C.F. Barenghi, Y.A. Sergeev, Europhys. Lett. 98, 26002 (2012)
A.W. Baggaley, C.F. Barenghi, Y.A. Sergeev, Phys. Rev. B 85, 060501(R) (2012)
A.W. Baggaley, J. Laurie, C.F. Barenghi, Phys. Rev. Lett. 109, 205304 (2012)
E.A.L. Henn, J.A. Seman, G. Roati, K.M.F. Magalhaes, V.S. Bagnato, Phys. Rev. Lett. 103, 045301 (2009)
M. Kobayashi, M. Tsubota, Phys. Rev. A 76, 045603 (2007)
W.J. Kwon, G. Moon, J. Choi, S.W. Seo, Y. Shin, Phys. Rev. A 90, 063627 (2014)
T. Simula, M.J. Davis, K. Helmerson, Phys. Rev. Lett. 113, 165302 (2014)
T.P. Billam, M.T. Reeves, B.P. Anderson, A.S. Bradley, Phys. Rev. Lett. 112, 145301 (2014)
P.H. Roberts, J. Grant, J. Phys. A: Math. Gen. 4, 55 (1971)
Author information
Authors and Affiliations
Corresponding author
Problems
Problems
5.1
Consider the bucket of Sects. 5.5 and 5.6 to now feature a harmonic potential \(V(r)=\frac{1}{2}m \omega _r^2 r^2\) perpendicular to the axis of the cylinder. Take the condensate to adopt the Thomas–Fermi profile.
-
(a)
Show that the energy of the vortex-free condensate is \(E_0=\pi m n_0 \omega _r^2 H_0 R_r^4 / 6\), where \(R_r\) is the radial Thomas–Fermi radius and \(n_0\) is the density along the axis.
-
(b)
Now estimate the kinetic energy \(E_\mathrm{kin}\) due to a vortex along the axis via Eq. (5.12). Use the fact that \(a_0 \ll R_r\) to simplify your final result.
-
(c)
Estimate the angular momentum of the vortex state, and hence estimate the critical rotation frequency at which the presence of a vortex becomes energetically favourable.
5.2
Use the LIA (Eq. (5.49)) to determine the angular frequency of rotation of a Kelvin wave of wave length \(\lambda =2\pi /k\) (where k is the wavenumber) on a vortex with circulation \(\kappa \).
5.3
Using the vortex point method and the complex potential, determine the translational speed of a vortex-antivortex pair (each of circulation \(\kappa \)) separated by the distance 2D.
5.4
Using the vortex point method and the complex potential, determine the period of rotation of a vortex-vortex pair (each of circulation \(\kappa \)) separated by the distance 2D.
5.5
Consider a homogeneous, isotropic, random vortex tangle (ultra-quantum turbulence) of vortex line density L, contained in a cubic box of size D. Show that the kinetic energy is approximately
where \(\rho \) is the density, \(\kappa \) the quantum of circulation, \(\ell \approx L^{-1/2}\) is the inter-vortex distance and \(a_0\) is the vortex core radius.
5.6
In an ordinary fluid of kinematic viscosity \(\nu \), the decay of the kinetic energy per unit mass, \(E'\), obeys the equation
where \(\omega \) is the rms vorticity. Consider ultra-quantum turbulence of vortex line density L. Define the rms superfluid vorticity as \(\omega =\kappa L\), and show that the vortex line density obeys the equation,
where the constant c is,
hence show that, for large times, the turbulence decays as
Rights and permissions
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Barenghi, C.F., Parker, N.G. (2016). Vortices and Rotation. In: A Primer on Quantum Fluids. SpringerBriefs in Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-42476-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-42476-7_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42474-3
Online ISBN: 978-3-319-42476-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)