Abstract
Our perceptions of cities until quite recently were that they were largely stable in spatial structure over long periods of time, decades, even centuries, and that this suggested that they were in equilibrium. Cities appeared similar from generation to generation and although there were superficial changes due to fashion and technology, their overall structures were unchanging. To a large extent, this view of cities in equilibrium is borne of thinking about them physically but as soon as we unpack their dynamics, we realise that this a superficial perception. Cities are always in disequilibrium. They are in fact far-from-equilibrium being maintained through a tension of many countervailing forces that break down and build up on many different spatial and temporal scales, thus all coalescing in strong volatility and heterogeneity in urban form and function. Here we first review the concept of equilibrium and dynamics, and then we introduce ideas about discontinuity drawing on ideas from catastrophe and chaos theory. We argue that we should think of cities as being far-from-equilibrium structures and allude to ideas about innovation and technological change that condition their dynamic entirely. Our conclusion is that what happens in cities is increasingly disconnected from their physical form and this is particularly the case in the contemporary world where changes to the built environment are ever out-of-sync with changes in human behaviours, activity locations, patterns of movement, and globalisation.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
If you slightly abstract your casual knowledge of a city by considering its physical form as a map or even a description of how its various activities, land uses and transportation systems are configured, and you then examine how these images have changed over past generations, you could be forgiven for thinking that cities are fairly stable in their form and function. They appear to be long lasting in their structure and change only slowly from decade to decade or even century to century. In one sense, cities of the medieval era have the same structure as those of today—relatively well-defined urban cores or central business districts (CBDs as they are now referred to), inner areas that house industries and poorer populations who are crammed into places near their work, and more open lower density tracts which form their suburbs. Of course the medieval city was a microcosm of today’s industrial and post-industrial city and of a very different scale. Its technology was massively different and consequently as populations could only travel limited distances—no more than 6 miles or so to work each day—cities were very much smaller. Only did they break through the one million population threshold when mechanical technologies were invented and disseminated for movement from the early nineteenth century onwards, but their structure has remained much the same to this day. However we now stand at another technological threshold with respect to the city and what it will be like in the future but before we engage in this debate, let us begin by describing what we know about cities in terms of their stability and dynamics over space and time.
From what we have said, cities appear to be in some sort of equilibrium over time in terms of their structure and even if this equilibrium were changing, a common assumption has been that this is a stable equilibrium. Perturb it a little and the city will return to its current state or a state only a little different from the one that existed before the perturbation. Evidence of this is all around us: look at a large city like London in 1915 and the same city today in 2015 from aerial imagery and you would see the ‘same’ kinds of clusters of urbanisation at the two periods, the first much smaller than the present but their spatial structure being much the same. Yet despite these evident similarities, there are little chinks in the armour of this notion that cities are in equilibrium which come from other casual observations. Old photographs show very different forms of behaviour in cities at different time periods, styles of dress differ markedly, and the way people travel has changed. Much has been reinforced from earlier eras but there has also been substantial change. In fact the notion that cities are in equilibrium has become something of a convenient myth. It has been reinforced somewhat by the fact that much of quantitative urban theory is predicated on explaining how urban markets work to produce patterns of population and employment densities, rents and transport costs that tie people to particular places in the city and generate profiles that suggest populations decline monotonically in density as they locate further and further from the core of the city. Such theories suggest that negative feedbacks reinforce these patterns and the very notion that we use the market as the economic mechanism to resolve the way people make decisions, forces us somewhat to assume that markets tend to clear with equilibrium being their dominant state. Living with markets in disequilibrium is something that we have found hard to articulate. Moreover, there has been little theorising about how cities might grow and change to account for radical discontinuities in technology and behaviour, at least other than in the most general conceptual terms.
Yet when you look at cities across wide spans of time, everything is different. Although cities look rather inert with respect to their physical form, the activities that take place in their buildings and locations differ markedly from generation to generation. For example in 1900, there were 75,000 manufacturing jobs in the City of London which then had a residential population of 27,000. In 2015 there were hardly any such jobs and the City’s population had fallen to 8100. During this period service jobs hardly grew at all but their composition changed dramatically to be dominated by financial services. The City has been rebuilt some three times since the second world war during the various building booms but the street pattern is more or less the same as it was in medieval times before the Great Fire in 1666. This makes for some confusion over the notion of what equilibrium one is trying to capture. In fact there are many types of equilibrium that might be sought in defining cities and as a corollary, many types of disequilibrium. In some respects, it is a fruitless task to try to merge all these different perspectives and to achieve any clarity in this kind of non-equilibrium social science, we must take one step back to go two steps forward in our discussion.
2 Equilibrium, Steady States, Feedback and Urban Dynamics
By the mid-twentieth century, the systems approach was in full ascendency in the social sciences with the notion that cities as well as many other functions of modern society were systems in equilibrium, maintained by strong negative feedback loops that returned the system to its steady state if perturbed. The notion that this steady state could evolve was also consistent with this concept of equilibrium since such a steady state could incorporate various kinds of progression in the form of new technologies, new behaviours and so on but at the end of the day, negative feedback would prevail. The steady state to which the system returned was much the same, perhaps differing by some quantitative measure but was not qualitatively different from any former equilibrium.
The notion of negative feedback is central to this concept of equilibrium. The city was regarded as something that was well-behaved: if new activities were added to its structure, then multiplier effects would work themselves out and provide a new equilibrium but not one that was intrinsically different from before. Most land use transport models, housing market models, and macro economic input-output models were fashioned around this concept of equilibrium being the product of multiplier effects that eventually and rather quickly died way. This conception of the city as being well-behaved was deeply ingrained in our mid-twentieth century mind-set so much so that planners and politicians never ever considered the fact that their schemes would not be absorbed into a willing medium and that they would bounce back in deleterious fashion: the notion of the city and society being dominated by such wicked problems was borne of such disastrous experiments [8]. At the pinnacle of the systems movement, the idea that the city could be seen as a machine and that planning might be regarded as a controller in cybernetic fashion was widely held, as evidenced in such books as McLoughlin’s (1973) Control and Urban Planning [19].
In this field, it is important to distinguish between questions of statics and dynamics and questions of equilibrium. If a city is in equilibrium, then we can assume its spatial structure can be simulated at a cross-section in time where any dynamic is subsumed by the forces that determine the equilibrium. In this sense, a simulation would be comparatively static, meaning that changes in the magnitude of the forces involved would produce a new static structure which would be closely related to the existing structure: the generic nature of the forces would not change, and it is this that makes predictions with such static equilibrium models only relevant to situations where there would be immediate, probably marginal change in the very short term. The first models of cities built 50 years ago such as that by Lowry (1964) for Pittsburgh were regarded as producing an ‘instant metropolis’ [16]. In these early days, there was much discussion about making such models dynamic but not so much about equilibrium per se. Two key issues were reflected in the discussion at that time. First there were several attempts to make such simulations semi- or pseudo-dynamic by exploiting the multipliers embedded in their equilibrium structure, that is by matching multipliers to increments or decrements of change and using the same model to simply add or subtract changes over time where these changes were simulated using the equilibrium model [3]. A second development was more theoretical and was based on assuming well-behaved dynamics which led to an equilibrium over time where the trajectories followed well-known paths such as those based on capacitated exponential (logistic) growth (and any subsequent decline). Forrester’s (1969) Urban Dynamics model was based on such a dynamic equilibrium but being more of a thought experiment—albeit based on the computational language of systems dynamics—than an empirical and operational application of any of the contemporary theories underpinning the ways cities were spatially and economically structured [12].
There were however many voices questioning this ideology of equilibrium. It was always felt that the equilibrium was precarious and if the boundaries of the problem changed a little then cities would look as they were in disequilibrium. The evidence for this however came both from what was happing to cities from the mid-twentieth century onwards as well as from intellectual responses to the then prevailing scientific view that equilibrium was the product a well-behaved dynamics. From the 1950s, western cities were racked with ethnic riots which flared spontaneously from multiple causations. Technology change was also evident in the way they began to sprawl while changes in employment structure reflecting de-industrialisation, globalisation and the rise of information technologies had substantial impacts on their spatial structuring. In fact, long standing monocentric structures did remain focussed on the CBD but new centres grew on the edge of cities and cities began to merge with one another in the denser urbanised regions. The picture now is one of much greater polycentricity everywhere.
Dynamics for the most part prior to the mid-twentieth century was mainly concerned with how physical phenomena changes in a continuous, largely smooth fashion. But there were many instances in the physical sciences were change was discontinuous and abrupt. Indeed various examples of functions which were continuous but not differentiable (such as Weierstrass’s function) had been discovered in the nineteenth century and the mathematics of irregularity was slowly beginning to be put on a stronger foundation. By the late 1960s, the idea that systems could change ‘catastrophically’ had been articulated. The notion that a system might continue quite smoothly for a long period of time manifesting a well-behaved trajectory but then suddenly switch largely as a confluence of tensions in the background conditions, was explored by Thom (1972) who invented catastrophe theory [22]. Immediately examples in the social sciences were identified such as prison riots, movements in share prices and related cycles which no longer appeared smooth. Over much longer time spans, this theory was also used to simulate the dramatic decline of cities and civilisations.
In the 1970s, ideas about equilibrium thus came under scrutiny with developments in catastrophe and bifurcation theory (which we will note below) that enabled those thinking about cities to introduce an entirely new set of dynamics that mirrored many features of cities in- and out-of-equilibrium. The notion that smooth change could give rise to discontinuities was clear enough but identifying conditions under which such changes could be explained was more problematic. Consequently many of the first forays into thinking of cities as dynamic non-equilibrium systems tended to demonstrate these notions using hypothetical examples. One of the best examples is Wilson’s [24] speculation of what happens when there is a switch in the relative balance of travel costs associated with travelling on public and private transport. Essentially this thesis suggests that if the cost of public transport rises substantially relative to private, then travellers will switch to private transport perhaps continuously in proportion to this change but also perhaps discontinuously all at once. But if the cost of public transport falls back to its initial level, travellers will not switch back to public transport, largely because they have found some hidden advantages in private travel— convenience and so on—which do not tend to be reflected in transport costs. Wilson demonstrated that you can model this as a cusp catastrophe and his argument seems appealing relative to what we know about mode switching and the decline in the patronage of public transport. His demonstration is purely hypothetical and it might be hard to find data for fitting such a model, but nonetheless the point is clear. Discontinuities in switching can be modelled using such strategies and this suggests that this kind of mechanism is likely to dominate many other changes in the structure of urban systems to which it might be applied.
3 From Catastrophe and Bifurcation to Chaos
Many hypothetical applications of this kind of non-equilibrium dynamics were applied to urban systems in the 1970s and 1980s with Amson [2] and Wilson [25] leading the way in applications of catastrophe theory. This was paralleled by a very different form of dynamics associated with urban systems that was reflected in the non-equilibrium thermodynamics pioneered by Prigogine [21] who introduced the very basic notion that a system which was embarked on a smooth trajectory of change might suddenly deviate onto one of a number of paths—essentially bifurcating onto one of several different paths dependent upon local conditions and probabilities of change that pertained to the system in question. Technological change and innovation provided the pertinent examples but in cities, the notion of rapid changes in some growth of activities such as retail and commercial centres—edge cities—provided the most obvious examples. The theory was pursued and demonstrated by Allen (1997) and simple models were applied to real urban systems such as Brussels [1]. Empirical work however has been minimal in applying these ideas for actual applications, being more like toy models developed with some fine tuning to real situations to demonstrate something a little more realistic than pure thought experiments.
Prigogine’s approach was strongly counter-intuitive with respect to physical systems in that it is based on turning around the laws of thermodynamics, introducing what to all intents and purposes is a reversible thermodynamics. The strong logic of thermodynamics is based on the notion that energy is continually used up in a workable form as it is converted into heat and that eventually the universe will reach a state of random disorder where its entropy will be at a maximum and no useful work is possible. This is the equilibrium that is implied in statistical physics. Prigogine argued that in social systems the opposite was the case. Order was always increasing as life continued to use energy to maintain, if not increase this order. Of course life in this interpretation is a local pocket of order in a sea of increasing disorder and in that sense, Prigogine’s theory did not fight against the general laws of thermodynamics. In the long run, the heat death of the universe is still incontrovertible, notwithstanding the fact that at this point in space and time, our own actions tend to counter the general increase in entropy that comes from the conversion of energy.
It is in this sense then that we can think of cities as being far-from-equilibrium. We will return to this view in the next section but it is useful to show these kinds of dynamics in cities that were demonstrated both in theory and through various stylised facts as these ideas were developed. Both [1] and [25] produced demonstrations that indicated how rapid changes in locational activities might occur using the kind of dynamics of bifurcation that could be associated with how an activity such as a shopping centre might suddenly sprout from a pattern of spatial population demand defined in the hinterland of any centre. In 1992, Garreau [13] published his important polemic on the edge city—cities that quickly grew as large retail and commercial centres on the edge of big cities competing for pride of place with the original CBDs around which most cities were formed. These centres tended to develop rapidly or not at all. Some were stillborn and it took some scrutiny of urban conditions to identify centres on the edge of cities that failed but the whole range of development possibilities pertained to such centres.
To an extent, the notion of retail development being associated with a bifurcation in activity locations fitted the conception of edge cities rather well. In fact, Wilson developed this concept of rapidly generated retail centres well before Garreau produced his commentary, for Wilson’s work was very much related to how one built supply-side dynamics into retail models [25, 26]. All we can do here is give a sketch of how he proceeded. Essentially he argued that cross-sectional equilibrium models of spatial interaction produced a picture of how the demand for facilities—in this case retail and commercial facilities—was stable at any point in time. The supply of these facilities was not typically part of these models for the dynamics of developer behaviour were hard to model and were for the most part excluded from such simulations. What Wilson did was to suggest that the development cycle might be approximated by a logistic supply equation which generated a level of activity through time to a capacity limit. So he embedded a spatial interaction model of the demand-side into a Lotka-Volterra style of logistic equation which mirrored how development might take place, that is how development might be supplied. What he demonstrated was that in such a nonlinear system of equations, one could produce dramatic growth in certain locations and none at all in others by tweaking the demand parameter of the model which was highly sensitive to radically changing the predicted pattern under certain parameter regimes. In short his extended equation system could be used to explore the different parameter values which would give rise to discontinuities (rapid changes which in fact were continuous in some sense) and might be seen as being edge city-like in form and function.
At much the same time, other approaches to characterising disequilibrium in social systems were being pursued. More fundamentally, several researchers explored the notion that certain very standard nonlinear logistic growth equations could generate bifurcations with respect to their trajectories, leading to oscillating equilibria which in the limit became chaotic, seemingly without rhyme or reason. The usual form for a population logistic is that it converges on the capacity limit as the system grows but for certain parameter values, this convergence becomes a regular oscillation. As the value of the parameter continues to change, this oscillation becomes more and more chaotic and in a limit, truly chaotic. If you were to observe a system changing in this way, it would be hard to figure out that one were dealing with a capacitated nonlinear system. In fact few instances of such systems have been observed in nature although some predator-prey systems appear to follow such oscillations. Most exploration has been intent on demonstrating paths to chaos and generalising such equations to a wider class leading to systems which have sensitive dependence on initial conditions. Feigenbaum [10] is accredited with identifying such chaos in the first instance in 1974 although others such as [17] and [18] amongst many, were involved in developing these ideas simultaneously from entirely different directions. In the late 1970s and 1980s, these ideas led to the science of chaos [14] with many speculations that social systems in general and city systems in particular contained the seeds of such instabilities. In this way, a new form of dynamics pertaining to cities emerged based on discontinuities in equilibria that were generated as catastrophes and bifurcations, often revealing themselves as chaos.
4 Cities as Far-from-Equilibrium Structures
We have already introduced the problem posed by Prigogine who introduced the theory that human systems in general and cities in particular are systems that preserve and attempt to increase order in the wider face of it being destroyed by nature. It is already pretty clear in this chapter and indeed throughout this book that the concept of equilibrium can change dramatically dependent upon its application. It is entirely likely that a system can be in equilibrium in one sense, out-of-equilibrium in another, in disequilibrium, and far-from-equilibrium all at the same time. Indeed our earlier example—the City of London—whose physical structure has remained somewhat inert and stable with respect to the street pattern but whose buildings are continually being regenerated and whose populations are forever changing dramatically in type and composition is such a case. Here however we will concentrate on a very different kind of equilibrium that is being maintained in the fight for order against chaos with respect to how cities use energy and introduce innovations. This is the idea of a system that is far-from-equilibrium that we can best articulate with respect to its physical form.
Excellent examples of very highly ordered cities are those that must be completely controlled from the top down. Ideal cities such Frank Lloyd Wright’s mile high tower The Illinois, Le Corbusier’s various schemes for The City of Tomorrow, and Dantzig and Saaty’s Compact City are examples where considerable energy needs to be continually expended to keep the planned structures intact and to avoid any individual changes to the urban fabric and its organisation [5]. Wright’s tower contained everyone in his ideal city—some 100,000 persons—while Le Corbusier suggested a city of 60 storey tower blocks centred in wide open parkland surrounded by residential blocks of some six storeys high housing some three million. Dantzig and Saaty suggested a more compact but equally fictitious proposal based on compressing activities horizontally and to some extent vertically for a city of some 250,000 which could be expanded segmentally to two million persons but located in a large empty hinterland. In each case if we were to divide the city expanse into small zones and allocate population accordingly, most of the land would be empty and where it was occupied, it would be extremely dense.
We might approximate such structures with a set of probabilities of occupation where most were zero and a few or even only a single cell in the limit were unity. In the Wright example, if the formal probabilities of allocation were given by p i where ∑ i p i = 1, then we would have \(p_{i} = 0,i\neq 1,\forall i\) and p 1 = 1 where location 1 was the tower itself. In contrast imagine a city where everyone was spread out evenly and where there was no advantage or preference for locating in any one of n cells compared to any other. Then p i = 1∕n. If we now compute the Shannon entropy H = −∑ i p i logp i for Wright’s mile high city where the entire population lived in the tower, the entropy would be zero; for a city spread out evenly—a flat sprawling city—the entropy would be logn. So the most disordered structure is the flat sprawling one while the mile high tower is the most ordered with an entropy of zero. To keep everyone in the mile high tower would involve a massive amount of energy—material and psychic—while letting everyone live where they wanted would involve very little organisation. So the mile high tower in this context is far-from-equilibrium but the sprawling structures are essentially random and disorganised and in effect represent the traditional kind of thermodynamic equilibrium.
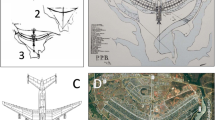
We might categorise all cities on this spectrum from order to chaos. A more visually structured example is reflected in a physical model of growth which is a diffusion limited by the space into which the phenomena might expand. It is well-known that such a diffusion-limited aggregation (DLA) model produces dendritic structures that reflect a system far-from-equilibrium. We can demonstrate how such a structure can be relaxed to imply ever more disordered equilibria—more compact and uniform structures compared to highly constrained forms which require severe constraints on where development can locate. It is worth illustrating how this kind of constrained structure can be simulated and in Fig. 1, we show a sequence of how the model to generate these kinds of structures actually works. We need to talk the reader through this to understand how such a structure emerges for we will then illustrate various examples of real cities that imply how such structures actually emerge.
Far-from equilibrium structures: analogues to city forms generated by diffusion from a central seed source. (a ) We plant a seed (the central dot) at the source site (the CBD) and at each time interval, it generates units of development (the light grey dots) that are projected onto the periphery. The unit then searches for an occupied site (which in the first instance is the seed site) by randomly walking across the space, where the dot with the arrows indicates such as random walk. Once it finds an occupied site, it sticks. Another unit is spawned and the walk begins again. In this way, the city is generated with a dendritic structure which is the default morphology
In Fig. 1a, we plant a seed at the centre of a space and this represents the fixed core—the CBD, say—from which the diffusion begins. Imagine that this seed continues to throw out units of development—growth—on a continuing basis but that these units have no capacity to locate on the seed site. They need to diffuse to nearby sites where there is space. If there are no constraints on such a structure, they will simply diffuse to the nearest vacant sites and there is nothing to constrain or limit the diffusion. It will simply spread in a random circular fashion around the source. We could quite easily ensure that the places closest to the source or seed had the capacity to take higher densities, thus mirroring the kind of competitive structures that exist in real cities but this would involve a degree of external constraint or organisation that would reduce the entropy from that associated with the purely random diffusion. We show the circular random diffusion and its growth in Fig. 1b, noting that as the number of cells increases the entropy rises as Shannon’s formula varies with the size of the system.
When we begin to impose constraints on where units might diffuse to, we lower the entropy in relative terms. The classic diffusion-limited aggregation model essentially imposes the condition that a cell that becomes developed must be already connected to the growing structure. Moreover the method of selecting a cell is one where the unit moves randomly amongst the empty cells in the space and as soon as it reaches an occupied cell, it sticks, forming part of the growing structure. To articulate this process, then we must assume that the unit of development is projected from the source to the periphery of the system and then begins its random walk in search of a cell that is adjacent to the growing structure and might then be occupied; or we need to compute a set of probabilities of occupation of the empty cells that are dependent on the relative positioning of all occupied and unoccupied cells, and use this field to determine the allocation.
This relative positioning gives added weight to those cells adjacent to the growing structure and particularly on the tips of the dendrites and lesser weight to those further away and the probabilities are computed so that this field is balanced. A walker or development unit once spawned from the source begins its walk across the existing structure and when it reaches an unoccupied cell, it selects this cell for fixing its location according to the occupation probability of this cell. Once this occurs, the probability field is altered and recomputed.
The process of random walking from the periphery—the former version of the model—is DLA, while the latter where the probability field is continually computed is the process of dielectric breakdown (DEB) but in essence, they lead to the same formations. When this sort of model is used to generate the growing structure, the kind of physical form that is produced is a dendrite where resources are clearly conserved by ensuring that those branches that have already been established become increasingly attractive to growth. The model contains all the elements of a far-from-equilibrium structure: emergence, path dependence, fractal structure, and positive feedback. We show this process in Fig. 1c where it is clear that the entropy lies between the more evenly spread random structure and the result that would occur if every unit of development were generated and planted on the source cell.
To illustrate the formation produced when the amount of order is much greater, one has to structure the probabilities of occupation to reflect this order. For example if everyone were required to live on the source site—in Wright’s mile high tower—then this would mean the probability of occupying this site were equal to 1 and all other cells zero. Another idealised structure might be a linear one where the probability of location were structured according to a linear routing to the central source site. Imagine a cell occupied by the source site. The probabilities of location in the immediate neighbourhood of this first cell are then equal to one another. If one is chosen randomly, thus breaking the symmetry, then the occupied cells provide a line of two cells. The probabilities are then determined by how close they are to this line—assuming the line of two cells marks out a transport route. Then the cells at each end of the line have higher probabilities of occupation than those anywhere else adjacent to the line because they are closer to transport to the source. If we proceed in this way, we generate a linear city as we show in Fig. 1d and the entropy of this structure is near zero largely because it takes a much greater amount of organisation to ensure that this kind of structure is developed.
When we examine the structures in Fig. 1, we can compare their entropies and recognise that those in (c) and (d) are farther-from-equilibrium than (b), their entropies are low in comparison to the more random equivalents such as the circular structure in Fig. 1b. One way of illustrating how close these kinds of structure are to those that we observe in real life is to choose a set of examples that reflect the skeletal structure of cities in terms of different space-filling regimes that clearly characterise the way development has taken place. The pure dendrite is not a structure that we see very often, perhaps not at all, although there are structures that approximate it. More likely we observe something that is not present in our diffusion model and that is a hierarchy of routes that we see quite clearly in many cities [4]. Moreover cities at different scales do show different dendritic forms despite the fact that there is strong self-similarity in structure across different levels due to the fact that cities tend to be fractal [7]. Without labouring the point, we have simply selected four cities that manifest different degrees of dendritic structure colouring in the land that is developed and making sure that the key dendritic structures that support land development—that move materials, people, and energies of various physical kinds from one location to another—are clearly visible (as we shown in Fig. 2).
To an extent, these approaches to equilibrium do not exist without an explicit dynamics. Models of these dynamics relate quite strongly to a whole class of models that partition cities into cells and then apply transition rules that mirror the fractal-like processes generating far-from-equilibrium forms that we have pictured in the abstract and in the real in Figures 1 and 2 [4, 23]. We simply point to the existence of this class of dynamic model which are very different from those that we introduced, albeit rather briefly, when we dealt with comparative static models earlier in this chapter. In fact agent-based models can be easily generalised from these cellular models. The diffusion model shown in Fig. 1 is essentially an agent-based model where the agents interact with each other and with the cells that they visit and occupy and there is a whole host of models that spin-off from these approaches that invoke a much richer dynamics and related concepts of non- and dis-equilibrium [9, 20]. These are important developments that add to the array of different kinds of equilibria in city systems but to conclude, we must examine those that pertain to really radical change and massive discontinuity that can be seen as being part of the dynamics of urban systems over much longer periods of time.
5 Creation and Destruction: Radical Change From Innovations in Technology
Dramatic change in cities usually takes place over long periods of time that relate to scientific and technological advances, to cultural movements, and to migrations of population associated with climatic or other physical conditions. Here we will focus on technology change because over the last 200 years and in modern times, we can easily observe the impact of new technologies on cities. But in past ages, cultural and economic change has been significant. For example, most of the cities of the ancient world are no longer in existence. Of the top 50 cities by population size known 500 years or so before the common era (BCE), none exist in the top 50 today and most have simply disappeared. Indeed there are only six of the biggest cities in the top 50 from the time of the Fall of Constantinople in 1453 in the top 50 today. This implies very substantial change in terms of an urban dynamics and by and large this has little to do with technological change. Rome reached about one million persons in the second century AD but the Empire could not hold, for cultural and political tensions as much as technology sealed its fate. The collapse that set in did not see a revival of cities until the Middle Ages, perhaps even as late as the modern era from the onset of the industrial revolution when the dynamic really did begin to change.
Apart from noting the dynamics pursued by Forrester [12] who essentially simulated a capacitated exponential growth for an hypothetical inner city system, most of the dynamics we have introduced do not follow cycles of any kind. When it comes to historical cycles, it is economic cycles that appear to coincide with technology change and over the last 200 years, the mechanical, electrical, and information revolutions based on the relevant inventions appear to have dominated successive waves of innovation. At present, the biosciences revolution appears to be dominant but so does the all-pervasive revolution in communications and computing that sets the current time apart from the previous three revolutions. The mechanical revolution dating from the steam engine dominated the world until the mid to late nineteenth century and this was then succeeded by the electrical with its invention of telecommunications, radio and television. By the mid-twentieth century, the revolution in computing had begun. These eras led to quite dramatic changes in the structure of cities: first as pointed out earlier, once the steam engine had been utilised for land transport, cities broke through their one million population capacity limit for the first time and megalopolis came onto the horizon. At first, this led to street car suburbs but then as mechanical technologies became all pervasive in the automobile, cities began to sprawl to the limits of daily travel to work. Electrical technologies merely reinforced this. Only in the last 50 years have they begun to change the nexus of communication in cities—the glue that holds the physical fabric together—but this has been as much due to the revolution in computing and communications, all based of course on electricity.
In terms of the physical built environment, we can define two broad stages in the evolution of cities from the pre-industrial era: first the city built around fixed rail and transit lines, and then the city built around the automobile. The first is public or collective transport, the second individual transport, both dependent on the use of material energies to power these technologies. We are fast entering a third era when information technologies in the form of media, email, web services and the great array of invisible communications that defy physical distance to a large extent are beginning to make an impact. These are reminiscent of the cycles or eras defined by Florida (2010) in his book The Great Reset [11]. How they are impacting on the physical form of cities is extremely difficult to unravel because many of these technologies are not easily visible in the same way as material technologies. We might then map these changes which we can see in the physical form of the city, albeit the most recent being most problematic, onto other cycles that appear to characterise urban change.
First, there is the material revolution in energies that really divides the last 200 years into the industrial and post-industrial age with the latter reflecting the transition from energy to information, from atoms to bits. And then there is the notion that the various sequence of technologies can be broken into a finer set of cycles—the most obvious being cycles of around 50 years first identified by Kondratieff [6]. These cycles involve changes in technologies that can be defined in terms of an innovative ideas phase, followed by development and thence some form of downswing to a kind of depression during which a new upswing in terms of inventions can be discerned. To this, Schumpeter added the idea that technology creates and then destroys perfectly workable infrastructures, even ideas, perhaps even information as the economic system supporting these changes seeks ever greater value from the products that are created [15]. This produces another layer of complexity dynamics with respect to cities. It reinforces the idea that cities can only be appreciated from multiple perspectives through multiple ideologies. The idea of equilibrium is everywhere one looks as is the idea of disequilibrium, and thus there is no such thing as a single equilibrium or disequilibrium as we have attempted to argue and portray in this chapter.
6 Reflections
Our thesis in this chapter has been that there are many types of equilibrium which we can recognise in city systems and consequently anything that departs from the steady state can be defined as a disequilibrium. Collectively all these characterisations might be brought together under the title non-equilibrium. In this chapter we have taken an explicitly physical approach to our social science. Cities are naturally viewed as physical and spatial systems and their patterns provide an obvious entry point into their study, their design and management. Indeed one of the reasons there is so much interest in cities is that we can use them to encapsulate many of the problems of modern society and attempt to understand them from the perspective of their form and function. Although it is controversial, solutions to these problems are often reflected in ways that we might alter the physical form of cities rather than attempting to change the behaviours more directly that have led to some of these problems. In a sense, this is a highly contentious point because it means that to solve urban problems, cities must be pushed out-of-equilibrium, out of their current condition to move to new equilibria that implies some better level of optimality.
The most promising perspective that we have indicated here is the idea that cities are far-from-equilibrium. Disentangling the concept of equilibrium from optimality is a very important consequence of thinking of cities as being out-of-equilibrium, far-from-equilibrium, or in non-equilibrium. In many senses, moving from equilibrium models of cities that have dominated the way we have thought of them during the last 50 years or so is an advance, and many of the ideas in other contributions in this book are also pointers to the progress in thinking of social systems in terms other than equilibria. It is not that equilibrium is an out-dated concept for it still represents a baseline which is a point of stability in our understanding of cities. But it is a point of departure rather than an end in itself as we have argued in diverse ways through the various perspectives we have introduced here.
References
Allen, P.M.: Cities and Regions as Self-Organizing Systems. London, Routledge (1997)
Amson, J.: Catastrophe theory: a contribution to the study of urban problems? Environ. Plan. B 2, 177–221 (1975)
Batty, M.: Pseudo-dynamic urban models. Ph.D. Thesis, University of Wales, Cardiff (1984). Available at http://www.casa.ucl.ac.uk/PhD.pdf
Batty, M.: The New Science of Cities. MIT, Cambridge, MA (2013)
Batty, M.: Optimal cities, ideal cities. Environ. Plan. B 42 (4), 571–573 (2015)
Batty, M.: Creative destruction, long waves and the age of the smart city. In: Knowles, R., Rozenblat, C. (eds.) Sir Peter Hall: Pioneer in Regional Planning, Transport and Urban Geography. Springer Briefs on Pioneers in Science and Practice No 52, pp. 81–97. Springer, Mosbach (2015)
Batty, M., Longley, P.A.: Modelling spatial morphologies fractal patterns from cellular automata. In: Abrahart, R.J., See, L.M. (eds.) Geocomputation, 2nd edn., pp. 23–48. CRC Press, Baton Rouge, FL (2014)
Churchman, C.W.: Wicked problems. Manag. Sci. 14, 141–142 (1967)
Crooks, A.T., Heppenstall, A.J.: Introduction to agent-based modelling. In: Heppenstall, A.J., Crooks, A.T., See, L.M., Batty, M. (eds.) Agent-Based Models of Geographical Systems, pp. 85–105. Springer, Berlin and New York (2014)
Feigenbaum, M.J.: Universal behavior in nonlinear systems. Phys. D 7, 16–39 (1983)
Florida, R.: The Great Reset: How the Post-Crash Economy Will Change the Way We Live and Work. Harper, New York (2010)
Forrester, J.W.: Urban Dynamics. MIT, Cambridge, MA (1969)
Garreau, J.: Edge City: Life on the New Frontier. Anchor Books, New York (1992)
Gleick, J.: Chaos: Making a New Science. Viking Books, New York (1987)
Leahy, W.H., McKee, D.L.: On goldfields, libraries, cities and Schumpeter, Am. Econ. 18, 142–144 (1974)
Lowry, I.S.: Model of metropolis. RM-4035-RC, The Rand Corporation, Santa Monica, CA (1964). Available at http://www.rand.org/content/dam/rand/pubs/research_memoranda/2006/RM4035.pdf
Mandelbrot, B.B.: Fractal aspects of the iteration of z = λ z(1 − z) for complex λ and z. Ann. N. Y. Acad. Sci. 357, 249–259 (1980)
May, R.M.: Simple mathematical models with very complicated dynamics. Nature 261, 459–467 (1976)
McLoughlin, J.B.: Control and Urban Planning. Faber and Faber, London (1973)
Murcio, R., Morphet, R., Gershenson, C., Batty, M.: Urban transfer entropy across scales. PLoS ONE 10 (7), e0133780 (2015). doi:10.1371/journal. pone.0133780
Prigogine, I.: The End of Certainty: Time, Chaos and the New Laws of Nature. Free Press, New York (1997)
Thom, R.: Structural Stability and Morphogenesis. W.A. Benjamin, New York (1972)
White, R., Engelen, G., Uljee, I.: Modeling Cities and Regions as Complex Systems: From Theory to Planning Applications. MIT, Cambridge, MA (2015)
Wilson, A.G.: Catastrophe theory and urban modelling: an application to modal choice. Environ. Plan. A 8, 351–356 (1976)
Wilson, A.G.: Catastrophe Theory and Bifurcation: Applications to Urban and Regional Systems. University of California Press, Berkeley, CA (1982)
Wilson, A.: Boltzmann, Lotka and Volterra and spatial structural evolution: an integrated methodology for some dynamical systems. J. R. Soc. Interface 5 (25), 865–871 (2008)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.
The images or other third party material in this chapter are included in the work's Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work's Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2017 The Author(s)
About this chapter
Cite this chapter
Batty, M. (2017). Cities in Disequilibrium. In: Johnson, J., Nowak, A., Ormerod, P., Rosewell, B., Zhang, YC. (eds) Non-Equilibrium Social Science and Policy. Understanding Complex Systems. Springer, Cham. https://doi.org/10.1007/978-3-319-42424-8_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-42424-8_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42422-4
Online ISBN: 978-3-319-42424-8
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)