Abstract
In order to evaluate spherical array processing algorithms comprehensively under many different acoustic conditions, it is indispensable to use simulated acoustic impulse responses (AIRs) to characterize the source–microphone acoustic channel, most typically in a room or other enclosed acoustic environment. The image method proposed by Allen and Berkley is a well-established way of doing this for point-to-point AIRs with sensors in free space. However, it does not account for the acoustic scattering introduced by a rigid sphere. In this chapter, we present a method for simulating the AIRs between a sound source and microphones positioned on a rigid spherical array. In addition, three examples are presented based on this method: an analysis of a diffuse reverberant sound field, a study of binaural cues in the presence of reverberation, and an illustration of the algorithm’s use as a mouth simulator.
Portions of this chapter were first published in the Journal of the Acoustical Society of America [17], and are reproduced in accordance with the Acoustical Society of America’s Transfer of Copyright Agreement. The content of [17] has been edited here for brevity and to standardize the notation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Vectors in Cartesian coordinates are denoted with a corner mark \(\llcorner \) to distinguish them from vectors in spherical coordinates, which are used throughout this book and will be introduced later in the chapter.
- 2.
This expression assumes the sign convention commonly used in electrical engineering, whereby the temporal Fourier transform is defined as \(\mathcal {F}(\omega ) = \int _{-\infty }^{\infty } f(t) e^{-i \omega t} \text {d}t\). For more information on this sign convention, the reader is referred to Sect. 2.3.
- 3.
Some texts [9] refer to the scattering effect as diffraction, although Morse and Ingard note that “When the scattering object is large compared with the wavelength of the scattered sound, we usually say the sound is reflected and diffracted, rather than scattered” [28], therefore in the case of spherical microphone arrays (particularly rigid ones which tend to be relatively small for practical reasons), scattering is possibly the more appropriate term.
- 4.
The sign in the powers of \(\beta \) is different from that in Allen and Berkley’s conventional image method, due to the change in the definition of
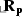 that is required for the SMIR method.
that is required for the SMIR method. - 5.
Very low frequencies are omitted due to the fact that the spherical Hankel function \(h_l(x)\) has a singularity around \(x = 0\).
- 6.
While the ray-tracing formula is frequency-independent, it has been shown [6] that ITDs actually exhibit some frequency dependence, and that because the ray-tracing concept applies to short wavelengths, this model yields only the high frequency time delay. Kuhn provides a more comprehensive discussion of this model and the frequency-dependence of ITDs [19]. It should be noted the simulation results in Fig. 4.8 are in broad agreement with Kuhn’s measured results at 3.0 kHz.
References
Abramowitz, M., Stegun, I.A. (eds.): Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications, New York (1972)
Allen, J.B., Berkley, D.A.: Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 65(4), 943–950 (1979)
Avni, A., Rafaely, B.: Sound localization in a sound field represented by spherical harmonics. In: Proceedings 2nd International Symposium on Ambisonics and Spherical Acoustics, pp. 1–5. Paris, France (2010)
Betlehem, T., Poletti, M.A.: Sound field reproduction around a scatterer in reverberation. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 89–92 (2009). doi:10.1109/ICASSP.2009.4959527
Botteldoore, D.: Finite-difference time-domain simulation of low-frequency room acoustic problems. J. Acoust. Soc. Am. 98(6), 3302–3308 (1995)
Brown, C., Duda, R.: A structural model for binaural sound synthesis. IEEE Trans. Speech Audio Process. 6(5), 476–488 (1998). doi:10.1109/89.709673
Chen, Z., Maher, R.C.: Addressing the discrepancy between measured and modeled impulse responses for small rooms. In: Proceedings of Audio Engineering Society Convention (2007)
Deller, J.R., Proakis, J.G., Hansen, J.H.L.: Discrete-Time Processing of Speech Signals. MacMillan, New York (1993)
Duda, R.O., Martens, W.L.: Range dependence of the response of a spherical head model. J. Acoust. Soc. Am. 104(5), 3048–3058 (1998). doi:10.1121/1.423886
Evans, M.J., Angus, J.A.S., Tew, A.I.: Analyzing head-related transfer function measurements using surface spherical harmonics. J. Acoust. Soc. Am. 104(4), 2400–2411 (1998)
Gumerov, N., Duraiswami, R.: Modeling the effect of a nearby boundary on the HRTF. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), vol. 5, pp. 3337–3340 (2001). doi:10.1109/ICASSP.2001.940373
Gumerov, N.A., Duraiswami, R.: Fast Multipole Methods for the Helmholtz Equation in Three Dimensions. Elsevier, Oxford (2005)
Habets, E.A.P., Benesty, J.: A two-stage beamforming approach for noise reduction and dereverberation. IEEE Trans. Audio, Speech, Lang. Process. 21(5), 945–958 (2013)
Jarrett, D.P.: Spherical microphone array impulse response (SMIR) generator. http://www.ee.ic.ac.uk/sap/smirgen/
Jarrett, D.P., Habets, E.A.P., Thomas, M.R.P., Gaubitch, N.D., Naylor, P.A.: Dereverberation performance of rigid and open spherical microphone arrays: theory and simulation. In: Proceedings Joint Workshop on Hands-Free Speech Communication and Microphone Arrays (HSCMA), pp. 145–150. Edinburgh (2011)
Jarrett, D.P., Habets, E.A.P., Thomas, M.R.P., Naylor, P.A.: Simulating room impulse responses for spherical microphone arrays. In: Proc. IEEE Intl. Conf. on Acoustics, Speech and Signal Processing (ICASSP), pp. 129–132. Prague, Czech Republic (2011)
Jarrett, D.P., Habets, E.A.P., Thomas, M.R.P., Naylor, P.A.: Rigid sphere room impulse response simulation: algorithm and applications. J. Acoust. Soc. Am. 132(3), 1462–1472 (2012)
Knudsen, V., Harris, C.: Acoustical Designing in Architecture. Wiley, New York (1950)
Kuhn, G.F.: Model for the interaural time differences in the azimuthal plane. J. Acoust. Soc. Am. 62(1), 157–167 (1977). doi:10.1121/1.381498
Kuttruff, H.: Room Acoustics, 4th edn. Taylor and Francis, London (2000)
Lehmann, E., Johansson, A.: Diffuse reverberation model for efficient image-source simulation of room impulse responses. IEEE Trans. Audio Speech Lang. Process. 18(6), 1429–1439 (2010). doi:10.1109/TASL.2009.2035038
Li, Z., Duraiswami, R.: Hemispherical microphone arrays for sound capture and beamforming. In: Proceedings of IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, pp. 106–109 (2005)
Logan, N.A.: Survey of some early studies of the scattering of plane waves by a sphere. Proc. IEEE 53(8), 773–785 (1965). doi:10.1109/PROC.1965.4055
Meyer, J., Agnello, T.: Spherical microphone array for spatial sound recording. In: Proc. Audio Engineering Society Convention, pp. 1–9. New York (2003)
Meyer, J., Elko, G.: A highly scalable spherical microphone array based on an orthonormal decomposition of the soundfield. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), vol. 2, pp. 1781–1784 (2002)
Meyer, J., Elko, G.W.: Position independent close-talking microphone. Signal Process. 86(6), 1254–1259 (2006). doi:10.1016/j.sigpro.2005.05.036
mh acoustics LLC: The Eigenmike microphone array. http://www.mhacoustics.com/mh_acoustics/Eigenmike_microphone_array.html
Morse, P.M., Ingard, K.U.: Theoretical Acoustics. International Series in Pure and Applied Physics. McGraw Hill, New York (1968)
Peterson, P.M.: Simulating the response of multiple microphones to a single acoustic source in a reverberant room. J. Acoust. Soc. Am. 80(5), 1527–1529 (1986)
Pietrzyk, A.: Computer modeling of the sound field in small rooms. In: Proceedings of AES International Conference on Audio, Acoustics and Small Spaces, vol. 2, pp. 24–31. Copenhagen (1998)
Radlović, B.D., Williamson, R., Kennedy, R.: Equalization in an acoustic reverberant environment: robustness results. IEEE Trans. Speech Audio Process. 8(3), 311–319 (2000)
Rafaely, B.: Plane-wave decomposition of the pressure on a sphere by spherical convolution. J. Acoust. Soc. Am. 116(4), 2149–2157 (2004)
Rafaely, B.: Analysis and design of spherical microphone arrays. IEEE Trans. Speech Audio Process. 13(1), 135–143 (2005). doi:10.1109/TSA.2004.839244
Sandel, T.T., Teas, D.C., Feddersen, W.E., Jeffress, L.A.: Localization of sound from single and paired sources. J. Acoust. Soc. Am. 27(5), 842–852 (1955). doi:10.1121/1.1908052
Savitzky, A., Golay, M.J.E.: Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 36(8), 1627–1639 (1964). doi:10.1021/ac60214a047
Sengupta, D.L.: The sphere. In: J.J. Bowman, T.B.A. Senior, P.L.E. Uslenghi (eds.) Electromagnetic and Acoustic Scattering by Simple Shapes, pp. 353–415. North-Holland (1969) (chap. 10)
Shinn-Cunningham, B.G., Kopco, N., Martin, T.J.: Localizing nearby sound sources in a classroom: binaural room impulse responses. J. Acoust. Soc. Am. 117(5), 3100–3115 (2005). doi:10.1121/1.1872572
Talantzis, F., Ward, D.B.: Robustness of multichannel equalization in an acoustic reverberant environment. J. Acoust. Soc. Am. 114(2), 833–841 (2003)
Ward, D.B.: On the performance of acoustic crosstalk cancellation in a reverberant environment. J. Acoust. Soc. Am. 110, 1195–1198 (2001)
Williams, E.G.: Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography, 1st edn. Academic Press, London (1999)
Author information
Authors and Affiliations
Corresponding author
Appendix: Spatial Correlation in a Diffuse Sound Field
Appendix: Spatial Correlation in a Diffuse Sound Field
The sound pressure at a position \(\mathbf {r} = (r,\varOmega )\) due to a unit amplitude plane wave incident from direction \(\varOmega _{\text {s}}\) is given by [40]
where \(\varphi (\varOmega _{\text {s}})\) is a random phase term and \(|\varphi (\varOmega _{\text {s}})|~=~1\). Assuming a diffuse sound field, the spatial cross-correlation between the sound pressure at two positions \(\mathbf {r} = (r,\varOmega )\) and \(\mathbf {r}' = (r,\varOmega ')\) is given by:
Using the orthonormality property of the spherical harmonics in (2.18) and the addition theorem in (2.23), we eliminate the cross terms followed by the sum over m and obtain

where \(\varTheta _{\mathbf {r},\mathbf {r}'}\) is the angle between \(\mathbf {r}\) and \(\mathbf {r}'\).
In the open sphere case, we can derive a simplified expression for \(C(\mathbf {r},\mathbf {r}',k)\). Firstly, we note that the expression in (4.25) is real, and therefore, for a reason which will soon become clear, \(C(\mathbf {r},\mathbf {r}',k)\) can advantageously be expressed as

where \(\mathfrak {I}\) denotes the imaginary part of a complex number. By substituting the open sphere mode strength \(b_l(k) = i^l j_l(kr)\) into (4.26), we obtain

Using \(\mathfrak {R}\{h_l^{(2)}(kr)\} = j_l(kr)\), where \(\mathfrak {R}\) denotes the real part of a complex number, we can now write (4.27) as

As the expression marked with a \(\star \) is real, its imaginary part is zero and (4.28) can be simplified to

Finally, using (4.7) and (4.8), we obtain the well-known spatial domain result for two omnidirectional receivers in a diffuse sound field [20, 31, 39]:
Rights and permissions
Copyright information
© 2017 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Jarrett, D.P., Habets, E.A.P., Naylor, P.A. (2017). Spherical Array Acoustic Impulse Response Simulation. In: Theory and Applications of Spherical Microphone Array Processing. Springer Topics in Signal Processing, vol 9. Springer, Cham. https://doi.org/10.1007/978-3-319-42211-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-42211-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-42209-1
Online ISBN: 978-3-319-42211-4
eBook Packages: EngineeringEngineering (R0)


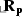 that is required for the SMIR method.
that is required for the SMIR method.