Abstract
Automated nuclear segmentation is essential in the analysis of most microscopy images. This paper presents a novel concavity-based method for the separation of clusters of nuclei in binary images. A heuristic rule, based on object size, is used to infer the existence of merged regions. Concavity extrema detected along the merged-cluster boundary are used to guide the separation of overlapping regions. Inner split contours of multiple concavities along the nuclear boundary are estimated via a series of morphological procedures. The algorithm was evaluated on images of H400 cells in monolayer cultures and compares favourably with the state-of-art watershed method commonly used to separate overlapping nuclei.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction and Related Work
Automated nuclear segmentation plays an important role in computer-assisted analysis of histopathological images. Improving the quality and accuracy of nuclear segmentation has become an increasingly important topic, for which numerous analytical procedures have been proposed. One main challenge is the separation of clusters of overlapping nuclei. These often appear as irregular shapes resulting from an overlap of the 3D extent of nuclei on 2D image projections. An additional complication is that the overlapping nucleus boundaries are often indistinct and make the algorithmic separation a non-trivial challenge. This is especially relevant for the diagnosis of many diseases, including cancer, where identifying and characterising cellular abnormalities play an important role. There has been extensive, well-focused research by various groups on the splitting of nuclear clusters; a review paper [1] addresses recent advances and current challenges with respect to this problem. The well-known watershed algorithm [2, 3] has been used to address region separation by creating unique ‘basins’ where nuclei are defined by the ridges bounding the basins. Although this can result in successful separation in some images, there are well-documented problems with over- and under-segmentation in cells/nuclei that overlap, particularly when the boundary gradients at the overlaps are weak. Other methods use measures of concavity of the cluster contour to find the nuclei [4–6] or use ellipse-fitting to infer the overlapping nuclei, one drawback being that the performance tends to be sensitive to fluctuations of the contours. Also, most methods detect but do not split clusters into individual nuclei segments in the 2D image. While it might not be possible to resolve this in all cases, such splittings are often necessary for extracting additional features (object counting, computing spatial relations) which are operationally useful even when derived from segmentations that include some mis-assigned pixels. Other methods [7–9] employ iterative split-line algorithms to generate inner edges, and use concavity points to construct edge-path graphs. From these, the possible combinations of lines linking every pair of concavity points are computed and the shortest set of lines satisfying certain conditions is generated at the final splitting step. The split-lines are generated subject to the conditions that they yield sub-contours with acceptable nuclear sizes and do not intersect with other lines. While this can produce reasonable results in simple cases, it often fails in complex configurations, for a number of reasons: (a) from all the possible combinations of split-lines it is difficult to identify which point pairs to link; (b) the number of split combinations increases dramatically with the number of concavity points, becoming computationally costly and slow; (c) object separation uses straight lines along the inferred boundaries, while real nuclear boundaries are curved; (d) iterative separation usually leads to over-segmentation, as illustrated later.
Here we propose a new method for the detection and separation of individual nuclei in clusters based on the geometrical characteristics of the cluster boundary, particularly contour curvature; this approach overcomes several limitations mentioned earlier. The expected positions and shapes of individual candidate nuclei are estimated and followed by a series of morphological operations that separate the cluster into individual nuclear regions. The validity and effectiveness of the proposed framework was assessed through a series of experiments on images of clumped nuclei.
2 The Proposed Algorithm
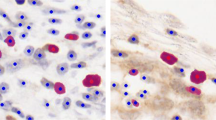
We investigated cluster separation on images of monolayers of H400 cells (an oral cancer cell line) grown on glass and captured at \(\times \)20 magnification (inter-pixel distance is 0.34 \(\upmu \)m) stained with Haematoxylin. These are typical conditions used in a variety of gene expression analyses. The haematoxylin (blue/violet) dye is primarily taken up by nucleic acids (therefore highlighting nuclei). Often eosin (pink dye) is used as a counter-stain, staining proteins in the intra- and extra-cellular compartments. A typical analysis of these cultures starts with a standard image pre-processing step such as colour deconvolution to unmix the dyes (if more than one is used) in order to facilitate extraction of the objects of interest. Nucleus segmentation is best performed on the Haematoxylin channel image owing to its aforementioned affinity to nucleic acids. Following this, a global thresholding method is applied to obtain a binary image of the nuclei where any clustered groups of nuclei would require separation. In the experiments described later, however, we work on a manually segmented ‘gold standard’ set of nuclear images. All imaging procedures were implemented on the popular ImageJ platform [10].
2.1 Identifying Potential Nuclei Clusters
This initial step extracts the boundaries of potential nuclear clusters R in the binary image \(I_1\) representing the nuclei when the area of R is larger than some empirically determined value. This is followed by a concavity analysis (explained in the next section), where identified concavity points S serve as the input to the following region-splitting algorithm. Large regions with no concavity points imply lack of overlap, in which case region-splitting is not required; whereas the presence of one or more concavity points indicates contours that potentially enclose two or more nuclei.
2.2 Concavity Point Detection
This step detects the most dominant set of concavity points in a region boundary. Concavity points represent junctions where overlapping occurs and they are used here to guide the subsequent separation steps. A closed region R is defined by an ordered set of N boundary points, say \(R = \{p_i | i \in \{1... N\}\}\). A point \(p_i\) corresponds to the ith boundary point and \(p_{i+1}\) and \(p_{i-1}\) are the next and previous boundary points, respectively. Determining concavity/convexity in a boundary relies on the mathematical property of two dimensional vectors defined along the periphery of the closed-loop region R. A two-dimensional vector \(V_1\) is defined between points \(p_{i-1}\) and \(p_i\), and a second one, \(V_2\), is defined between points \(p_{i+1}\) and \(p_i\). The cross product \(V_1 \times V_2\) characterizes the boundary curvature. If the boundary points are ordered in the clockwise direction, then a point \(p_i \in R\) belongs to a concave segment if \(V_1 \times V_2 \le 0\). To reduce the sensitivity of the algorithm to small fluctuations and noise, a tolerance value gap representing the length of the vectors is introduced. Similarly to the approach in [7], the most dominant concavity point is then selected from each detected concave segment, based on the angle between contour points. The selected point s corresponds to the deepest indentation between two overlapping nuclei, minimising the angle \(Angle(p_i)= \pi - \arccos \left( \frac{{(p_i - p_{i-gap})} \cdot {(p_{i+gap} - p_i)}}{\Vert p_i - p_{i-gap}\Vert \Vert p_{i+gap} - p_i \Vert }\right) \) between the vectors. The final list of concavity points, S, is passed as an input to the following splitting algorithm.
2.3 Region-Splitting Algorithm
The presence of a single concavity point (\(s_1 \in S\)) in the cluster boundary indicates a potential overlap of two individual nuclei. In this special case, the algorithm creates a 4-connectedFootnote 1 split-line that links \(s_1\) to the midpoint, \(p_{i}\), where i corresponds to the middle position of the opposite convex boundary. It is worthwhile mentioning that other splitting procedures such as the watershed separation would fail to produce split-lines in these cases.
On the other hand, two or more concavity points along the boundary imply potential overlap between multiple nuclei. The proposed model takes as input a region of clustered nuclei with multiple detected concavity points and returns the optimal inner separating boundaries. The whole process is summarized in Fig. 1 (using a synthetic cluster region)Footnote 2 and it consists of the following steps:
1. Convex Contour Extraction. This step extracts the coordinates and number of pixels located on convex segments between each consecutive pair of concavity points (see Fig. 1(b)). For robustness, the algorithm only considers convex segments that are large enough to fit a candidate cell. A given value \(\theta _1\) serves as a threshold for detecting effective convex regions.
2. Circle Fitting. Least-squares fitting [11] is used to compute the best fitting circles to the set of points in each of the convex segments, and each circle corresponds now to a candidate individual nucleus, as shown in Fig. 1(c). With each circle crl with centre \(c \in \check{C}\) and radius rad is associated a pair of consecutive concavity points, \(s_n, s_{n+1} \in S\), located on the cluster boundary. The circles are inspected and modified before nuclear separation takes place, as follows. The algorithm constrains the radii to be less than an empirically determined threshold \(\theta _2\), estimated in advance, which corresponds to the maximum radius of a real nucleus, then it replaces radii larger than this with this threshold value. As for circle centres in \(\check{C}\), on rare occasions they might be located outside the clustered nuclear region R. The algorithm corrects this by recursively shifting the circle centre coordinates, in small increments, towards their corresponding convex segments until it is repositioned inside R. To do this, the recursive shift checks the intensity value of a centre point in image \(I_1\).
3. Estimating Candidate Nuclei. The circle centres provide an a priori estimation of the expected position of the nuclei in the cluster. We noted that clusters are likely to have regions with two closely opposing convex segments. The procedure described so far would yield two partially overlapping circular zones with adjacent centres, see Fig. 1(c). Intuitively, however, an observer with a range of possible nuclear sizes and shapes in mind would conclude that opposing segments are likely to correspond to only one rounded object, not two. To resolve this, the algorithm checks the pairwise distance between all the assigned centres. Consider a circle \(crl_a\), with centre \(c_a\), radius \(rad_a\) and concavity points (\(s_a, s_{a+1}\)). To find whether another centre \(c_b\) (located in circle \(crl_b\) with radius \(rad_b\) and concavity points (\(s_b, s_{b+1}\))) is inside the circle \(crl_a\), we measure the Euclidean distance \(\check{D}\) between \(c_a\) and \(c_b\). Point \(c_b\) is inside \(crl_a\) if \(\check{D} \le rad_a\). Accordingly, the status of centre \(c_b\) with respect to \(c_a\) is set to Binary Centres (\(\varvec{BC}\)) if (\(\check{D} \le rad_a\) and \((s_a, s_{a+1}) \not = (s_b,s_{b+1})\)), implying their close proximity, representing a single candidate object. This is shown in Fig. 1(c) in blob pairs [L,C] and [J,E].
It might be argued, however, that nuclear boundaries often take the form of ellipses rather than circles, while the procedure above aims to detect near-by centres of overlapping circles. In other words, the distance between the two centres \(c_a\) and \(c_b\) might be larger than the radius \(rad_a\) in the case of elliptical candidate nuclei. This situation, illustrated in blob pair [K, D] in Fig. 1(c), is not detected by our algorithm so far, and would lead to an incorrect separation into two assumed circular objects instead of a single elliptical object. To provide a viable segmentation of overlapping elliptical objects, the algorithm introduces a correction factor, namely \(\check{O}\), that is multiplied by the radius \(rad_a\). This factor increases the distance span that is to be compared with \(\check{D}\), thereby allowing for the detection of elliptical objects. Accordingly, \(\forall (c_a, c_b) \in \check{C}\), the status of centre \(c_b\) with respect to \(c_a\) is assigned as \(\varvec{BC}\) if (\(\check{D} \le rad_a \times \check{O}\) and \((s_a, s_{a+1}) \not = (s_b,s_{b+1})\)), otherwise, it is assigned as \(\varvec{SC}\) (Single Centre), as shown in blobs M, A, B, F, G, H, I in Fig. 1(c). Note that, if the status of \(c_b\) is deemed to be \(\varvec{BC}\) with respect to \(c_a\), then the algorithm imposes the same \(\varvec{BC}\) relation on \(c_a\), and saves the concavity information of both centres.
4. Morphological Operations for Cluster Splitting. This step produces the final inner edges to separate the overlapping nuclei by means of a series of mathematical morphology operations [12]. The idea revolves around geodesic dilations, without merging, of seeds representing single regions belonging uniquely to each candidate object. This principle is similar to the well-known watershed separation method (natively available in ImageJ [10]), but while that method uses the ultimate eroded points as seeds (often leading to over-segmentation) our approach uses much larger seeds derived from the regions containing convex segments and estimated centres of regions. This avoids the over-segmentation typical of the watershed method. The seed image is created as follows. On a new blank binary image \(I_2\), a preliminary set of line segments is drawn. Their positions depend on the status of the candidate object centres (each of which is located between a pair of concavity points as described earlier). If a centre is labelled as \(\varvec{BC}\) with respect to another (i.e., together representing a single candidate nucleus), the algorithm retrieves the concavity information relative to both centres and draws two lines, each linking one of the two pairs of associated concavity points from the opposite sides of the boundary. The order of linking these is given by the encoding order in the cluster boundary. Furthermore, if a centre is labelled as \(\varvec{SC}\) (i.e., representing a single candidate object) then two lines are drawn, linking the circle centre to each of the surrounding concavity points. Some of the resulting lines, as illustrated in Fig. 1(d), might create closed polygons, which are then filled. This is followed by subtracting the image \(I_2\) from the original image \(I_1\), yielding a seed image \(I_3\), which retains some parts of the original cluster, as seen in Fig. 1(e). Since each segmented sub-region (seed) is now unique to a detected object in the cluster, these can then be conditionally dilated to form individual nuclear objects by means of a geodesic dilation operation, without merging, of the seed image \(I_3\), inside the original image \(I_1\) which acts as a mask. The dilation progresses with two restrictions, one being the mask extent of the original cluster and the other a logical operation that prevents pixels connected to different seeds from merging. The geodesic dilation of seed \(I_3\) with respect to the mask \(I_1\) is defined as \(D_{(I_1)} (I_3 )=(I_3 \oplus B) \cap I_1\), where \(\oplus \) denotes the dilation of \(I_3\) with the structure element B, and \(\cap \) performs a pixel-wise logical AND (intersection) between the dilated image and the mask \(I_1\). The final segmentation result is depicted in Fig. 1(f). The separation results of the watershed [2, 3] and iterative split-line methods [7–9] are shown in Fig. 1(g) and (h), yielding under- and over- segmentation, respectively.
3 Experiments and Evaluation
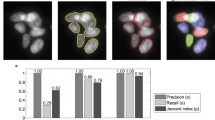
Our proposed method was tested using four large monolayer images of H400 cells. A total of 2610 nuclei were hand-drawn by one of us to produce a gold-standard set, which was used to obtain another set of binary images.Footnote 3 Among these, a total of 497 nuclei formed 203 clusters with various degrees of complexity in their fused boundaries. Potential clusters were processed when their area was larger than 1600 pixels\(^{2}\) and contained concavity points. The optimal range of parameter values were initially chosen before applying to the tested images. The optimal values of gap and \(\check{O}\) depended on the geometry and size of the cluster, so they were tested at values of {5, 10, 15} and {2, 3}, respectively. Those were the values that generated regions with the highest circularity and within the optimal nuclear area. The thresholds \(\theta _1\) and \(\theta _2\) were constrained to be larger than 20 and less than 20 pixels, respectively. The qualitative results shown in Fig. 2 (upper row) demonstrate the ability of our algorithm to resolve complex clusters (with four or more overlapping nuclei) while avoiding over- and under-segmentation. The procedure can generate contours close to actual nucleus boundaries. The lower rows of Fig. 2 show the superiority of our approach over the watershed separation, which generates spurious edges in some simple configurations.
Quantitative results (summarized in Table 1) were obtained using three different measures. Our segmentation result was compared visually with the gold-standard to estimate the True Positive Rate \(TPR=\frac{TP}{TP+FN}\) and the Positive Predictive Value \(PPV=\frac{TP}{TP+FP}\), where the True Positives (TP), False Positives (FP), and False Negatives (FN) are the numbers of correctly detected nuclei, incorrectly detected nuclei, and undetected nuclei, respectively. The third measure was given by the Jaccard Index (JI), which is defined as the ratio \(JI = \frac{|\check{G} \cap I|}{|\check{G} \cup I|}\) between the pixel-counts of the intersection and union of the gold-standard segmented image \(\check{G}\) and the test segmentation I. The JI ranges from 0 (no overlap between the images) to 1 (complete congruence). Note that the line-of-sight 2D projections of the gold-standard images show inferred overlapping nuclear boundaries which cannot be separated and represented in a single binary image. The JI match of \(\check{G}\) and I is measured as follows. Using standard morphological operations we (i) extract the symmetric difference of the filled overlapping regions with respect to their filled intersections (‘lenses’) to generate a set of ‘lunes’; (ii) separate the lunes into their component parts by a morphological erosion, (iii) apply a binary dilation without merging operation to the separated lune parts within a mask image (the merged filled nuclear profiles). The split-line generated in each of the lens-like regions approximates their medial-axis transform. Overall, the proposed method outperforms the classical watershed in terms of TPR, PPV and JI. During the experiments, we observed that the algorithm preserves the ellipticity of the reconstructed nuclear regions, and in particular it outperforms watershed segmentation in clusters that lack prominent ‘necks’; it is, however, sensitive to the gap and \(\check{O}\) parameters.
4 Conclusion
We presented a novel mathematical morphology-based algorithm for separating clustered binary nuclear profiles. Concavity features of the cluster boundary are extracted and guide the subsequent region-splitting steps. Optimal split boundaries are computed using a series of morphological operations. Unlike in iterative split-line models, our non-iterative algorithm provides separation while avoiding over-segmentation. Qualitative and quantitative results tested on hand-segmented datasets of images of H400 cells verify that the segmentation accuracy of the proposed method outperforms the watershed separation approach.
Notes
- 1.
Our binary image objects are 8-connected in a 4-connected background.
- 2.
Boundaries in Fig. 1(b) are thickened for display purposes.
- 3.
Hand-segmented nuclei regions were filled in white and the background in black. As a result, nuclei with overlapping boundaries will appear in clusters and the ones with separated boundaries will appear individually.
References
Irshad, H., Veillard, A., Roux, L., Racoceanu, D.: Methods for nuclei detection, segmentation, and classification in digital histopathology: a review-current status and future potential. Biomed. Eng. 7, 97–114 (2014)
Beucher, S., Lantuejoul, C.: Use of watersheds in contour detection. In: Proceedings of the International Workshop on Image Processing, Real-Time Edge and Motion Detection/Estimation, CCETT/IRISA, pp. 17–21 (1979)
Gran, V., Mewes, A.U.J., Alcaniz, M., Kikinis, R., Warfield, S.K.: Improved watershed transform for medical image segmentation using prior information. IEEE Trans. Med. Imag. 23(4), 447–458 (2004)
Bai, X., Sun, C., Zhou, F.: Splitting touching cells based on concave points and ellipse fitting. Pattern Recog. 42(11), 2434–2446 (2009)
Plissiti, M.E., Louka, E., Nikou, C.: Splitting of overlapping nuclei guided by robust combinations of concavity points. In: SPIE 9034, Medical Imaging 2014: Image Processing, 903431 (2014)
Zafari, S., Eerola, T., Sampo, J., Kalviainen, H., Haario, H.: Segmentation of overlapping elliptical objects in silhouette images. IEEE Trans. Image Process. 24(12), 5942–5952 (2015)
Fatakdawala, H., Basavanhally, A., Jun, X., Bhanot, G., Ganesan, S., Feldman, M., Tomaszewski, J., Madabhushi, A.: Expectation maximization driven geodesic active contour with overlap resolution (EMaGACOR): application to lymphocyte segmentation on breast cancer histopathology. In: Ninth IEEE International Conference on Bioinformatics and BioEngineering, pp. 69–76 (2009)
Kong, H., Gurcan, M., Belkacem-Boussaid, K.: Partitioning histopathological images: an integrated framework for supervised color-texture segmentation and cell splitting. IEEE Trans. Med. Imaging 30(9), 1661–1677 (2011)
Latorre, A., Alonso-Nanclares, L., Muelas, S., Peña, J.M., Defelipe, J.: Segmentation of neuronal nuclei based on clump splitting and a two-step binarization of images. Expert Syst. Appl. 40(16), 6521–6530 (2013)
Rasband, W.S. (1997-2016) ImageJ, U.S. National Institutes ofHealth, Bethesda, Maryland, USA. http://imagej.nih.gov/ij/
Pratt, V.: Direct least-squares fitting of algebraic surfaces. In: Stone, M.C. (ed.) 14th Annual Conference on Computer Graphics and Interactive Techniques, pp. 145–152. ACM, New York (1987)
Dougherty, E.: Mathematical Morphology in Image Processing. CRC Press, Boca Raton (1992)
Acknowledgments
The research reported in this paper was supported by the Engineering and Physical Sciences Research Council (EPSRC), UK through funding under grant EP/M023869/1 “Novel context-based segmentation algorithms for intelligent microscopy”.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.
The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2016 The Author(s)
About this paper
Cite this paper
Fouad, S., Landini, G., Randell, D., Galton, A. (2016). Morphological Separation of Clustered Nuclei in Histological Images. In: Campilho, A., Karray, F. (eds) Image Analysis and Recognition. ICIAR 2016. Lecture Notes in Computer Science(), vol 9730. Springer, Cham. https://doi.org/10.1007/978-3-319-41501-7_67
Download citation
DOI: https://doi.org/10.1007/978-3-319-41501-7_67
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-41500-0
Online ISBN: 978-3-319-41501-7
eBook Packages: Computer ScienceComputer Science (R0)