Fermions

Abstract

Classical theories starting with continuous degrees of freedom will typically generate bosonic quantum objects; fermionic quantum objects in turn, arise when a classical system contains discrete degrees of freedom—typically: flip-flops. Here, we explain how anti-commuting operators enter the scene, and illustrate the situation using an elegant model: the idealized notion of a ‘neutrino’. What do neutrinos have in common with infinite, at sheets, and where does spin $\frac{1}{2}$ come from? The associated mathematical tool kit is quite delicate.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 The Jordan–Wigner Transformation

In order to find more precise links between the real quantum world on the one hand and deterministic automaton models on the other, much more mathematical machinery is needed. For starters, fermions can be handled in an elegant fashion.

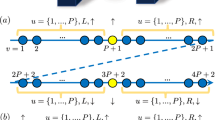
Take a deterministic model with $M$ states in total. The example described in Fig. 2.2 (page 26), is a model with $M=31$ states, and the evolution law for one time step is an element $P$ of the permutation group for $M=31$ elements: $P\in P_{M}$. Let its states be indicated as $|1\rangle,\ldots, |M\rangle$. We write the single time step evolution law as:

$$\begin{aligned} |i\rangle_{t}\rightarrow|i\rangle_{t+\delta t}=|P(i) \rangle_{t}=\sum_{j=1}^{M}P_{ij}|j \rangle _{t} , \quad i=1,\ldots,M , \end{aligned}$$

(15.1)

where the latter matrix $P$ has matrix elements $\langle j|P|i\rangle$ that consists of 0s and 1s, with one 1 only in each row and in each column. As explained in Sect. 2.2.2, we assume that a Hamiltonian matrix $H^{\mathrm{op}}_{ij}$ is found such that (when normalizing the time step $\delta t$ to one)

$$\begin{aligned} \langle j|P|i\rangle= \bigl(e^{-iH^{\mathrm{op}}}\bigr)_{ji} , \end{aligned}$$

(15.2)

where possibly a zero point energy $\delta E$ may be added that represents a conserved quantity: $\delta E$ only depends on the cycle to which the index $i$ belongs, but not on the item inside the cycle.

We now associate to this model a different one, whose variables are Boolean ones, taking the values 0 or 1 (or equivalently, $+1$ or −1) at every one of these $M$ sites. This means that, in our example, we now have $2^{M}=2{,}147{,}483{,}648$ states, one of which is shown in Fig. 15.1. The evolution law is defined such that these Boolean numbers travel just as the sites in the original cogwheel model were dictated to move. Physically this means that, if in the original model, exactly one particle was moving as dictated, we now have $N$ particles moving, where $N$ can vary between 0 and $M$. In particle physics, this is known as “second quantization”. Since no two particles are allowed to sit at the same site, we have fermions, obeying Pauli’s exclusion principle.

Fig. 15.1

The “second quantized” version of the multiple-cogwheel model of Fig. 2.2. Black dots represent fermions

To describe these deterministic fermions in a quantum mechanical notation, we first introduce operator fields $\phi_{i}^{\mathrm{op}}$, acting as annihilation operators, and their Hermitian conjugates, $\phi _{i}^{\mathrm{op} \dagger}$, which act as creation operators. Denoting our states as $|n_{1},n_{2},\ldots,n_{M}\rangle$, where all $n$’s are 0 or 1, we postulate

$$\begin{aligned} \begin{aligned} \phi^{\mathrm{op}}_{i}|n_{1},\ldots, n_{i},\ldots, n_{M}\rangle&=n_{i} |n_{1}, \ldots,n_{i}-1,\ldots,n_{M} \rangle , \\ \phi_{i}^{\mathrm{op}\dagger} |n_{1},\ldots, n_{i}, \ldots, n_{M}\rangle &=(1-n_{i}) |n_{1}, \ldots,n_{i}+1,\ldots,n_{M}\rangle , \end{aligned} \end{aligned}$$

(15.3)

At one given site $i$, these fields obey (omitting the superscript ‘op’ for brevity):

$$\begin{aligned} ( \phi_{i})^{2}=0,\qquad\phi_{i}^{\dagger}\phi_{i}+\phi_{i} \phi_{i}^{\dagger}= \Bbb{I} , \end{aligned}$$

(15.4)

where $\Bbb {I}$ is the identity operator; at different sites, the fields commute: $\phi_{i}\phi_{j}=\phi_{j}\phi_{i}$; $\phi _{i}^{\dagger}\phi_{j}=\phi_{j}\phi^{\dagger}_{i}$, if $i\ne j$.

To turn these into completely anti-commuting (fermionic) fields, we apply the so-called Jordan-Wigner transformation [54]:

$$\begin{aligned} \psi_{i}=(-1)^{n_{1}+\cdots+n_{i-1}}\phi_{i}, \end{aligned}$$

(15.5)

where $n_{i}=\phi^{\dagger}_{i}\phi_{i}=\psi^{\dagger}_{i}\psi_{i}$ are the occupation numbers at the sites $i$, i.e., we insert a minus sign if an odd number of sites $j$ with $j< i$ are occupied. As a consequence of this well-known procedure, one now has

$$\begin{aligned} \psi_{i}\psi_{j}+\psi_{j} \psi_{i}=0,\qquad\psi _{i}^{\dagger}\psi_{j}+\psi_{j}\psi_{i}^{\dagger}=\delta _{ij},\quad\forall(i,j). \end{aligned}$$

(15.6)

The virtue of this transformation is that the anti-commutation relations (15.6) stay unchanged after any linear, unitary transformation of the $\psi_{i}$ as vectors in our $M$-dimensional vector space, provided that $\psi_{i}^{\dagger}$ transform as contra-vectors. Usually, the minus signs in Eq. (15.5) do no harm, but some care is asked for.

Now consider the permutation matrix $P$ and write the Hamiltonian in Eq. (15.2) as a lower case $h_{ij}$; it is an $M\times M$ component matrix. Writing $U_{ij}(t)= (e^{-iht})_{ij}$, we have, at integer time steps, $P_{\mathrm{op}}^{t}=U^{\mathrm{op}}(t)$. We now claim that the permutation that moves the fermions around, is generated by the Hamiltonian $H^{\mathrm{op}}_{F}$ defined as

$$ H^{\mathrm{op}}_{F}=\sum_{ij} \psi^{\dagger}_{j}h_{ji} \psi_{i}. $$

(15.7)

This we prove as follows:

Let

$$\begin{aligned} \begin{aligned} \psi_{i}(t)&=e^{iH^{\mathrm{op}}_{F}t} \psi_{i} e^{-iH^{\mathrm{op}}_{F} t}, \\ {\mathrm{d}\over \mathrm{d}t}e^{-iH^{\mathrm{op}}_{F}t}&=-iH^{\mathrm{op}}_{F} e^{-iH^{\mathrm{op}}_{F}t}=-i e^{-iH^{\mathrm{op}}_{F}t}H^{\mathrm{op}}_{F}; \end{aligned} \end{aligned}$$

(15.8)

Then

$$\begin{aligned} {\mathrm{d}\over \mathrm{d}t}\psi_{k}(t) =& i e^{iH^{\mathrm{op}}_{F}t}\sum _{ij}\bigl[\psi _{j}^{\dagger}h_{ji}\psi_{i},\psi_{k}\bigr]e^{-iH^{\mathrm{op}}_{F}t} \end{aligned}$$

(15.9)

$$\begin{aligned} =& ie^{iH^{\mathrm{op}}_{F}t}\sum_{ij}h_{ji} \bigl(-\bigl\{ \psi ^{\dagger}_{j},\psi_{k}\bigr\} \psi_{i}+\psi^{\dagger}_{j}\{\psi_{i}, \psi_{k}\} \bigr)e^{-iH^{\mathrm{op}}_{F}t} \end{aligned}$$

(15.10)

$$\begin{aligned} =&-ie^{iH^{\mathrm{op}}_{F}t}\sum_{i} h_{ki} \psi_{i}e^{-iH^{\mathrm{op}}_{F}t}=-i\sum_{i}h_{ki} \psi_{i}(t), \end{aligned}$$

(15.11)

where the anti-commutator is defined as $\{A,B\}\equiv AB+BA$ (note that the second term in Eq. (15.10) vanishes).

This is the same equation that describes the evolution of the states $|k\rangle$ of the original cogwheel model. So we see that, at integer time steps $t$, the fields $\psi_{i}(t)$ are permuted according to the permutation operator $P^{t}$. Note now, that the empty state $|0\rangle$ (which is not the vacuum state) does not evolve at all (and neither does the completely filled state). The $N$ particle state ($0\le N\le M$), obtained by applying $N$ copies of the field operators $\psi^{\dagger}_{i}$, therefore evolves with the same permutator. The Jordan Wigner minus sign, (15.5), gives the transformed state a minus sign if after $t$ permutations the order of the $N$ particles has become an odd permutation of their original relative positions. Although we have to be aware of the existence of this minus sign, it plays no significant role in most cases. Physically, this sign is not observable.

The importance of the procedure displayed here is that we can read off how anti-commuting fermionic field operators $\psi_{i}$, or $\psi _{i}(x)$, can emerge from deterministic systems. The minus signs in their (anti-)commutators is due to the Jordan-Wigner transformation (15.5), without which we would not have any commutator expressions at all, so that the derivation (15.11) would have failed.

The final step in this second quantization procedure is that we now use our freedom to perform orthogonal transformations among the fields $\psi$ and $\psi^{\dagger}$, such that we expand them in terms of the eigenstates $\psi(E_{i})$ of the one-particle Hamiltonian $h_{ij}$. Then the state $|\emptyset\rangle$ obeying

$$\begin{aligned} \psi(E_{i})|\emptyset\rangle=0 \quad \hbox{if } E_{i}>0; \qquad\psi^{\dagger}(E_{i})|\emptyset\rangle=0 \quad \hbox{if}\quad E_{i}< 0, \end{aligned}$$

(15.12)

has the lowest energy of all. Now, that is the vacuum state, as Dirac proposed. The negative energy states are interpreted as holes for antiparticles. The operators $\psi(E)$ annihilate particles if $E>0$ or create antiparticles if $E<0$. For $\psi^{\dagger}(E)$ it is the other way around. Particles and antiparticles now all carry positive energy. Is this then the resolution of the problem noted in Chap. 14? This depends on how we handle interactions, see Chap. 9.2 in Part I, and we discuss this important question further in Sect. 22.1 and in Chap. 23.

The conclusion of this section is that, if the Hamiltonian matrix $h_{ij}$ describes a single or composite cogwheel model, leading to classical permutations of the states $|i\rangle$, $i=1,\ldots,M$ , at integer times, then the model with Hamiltonian (15.7) is related to a system where occupied states evolve according to the same permutations, the difference being that now the total number of states is $2^{M}$ instead of $M$. And the energy is always bounded from below.

One might object that in most physical systems the Hamiltonian matrix $h_{ij}$ would not lead to classical permutations at integer time steps, but our model is just a first step. A next step could be that $h_{ij}$ is made to depend on the values of some local operator fields $\varphi(x)$. This is what we have in the physical world, and this may result if the permutation rules for the evolution of these fermionic particles are assumed to depend on other variables in the system.

In fact, there does exist a fairly realistic, simplified fermionic model where $h_{ij}$ does appear to generate pure permutations. This will be exhibited in the next section.

A procedure for bosons should go in analogous ways, if one deals with bosonic fields in quantum field theory. However, a relation with deterministic theories is not as straightforward as in the fermionic case, because arbitrarily large numbers of bosonic particles may occupy a single site. To mitigate this situation, the notion of harmonic rotators was introduced, which also for bosons only allows finite numbers of states. We can apply more conventional bosonic second quantization in some special two-dimensional theories, see Sect. 17.1.1.

How second quantization is applied in standard quantum field theories is described in Sect. 20.3.

2 ‘Neutrinos’ in Three Space Dimensions

In some cases, it is worth-while to start at the other end. Given a typical quantum system, can one devise a deterministic classical automaton that would generate all its quantum states? We now show a new case of interest.

One way to determine whether a quantum system may be mathematically equivalent to a deterministic model is to search for a complete set of beables. As defined in Sect. 2.1.1, beables are operators that may describe classical observables, and as such they must commute with one another, always, at all times. Thus, for conventional quantum particles such as the electron in Bohr’s hydrogen model, neither the operators $x$ nor $p$ are beables because $[x(t)$, $x(t')]\ne0$ and $[p(t),p(t')]\ne 0$ as soon as $t\ne t'$. Typical models where we do have such beables are ones where the Hamiltonian is linear in the momenta, such as in Sect. 12.3, Eq. (12.18), rather than quadratic in $p$. But are they the only ones?

Maybe the beables only form a space–time grid, whereas the data on points in between the points on the grid do not commute. This would actually serve our purpose well, since it could be that the physical data characterizing our universe really do form such a grid, while we have not yet been able to observe that, just because the grid is too fine for today’s tools, and interpolations to include points in between the grid points could merely have been consequences of our ignorance.

Beables form a complete set if, in the basis where they are all diagonal, the collection of eigenvalues completely identify the elements of this basis.

No such systems of beables do occur in Nature, as far as we know today; that is, if we take all known forces into account, all operators that we can construct today cease to commute at some point. We can, and should, try to search better, but, alternatively, we can produce simplified models describing only parts of what we see, which do allow transformations to a basis of beables. In Chap. 12.1, we already discussed the harmonic rotator as an important example, which allowed for some interesting mathematics in Chap. 13. Eventually, its large $N$ limit should reproduce the conventional harmonic oscillator. Here, we discuss another such model: massless ‘neutrinos’, in 3 space-like and one time-like dimension.

A single quantized, non interacting Dirac fermion obeys the Hamiltonian¹

$$\begin{aligned} H^{\mathrm{op}}=\alpha_{i}p_{i}+\beta m, \end{aligned}$$

(15.13)

where $\alpha_{i},\beta$ are Dirac $4\times4$ matrices obeying

$$\begin{aligned} \alpha_{i}\alpha_{j}+\alpha_{j} \alpha_{i}=2\delta _{ij};\qquad\beta^{2}=1;\qquad \alpha_{i}\beta+\beta\alpha _{i}=0. \end{aligned}$$

(15.14)

Only in the case $m=0$ can we construct a complete set of beables, in a straightforward manner.² In that case, we can omit the matrix $\beta$, and replace $\alpha_{i}$ by the three Pauli matrices, the $2\times2$ matrices $\sigma_{i}$. The particle can then be looked upon as a massless (Majorana or chiral) “neutrino”, having only two components in its spinor wave function. The neutrino is entirely ‘sterile’, as we ignore any of its interactions. This is why we call this the ‘neutrino’ model, with ‘neutrino’ between quotation marks.

There are actually two choices here: the relative signs of the Pauli matrices could be chosen such that the particles have positive (left handed) helicity and the antiparticles are right handed, or they could be the other way around. We take the choice that particles have the right handed helicities, if our coordinate frame $(x,y,z)$ is oriented as the fingers 1,2,3 of the right hand. The Pauli matrices $\sigma _{i}$ obey

$$\begin{aligned} \sigma_{1}\sigma_{2}=i\sigma_{3},\qquad \sigma_{2} \sigma_{3}=i\sigma_{1},\qquad \sigma_{3}\sigma_{1}=i\sigma_{2};\qquad \sigma_{1}^{2}=\sigma_{2}^{2}= \sigma_{3}^{2}=1. \end{aligned}$$

(15.15)

The beables are:

$$\begin{aligned} \bigl\{ \mathcal{O}^{\mathrm{op}}_{i}\bigr\} =&\{\hat{q},s, r\},\quad\hbox{where} \\ \hat{q}_{i} \equiv&\pm p_{i}/|p|,\quad s\equiv \hat{q} \cdot\vec{\sigma},\quad r\equiv{\textstyle{1\over 2}}(\hat{q}\cdot\vec{x}+\vec{x} \cdot\hat{q}). \end{aligned}$$

(15.16)

To be precise, $\hat{q}$ is a unit vector defining the direction of the momentum, modulo its sign. What this means is that we write the momentum $\vec{p}$ as

$$\begin{aligned} \vec{p}=p_{r}\hat{q}, \end{aligned}$$

(15.17)

where $p_{r}$ can be a positive or negative real number. This is important, because we need its canonical commutation relation with the variable $r$, being $[r,p_{r}]=i$, without further restrictions on $r$ or $p_{r}$. If $p_{r}$ would be limited to the positive numbers $|p|$, this would imply analyticity constraints for wave functions $\psi( r )$.

The caret $\ \hat{}\$ on the operator $\hat{q}$ is there to remind us that it is a vector with length one, $|\hat{q}|=1$. To define its sign, one could use a condition such as $\hat{q}_{z}>0$. Alternatively, we may decide to keep the symmetry $P_{\mathrm{int}}$ (for ‘internal parity’),

$$\begin{aligned} \hat{q}\leftrightarrow-\hat{q},\qquad p_{r}\leftrightarrow-p_{r} , \qquad r\leftrightarrow-r, \qquad s\leftrightarrow-s, \end{aligned}$$

(15.18)

after which we would keep only the wave functions that are even under this reflection. The variable $s$ can only take the values $s=\pm1,$ as one can check by taking the square of $\hat{q}\cdot \vec{\sigma}$. In the sequel, the symbol $\hat{p}$ will be reserved for $\hat{p}=+\vec{p}/|p|$, so that $\hat{q}=\pm\hat{p}$.

The last operator in Eq. (15.16), the operator $r$, was symmetrized so as to guarantee that it is Hermitian. It can be simplified by using the following observations. In the $\vec{p}$ basis, we have

$$\begin{aligned} & \begin{aligned} {}&\vec{x}=i{\partial\over \partial\vec{p}};\qquad {\partial\over \partial\vec{p}} p_{r}=\hat{q};\\ &[x_{i},p_{r}]=i\hat{q}_{i};\qquad[x_{i},\hat{q}_{j} ]= {i\over p_{r}}(\delta_{ij}-\hat{q}_{i}\hat{q}_{j}); \end{aligned} \end{aligned}$$

(15.19)

$$\begin{aligned} &x_{i}\hat{q}_{i}-\hat{q}_{i}x_{i}= {2i\over p_{r}}\quad \rightarrow\quad {\textstyle{1\over 2}}(\hat{q}\cdot\vec{x}+\vec{x}\cdot\hat{q})=\hat{q}\cdot\vec{x}+{i\over p_{r}}. \end{aligned}$$

(15.20)

This can best be checked first by checking the case $p_{r}=|p|>0, \hat{q}=\hat{p}$, and noting that all equations are preserved under the reflection symmetry (15.18).

It is easy to check that the operators (15.16) indeed form a completely commuting set. The only non-trivial commutator to be looked at carefully is $[r,\hat{q}]=[\hat{q}\cdot\vec{x}, \hat{q} ]$ . Consider again the $\vec{p}$ basis, where $\vec{x}=i\partial /\partial\vec{p}$ : the operator $\vec{p}\cdot\partial/\partial\vec{p}$ is the dilatation operator. But, since $\hat{q}$ is scale invariant, it commutes with the dilatation operator:

$$\begin{aligned} \biggl[\vec{p}\cdot{\partial\over \partial\vec{p}}, \hat{q}\biggr] =0 . \end{aligned}$$

(15.21)

Therefore,

$$\begin{aligned}{} [\hat{q}\cdot\vec{x},\hat{q}]=i\biggl[p_{r}^{-1}\vec{p}\cdot{\partial\over \partial\vec{p}}, \hat{q}\biggr]=0, \end{aligned}$$

(15.22)

since also $[p_{r},\hat{q}]=0$, but of course we could also have used Eq. (15.19), # 4.

The unit vector $\hat{q}$ lives on a sphere, characterized by two angles $\theta$ and $\varphi$. If we decide to define $\hat{q}$ such that $q_{z}>0$ then the domains in which these angles must lie are:

$$\begin{aligned} 0\le\theta\le\pi/2,\qquad0\le\varphi< 2\pi. \end{aligned}$$

(15.23)

The other variables take the values

$$\begin{aligned} s=\pm1, \qquad-\infty< r< \infty. \end{aligned}$$

(15.24)

An important question concerns the completeness of these beables and their relation to the more usual operates $\vec{x}, \vec{p}$ and $\vec{\sigma}$, which of course do not commute so that these themselves are no beables. This we discuss in the next subsection, which can be skipped at first reading. For now, we mention the more fundamental observation that these beables can describe ontological observables at all times, since the Hamiltonian (15.13), which here reduces to

$$\begin{aligned} H=\vec{\sigma}\cdot\vec{p}, \end{aligned}$$

(15.25)

generates the equations of motion

$$\begin{aligned} &{\mathrm{d}\over \mathrm{d}t}\vec{x} =-i[\vec{x},H]= \vec{\sigma},\qquad {\mathrm{d}\over \mathrm {d}t}\vec{p}=0,\qquad{\mathrm{d}\over \mathrm{d}t}\sigma_{i}= 2\varepsilon _{ijk}p_{j}\sigma_{k}; \end{aligned}$$

(15.26)

$$\begin{aligned} & \begin{aligned} {}&{\mathrm{d}\over \mathrm{d}t}\hat{p}=0;\qquad {\mathrm{d}\over \mathrm{d}t}(\hat{p}\cdot\vec{\sigma})=2\varepsilon_{ijk} (p_{i}/|p|) p_{j} \sigma_{k}=0, \\ {}&{\mathrm{d}\over \mathrm{d}t}(\hat{p}\cdot\vec{x})=\hat{p}\cdot\vec{\sigma}, \end{aligned} \end{aligned}$$

(15.27)

where $\hat{p}=\vec{p}/|p|=\pm\hat{q}$, and thus we have:

$$\begin{aligned} {\mathrm{d}\over \mathrm{d}t}\theta=0,\qquad {\mathrm{d}\over \mathrm{d}t}\varphi=0, \qquad{\mathrm{d}\over \mathrm{d}t}s=0,\qquad{\mathrm{d}\over \mathrm{d}t}r=s=\pm 1. \end{aligned}$$

(15.28)

The physical interpretation is simple: the variable $r$ is the position of a ‘particle’ projected along a predetermined direction $\hat{q}$, given by the two angles $\theta$ and $\varphi$, and the sign of $s$ determines whether it moves with the speed of light towards larger or towards smaller $r$ values, see Fig. 15.2.

Fig. 15.2

The beables for the “neutrino”, indicated as the scalar $r$ (distance of the sheet from the origin), the Boolean $s$, and the unit vectors $\hat {q}, \hat{\theta}$, and $\hat{\varphi}$. $O$ is the origin of 3-space

Note, that a rotation over $180^{\circ}$ along an axis orthogonal to $\hat{q}$ may turn $s$ into $-s$, which is characteristic for half-odd spin representations of the rotation group, so that we can still consider the neutrino as a spin ${1\over 2}$ particle.³

What we have here is a representation of the wave function for a single ‘neutrino’ in an unusual basis. As will be clear from the calculations presented in the subsection below, in this basis the ‘neutrino’ is entirely non localized in the two transverse directions, but its direction of motion is entirely fixed by the unit vector $\hat{q}$ and the Boolean variable $s$. In terms of this basis, the ‘neutrino’ is a deterministic object. Rather than saying that we have a particle here, we have a flat sheet, a plane. The unit vector $\hat{q}$ describes the orientation of the plane, and the variable $s$ tells us in which of the two possible directions the plane moves, always with the speed of light. Neutrinos are deterministic planes, or flat sheets. The basis in which the operators $\hat{q}, r$, and $s$ are diagonal will serve as an ontological basis.

Finally, we could use the Boolean variable $s$ to define the sign of $\hat{q}$, so that it becomes a more familiar unit vector, but this can better be done after we studied the operators that flip the sign of the variable $s$, because of a slight complication, which is discussed when we work out the algebra, in Sects. 15.2.1 and 15.2.2.

Clearly, operators that flip the sign of $s$ exist. For that, we take any vector $\hat{q}'$ that is orthogonal to $\hat{q}$. Then, the operator $\hat{q}'\cdot\vec{\sigma}$ obeys $(\hat{q}'\cdot\vec{\sigma}) s=-s (\hat{q}'\cdot\vec{\sigma})$ , as one can easily check. So, this operator flips the sign. The problem is that, at each point on the sphere of $\hat{q}$ values, one can take any unit length superposition of two such vectors $\hat{q}'$ orthogonal to $\hat{q}$. Which one should we take? Whatever our choice, it depends on the angles $\theta$ and $\varphi$. This implies that we necessarily introduce some rather unpleasant angular dependence. This is inevitable; it is caused by the fact that the original neutrino had spin ${1\over 2}$, and we cannot mimic this behaviour in terms of the $\hat{q}$ dependence because all wave functions have integral spin. One has to keep this in mind whenever the Pauli matrices are processed in our descriptions.

Thus, in order to complete our operator algebra in the basis determined by the eigenvalues $\hat{q},s,$ and $r$, we introduce two new operators whose squares ore one. Define two vectors orthogonal to $\hat{q}$, one in the $\theta$-direction and one in the $\varphi$ -direction:

$$ \begin{aligned} \hat{q}&=\begin{pmatrix}q_{1}\cr q_{2}\cr q_{3}\end{pmatrix},\qquad\hat{\theta}={1\over \sqrt {q_{1}^{2}+ q_{2}^{2}}} \begin{pmatrix} q_{3}q_{1}\cr q_{3} q_{2}\cr q_{3}^{2}-1 \end{pmatrix},\\ \hat{\varphi}&={1\over \sqrt{ q_{1}^{2}+ q_{2}^{2}}}\begin{pmatrix}-q_{2}\cr q_{1}\cr 0\end{pmatrix}. \end{aligned} $$

(15.29)

All three are normalized to one, as indicated by the caret. Their components obey

$$\begin{aligned} q_{i}=\varepsilon_{ijk}\theta_{j} \varphi_{k},\qquad \theta_{i}=\varepsilon_{ijk} \varphi_{j} q_{k},\qquad\varphi_{i}= \varepsilon_{ijk}q_{j}\theta_{k}. \end{aligned}$$

(15.30)

Then we define two sign-flip operators: write $s=s_{3}$, then

$$\begin{aligned} s_{1}=\hat{\theta}\cdot\vec{\sigma},\qquad s_{2}=\hat{\varphi}\cdot\vec{\sigma},\qquad s_{3}=s=\hat{q}\cdot\vec{\sigma}. \end{aligned}$$

(15.31)

They obey:

$$\begin{aligned} s_{i}^{2}={\Bbb {I}},\qquad s_{1} s_{2}=is_{3},\qquad s_{2} s_{3}=is_{1} ,\qquad s_{3}s_{1}=is_{2}. \end{aligned}$$

(15.32)

Considering now the beable operators $\hat{q}, r,$ and $s_{3}$, the translation operator $p_{r}$ for the variable $r$, the spin flip operators (“changeables”) $s_{1}$ and $s_{2}$, and the rotation operators for the unit vector $\hat{q}$, how do we transform back to the conventional neutrino operators $\vec{x}$, $\vec{p}$ and $\vec{\sigma}$?

Obtaining the momentum operators is straightforward:

$$\begin{aligned} p_{i}=p_{r}\hat{q}_{i}, \end{aligned}$$

(15.33)

and also the Pauli matrices $\sigma_{i}$ can be expressed in terms of the $s_{i}$, simply by inverting Eqs. (15.31). Using Eqs. (15.29) and the fact that $q_{1}^{2}+q_{2}^{2}+q_{3}^{2}=1$, one easily verifies that

$$\begin{aligned} \sigma_{i}=\theta_{i} s_{1}+ \varphi_{i} s_{2}+q_{i} s_{3}. \end{aligned}$$

(15.34)

However, to obtain the operators $x_{i}$ is quite a bit more tricky; they must commute with the $\sigma_{i}$. For this, we first need the rotation operators $\vec{L}^{\mathrm{ont}}$ . This is not the standard orbital or total angular momentum. Our transformation from standard variables to beable variables will not be quite rotationally invariant, just because we will be using either the operator $s_{1}$ or the operator $s_{2}$ to go from a left-moving neutrino to a right moving one. Note, that in the standard picture, chiral neutrinos have spin ${1\over 2}$. So flipping from one mode to the opposite one involves one unit $\hbar$ of angular momentum in the plane. The ontological basis does not refer to neutrino spin, and this is why our algebra gives some spurious angular momentum violation. As long as neutrinos do not interact, this effect stays practically unnoticeable, but care is needed when either interactions or mass are introduced.

The only rotation operators we can start off with in the beable frame, are the operators that rotate the planes with respect to the origin of our coordinates. These we call $\vec{L}^{\mathrm{ont}}$:

$$ L_{i}^{\mathrm{ont}}=-i\varepsilon_{ijk} q_{j}{\partial \over \partial q_{k}}. $$

(15.35)

By definition, they commute with the $s_{i}$, but care must be taken at the equator, where we have a boundary condition, which can be best understood by imposing the symmetry condition (15.18).

Note that the operators $L^{\mathrm{ont}}_{i}$ defined in Eq. (15.35) do not coincide with any of the conventional angular momentum operators because those do not commute with the $s_{i}$, as the latter depend on $\hat{\theta}$ and $\hat{\varphi}$. One finds the following relation between the angular momentum $\vec{L}$ of the neutrinos and ${\vec{L}}^{\mathrm{ont}}$:

$$\begin{aligned} L_{i}^{\mathrm{ont}}\equiv L_{i}+{\textstyle{1\over 2}} \biggl(\theta_{i} s_{1}+\varphi_{i} s_{2}-{q_{3}\theta_{i}\over \sqrt{1-q_{3}^{2}}} s_{3} \biggr); \end{aligned}$$

(15.36)

the derivation of this equation is postponed to Sect. 15.2.1.

Since $\vec{J}=\vec{L}+{1\over 2}\vec{\sigma}$, one can also write, using Eqs. (15.34) and (15.29),

$$\begin{aligned} L_{i}^{\mathrm{ont}}=J_{i}-{1\over 1-q_{3}^{2}}\begin{pmatrix}q_{1}\cr q_{2}\cr0\end{pmatrix}s_{3} . \end{aligned}$$

(15.37)

We then derive, in Sect. 15.2.1, Eq. (15.60), the following expression for the operators $x_{i}$ in the neutrino wave function, in terms of the beables $\hat{q},r$ and $s_{3}$, and the changeables⁴ $L_{k}^{\mathrm{ont}}, p_{r}, s_{1}$ and $s_{2}$:

$$\begin{aligned} x_{i} =& q_{i}\biggl(r-{i\over p_{r}}\biggr)+ \varepsilon_{ijk}q_{j} L^{\mathrm{ont}}_{k}/p_{r} \\ &{}+{1\over 2p_{r}} \biggl(-\varphi_{i}s_{1}+ \theta_{i}s_{2}+ {q_{3}\over \sqrt{1-q_{3}^{2}}} \varphi_{i}s_{3} \biggr) \end{aligned}$$

(15.38)

(note that $\theta_{i}$ and $\varphi_{i}$ are beables since they are functions of $\hat{q}$).

The complete transformation from the beable basis to one of the conventional bases for the neutrino can be derived from

$$\begin{aligned} \langle\vec{p},\alpha|\hat{q},p_{r},s\rangle =p_{r} \delta^{3}(\vec{p}-\hat{q}p_{r})\chi _{\alpha}^{s}( \hat{q}), \end{aligned}$$

(15.39)

where $\alpha$ is the spin index of the wave functions in the basis where $\sigma_{3}$ is diagonal, and $\chi^{s}_{\alpha}$ is a standard spinor solution for the equation $(\hat{q}\cdot\vec{\sigma}_{\alpha\beta}) \chi^{s}_{\beta}(\hat{q})=s\chi^{s}_{\alpha}(\hat{q})$.

In Sect. 15.2.2, we show how this equation can be used to derive the elements of the unitary transformation matrix mapping the beable basis to the standard coordinate frame of the neutrino wave function basis⁵ (See Eq. 15.83):

$$ \langle\vec{x},\alpha|\hat{q},r,s \rangle= {i\over 2\pi} \delta'(r-\hat{q}\cdot\vec{x})\chi _{\alpha}^{s}( \hat{q}), $$

(15.40)

where $\delta'(z)\equiv{\mathrm{d}\over \mathrm{d}z}\delta (z)$. This derivative originates from the factor $p_{r}$ in Eq. (15.39), which is necessary for a proper normalization of the states.

2.1 Algebra of the Beable ‘Neutrino’ Operators

This subsection is fairly technical and can be skipped at first reading. It derives the results mentioned in the previous section, by handling the algebra needed for the transformations from the $(\hat{q},s,r)$ basis to the $(\vec{x},\sigma_{3})$ or $(\vec{p}, \sigma_{3})$ basis and back. This algebra is fairly complex, again, because, in the beable representation, no direct reference is made to neutrino spin. Chiral neutrinos are normally equipped with spin $+{1\over 2}$ or $-{1\over 2}$ with spin axis in the direction of motion. The flat planes that are moving along here, are invariant under rotations about an orthogonal axis, and the associated spin-angular momentum does not leave a trace in the non-interacting, beable picture.

This forces us to introduce some axis inside each plane that defines the phases of the quantum states, and these (unobservable) phases explicitly break rotation invariance.

We consider the states specified by the variables $s$ and $r$, and the polar coordinates $\theta$ and $\varphi$ of the beable $\hat{q}$, in the domains given by Eqs. (15.23), (15.24). Thus, we have the states $|\theta,\varphi,s,r\rangle$. How can these be expressed in terms of the more familiar states $|\vec{x},\sigma _{z}\rangle$ and/or $|\vec{p},\sigma_{z}\rangle$, where $\sigma_{z}=\pm1$ describes the neutrino spin in the $z$-direction, and vice versa?

Our ontological states are specified in the ontological basis spanned by the operators $\hat{q}, s(=s_{3}),$ and $r$. We add the operators (changeables) $s_{1}$ and $s_{2}$ by specifying their algebra (15.32), and the operator

$$\begin{aligned} p_{r}=-i\partial/\partial r;\qquad[r,p_{r}]=i. \end{aligned}$$

(15.41)

The original momentum operators are then easily retrieved. As in Eq, (15.17), define

$$\begin{aligned} \vec{p}=p_{r}\hat{q}. \end{aligned}$$

(15.42)

The next operators that we can reproduce from the beable operators $\hat{q}, r$, and $s_{1,2,3}$ are the Pauli operators $\sigma _{1,2,3}$:

$$\begin{aligned} \sigma_{i}=\theta_{i} s_{1}+ \varphi_{i} s_{2}+q_{i} s_{3}. \end{aligned}$$

(15.43)

Note, that these now depend non-trivially on the angular parameters $\theta$ and $\varphi$, since the vectors $\hat{\theta}$ and $\hat{\varphi}$, defined in Eq. (15.29), depend non-trivially on $\hat{q}$, which is the radial vector specified by the angles $\theta$ and $\varphi$. One easily checks that the simple multiplication rules from Eqs. (15.32) and the right-handed orthonormality (15.30) assure that these Pauli matrices obey the correct multiplication rules also. Given the trivial commutation rules for the beables, $[q_{i},\theta_{j}]= [q_{i},\varphi_{j}]=0$, and $[p_{r},q_{i}]=0$, one finds that $[p_{i}, \sigma _{j}]=0$, so here, we have no new complications.

Things are far more complicated and delicate for the $\vec{x}$ operators. To reconstruct an operator $\vec{x}=i\partial/\partial\vec{p}$, obeying $[x_{i}, p_{j}]=i\delta_{ij}$ and $[x_{i},\sigma_{j}]=0$, we first introduce the orbital angular momentum operator

$$\begin{aligned} L_{i}=\varepsilon_{ijk}x_{i}p_{k}=-i \varepsilon_{ijk} q_{j}{\partial\over \partial q_{k}} \end{aligned}$$

(15.44)

(where $\sigma_{i}$ are kept fixed), obeying the usual commutation rules

$$\begin{aligned}{} [L_{i},L_{j}]=i\varepsilon_{ijk}L_{k} , \qquad[L_{i}, q_{j}]=i\varepsilon_{ijk} q_{k},\qquad [L_{i},p_{j}]=i \varepsilon_{ijk}p_{k}, \hbox{ etc.}, \end{aligned}$$

(15.45)

while $[L_{i},\sigma_{j}]=0$. Note, that these operators are not the same as the angular momenta in the ontological frame, the $L_{i}^{\mathrm{ont}}$ of Eq. (15.35), since those are demanded to commute with $s_{j}$, while the orbital angular momenta $L_{i}$ commute with $\sigma _{j}$. In terms of the orbital angular momenta (15.44), we can now recover the original space operators $x_{i}, i=1,2,3$, of the neutrinos:

$$\begin{aligned} x_{i}=q_{i}\biggl(r-{i\over p_{r}}\biggr)+ \varepsilon_{ijk}q_{j} L_{k}/p_{r} . \end{aligned}$$

(15.46)

The operator $1/p_{r}$, the inverse of the operator $p_{r}=-i\partial /\partial r$ , should be $-i$ times the integration operator. This leaves the question of the integration constant. It is straightforward to define that in momentum space, but eventually, $r$ is our beable operator. For wave functions in $r$ space, $\psi(r,\ldots)=\langle r,\ldots|\psi\rangle$, where the ellipses stand for other beables (of course commuting with $r$), the most careful definition is:

$$\begin{aligned} {1\over p_{r}}\psi( r )\equiv \int_{-\infty}^{\infty}{\textstyle{1\over 2}}i \operatorname{sgn} \bigl(r-r'\bigr)\psi\bigl(r'\bigr) \mathrm{d}r', \end{aligned}$$

(15.47)

which can easily be seen to return $\psi( r )$ when $p_{r}$ acts on it. “sgn(x)” stands for the sign of $x$. We do note that the integral must converge at $r\rightarrow\pm \infty$. This is a restriction on the class of allowed wave functions: in momentum space, $\psi$ must vanish at $p_{r}\rightarrow0$. Restrictions of this sort will be encountered more frequently in this book.

The anti Hermitian term $-i/p_{r}$ in Eq. (15.46) arises automatically in a careful calculation, and it just compensates the non hermiticity of the last term, where $q_{j}$ and $L_{k}$ should be symmetrized to get a Hermitian expression. $L_{k}$ commutes with $p_{r}$. The $x_{i}$ defined here ends up being Hermitian.

This perhaps did not look too hard, but we are not ready yet. The operators $L_{i}$ commute with $\sigma_{j}$, but not with the beable variables $s_{i}$. Therefore, an observer of the beable states, in the beable basis, will find it difficult to identify our operators $L_{i}$. It will be easy for such an observer to identify operators $L_{i}^{\mathrm{ont}}$, which generate rotations of the $q_{i}$ variables while commuting with $s_{i}$. He might also want to rotate the Pauli-like variables $s_{i}$, employing a rotation operator such as ${1\over 2}s_{i}$, but that will not do, first, because they no longer obviously relate to spin, but foremost, because the $s_{i}$ in the conventional basis have a much less trivial dependence on the angles $\theta$ and $\varphi$, see Eqs. (15.29) and (15.31).

Actually, the reconstruction of the $\vec{x}$ operators from the beables will show a non-trivial dependence on the variables $s_{i}$ and the angles $\theta$ and $\varphi$. This is because $\vec{x}$ and the $s_{i}$ do not commute. From the definitions (15.29) and the expressions (15.29) for the vectors $\hat{\theta}$ and $\hat{\varphi}$, one derives, from judicious calculations:

$$\begin{aligned} {} [x_{i},\theta_{j}] =& {i\over p_{r}} \biggl( {q_{3}\over \sqrt{1-q_{3}^{2}}} \varphi_{i}\varphi_{j}- \theta_{i}q_{j} \biggr), \end{aligned}$$

(15.48)

$$\begin{aligned} {} [x_{i},\varphi_{j}] =&{-i\varphi_{i}\over p_{r}} \biggl(q_{j}+{\theta_{j} q_{3}\over \sqrt {1-q_{3}^{2}}} \biggr), \end{aligned}$$

(15.49)

$$\begin{aligned} {}[x_{i},q_{j}] =&{i\over p_{r}}( \delta_{ij}-q_{i}q_{j}) . \end{aligned}$$

(15.50)

The expression $q_{3}/\sqrt{1-q_{3}^{2}}=\cot(\theta)$ emerging here is singular at the poles, clearly due to the vortices there in the definitions of the angular directions $\theta$ and $\varphi$.

From these expressions, we now deduce the commutators of $x_{i}$ and $s_{1,2,3}$:

$$\begin{aligned} {}[x_{i},s_{1}] =&{i\over p_{r}} \biggl( { \varphi_{i}q_{3}\over \sqrt{1-q_{3}^{2}}} s_{2}-\theta_{i}s_{3} \biggr), \end{aligned}$$

(15.51)

$$\begin{aligned} {}[x_{i},s_{2}] =& {-i\over p_{r}} \varphi_{i} \biggl(s_{3}+{ q_{3}\over \sqrt{1- q_{3}^{2}}}s_{1} \biggr) , \end{aligned}$$

(15.52)

$$\begin{aligned} {}[x_{i},s_{3}] =&{i\over p_{r}}( \sigma_{i}- q_{i}s_{3})={i\over p_{r}}( \theta _{i} s_{1}+ \varphi_{i} s_{2}). \end{aligned}$$

(15.53)

In the last expression Eq. (15.43) for $\vec{\sigma}$ was used. Now, observe that these equations can be written more compactly:

$$\begin{aligned}{} [x_{i},s_{j}]={\textstyle{1\over 2}} \biggl[ {1\over p_{r}} \biggl(- \varphi _{i}s_{1}+ \theta_{i} s_{2}+{ q_{3} \varphi_{i}\over \sqrt{1- q_{3}^{2}}}s_{3} \biggr), s_{j} \biggr] . \end{aligned}$$

(15.54)

To proceed correctly, we now need also to know how the angular momentum operators $L_{i}$ commute with $s_{1,2,3}$. Write $L_{i}=\varepsilon_{ijk}x_{j} \hat{q}_{k}p_{r}$, where only the functions $x_{i}$ do not commute with the $s_{j}$. It is then easy to use Eqs. (15.51)–(15.54) to find the desired commutators:

$$\begin{aligned}{} [L_{i},s_{j}]={\textstyle{1\over 2}} \biggl[- \theta_{i}s_{1}-\varphi _{i}s_{2}+ {q_{3} \theta_{i}\over \sqrt {1-q_{3}^{2}}}s_{3}, s_{j} \biggr], \end{aligned}$$

(15.55)

where we used the simple orthonormality relations (15.30) for the unit vectors $\hat{\theta}, \hat{\varphi}$, and $\hat {q}$. Now, this means that we can find new operators $L_{i}^{\mathrm{ont}}$ that commute with all the $s_{j}$:

$$\begin{aligned} L_{i}^{\mathrm{ont}}\equiv L_{i}+{\textstyle{1\over 2}} \biggl(\theta_{i} s_{1}+\varphi_{i} s_{2}-{q_{3}\theta_{i}\over \sqrt{1-q_{3}^{2}}} s_{3} \biggr),\qquad \bigl[L_{i}^{\mathrm{ont}},s_{j}\bigr]=0, \end{aligned}$$

(15.56)

as was anticipated in Eq. (15.36). It is then of interest to check the commutator of two of the new “angular momentum” operators. One thing we know: according to the Jacobi identity, the commutator of two operators $L_{i}^{\mathrm{ont}}$ must also commute with all $s_{j}$. Now, expression (15.56) seems to be the only one that is of the form expected, and commutes with all $s$ operators. It can therefore be anticipated that the commutator of two $L^{\mathrm{ont}}$ operators should again yield an $L^{\mathrm{ont}}$ operator, because other expressions could not possibly commute with all $s$. The explicit calculation of the commutator is a bit awkward. For instance, one must not forget that $L_{i}$ also commutes non-trivially with $\cot(\theta)$:

$$\begin{aligned} \biggl[L_{i},{q_{3}\over \sqrt{1-q_{3}^{2}}}\biggr]={i\varphi_{i}\over 1-q_{3}^{2}} . \end{aligned}$$

(15.57)

But then, indeed, one finds

$$\begin{aligned} \bigl[L^{\mathrm{ont}}_{i},L^{\mathrm{ont}}_{j} \bigr]=i\varepsilon_{ijk}L^{\mathrm{ont}}_{k}. \end{aligned}$$

(15.58)

The commutation rules with $q_{i}$ and with $r$ and $p_{r}$ were not affected by the additional terms:

$$\begin{aligned} \bigl[L^{\mathrm{ont}}_{i},q_{j}\bigr]=i \varepsilon_{ijk}q_{k},\qquad\bigl[L_{i}^{\mathrm{ont}}, r\bigr]=\bigl[L_{i}^{\mathrm{ont}} ,p_{r}\bigr]=0. \end{aligned}$$

(15.59)

This confirms that we now indeed have the generator for rotations of the beables $q_{i}$, while it does not affect the other beables $s_{i}, r$ and $p_{r}$.

Thus, to find the correct expression for the operators $\vec{x}$ in terms of the beable variables, we replace $L_{i}$ in Eq. (15.46) by $L_{i}^{\mathrm{ont}}$, leading to

$$\begin{aligned} x_{i} =& q_{i}\biggl(r-{i\over p_{r}}\biggr)+ \varepsilon_{ijk}q_{j} L^{\mathrm{ont}}_{k}/p_{r} \\ &{}+{1\over 2p_{r}} \biggl(-\varphi_{i}s_{1}+ \theta_{i}s_{2}+{q_{3}\over \sqrt {1-q_{3}^{2}}} \varphi_{i} s_{3} \biggr). \end{aligned}$$

(15.60)

This remarkable expression shows that, in terms of the beable variables, the $\vec{x}$ coordinates undergo finite, angle-dependent displacements proportional to our sign flip operators $s_{1}, s_{2}$, and $s_{3}$. These displacements are in the plane. However, the operator $1/p_{r}$ does something else. From Eq. (15.47) we infer that, in the $r$ variable,

$$\begin{aligned} \langle r_{1}|{1\over p_{r}}|r_{2}\rangle= {\textstyle{1\over 2}}i\operatorname{sgn}(r_{1}-r_{2}). \end{aligned}$$

(15.61)

Returning now to a remark made earlier in this chapter, one might decide to use the sign operator $s_{3}$ (or some combination of the three $s$ variables) to distinguish opposite signs of the $\hat{q}$ operators. The angles $\theta$ and $\varphi$ then occupy the domains that are more usual for an $S_{2}$ sphere: $0<\theta<\pi$, and $0<\varphi\le 2\pi$. In that case, the operators $s_{1,2,3}$ refer to the signs of $\hat{q}_{3}, r$ and $p_{r}$. Not much would be gained by such a notation.

The Hamiltonian in the conventional basis is

$$\begin{aligned} H=\vec{\sigma}\cdot\vec{p}. \end{aligned}$$

(15.62)

It is linear in the momenta $p_{i}$, but it also depends on the non commuting Pauli matrices $\sigma_{i}$. This is why the conventional basis cannot be used directly to see that this is a deterministic model. Now, in our ontological basis, this becomes

$$\begin{aligned} H=sp_{r}. \end{aligned}$$

(15.63)

Thus, it multiplies one momentum variable with the commuting operator $s$. The Hamilton equation reads

$$\begin{aligned} {\mathrm{d}r\over \mathrm{d}t} =s, \end{aligned}$$

(15.64)

while all other beables stay constant. This is how our ‘neutrino’ model became deterministic. In the basis of states $|\hat{q},r,s \rangle$ our model clearly describes planar sheets at distance $r$ from the origin, oriented in the direction of the unit vector $\hat{q}$, moving with the velocity of light in a transverse direction, given by the sign of $s$.

Once we defined, in the basis of the two eigenvalues of $s$, the two other operators $s_{1}$ and $s_{2}$, with (see Eqs. (15.32))

$$\begin{aligned} s_{1}=\begin{pmatrix}0&1\cr1&0\end{pmatrix},\qquad s_{2}=\begin{pmatrix}0&-i\cr i&0\end{pmatrix},\qquad s_{3}=s=\begin{pmatrix}1&0\cr0&-1\end{pmatrix}, \end{aligned}$$

(15.65)

in the basis of states $|r\rangle$ the operator $p_{r}=-i\partial/\partial r$, and, in the basis $|\hat{q}\rangle$ the operators $L_{i}^{\mathrm{ont}}$ by

$$\begin{aligned} \begin{aligned} \bigl[L^{\mathrm{ont}}_{i},L^{\mathrm{ont}}_{j}\bigr]&=i\varepsilon_{ijk}L^{\mathrm{ont}}_{k} ,\qquad\bigl[L_{i}^{\mathrm{ont}} ,q_{j}\bigr]=i \varepsilon_{ijk}q_{k},\\ \bigl[L^{\mathrm{ont}}_{i}, r\bigr]&=0, \qquad\bigl[L^{\mathrm{ont}}_{i}, s_{j} \bigr]=0, \end{aligned} \end{aligned}$$

(15.66)

we can write, in the ‘ontological’ basis, the conventional ‘neutrino’ operators $\vec{\sigma}$ (Eq. (15.43)), $\vec{x}$ (Eq. (15.60)), and $\vec{p}$ (Eq. (15.42)). By construction, these will obey the correct commutation relations.

2.2 Orthonormality and Transformations of the ‘Neutrino’ Beable States

The quantities that we now wish to determine are the inner products

$$\begin{aligned} \langle\vec{x},\sigma_{z}|\theta,\varphi ,s,r\rangle,\qquad\langle \vec{p},\sigma_{z}|\theta,\varphi ,s,r\rangle. \end{aligned}$$

(15.67)

The states $|\theta,\varphi,s,r\rangle$ will henceforth be written as $| \hat{q},s,r\rangle$. The use of momentum variables $\hat{q}\equiv\pm \vec{p}/|p|, q_{z}>0,$ together with a real parameter $r$ inside a Dirac bracket will always denote a beable state in this subsection.

Special attention is required for the proper normalization of the various sets of eigenstates. We assume the following normalizations:

$$\begin{aligned} \bigl\langle \vec{x},\alpha|\vec{x}',\beta\bigr\rangle =& \delta^{3}\bigl(\vec{x}-\vec{x}'\bigr) \delta_{\alpha \beta}, \end{aligned}$$

(15.68)

$$\begin{aligned} \bigl\langle \vec{p},\alpha|\vec{p}',\beta\bigr\rangle =&\delta ^{3}\bigl(\vec{p}-\vec{p}'\bigr)\delta_{\alpha\beta }, \end{aligned}$$

(15.69)

$$\begin{aligned} \langle\vec{x},\alpha|\vec{p},\beta\rangle =&(2\pi)^{-3/2} e^{i\vec{p}\cdot\vec{x}}\delta_{\alpha\beta}; \end{aligned}$$

(15.70)

$$\begin{aligned} \bigl\langle \hat{q},r,s|\hat{q}',r', s'\bigr\rangle =&\delta ^{2}\bigl(\hat{q},\hat{q} '\bigr)\delta\bigl(r-r'\bigr)\delta_{ss'} , \end{aligned}$$

(15.71)

$$\begin{aligned} \delta^{2}\bigl(\hat{q}, \hat{q}'\bigr) \equiv& {\delta(\theta-\theta')\delta(\varphi-\varphi') \over \sin\theta} , \end{aligned}$$

(15.72)

and $\alpha$ and $\beta$ are eigenvalues of the Pauli matrix $\sigma_{3}$; furthermore,

$$\begin{aligned} \begin{aligned} \int\delta^{3}\vec{x}\sum_{\alpha}| \vec{x},\alpha \rangle \langle\vec{x},\alpha| &=\Bbb {I}= \int\mathrm{d}^{2}\hat{q} \int_{-\infty}^{\infty}\mathrm{d}r \sum _{s=\pm}|\hat{q},r,s\rangle \langle\hat{q},r,s|; \\ \int\mathrm{d}^{2}\hat{q} &\equiv \int_{0}^{\pi/2}\sin\theta\, \mathrm{d}\theta \int_{0}^{2\pi }\mathrm{d}\varphi. \end{aligned} \end{aligned}$$

(15.73)

The various matrix elements are now straightforward to compute. First we define the spinors $\chi_{\alpha}^{\pm}(\hat{q})$ by solving

$$\begin{aligned} (\hat{q}\cdot\vec{\sigma}_{\alpha\beta})\chi ^{s}_{\beta}=s \chi^{s}_{\alpha};\qquad\begin{pmatrix} q_{3}-s&q_{1}-iq_{2}\cr q_{1}+iq_{2}&-q_{3}-s\end{pmatrix} \begin{pmatrix}\chi^{s}_{1}\cr\chi^{s}_{2}\end{pmatrix}=0, \end{aligned}$$

(15.74)

which gives, after normalizing the spinors,

$$\begin{aligned} \begin{aligned} \chi^{+}_{1}(\hat{q})&=\sqrt {{\textstyle{1\over 2}}(1+q_{3})};\qquad \chi^{-}_{1}(\hat{q})= -\sqrt{{\textstyle{1\over 2}}(1-q_{3})}; \\ \chi ^{+}_{2}(\hat{q})&={q_{1}+iq_{2}\over \sqrt{2(1+q_{3})}};\qquad \chi^{-}_{2}(\hat{q})={q_{1}+iq_{2}\over \sqrt {2(1-q_{3})}} , \end{aligned} \end{aligned}$$

(15.75)

where not only the equation $s_{3}\chi^{\pm}_{\alpha}=\pm\chi^{\pm}_{\alpha}$ was imposed, but also

$$\begin{aligned} s_{1\beta}^{\alpha}\chi^{\pm}_{\alpha}=\chi ^{\mp}_{\beta},\qquad s_{2\beta}^{ \alpha} \chi^{\pm}_{\alpha}=\pm i\chi^{\mp}_{\beta}, \end{aligned}$$

(15.76)

which implies a constraint on the relative phases of $\chi^{+}_{\alpha}$ and $\chi^{-}_{\alpha}$. The sign in the second of these equations is understood if we realize that the index $s$ here, and later in Eq. (15.80), is an upper index.

Next, we need to know how the various Dirac deltas are normalized:

$$\begin{aligned} \mathrm{d}^{3}\vec{p}=p_{r}^{2} \mathrm{d}^{2}\hat{q}\mathrm {d}p_{r};\qquad \delta^{3}\bigl(\hat{q}p_{r}-\hat{q} ' p_{r}'\bigr)={1\over p_{r}^{2}} \delta^{2}\bigl(\hat{q},\hat{q}'\bigr)\delta \bigl(p_{r}-p_{r}'\bigr), \end{aligned}$$

(15.77)

We demand completeness to mean

$$\begin{aligned} &\int\mathrm{d}^{2}\hat{q} \int_{-\infty }^{\infty}\mathrm{d}p_{r}\sum _{s\,=\,\pm }\langle\vec{p},\alpha|\hat{q}, p_{r},s\rangle \langle\hat{q},p_{r},s| \vec{p}',\alpha'\rangle\, =\,\delta_{\alpha\alpha'} \delta^{3}\bigl(\vec{p}-\vec{p}'\bigr); \end{aligned}$$

(15.78)

$$\begin{aligned} &\int\mathrm{d}^{3}\vec{p}\sum_{\alpha\,=\,1}^{2} \langle \hat{q}, p_{r}, s | \vec{p}, \alpha \rangle \langle \vec{p}, \alpha | \hat{q} ', p_{r}', s' \rangle\,=\, \delta^{2}\bigl(\hat{q}, \hat{q} '\bigr)\delta\bigl(p_{r}-p_{r} '\bigr) \delta_{s s'}, \end{aligned}$$

(15.79)

which can easily be seen to imply⁶

$$\begin{aligned} \langle\vec{p},\alpha | \hat{q}, p_{r}, s\rangle =p_{r} \delta^{3}(\vec{p}-\hat{q} p_{r})\chi _{\alpha}^{s}( \hat{q}), \end{aligned}$$

(15.80)

since the norm $p_{r}^{2}$ has to be divided over the two matrix terms in Eqs (15.78) and (15.79).

This brings us to derive, using $\langle r | p_{r} \rangle =(2\pi )^{-1/2} e^{ i p_{r} r}$,

$$ \langle \vec{p}, \alpha | \hat{q}, r, s \rangle={1\over \sqrt{2\pi}} {1\over p_{r}} \delta^{2} \biggl({\pm\vec{p}\over |p|} , \hat{q} \biggr)e^{-i(\hat{q}\cdot\vec{p} ) r}\chi_{\alpha}^{s}(\hat{q}), $$

(15.81)

where the sign is the sign of $p_{3}$.

The Dirac delta in here can also be denoted as

$$\begin{aligned} \delta^{2} \biggl({\pm\vec{p}\over |p|} ,\hat{q} \biggr)=(\hat{q} \cdot\vec{p} )^{2} \delta ^{2}(\vec{p}\wedge\hat{q}), \end{aligned}$$

(15.82)

where the first term is a normalization to ensure the expression to become scale invariant, and the second just forces $\vec{p}$ and $\hat{q}$ to be parallel or antiparallel. In the case $\hat {q}=(0,0,1)$, this simply describes $p_{3}^{2} \delta(p_{1}) \delta(p_{2})$.

Finally then, we can derive the matrix elements $\langle \vec{x}, \alpha | \hat{q}, r, s \rangle$. Just temporarily, we put $\hat{q}$ in the 3-direction: $\hat{q}=(0,0,1)$,

$$\begin{aligned} \langle \vec{x}, \alpha | \hat{q}, r, s \rangle =&{1\over \sqrt{2\pi}}(2 \pi )^{-3/2} \int\mathrm{d}^{3}\vec{p} {(\hat{q}\cdot\vec{p} )^{2}\over p_{r}} \delta^{2}(\vec{p}\wedge\hat{q}) e^{-i(\hat{q}\cdot\vec{p} ) r+i \vec{p}\cdot\vec{x}}\chi_{\alpha}^{s}( \hat{q}) \\ =&{1\over (2\pi)^{2}} \int\mathrm{d}^{3}\vec{p} p_{3} \delta(p_{1}) \delta(p_{2}) e^{i p_{3}(x_{3}-r)} \chi_{\alpha}^{s}(\hat{q}) \\ =&{1\over 2\pi}{i\mathrm{d}\over \mathrm{d}r}\delta(r-\hat {q}\cdot\vec{x} ) \chi_{\alpha}^{s}(\hat{q})={i\over 2\pi}\delta '(r-\hat{q}\cdot\vec{x} ) \chi_{\alpha}^{s}( \hat{q}). \end{aligned}$$

(15.83)

With these equations, our transformation laws are now complete. We have all matrix elements to show how to go from one basis to another. Note, that the states with vanishing $p_{r}$, the momentum of the sheets, generate singularities. Thus, we see that the states $| \psi \rangle$ with $\langle p_{r}=0 | \psi \rangle\ne0$, or equivalently, $\langle \vec{p}=0 | \psi \rangle\ne0$, must be excluded. We call such states ‘edge states’, since they have wave functions that are constant in space (in $r$ and also in $\vec{x}$), which means that they stretch to the ‘edge’ of the universe. There is an issue here concerning the boundary conditions at infinity, which we will need to avoid. We see that the operator $1/p_{r}$, Eq. (15.47), is ill defined for these states.

2.3 Second Quantization of the ‘Neutrinos’

Being a relativistic Dirac fermion, the object described in this chapter so-far suffers from the problem that its Hamiltonian, (15.25) and (15.63), is not bounded from below. There are positive and negative energy states. The cure will be the same as the one used by Dirac, and we will use it again later: second quantization. We follow the procedure described in Sect. 15.1: for every given value of the unit vector $\hat{q}$, we consider an unlimited number of ‘neutrinos’, which can be in positive or negative energy states. To be more specific, one might, temporarily, put the variables $r$ on a discrete lattice:

$$\begin{aligned} r=r_{n}=n \delta r, \end{aligned}$$

(15.84)

but often we ignore this, or in other words, we let $\delta r$ tend to zero.

We now describe these particles, having spin ${1\over 2}$, by anti-commuting fermionic operators. We have operator fields $\psi_{\alpha}(\vec{x} )$ and $\psi_{\alpha}^{\dagger}(\vec{x} )$ obeying anticommutation rules,

$$\begin{aligned} \bigl\{ \psi_{\alpha}(\vec{x} ), \psi_{\beta}^{\dagger}\bigl( \vec{x} ' \bigr)\bigr\} =\delta^{3}\bigl(\vec{x}-\vec{x} '\bigr)\delta_{\alpha\beta}. \end{aligned}$$

(15.85)

Using the transformation rules of Sect. 15.2.2, we can transform these fields into fields $\psi(\hat{q},r,s)$ and $\psi^{\dagger}(\hat{q},r,s)$ obeying

$$\begin{aligned} \bigl\{ \psi(\hat{q},r,s), \psi^{\dagger}\bigl(\hat{q} ',r',s' \bigr)\bigr\} = \delta^{2}\bigl(\hat{q},\hat{q} ' \bigr) \delta \bigl(r-r'\bigr)\delta_{s s'}\rightarrow\delta^{2}\bigl(\hat{q},\hat{q} '\bigr) \delta_{n n'} \delta_{s s'}. \end{aligned}$$

(15.86)

At any given value of $\hat{q}$ (which could also be chosen discrete if so desired), we have a straight line of $r$ values, limited to the lattice points (15.84). On a stretch of $N$ sites of this lattice, we can imagine any number of fermions, ranging from 0 to $N$. Each of these fermions obeys the same evolution law (15.64), and therefore also the entire system is deterministic.

There is no need to worry about the introduction of anti-commuting fermionic operators (15.85), (15.86). The minus signs are handled through the Jordan-Wigner transformation, implying that the creation or annihilation of a fermion that has an odd number of fermions at one side of it, will be accompanied by an artificial minus sign. This minus sign has no physical origin but is exclusively introduced in order to facilitate the mathematics with anti-commuting fields. Because, at any given value of $\hat{q}$, the fermions propagate on a single line, and they all move with the same speed in one direction, the Jordan-Wigner transformation is without complications. Of course, we still have not introduced interactions among the fermions, which indeed would not be easy as yet.

This ‘second quantized’ version of the neutrino model has one big advantage: we can describe it using a Hamiltonian that is bounded from below. The argument is identical to Dirac’s own ingenious procedure. The Hamiltonian of the second quantized system is (compare the first quantized Hamiltonian (15.25)):

$$\begin{aligned} H= \int\mathrm{d}^{3}\vec{x}\sum_{\alpha}\psi^{* \alpha}(\vec{x})h_{\alpha}^{\beta}\psi_{\beta}(\vec{x}),\quad h_{\alpha}^{\beta}=-i\vec{\sigma}_{\alpha}^{\beta } \cdot{\partial\over \partial\vec{x}}. \end{aligned}$$

(15.87)

Performing the transformation to the beable basis described in Sect. 15.2.2, we find

$$ H= \int\mathrm{d}^{2}\hat{q} \int\mathrm{d}r\sum_{s} \psi^{*}( \hat{q},r,s) (-i s) {\partial\over \partial r}\psi(\hat{q}, r,s). $$

(15.88)

Let us denote the field in the standard notation as $\psi^{ \mathrm {stand} }_{\alpha}(\vec{x})$ or $\psi^{ \mathrm{stand} }_{\alpha}(\vec{p})$, and the field in the ‘beable’ basis as $\psi^{\mathrm{ont}}_{s}(\hat{q}, r)$. Its Fourier transform is not a beable field, but to distinguish it from the standard notation we will sometimes indicate it nevertheless as $\psi^{\mathrm{ont}}_{s}(\hat{q}, p_{r})$.

In momentum space, we have (see Eq. 15.39):

$$\begin{aligned} \psi^{ \mathrm{stand} }_{\alpha}(\vec{p} ) =&{1\over p_{r}}\sum _{s}\chi^{s}_{\alpha}(\hat{q}) \psi ^{\mathrm{ont}}_{s}(\hat{q}, p_{r}); \end{aligned}$$

(15.89)

$$\begin{aligned} \qquad\psi^{\mathrm{ont}}_{s}(\hat{q}, p_{r}) =&p_{r} \sum_{\alpha}\chi ^{s}_{\alpha}(\hat{q})^{*} \psi ^{ \mathrm{stand} }_{\alpha}(\vec{p}),\quad\vec{p}\equiv\hat{q} p_{r}, \end{aligned}$$

(15.90)

where ‘stand’ stands for the standard representation, and ‘ont’ for the ontological one, although we did the Fourier transform replacing the variable $r$ by its momentum variable $p_{r}$. The normalization is such that

$$\begin{aligned} \sum_{\alpha}\int\mathrm{d}^{3}\vec{p} \bigl|\psi^{ \mathrm{stand} }_{\alpha}( \vec{p} )\bigr|^{2}=\sum_{s} \int_{\hat {q}_{3}>0}\mathrm{d}^{2}\hat{q} \int_{-\pi/\delta r}^{\pi/\delta r}\mathrm{d}p_{r}\bigl| \psi^{\mathrm{ont}}_{s}(\hat{q},p_{r})\bigr|^{2}, \end{aligned}$$

(15.91)

see Eqs. (15.77)–(15.80).

In our case, $\psi$ has only two spin modes, it is a Weyl field, but in all other respects it can be handled just as a massless Dirac field. Following Dirac, in momentum space, each momentum $\vec{p}$ has two energy eigenmodes (eigenvectors of the operator $h^{\beta}_{\alpha}$ in the Hamiltonian (15.87)), which we write, properly normalized, as

$$\begin{aligned} u^{{ \mathrm{stand} }\pm}_{\alpha}(\vec{p} )={1\over \sqrt{2|p|(|p|\pm p_{3})}}\begin{pmatrix} \pm|p|+p_{3}\cr p_{1}+ip_{2}\end{pmatrix}; \qquad E=\pm|p|. \end{aligned}$$

(15.92)

Here, the spinor lists the values for the index $\alpha=1,2$. In the basis of the beables:

$$\begin{aligned} u^{\mathrm{ont} \pm}_{s}(\hat{q},p_{r}) =&\begin{pmatrix} 1\cr0\end{pmatrix}\quad \hbox{if } \pm p_{r}>0, \quad \begin{pmatrix}0\cr1\end{pmatrix}\quad \hbox{if }\pm p_{r}< 0; \end{aligned}$$

(15.93)

$$\begin{aligned} E =&\pm|p_{r}|. \end{aligned}$$

(15.94)

Here, the spinor lists the values for the index $s=+$ and −.

In both cases, we write

$$\begin{aligned} \psi(\vec{p}) =&u^{+} a_{1}(\vec{p} )+u^{-} a_{2}^{\dagger}(-\vec{p} );\qquad \{a_{1}, a_{2}\}=\bigl\{ a_{1}, a_{2}^{\dagger}\bigr\} =0, \end{aligned}$$

(15.95)

$$\begin{aligned} \bigl\{ a_{1}(\vec{p} ), a_{1}^{\dagger}\bigl(\vec{p} '\bigr)\bigr\} =&\bigl\{ a_{2}(\vec{p} ), a_{2}^{\dagger}\bigl(\vec{p} '\bigr)\bigr\} = \delta^{3}\bigl(\vec{p}-\vec{p} '\bigr)\ \ \hbox{or}\ \ \delta \bigl(p_{r}-p_{r}'\bigr) \delta^{2}\bigl(\hat{q}, \hat{q} '\bigr) ; \end{aligned}$$

(15.96)

$$\begin{aligned} H^{\mathrm{op}} =&|p| \bigl(a_{1}^{\dagger}a_{1}+a_{2}^{\dagger}a_{2}-1\bigr), \end{aligned}$$

(15.97)

where $a_{1}$ is the annihilation operator for a particle with momentum $\vec{p}$, and $a_{2}^{\dagger}$ is the creation operator for an antiparticle with momentum $-\vec{p}$. We drop the vacuum energy −1 . In case we have a lattice in $r$ space, the momentum is limited to the values $|\vec{p} |=|p_{r}|<\pi/\delta r$.

3 The ‘Neutrino’ Vacuum Correlations

The vacuum state $|\emptyset\rangle$ is the state of lowest energy. This means that, at each momentum value $\vec{p}$ or equivalently, at each $(\hat{q}, p_{r})$, we have

$$\begin{aligned} a_{i}|\emptyset\rangle=0, \end{aligned}$$

(15.98)

where $a_{i}$ is the annihilation operator for all states with $H=\sigma \cdot\vec{p}=s p_{r}>0$, and the creation operator if $H<0$. The beable states are the states where, at each value of the set $(\hat{q}, r, s)$ the number of ‘particles’ is specified to be either 1 or 0. This means, of course, that the vacuum state (15.98) is not a beable state; it is a superposition of all beable states.

One may for instance compute the correlation functions of right- and left moving ‘particles’ (sheets, actually) in a given direction. In the beable (ontological) basis, one finds that left-movers are not correlated to right movers, but two left-movers are correlated as follows:

$$\begin{array}{rcl}& & P(r_1,r_2)-P(r_1)P(r_2)\\ & & =\delta r^2{〈\mathrm{\varnothing }|{\psi }_s^{\ast }(r_1){\psi }_s(r_1){\psi }_s^{\ast }(r_2){\psi }_s(r_2)|\mathrm{\varnothing }〉}_{\mathrm{conn}}\\ & & ={\left|\frac{\delta r}{2\pi }{\int }_0^{\pi /\delta r}\mathrm{d}p{e}^{ip(r_2-r_1)}\right|}^2=\{\begin{array}{cc}\frac{\delta r^2}{{\pi }^2{|r_1-r_{2\phantom{{|}_{|}}}|}^2}& \text{if }\frac{r_1-r_2\phantom{{|}_g}}{\delta r}=\text{odd },\\ \frac{1}{4}{\delta }_{r_1,r_2}& \text{if }\frac{r_1-r_2\phantom{{|}_g}}{\delta r}=\text{even},\end{array}\end{array}$$

(15.99)

where $\delta r ^{2}$, the unit of distance between two adjacent sheets squared, was added for normalization, and ‘conn’ stands for the connected diagram contribution only, that is, the particle and antiparticle created at $r_{2}$ are both annihilated at $r_{1}$. The same applies to two right movers. In the case of a lattice, where $\delta r$ is not yet tuned to zero, this calculation is still exact if $r_{1}-r_{2}$ is an integer multiple of $\delta r$. Note that, for the vacuum, $P(r)=P(r,r)={1\over 2}$.

An important point about the second quantized Hamiltonian (15.87), (15.88): on the lattice, we wish to keep the Hamiltonian (15.97) in momentum space. In position space, Eqs. (15.87) or (15.88) cannot be valid since one cannot differentiate in the space variable $r$. But we can have the induced evolution operator over finite integer time intervals $T=n_{t} \delta r$. This evolution operator then displaces left movers one step to the left and right movers one step to the right. The Hamiltonian (15.97) does exactly that, while it can be used also for infinitesimal times; it is however not quite local when re-expressed in terms of the fields on the lattice coordinates, since now momentum is limited to stay within the Brillouin zone $|p_{r}|<\pi/\delta r$. This feature, which here does not lead to serious complications, is further explained, for the bosonic case, in Sect. 17.1.1.

Correlations of data at two points that are separated in space but not in time, or not sufficiently far in the time-like direction to allow light signals to connect these two points, are called space-like correlations. The space-like correlations found in Eq. (15.99) are important. They probably play an important role in the mysterious behaviour of the beable models when Bell’s inequalities are considered, see Part I, Chap. 3.6 and beyond.

Note that we are dealing here with space-like correlations of the ontological degrees of freedom. The correlations are a consequence of the fact that we are looking at a special state that is preserved in time, a state we call the vacuum. All physical states normally encountered are template states, deviating only very slightly from this vacuum state, so we will always have such correlations.

In the chapters about Bell inequalities and the Cellular Automaton Interpretation (Sect. 5.2 and Chap. 3 of Part I), it is argued that the ontological theories proposed in this book must feature strong, space-like correlations throughout the universe. This would be the only way to explain how the Bell, or CHSH inequalities can be so strongly violated in these models. Now since our ‘neutrinos’ are non interacting, one cannot really do EPR-like experiments with them, so already for that reason, there is no direct contradiction. However, we also see that strong space-like correlations are present in this model.

Indeed, one’s first impression might be that the ontological ‘neutrino sheet’ model of the previous section is entirely non local. The sheets stretch out infinitely far in two directions, and if a sheet moves here, we immediately have some information about what it does elsewhere. But on closer inspection one should concede that the equations of motion are entirely local. These equations tell us that if we have a sheet going through a space–time point $x$, carrying a sign function $s$, and oriented in the direction $\hat{q}$, then, at the point $x$, the sheet will move with the speed of light in the direction dictated by $\hat{q}$ and $\sigma$. No information is needed from points elsewhere in the universe. This is locality.

The thing that is non local is the ubiquitous correlations in this model. If we have a sheet at $(\vec{x}, t)$, oriented in a direction $\hat{q}$, we instantly know that the same sheet will occur at other points $(\vec{y}, t)$, if $\hat{q}\cdot(\vec{y}-\vec{x} )=0$, and it has the same values for $\hat{q}$ and $\sigma$. It will be explained in Chap. 20, Sect. 20.7, that space-like correlations are normal in physics, both in classical systems such as crystals or star clusters and in quantum mechanical ones such as quantized fields. In the neutrino sheets, the correlations are even stronger, so that assuming their absence is a big mistake when one tries to draw conclusions from Bell’s theorem.