The Continuum Limit of Cogwheels, Harmonic Rotators and Oscillators

Abstract

It is shown how the mathematics has to be set up that is needed to relate classical and quantum mechanical periodic worlds, in the case both contain large numbers of states, while, eventually, we wish to introduce perturbations and interactions.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In the $N\rightarrow \infty$ limit, a cogwheel will have an infinite number of states. The Hamiltonian will therefore also have infinitely many eigenstates. We have seen that there are two ways to take a continuum limit. As $N\rightarrow \infty$, we can keep the quantized time step fixed, say it is 1. Then, in the Hamiltonian (2.24), we have to allow the quantum number $k$ to increase proportionally to $N$, keeping $\kappa =k/N$ fixed. Since the time step is one, the Hamiltonian eigenvalues, $2\pi\kappa$, now lie on a circle, or, we can say that the energy takes values in the continuous line segment $[0,2\pi)$ (including the point 0 but excluding the point $2\pi$). Again, one may add an arbitrary constant $\delta E$ to this continuum of eigenvalues. What we have then, is a model of an object moving on a lattice in one direction. At the beat of a clock, a state moves one step at a time to the right. This is the rack, introduced in Sect. 12.2. The second-quantized version is handled in Sect. 17.1.

The other option for a continuum limit is to keep the period $T$ of the cogwheel constant, while the time quantum $\delta t$ tends to zero. This is also a cogwheel, now with infinitely many, microscopic teeth, but still circular. Since now $N\delta t=T$ is fixed, the ontological¹ states of the system can be described as an angle:

$$\begin{aligned} 2\pi n/N\rightarrow \varphi ,\qquad{\mathrm {d}\over \mathrm{d}t}\varphi (t)= {2\pi\over T}. \end{aligned}$$

(13.1)

The energy eigenvalues become

$$\begin{aligned} E_{k}=2\pi k/T+\delta E, \quad k=0,1,\ldots, \infty. \end{aligned}$$

(13.2)

If $\delta E$ is chosen to be $\pi/T$, we have the spectrum $E_{k}=(2\pi /T)(k+{1\over 2})$. This is the spectrum of a harmonic oscillator. In fact, any periodic system with period $T$, and a continuous time variable can be characterized by defining an angle $\varphi$ obeying the evolution equation (13.1), and we can attempt to apply a mapping onto a harmonic oscillator with the same period.

Mappings of one model onto another one will be frequently considered in this book. It will be of importance to understand what we mean by this. If one does not put any constraint on the nature of the mapping, one would be able to map any model onto any other model; physically this might then be rather meaningless. Generally, what we are looking for are mappings that can be prescribed in a time-independent manner. This means that, once we know how to solve the evolution law for one model, then after applying the mapping, we have also solved the evolution equations of the other model. The physical data of one model will reveal to us how the physical data of the other one evolve.

This requirement might not completely suffice in case a model is exactly integrable. In that case, every integrable model can be mapped onto any other one, just by considering the exact solutions. In practice, however, time independence of the prescription can be easily verified, and if we now also require that the mapping of the physical data of one model onto those of the other is one-to-one, we can be confident that we have a relation of the kind we are looking for. If now a deterministic model is mapped onto a quantum model, we may demand that the classical states of the deterministic model map onto an orthonormal basis of the quantum model. Superpositions, which look natural in the quantum system, might look somewhat contrived and meaningless in the deterministic system, but they are certainly acceptable as describing probabilistic distributions in the latter. This book is about these mappings.

We have already seen how a periodic deterministic system can produce a discrete spectrum of energy eigenstates. The continuous system described in this section generates energy eigenstates that are equally spaced, and range from a lowest state to $E\rightarrow \infty$. Mapping this onto the harmonic oscillator, seems to be straightforward; all we have to do is map these energy eigenstates onto those of the oscillator, and since these are also equally spaced, both systems will evolve in the same way. Of course this is nothing to be surprized about: both systems are integrable and periodic with the same period $T$.

For the rest of this section, we will put $T=2\pi$. The Hamiltonian of this harmonic oscillator can then be chosen to be²

$$\begin{aligned} H_{\mathrm{op}}={\textstyle{1\over 2}}\bigl(p^{2}+x^{2}-1 \bigr);\qquad H_{\mathrm{op}}|n\rangle _{H} = n|n\rangle _{H},\quad n=0,1,\ldots,\infty. \end{aligned}$$

(13.3)

The subscript ${\scriptstyle{H}}$ reminds us that we are looking at the eigenstates of the Hamiltonian $H_{\mathrm{op}}$. For later convenience, we subtracted the zero point energy.³

In previous versions of this book’s manuscript, we described a mapping that goes directly from a deterministic (but continuous) periodic system onto a harmonic oscillator. Some difficulties were encountered with unitarity of the mapping. At first sight, these difficulties seemed not to be very serious, although they made the exposition less than transparent. It turned out, however, that having a lower bound but not an upper bound on the energy spectrum does lead to pathologies that we wish to avoid.

It is much better to do the mapping in two steps: have as an intermediate model the harmonic rotator, as was introduced in Chap. 12.1. The harmonic rotator differs from the harmonic oscillator by having not only a ground state, but also a ceiling. This makes it symmetric under sign switches of the Hamiltonian. The lower energy domain of the rotator maps perfectly onto the harmonic oscillator, while the transition from the rotator to the continuous periodic system is a straightforward limiting procedure.

Therefore, let us first identify the operators $x$ and $p$ of the harmonic rotator, with operators in the space of the ontological states $|\varphi \rangle _{\mathrm{ont}}$ of our periodic system. This is straightforward, see Eqs. (12.3). In the energy basis of the rotator, we have the lowering operator $L_{-}$ and the raising operator $L_{+}$ which give to the operators $x$ and $p$ the following matrix elements between eigenstates $|m\rangle ,-\ell\le m\le\ell,$ of $H_{\mathrm{op}}$:

$$\begin{aligned} \begin{aligned} \langle m-1|x|m\rangle &={\textstyle{1\over 2}}\sqrt{(m+\ell )(\ell+1-m)\over \ell}= \langle m|x|m-1\rangle , \\ \langle m-1|p|m\rangle &=-{\textstyle{1\over 2}}i\sqrt{(m+\ell)(\ell +1-m)\over \ell}= -\langle m|p|m-1\rangle , \end{aligned} \end{aligned}$$

(13.4)

while all other matrix elements vanish.

1 The Operator $\varphi _{\mathrm{op}}$ in the Harmonic Rotator

As long as the harmonic rotator has finite $\ell$, the operator $\varphi _{\mathrm{op}}$ is to be replaced by a discrete one:

$$\begin{aligned} \varphi _{\mathrm{op}}={2\pi\over 2\:\!\ell+1}\sigma ,\quad\sigma =-\ell,- \ell+1,\ldots,+\ell. \end{aligned}$$

(13.5)

By discrete Fourier transformations, one derives that the discrete function $\varphi (\sigma )$ obeys the finite Fourier expansion,

$$\begin{aligned} \sigma = i\sum_{k=1}^{2\ell} {(-1)^{k}\over 2\sin { ({\pi k\over 2\ell +1} )}}e^{\textstyle{2\pi i k\sigma \over 2\ell+1}}. \end{aligned}$$

(13.6)

By modifying some phase factors, we replace the relations (2.21) and (2.22) by

$$\begin{aligned} |m\rangle _{H} \equiv&{1\over \sqrt{2\ell+1}}\sum _{\sigma =-\ell}^{\ell}e^{\textstyle{2\pi i m\sigma \over 2\ell+1}}|\sigma \rangle _{\mathrm{ont}}, \end{aligned}$$

(13.7)

$$\begin{aligned} |\sigma \rangle _{\mathrm{ont}} =&{1\over \sqrt{2\ell+1}}\sum _{m=-\ell}^{\ell}e^{\textstyle {-2\pi i m\sigma \over 2\ell+1}}|m\rangle _{H} \end{aligned}$$

(13.8)

(which symmetrizes the Hamiltonian eigenvalues $m$, now ranging from $-\ell$ to $\ell$).

One now sees that the operator $e^{\textstyle{2\pi i\over 2\ell +1}\sigma }$ increases the value $m$ by one unit, with the exception of the state $|m=\ell\rangle$, which goes to $|m=-\ell\rangle$. Therefore,

$$\begin{aligned} \begin{aligned} e^{\textstyle{2\pi i\sigma \over 2\ell+1}}&=(\ell +1-H)^{-1/2}L_{+} (\ell+1+H)^{-1/2}+|-\ell \,\rangle \langle\, \ell\,|\,; \\ e^{\textstyle{-2\pi i\sigma \over 2\ell+1}}&=(\ell+1+H)^{-1/2} L_{-}(\ell +1-H)^{-1/2}+|\,\ell \,\rangle \langle\, -\ell\,|\,, \end{aligned} \end{aligned}$$

(13.9)

and Eq. (13.6) can now be written as

$$\begin{aligned} \begin{aligned} \langle m+k|\sigma |m\rangle &={i(-1)^{k}\over 2\sin ({\pi k\over 2\ell +1} )},\quad k\ne0, \\ \langle m|\sigma |m\rangle &=0. \end{aligned} \end{aligned}$$

(13.10)

Equations (13.9) can easily be seen to be unitary expressions, for all $\ell$ in the harmonic rotator. Care was taken to represent the square roots in the definitions of $L_{\pm}$ correctly: since now $|H|\le\ell$, one never encounters division by 0. The quantity $m+k$ characterizing the state in Eq. (13.10) must be read Modulo $2\ell+1$, while observing the fact that for half-odd-integer values of $\ell$ the relations (13.7) and (13.8) are both anti periodic with period $2\ell+1$.

The operator $\sigma$ in Eqs. (13.9) and (13.10) can now be seen to evolve deterministically:

$$\begin{aligned} \sigma (t)=\sigma (0)+(2\ell+1)t/ T. \end{aligned}$$

(13.11)

The eigenstates $|\varphi \rangle$ of the operator $\varphi _{\mathrm{op}}$ are closely related to Glauber’s coherent states in the harmonic oscillator [42], but our operator $\varphi _{\mathrm{op}}$ is Hermitian and its eigenstates are orthonormal; Glauber’s states are eigenstates of the creation or annihilation operators, which were introduced by him following a different philosophy. Orthonormality is a prerequisite for the ontological states that are used in this work.

2 The Harmonic Rotator in the $x$ Frame

In harmonic oscillators, it is quite illuminating to see how the equations look in the coordinate frame. The energy eigen states are the Hermite functions. It is an interesting exercise in mathematical physics to investigate how the ontological operator (beable) $\varphi _{\mathrm{op}}$ can be constructed as a matrix in $x$-space. As was explained at the beginning of this chapter however, we refrain from exhibiting this calculation as it might lead to confusion.

The operator $\varphi _{\mathrm{op}}$ is represented by the integer $\sigma$ in Eq. (13.5). This operator is transformed to the energy basis by Eqs. (13.7) and (13.8), taking the form (13.9). In order to transform these into $x$ space, we first need the eigen states of $L_{x}$ in the energy basis. This is a unitary transformation requiring the matrix elements $\langle m_{3}|m_{1}\rangle$, where $m_{3}$ are the eigen values of $L_{3}$ and $m_{1}$ those of $L_{x}$. Using the ladder operators $L_{\pm}$, one finds the useful recursion relation

$$ \textstyle\begin{array}[b]{rcl} 2m_{1}\langle m_{1}|m_{3}\rangle &=& \sqrt{(\ell +m_{3}+1) (\ell-m_{3})}\langle m_{1}|m_{3}+1 \rangle \\ &&{}+\sqrt{(\ell+m_{3}) (\ell+1-m_{3})}\langle m_{1}|m_{3}-1\rangle , \end{array} $$

(13.12)

First remove the square roots by defining new states $\|m_{3}\rangle$ and $\|m_{1}\rangle$:

$$\begin{aligned} \begin{aligned} \|m_{3}\rangle &\equiv\sqrt{(\ell+m_{3})!(\ell -m_{3})!}|m_{3}\rangle , \\ \|m_{1}\rangle &\equiv\sqrt{(\ell+m_{1})!( \ell-m_{1})!} |m_{1}\rangle . \end{aligned} \end{aligned}$$

(13.13)

For them, we have

$$\begin{aligned} L_{\pm}\|m_{3}\rangle =(\ell\mp m_{3})\|m_{3} \rangle , \end{aligned}$$

(13.14)

so that the inner products of these new states obey

$$\begin{aligned} \begin{aligned} 2m_{1}\langle m_{1}|\!|\!|m_{3}\rangle &=( \ell-m_{3}) \langle m_{1}|\!|\!|m_{3}+1\rangle +(\ell +m_{3})\langle m_{1}|\!|\!|m_{3}\rangle ; \\ \langle m_{1}|\!|\!|m_{3}\rangle &=\langle m_{3}|\!|\!|m_{1}\rangle . \end{aligned} \end{aligned}$$

(13.15)

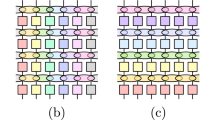
These equations can easily be inserted in a numerical procedure to determine the matrix elements of the transformation to the ‘coordinate frame’ $L_{x}$. With Eqs. (13.7) and (13.8), we now find the elements $\langle m_{1}|\sigma \rangle$ of the matrix relating the beable eigen states $|\sigma \rangle _{\mathrm{ont}}$ to the $x$ eigen states of $L_{x}$. A graphic expression of the result (for $\ell=40$), is displayed in Fig. 13.1. We see in Fig. 13.1b that the ontological variable is loosely following the template degree of freedom $x=m_{1}/\sqrt{\ell}$, just as it will follow the momentum $p=-m_{2}/\sqrt{\ell}$, with a $90^{\circ}$ phase shift.

Fig. 13.1

a Plot of the inner products $\langle m_{3}|m_{1}\rangle$; b Plot of the transformation matrix $\langle m_{1}|\sigma \rangle _{\mathrm{ont}}$ (real part). Horiz.: $m_{1}$, vert.: $\sigma$