Reliability and Preventive Maintenance

Abstract

In this chapter, the authors explain how to perform the core analysis of a Reliability Centered Maintenance (RCM) process for an offshore wind turbine. The aim is to provide an engineering guide which can improve the maintenance of the system, and consequently increases its availability and the production of energy. The initial investigations have been carried out using a database for an onshore 5 MW wind turbine; the data has then been converted using a proper conversion factor, so that it can be used for a 10 MW offshore turbine case. The reliability and availability of the entire offshore wind turbine have been calculated through Reliability Prediction and a Reliability Block Diagram (RBD). In addition, a failure mode analysis is done using FMECA, in order to identify the most important failure modes in a risk priority order, and to the note the effect of propagation of each functional failure. The maintenance part of the RCM analysis has also been studied, to facilitate the creation of an optimum packaging of preventive maintenance tasks, which can help to avoid the functional failures of items throughout the system. Although the main target of the RCM is to reduce the downtime of the wind turbine, a reduction in Life Cycle Costs can be also accomplished through this process.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Overview

During last 20 years, a great number of new technologies have been introduced in the field of green energy systems. The gradual appearance of different devices for energy production using renewable resources, have required novel research into improving the efficiency, in terms of both performances and costs. Taking such developments into consideration, reliability, availability and maintainability studies represent an essential investigation in order to identify how to optimize the design and the life cycle management from a cost/efficiency point of view.

The relevance of this topic has been well understood by the European Commission, as they promoted a research project named Reliawind (2011) between 2008 and 2011, for an on-shore wind turbine generator system. One of the aims of this research, in the work package led by Relex Italia s.r.l., was to assess the reliability for a 5 MW onshore wind turbine by creating a reliability model.

In 2014, the industry took a further step forward when the MARE-WINT project was approved. A new complete study on a wind turbine generator has been planned increasing generated power capacity to 10 MW and moving the wind turbine from onshore to an offshore environment. These changes reflect the improving design and concept for wind energy generation.

For a better explanation, Fig. 15.1 depicts the supportability analysis method derived from the procedure applied in the aeronautics and aerospace industries. This method has been used to initiate the current research; however, this method is quite extensive, and it was not possible to feasibly fulfill each and every component. Therefore, the attention has been focused on the core of this procedure (colored in pink) which can reasonably be considered the essential part.

Fig. 15.1

Supportability analysis method

As shown in Fig. 15.2, the knowledge acquired during Reliawind project, the reliability model, and the database have been used as starting point for the current work. An accurate study on the best power and environmental conversion factor has been conducted and a new reliability model, for reliability prediction and reliability block diagram studies, has been developed. Meanwhile an investigation into failure modes, classified by severity, has been conducted in order to identify riskiest failures for the system both from safety/environmental and economic/operational point of view. The second and third part of the research mainly consists of the Reliability Centered Maintenance analysis—which has made it possible to optimize a maintenance plan with respect to all information collected in the previously analysis. The detailed procedure is described in the following chapter.

Fig. 15.2

MARE-WINT research

2 Offshore Wind Turbine Configuration

There are several wind turbine configurations which could be studied and compared in future works.

Fig. 15.3

Whole hierarchy offshore wind turbine

Figure 15.3 shows the whole hierarchy system which has been used in order to develop the reliability model. Main assembly and sub-assembly characteristics have been described as follows:

• The Rotor Module is composed of a hydraulic pitch system which optimizes the position of the blades based on the wind direction. It is also the primary brake system for the wind turbine.

• The Drive Train Module transmits wind forces and torque from the rotor to the main shaft. It is done through a gearbox which is a combination of a planetary stage, followed by two parallel stages, and a mechanical brake.

• Four electrical yaw gears with motor brakes are included into the Nacelle Module. The yaw system rotates the top part of the nacelle into the upwind direction to maximize power production and minimize loads.

• A doubly fed induction generator (DFIG) with rated power 10 MW Power Module has been selected.

• A converter is connected between the generator and the grid. It is a four quadrant converter with the insulated gated bipolar transistor (IGBT) on the generator-side. An active crowbar unit is placed on the generator-side to ensure the compliance with grid requirements. The converter is located in the rear part of the nacelle.

3 Reliability Prediction

Reliability prediction is a quantitative analysis technique that has been used to predict the failure rate (λ) of an offshore wind turbine (OWT) using an established model with defined operating conditions. The goal of reliability prediction is to predict the rate at which components and systems fail.

3.1 Definition and Assumptions

The general formulation for the reliability through time is shown as Eq. (15.1):

$$ R(t)={e}^{-{\int^{t}_{0}}\lambda (x)dx} $$

(15.1)

where R is the reliability and λ is the failure rate (number of failures per million of hours) and t is the time.

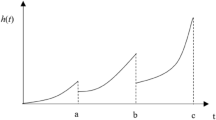
A component’s lifetime is often described by three phases. During first phase, the failure rate decreases down early with time and failures are attributable to manufacturing and quality problems. After that in the second phase, failure rate λ(t) is approximately constant (chance failures). In the third phase, the failure rate increases with time due to aging, wear out, fatigue, etc. If it is assumed that the failure rate is constant along time (2nd phase), we get Eq. (15.2):

$$ \uplambda \left(\mathrm{t}\right)=\uplambda $$

(15.2)

Using Eq. (15.2), the reliability function shown in Eq. (15.1) can be expressed as Eq. (15.3):

$$ R(t)={e}^{-\lambda t} $$

(15.3)

The reliability exponential function (Eq. 15.3) has been selected as the way to describe the component’s reliability.

3.2 Reliability Prediction Data-Base

Since published reliability data of offshore wind farms does not exist, it has been necessary to convert the failure rate data from onshore to offshore using published data of onshore wind turbines. Before starting the reliability prediction, a literature review of published data sources (e.g. Windstats, WMEP, LWP and Swedish Wind) was conducted, and the Reliawind data-base was chosen as being the most suitable for this research.

3.2.1 Reliawind Data-Base

Reliawind is a project in which the reliability of large wind turbines (5 MW) was investigated. Recommended methods of measuring reliability and processing data from onshore wind turbines and wind farms were studied. During this project a large data-base, containing data on more than a thousand items, was developed. The project ran from 2008 to March, with active involvement of ten partners.

3.2.2 Conversion Factor

Since our current turbine operates in a different environment, and has different parameters compared to the Reliawind turbine, a conversion factor has been introduced to convert the database data of the 5 MW onshore wind turbine to that of a 10 MW offshore wind turbine. This factor has been derived as combination of two parameters (Karyotakis 2011; Davidson and Hunsley 1994). The first parameter “K ₁”, takes into consideration the environmental stress; “K ₂” is based on the power rating stress.

K _1 offshore is the environmental stress factor and it is defined as the effect of environmental condition (e.g. weather and humidity condition) on the offshore wind turbine.

K _2 offshore is the power rating stress factor that depends on the operating power ranges of the wind turbine.

It is well known that offshore wind farms are exposed to higher power rating stress factor and adverse environment. Thus, Eq. (15.4) is used to describe the failure rate for the offshore wind turbine:

$$ {\lambda}_{offshore}={\lambda}_{onshore}\cdot \left({K}_{1\ offshore}\cdot {K}_{2\ offshore}\right) $$

(15.4)

Table 15.1 shows how the value of the environment stress conversion factors varies, depending on the environmental conditions.

Table 15.1 Environmental stress factor

In our case, K₁ is considered to be ‘Naval Sheltered’ for items within the nacelle. ‘Naval Exposed’ is chosen for the items that are fully exposed to marine environment. K_1 onshore is considered to be ‘Ground Based’ (K_1 onshore = 1); K_1 offshore is assumed to be between naval sheltered and exposed ($1,5\le {\mathrm{K}}_{1\ \mathrm{offshore}}\le 2$).

The other parameter, K₂, is obtained by taking into consideration the ‘windiness’ of the wind farm site. The windiness of the OWT is measured by the capacity factor of the wind turbine. This average capacity factor is assumed to be 25 % for onshore, 35 % for near-offshore and 45 % for far-offshore (Boccard 2009; BWEA 2000; CA-OWEE 2001; DTI 2002); in our case, the wind farm is considered to be ‘near-offshore’.

Table 15.2 shows the exponential relationship between the power rating stress factor and the component nominal rating. Values from Table 15.2 are plotted on Fig. 15.4 and the equation of the curve can be derived from the values showed in Table 15.2. As per the previous considerations, the difference between the average capacity factor for ‘far-offshore’ and ‘onshore’ is 20 % (45 %–25 %). Accepting a capacity factor of 25 % as the average onshore (assumed as a PCNR value of 100 %), and assuming that K_2 onshore is equal to 1 (from Table 15.2), the PCNR of far-offshore is calculated as: $45\%-25\%+100\%=120\%$.

Table 15.2 Power rating stress factor for mechanical components

Fig. 15.4

Percentage of component nominal rating plotted against stress factor K₂. Graph constructed based on the data presented in Table 15.2

Similarly, if—from Table 15.2—${\mathrm{K}}_{2\ \mathrm{far}-\mathrm{offshore}}$ is equal to 2, the PCNR of near offshore can calculated by using the same method which has been used for the far-offshore case; assuming a near offshore capacity factor of 35 %; the PNCR of near-offshore is then: $35\%-25\%+100\%=110\%$. ${\mathrm{K}}_{2\ \mathrm{near}-\mathrm{offshore}}$ is then calculated through Eq. (15.5), using this PCNR value of 110 %:

$$ {K}_2=0.0541\cdot {\mathrm{e}}^{0.0301*\mathrm{PCNR}} $$

(15.5)

As a result, ${\mathrm{K}}_{2\ \mathrm{near}-\mathrm{offshore}}$ is equal to 1.483. Then, Eq. (15.6) can be obtained by introducing ${\mathrm{K}}_{2\ \mathrm{near}-\mathrm{offshore}}$ into Eq. (15.4):

$$ {\lambda}_{offshore}={\lambda}_{onshore}\left({K}_{1\ offshore}\cdot 1.483\right) $$

(15.6)

3.3 Reliability Prediction Results

The system failure rate value obtained from the reliability prediction analysis is 1866.36 failures per million hours. Figure 15.5 shows the number of failures per year associated with each sub-system (the failures of the auxiliary equipment are not included in Fig. 15.5).

Fig. 15.5

Results reliability prediction on sub-systems

4 Reliability Block Diagram

4.1 Definition and Assumptions

A Reliability Block Diagram (RBD) is a visual representation of the parts of the system, through blocks (representing items) linked together (Fig. 15.6). An RBD also shows how various parts are connected logically to fulfill the system requirements.

Fig. 15.6

Development of RBD within a system

Since reliability predictions assume that all components in a system are in series, they cannot be used to analyze a system with redundant components. RBDs are used to evaluate the reliability of systems that are complex in their configurations. RBDs also provide an efficient and effective way to compare various configurations to identify the best overall system design. An example of a RBD for the OWT that presents redundancies is depicted in Fig. 15.7. The pitch system RBD shows how the main line is connected in standby configuration with the emergency line. A functional reliability model is created in order to evaluate the real configuration on the typical 10 MW wind turbine, and shown in Fig. 15.8.

Fig. 15.7

Pitch system RBD

Fig. 15.8

Main RBD of the offshore wind turbine

The goal of the Reliability Block Diagram is to determine the reliability and maintainability metrics—such as Reliability, Availability, Failure rate and MTTR (mean time to repair)—for a complete system. The elements which are necessary for the required function are connected in series, while elements which can fail with no effect on the required function are connected with redundancies. There are three types of redundancies: parallel, load sharing and standby.

4.2 Inherent Availability

The Availability is the probability that the system is operating satisfactorily at any point in time when used under stated conditions; here, the time considered includes operating time, active repair time, administrative time and logistic time. Through this parameter, one can calculate the inherent availability, in which the proportion of the total time that the item is available is the steady-state availability. Therefore, the availability of an item is a function of its failure rate $\lambda$ and of its repair or replacement rate μ. The difference between repairable and non-repairable system is illustrated graphically in Fig. 15.9. For a simple unit with a constant failure rate and a constant mean repair rate, μ is shown as Eq. (15.7):

Fig. 15.9

(a) Non-reparable system and (b) reparable system

$$ \upmu =\frac{1}{\mathrm{MTTR}} $$

(15.7)

Then, Eq. (15.8) can be derived to calculate the steady-state availability:

$$ \mathrm{A}=\frac{\mathrm{MTBF}}{\mathrm{MTBF}+\mathrm{MTTR}}=\frac{\upmu}{\uplambda +\upmu} $$

(15.8)

4.3 Reliability Block Diagram Results

RBD results for our study are shown in Figs. 15.10 and 15.11. From Fig. 15.11, it can be seen that the MTBF is equal to 3723.37 h (2.37 failures per year). According to theory, the value of MTBF is the time at which the reliability value is 0.37. The inherent availability is calculated with a year mission time (8760 h), and at that time the value of inherent availability is about 99 %.

Fig. 15.10

Results RBD on sub-systems

Fig. 15.11

Reliability through time in a year operation

5 Failure Mode, Effects and Criticality Analysis

5.1 Definition

A Failure Mode, Effects and Criticality Analysis (FMECA) is one of the most used analysis tools in the engineering field for developing designs, processes and services. To develop a FMECA, potential failure modes are analyzed to determine their effects all along the system, and classified according to their severity (FMEA) and probability of occurrence (FMECA).

5.2 Objectives

The main target of this analysis is to identify the weakest parts of the OWT, understand their failure modes and the associated effects, and then improve their availability by introducing possible redundancies or design changes, and updating the preventive maintenance. Other objectives that are possible to achieve through this analysis are:

• Anticipate the most important problems.

• Prevent failures from occurring.

• Minimize the failure consequences as cost effectively as possible.

• Give technical information to maintenance personnel about failures that might come out during system life.

• Compare results with previous maintenance reports and update the analysis.

• Provide necessary information to create a cost/benefit analysis.

• Provide those modes that need preventive maintenance in a risk priority order.

5.3 Method

A FMECA is a bottom up approach analysis by which the system design and performance are studied. With this analysis the potential failure modes are defined, as well as the occurrence and severity of each failure effect associated to them. The analysis can be done in two ways: component level (referred as component FMEA) or functional level (referred as functional FMEA). A component FMECA has been chosen based on the tasks 101 and 102 (Table 15.3) of the military standard MIL-STD-1629A from the Department of Defense of USA (DoD 1980).

Table 15.3 FMECA MIL-STD-1629 tasks

5.4 Approach

A FMECA can be initiated at any system level but due to the complexity, huge amount of components and the lack of data, a proper level of indenture of our OWT has been chosen: the FMEA has been performed starting from the component level, while the FMECA starts from the line replaceable unit (LRU) level. A bottom-up approach is used, noting the failure modes of the lowest level items of the system and then moving up the hierarchy and noting the effect of the failure to the end item (the OWT itself). Figure 15.12 illustrates the distribution mentioned before.

Fig. 15.12

Example of the hierarchy structure used to perform the FMECA

5.5 Criticality

A criticality analysis completes the FMEA by using two parameters: occurrence and severity. With these parameters the risky parts of the systems are identified. Calculating criticality numbers gives us the possibility to define the criticality of each item and its associated failure modes from a quantitative point of view; however, this method is only used when enough data is available. The mode criticality number “C_m” and the item criticality number “C_r” (see Table 15.4), can be calculated according to definitions in MIL-HDBK-1629 (DoD 1980).

Table 15.4 Criticality numbers description from MIL-HDBK-1629

These numbers are defined using Eqs. (15.9) and (15.10):

$$ {\mathrm{C}}_{\mathrm{m}}=\upalpha *\upbeta *{\uplambda}_p*\mathrm{t}\vspace*{-20pt} $$

(15.9)

$$ {\mathrm{C}}_{\mathrm{r}}={\displaystyle \sum_n^j}{\left({\mathrm{C}}_{\mathrm{m}}\right)}_n\mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{n}=1,2\dots \mathrm{j} $$

(15.10)

• C_r = Criticality number for the item

• C_m = Criticality number for a failure mode under a particular severity classification.

• α = Failure mode ratio. The probability, expressed as a decimal fraction, that the part or item will fail in the identified mode.

• λ_p = Part failure rate.

• β = Conditional probability of mission loss given that the failure mode has occurred. Table 15.5 defines β values.

  Table 15.5 β classification from MIL-HDBK-1629

• t = Mission time.

• n = Failure modes in the items that fall under a particular severity classification.

• j = Last failure mode in the item under the severity classification.

Alternatively, a qualitative method can be used, which allows us to represent the criticality results using a Risk Matrix. The matrix is constructed by inserting the total number of OWT failure modes in the matrix areas representing the severity classification and the frequency level assigned. The frequency is calculated as the ratio between failure mode probability of occurrence in a certain time interval, and the overall system probability of occurrence in the same time interval, as Eq. (15.11):

$$ \mathrm{f}=\frac{\uplambda_{\mathrm{p}}*\upalpha *\mathrm{t}}{\uplambda_{\mathrm{s}}*\mathrm{t}}=\frac{\uplambda_{\mathrm{p}}*\upalpha}{\uplambda_{\mathrm{s}}} $$

(15.11)

• f = Frequency

• α = Failure mode ratio. The probability, expressed as a decimal fraction, that the part or item will fail in the identified mode.

• λ_p = Part failure rate.

• λ_s = Total system failure rate.

The results of the analysis for our OWT are summarized in the Criticality Matrix shown in Fig. 15.13, in which three risk areas can be identified:

Fig. 15.13

Risk matrix

• Green area (Low occurrence and low severity) indicates that the risk associated to that failure mode located on it, is acceptable or well controlled. This area refers to those placed in minor severity with frequency from I to III, marginal severity with frequency I and II, critical severity with frequency I.

• Red area (High occurrence and high severity) indicates that actions must be taken to decrease the severity associated to that failure mode and occurrence of the failure modes placed on it. This area refers to those placed in marginal severity with frequency V, in critical severity with frequency IV and V and catastrophic severity with frequency from III to V.

• Yellow area (Medium risk) gathers those failure modes which must be monitored and controlled. This area refers to those modes placed in minor severity with frequency IV and V, marginal severity with frequency III and IV, critical severity with frequency II and III, and catastrophic severity with frequency I and II.

The matrix provides a way to identify and compare failure modes, with respect to their associated severity and frequency. Severity degrees assigned to failure modes are described in Table 15.6. A classification of frequency is given in Table 15.7.

Table 15.6 Severity classification

Table 15.7 Frequency/occurrence classification

5.6 Process

The ‘bottom-up’ procedure for component FMECA is the following:

• 1. Construct a OWT FMECA system tree;

• 2. Identify all potential items;

• 3. Evaluate failure modes (from mode library) of each component;

• 4. Evaluate the local effect for each component failure mode;

• 5. Roll-up all local effects at higher level (at higher level, the rolled-up effect becomes the failure mode at that level);

• 6. Repeat step 5 until system level;

• 7. For each end effect at system level identify the detection, severity and occurrence;

• 8. Build down the FMECA by transferring all the end system effects and severity to sub-system, assembly and component level.

5.7 Limitations

FMEA takes into consideration only non-simultaneous failure modes. In other words, each failure mode is considered individually, assuming that other system items work as usual. Effects of multiple item failures on wind turbine functions and redundant items are not covered by FMEA. These events are usually studied for those systems or sub-systems that perform safety functions by the Fault Tree Analysis (FTA) and Markov analysis.

5.8 Results

Due to the complexity of the full FMECA just the consequential results are shown in this section, which are related to the hierarchical structure described in Sect. 15.5.4.

5.8.1 Risk Matrix and Criticality Evaluation

A risk matrix is probably one of the most widespread tools for risk evaluation. Figure 15.13 reports the number of failure modes that lead to the end effect with each particular combination of severity and frequency values.

Figure 15.13 shows seven failure modes located in yellow zones where actions to control or monitor them must be taken (three of them are: The Drive train Module Failure, the Power Module Failure and the Structural Module Failure). Twenty-four failure modes, whose risk is considered to be low are in the green areas. Three failure modes are located in the red areas where mitigating actions must be taken (The Auxiliary Power Equipment Failure in Marginal-Frequent, The Rotor Module Failure in Critical-Frequent, and the Nacelle Module Failure in Catastrophic-Occasional).

The results of the Auxiliary Power Equipment are due to the large amount of items contained within it, while for the Rotor Module this result is due to the high failure rate of the Blades assembly. For the Nacelle Module Failure, the reason why it is placed in a red zone is because the Nacelle is one of the main structures of the WT where the majority of the main assemblies are located.

From what is presented in Sect. 15.4.3, the MTBF of the system is 3723.37 h (2.37 failures per year). For this reason, the time until system fails has been taken as the mission time.

As mentioned in Sect. 15.5.5, another quantitative analysis has been performed, the results of which are shown in Fig. 15.14. From Fig. 15.14, it can be seen that:

Fig. 15.14

Item criticality number (Cr) distribution

• Six marginal failure modes have the highest criticality number for the system.

• Nine critical failure modes have almost the same criticality number as Marginal failure modes.

• Seventeen ‘minor’ failure modes have more than three times criticality compared to the two ‘Catastrophic’ failure modes, but less than half the value of criticality number compared to Marginal and Critical failure modes.

Equation (15.12) is derived from Eqs. (15.9), (15.10) and (15.11), and it can help to explain why the item criticality numbers are so high for the less severe modes:

$$ {C}_r={\displaystyle \sum_n^j}\left(\,{f}_n*t*\upbeta *{\uplambda}_s\right) $$

(15.12)

Considering that “t” does not change, λ_s is constant and β values are the same for all failure modes, one can obtain Eq. (15.13):

$$ {C}_r=k*{\displaystyle \sum_n^j}{\,f}_n $$

(15.13)

Therefore, for the marginal classification, high values of frequency and a high number of failure modes are the reason for high item criticality numbers.

5.8.2 Mode Criticalities at System Level

The ten modes with the highest criticalities are reported in Fig. 15.15. Blades are well known as the parts that most suffer in wind turbines due to their continuous work under adverse environmental conditions; in fact Rotor Module Failure (which includes the Blades) is characterized by the highest mode criticality value (mode criticality of 2.88).

Fig. 15.15

Top 10 mode criticalities

Unifying all Auxiliary Equipment failure modes would lead to the highest mode criticality (3.41), simply due to the large amount of assemblies contained in this sub-system; however these failure modes have been sorted based on the equipment in which they can manifest.

Even with the aforementioned equipment separated, the second highest mode criticality belongs to Auxiliary Power Equipment Failure, while the third and fourth positions are taken by WT Auxiliary Equipment Failure and Air Conditioning Equipment Failure, respectively.

The remaining failures with the lowest values of mode criticality belong to Condition Monitoring System Failure, Control and Safety System Failure, Nacelle Module Failure, Drive Train Module Failure and Power Module Failure.

5.8.3 Risk Priority Number (RPN)

RPN is a criticality study in which the severity, occurrence and detection are multiplied in order to obtain information about the riskiest failure modes. Thus, greater attention is paid to critical parts. Equation (15.14) is used to obtain RPN numbers:

$$ \mathrm{R}\mathrm{P}\mathrm{N}=\mathrm{Severity}*\mathrm{Occurrence}*\mathrm{Detection} $$

(15.14)

Figure 15.16 shows the consequent risk priority classification with the highest RPNs of the OWT.

Fig. 15.16

Top 10 RPN

Table 15.8 Detection classification

In this case, Rotor Module Failure is still in first position because of its high occurrence and severity and also its low detection level comparing to the others, followed now by the Structural Module Failure and the Nacelle Module Failure due to its high severity and low detection. The rest of the failure modes have such combinations that give them a gradual position on the graph until getting a value of 200 for the last two modes.

It is important to note that the mode criticality graph and the RPN graph give different lists of the riskiest failure modes of the OWT. This is because the mode criticality analysis focuses on the probability of occurrence, while the RPN analysis considers the detection parameter combined with severity and occurrence. All RPN values related to severity, occurrence and detection, and used to perform this analysis, are listed in Tables 15.6, 15.7 and 15.8 respectively.

6 Preventive Maintenance (PM)

During the Wind Turbine life different types of maintenance tasks are required in order to retain or restore its operation. In this section, we explain how to apply the “NAVAIR 00-25-403” procedure to define the PM tasks for our OWT (NAVAIR 2003). This standard explains a complete reliability centered maintenance (RCM) process which can be applied for almost any system.

6.1 Definition

Preventive Maintenance looks at actions that can be used to extend the useful life of system with a good cost-benefit relation, whilst simultaneously ensuring the safety of the system. PM tasks are generally performed during an intended downtime, though they can also be performed during corrective maintenance and even while the system is running (Predictive Maintenance using nondestructive inspection techniques).

6.2 Preventive Maintenance Tasks Classification

6.2.1 Scheduled Tasks

Scheduled task are those which are performed in set intervals of time. These intervals can be measured in different units depending on how the system operates (e.g. cycles, time and events). The main units used in the Wind Turbine tasks are units of time: hours, days months and years. Scheduled tasks include:

• Servicing (S): this task involves the replenishment of consumables that are wasted overtime, as for example oil and fuel. Usually no further analysis should be done for these tasks due to they should be performed according to their manufacturer’s instructions, which include information about how often, how to do it, level of disassembly, operator skills and other maintenance requirements.

• Lubrication (L): this task is applied to those components that must be lubricated periodically according to design specifications. As for S tasks, manufacturers give the instructions to perform it as well as its intervals to be applied

• Hard Time (HT): It consists of the replacement or restoration of the item before it fails. This task is performed when the degradation of the item cannot be detected. The degradation phase of the item is called “Wear Out”, which shows different increases of the probability of failure with time depending on the type of component. The time to perform the task is established according to the consequences of the effects that the item failure causes. If the consequences are safety/environmental related, the limit time to perform the task will be established before the wear out age while if the consequences are operational/economic related the limit time will be flexibly established before the functional failure.

• Failure Finding (FF): this schedule task allows finding functional failures that have already occurred but are not apparent to the operators/maintainers, also called hidden failures. Emergency or back-up systems such as firefighting system or pumps in the hydraulic system are examples of elements that are subjected to Failure Finding task.

6.2.2 On Condition Task

On Condition (OC) tasks are periodical or continuous inspections. In contrast to HT tasks, these have a well-defined degradation period where the potential failure indicates that a functional failure will occur. Periodic and continuous inspections ensure that the items work until a potential failure comes along, extending its useful life, and therefore decreasing its maintenance costs. Once the potential failure is found, the next inspections are performed with flexible intervals of time in order to find the right time to take corrective actions. Periodical inspections range from simple visual checks to non-destructive inspections which need specialized equipment. The most used continuous inspection in wind turbines is condition monitoring. Condition monitoring is usually used for failure modes whose functional failures have environmental/safety-related effects, as these need to be continuously controlled.

6.3 Significant Function Selection

System failures may have different levels of function losses. Hence, functions are classified as “Significant Function (SF)” or “Non-SF”, depending on whether the consequences of these failures may lead to any losses of function, or effects, in terms of safety, environment, operations or economic impacts.

6.3.1 Significant Function (SF) Logic

Function failures have been analyzed through several questions which identify all significant failures. Items may have more than one significant function and each one should be analyzed individually. Functions which are not significant are not taken into consideration. The logic diagram shown in Fig. 15.17 has been followed in order to identify all significant functions.

Fig. 15.17

Significant function selection logic diagram

The diagram is composed of four questions, that point out which loss of function has adverse effects on safety, environment, operations and economic impacts—and if the function is already protected by an existing PM task. The significant function selection logic diagram is represented in Fig. 15.17. All functions are followed through the diagram in order to classify them in “SF” or “Non-SF”. If the four questions’ in Fig. 15.17 are answered as “No”, the function is classified as “Non-SF”. A positive answer is enough to consider the function as a “SF”. The SF Identification process ensures that all functions and effects have been taken into consideration before a Task Evaluation analysis is developed.

6.4 Task Evaluation

A ‘task decision logic’ process must be undertaken using the Decision Logic Diagram (Fig. 15.18), after SFs have been identified.

Fig. 15.18

Decision logic

An appropriate failure management strategy is implemented in order to accept, eliminate or decrease the consequences of functional failures. All possible Predictive Maintenance tasks have been studied to cover each functional failure through the Decision Logic Diagram shown in Fig. 15.18.

The study of each functional failure or failure mode effect goes through different branches depending on its circumstances, which finally identifies the suitable options in a two-step process. A failure that is not apparent under normal circumstances is classified as “hidden” because it only appears when a dormant function is activated. Both evident and hidden failures have adverse impacts which require actions, but if for each mode more than one action is possible, an economic and operational impact study is required to identify the best option.

The Decision logic branches identify four types of PM tasks: Lubrication tasks, OC tasks, HT tasks, and FF tasks which have been explained before. Task evaluations are shown for the MV Switchgear and Transformer in Fig. 15.19; evaluating all the failure effects and reporting that the failures on these parts are “evident” for the crew with an economic/operational impact, is what the decision logic shown in Fig. 15.19 can provide, as an example.

Fig. 15.19

Example of decision logic for the MV Switchgear and Transformer

In other words, this is the process in which the best suited task is selected to prevent and deal with each failure mode. If tasks cannot completely prevent the functional failure, the consequences must be reduced until they are acceptable. The available suitable tasks are identified in order to deal with each failure mode through the task selection in the next Sect. 15.6.5.

6.5 Task Selection

Once all possible maintenance tasks are known, the following step is the task selection. This evaluation process is done by looking through suitable tasks and taking into account cost analysis and operational consequences, thus determining which one deals better with a given failure mode.

6.5.1 Cost

Costs are evaluated for each task, including consumables cost, charter cost for the kind of vessel that is used for the preventive tasks, crew cost, energy losses cost and transportation cost. Costs are measured in euros (€). Special attention has been paid to those activities or resources which play an important role in offshore maintenance: for instance, the energy losses during activity maintenance have been taken under consideration as well as fuel consumptions. All costs have been assumed under a literature review (Krohn et al. 2009; Malcolm and Hansen 2006; Myhr et al. 2014; Poore and Walford 2008; IRENA 2012; RAB 2010; The Crown Estate 2010). Equation (15.15) shows how the overall cost is based on associated costs:

$$ \mathrm{C}={\mathrm{C}}_{\mathrm{C}\mathrm{onsumables}}+{\mathrm{C}}_{\mathrm{Vessel}}+{\mathrm{C}}_{\mathrm{transportation}}+{\mathrm{C}}_{\mathrm{C}\mathrm{rew}}+{\mathrm{C}}_{\mathrm{Losses}} $$

(15.15)

C_Consumables is the cost of the consumables. Assuming that vessels and equipment are needed, costs such as the rental vessel and equipment cost—C_Vessel—are also taken into account. C_{transportation} is the cost based on transportation from the harbor to the wind farm. It is represented by Eq. (15.16):

$$ {\mathrm{C}}_{\mathrm{Transportation}}=\mathrm{d}\cdot {\mathrm{C}}_1 $$

(15.16)

• $d= Distance\ from\ harbor\ to\ wind\ farm\ \mathrm{and}\ \mathrm{come}\ \mathrm{back}\ (km)$.

• ${C}_1= Fuel\ cost\left(\raisebox{1ex}{${\textsf{C}\hspace{-1.7ex}{=}} $}\!\left/ \!\raisebox{-1ex}{$Km$}\right.\right)$.

C_Crew, the crew cost is based on Eq. (15.17):

$$ {\mathrm{C}}_{\mathrm{C}\mathrm{rew}}=\mathrm{t}\cdot {\mathrm{C}}_{\mathrm{d}}\left({\mathrm{t}}_{\mathrm{d}}+{\mathrm{t}}_0+{\mathrm{t}}_{\mathrm{r}}\right) $$

(15.17)

• $t= Number\ of\ technicians$.

• ${C}_d= Cost\ technicians\ per\ \mathrm{hour}\ \left(\raisebox{1ex}{${\textsf{C}\hspace{-1.7ex}{=}} $}\!\left/ \!\raisebox{-1ex}{$ hours$}\right.\right)$.

• ${t}_d= Transportation\ time,\ round\ trip\ \left(\mathrm{hours}\right)$.

• ${t}_0= Time\ to\ adjust\ the\ actions\ (hours)$. It has been assumed as 2 h.

• ${t}_r= Time\ to\ \mathrm{develop}\ \mathrm{the}\ \mathrm{preventive}\ \mathrm{task}\ (hours)$.

C_Losses, the cost associated with losses of energy can be calculated via Eq. (15.18):

$$ {\mathrm{C}}_{\mathrm{L}\mathrm{osses}}=\left({\mathrm{t}}_{\mathrm{r}}\right)\cdot {\mathrm{C}}_{\mathrm{L}} $$

(15.18)

• ${C}_L=W\cdot E\cdot {C}_{factor}$.

• $W= Power\ Ratio(MW)$.

• $E= Electricity\ price={\textsf{C}\hspace{-1.7ex}{=}} /\mathrm{M}\mathrm{W}\mathrm{h}$.

Table 15.9 shows assumptions about C_Crew and C_Losses. Other general assumptions have been established as follows:

Table 15.9 General assumptions

• The nominal power of the offshore wind turbine is 10 MW.

• A distance from harbor to wind farm of 30 Km.

• Logistic delays have not been taken into account.

• The weather window is always perfect to develop the replacement and there is no environmental condition by which to wait in onshore until the maintenance could begin (e.g. wave height).

A Crew Transfer Vessel has been selected in order to carry out the preventive tasks. This vessel is selected for the replacement of items with small and low weight. The role is to transport the crew to the OWT and items of a few tones. Characteristics of the selected vessel are shown in Table 15.10.

Table 15.10 Crew Transfer Vessel features

6.5.2 Operational Consequences

The right tasks have to ensure that there are no operational consequences in the OWT. A balance between cost and operational impact should be chosen: a less expensive task will not be selected unless it fits in a work package without operational consequences. As an example, the most suited maintenance tasks associated with each failure mode are shown in Table 15.11, for several Transformer parts.

Table 15.11 Maintenance task assignation

6.6 Packaging

After selecting the best-suited tasks the next step is to adjust all these tasks in work packages by different criteria in an optimal way. In the first phase of packaging, a proper metric for all the tasks must be selected in order to organize them along the timeline. When converting the metrics of an environmental/safety-related task, special care should be taken, ensuring that the time to perform the task is not exceeded with the new metric. Although the first timeline graph with all the maintenance tasks can suggest a first packaging strategy based on the frequency of the maintenance tasks, the second phase includes other criteria to group the tasks that should also be taken into consideration.

In the second phase, tasks with common characteristics are grouped according to their maintenance level, kind of skills needed, equipment required, task intervals, transportation, etc. While grouping maintenance tasks, the environmental/safety related ones usually set the time for other tasks, due to their less flexible intervals of time which cannot be exceeded.

In the third and last step, the final packaging is developed, introducing other important factors such as the operational impact of the work package (e. g. downtime) or the ability to perform tasks in parallel, managed by previous analysis and engineering criteria. The target, at this point, is to reduce the downtime of the wind turbine as much as possible while maintenance tasks are being performed. The more the maintenance time is reduced, the lesser costs of maintenance; consequently the availability of the wind turbine, and the energy produced, is also greater.

However, factors, such as labor hours (7–9 h and sometimes more) or the reduced spaces to work (limited crew) can make it difficult to obtain optimal packages. Sometimes tasks do not fit into the established work packages, and may have to be performed as “Special Inspections”. Usually, these inspections have:

• A different kind of vessel: Depending on the component, on which the task is going to be performed, the necessities and equipment needed to access it may be different; consequently, the vessels used will also vary. Usually, three or four kinds of vessels take part in PM programs.

• A different interval: Sometimes, the time to perform a preventive task is very different from the time required for other tasks. This may be due to the item operation, environment requirements, etc. This makes it harder to couple the task to others.

When new tasks or changes on them are being implemented, and they contain the usage of hazardous materials or the emission of contaminant, special authorizations are required. For instance, during the recoating of blades, the use of solvents, certain types of lubricants, and some non-destructive inspection materials may need to be regulated and/or certificated before the task is performed.

In the following example, 59 maintenance tasks from the power module have been packaged. The power module is divided in five parts: Medium Voltage Switchgear (MVS), Generator (GE), Converter (CONV), Transformer (TRANS) and Power Feeder Cables (PFC). The maintenance tasks are numbered as shown in Table 15.12.

Table 15.12 Maintenance task classification by sub-systems

The descriptions of some key tasks are shown in Table 15.13. In this case, the system is already operating and the intervals are taken from manufacturers’ manuals. If the system is in an early design phase, other analyses should be performed to define task intervals. When all the intervals are identified, they are grouped every four months (4 M), six months (6 M), annually (A), two years (2 Y), three years (3 Y), and five years (5 Y) and six years (6 Y). Table 15.14 shows the first packaged tasks by their intervals for the Medium Voltage Switchgear and the Generator.

Table 15.13 Maintenance task descriptions

Table 15.14 Packaged tasks by intervals for MVS and GE

The tasks using common equipment are highlighted with the same colors. In Table 15.14, the red color (task number 1) refers to cleaning products and tools for cleaning; the yellow color (task number 2) means advanced tools for electrical tests; green indicates (task number 3, 10 and 11) basic tools for electrical tests; flesh color (task number 4 and 17) indicated lubricants; blue color (task number 12, 15, 18 and 19) depicts temperature and vibration test tools; and purple color pertains to advanced test tools.

Once the tasks are defined and classified by intervals of time, they have to be arranged in a lifeline. In our case, the tasks have been organized for 6 years (the maximum interval) and distributed over 3 different months with 2 days of work in each one. The simple reason why the workload is distributed in 2 days is because the work package has many working hours that do not fit in the limited labor hours. The months to perform the work packages are chosen based on the best weather periods of the year; the same for applies for the working days in each month, as certain weather conditions must be met. Table 15.15 shows the distribution of tasks for the first month (March) of work and for the first 6 years. The tasks highlighted in Table 15.15 are in accordance with the previous ones shown in Tables 15.13 and 15.14 (which follow the criteria previously explained for the packaging).

Table 15.15 Packaged tasks for the first 6 years

The crew on board the vessel is divided in two teams which work in parallel—thus the time to perform the maintenance tasks is considerably reduced. Table 15.16 summarizes the working time for each year, for the first month and each work team.

Table 15.16 Working hours for the first 6 years

Consider the second working day and first work team, with a short working time of 1.8 h. The 1.8 h could have been better packaged with just one work team; however, further analyses for other sub-systems led to other maintenance tasks, that also need to be packaged with the same work team; additionally, there is the possibility that the labor time of the day can be limited to around 8 h.

Table 15.17 shows the different cases taken into account when packaging. In the case of October, a more flexible labor time is assumed (where it is reaches 11 labor hours)—and so there is only one day of work. However, as it was mentioned before, when the maintenance plan is also performed for the rest of the sub-systems, these times will be readjusted. In the case of July, the two working teams cannot work in parallel because of the limited space in the nacelle; therefore they are separated in 2 days of work.

Table 15.17 Packaging overview for year 0

6.7 Age Exploration (AE)

In the process to elaborate PM programs, assumed data is necessary. An AE updates the data during different analyses.

6.8 Repackaging

In order to improve the work packages there are periodic reviews of:

• Time to perform the task

• Task interval

• Work package interval

• Maintenance process

• Techniques and technologies used

The maintenance documentation from field, which contains the information as previously mentioned, should be reviewed with maintainers to verifying whether the analysis results are realistic.

7 Conclusions

The reliability analysis for a 10 MW offshore wind turbine has identified which sub-systems, assemblies and sub-assemblies have a high failure rate. The sub-systems with highest failure rate are Rotor Module, and Drive Train Module. In particular, the Rotor Module is exposed to high stress and fatigue during its operation time due to uneven high air pressure around it. It should be also noted that the gearbox does not appear to be one of the less reliable assemblies of an OWT as it might be expected. These results also verify the results of the Reliawind project.

The RBD shows an OWT failure rate of 2.37 failures per year, which is about twice as large as an onshore wind turbine failure rate. This value could be accepted for an onshore wind turbine; however it is a high failure rate for an OWT due to the limited accessibility to perform preventive or corrective maintenance.

The huge dimensions of the wind turbine, its complexity and the environment increase the failure rate of the system. Through quality improvements of components, and by using condition monitoring on critical assemblies, the downtime can be reduced—allowing for an accurate scheduled maintenance to be developed.

Nowadays, availability improvements have been sought, in order to reduce energy losses and make offshore wind energy more profitable. In general, commercial offshore wind turbines can achieve an availability value of about 90 %, but, depending on the maintenance assumptions, this value can increase to 95 %. However in this analysis, logistic delays, maintenance delays and supply delays have not been taken into account; therefore, an availability value (inherent availability) of 99 % has been achieved.

Regarding the FMECA study, it can be concluded that the change in environment increases the probability of certain failures, directly or indirectly. For the Rotor Module and the Structural Module, the analysis confirms that their failures are mainly caused by the hazardous environment. For the Drive Train Module and Rotor Module, the abrupt changes in wind direction lead to continuous variation on their load conditions, and consequently cause stress and fatigue. As the OWT usually works in extreme temperature conditions, the Air Conditioning Equipment has to increase its power to maintain suitable environmental conditions, and this leads to an increase in its failure rate.

From the result of the RPN and Mode Criticalities analysis, it can be seen how each method can give different lists of riskiest parts of the system; for this reason both analysis are suggested in order not to leave any important failure mode out of consideration.

A successfully scheduled PM program can reduce maintenance costs and increase the availability of the OWT without risks for the system, personnel or environment. Throughout the packaging study, it has been seen that clear criteria combined with expert engineering judgment can make the process much easier.

The fact that the wind turbine is placed in an offshore environment affects the PM program due to drawbacks such as limited labor hours, expensive means of transport, expensive maintenance tasks, the difficulty to proceed with certain corrective actions, and the difficulty to perform some preventive tasks, amongst other factors. Nonetheless, with the right tools and procedures, offshore wind can be made more reliable and feasible.