Critical Sensor Density for Event-Driven Data-Gathering in Delay and Lifetime Constrained WSN

Abstract

In rare-event detection wireless sensor network (WSN) applications maximizing lifetime and minimizing end-to-end delay (e-delay) are important factors in designing a cost-efficient network, which can be achieved using asynchronous sleep/wake (s/w) scheduling techniques and anycasting data-forwarding strategies, respectively. In this paper, we address the problem of finding an optimal cost WSN that satisfies given delay constraint and lifetime requirement, assuming random uniform deployment of nodes in a circular-shaped Field-of-Interest (FoI) and estimate the maximum of minimum expected e-delay in an anycasting forwarding technique for a given sensor density. We use this analysis to find the critical expected sensor density that satisfies given e-delay constraint, and lifetime requirement. We also validate our analysis.

1 Introduction

In rare event driven data gathering applications like, intrusion detection, tsunami detection, forest-fire detection, and many more, nodes remain idle for most of the time until an event occurs. Extending lifetime while maintaining delay and coverage constraints, are the most essential quality of service parameters. In WSN, energy consumption is reduced using s/w scheduling techniques where the communication device is switched off when no event is detected in the vicinity. Nodes exchange synchronization messages in synchronous s/w scheduling protocols. Whereas, in asynchronous s/w scheduling technique sensor nodes wake up independently without any s/w synchronization. In the rare event detection scenario, asynchronous s/w scheduling techniques conserve more energy compared to synchronous s/w scheduling because of additional energy required in synchronization.

Several asynchronous s/w scheduling techniques are proposed in the literature. Generally, e-delay and lifetime depend on wake up rate of sensor nodes. With higher wake up rate, nodes consume more energy with reduced e-delay, and vice versa. Although there are other factors like queuing delay and clock skew that affects overall e-delay of the network, but wake up rate is the most dominating. Hence, in this paper we consider wake up rate as the governing factor of e-delay and lifetime The lifetime is the time duration of the first node depletes its energy completely in the network.

In anycasting strategy, packet is forwarded to the first node that wakes up within a set of candidate nodes. Since each node maintains a set of forwarding nodes, compared to a single forwarding node in traditional approaches, anycasting strategy decreases expected waiting time significantly, which in turn decreases e-delay [1].

In anycasting forwarding strategy, density also govern e-delay and lifetime. With increasing density, e-delay may decrease for a given wake up rate. In contrary, for a given e-delay, increasing density may result in increasing overall lifetime of the network. In order to increase network lifetime, for a given e-delay constraint, one can decrease the wake up rate by increasing the density. But, increasing density increases the overall cost of the network. Hence, we address the problem: what is the critical sensor density that satisfies given delay constraint and lifetime requirement, when nodes follow anycasting forwarding strategy? We use a stochastic approach to estimate expected e-delay for a given sensor density and use this analysis to find the critical sensor density that satisfies given requirements.

The next section reviews the significant contributions in the literature. Section 3 derives stochastic analysis to estimate expected e-delay for given sensor density and Sect. 4 uses this analysis to estimate critical sensor density. We validate our analysis using ns2 simulation in the fifth section and the final section points to the future work direction.

2 Related Work

Anycasting strategy first applied to wireless networks by Awerbuch et al. in [3]. In [4], the authors used the shortest path anycasting tree to route a data-packet. In [5, 6] the authors proposed heuristic anycasting protocols that exploit geographical distance to the sink in order to minimize e-delay. In [7–9], the authors used hop-count information to minimize delay along the routing path. Whereas in [10], the authors used both hop-count and power consumption metrics to reduce the overall cost of forwarding a data-packet from a source to the sink.

In anycasting based forwarding strategy if the number of nodes in a forwarding set increases, expected one hop delay decreases. Adding more nodes to the forwarding set may increase expected e-delay, especially when the newly added nodes have larger expected e-delay. Hence, nodes must be added to the forwarding set according to their expected e-delay. Based on this observation, Kim et al. proposed an anycasting forwarding technique, in which neighboring nodes are added to the forwarding set only when they collectively minimize overall expected e-delay [1]. But packets may follow a longer route to the base station. In order to minimize this effect, the same authors developed a delay optimal anycasting scheme [2], where nodes do not immediately forward the packet, instead they wait for some time and then opportunistically forward only when expected delay involves for waiting is more.

Motivation: For given strict delay constraint, the lifetime is proportional to the density of the network. If the number of nodes in forwarding set increases with increasing density, the wake up rate decreases in order to maintain given delay constraint. This in-turn increases the lifetime of the sensor nodes. Hence with given delay, coverage, and lifetime constraint, the density of the overall FoI can be adjusted according to the requirements. Although, the analysis provided in [1, 2] calculates expected lifetime of a node, with periodic wake up rate, but not directly applicable for satisfying the expected lifetime constraint. For given delay, coverage and lifetime requirements, deployment density over the FoI must be minimized to reduce the overall cost of sensor network. The proposed anycasting forwarding techniques [1, 2, 5–9] in the literature are unable to provide any analysis for expected lifetime varying sensor density.

3 Expected E-Delay

We use a stochastic approach to calculate expected e-delay of a randomly chosen sensor i, located at a distance $dis_i$ from the base-station in a circular shaped FoI. The nodes that can directly communicate with the base-station, can forward the data-packet immediately, since the base-station is awake all the time. In general, if the distance of a node from the base-station increases, the number of hops required to send a data-packet also increases, which in-turn increases e-delay. The maximum e-delay is nothing but the end-to-end delay of the node located at the farthest point from base-station.

Fig. 1.

Example of packet forwarding protocol

3.1 Expected E-Delay for a Fixed Size Forwarding Set

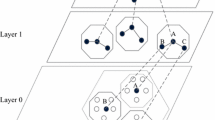
We assume random uniform deployment of nodes in a circular-shaped Field-of-Interest (FoI). We also assume that a sensor located at a point c, can only communicate perfectly within a circular region of radius C centered at c, which is denoted by A(c, C). We follow the forwarding strategy given in [1, 2]. Before sending a packet, a node sends a beacon signal, followed by an ID signal, and listens for acknowledgment. If any node hears the beacon (followed by ID), it sends acknowledgment only if it belongs to the forwarding set, else go to sleep and wakes up after $\frac{1}{w}$, where w denotes the asynchronous periodic wake up rate (as shown in Fig. 1, redrawn from [1]). Hence, the probability of any node in the forwarding set wakes up at $h^{th}$ beacon signal is defined as $p_w=\frac{{{t_I}}}{{1/{w}}}$, if $h < \frac{1/{w}}{t_I}$, else 1, where $t_I=t_A+t_B+t_C$ [1]. Moreover, $h_{max}=\frac{1/{w}}{t_I}$ denotes the total number of beacons.

Let $\{i_{1},i_{2},...,i_{k}\}$ be the forwarding set of node i. Let W be the event that denotes the set of forwarding nodes wake up during their respective beacon intervals. The probability of the event W, denoted by P(W), is $(p_w)^k$. Let X be the event denotes no node wakes up during the first $h-1$ beacons, j nodes wake up during the $h^{th}$ beacon, and remaining $k-j$ nodes wake up during the last $h_{max}-h$ beacons. The probability of X, P(X), is given by,

$$\begin{aligned} P(X) = ^k{C_j}{(h_{max} - h)^{k - j}}{\left( {{p_w}} \right) ^k}, \end{aligned}$$

(1)

since there are $^k{C_j}$ different possible sets of nodes that can wake up during $h^{th}$ beacon and remaining $(k-j)$ nodes wake up during the remaining $(h_{max}-h)$ beacons in $(h_{max}-h)^{k-j}$ different ways. Let $W_h$ denotes the event that the packet is forwarded after h beacon intervals so that no node wakes-up during first $(h-1)$ beacons and at least one node wakes up during $h^{th}$ beacon and remaining nodes wake up during remaining $(h_{max}-h)$ beacons. Hence, the probability of the packet is forwarded after $h^{th}$ beacon is,

$$\begin{aligned} P({W_{h}}) = \sum \limits _{j = 1}^k {^k{C_j}{{(h_{max}-h)}^{k - j}}{{\left( {{p_w}} \right) }^k}}. \end{aligned}$$

(2)

Hence expected one hop delay is given by

$$\begin{aligned} {d_{k,w}} = \sum \limits _{h = 1}^{\left\lfloor {\frac{{1/w}}{{{t_I}}}} \right\rfloor } {{P(W_{h})}*h} + t_D, \end{aligned}$$

(3)

where, $t_D$ denotes the transmission delay. The expected e-delay of a node i is the sum of the expected one hop delay and the expected e-delay of the nodes in its forwarding set. Since, every node in forwarding set has equal asynchronous periodic wake up rate w, the probability of the packet is forwarded to any node is $\frac{1}{k}$, and the expected e-delay of its forwarding set nodes is $\sum \limits _{j = 1}^k {\frac{1}{k}*{D_{i_j,k,w}}}$, for $1 \le j \le k$, where $D_{i_j,k,w},$ denotes the respective expected e-delay of node $i_j$. Hence, follows the lemma.

Lemma 1

Let $\{i_{1},i_{2},...,i_{k}\}$ be the forwarding set of node i. If $D_{i_j,k,w},$ denotes the respective expected e-delay of node $i_j$, for $1 \le j \le k$, then expected e-delay of node i, such that $(i \ne j),$ is given by ${D_{i,k,w}} = {d_{k,w}} + \sum \limits _{j = 1}^k {\frac{1}{k}*{D_{i_j,k,w}}}$, where ${d_{k,w}}=\sum \limits _{h = 1}^{\left\lfloor {\frac{{1/w}}{{{t_I}}}} \right\rfloor } {{P(W_{h,k})}*h}+t_D$.

3.2 Estimation of E-Delay of a Circular-Shaped FoI

Note that the overall e-delay decreases if neighboring nodes with less e-delay are given priority for including in the forwarding set [1]. Increasing the number of nodes in the forwarding set decreases expected one-hop delay but may increase expected e-delay of its forwarding set nodes. Hence in order to reduce expected e-delay for a node i, only neighboring nodes which collectively minimizes overall expected e-delay, are included in its forwarding set. Note that when density remains constant, with increasing distance from the base station may increase the overall e-delay but not decreases it. Hence, a linear search within the neighboring nodes, with higher priority for the nodes closer to the base-station, efficiently selects the forwarding set which minimizes overall expected e-delay. Expected e-delay of a given FoI is the expected e-delay of the farthest node from the base-station.

Fig. 2.

Example of our analysis

E-delay of the nodes are estimated in the increasing order of their distance from the base-station. We estimate e-delay of the nodes closer to the base-station first, and use the results to estimate the e-delay of their neighbors which are away from the base-station. Since the base-station is always awake, the e-delay of the nodes within the communication range of the base-station is equal to transmission delay, $t_D$. We denote this direct communication circle by $C_D$.

In order to estimate maximum expected e-delay, we divide the FoI into rings using concentric circles centered at base-station, and estimate the expected e-delay for a randomly chosen node in each ring. First we estimate the expected e-delay of a randomly chosen node within the first ring using the e-delay of nodes within the direct communication range of the base-station. Assuming base-station is positioned at $b_p$, we estimate the minimum expected e-delay of a randomly chosen node i within the circular annulus $CA(b_p,C,C+\delta _1)$, such that the neighboring nodes closer to base-station belongs to $C_D$. The circular annulus $CA(b_p,R_i,R_j)$ between two concentric circles, centered at $b_p$ with radii $R_i,R_j$, such that $R_j>R_i$, is defined as the area between their boundaries. In order to estimate $\delta _1$, we first define the effective forwarding region of communication.

For a node i at a distance $dis_i$ from the base station, the effective forwarding region of communication $EC_i$ is the intersection of the open circular area with radius $dis_i$ centered at the base-station and communication region of node i, as shown in Fig. 2(a). The following lemma quantifies the effective forwarding region of communication which can be verified using simple geometry.

Lemma 2

Area of the effective forwarding region of communication of node i at a distance $dis_i$ from the base station with communication range C such that $dis_i>C$, is $||EC_i||={\cos ^{- 1}}\left( {\frac{C}{{2di{s_i}}}} \right) {C^2} + {\cos ^{- 1}}\left( {1 - \frac{{{C^2}}}{{2di{s_i}}}} \right) di{s_i}^2 - di{s_i}\sqrt{{C^2} - \frac{{{C^2}}}{{2di{s_i}}}}$.

Let $\delta _1$ denotes the maximum width of the circular annulus $CA(b_p,C,C+\delta _1)$, such that the effective forwarding region of communication $EC_i$ is expected to contain only neighbors which are in the direct communication range of the base-station. In order to estimate the expected value of $\delta _1$, we use the following lemma which estimates the intersection of a circle and the effective forwarding region of communication of a random node, and can be proved using simple geometry.

Lemma 3

Consider a node i at a distance $dis_i$ from the base station, with communication range C. The intersection of a circle centered at base-station ($b_p$) with radius $R_j=dis_i-\delta ,0<\delta \le C,$ and the effective forwarding region of communication of node i, can be given as

Since the effective forwarding region of communication contains only neighbors that are in the direct communication range of the base-station, the expected number of nodes in the shaded region in Fig. 2(a) of a node i is one, which is node i itself. Moreover, the expected area of the shaded region in Fig. 2(a) is $\frac{1}{\lambda }$, where $\lambda$ denotes the node density. The expected maximum value of $\delta _1$ can be found by solving the following equation.

$$\begin{aligned} EC_i - CI(dis_i,\delta _1) = \frac{1}{\lambda } . \end{aligned}$$

(4)

We assume that Eq. 4 can be solved in constant time because it is a single variable equation. In the following lemma we estimate the minimum expected e-delay of a node belongs to $CA(b_p,C,C+\delta _1)$.

Lemma 4

The expected minimum e-delay of a randomly chosen node i within the circular annulus $CA(b_p,C,C+\delta _1)$ such that the effective forwarding region of communication, $EC_i$ is expected to contain only neighbors which can directly communicate with base-station, is ${D_{i,k,w}} = \sum \limits _{h = 1}^{\left\lfloor {\frac{{1/w}}{{{t_I}}}} \right\rfloor } {{p_{h,k,w}}*h} + t_D$, where $k=EC_i*\lambda -1$ and $\lambda$ denotes the density.

Proof

Since $C<dis_j \le C+\delta _1$ and the effective forwarding region of communication $EC_i$ is expected to contain only neighbors which can directly communicate with the base-station, then the expected number of sensors belong to this area is $||EC_i||*\lambda - 1$. Since these nodes have minimum e-delay $t_D$, the overall e-delay of node i decreases if more nodes are included in its forwarding set. Hence, the minimum expected e-delay of node i is,

$$\begin{aligned} {D_{i,k,w}} = \sum \limits _{h = 1}^{\left\lfloor {\frac{{1/w}}{{{t_I}}}} \right\rfloor } {{p_{h,k,w}}*h} + t_D, \end{aligned}$$

(5)

where $k=||EC_i||*\lambda -1$.

We gradually increase the distance from the base-station in steps of $\gamma$, and estimate the minimum expected e-delay. We calculate the expected e-delay of a random node i at a distance $C+\delta _1+m\gamma$ for $m \in N$, using the estimated expected e-delay of the nodes which are within the distance $C+\delta _1+(m-1)\gamma$ from the base-station.

We divide the effective forwarding region of communication $EC_i$, into several sectoral annuli such that every sectoral annulus is expected to contain only one node, as shown in Fig. 2(b), for $1 \le j \le k$, where $k=||EC_i||*\lambda -1$. The $j^{th}$ sectoral annulus $SA_{i,j}(\beta _{i_{j1}},\beta _{i_{j2}})$ of node i, between two concentric circles, centered at $b_p$ with radii $\beta _{i_{j1}},\beta _{i_{j2}}$, such that $\beta _{i_{j1}}>\beta _{i_{j2}}$, is defined as the intersection of the area between their boundaries and $EC_i$.

Let $i_{1}$ denotes the closest sectoral annulus to the base-station. $\beta _{i_{11}}$ is equal to $dis_i-C$. $\beta _{i_{12}}$ can be found by solving the following equation.

$$\begin{aligned} CI(dis_i,\beta _{i_{12}}-(dis_i-C)) = \frac{1}{\lambda } . \end{aligned}$$

(6)

Note that $\beta _{i_{21}}=\beta _{i_{12}}$. Moreover, $\beta _{i_{j1}}=\beta _{i_{(j-1)}{2}}$, for $2 \le j \le k$. For an arbitrary $i_j$, $\beta _{i_{j2}}$ can be calculated by solving the following equation.

$$\begin{aligned} CI(dis_i,\beta _{i_{j2}}-\beta _{i_{j1}}) = \frac{1}{\lambda } , \end{aligned}$$

(7)

for $1 \le j \le k$. We assume the Eqs. 6 and 7 can be solved in constant time because these are single variable equations.

We first estimate the expected minimum e-delay of a random node within $j^{th}$ sectoral annulus, for $1 \le j \le k$, and use these to estimate expected minimum e-delay of a random node i.

Consider a random sectoral annulus $SA_{i,j}(\beta _{i_{j1}},\beta _{i_{j2}})$. Assume $m_{i_1}$ be the largest integer such that $C+\delta _1+ m_{i_1}\gamma \le \beta _{i_{j1}}$ and $m_{i_2}$ be the smallest integer such that $C+\delta _1+m_{i_1}\gamma \ge \beta _{i_{j2}}$. In order to calculate the expected e-delay of a random node belongs to $SA_{i,j}(\beta _{i_{j1}},\beta _{i_{j2}})$, we use the expected e-delay of nodes at distances $C+\delta _1+(m_{i_1}+1)\gamma ,C+\delta _1+(m_{i_1}+2)\gamma ,...,C+\delta _1+m_{i_2}\gamma$. The node can belong to any one of the areas induced by the intersection between $SA_{i,j}(\beta _{i_{j1}},\beta _{i_{j2}})$ and the ring formed by the circular annuli $CA(b_p,C+\delta _1+t\gamma ,C+\delta _1+(t+1)\gamma )$, where $m_{i_1} \le t \le (m_{i_2} -1)$. In fact, estimated minimum expected e-delay of a random node belongs to $SA_{i,j}(\beta _{i_{j1}},\beta _{i_{j2}})$ is proportional to the area induced by the intersection between $SA_{i,j}(\beta _{i_{j1}},\beta _{i_{j2}})$ and the ring formed by the corresponding circular annuli.

Area induced by $SA_{i,j}(C+\delta _1+m_{i_1}\gamma ,C+\delta _1+(m_{i_1}+1)\gamma )$ is $CI(dis_i,dis_i-(C+\delta _1+(m_{i_1}+1)\gamma ))- \frac{1}{\lambda }(k-j)$. Moreover, the area induced by $SA_{i,j}(C+\delta _1+t\gamma ,C+\delta _1+(t+1)\gamma )$ for $m_{i_1} < t \le (m_{i_2}-1)$ is,

$$\begin{aligned} ||SA_{i,j}(C+\delta _1+t\gamma ,C+\delta _1+(t+1)\gamma )|| = CI({dis_i,{dis_i-(C+\delta _1+t\gamma )}}) \\ - \sum \limits _{s = 1}^{t - 1} {\left\| SA_{i,j}(C+\delta _1+s\gamma ,C+\delta _1+(s+1)\gamma ) \right\| }-\frac{1}{\lambda }(k-j). \end{aligned}$$

The probability of node $i_j$ belongs to $SA_{i,j}(C+\delta _1+t\gamma ,C+\delta _1+(t+1)\gamma )$ is $||SA_{i,j}(C+\delta _1+t\gamma ,C+\delta _1+(t+1)\gamma )||\lambda$. Let $D_{i_j,t\gamma }$ denotes the minimum expected e-delay of a random node within $SA_{i,j}(C+\delta _1+t\gamma ,C+\delta _1+(t+1)\gamma )$. Hence, an upper bound for the expected e-delay $D_{i_j}$ of node $i_j$, is $\sum \limits _{t = m_{i_1}}^{(m_{i_2}-1)} {||SA_{i,j}(C+\delta _1+t\gamma ,C+\delta _1+(t+1)\gamma )||\lambda D_{i_j,t\gamma }}$.

We use expected e-delay $D_{i_j}$ of a random node belongs to ${i_j}^{th}$ sectoral annulus, to find the minimum expected e-delay of node i at a distance $dis_i=C+\delta _1+m\gamma$. Consider a randomly chosen node i at a distance $dis_i=C+\delta _1+m\gamma$ from the base-station. We divide the effective forwarding region of communication $EC_i$, into $EC_i*\lambda -1$ sectoral annuli such that every sectoral annulus is expected to contain only one node. Assuming $D_{i_j}$ denotes the estimated minimum expected e-delay for a randomly selected node within circular annulus $i_j$, for $1 \le j \le (EC_i*\lambda - 1)$, which is calculated as shown earlier using the minimum expected e-delay of nodes at distances $C+\delta _1+\gamma ,C+\delta _1+2\gamma ,...,C+\delta _1+(m-1)\gamma$. A linear search over the nodes at every sectoral annulus, with higher priority given to nodes closer to the base-station effectively selects $k'$ required number of nodes in the forwarding set, that minimizes overall e-delay [1]. Hence, minimum expected e-delay of node i is upper bounded by,

$$\begin{aligned} {D_{i,{k'},w}} = {d_{{k'},w}} + \sum \limits _{j = 1}^{k'} {\frac{1}{k'}*{D_{i_j}}}, \end{aligned}$$

(8)

where ${d_{k',w}}=\sum \limits _{h = 1}^{\left\lfloor {\frac{{1/w}}{{{t_I}}}} \right\rfloor } {{P(W_{h,k'})}*h}+t_D$. Hence, follows the theorem.

Theorem 1

Assume $D_{i_j}$ denotes the estimated minimum expected e-delay for a randomly selected node within circular annulus $SA_{i,j}(\beta _{i_{j1}},\beta _{i_{j2}})$ of node i at distance $dis_i=C+\delta _1+m\gamma$ from the base station, for $1 \le j \le (EC_i*\lambda - 1)$. Let $k'$ nodes are included in the forwarding set. An upper bound on minimum expected e-delay of node i is ${D_{i,{k'},w}} = {d_{{k'},w}} + \sum \limits _{j = 1}^{k'} {\frac{1}{k'}*{D_{i_j}}}$, where ${d_{k',w}}=\sum \limits _{h = 1}^{\left\lfloor {\frac{{1/w}}{{{t_I}}}} \right\rfloor } {{P(W_{h,k'})}*h}+t_D$.

In order to estimate the maximum of minimum e-delay in the FoI, we gradually increase the distance (such that $dis_i>\delta _1$) of a random node i from the base-station, by small $\gamma$, and estimate the minimum expected e-delay of a node at this distance. We keep on increasing $dis_i$ till we reach the farthest point which is at a distance equal to the radius of FoI.

In the next section, we use this analysis to find the critical sensor density required to satisfy the given e-delay constraint and lifetime requirement.

4 Critical Sensor Density

Assume sensor nodes are deployed with the initial energy Q and consume average energy E during a wake up interval, the energy required for wake up. Average wake up rate w of a node can be given as $\frac{Q}{LE}$, where L is required lifetime constraint. The expected e-delay $D_e$ of the FoI can be found using the analysis given in the previous section, for a given density. If the maximum of minimum expected e-delay $D_e$ in FoI is greater than the delay constraint D, it is necessary to increase the density. The minimum sensor density $\lambda _m$ is defined as the density required to satisfy the coverage requirement, which can be found using the methods described in [11]. In order to find the critical sensor density $\lambda _c$ required to satisfy given delay D and lifetime constraint L, we formulate the problem as follows.

$$\begin{aligned}&\mathop {\min }\limits _{\lambda _c}\,\{{||A||*{\lambda _{c}}*C} \} \,\,\,\,\,\, subject \,\, to \\&\,\,\,\,\,\, D_{e} \le D, \lambda _{m} \le \lambda _{c},\,\,\, and \,\, D_{e},L,\lambda _{c} > 0, \end{aligned}$$

where C denotes the cost of any sensor.

In order to find an upper bound $\lambda _u$ for the critical sensor density that satisfies given delay constraint D and lifetime requirement L, we exponentially increase the density $\lambda$ from $\lambda _m$ and find $\lambda _{u}$ that satisfies the delay constraint using Sect. 3.2, with the average wake up rate $w=\frac{Q}{LE}$. Next we use binary search between $\lambda _u$ and $\frac{\lambda _u}{2}$ to find the critical sensor density $\lambda _c$ that minimizes the overall deployment cost.

5 Validation

In order to verify the estimation of the maximum of minimum expected e-delay and the critical sensor density for given delay and lifetime constraints, we evaluate numerically the methods described in Sects. 3.2 and 4, and compare these with that obtained in a ns2 simulation.

We deploy sensor nodes with 200 m communication range, using uniform distribution in a circular shaped FoI of radius 1000 m. For simplicity we place the base-station at the center of the FoI. We set data-rate to be 19.2 kbps. We also set respectively transmission and receiving/idle power as 19.5 mW and 13.0 mW. The data and beacon/control packet length is set to 8 byte and 3 byte, respectively. The sensor nodes follow anycasting forwarding strategy [1].

Fig. 3.

Validating the estimated expected e-delay

5.1 Validating Estimated Expected E-Delay

In this section we validate the estimated maximum of minimum expected e-delay obtained from numerical evaluation given in Sect. 3.2 and compare it with simulation results. In order to calculate the maximum of minimum e-delay in each experiment, we select the farthest node from the base-station and calculate its average e-delay by simulating 100 events originating at this node. We repeat the experiment for 100 times by changing the seed of uniform deployment. The average of maximum e-delay of the simulation results along with the numerical estimations are shown in Fig. 3. Our numerical estimation are close to the simulation results for various scenarios.

Impact of wake up interval: The average maximum e-delay for different wake up intervals are shown in Fig. 3(a), for 1000 nodes. As wake up interval increases, average maximum e-delay also increases. This is because, if wake up interval increases, expected one-hop delay increases, which in-turn increases e-delay. It can also be noted that the estimation results are always higher than the simulation results.

Impact of density: In order to show the effectiveness of our approach at different densities, we varied the number of nodes deployed. For a fixed wake up interval 500 ms results are shown in Fig. 3(b). Note that, increasing the number of nodes in the given FoI, decreases expected one hop delay, which in turn decreases expected e-delay. The percentage of over estimation on maximum expected e-delay is almost same for different densities.

Impact of FoI: The average maximum e-delay for different areas of FoI are shown in Fig. 3(c), for a wake up interval 500 ms. As radius of circular shaped FoI increases with fixed density, e-delay also increases rapidly. This is because, if the radius of FoI increases, maximum number of hops from the farthest node increases as well, which in turn increases e-delay. Moreover, it can also be noted that the estimation results are always higher than the simulation results.

5.2 Validating Critical Sensor Density

In this section we validate the estimated critical sensor density $\lambda _c$, for given delay and lifetime constraints, obtained from numerical evaluation given in Sect. 4 and compare it with simulation results. We gradually increase the sensor density and find the critical sensor density that satisfies given delay constraint and lifetime requirement using simulation. Our numerical estimation is close to the simulation results for various scenarios.

Impact of E-delay: We compare the numerically estimated critical sensor density with that of simulation, for different delay constraint and fixed wake up interval 500 ms(refer Fig. 4(a)). As given e-delay constraint increases, critical sensor density decreases. This is because, increasing critical sensor density decreases expected one hop delay, which in turn decreases expected e-delay.

Fig. 4.

Validating critical sensor

Impact of lifetime: Critical sensor densities for different lifetime requirements are shown in Fig. 4(b), for a fixed delay constraint as 10 ms. When lifetime requirement increases, the critical sensor density also increases. This is because, increasing lifetime decrease wake up interval, which in turn decreases expected one-hop and e-delay. In order to maintain the given delay constraint, the critical sensor density needs to be increased.

6 Conclusion and Future Work

In this work we estimated the maximum expected e-delay for circular shaped FoI with given density and used this analysis to find the critical sensor density that satisfies given delay constraint and lifetime requirement. Similar analysis can be extended to estimate the critical sensor density for a convex-shaped FoI. In a convex-shaped FoI, for a node i, the actual effective forwarding area of communication is nothing but the intersection of the given FoI and the effective forwarding area of communication. We also believe that this work would motivate further research in estimating critical sensor density problem for heterogeneous WSNs. Note that we assumed the communication range to be 2-D in our analysis. Whereas, our work can also be extended for a WSN consists of sensor nodes with 3-D communication range.