Basket Option Pricing and Implied Correlation in a One-Factor Lévy Model

Abstract

In this paper we employ a one-factor Lévy model to determine basket option prices. More precisely, basket option prices are determined by replacing the distribution of the real basket with an appropriate approximation. For the approximate basket we determine the underlying characteristic function and hence we can derive the related basket option prices by using the Carr–Madan formula. We consider a three-moments-matching method. Numerical examples illustrate the accuracy of our approximations; several Lévy models are calibrated to market data and basket option prices are determined. In the last part we show how our newly designed basket option pricing formula can be used to define implied Lévy correlation by matching model and market prices for basket options. Our main finding is that the implied Lévy correlation smile is flatter than its Gaussian counterpart. Furthermore, if (near) at-the-money option prices are used, the corresponding implied Gaussian correlation estimate is a good proxy for the implied Lévy correlation.

1 Introduction

Nowadays, an increased volume of multi-asset derivatives is traded. An example of such a derivative is a basket option. The basic version of such a multivariate product has the same characteristics as a vanilla option, but now the underlying is a basket of stocks instead of a single stock. The pricing of these derivatives is not a trivial task because it requires a model that jointly describes the stock prices involved.

Stock price models based on the lognormal model proposed in Black and Scholes [6] are popular choices from a computational point of view; however, they are not capable of capturing the skewness and kurtosis observed for log returns of stocks and indices. The class of Lévy processes provides a much better fit for the observed log returns and, consequently, the pricing of options and other derivatives in a Lévy setting is much more reliable. In this paper we consider the problem of pricing multi-asset derivatives in a multivariate Lévy model.

The most straightforward extension of the univariate Black and Scholes model is based on the Gaussian copula model, also called the multivariate Black and Scholes model. In this framework, the stocks composing the basket at a given point in time are assumed to be lognormally distributed and a Gaussian copula is connecting these marginals. Even in this simple setting, the price of a basket option is not given in a closed form and has to be approximated; see e.g. Hull and White [23], Brooks et al. [8], Milevsky and Posner [39], Rubinstein [42], Deelstra et al. [18], Carmona and Durrleman [12] and Linders [29], among others. However, the normality assumption for the marginals used in this pricing framework is too restrictive. Indeed, in Linders and Schoutens [30] it is shown that calibrating the Gaussian copula model to market data can lead to non-meaningful parameter values. This dysfunctioning of the Gaussian copula model is typically observed in distressed periods. In this paper we extend the classical Gaussian pricing framework in order to overcome this problem.

Several extensions of the Gaussian copula model are proposed in the literature. For example, Luciano and Schoutens [32] introduce a multivariate Variance Gamma model where dependence is modeled through a common jump component. This model was generalized in Semeraro [44], Luciano and Semeraro [33], and Guillaume [21]. A stochastic correlation model was considered in Fonseca et al. [19]. A framework for modeling dependence in finance using copulas was described in Cherubini et al. [14]. The pricing of basket options in these advanced multivariate stock price models is not a straightforward task. There are several attempts to derive closed form approximations for the price of a basket option in a non-Gaussian world. In Linders and Stassen [31], approximate basket option prices in a multivariate Variance Gamma model are derived, whereas Xu and Zheng [48, 49] consider a local volatility jump diffusion model. McWilliams [38] derives approximations for the basket option price in a stochastic delay model. Upper and lower bounds for basket option prices in a general class of stock price models with known joint characteristic function of the logreturns are derived in Caldana et al. [10].

In this paper we start from the one-factor Lévy model introduced in Albrecher et al. [1] to build a multivariate stock price model with correlated Lévy marginals. Stock prices are assumed to be driven by an idiosyncratic and a systematic factor. The idea of using a common market factor is not new in the literature and goes back to Vasicek [47]. Conditional on the common (or market) factor, the stock prices are independent. We show that our model generalizes the Gaussian model (with single correlation). Indeed, the idiosyncratic and systematic components are constructed from a Lévy process. Employing a Brownian motion in that construction delivers the Gaussian copula model, but other Lévy models arise by employing different Lévy processes like VG, NIG, Meixner, etc. As a result, this new one-factor Lévy model is more flexible and can capture other types of dependence.

The correlation is by construction always positive and, moreover, we assume a single correlation. Stocks can, in reality, be negatively correlated and correlations between different stocks will differ. From a tractability point of view, however, reporting a single correlation number is often preferred over $n(n-1)/2$ pairwise correlations. The single correlation can be interpreted as a mean level of correlation and provides information about the general dependence among the stocks composing the basket. Such a single correlation appears, for example, in the construction of a correlation swap. Therefore, our framework may have applications in the pricing of such correlation products. Furthermore, calibrating a full correlation matrix may require an unrealistically large amount of data if the index consists of many stocks.

In the first part of this paper, we consider the problem of finding accurate approximations for the price of a basket option in the one-factor Lévy model. In order to value a basket option, the distribution of this basket has to be determined. However, the basket is a weighted sum of dependent stock prices and its distribution function is in general unknown or too complex to work with. Our valuation formula for the basket option is based on a moment-matching approximation. To be more precise, the (unknown) basket distribution is replaced by a shifted random variable having the same first three moments than the original basket. This idea was first proposed in Brigo et al. [7], where the Gaussian copula model was considered. Numerical examples illustrating the accuracy and the sensitivity of the approximation are provided.

In the second part of the paper we show how the well-established notions of implied volatility and implied correlation can be generalized in our multivariate Lévy model. We assume that a finite number of options, written on the basket and the components, are traded. The prices of these derivatives are observable and will be used to calibrate the parameters of our stock price model. An advantage of our modeling framework is that each stock is described by a volatility parameter and that the marginal parameters can be calibrated separately from the correlation parameter. We give numerical examples to show how to use the vanilla option curves to determine an implied Lévy volatility for each stock based on a Normal, VG, NIG, and Meixner process and determine basket option prices for different choices of the correlation parameter.

An implied Lévy correlation estimate arises when we tune the single correlation parameter such that the model price exactly hits the market price of a basket option for a given strike. We determine implied correlation levels for the stocks composing the Dow Jones Industrial Average in a Gaussian and a Variance Gamma setting. We observe that implied correlation depends on the strike and in the VG model, this implied Lévy correlation smile is flatter than in the Gaussian copula model. The standard technique to price non-traded basket options (or other multi-asset derivatives) is by interpolating on the implied correlation curve. It is shown in Linders and Schoutens [30] that in the Gaussian copula model, this technique can sometimes lead to non-meaningful correlation values. We show that the Lévy version of the implied correlation solves this problem (at least to some extent). Several papers consider the problem of measuring implied correlation between stock prices; see e.g. Fonseca et al. [19], Tavin [46], Ballotta et al. [4], and Austing [2]. Our approach is different in that we determine implied correlation estimates in the one-factor Lévy model using multi-asset derivatives consisting of many assets (30 assets for the Dow Jones). When considering multi-asset derivatives with a low dimension, determining the model prices of these multi-asset derivatives becomes much more tractable. A related paper is Linders and Stassen [31], where the authors also use high-dimensional multi-asset derivative prices for calibrating a multivariate stock price model. However, whereas the current paper models the stock returns using correlated Lévy distributions, the cited paper uses time-changed Brownian motions with a common time change.

2 The One-Factor Lévy Model

We consider a market where n stocks are traded. The price level of stock j at some future time $t,\ 0\le t \le T$ is denoted by $S_j(t)$. Dividends are assumed to be paid continuously and the dividend yield of stock j is constant and deterministic over time. We denote this dividend yield by $q_j$. The current time is $t=0$. We fix a future time T and we always consider the random variables $S_j(T)$ denoting the time-T prices of the different stocks involved. The price level of a basket of stocks at time T is denoted by S(T) and given by

$$ S(T)=\sum _{j=1}^n w_j S_j(T), $$

where $w_j>0$ are weights which are fixed upfront. In case the basket represents the price of the Dow Jones, the weights are all equal. If this single weight is denoted by w, then 1 / w is referred to as the Dow Jones Divisor.¹ The pay-off of a basket option with strike K and maturity T is given by $\left( S(T)-K \right) _+$, where $(x)_+=\max (x,0).$ The price of this basket option is denoted by C[K, T]. We assume that the market is arbitrage-free and that there exists a risk-neutral pricing measure $\mathbb {Q}$ such that the basket option price C[K, T] can be expressed as the discounted risk-neutral expected value. In this pricing formula, discounting is performed using the risk-free interest rate r, which is, for simplicity, assumed to be deterministic and constant over time. Throughout the paper, we always assume that all expectations we encounter are well-defined and finite.

2.1 The Model

The most straightforward way to model dependent stock prices is to use a Black and Scholes model for the marginals and connect them with a Gaussian copula. A crucial (and simplifying) assumption in this approach is the normality assumption. It is well-known that log returns do not pass the test for normality. Indeed, log returns exhibit a skewed and leptokurtic distribution which cannot be captured by a normal distribution; see e.g. Schoutens [43].

We generalize the Gaussian copula approach by allowing the risk factors to be distributed according to any infinitely divisible distribution with known characteristic function. This larger class of distributions increases the flexibility to find a more realistic distribution for the log returns. In Albrecher et al. [1] a similar framework was considered for pricing CDO tranches; see also Baxter [5]. The Variance Gamma case was considered in Moosbrucker [40, 41], whereas Guillaume et al. [22] consider the pricing of CDO-squared tranches in this one-factor Lévy model. A unified approach for these CIID models (conditionally independent and identically distributed) is given in Mai et al. [36].

Consider an infinitely divisible distribution for which the characteristic function is denoted by $\phi$. A stochastic process X can be built using this distribution. Such a process is called a Lévy process with mother distribution having the characteristic function $\phi$. The Lévy process $X=\left\{ X(t) | t \ge 0 \right\}$ based on this infinitely divisible distribution starts at zero and has independent and stationary increments. Furthermore, for $s,t \ge 0$ the characteristic function of the increment $X(t+s)-X(t)$ is $\phi ^s$.

Assume that the random variable L has an infinitely divisible distribution and denote its characteristic function by $\phi _L$. Consider the Lévy process $X=\left\{ X(t) | t \in [0,1] \right\}$ based on the distribution L. We assume that the process is standardized, i.e. $\mathbb {E}[X(1)]=0$ and $\text {Var}[X(1)]=1$. One can then show that $\text {Var}[X(t)]=t$, for $t\ge 0$. Define also a series of independent and standardized processes $X_j=\left\{ X_j(t) | t \in [0,1] \right\}$, for $j=1,2,\ldots , n$. The process $X_j$ is based on an infinitely divisible distribution $L_j$ with characteristic function $\phi _{L_j}$. Furthermore, the processes $X_1, X_2, \ldots ,X_n$ are independent from X. Take $\rho \in [0,1]$. The r.v. $A_j$ is defined by

$$\begin{aligned} A_j=X(\rho ) + X_j(1-\rho ), \quad j=1,2,\ldots n. \end{aligned}$$

(1)

In this construction, $X(\rho )$ and $X_j(1-\rho )$ are random variables having the characteristic function $\phi _L^{\rho }$ and $\phi _{L_j}^{1-\rho }$, respectively. Denote the characteristic function of $A_j$ by $\phi _{A_j}$. Because the processes X and $X_j$ are independent and standardized, we immediately find that

$$\begin{aligned} \mathbb {E}[A_j]=0,\quad \text {Var}[A_j]=1\quad \text {and} \quad {\phi _{A_j}(t)=\phi _L^{\rho }(t)\phi _{L_j}^{1-\rho }(t),\quad \text {for}\ j=1,2,\ldots ,n.} \end{aligned}$$

(2)

Note that if X and $X_j$ are both Lévy processes based on the same mother distribution L, we obtain the equality $A_j\overset{\text {d}}{=}L$.

The parameter $\rho$ describes the correlation between $A_i$ and $A_j$, if $i\ne j$. Indeed, it was proven in Albrecher et al. [1] that in case $A_j$, $j=1,2,\ldots ,n$ is defined by (1), we have that

$$\begin{aligned} \text {Corr}\left[ A_i,A_j \right] =\rho . \end{aligned}$$

(3)

We model the stock price levels $S_j(T)$ at time T for $j=1,2,\ldots ,n$ as follows

$$\begin{aligned} S_j(T)=S_j(0)\text {e}^{\mu _j T+\sigma _j\sqrt{T} A_j},\quad j=1,2,\ldots ,n, \end{aligned}$$

(4)

where $\mu _j \in \mathbb {R}$ and $\sigma _j >0$. Note that in this setting, each time-T stock price is modeled as the exponential of a Lévy process. Furthermore, a drift $\mu _j$ and a volatility parameter $\sigma _j$ are added to match the characteristics of stock j. Our model, which we will call the one-factor Lévy model, can be considered as a generalization of the Gaussian model. Indeed, instead of a normal distribution, we allow for a Lévy distribution, while the Gaussian copula is generalized to a Lévy-based copula.² This model can also, at least to some extent, be considered as a generalization to the multidimensional case of the model proposed in Corcuera et al. [17] and the parameter $\sigma _j$ in (4) can then be interpreted as the Lévy space (implied) volatility of stock j. The idea of building a multivariate asset model by taking a linear combination of a systematic and an idiosyncratic process can also be found in Kawai [26] and Ballotta and Bonfiglioli [3].

2.2 The Risk-Neutral Stock Price Processes

If we take

$$\begin{aligned} \mu _j=(r-q_j)-\frac{1}{T}\log \phi _L\left( -\textsf {i}\sigma _j\sqrt{T}\right) , \end{aligned}$$

(5)

we find that

$$ \mathbb {E}[S_j(T)]=\text {e}^{(r-q_j)T}S_j(0), \quad j=1,2,\ldots ,n. $$

From expression (5) we conclude that the risk-neutral dynamics of the stocks in the one-factor Lévy model are given by

$$\begin{aligned} S_j(T)=S_j(0)\text {e}^{(r-q_j-\omega _j)T+\sigma _j\sqrt{T} A_j}, \quad j=1,2,\ldots ,n, \end{aligned}$$

(6)

where $\omega _j=\log \phi _L\left( -\textsf {i}\sigma _j\sqrt{T}\right) /T$. We always assume $\omega _j$ to be finite. The first three moments of $S_j(T)$ can be expressed in terms of the characteristic function $\phi _{A_j}$. By the martingale property, we have that $\mathbb {E}\left[ S_j(T)\right] =S_j(0)\text {e}^{(r-q_j)T}$. The risk-neutral variance $\text {Var}\left[ S_j(T) \right]$ can be written as follows

$$\begin{aligned} \text {Var}\left[ S_j(T) \right] =S_j(0)^2\text {e}^{2(r-q_j)T}\left( \text {e}^{-2\omega _j T}\phi _{A_j}\left( -\textsf {i}2\sigma _j \sqrt{T} \right) -1\right) . \end{aligned}$$

The second and third moment of $S_j(T)$ are given by:

$$\begin{aligned} \mathbb {E}\left[ S_j(T)^2 \right]= & {} \mathbb {E}[S_j(T)]^2\frac{\phi _{A_j}\left( -\textsf {i}2\sigma _j\sqrt{T} \right) }{\phi _{A_j}\left( -\textsf {i}\sigma _j\sqrt{T} \right) ^2},\\ \mathbb {E}\left[ S_j(T)^3 \right]= & {} \mathbb {E}[S_j(T)]^3\frac{\phi _{A_j}\left( -\textsf {i}3\sigma _j\sqrt{T} \right) }{\phi _{A_j}\left( -\textsf {i}\sigma _j\sqrt{T} \right) ^3}. \end{aligned}$$

We always assume that these quantities are finite. If the process $X_j$ has mother distribution L, we can replace $\phi _{A_j}$ by $\phi _L$ in expression (5) and in the formulas for $\mathbb {E}\left[ S_j(T)^2 \right]$ and $\mathbb {E}\left[ S_j(T)^3 \right]$. From here on, we always assume that all Lévy processes are built on the same mother distribution. However, all results remain to hold in the more general case.

3 A Three-Moments-Matching Approximation

In order to price a basket option, one has to know the distribution of the random sum S(T), which is a weighted sum of dependent random variables. This distribution is in most situations unknown or too cumbersome to work with. Therefore, we search for a new random variable which is sufficiently ‘close’ to the original random variable, but which is more attractive to work with. More concretely, we introduce in this section a new approach for approximating C[K, T] by replacing the sum S(T) with an appropriate random variable $\widetilde{S}(T)$ which has a simpler structure, but for which the first three moments coincide with the first three moments of the original basket S(T). This moment-matching approach was also considered in Brigo et al. [7] for the multivariate Black and Scholes model.

Consider the Lévy process $Y=\left\{ Y(t) \mid 0 \le t \le 1 \right\}$ with infinitely divisible distribution L. Furthermore, we define the random variable A as

$$ A=Y(1). $$

In this case, the characteristic function of A is given by $\phi _L$. The sum S(T) is a weighted sum of dependent random variables and its cdf is unknown. We approximate the sum S(T) by $\widetilde{S}(T)$, defined by

$$\begin{aligned} \widetilde{S}(T)=\bar{S}(T)+\lambda , \end{aligned}$$

(7)

where $\lambda \in \mathbb {R}$ and

$$\begin{aligned} \bar{S}(T)=S(0)\exp \left\{ (\bar{\mu }-\bar{\omega })T+\bar{\sigma }\sqrt{T}A\right\} . \end{aligned}$$

(8)

The parameter $\bar{\mu } \in \mathbb {R}$ determines the drift and $\bar{\sigma }>0$ is the volatility parameter. These parameters, as well as the shifting parameter $\lambda$, are determined such that the first three moments of $\widetilde{S}(T)$ coincide with the corresponding moments of the real basket S(T). The parameter $\bar{\omega }$, defined as follows

$$ \bar{\omega }=\frac{1}{T}\log \phi _L\left( -\textsf {i}\bar{\sigma }\sqrt{T} \right) , $$

is assumed to be finite.

3.1 Matching the First Three Moments

The first three moments of the basket S(T) are denoted by $m_1, m_2$, and $m_3$ respectively. In the following lemma, we express the moments $m_1, m_2$, and $m_3$ in terms of the characteristic function $\phi _L$ and the marginal parameters. A proof of this lemma is provided in the appendix.

Lemma 1

Consider the one-factor Lévy model (6) with infinitely divisible mother distribution L. The first two moments $m_1$ and $m_2$ of the basket S(T) can be expressed as follows

$$\begin{aligned} m_1= & {} \sum _{j=1}^n w_j \mathbb {E}\left[ S_j(T) \right] , \end{aligned}$$

(9)

$$\begin{aligned} m_2= & {} \sum _{j=1}^n\sum _{k=1}^n w_j w_k \mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] \left( \frac{\phi _L\left( -\textsf {i}(\sigma _j+\sigma _k)\sqrt{T} \right) }{\phi _L\left( -\textsf {i}\sigma _j\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k\sqrt{T} \right) }\right) ^{\rho _{j,k}}, \end{aligned}$$

(10)

where

$$ \rho _{j,k} = \left\{ \begin{array}{ll} \rho , &{}\text {if}\ j\ne k; \\ 1, &{} \text {if}\ j = k. \end{array} \right. $$

The third moment $m_3$ of the basket S(T) is given by

$$\begin{aligned} m_3= & {} \sum _{j=1}^n\sum _{k=1}^n \sum _{l=1}^n w_j w_k w_l \mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] \mathbb {E}\left[ S_l(T) \right] \nonumber \\&\times \frac{\phi _L\left( -\textsf {i}\left( \sigma _j + \sigma _k + \sigma _l \right) \sqrt{T}\right) ^{\rho }}{\phi _L\left( -\textsf {i}\sigma _j\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _l\sqrt{T} \right) } A_{j,k,l}, \end{aligned}$$

(11)

where

$$ A_{j,k,l} = \left\{ \begin{array}{ll} \left( \phi _L\left( -\textsf {i}\sigma _j\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _l\sqrt{T} \right) \right) ^{1-\rho }, &{} \text {if}\ j\ne k, k\ne l\text { and }j\ne l; \\ \left( \phi _L\left( -\textsf {i}(\sigma _j+\sigma _k)\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _l\sqrt{T} \right) \right) ^{1-\rho }, &{} \text {if}\ j = k, k\ne l; \\ \left( \phi _L\left( -\textsf {i}(\sigma _k+\sigma _l)\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _j\sqrt{T} \right) \right) ^{1-\rho }, &{} \text {if}\ j \ne k, k= l; \\ \left( \phi _L\left( -\textsf {i}(\sigma _j+\sigma _l)\sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k\sqrt{T} \right) \right) ^{1-\rho }, &{} \text {if}\ j = l, k\ne l; \\ \phi _L\left( -\textsf {i}\left( \sigma _j + \sigma _k + \sigma _l \right) \sqrt{T}\right) ^{1-\rho }, &{} \text {if}\ j = k=l. \end{array} \right. $$

In Sect. 2.2 we derived the first three moments for each stock j, $j=1,2,\ldots ,n$. Taking into account the similarity between the price $S_j(T)$ defined in (6) and the approximate r.v. $\bar{S}(T)$, defined in (8), we can determine the first three moments of $\bar{S}(T)$:

$$\begin{aligned} \mathbb {E}\left[ \bar{S}(T) \right]= & {} S(0)\text {e}^{\bar{\mu }T}=:\xi ,\\ \mathbb {E}\left[ \bar{S}(T)^2 \right]= & {} \mathbb {E}\left[ \bar{S}(T) \right] ^2 \frac{\phi _L\left( -\textsf {i}2\bar{\sigma }\sqrt{T} \right) }{\phi _L\left( -\textsf {i}\bar{\sigma }\sqrt{T} \right) ^2}=:\xi ^2\alpha , \\ \mathbb {E}\left[ \bar{S}(T)^3 \right]= & {} \mathbb {E}\left[ \bar{S}(T) \right] ^3 \frac{\phi _L\left( -\textsf {i}3\bar{\sigma }\sqrt{T} \right) }{\phi _L\left( -\textsf {i}\bar{\sigma }\sqrt{T} \right) ^3}=:\xi ^3\beta . \end{aligned}$$

These expressions can now be used to determine the first three moments of the approximate r.v. $\widetilde{S}(T)$:

$$\begin{aligned} \mathbb {E}\left[ \widetilde{S}(T) \right]= & {} \mathbb {E}\left[ \bar{S}(T) \right] + \lambda , \\ \mathbb {E}\left[ \widetilde{S}(T)^2 \right]= & {} \mathbb {E}\left[ \bar{S}(T)^2 \right] + \lambda ^2 + 2\lambda \mathbb {E}\left[ \bar{S}(T)\right] , \\ \mathbb {E}\left[ \widetilde{S}(T)^3 \right]= & {} \mathbb {E}\left[ \bar{S}(T)^3 \right] + \lambda ^3 + 3\lambda ^2 \mathbb {E}\left[ \bar{S}(T)\right] +3\lambda \mathbb {E}\left[ \bar{S}(T)^2\right] . \end{aligned}$$

Determining the parameters $\bar{\mu }$, $\bar{\sigma }$ and the shifting parameter $\lambda$ by matching the first three moments, results in the following set of equations

$$\begin{aligned} m_1= & {} \xi +\lambda , \\ m_2= & {} \xi ^2\alpha + \lambda ^2 + 2\lambda \xi , \\ m_3= & {} \xi ^3 \beta + \lambda ^3 +3\lambda ^2\xi + 3\lambda \xi ^2\alpha . \end{aligned}$$

These equations can be recast in the following set of equations

$$\begin{aligned} \lambda= & {} m_1- \xi , \\ \xi ^2= & {} \frac{m_2-m_1^2}{\alpha -1}, \\ 0= & {} \left( \frac{m_2-m_1^2}{\alpha -1} \right) ^{3/2}\left( \beta + 2-3\alpha \right) +3m_1m_2-2m_1^3-m_3. \end{aligned}$$

Remember that $\alpha$ and $\beta$ are defined by

$$ \alpha =\frac{\phi _L\left( -\textsf {i}2\bar{\sigma }\sqrt{T}\right) }{\phi _L\left( -\textsf {i}\bar{\sigma }\sqrt{T}\right) ^2} \quad \text {and}\quad \beta =\frac{\phi _L\left( -\textsf {i}3\bar{\sigma }\sqrt{T}\right) }{\phi _L\left( -\textsf {i}\bar{\sigma }\sqrt{T}\right) ^3}. $$

Solving the third equation results in the parameter $\bar{\sigma }$. Note that this equation does not always have a solution. This issue was also discussed in Brigo et al. [7] for the Gaussian copula case. However, in our numerical studies we did not encounter any numerical problems. If we know $\bar{\sigma }$, we can also determine $\xi$ and $\lambda$ from the first two equations. Next, the drift $\bar{\mu }$ can be determined from

$$ \bar{\mu }=\frac{1}{T}\log \frac{\xi }{S(0)}. $$

3.2 Approximate Basket Option Pricing

The price of a basket option with strike K and maturity T is denoted by C[K, T]. This unknown price is approximated in this section by $C^{MM}[K,T]$, which is defined as

$$ C^{MM}[K,T] = \text {e}^{-rT}\mathbb {E}\left[ \left( \widetilde{S}(T)-K\right) _+ \right] . $$

Using expression (7) for $\widetilde{S}(T)$, the price $C^{MM}[K,T]$ can be expressed as

$$ C^{MM}[K,T] = \text {e}^{-rT}\mathbb {E}\left[ \left( \bar{S}(T)-(K-\lambda )\right) _+ \right] . $$

Note that the distribution of $\bar{S}(T)$ is also depending on the choice of $\lambda$. In order to determine the price $C^{MM}[K,T]$, we should be able to price an option written on $\bar{S}(T)$, with a shifted strike $K-\lambda$. Determining the approximation $C^{MM}[K,T]$ using the Carr–Madan formula requires knowledge about the characteristic function $\phi _{\log \bar{S}(T)}$ of $\log \bar{S}(T)$:

$$ \phi _{\log \bar{S}(T)}(u)=\mathbb {E}\left[ \text {e}^{\textsf {i}u\log \bar{S}(T)} \right] . $$

Using expression (8) we find that

$$ \phi _{\log \bar{S}(T)}(u)=\mathbb {E}\left[ \exp \left\{ \textsf {i}u\left( \log S(0) + (\bar{\mu } -\bar{\omega })T +\bar{\sigma }\sqrt{T}A\right) \right\} \right] . $$

The characteristic function of A is $\phi _L$, from which we find that

$$ \phi _{\log \bar{S}(T)}(u)=\exp \left\{ \textsf {i}u\left( \log S(0) + (\bar{\mu } -\bar{\omega })T\right) \right\} \phi _L\left( u\bar{\sigma }\sqrt{T} \right) . $$

Note that nowhere in this section we used the assumption that the basket weights $w_j$ are strictly positive. Therefore, the three-moments-matching approach proposed in this section can also be used to price, e.g. spread options. However, for pricing spread options, alternative methods exist; see e.g. Carmona and Durrleman [11], Hurd and Zhou [24] and Caldana and Fusai [9].

3.3 The FFT Method and Basket Option Pricing

Consider the random variable X. In this section we show that if the characteristic function $\phi _{\log X}$ of this r.v. X is known, one can approximate the discounted stop-loss premium

$$ \text {e}^{-rT}\mathbb {E}\left[ \left( X-K \right) _+\right] , $$

for any $K>0$.

Let $\alpha >0$ and assume that $\mathbb {E}\left[ X^{\alpha +1} \right]$ exists and is finite. It was proven in Carr and Madan [13] that the price $\text {e}^{-rT}\mathbb {E}\left[ \left( X-K \right) _+\right]$ can be expressed as follows

$$\begin{aligned} \text {e}^{-rT}\mathbb {E}\left[ \left( X-K \right) _+\right] = \frac{\text {e}^{-\alpha \log (K)}}{\pi }\int _0^{+\infty }\exp \left\{ -\textsf {i}v \log (K) \right\} g(v)\text {d}v, \end{aligned}$$

(12)

where

$$\begin{aligned} g(v)=\frac{\text {e}^{-rT}\phi _{\log X}\left( v-(\alpha +1)\textsf {i} \right) }{\alpha ^2+\alpha -v^2+\textsf {i}(2\alpha +1)v}. \end{aligned}$$

(13)

The approximation $C^{MM}[K,T]$ was introduced in Sect. 3 and the random variable X now denotes the moment-matching approximation $\widetilde{S}(T)=\bar{S}(T)+\lambda$. The approximation $C^{MM}[K,T]$ can then be determined as the option price written on $\bar{S}(T)$ and with shifted strike price $K-\lambda$.

4 Examples and Numerical Illustrations

The Gaussian copula model with equicorrelation is a member of our class of one-factor Lévy models. In this section we discuss how to build the Gaussian, Variance Gamma, Normal Inverse Gaussian, and Meixner models. However, the reader is invited to construct one-factor Lévy models based on other Lévy-based distributions; e.g. CGMY, Generalized hyperbolic, etc. distributions.

Table 1 Overview of infinitely divisible distributions

Table 1 summarizes the Gaussian, Variance Gamma, Normal Inverse Gaussian, and the Meixner distributions, which are all infinitely divisible. In the last row, it is shown how to construct a standardized version for each of these distributions. We assume that L is distributed according to one of these standardized distributions. Hence, L has zero mean and unit variance. Furthermore, the characteristic function $\phi _L$ of L is given in closed form. We can then define the Lévy processes X and $X_j$, $j=1,2,\ldots ,n$ based on the mother distribution L. The random variables $A_j$, $j=1,2,\ldots ,n$, are modeled using expression (1).

4.1 Variance Gamma

Although pricing basket option under a normality assumption is tractable from a computational point of view, it introduces a high degree of model risk; see e.g. Leoni and Schoutens [28]. The Variance Gamma distribution has already been proposed as a more flexible alternative to the Brownian setting; see e.g. Madan and Seneta [34] and Madan et al. [35].

Table 2 Basket option prices in the one-factor VG model with $S_1(0)=40,\ S_2(0)=50,\ S_3(0)=60,\ S_4(0)=70$, and $\rho =0$

We consider two numerical examples where L has a Variance Gamma distribution with parameters $\sigma = 0.5695, \nu = 0.75, \theta = -0.9492, \mu = 0.9492$. Table 2 contains the numerical values for the first illustration, where a four-basket option paying $\left( \frac{1}{4}\sum _{j=1}^4 S_j(T)-K\right) _+$ at time T is considered. We use the following parameter values: $r=6\,\%$, $T=0.5$, $\rho =0$ and $S_1(0)=40,\ S_2(0)=50,\ S_3(0)=60,\ S_4(0)=70$. These parameter values are also used in Sect. 5 of Korn and Zeytun [27]. We denote by $C^{mc}[K,T]$ the corresponding Monte Carlo estimate for the price C[K, T]. Here, $10^7$ number of simulations are used. The approximation of the basket option price C[K, T] using the moment-matching approach outlined in Sect. 3 is denoted by $C^{MM}[K,T]$. A comparison between the empirical density and the approximate density is provided in Fig. 1.

In the second example, we consider the basket $S\left( T\right) =w_{1}X_{1}\left( T\right) +w_{2}X_{2}\left( T\right) ,$ written on two non-dividend paying stocks. We use as parameter values the ones also used in Sect. 7 of Deelstra et al. [18], hence $r=5\,\%$, $X_{1}\left( 0\right) =X_{2}\left( 0\right) =100$, and $w_{1}=w_{2}=0.5.$ Table 3 gives numerical values for these basket options. Note that strike prices are expressed in terms of forward moneyness. A basket strike price K has forward moneyness equal to $K/ \mathbb {E}\left[ S\right] .$ We can conclude that the three-moments-matching approximation gives acceptable results. For far out-of-the-money call options, the approximation is not always able to closely approximate the real basket option price.

We also investigate the sensitivity with respect to the Variance Gamma parameters $\sigma , \nu$, and $\theta$ and to the correlation parameter $\rho$. We consider a basket option consisting of 3 stocks, i.e. $n=3$. From Tables 2 and 3, we observe that the error is the biggest in case we consider different marginal volatilities and the option under consideration is an out-of-the-money basket call. Therefore, we put $\sigma _1=0.2, \sigma _2=0.4, \sigma _3=0.6$ and we determine the prices $C^{mc}[K,T]$ and $C^{MM}[K,T]$ for $K=105.13$. The other parameter values are: $r=0.05, \rho =0.5, w_1=w_2=w_3=1/3$ and $T=1$. The first panel of Fig. 2 shows the relative error for varying $\sigma$. The second panel of Fig. 2 shows the relative error in function of $\nu$. The sensitivity with respect to $\theta$ is shown in the third panel of Fig. 2. Finally, the fourth panel of Fig. 2 shows the relative error in function of $\rho$.

The numerical results show that the approximations do not always manage to closely approximate the true basket option price. Especially when some of the volatilities deviate substantially from the other ones, the accuracy of the approximation deteriorates. The dysfunctioning of the moment-matching approximation in the Gaussian copula model was already reported in Brigo et al. [7]. However, in order to calibrate the Lévy copula model to available option data, the availability of a basket option pricing formula which can be evaluated in a fast way, is of crucial importance. Table 4 shows the CPU times³ for the one-factor VG model for different basket dimensions. The calculation time of approximate basket option prices when 100 stocks are involved is less than one second. Therefore, the moment-matching approximation is a good candidate for calibrating the one-factor Lévy model.

Fig. 1

Probability density function of the real basket (solid line) and the approximate basket (dashed line). The basket option consists of 4 stocks and $r=0.06, \rho =0, T=1/2, w_1=w_2=w_3=w_4=\frac{1}{4}$. All volatility parameters are equal to $\sigma$

Table 3 Basket option prices in the one-factor VG model with $r=0.05, w_1=w_2=0.5, X_1(0)=X_2(0)=100$ and $\sigma _1=\sigma _2$

Fig. 2

Relative error in the one-factor VG model for the three-moments-matching approximation. The basket option consists of 3 stocks and $r=0.05, \rho =0.5, T=1, \sigma _1=0.2, \sigma _2=0.4, \sigma _3=0.6, w_1=w_2=w_3=\frac{1}{3}$. The strike price is $K=105.13$. In the benchmark model, the VG parameters are $\sigma = 0.57, \nu = 0.75, \theta = -0.95, \mu = 0.95$

Table 4 The CPU time (in seconds) for the one-factor VG model for increasing basket dimension n

4.2 Pricing Basket Options

In this subsection we explain how to determine the price of a basket option in a realistic situation where option prices of the components of the basket are available and used to calibrate the marginal parameters. In our example, the basket under consideration consists of 2 major stock market indices ($n=2$), the S&P500 and the Nasdaq:

$$ \text {Basket} = w_1 \text {S} \& \text {P 500} +w_2\text {Nasdaq}. $$

The pricing date is February 19, 2009 and we determine prices for the Normal, VG, NIG, and Meixner case. The details of the basket are listed in Table 5. The weights $w_1$ and $w_2$ are chosen such that the initial price S(0) of the basket is equal to 100. The maturity of the basket option is equal to 30 days.

The S&P 500 and Nasdaq option curves are denoted by $C_1$ and $C_2$, respectively. These option curves are only partially known. The traded strikes for curve $C_j$ are denoted by $K_{i,j},\ i=1,2, \ldots ,N_j$, where $N_j>1$. If the volatilities $\sigma _1$ and $\sigma _2$ and the characteristic function $\phi _L$ of the mother distribution L are known, we can determine the model price of an option on asset j with strike K and maturity T. This price is denoted by $C_j^{model}[K,T; \varTheta , \sigma _j]$, where $\varTheta$ denotes the vector containing the model parameters of L. Given the systematic component, the stocks are independent. Therefore, we can use the observed option curves $C_1$ and $C_2$ to calibrate the model parameters as follows:

Algorithm 1

(Determining the parameters $\varTheta$ and $\sigma _j$ of the one-factor Lévy model)

• Step 1: Choose a parameter vector $\varTheta$.

• Step 2: For each stock $j=1,2,\ldots ,n$, determine the volatility $\sigma _j$ as follows:

  $$ \sigma _j=\arg \min _{\sigma } \frac{1}{N_j}\sum _{i=1}^{N_j} \frac{\left| C_j^{model}[K_{i,j},T; \varTheta , \sigma ]-C_j[K_{i,j}] \right| }{C_j[K_{i,j}]}, $$

• Step 3: Determine the total error:

  $$ \text {error}= \sum _{j=1}^n \frac{1}{N_j}\sum _{i=1}^{N_j} \frac{\left| C_j^{model}[K_{i,j},T; \varTheta , \sigma _j]-C_j[K_{i,j}] \right| }{C_j[K_{i,j}]}. $$

  Repeat these three steps until the parameter vector $\varTheta$ is found for which the total error is minimal. The corresponding volatilities $\sigma _1,\sigma _2,\ldots ,\sigma _n$ are called the implied Lévy volatilities.

Only a limited number of option quotes is required to calibrate the one-factor Lévy model. Indeed, the parameter vector $\varTheta$ can be determined using all available option quotes. Additional, one volatility parameter has to be determined for each stock. However, other methodologies for determining $\varTheta$ exist. For example, one can fix the parameter $\varTheta$ upfront, as is shown in Sect. 5.2. In such a situation, only one implied Lévy volatility has to be calibrated for each stock.

Table 5 Input data for the basket option

Table 6 One-factor Lévy models: Calibrated model parameters

Table 7 Basket option prices for the basket given in Table 5

The calibrated parameters together with the calibration error are listed in Table 6. Note that the relative error in the VG, Meixner, and NIG case is significantly smaller than in the normal case. Using the calibrated parameters for the mother distribution L together with the volatility parameters $\sigma _1$ and $\sigma _2$, we can determine basket option prices in the different model settings. Note that here and in the sequel of the paper, we always use the three-moments-matching approximation for determining basket option prices. We put $T=30$ days and consider the cases where the correlation parameter $\rho$ is given by 0.1, 0.5, and 0.8. The corresponding basket option prices are listed in Table 7. One can observe from the table that each model generates a different basket option price, i.e. there is model risk. However, the difference between the Gaussian and the non-Gaussian models is much more pronounced than the difference within the non-Gaussian models. We also find that using normally distributed log returns, one underestimates the basket option prices. Indeed, the basket option prices $C^{VG}[K,T], C^{Meixner}[K,T]$ and $C^{NIG}[K,T]$ are larger than $C^{BLS}[K,T]$. In the next section, however, we encounter situations where the Gaussian basket option price is larger than the corresponding VG price for out-of-the-money options. The reason for this behavior is that marginal log returns in the non-Gaussian situations are negatively skewed, whereas these distributions are symmetric in the Gaussian case. This skewness results in a lower probability of ending in the money for options with a sufficiently large strike (Fig. 3).

Fig. 3

Implied market and model volatilities for February 19, 2009 for the S&P 500 (left) and the Nasdaq (right), with time to maturity 30 days

5 Implied Lévy Correlation

In Sect. 4.2 we showed how the basket option formulas can be used to obtain basket option prices in the Lévy copula model. The parameter vector $\varTheta$ describing the mother distribution L and the implied Lévy volatility parameters $\sigma _j$ can be calibrated using the observed vanilla option curves $C_j[K,T]$ of the stocks composing the basket S(T); see Algorithm 1. In this section we show how an implied Lévy correlation estimate $\rho$ can be obtained if in addition to the vanilla options, market prices for a basket option are also available.

We assume that S(T) represents the time-T price of a stock market index. Examples of such stock market indices are the Dow Jones, S&P 500, EUROSTOXX 50, and so on. Furthermore, options on S(T) are traded and their prices are observable for a finite number of strikes. In this situation, pricing these index options is not a real issue; we denote the market price of an index option with maturity T and strike K by C[K, T]. Assume now that the stocks composing the index can be described by the one-factor Lévy model (6). If the parameter vector $\varTheta$ and the marginal volatility vector $\underline{\sigma }=(\sigma _1,\sigma _2,\ldots ,\sigma _n)$ are determined using Algorithm 1, the model price $C^{model}[K,T;\underline{\sigma }, \varTheta , \rho ]$ for the basket option only depends on the choice of the correlation $\rho$. An implied correlation estimate for $\rho$ arises when we match the model price with the observed index option price.

Definition 1

(Implied Lévy correlation) Consider the one-factor Lévy model defined in (6). The implied Lévy correlation of the index S(T) with moneyness $\pi =S(T)/S(0)$, denoted by $\rho \left[ \pi \right]$, is defined by the following equation:

$$\begin{aligned} C^{model}\left[ K,T;\underline{\sigma }, \varTheta , \rho \left[ \pi \right] \right] =C[K,T], \end{aligned}$$

(14)

where $\underline{\sigma }$ contains the marginal implied volatilities and $\varTheta$ is the parameter vector of L.

Determining an implied correlation estimate $\rho \left[ K/S(0) \right]$ requires an inversion of the pricing formula $\rho \rightarrow C^{model}[K,T;\underline{\sigma }, \varTheta , \rho ]$. However, the basket option price is not given in a closed form and determining this price using Monte Carlo simulation would result in a slow procedure. If we determine $C^{model}[K,T;\underline{\sigma }, \varTheta , \rho ]$ using the three-moments-matching approach, implied correlations can be determined in a fast and efficient way. The idea of determining implied correlation estimates based on an approximate basket option pricing formula was already proposed in Chicago Board Options Exchange [15], Cont and Deguest [16], Linders and Schoutens [30], and Linders and Stassen [31].

Note that in case we take L to be the standard normal distribution, $\rho [\pi ]$ is an implied Gaussian correlation; see e.g. Chicago Board Options Exchange [15] and Skintzi and Refenes [45]. Equation (14) can be considered as a generalization of the implied Gaussian correlation. Indeed, instead of determining the single correlation parameter in a multivariate model with normal log returns and a Gaussian copula, we can now extend the model to the situation where the log returns follow a Lévy distribution. A similar idea was proposed in Garcia et al. [20] and further studied in Masol and Schoutens [37]. In these papers, Lévy base correlation is defined using CDS and CDO prices.

The proposed methodology for determining implied correlation estimates can also be applied to other multi-asset derivatives. For example, implied correlation estimates can be extracted from traded spread options [46], best-of basket options [19], and quanto options [4]. Implied correlation estimates based on various multi-asset products are discussed in Austing [2].

5.1 Variance Gamma

In order to illustrate the proposed methodology for determining implied Lévy correlation estimates, we use the Dow Jones Industrial Average (DJ). The DJ is composed of 30 underlying stocks and for each underlying we have a finite number of option prices to which we can calibrate the parameter vector $\varTheta$ and the Lévy volatility parameters $\sigma _j$. Using the available vanilla option data for June 20, 2008, we will work out the Gaussian and the Variance Gamma case.⁴ Note that options on components of the Dow Jones are of American type. In the sequel, we assume that the American option price is a good proxy for the corresponding European option price. This assumption is justified because we use short term and out-of-the-money options.

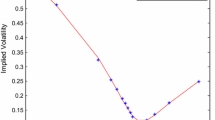
The single volatility parameter $\sigma _j$ is determined for stock j by minimizing the relative error between the model and the market vanilla option prices; see Algorithm 1. Assuming a normal distribution for L, this volatility parameter is denoted by $\sigma _j^{BLS}$, whereas the notation $\sigma _j^{VG},\ j=1,2,\ldots ,n$ is used for the VG model. For June 20, 2008, the parameter vector $\varTheta$ for the VG copula model is given in Table 9 and the implied volatilities are listed in Table 8. Figure 4 shows the model (Gaussian and VG) and market prices for General Electric and IBM, both members of the Dow Jones, based on the implied volatility parameters listed in Table 8. We observe that the Variance Gamma copula model is more suitable in capturing the dynamics of the components of the Dow Jones than the Gaussian copula model.

Given the volatility parameters for the Variance Gamma case and the normal case, listed in Table 8, the implied correlation defined by Eq. (14) can be determined based on the available Dow Jones index options on June 20, 2008. For a given index strike K, the moneyness $\pi$ is defined as $\pi =K/S(0)$. The implied Gaussian correlation (also called Black and Scholes correlation) is denoted by $\rho ^{BLS}\left[ \pi \right]$ and the corresponding implied Lévy correlation, based on a VG distribution, is denoted by $\rho ^{VG}\left[ \pi \right]$. In order to match the vanilla option curves more closely, we take into account the implied volatility smile and use a volatility parameter with moneyness $\pi$ for each stock j, which we denote by $\sigma _j[\pi ]$. For a detailed and step-by-step plan for the calculation of these volatility parameters, we refer to Linders and Schoutens [30].

Table 8 Implied Variance Gamma volatilities $\sigma _j^{VG}$ and implied Black and Scholes volatilities $\sigma _j^{BLS}$ for June 20, 2008

Table 9 Calibrated VG parameters for different trading days

Fig. 4

Option prices and implied volatilities (model and market) for Exxon Mobile and IBM on June 20, 2008 based on the parameters listed in Table 8. The time to maturity is 30 days

Fig. 5

Implied correlation smile for the Dow Jones, based on a Gaussian (dots) and a one-factor Variance Gamma model (crosses) for June 20, 2008

Figure 5 shows that both the implied Black and Scholes and implied Lévy correlation depend on the moneyness $\pi$. However, for low strikes, we observe that $\rho ^{VG}\left[ \pi \right] <\rho ^{BLS}\left[ \pi \right]$, whereas the opposite inequality holds for large strikes, making the implied Lévy correlation curve less steep than its Black and Scholes counterpart. In Linders and Schoutens [30], the authors discuss the shortcomings of the implied Black and Scholes correlation and show that implied Black and Scholes correlations can become larger than one for low strike prices. Our more general approach and using the implied Lévy correlation solves this problem at least to some extent. Indeed, the region where the implied correlation stays below 1 is much larger for the flatter implied Lévy correlation curve than for its Black and Scholes counterpart. We also observe that near the at-the-money strikes, VG and Black and Scholes correlation estimates are comparable, which may be a sign that in this region, the use of implied Black and Scholes correlation (as defined in Linders and Schoutens [30]) is justified. Figure 7 shows implied correlation curves for March, April, July and August, 2008. In all these situations, the time to maturity is close to 30 days. The calibrated parameters for each trading day are listed in Table 9.

We determine the implied correlation $\rho ^{VG}[\pi ]$ such that model and market quote for an index option with moneyness $\pi =K/S(0)$ coincide. However, the model price is determined using the three-moments-matching approximation and may deviate from the real model price. Indeed, we determine $\rho ^{VG}[\pi ]$ such that $C^{MM}\left[ K,T;\underline{\sigma }, \varTheta , \rho \left[ \pi \right] \right] =C[K,T]$. In order to test if the implied correlation estimate obtained is accurate, we determine the model price $C^{mc}\left[ K,T;\underline{\sigma }, \varTheta , \rho \left[ \pi \right] \right]$ using Monte Carlo simulation, where we plug in the volatility parameters and the implied correlation parameters. The results are listed in Table 10 and shown in Fig. 6. We observe that model and market prices are not exactly equal, but the error is still acceptable.

Table 10 Market quotes for Dow Jones Index options for different basket strikes on June 20, 2008

5.2 Double Exponential

In the previous subsection, we showed that the Lévy copula model allows for determining robust implied correlation estimates. However, calibrating this model can be a computational challenging task. Indeed, in case we deal with the Dow Jones Industrial Average, there are 30 underlying stocks and each stock has approximately 5 traded option prices. Calibrating the parameter vector $\varTheta$ and the volatility parameters $\sigma _j$ has to be done simultaneously. This contrasts sharply with the Gaussian copula model, where the calibration can be done stock per stock.

Fig. 6

Dow Jones option prices: Market prices (circles) and the model prices using a one-factor Variance Gamma model and the implied VG correlation smile (crosses) for June 20, 2008

Fig. 7

Implied correlation smile for the Dow Jones, based on a Gaussian (dots) and a one-factor Variance Gamma model (crosses) for different trading days

In this subsection we consider a model with the computational attractive calibration property of the Gaussian copula model, but without imposing any normality assumption on the marginal log returns. To be more precise, given the convincing arguments exposed in Fig. 7 we would like to keep L a $VG(\sigma , \nu , \theta , \mu )$ distribution. However, we do not calibrate the parameter vector $\varTheta =\left( \sigma , \nu , \theta , \mu \right)$ to the vanilla option curves, but we fix these parameters upfront as follows

$$\begin{aligned} \mu = 0,\quad \theta = 0,\quad \nu = 1\quad \text {and}\quad \sigma = 1. \end{aligned}$$

In this setting, L is a standardized distribution and its characteristic function $\phi _L$ is given by

$$ \phi _L(u)=\frac{1}{1+\frac{u^2}{2}},\quad u \in \mathbb {R}. $$

From its characteristic function, we see that L has a Standard Double Exponential distribution, also called Laplace distribution, and its pdf $f_L$ is given by

$$f_L(u)=\frac{\sqrt{2}}{2}\text {e}^{-\frac{|u|}{\sqrt{2}}}$$

Fig. 8

Implied correlation smiles in the one-factor Variance Gamma and the Double Exponential model

The Standard Double Exponential distribution is symmetric and centered around zero, while it has variance 1. Note, however, that it is straightforward to generalize this distribution such that it has center $\mu$ and variance $\sigma ^2$. Moreover, the kurtosis of this Double Exponential distribution is 6.

By using the Double Exponential distribution instead of the more general Variance Gamma distribution, some flexibility is lost for modeling the marginals. However, the Double Exponential distribution is still a much better distribution for modeling the stock returns than the normal distribution. Moreover, in this simplified setting, the only parameters to be calibrated are the marginal volatility parameters, which we denote by $\sigma _j^{DE}$, and the correlation parameter $\rho ^{DE}$. Similar to the Gaussian copula model, calibrating the volatility parameter $\sigma _j^{DE}$ only requires the option curve of stock j. As a result, the time to calibrate the Double Exponential copula model is comparable to its Gaussian counterpart and much shorter than the general Variance Gamma copula model.

Consider the DJ on March 25, 2008. The time to maturity is 25 days. We determine the implied marginal volatility parameter for each stock in a one-factor Variance Gamma model and a Double Exponential framework. Given this information, we can determine the prices $C^{VG}[K,T]$ and $C^{DE}[K,T]$ for a basket option in a Variance-Gamma and a Double Exponential model, respectively. Figure 8 shows the implied Variance Gamma and the Double Exponential correlations. We observe that the implied correlation based on a one-factor VG model is larger than its Double Exponential counterpart for a moneyness bigger than one, whereas both implied correlation estimates are relatively close to each other in the other situation.

6 Conclusion

In this paper we introduced a one-factor Lévy model and we proposed a three-moments-matching approximation for pricing basket options. Well-known distributions like the Normal, Variance Gamma, NIG, Meixner, etc., can be used in this one-factor Lévy model. We calibrate these different models to market data and determine basket option prices for the different model settings. Our newly designed (approximate) basket option pricing formula can be used to define implied Lévy correlation. The one-factor Lévy model provides a flexible framework for deriving implied correlation estimates in different model settings. Indeed, by employing a Brownian motion and a Variance Gamma process in our model, we can determine Gaussian and VG-implied correlation estimates, respectively. We observe that the VG implied correlation is an improvement of the Gaussian-implied correlation.

Appendix: Proof of Lemma 1

The proof for expression (9) is straightforward.

Starting from the multinomial theorem, we can write the second moment $m_2$ as follows

$$\begin{aligned} m_2= & {} \mathbb {E}\left[ \left( w_1S_1(T)+w_2S_2(T)+\ldots w_n S_n(T) \right) ^2 \right] \\= & {} \mathbb {E}\left[ \sum _{i_1+i_2+\ldots +i_n=2} \frac{2}{i_1!i_2!\ldots i_n!} \prod _{j=1}^n \left( w_j S_j(T)\right) ^{i_j} \right] . \end{aligned}$$

Considering the cases $(i_n=0)$, $(i_n=1)$ and $(i_n=2)$ separately, we find

$$\begin{aligned} m_2= & {} \mathbb {E}\left[ \left( \sum _{j=1}^{n-1}w_j S_j(T) \right) ^2 + 2w_n S_n(T)\sum _{j=1}^{n-1}w_j S_j(T)+w_j^2S_n^2(T)\right] . \end{aligned}$$

Continuing recursively gives

$$\begin{aligned} m_2 = \sum _{j=1}^n \sum _{k=1}^n w_j w_k \mathbb {E}\left[ S_j(T) S_k(T) \right] . \end{aligned}$$

(15)

We then find that

$$\begin{aligned} m_2= & {} \sum _{j=1}^n \sum _{k=1}^n w_j w_k S_j(0) S_k(0) \\&\times \,\mathbb {E}\left[ \exp \left\{ (2r-q_j-q_k-\omega _j - \omega _k)T+(\sigma _j A_j + \sigma _k A_k)\sqrt{T} \right\} \right] \\= & {} \sum _{j=1}^n \sum _{k=1}^n w_j w_k \frac{\mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] }{\phi _L\left( -\textsf {i}\sigma _j \sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k \sqrt{T} \right) }\mathbb {E}\left[ \exp \left\{ (\sigma _j A_j + \sigma _k A_k)\sqrt{T} \right\} \right] .\\ \end{aligned}$$

In the last step, we used the Expression $\omega _j=\log \phi _L\left( \textsf {i}\sigma _j\sqrt{T} \right) /T$. If we use expression (1) to decompose $A_j$ and $A_k$ in the common component $X(\rho )$ and the independent components $X_j(1-\rho )$ and $X_k(1-\rho )$, we find the following expression for $m_2$

$$ m_2 = \sum _{j=1}^n \sum _{k=1}^n w_j w_k \frac{\mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] }{\phi _L\left( -\textsf {i}\sigma _j \sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k \sqrt{T} \right) } \mathbb {E}\left[ \text {e}^{(\sigma _j + \sigma _k)X(\rho )}\text {e}^{\sigma _j \sqrt{T}X_j(1-\rho )}\text {e}^{\sigma _k \sqrt{T}X_k(1-\rho )}\right] . $$

The r.v. $X(\rho )$ is independent from $X_j(1-\rho )$ and $X_k(1-\rho )$. Furthermore, the characteristic function of $X(\rho )$ is $\phi _L^{\rho }$, which results in

$$\begin{aligned} m_2= & {} \sum _{j=1}^n \sum _{k=1}^n w_j w_k \frac{\mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] }{\phi _L\left( -\textsf {i}\sigma _j \sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k \sqrt{T} \right) } \phi _L\left( -\textsf {i}(\sigma _j + \sigma _k)\sqrt{T} \right) ^{\rho }\\&\times \, \mathbb {E}\left[ \text {e}^{\sigma _j \sqrt{T}X_j(1-\rho )}\text {e}^{\sigma _k \sqrt{T}X_k(1-\rho )}\right] . \end{aligned}$$

If $j\ne k$, $X_j(1-\rho )$ and $X_k(1-\rho )$ are i.i.d. with characteristic function $\phi _L^{1-\rho }$, which gives the following expression for $m_2$:

$$\begin{aligned} m_2= & {} \sum _{j=1}^n \sum _{k=1}^n w_j w_k \mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] \left( \frac{\phi _L\left( -\textsf {i}(\sigma _j + \sigma _k)\sqrt{T} \right) }{\phi _L\left( -\textsf {i}\sigma _j \sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k \sqrt{T} \right) }\right) ^{\rho }. \\ \end{aligned}$$

If $j=k$, we find that

$$ \mathbb {E}\left[ \text {e}^{\sigma _j \sqrt{T}X_j(1-\rho )}\text {e}^{\sigma _k \sqrt{T}X_k(1-\rho )}\right] = \phi _L\left( -\textsf {i}\left( \sigma _j+\sigma _k \right) \sqrt{T}\right) , $$

which gives

$$\begin{aligned} m_2= & {} \sum _{j=1}^n \sum _{k=1}^n w_j w_k \mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] \frac{\phi _L\left( -\textsf {i}(\sigma _j + \sigma _k)\sqrt{T} \right) }{\phi _L\left( -\textsf {i}\sigma _j \sqrt{T} \right) \phi _L\left( -\textsf {i}\sigma _k \sqrt{T} \right) }. \\ \end{aligned}$$

This proves expression (10) for $m_2$.

We can write $m_3$ as follows

$$\begin{aligned} m_3= & {} \mathbb {E}\left[ \left( \sum _{j=1}^n w_jS_j(T)\right) ^3 \right] \\= & {} \mathbb {E}\left[ \left( \sum _{j=1}^n w_jS_j(T)\right) ^2\sum _{l=1}^n w_l S_l(T) \right] . \end{aligned}$$

Using expression (15), we find the following Expression for $m_3$:

$$\begin{aligned} m_3= & {} \mathbb {E}\left[ \left( \sum _{j=1}^n \sum _{k=1}^n w_j w_k S_j(T) S_k(t)\right) \sum _{l=1}^n w_l S_l(T) \right] \\= & {} \sum _{j=1}^n \sum _{k=1}^n \sum _{l=1}^n w_j w_k w_l \mathbb {E}\left[ S_j(T) S_k(T) S_l(T) \right] . \end{aligned}$$

Similar calculations as for $m_2$ result in

$$\begin{aligned} m_3= & {} \sum _{j=1}^n \sum _{k=1}^n \sum _{l=1}^n w_j w_k w_l\mathbb {E}\left[ S_j(T) \right] \mathbb {E}\left[ S_k(T) \right] \mathbb {E}\left[ S_l(T) \right] \\&\times \,\frac{\phi _L\left( -\textsf {i}(\sigma _j+\sigma _k+\sigma _l) \sqrt{T}\right) ^{\rho }}{\phi _L\left( -\textsf {i}\sigma _j \sqrt{T}\right) \phi _L\left( -\textsf {i}\sigma _k \sqrt{T}\right) \phi _L\left( -\textsf {i}\sigma _l \sqrt{T}\right) }A_{j,k,l}, \end{aligned}$$

where

$$ A_{j,k,l}=\mathbb {E}\left[ \text {e}^{\sigma _j \sqrt{T}X_j(1-\rho )}\text {e}^{\sigma _k \sqrt{T}X_k(1-\rho )}\text {e}^{\sigma _l \sqrt{T}X_l(1-\rho )} \right] . $$

Differentiating between the situations $\left( j=k=l\right)$, $\left( j=k, k \ne l\right)$, $\left( j \ne k, k=l \right)$, $(j\ne k, k\ne l, j=l)$ and $\left( j\ne k\ne l, j \ne l \right)$, we find expression (11).