To the Question of Learnability of a Spiking Neuron with Spike-Timing-Dependent Plasticity in Case of Complex Input Signals

Abstract

Results of investigations of learnability of a spiking neuron in case of complex input signals which encode binary vectors are presented. The disadvantages of the supervised learning protocol with stimulating the neuron by current impulses in desired moments of time are analyzed.

1 Introduction

Currently there is a number of publications [1, 2] devoted to the various approaches to make spiking neural networks learn to respond with the desired output to an input. Among them learning by spike timing-dependent plasticity (STDP) looks like more biologically inspired and clear. Provided that the neuron can produce the desired output in response to the given input with some values of its adjustable parameters (i.e. synaptic weights), the question is when that desired parameters can be reached during learning, starting from random initial ones.

Legenstein et al. proved that STDP enables to realise supervised learning for any input-output transformation that the neuron could in principle implement in a stable manner. This fact was shown for Leaky Integrate-and-Fire neuron model, all-to-all spike pairing scheme in the STDP rule and simple forms of input signal, each synapse receiving Poisson trains of constant mean frequency. In [3] the same experiment was conducted with reduced symmetric spike pairing scheme, which is more biologically plausible according to [4].

In this study we investigate, following the protocol suggested in [5], the learnability of a spiking neuron in case of complex input signals. In Sect. 3.2 it is shown that synaptic weights, with which the neuron divides a set of binary vectors encoded by spike trains into two classes, can be reached during learning.

In this case the learning performance depends on the supervised learning implementation because of possible presence of undesired (unforced) spikes of neuron or absence of desired ones. To investigate the learning in idealized case without a spiking neuron at all, in Sect. 3.3 learning is performed without neuron, calculating weight change only on base of prepared couple of input and output signals.

In Sect. 3.4 the existence of short-term plasticity in the synapse model is shown to be not necessary for learning.

2 Materials and Methods

2.1 Neuron Model

In the Leaky Integrate-and-Fire neuron model the membrane potential V changes with time as following:

$$ \begin{array}{*{20}l} {\frac{dV}{dt} = \frac{{ - \left( {V(t) - V_{\text{resting}} } \right)}}{{\tau_{\text{m}} }} + \frac{{I_{\text{syn}} (t)}}{{C_{\text{m}} }} + \frac{{I_{\text{ext}} }}{{C_{\text{m}} }},} \hfill \\ {{\text{when}}\;V \ge V_{\text{th}} ,V \to V_{\text{reset}} .} \hfill \\ \end{array} $$

where $V_{\text{resting}}$ was chosen to be 0 mV, $\tau_{\text{m}} = 30\,{\text{ms}}$ is the membrane potential relaxation time constant, $C_{\text{m}} = 30\,{\text{pF}}$ is the membrane capacitance, $I_{\text{ext}} = 13.5\,{\text{pA}}$ is constant background stimulation current, $V_{\text{reset}} = 14.2\,{\text{mV}}$, and $I_{\text{syn}} (t)$ is total incoming current through synapses. The refractory period was 3 ms for excitatory neurons and 6 ms for inhibitory ones.

As the synapse model we used postsynaptic current of exponentially decaying form along with the Maass-Markram short-term plasticity [6], taking all parameters as in [5].

2.2 Spike-Timing-Dependent Plasticity

STDP [7] is a biologically inspired long-term plasticity model, in which for each synapse a weight $0 \le w \le w_{ \hbox{max} }$, characterizing its strength, is given, and in the additive STDP form it changes according to the following rule [4]:

$$ \varDelta w = \left\{ {\begin{array}{*{20}l} { - W_{ - } \cdot {\text{e}}^{{ - \frac{{t_{\text{pre}} - t_{\text{post}} }}{{\tau_{ - } }}}} } \hfill & {{\text{if}}\;\;t_{\text{pre}} - t_{\text{post}} > 0;} \hfill \\ {W_{ + } \cdot {\text{e}}^{{ - \frac{{t_{\text{post}} - t_{\text{pre}} }}{{\tau_{ + } }}}} } \hfill & {{\text{if}}\;\;t_{\text{pre}} - t_{\text{post}} < 0.} \hfill \\ \end{array} } \right. $$

(1)

with the auxiliary clause preventing the weight from falling below zero or exceeding the maximum value $w_{ \hbox{max} }$:

$$ {\text{if}}\;w + \varDelta w > w_{\hbox{max} } \;{\text{or}}\;w + \varDelta w < 0,{\text{then}}\;\varDelta w = 0. $$

Here $t_{\text{pre}}$ is the presynaptic spike moment, $t_{\text{post}}$ is the postsynaptic spike moment, weight depression amplitude $W_{ + } = 0,3$, and weight potentiation amplitude $W_{ - } = \alpha \cdot W_{ + }$, so that $\alpha$ controls how much the depression is stronger than the potentiation.

An important part of STDP rule is the scheme of pairing pre-and postsynaptic spikes when evaluating weight change. We used the reduced symmetric scheme, in which each presynaptic spike is paired with the closest preceding postsynaptic, each post- with the closest preceding pre-, and no more than once can a spike be accounted in pre-before-post pair and once in post-before-pre one.

2.3 The Learning Protocol

The following protocol suggested in [5] is to force the synaptic weights of a neuron to converge to the target weights:

• 1. Obtaining the teacher signal

  The neuron’s weights are set equal to the target, STDP is disabled, and the neuron’s response to the input trains is recorded as the desired output.

• 2. Learning

  The neuron’s weights are set random (but about 4 times smaller than the target ones), STDP is turned on, and the same input trains are given to the neuron’s incoming synapses. During this the neuron is stimulated by the teacher signal, obtained from the desired output train by replacing spikes with 0.2-ms-duration current impulses of 2 mA (which is at least three orders more than typical magnitude of synaptic current).

3 Experiments and Results

3.1 The Experiment Technique

The experiment configuration was chosen as in [5] in order to meet succession to the case of more simple input signals considered there. The single neuron had 90 excitatory and 10 inhibitory synapses. The neuron threshold was adjusted for each input signal to reach mean spiking rate of approximately 25 Hz. The maximum synaptic weights in the STDP rule (1) were chosen from the normal distribution with the mean of 54 and standard deviation of 10.8, values less than 21.6 and more than 86.4 being replaced by 21.6 and 86.4 correspondingly.

For the implementation of neuron and synapse models we used the NEST simulator [8].

As a measure for learning performance the deviation $\beta$ between current and target weights was used:

$$ \beta (t) = \frac{{\sum\nolimits_{i = 1}^{90} {\left| {W^{i} (t) - W_{\text{target}}^{i} } \right|} }}{{\sum\nolimits_{i = 1}^{90} {W_{\text{target}}^{i} } }} $$

So, the closer $\beta$ is to 0, the more successful the learning is.

3.2 Learning Weights with Which the Neuron Classifies Binary Vectors

The aim of this section is to ensure whether a neuron can learn by the learning protocol under consideration such target synaptic weights that allow it to do the classification task. By doing the classification task we mean the neuron producing relatively high frequency in response to inputs represented by vectors from one class, and relatively low frequency in response to vectors from the other class. Binary vectors are encoded by spike trains, a vector component of 1 meaning high-frequency trains presented to the corresponding synapse or group of synapses, and a component of 0 being encoded by low mean frequency trains.

The output frequency of a neuron apparently must depend on how many spikes are given to the synapses having non-zero weights. Indeed, the output frequency depends almost monotonously from scalar product $(\vec{w},\vec{S})$ of weights vector $\vec{w}$ by binary vector $\vec{S}$ describing input signal. This allows to obtain manually the weights with which the neuron classifies binary vectors. Six 100-dimensional binary vectors were generated, each having 50 components equal to 0 and 50 components equal to 1. Three vectors were randomly decided to belong to one class, and the other three—to the other class. Figure 1 shows that with the chosen target weights the difference between the neuron’s frequencies in response to vectors from different classes is distinctly higher than difference in response to vectors from one class.

Fig. 1

For each of 6 binary vectors mean output frequency in response to the input described by that vector (a vector component of 1 corresponds to 30-Hz Poisson train, a component of 0–10 Hz), and averaged over 5 inputs described by the same vector, each presented for 100 s, is given (gray bars), along with the scalar product of that vector by the excitatory synaptic weights vector (black crosses)

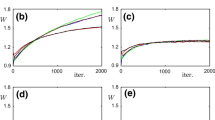
So, the weights with which the neuron classifies binary vectors were obtained, and such weights could emerge as the result of learning, as can be seen on Fig. 2. Since learning was less successful than in [9] ($\beta$ never descended below 0.1, while in [9] it was less than 0.1), we tried changing the ratio $\alpha$ of weight decreasing amplitude $W_{ - }$ to weight increasing amplitude $W_{ + }$ in the STDP weight update rule (1), and the higher $\alpha$ is, the more successful the learning is.

Fig. 2

$\beta (t)$ during training LIF neuron with different $\alpha = \frac{{W_{ - } }}{{W_{ + } }}$ in the STDP rule. 6 binary vectors presented one after another were used as input, a vector component of 1 coding a 100-s-long Poisson train with mean frequency of 30 Hz, a component of 0–10 Hz. Inhibitory synapses were always receiving 30 Hz trains

3.3 Learning Without a Neuron, Based Only on Input and Output Signals and STDP Rule

The reason of rather poor weights convergence in the previous section is the emergence of unforced spikes, i.e. caused by the incoming synaptic currents instead of teacher impulses, and therefore differing from the desired output. To confirm it we introduced the learning protocol without neuron, in which spike pairing scheme is applied to the inputs and the desired output. Such a protocol provides the idealised way of learning, with no difference between the postsynaptic train and the desired output. The “without neuron’’ curve on Fig. 3 shows that learning without a neuron is more successful than the one with neuron, copied from the previous section.

Fig. 3

$\beta (t)$ during learning: gray with LIF neuron, black without neuron, with the same desired output train obtained with LIF. Half of excitatory and all inhibitory synapses received Poisson trains with mean frequency of 30 Hz, and another half of excitatory synapses—10 Hz Poisson trains

As a result, we conclude that differences in the learning performance of the protocols with and without the neuron are caused by the disadvantages of the protocol of presenting the teacher signal to the neuron in the form of current impulses, while, if the learning with some input and output trains was unsuccessful even without neuron, the reason would be that such input-output transformation cannot be learnt ever.

3.4 Learning Without Short-Term Plasticity

In [5] long-term plasticity model STDP was used along with Maass-Markram short-term plasticity model, but whether the existence of the latter is necessary for the weights convergence, was not stated clearly.

If one just removes the short-term plasticity variables u(t) and R(t) from the synaptic current equation, no learning is possible. The reason is that after long time of simulation (more than 20 s) u keeps fluctuating around about 1/2, while R—around about 1/8, so, removing u and R, the amplitude of synaptic current becomes about 16 times higher, which will inevitably cause undesired (see Sect. 3.3) spikes.

Nevertheless, if the synaptic current is multiplied by 0.04, which is roughly the typical mean value of $u \cdot R$ during simulation, the learning does take place (Fig. 4).

Fig. 4

$\beta (t)$ during training LIF neuron with and without Maass-Markram short-term plasticity. In the case without the synaptic current was being multiplied by 0.04. All synapses received Poisson trains with mean frequency of 20 Hz

4 Conclusion

Neuron learning can be performed using STDP not only with simple input signals, but with different complicated ones too. Slightly less accuracy in this case is caused by disadvantages of the protocol of stimulating neuron with current impulses during learning.

Changing the ratio of weight depression amplitude to weight potentiation amplitude can significantly affect the learning performance.

The existence of short-term plasticity is not necessary for learning.