Abstract
In this chapter, the evolutionary and revolutionary developments of microscopic imaging are overviewed with focus on ultrashort light and electrons pulses; for simplicity, we shall use the term “ultrafast” for both. From Alhazen’s camera obscura, to Hooke and van Leeuwenhoek’s optical micrography, and on to three- and four-dimensional (4D) electron microscopy, the developments over a millennium have transformed humans’ scope of visualization. The changes in the length and time scales involved are unimaginable, beginning with the visible shadows of candles at the centimeter and second scales, and ending with invisible atoms with space and time dimensions of sub-nanometer and femtosecond, respectively. With these advances it has become possible to determine the structures of matter and to observe their elementary dynamics as they fold and unfold in real time, providing the means for visualizing materials behavior and biological function, with the aim of understanding emergent phenomena in complex systems. Both light and light-generated electrons are now at the forefront of femtosecond and attosecond science and technology, and the scope of applications has reached beyond the nuclear motion as electron dynamics become accessible.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Origins
The ever-increasing progress made by humans in making the very small and the very distant visible and tangible is truly remarkable. The human eye has spatial and temporal resolutions that are limited to about 100 μm and a fraction of a second, respectively. Today we are aided by tools that enable the visualization of objects that are below a nanometer in size and that move in femtoseconds ([98] and the references therein). This chapter, which is based on review articles by the author [94, 99–101], some commentaries [83–85, 87], and a book [103], provides a road map for the evolutionary and revolutionary developments in the fields of ultrafast light and electrons used to image the invisibles of matter.
How did it all begin? Surely, the power of light for observation has been with humans since their creation. Stretching back over six millennia, one finds its connection to the science of time clocking [95] (first in calendars) and to the mighty monotheistic faiths and rituals (Fig. 3.1). Naturally, the philosophers of the past must have been baffled by the question: what is light and what gives rise to the associated optical phenomena?
The significance of the light–life interaction as perceived more than three millennia ago, at the time of Akhenaton and Nefertiti. Note the light’s “ray diagram” from a spherical source, the Sun. Adapted from Zewail [96]
A leading contribution to this endeavor was made by the Arab polymath Alhazen (Ibn al-Haytham; AD 965–1040) nearly a millennium ago. He is recognized for his quantitative experimentation and thoughts on light reflection and refraction, and is also credited with explaining correctly the mechanism of vision, prior to the contributions of Kepler, Descartes, Da Vinci, Snell, and Newton. But of relevance to our topic is his conceptual analysis of the camera obscura, the “dark chamber,” which aroused the photographic interests of J. W. Strutt (later known as Lord Rayleigh) in the 1890s [81]. Alhazen’s idea that light must travel along straight lines and that the object is inverted in the image plane is no different from the modern picture of ray diagrams taught in optics today (Fig. 3.2). His brilliant work was published in the Book of Optics or, in Arabic, Kitab al-Manazir.
2 Optical Microscopy and the Phenomenon of Interference
In the fourteenth and fifteenth centuries, the art of grinding lenses was perfected in Europe, and the idea of optical microscopy was developed. In 1665, Robert Hooke (the scientist who coined the word “cell”) published his studies in Micrographia ([39]; Fig. 3.3), and among these studies was a description of plants, feathers, as well as cork cells and their ability to float in water. Contemporaneously, Anton van Leeuwenhoek used a simple, one-lens microscope to examine blood, insects, and other objects, and was the first to visualize bacteria, among other microscopic objects.
Microscopy time line, from camera obscura to 3D electron microscopes. 4D ultrafast electron microscopy and diffraction were developed a decade ago (see Sec. 3.7). The top inset is the frontispiece of Hooke’s [39] Micrographia published by the Royal Society of London. In the frontispiece to Hevelius’s Selenographia (bottom inset), Ibn al-Haytham represents Ratione (the use of reason) with his geometrical proof and Galileo represents Sensu (the use of the senses) with his telescope. The two scientists hold the book’s title page between them, suggesting a harmony between the methods [72, 80]. Adapted from Zewail and Thomas [98]
More than a 100 years later, an experiment by the physicist, physician, and Egyptologist, Thomas Young, demonstrated the interference of light, an experiment that revolutionized our view of the nature of light. His double-slit experiment of 1801 performed at the Royal Institution of Great Britain led to the rethinking of Newton’s corpuscular theory of light. Of relevance here is the phenomenon of diffraction due to interferences of waves (coherence). Much later, such diffraction was found to yield the (microscopic) interatomic distances characteristic of molecular and crystal structures, as discovered in 1912 by von Laue and elucidated later that year by W. L. Bragg.
Resolution in microscopic imaging was brought to a whole new level by two major developments in optical microscopy. In 1878, Ernst Abbe formulated a mathematical theory correlating resolution to the wavelength of light (beyond what we now designate the empirical Rayleigh criterion for incoherent sources), and hence the optimum parameters for achieving higher resolution. At the beginning of the twentieth century, Richard Zsigmondy, by extending the work of Faraday and Tyndall, developed the “ultramicroscope” to study colloidal particles; for this work, he received the Nobel Prize in Chemistry in 1925. Then came the penetrating developments in the 1930s by Frits Zernike, who introduced the phase-contrast concept in microscopy; he, too, received the Nobel Prize, in Physics, in 1953. It was understood that the spatial resolution of optical microscopes was limited by the wavelength of the visible light used. Recently, optical techniques have led to considerable improvement in the spatial resolution, and the 2014 Nobel Prize in Chemistry was awarded to Eric Betzig, Stefan Hell, and William Moerner for reaching the spatial resolution beyond the diffraction limit.
3 The Temporal Resolution: From Visible to Invisible Objects
In 1872 railroad magnate Leland Stanford wagered $25,000 that a galloping horse, at some point in stride, lifts all four hooves off the ground. To prove it, Stanford employed English photographer Eadweard Muybridge. After many attempts, Muybridge developed a camera shutter that opened and closed for only two thousandths of a second, enabling him to capture on film a horse flying through the air (Fig. 3.4). During the past century, all scientific disciplines from astrophysics to zoology have exploited “high-speed” photography to understand motion of objects and animals that are quicker than the eye can follow.
Ultrafast and fast motions. The snapshots of a galloping horse in the upper panel were taken in 1887 by Eadweard Muybridge. He photographed a single horse and the shutter speed was 0.002 s per frame. In the molecular case ( femtochemistry), a ten-orders-of-magnitude improvement in the temporal resolution was required, and methods for synchronization of billions of molecules had to be developed. The yellow surface in the lower panel represents the energy landscape for the transitory journey of the chemical reaction. Adapted from Zewail [94, 95]
The time resolution, or shutter speed, needed to photograph the ultrafast motions of atoms and molecules is beyond any conventional scale. When a molecule breaks apart into fragments or when it combines with another to form a new molecule, the chemical bonds between atoms break or form in less than a trillionth of a second, or one picosecond. Scientists have hoped to observe molecular motions in real time and to witness the birth of molecules: the instant at which the fate of the molecular reaction is decided and the final products are determined. Like Muybridge, they needed to develop a shutter, but it had to work ten billion times faster than that of Muybridge.
In the 1980s, our research group at the California Institute of Technology developed new techniques to observe the dynamics of molecules in real time [95]. We integrated our system of advanced lasers with molecular beams, rays of isolated molecules, to a point at which we were able to record the motions of molecules as they form and break chemical bonds on their energy landscapes (Fig. 3.4). The chemical reaction can now be seen as it proceeds from reactants through transition states, the ephemeral structures between reactants and products, and finally to products—chemistry as it happens!
Because transition states exist for less than a trillionth of a second, the time resolution should be shorter—a few quadrillionths of a second, or a few femtoseconds (1 fs is equal to 10−15 s). A femtosecond is to a second what a second is to 32 million years. Furthermore, whereas in 1 s light travels nearly 300,000 km—almost the distance between the Earth and the Moon—in 1 fs light travels 0.3 μm, about the diameter of the smallest bacterium.
Over half a century ago, techniques were introduced to study the so-called chemical intermediates using fast kinetics. Ronald Norrish and George Porter of the University of Cambridge and Manfred Eigen of the Max Planck Institute for Physical Chemistry were able to resolve chemical events that lasted about a thousandth of a second, and in some cases a millionth of a second. This time scale was ideal for the intermediates studied, but too long for capturing the transition states—by orders of magnitude for what was needed. Over the millisecond—or even the nano/picosecond—time scale, the transition states are not in the picture, and hence not much is known about the reaction scenery.
Chemist Sture Forsén of Lund University came up with an insightful analogy that illustrates the importance of understanding transitory stages in the dynamics. He compared researchers to a theater audience watching a drastically shortened version of a classical drama. The audience is shown only the opening scenes of, say, Hamlet and its finale. Forsén writes, “The main characters are introduced, then the curtain falls for change of scenery and, as it rises again, we see on the scene floor a considerable number of ‘dead’ bodies and a few survivors. Not an easy task for the inexperienced to unravel what actually took place in between” [25].
The principles involved in the ultrafast molecular “camera” [42] have some similarity to those applied by Muybridge. The key to his work was a special camera shutter that exposed a film for only 0.002 s. To set up the experiment, Muybridge spaced 12 of these cameras half a meter apart alongside a horse track. For each camera he stretched a string across the track to a mechanism that would trigger the shutter when a horse broke through the string. With this system, Muybridge attained a resolution in each picture of about two centimeters, assuming the horse was galloping at a speed of about 10 m/s. (The resolution, or definition, is simply the velocity of the motion multiplied by the exposure time.) The speed of the motion divided by the distance between cameras equals the number of frames per second—20 in this case. The motion within a picture becomes sharper as the shutter speed increases. The resolution of the motion improves as the distance between the cameras decreases.
Two aspects are relevant to the femtosecond, molecular camera (Fig. 3.5). First, a continuous motion is broken up into a series of snapshots or frames. Thus, one can slow down a fast motion as much as one likes so that the eye can see it. Second, both methods must produce enough frames in rapid succession so that the frames can be reassembled to give the illusion of a continuous motion. The change in position of an object from one frame to the next should be gradual, and at least 30 frames should be taken to provide 1 s of the animation. In our case—the femtosecond, molecular camera—the definition of the frame and the number of frames per second must be adjusted to resolve the elementary nuclear motions of reactions and, most importantly, the ephemeral transition states. The frame definition must be shorter than 0.l nm. Because the speed of the molecular motion is typically 1 km/s, the shutter resolution must be in a time range of better than 100 fs.
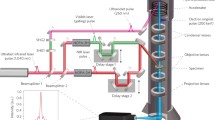
“The fastest camera in the world” [42] records what happens during a molecular transformation by initiating the reaction with a femtosecond laser pulse (“start pulse,” red). A short time later a second pulse (“observation pulse,” blue) takes a “picture” of the reacting molecule(s). By successively delaying the observation pulse in relation to the start pulse a “film” is obtained of the course of the reaction. With this first ultrafast “camera” built at Caltech, the ephemeral transition states were identified and characterized. The bottom inset shows part of the camera. It is a complex array of lasers, mirrors, lenses, prisms, molecular beams, detection equipment, and more. Adapted from Zewail [95]
Experimentally, we utilize the femtosecond pulses in the configuration shown in Fig. 3.5. The first femtosecond pulse, called the pump pulse, hits the molecule to initialize the reaction and set the experimental clock “at zero.” The second laser pulse, called the probe pulse, arrives several femtoseconds later and records a snapshot of the reaction at that particular instant. Like the cameras in Muybridge’s experiment, the femtosecond, molecular camera records successive images at different times in order to obtain information about different stages of the reaction. To produce time delays between the pump and the probe pulses, we initially tune the optical system so that both pulses reach the specimen at the same time. We then divert the probe pulse so that it travels a longer distance than does the pump pulse before it reaches the specimen (Fig. 3.5). If the probe pulse travels one micrometer farther than the pump pulse, it will be delayed 3.33 fs, because light travels at 300,000 km/s. Accordingly, pulses that are separated by distances of 1–100 μm resolve the motion during 3.33–333 fs periods. A shutter speed of a few femtoseconds is beyond the capability of any camera based on mechanical or electrical devices. When the probe pulse hits the molecule, it does not then transmit an image to a detector; see below. Instead the probe pulse interacts with the molecule, and then the molecule emits, or absorbs, a spectrum of light (Fig. 3.6) or changes its mass.
Femtosecond spectroscopy of transient species. A given state of a molecular system can be identified by the light that the molecule absorbs. When atoms in a molecule are relatively close together, they tend to absorb long wavelengths of light (red, for example). When the atoms are farther apart, they tend to absorb short wavelengths of light (blue, for instance). The change in the spectrum is the fingerprint of the atoms in motion. Adapted from Zewail [94]
When my colleague and friend Richard Bernstein of the University of California at Los Angeles learned about the femtosecond, molecular camera, he was very enthusiastic about the development, and we discussed the exciting possibilities created by the technique. At his house in Santa Monica, the idea of naming the emerging field of research femtochemistry was born. The field has now matured in many laboratories around the globe, and it encompasses applications in chemistry, biology, and materials science.
4 Electron Microscopy: Time-Averaged Imaging
Just before the dawn of the twentieth century, in 1897, electrons, or the corpuscles of J. J. Thomson, were discovered, but they were not conceived as imaging rays until Louis de Broglie formulated the concept of particle–wave duality in 1924. The duality character of an electron, which is quantified in the relationship λ deBroglie = h/p, where h is Planck’s constant and p is the momentum of the particle, suggested the possibility of achieving waves of picometer wavelength, which became essential to the understanding of diffraction and imaging. The first experimental evidence of the wave character of the electron was established in 1927 by Davisson and Germer (diffraction from a nickel surface) and, independently, by G. P. Thomson (the son of J. J. Thomson), who, with Reid, observed diffraction of electrons penetrating a thin foil. Around the same time, in 1923, Dirac postulated the concept of “single-particle interference.”
With these concepts in the background, Knoll and Ruska [46] invented the electron microscope (EM), in the transmission mode—TEM, using accelerated electrons. Initially the resolution was close to that of optical microscopy, but, as discussed below, it now reaches the atomic scale! Many contributions (Fig. 3.3) to this field have laid the foundation ([56] and the references therein, [77, 79]) for advances of the fundamentals of microscopy and for recent studies of electron interferometry [88, 89]. A comprehensive overview is given by Zewail and Thomas [98].
5 2D Imaging and Visualization of Atoms
The first images of individual atoms were obtained in 1951 by Müller [64, 86, 90], who introduced the technique of field-ion microscopy to visualize them at fine tips of metals and alloys, and to detect vacancies and atomic steps and kinks at surfaces. With the invention of field-emission sources and scanning TEM, pioneered in 1970 by Crewe, isolated heavy atoms became readily visible [15, 82]. (The scanning tunneling microscope was developed in the 1980s and made possible atomic-scale images of conducting surfaces.) Today, with aberration-corrected microscopes, imaging has reached a resolution of less than an ångström [65]. This history would be incomplete if I did not mention that the totality of technical developments and applications in the investigations of inorganic and organic materials have benefited enormously from the contributions of many other scientists, and for more details I refer the reader to the books by Cowley [14], Humphreys [41], Gai and Boyes [28], Spence [78], and Hawkes and Spence [34], and the most recent papers by Hawkes [33] and Howie [40].
6 The Third Dimension and Biological Imaging
Biological EM has been transformed by several major advances, including electron crystallography, single-particle tomography, and cryo-microscopy, aided by large-scale computational processing. Beginning with the 1968 electron crystallography work of DeRosier and Klug, see [45], 3D density maps became retrievable from EM images and diffraction patterns. Landmark experiments revealing the high-resolution structure from 2D crystals, single-particle 3D cryo-EM images of different but identical particles (6 Å resolution), and 3D cryo-EM images of the same particle (tomography with 6 Å resolution) represent the impressive progress made. Recently, another milestone in EM structural determination has been reported [2, 51]. Cryo-EM is giving us the first glimpse of mitochondrial ribosome at near-atomic resolution, and, as importantly, without the need for protein crystallization or extensive protocols of purification. In this case, the biological structure is massive, being three megadalton in content, and the subunit has a 39 protein complex which is clearly critical for the energy-producing function of the organelle. Using direct electron detection, a method we involved in the first ultrafast electron diffraction (UED) experiments [18, 91], the spatial resolution reached was 3.2 Å. With the recent structural advances made by the EM groups at the University of California, San Francisco (ion channels), Max Planck Institute of Biophysics, Frankfurt am Main (hydrogenase), and others, it is clear that EM is leading the way in the determination of macromolecular (and noncrystalline!) structures; the highlight by Kühlbrandt [51] provides the relevant references. The determined structures, however, represent an average over time.
With these methods, the first membrane protein structure was determined, the first high-resolution density maps for the protein shell of an icosahedral virus were obtained, and the imaging of whole cells was accomplished. Minimizing radiation damage by embedding the biological macromolecules and machines in vitreous ice affords a non-invasive, high-resolution imaging technique for visualizing the 3D organization of eukaryotic cells, with their dynamic organelles, cytoskeletal structure, and molecular machines in an unperturbed context, with an unprecedented resolution. I refer the reader to the papers by Henderson [35], Sali et al. [73], Crowther [16], and Glaeser [30], and the books by Glaeser et al. [31] and by Frank [27]. The Nobel paper by Roger Kornberg [48] on RNA polymerase II (pol II) transcription machinery is a must for reading. Recently, Henderson commented in a Nature article on the overzealous claims made by some in the X-ray laser community, emphasizing the unique advantages of electron microscopy and its cryo-techniques for biological imaging [36].
7 4D Ultrafast Electron Microscopy
Whereas in all of the above methods the processes of imaging, diffraction, and chemical analysis have been conducted in a static (time-averaged) manner, with the advent of femtosecond light pulses it has now become possible to unite the temporal domain with the (3D) spatial one, thereby creating 4D electron micrographs (Fig. 3.7; [99, 102]); the new approach is termed 4D ultrafast electron microscopy or—for short—4D UEM. This development owes its success to the advancement of the concept of coherent single-electron imaging [99], with the electron packets being liberated from a photocathode using femtosecond optical pulses. In such a mode of electron imaging, the repulsion between electrons is negligible, and thus atomic-scale spatiotemporal resolution can be achieved. Atomic motions, phase transitions, mechanical movements, and the nature of fields at interfaces are examples of phenomena that can be charted in unprecedented structural detail at a rate that is ten orders of magnitude faster than hitherto (Figs. 3.4, 3.8, and 3.9; see also the review article [24]).
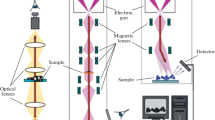
Concept of single-electron 4D UEM. A standard electron microscope records still images of a nanoscopic sample by sending a beam of electrons through the sample and focusing it onto a detector. By employing single-electron pulses, a 4D electron microscope produces movie frames representing time steps as short as femtoseconds (10−15 s). Each frame of the nanomovie is built up by repeating this process thousands of times with the same delay and combining all the pixels from the individual shots. The microscope may also be used in other modes, e.g., with one many-electron pulse per frame, depending on the kind of movie to be obtained. The single-electron mode produces the finest spatial resolution and captures the shortest time spans in each frame. Adapted from Zewail [101]
Nano-cantilevers in action. A 50-nm-wide cantilever made of a nickel-titanium alloy oscillates after a laser pulse excites it. Blue boxes highlight the movement in 3D. The full movie has one frame every 10 ns. Material properties determined from these oscillations would influence the design of nanomechanical devices. Adapted from Kwon et al. [52]
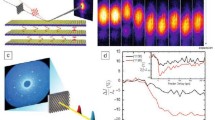
Principles of PINEM and experimental examples. (a) Left frame shows the moment of arrival of the electron packet at the nanotube prior to the femtosecond laser pulse excitation (t < 0); no spatiotemporal overlap has yet occurred. Middle frame shows the precise moment at t = 0 when the electron packet, femtosecond laser pulse, and evanescent field are at maximum overlap at the carbon nanotube. Right frame depicts the process during and immediately after the interaction (t > 0) when the electron gains/loses energy equal to integer multiples of femtosecond laser photons. (b) PINEM electron energy spectrum obtained at t = 0. The spectrum is given in reference to the loss/gain of photon quanta by the electrons with respect to the zero loss peak (ZLP). (c) Image taken with the E-field polarization of the femtosecond laser pulse being perpendicular to the long-axis of the carbon nanotube at t = 0, when the interaction between electrons, photons, and the evanescent field is at a maximum. (d) Near-fields of a nanoparticle pair with an edge-to-edge distance of 47 nm with false-color mapping. When the separation between the particles is reduced from 47 to 32 nm, a “channel” is formed between them. Adapted from Barwick et al. [3], Yurtsever et al. [93]
Furthermore, because electrons are focusable and can be pulsed at these very high rates, and because they have appreciable inelastic cross sections, UEM yields information in three distinct ways: in real space, in reciprocal space, and in energy space, all with the changes being followed in the ultrafast time domain. Convergent-beam imaging was shown to provide nanoscale diffraction of heterogeneous ensembles [92], and the power of tomography was also demonstrated for a complex structure [53]. Perhaps the most significant discovery in UEM was the photon induced near-field electron microscopy (PINEM; [3]), which uncovered the nature of the electromagnetic field in nanostructures; shown in Fig. 3.9 are images for PINEM of a single carbon nanotube and the coherent interaction between two particles at nanoscale separations. For biological PINEM imaging [23], see the upcoming Sect. 3.9. Thus, besides structural imaging, the energy landscapes of macromolecules, chemical compositions, and valence and core-energy states can be studied. The 3D structures (from tomography) can also be visualized.
Figure 3.10 depicts the space and time dimensions of UEM, and—for comparison—those of TEM. The boundaries of the time resolution are representative of the transition from the millisecond video speed used in TEM imaging, to the fast, or high-speed nanosecond-to-microsecond imaging, and on to the ultrafast femtosecond-to-attosecond imaging regime. The spatial resolution in the high-speed, nanosecond domain indicated in the Figure is limited by electron–electron (space–charge) repulsion in the nanosecond pulses of electrons. The UEM landscape is that of single-electron imaging, which, owing to the absence of inter-electron repulsion, reaches the spatial resolution of the TEM, but with the temporal resolution being ultrafast. Examples of time-averaged EM and of UEM studies can be found in [98]. The key concepts pertinent to UEM are outlined in Fig. 3.7.
Resolutions in space and time achieved in electron microscopy. The focus here is on the comparison of ultrafast electron microscopy (UEM) and transmission electron microscopy (TEM), but other variants of the techniques (scanning EM, tomography and holography, as well as electron spectroscopy) can similarly be considered. The horizontal dimension represents the spatial resolution achieved from the early years of EM to the era of aberration-corrected instruments. The vertical axis depicts the temporal resolution scale achieved up to the present time and the projected extensions into the near future. The domains of “fast” and “ultrafast” temporal resolutions are indicated by the areas of high-speed microscopy (HSM) and ultrafast electron microscopy (UEM), respectively [98]. Care should be taken in not naming the HSM “ultrafast electron microscopy”. Adapted from Zewail [99]
8 Coherent Single-Electrons in Ultrafast Electron Microscopy
The concept of single-electron imaging is based on the premise that the trajectories of coherent and timed, single-electron packets can provide an image equivalent to that obtained using many electrons in conventional microscopes. Unlike the random electron distribution of conventional microscopes, in UEM the packets are timed with femtosecond precision, and each electron has a unique coherence volume. As such, each electron of finite de Broglie wavelength is (transversely) coherent over the object length scale to be imaged, with a longitudinal coherence length that depends on its velocity. On the detector, the electron produces a “click” behaving as a classical particle, and when a sufficient number of such clicks are accumulated stroboscopically, the whole image emerges (Fig. 3.7). This was the idea realized in electron microscopy for the first time at Caltech. Putting it in Dirac’s famous dictum: each electron interferes only with itself. In the microscope, this “stop-motion imaging” yields a real-time movie of the process, and the methodology being used is similar to that described in Sect. 3.3. We note that, in contrast with Muybridge’s experiments, which deal with a single object (the horse), here we have to synchronize the motion of numerous independent atoms or molecules so that all of them have reached a similar point in the course of their structural evolution; to achieve such synchronization for millions—or billions—of the studied objects, the relative timing of the clocking and probe pulses must be of femtosecond precision, and the launch configuration must be defined to sub-ångström resolution.
Unlike with photons, in imaging with electrons we must also consider the consequences of the Pauli exclusion principle. The maximum number of electrons that can be packed into a state (or a cell of phase space) is two, one for each spin; in contrast, billions of photons can be condensed in a state of the laser radiation. This characteristic of electrons represents a fundamental difference in what is termed the “degeneracy,” or the mean number of electrons per cell in phase space. Typically it is about 10−4 to 10−6 but it is possible in UEM to increase the degeneracy by orders of magnitude, a feature that could be exploited for studies in quantum electron optics [98]. I note here that the definition of “single-electron packet” is reserved for the case when each timed packet contains one or a small number of electrons such that coulombic repulsion is effectively absent.
At Caltech, three UEM microscopes operate at 30, 120, and 200 keV. Upon the initiation of the structural change by heating of the specimen, or through electronic excitation, using the ultrashort clocking pulse, a series of frames for real space images, and similarly for diffraction patterns or electron-energy-loss spectra (EELS), is obtained. In the single-electron mode of operation, which affords studies of reversible processes or repeatable exposures, the train of strobing electron pulses is used to build up the image. By contrast, in the single-pulse mode, each recorded frame is created with a single pulse that contains 104–106 electrons. One has the freedom to operate the apparatus in either single-electron or single-pulse mode.
It is known from the Rayleigh criterion that, with a wavelength λ of the probing beam, the smallest distance that can be resolved is given by approximately 0.5 λ. Thus, in conventional optical microscopy, green light cannot resolve distances smaller than approximately 3000 Å (300 nm). Special variants of optical microscopy can nowadays resolve small objects of sub-hundreds of nanometers in size, which is below the diffraction limit ([37] and the references therein). When, however, an electron is accelerated in a 100 kV microscope, its wavelength approaches 4 × 10−2 Å, i.e., the picometer scale, a distance far shorter than that separating the atoms in a solid or molecule. The resolution of an electron microscope can, in principle, reach the sub-ångström limit [66]. One important advantage in optical microscopy is the ability to study objects with attached chromophores in water. Advances in environmental EM [28] for the studies of catalysis have been achieved, and liquid-cell EM ([17] and the references therein) has been successful in the studies of nanomaterials and cells.
Of the three kinds of primary beams (neutrons, X-rays, and electrons) suitable for structural imaging, the most powerful are coherent electrons, which are readily produced from field-emission guns [98]. The source brightness, as well as the temporal and spatial coherence of such electrons, significantly exceeds the values achievable for neutrons and X-rays: moreover, the minimum probe diameter of an electron beam is as small as 1 Å, and its elastic mean free path is approximately 100 Å (for carbon), much less than for neutrons and X-rays [35]. For larger samples and for those studied in liquids, X-ray absorption spectroscopy, when time-resolved, provides unprecedented details of energy pathways and electronic structural changes [8, 11, 43]. It is significant to note that in large samples the precision is high but it represents an average over the micrometer-scale specimens.
As a result of these developments and inventions, new fields of research continue to emerge. First, by combining energy-filtered electron imaging with electron tomography, chemical compositions of sub-attogram (less than 10−18 g) quantities located at the interior of microscopic or mesoscopic objects may be retrieved non-destructively. Second, transmission electron microscopes fitted with field-emission guns to provide coherent electron rays can be readily adapted for electron holography to record the magnetic fields within and surrounding nanoparticles or metal clusters, thereby yielding the lines of force of, for example, a nanoferromagnet encapsulated within a multi-walled carbon nanotube. Third, advances in the design of aberration-corrected high-resolution EMs have greatly enhanced the quality of structural information pertaining to nanoparticle metals, binary semiconductors, ceramics, and complex oxides. Moreover, electron tomography sheds light on the shape, size, and composition of materials. Finally, with convergent-beam and near-field 4D UEM [3, 92], the structural dynamics and plasmonics of a nanoscale single site (particle), and of nanoscale interface fields, can be visualized, reaching unprecedented resolutions in space and time [98].
9 Visualization and Complexity
Realization of the importance of visualization and observation is evident in the exploration of natural phenomena, from the very small to the very large. A century ago, the atom appeared complex, a “raisin or plum pie of no structure,” until it was visualized on the appropriate length and time scales. Similarly, with telescopic observations, a central dogma of the cosmos was changed and complexity yielded to the simplicity of the heliocentric structure and motion in the entire Solar System. From the atom to the universe, the length and time scales span extremes of powers of 10. The electron in the first orbital of a hydrogen atom has a “period” of sub-femtoseconds, and the size of atoms is on the nanometer scale or less. The lifetime of our universe is approximately 13 billion years and, considering the light year (approx. 1016 m), its length scale is of the order of 1026 m. In between these scales lies the world of life processes, with scales varying from nanometers to centimeters and from femtoseconds to seconds.
In the early days of DNA structural determination (1950s), a cardinal concept, in vogue at that time, was encapsulated in Francis Crick’s statement: If you want to know the function, determine the structure. This view dominated the thinking at the time, and it was what drove Max Perutz and John Kendrew earlier in their studies of proteins. But as we learn more about complexity, it becomes clear that the so-called structure–function correlation is insufficient to establish the mechanisms that determine the behavior of complex systems [98]. For example, the structures of many proteins have been determined, but we still do not understand how they fold, how they selectively recognize other molecules, how the matrix water assists folding and the role it plays in directionality, selectivity, and recognition; see, e.g., [61] for protein behavior in water (hydrophobic effect) and [62] for complexity, even in isolated systems. The proteins hemoglobin and myoglobin (a subunit of hemoglobin) have unique functions: the former is responsible for transporting oxygen in the blood of vertebrates, while the latter carries and stores oxygen in muscle cells. The three-dimensional structures of the two proteins have been determined (by Perutz and Kendrew), but we still do not understand the differences in behavior in the oxygen uptake by these two related proteins, the role of hydration, and the exact nature of the forces that control the dynamics of oxygen binding and liberation from the haem group. Visualization of the changing structures during the course of their functional operation is what is needed (see, e.g., [12, 75]).
In biological transformations, the energy landscape involves very complicated pathways, including those that lead to a multitude of conformations, with some that are “active” and others that are “inactive” in the biological function. Moreover, the landscapes define “good” and “bad” regions, the latter being descriptive of the origin of molecular diseases. It is remarkable that the robustness and function of these “molecules of life” are the result of a balance of weak forces—hydrogen bonding, electrostatic forces, dispersion, and hydrophobic interactions—all of energy of the order of a few kcal·mol−1, or approximately 0.1 eV or less. Determination of time-averaged molecular structures is important and has led to an impressive list of achievements, for which more than ten Nobel Prizes have been awarded, but the structures relevant to function are those that exist in the non-equilibrium state. Understanding their behavior requires an integration of the trilogy: structure, dynamics, and function.
Figure 3.11 depicts the experimental PINEM field of Escherichia coli bacterium which decays on the femtosecond time scale; in the same Figure, we display the conceptual framework of cryo-UEM for the study of folding/unfolding in proteins. Time-resolved cryo-EM has been successfully introduced in the studies of amyloids [21, 22]. In parallel, theoretical efforts ([57–60, 98] and the references therein) have been launched at Caltech to explore the areas of research pertaining to biological structures, dynamics, and the energy landscapes, with focus on the elementary processes involved.
Biological UEM. (a) An Escherichia coli bacterium imaged with PINEM. A femtosecond laser pulse generates an evanescent electromagnetic field in the cell’s membrane at time zero. By collecting only the imaging electrons that gained energy from this field, the technique produces high-contrast, relatively high-spatial resolution snapshot of the membrane. The false-color contour plot depicts the intensity recorded. The method can capture events occurring on very short timescales, as is evinced by the field’s significant decay after 200 fs. The field vanishes by 2000 fs. (b) By adapting the technique called cryo-imaging, we proposed the use of 4D UEM for the observation of biological processes such as protein folding. A glassy (noncrystalline) ice holds the protein. For each shot of the movie, a laser pulse melts the ice around the sample, causing the protein to unfold in the warm water. The movie records the protein refolding before the water cools and refreezes. The protein could be anchored to the substrate to keep it in the same position for each shot. Adapted from Flannigan et al. [23], Zewail [101]
Large-scale complexity is also evident in correlated physical systems exhibiting, e.g., superconductivity, phase transitions, or self-assembly, and in biological systems with emergent behavior [96]. For materials, an assembly of atoms in a lattice can undergo a change, which leads to a new structure with properties different from the original ones. In other materials, the structural transformation leads to a whole new material phase, as in the case of metal–insulator phase transitions. Questions of fundamental importance pertain to the time and length scales involved and to the elementary pathways that describe the mechanism. Recently, a number of such questions have been addressed by means of 4D electron imaging. Of significance are two regimes of structural transformation: the first one involves an initial (coherent) bond dilation that triggers unit-cell expansion and phase growth [5, 9], and the second one involves phase transformations in a diffusionless (collective) process that emerges from an initial random motion of atoms [67]. The elementary processes taking place in superconducting materials are now being examined [26] by direct probing of the “ultrafast phonons,” which are critically involved, and—in this laboratory—by studying the effect of optical excitation [10, 29] in ultrafast electron crystallography (UEC).
10 Attosecond Pulse Generation
For photons, attosecond pulse generation has already been demonstrated [49], and with a unique model that describes the processes involved [13]. Several review articles have detailed the history shaped by many involved in the field and the potential for applications; I recommend the reviews by Corkum [44], Krausz and Stockman [50], and Vrakking [55], and the critique by Leone et al. [54]. It is true that the pulse width can approach the 100 attosecond duration or less (see Fig. 3.12 for the electric field pattern), yielding a few-cycles-long pulse. However, there is a price to pay; the band width in the energy domain becomes a challenge in designing experiments. A 20-attosecond pulse has an associated energy bandwidth of ΔE ≈ 30 eV. In the femtochemistry domain, the bandwidth permits the mapping of dynamics on a given potential energy surface, and with selectivity for atomic motions. With electrons, processes of ionization and electron density change can be examined, but not with the selectivity mentioned above, as the pulse energy width covers, in case of molecules, numerous energy states. Experimental success has so far been reported for ionized atoms, Auger processes, and the direct measurement of the current produced by valence–conduction-band excitation in SiO2.
Electron pulse coherence and its packets, together with measured attosecond pulse envelope. (a) Single-electron packets and electron pulses. Shown are the effective pulse parameters and the coherence time involved. Each single-electron (blue) is a coherent packet consisting of many cycles of the de Broglie wave and has different timing due to the statistics of generation. On average, multiple single-electron packets form an effective electron pulse (dotted envelope). (b) Electric field of a few-cycle laser pulse impinging on an SiO2 sample. Adapted from Baum and Zewail [7], Krausz and Stockman [50]
On the other hand, for electrons in UEM, the challenge is to push the limit of the temporal width into the femtosecond domain and on to the attosecond regime. Several schemes have been proposed and discussed in the review article by Baum and Zewail [7]. In Fig. 3.12 we display a schematic for a single-electron packet and pulse. The electron trajectories obtained for the temporal optical-grating, tilted-pulses, and temporal-lens methodology are given in Fig. 3.13. One well-known technique is that of microwave compression [20] of electron pulses, which has recently been applied in femtosecond electron diffraction setups [63].
Schemes for creating and measuring attosecond compressed electron packets. (a) Temporal lensing. To measure the duration of the attosecond pulses, a second co-propagating standing wave is made to coincide with the electron pulse at the focal position. Instead of using a temporal delay, a phase shift, Δφ, is introduced into one of the laser pulses that creates the probing standing wave. By varying this phase shift, the nodes of the standing wave shift position. The average electron energy can thus be plotted vs. this phase shift. As the electron pulses become shorter than the period of the standing wave, the change in the average energy will increase. To use the attosecond electron pulse train as a probing beam in a UEM, the specimen would need to be positioned where the second standing wave appears in the figure; see Sec. 3.10. (b– e) Temporal optical gratings for the generation of free attosecond electron pulses for use in diffraction. (b) A femtosecond electron packet (blue) is made to co-propagate with a moving optical intensity grating (red). (c) The ponderomotive force pushes electrons toward the minima and thus creates a temporal lens. (d) The induced electron chirp leads to compression to the attosecond duration at a later time. (e) The electron pulse duration from 105 trajectories reaches into the domain of few attoseconds. Adapted from Barwick and Zewail [4], Baum and Zewail [7]
A more promising method for compression directly to the attosecond domain involves the creation of “temporal lenses” made by ultrashort laser pulses [6, 38]. The technique relies on the ponderomotive force (or ponderomotive potential) that influences electrons when they encounter an intense electromagnetic field. To create trains of attosecond electron pulses, appropriate optical intensity patterns have to be synchronized with the electron pulse. This is done by using counter-propagating laser pulses to create a standing optical wave that must be both spatially and temporally overlapped with the femtosecond electron pulse to get the desired compression. To make the standing wave in the rest frame of the electron pulse, the two counter-propagating electromagnetic waves must have different frequencies [6] or be angled appropriately [38]; see Fig. 3.13.
The standing wave that appears in the rest frame of the traveling electron pulse introduces a series of high and low intensity regions, and in this periodic potential each of the individual ponderomotive potential “wells” causes a compression of the local portion of the electron pulse that encounters it [38]. After interaction with the optical potential well, the electrons that have encountered steep intensity gradients get sped up or slowed down, depending on their position in the potential. After additional propagation, the electron pulse self-compresses into a train of attosecond pulses, with the pulse train spacing being equal to the periodicity of the optical standing wave. By placing the compression potential at an appropriate distance before the specimen, the pulse maximally compresses when encountering the system under study.
11 Optical Gating of Electrons and Attosecond Electron Microscopy
As discussed in this chapter, PINEM can be used to generate attosecond pulses [7]. Theoretically, it was clear that spatial and temporal coherences of partial waves (the so-called Bessel functions) can produce attosecond pulse trains, whereas incoherent waves cannot [68–70]. With this in mind, such pulse trains have been generated [19, 47], and the coherent interference of a plasmonic near-field was visualized [71]. Very recently at Caltech, we have developed a new variant of PINEM, which constitutes a breakthrough in electron pulse slicing and imaging.
In all the previous experiments conducted in 4D ultrafast electron microscopy, only “one optical pulse” is used to initiate the change in the nanostructure. In a recent report [32], based on the conceptual framework given by Park and Zewail [70], we have used “two optical pulses” for the excitation and “one electron pulse” for probing. The implementation of this pulse sequence led to the concept of “photon gating” of electron pulses, as shown in Fig. 3.14. The sequence gives rise to an electron pulse width limited only by the optical-gate pulse width. A picosecond electron pulse was shown to compress into the femtosecond width of the exciting optical pulse. This is a very important advance with the potential for reaching the attosecond time domain with many applications in 4D materials visualization.
Ultrafast “optical gating” of electrons using three-pulse sequence in PINEM. (a) PINEM spectrum at τ 1 = 0 fs, which consists of discrete peaks on the higher and lower energy sides of the zero loss peak (ZLP) separated by multiple photon-energy quanta (2.4 eV). The shaded curve presents the normalized ZLP measured at τ 1 = 1000 fs. (b) PINEM spectrogram of photon–electron coupling of the first optical and electron pulse as a function of the first optical pulse delay (τ 1). The ZLP area between −1.5 eV and 1.5 eV has been reduced for visualization of the adjacent discrete peaks. Optical gating is clearly manifested in the narrow strip corresponding to the width of the optical pulse (210 ± 35 fs) shown in red in the vertical plane at right, which is superimposed on the ultrafast electron pulse (1000 fs) in blue. The material studied is vanadium dioxide nanoparticles which undergo metal-to-insulator phase transition when appropriately excited. Adapted from Hassan et al. [32]
12 Conclusion
The generation of femtosecond light has its origins in several advances: mode locking by Anthony DeMaria, dye lasers by Peter Sorokin and Fritz Schäfer, colliding pulses in dye lasers by Erich Ippen and Chuck Shank (see the books edited by Schäfer and Shapiro [74, 76]); chirped pulse amplification by Gérard Mourou; white-light continuum by Bob Alfano and colleagues; and the streaking methods by Dan Bradley, and others, have all contributed to the advances made. Prior to the development of femtochemistry, there were significant contributions made in picosecond chemistry and physics (by Peter Rentzepis, Ken Eisenthal, the late Robin Hochstrasser, and Wolfgang Kaiser). In our laboratories at Caltech, the development of femtochemistry in the 1980s involved the use of spectroscopy, photoelectron detection, and mass spectrometry. But nothing can be compared with the capability we developed from the year 2000 and until now for microscopy imaging in 4D UEM.
The microscope is arguably one of the two most powerful human-made instruments of all time, the other being the telescope. To our vision they brought the very small and the very distant. Robert Hooke, for his Micrographia, chose the subtitle: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon. These words were made in reference to conventional optical microscopes; the spatial resolution of them is being limited by the wavelength of visible light—the Rayleigh criterion, as mentioned above. The transmission electron microscope, since its invention in the 1930s, has provided the wavelength of picometers, taking the field of imaging beyond the “minutes” of the seventeenth century Micrographia—it has now become possible to image individual atoms, and the scope of applications spans essentially all of the physical sciences as well as biology.
With 4D ultrafast electron microscopy, the structures determined are no longer “time-averaged” over seconds of recording. They can be seen as frames of a movie that elucidates the nature of the processes involved. We have come a long way from the epochs of the camera obscura of Alhazen and Hooke’s Micrographia, but I am confident that new research fields will continue to emerge in the twenty-first century, especially within frontiers at the intersection of physical, chemical, and biological sciences [97]. Indeed, the microscopic invisible has become visible—thanks to ultrafast photons and electrons.
References
Al-Hassani STS, Woodcock E, Saoud R (eds) (2006) 1001 inventions: Muslim heritage in our world. Foundation for Science, Technology and Civilization, Manchester
Amunts A, Brown A, Bai X et al (2014) Structure of the yeast mitochondrial large ribosomal subunit. Science 343:1485–1489
Barwick B, Flannigan DJ, Zewail AH (2009) Photon induced near-field electron microscopy. Nature 462:902–906
Barwick B, Zewail AH (2015) Photonics and plasmonics in 4D ultrafast electron microscopy. ACS Photonics 2:1391–1402
Baum P, Yang DS, Zewail AH (2007) 4D visualization of transitional structures in phase transformations by electron diffraction. Science 318:788–792
Baum P, Zewail AH (2007) Attosecond electron pulses for 4D diffraction and microscopy. Proc Natl Acad Sci U S A 104:18409–18414
Baum P, Zewail AH (2009) 4D attosecond imaging with free electrons: diffraction methods and potential applications. Chem Phys 366:2–8
Bressler C, Milne C, Pham VT et al (2009) Femtosecond XANES study of the light-induced spin crossover dynamics in an iron(II) complex. Science 323:489–492
Cavalleri A (2007) All at once. Science 318:755–756
Carbone F, Yang DS, Giannini E et al (2008) Direct role of structural dynamics in electron-lattice coupling of superconducting cuprates. Proc Natl Acad Sci USA 105:20161–20166
Chergui M, Zewail AH (2009) Electron and X-ray methods of ultrafast structural dynamics: advances and applications. Chem Phys Chem 10:28–43
Cho HS, Schotte F, Dashdorj N et al (2013) Probing anisotropic structure changes in proteins with picosecond time-resolved small-angle X-ray scattering. J Phys Chem B 117:15825–15832
Corkum PB, Krausz F (2007) Attosecond science. Nat Phys 3:381–387
Cowley JM (1995) Diffraction physics, 3rd edn. Elsevier, Amsterdam
Crewe AV, Wall J, Langmore J (1970) Visibility of single atoms. Science 168:1338–1340
Crowther RA (2008) The Leeuwenhoek lecture 2006. Microscopy goes cold: frozen viruses reveal their structural secrets. Philos Trans R Soc B 363:2441–2451
de Jonge N, Peckys DB, Kremers GJ et al (2009) Electron microscopy of whole cells in liquid with nanometer resolution. Proc Natl Acad Sci U S A 106:2159–2164
Dantus M, Kim SB, Williamson JC et al (1994) Ultrafast electron diffraction V: experimental time resolution and applications. J Phys Chem 98:2782–2796
Feist A, Echternkamp KE, Schauss J et al (2015) Quantum coherent optical phase modulation in an ultrafast transmission electron microscope. Nature 521:200–203
Fill E, Veisz L, Apolonski A et al (2006) Sub-fs electron pulses for ultrafast electron diffraction. New J Phys 8:272
Fitzpatrick AWP, Lorenz UJ, Vanacore GM et al (2013) 4D Cryo-electron microscopy of proteins. J Am Chem Soc 135:19123–19126
Fitzpatrick AWP, Park ST, Zewail AH et al (2013) Exceptional rigidity and biomechanics of amyloid revealed by 4D electron microscopy. Proc Natl Acad Sci USA 110:10976–10981
Flannigan DJ, Barwick B, Zewail AH (2010) Biological imaging with 4D ultrafast electron microscopy. Proc Natl Acad Sci U S A 107:9933–9937
Flannigan DJ, Zewail AH (2012) 4D electron microscopy: principles and applications. Acc Chem Res 45:1828–1839
Forsén S (1992) The Nobel prize for chemistry. In: Frängsmyr T, Malmstrøm BG (eds) Nobel lectures in chemistry, 1981–1990. World Scientific, Singapore, p 257, transcript of the presentation made during the 1986 Nobel Prize in chemistry award ceremony
Först M, Mankowsky R, Cavalleri A (2015) Mode-selective control of the crystal lattice. Acc Chem Res 48:380–387
Frank J (2006) Three-dimensional electron microscopy of macromolecular assemblies: visualization of biological molecules in their native state. Oxford University Press, New York
Gai PL, Boyes ED (2003) Electron microscopy in heterogeneous catalysis. Series in microscopy in materials science. IOP Publishing, Bristol
Gedik N, Yang DS, Logvenov G et al (2007) Nonequilibrium phase transitions in cuprates observed by ultrafast electron crystallography. Science 316:425–429
Glaeser RM (2008) Macromolecular structures without crystals. Proc Natl Acad Sci U S A 105:1779–1780
Glaeser RM, Downing K, DeRosier D et al (2007) Electron crystallography of biological macromolecules. Oxford University Press, New York
Hassan MT, Liu H, Baskin JS et al (2015) Photon gating in four-dimensional ultrafast electron microscopy. Proc Natl Acad Sci U S A 112:12944–12949
Hawkes PW (2009) Aberration correction: past and present. Phil Trans R Soc A 367:3637–3664
Hawkes PW, Spence JCH (eds) (2007) Science of microscopy. Springer, New York
Henderson R (1995) The potential and limitations of neutrons, electrons and X-rays for atomic resolution microscopy of unstained biological molecules. Q Rev Biophys 28:171–193
Henderson R (2002) Excitement over X-ray lasers is excessive. Nature 415:833
Hell SW (2015) Nanoscopy with focused light. Angew Chem Int Ed 54:8054–8066, transcript of the Nobel lecture given in 2014
Hilbert SA, Uiterwaal C, Barwick B et al (2009) Temporal lenses for attosecond and femtosecond electron pulses. Proc Natl Acad Sci U S A 106:10558–10563
Hooke R (1665) Micrographia: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon. Royal Society, London
Howie A (2009) Aberration correction: zooming out to overview. Phil Trans R Soc A 367:3859–3870
Humphreys CJ (ed) (2002) Understanding materials: a festschrift for Sir Peter Hirsch. Maney, London
Jain VK (1995) The world’s fastest camera. The World and I 10:156–163
Kim TK, Lee JH, Wulff M et al (2009) Spatiotemporal kinetics in solution studied by time-resolved X-ray liquidography (solution scattering). Chem Phys Chem 10:1958–1980
Kim KT, Villeneuve DM, Corkum PB (2014) Manipulating quantum paths for novel attosecond measurement methods. Nat Photonics 8:187–194
Klug A (1983) From macromolecules to biological assemblies. Angew Chem Int Ed 22:565–636, transcript of the Nobel lecture given in 1982
Knoll M, Ruska E (1932) Das Elektronenmikroskop. Z Phys 78:318–339
Kociak M (2015) Microscopy: quantum control of free electrons. Nature 521:166–167
Kornberg R (2007) The molecular basis of eukaryotic transcription. Angew Chem Int Ed 46:6956–6965, transcript of the Nobel lecture given in 2006
Krausz F, Ivanov M (2009) Attosecond physics. Rev Mod Phys 81:163–234
Krausz F, Stockman MI (2014) Attosecond metrology: from electron capture to future signal processing. Nat Photonics 8:205–213
Kühlbrandt W (2014) The resolution revolution. Science 343:1443–1444
Kwon OH, Park HS, Baskin JS et al (2010) Nonchaotic, nonlinear motion visualized in complex nanostructures by stereographic 4D electron microscopy. Nano Lett 10:3190–3198
Kwon OH, Zewail AH (2010) 4D electron tomography. Science 328:1668–1673
Leone SR, McCurdy CW, Burgdörfer J et al (2014) What will it take to observe processes in ‘real time’? Nat Photonics 8:162–166
Lépine F, Ivanov MY, Vrakking MJJ (2014) Attosecond molecular dynamics: fact or fiction? Nat Photonics 8:195–204
Lichte H (2002) Electron interference: mystery and reality. Philos Trans R Soc Lond A 360:897–920
Lin MM, Shorokhov D, Zewail AH (2006) Helix-to-coil transitions in proteins: helicity resonance in ultrafast electron diffraction. Chem Phys Lett 420:1–7
Lin MM, Meinhold L, Shorokhov D et al (2008) Unfolding and melting of DNA (RNA) hairpins: the concept of structure-specific 2D dynamic landscapes. Phys Chem Chem Phys 10:4227–4239
Lin MM, Shorokhov D, Zewail AH (2009) Structural ultrafast dynamics of macromolecules: diffraction of free DNA and effect of hydration. Phys Chem Chem Phys 11:10619–10632
Lin MM, Shorokhov D, Zewail AH (2009) Conformations and coherences in structure determination by ultrafast electron diffraction. J Phys Chem A 113:4075–4093
Lin MM, Zewail AH (2012) Protein folding: simplicity in complexity. Ann Phys 524:379–391
Lin MM, Shorokhov D, Zewail AH (2014) Dominance of misfolded intermediates in the dynamics of α-helix folding. Proc Natl Acad Sci U S A 111:14424–14429
Mancini GF, Mansart B, Pagano S et al (2012) Design and implementation of a flexible beamline for fs electron diffraction experiments. Nucl Instrum Methods Phys Res A 691:113–122
Müller EW (1951) Das Feldionenmikroskop. Z Phys 131:136–142
Nellist PD, Chisholm MF, Dellby N et al (2004) Direct sub-ångström imaging of a crystal lattice. Science 305:1741
O’Keefe MA (2008) Seeing atoms with aberration-corrected sub-ångström electron microscopy. Ultramicroscopy 108:196–209
Park HS, Kwon OH, Baskin JS et al (2009) Direct observation of martensitic phase-transformation dynamics in iron by 4D single-pulse electron microscopy. Nano Lett 9:3954–3962
Park ST, Lin MM, Zewail AH (2010) Photon induced near-field electron microscopy (PINEM): theoretical and experimental. New J Phys 12:123028
Park ST, Kwon OH, Zewail AH (2012) Chirped imaging pulses in four-dimensional electron microscopy: femtosecond pulsed hole burning. New J Phys 14:053046
Park ST, Zewail AH (2012) Enhancing image contrast and slicing electron pulses in 4D near-field electron microscopy. Chem Phys Lett 521:1–6
Piazza L, Lummen TTA, Quiñonez E et al (2015) Simultaneous observation of the quantization and the interference pattern of a plasmonic near-field. Nat Commun 6:6407
Sabra AI (2003) Ibn al-Haytham. Harvard Mag 9–10:54–55
Sali A, Glaeser RM, Earnest T et al (2003) From words to literature in structural proteomics. Nature 422:216–225
Schäfer FP (ed) (1973) Dye lasers (Topics in applied physics, vol. 1) Springer, Heidelberg
Schotte F, Cho HS, Kaila VRI et al (2012) Watching a signaling protein function in real time via 100-ps time-resolved Laue crystallography. Proc Natl Acad Sci USA 109:19256–19261
Shapiro SL (ed) (1977) Ultrashort light pulses, picosecond techniques and applications (Topics in applied physics, vol. 18) Springer, Heidelberg
Silverman MP, Strange W, Spence JCH (1995) The brightest beam in science: new directions in electron microscopy and interferometry. Am J Phys 63:800–813
Spence JCH (2003) High-resolution electron microscopy, (Monographs on the physics and chemistry of materials, vol. 60), 3rd edn. Oxford University Press, New York
Spence JCH (2009) Electron interferometry. In: Greenberger D, Hentschel K, Weinert F (eds) Compendium of quantum physics: concepts, experiments, history and philosophy. Springer, Berlin, pp 188–195
Steffens B (2007) Ibn al-Haytham: first scientist. Morgan Reynolds, Greensboro
Strutt JW (1891) On pin-hole photography. Philos Mag 31:87–99
Thomas JM (1979) Direct imaging of atoms. Nature 281:523–524
Thomas JM (1991) Femtosecond diffraction. Nature 351:694–695
Thomas JM (2004) Ultrafast electron crystallography: the dawn of a new era. Angew Chem Int Ed 43:2606–2610
Thomas JM (2005) A revolution in electron microscopy. Angew Chem Int Ed 44:5563–5566
Thomas JM (2008) Revolutionary developments from atomic to extended structural imaging. In: Zewail AH (ed) Physical biology: from atoms to medicine. Imperial College Press, London, pp 51–114
Thomas JM (2009) The renaissance and promise of electron energy-loss spectroscopy. Angew Chem Int Ed 48:8824–8826
Tonomura A (1998) The quantum world unveiled by electron waves. World Scientific, Singapore
Tonomura A (1999) Electron holography, 2nd edn. Springer, Berlin
Tsong TT (2006) Fifty years of seeing atoms. Phys Today 59:31–37
Williamson JC, Cao J, Ihee H et al (1997) Clocking transient chemical changes by ultrafast electron diffraction. Nature 386:159–162
Yurtsever A, Zewail AH (2009) 4D nanoscale diffraction observed by convergent-beam ultrafast electron microscopy. Science 326:708–712
Yurtsever A, Baskin JS, Zewail AH (2012) Entangled nanoparticles: discovery by visualization in 4D electron microscopy. Nano Lett 12:5027–5032
Zewail AH (1990) The birth of molecules. Sci Am 263:76–82
Zewail AH (2000) Femtochemistry: atomic-scale dynamics of the chemical bond using ultrafast lasers. In: Frängsmyr T (ed) Les prix nobel: the nobel prizes 1999. Almqvist & Wiksell, Stockholm, pp 110–203, Also published in Angew Chem Int Ed 39:2587–2631; transcript of the Nobel lecture given in 1999
Zewail AH (2008) Physical biology: 4D visualization of complexity. In: Zewail AH (ed) Physical biology: from atoms to medicine. Imperial College Press, London, pp 23–49
Zewail AH (2009) Chemistry at a historic crossroads. Chem Phys Chem 10:23
Zewail AH, Thomas JM (2009) 4D electron microscopy: imaging in space and time. Imperial College Press, London
Zewail AH (2010) 4D electron microscopy. Science 328:187–193
Zewail AH (2010) Micrographia of the 21st century: from camera obscura to 4D microscopy. Philos Trans R Soc Lond A 368:1191–1204
Zewail AH (2010) Filming the invisible in 4D. Sci Am 303:74–81
Zewail AH (2012) 4D imaging in an ultrafast electron microscope. US Patent 8,203,120
Zewail AH (2014) 4D visualization of matter: recent collected works. Imperial College Press, London
Acknowledgements
The research summarized in this contribution had been carried out with support from the National Science Foundation (DMR-0964886) and the Air Force Office of Scientific Research (FA9550-11-1-0055) in the Physical Biology Center for Ultrafast Science and Technology (UST), which is supported by the Gordon and Betty Moore Foundation at Caltech.
During the forty-years-long research endeavor at Caltech, I had the pleasure of working with some 400 research associates, and without their efforts the above story would not have been told. References are included here to highlight selected contributions, but the work in its totality could not be covered because of the limited space and the article focus.
I am especially grateful to Dr. Dmitry Shorokhov, not only for his technical support but also for the intellectual discussions of the science involved and possible future projects. Dr. Dmitry Shorokhov, together with Dr. Milo Lin, has made major contributions to biological dynamics in the isolated phase (see Sec. 3.9).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.
The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Zewail, A.H. (2016). Ultrafast Light and Electrons: Imaging the Invisible. In: Al-Amri, M., El-Gomati, M., Zubairy, M. (eds) Optics in Our Time. Springer, Cham. https://doi.org/10.1007/978-3-319-31903-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-31903-2_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-31902-5
Online ISBN: 978-3-319-31903-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)