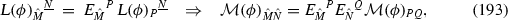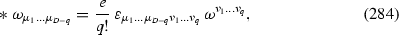Skip to main content
SpringerLink
Log in

Introductory Lectures on Extended Supergravities and Gaugings

  • Conference paper
  • First Online:
Book cover Theoretical Frontiers in Black Holes and Cosmology

Part of the book series: Springer Proceedings in Physics ((SPPHY,volume 176))

Abstract

In an ungauged supergravity theory, the presence of a scalar potential is allowed only for the minimal \(N=1\) case. In extended supergravities, a non-trivial scalar potential can be introduced without explicitly breaking supersymmetry only through the so-called gauging procedure. The latter consists in promoting a suitable global symmetry group to local symmetry to be gauged by the vector fields of the theory. Gauged supergravities provide a valuable approach to the study of superstring flux-compactifications and the construction of phenomenologically viable, string-inspired models. The aim of these lectures is to give a pedagogical introduction to the subject of gauged supergravities, covering just selected issues and discussing some of their applications.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    In part they originate from gauge symmetries associated with the higher dimensional antisymmetric tensor fields.

  2. 2.

    Using the “mostly minus” convention and \(8\pi \mathrm {G}_{\textsc {n}}=c=\hbar =1\).

  3. 3.

    A solvable Lie group \(G_S\) can be described (locally) as a the Lie group generated by solvable Lie algebra \({\mathscr {S}}\): \(G_S=\mathrm {exp}({\mathscr {S}}) \). A Lie algebra \({\mathscr {S}}\) is solvable iff, for some \(k>0\), \(\mathbf{D}^k {\mathscr {S}}=0\), where the derivative \(\mathbf{D}\) of a Lie algebra \(\mathfrak {g}\) is defined as follows: \(\mathbf{D}\mathfrak {g}\equiv [\mathfrak {g},\mathfrak {g}]\), \(\mathbf{D}^n\mathfrak {g}\equiv [\mathbf{D}^{n-1}\mathfrak {g},\mathbf{D}^{n-1}\mathfrak {g}]\). In a suitable basis of a given representation, elements of a solvable Lie group or a solvable Lie algebra are all described by upper (or lower) triangular matrices.

  4. 4.

    The symplectic indices \(M,\,N,\dots \) are raised (and lowered) with the symplectic matrix \(\mathbb {C}^{MN}\) (\(\mathbb {C}_{MN}\)) using north-west south-east conventions: \(X^{M}=\mathbb {C}^{MN}\,X_{N}\) (and \(X_M=\mathbb {C}_{NM}\,X^{N}\)).

  5. 5.

    A special Kähler manifold is in general characterized by the product of a \(\mathrm{U}(1)\)-bundle, associated with its Kähler structure (with respect to which the manifold is Hodge Kähler), and a flat symplectic bundle. See for instance [19] for an in depth account of this issue.

  6. 6.

    We label the new basis by underlined indices.

  7. 7.

    The electric and magnetic charges (e, m) are expressed in the rationalized-Heaviside-Lorentz (RHL) system of units.

  8. 8.

    Here we only consider local transformations on the fields.

  9. 9.

    We define \(w_\mu \equiv w_s\,\partial _\mu \phi ^s\).

  10. 10.

    This is a schematic representation in which we have suppressed the Lorentz indices and gamma-matrices.

  11. 11.

    The gravitino field has an additional term \(\mathscr {D}\varepsilon \) which is its variation as the gauge field of local supersymmetry.

  12. 12.

    We describe by hatted-indices those pertaining to the symplectic frame in which the Lagrangian is defined.

  13. 13.

    Here we use the following convention for the definition of the components of a form: \(\omega _{(p)}=\frac{1}{p!}\,\omega _{\mu _1\dots \mu _p}\,dx^{\mu _1}\wedge \dots dx^{\mu _p}\).

  14. 14.

    The ellipses refer to terms containing the vector field strengths.

  15. 15.

    In the formulas below we use the coset representative in which the first index (acted on by G) is in the generic symplectic frame defined by the matrix E and which is then related to the same matrix in the electric frame (labeled by hatted indices) as follows:

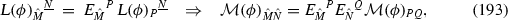
    figure d

    last equation being (68).

  16. 16.

    Recall that in maximal supergravity the locality constraint follows from the linear and the closure ones.

  17. 17.

    In a generic gauged model, supersymmetry further require the fermion shifts to be related by differential “gradient flow” relations [29] which can e shown to follow from the identification of the shifts with components of the \(\mathbb {T}\)-tensor and the geometry of the scalar manifold.

  18. 18.

    The \(H_\mathrm{R}=\mathrm{U}(2)\)-generators \(\{J_{\mathbf{a}}\}\) naturally split into a \(\mathrm{U}(1)\)-generator \(J_0\) of the Kähler transformations on \(\mathscr {M}_{\textsc {sk}}\) and \(\mathrm{SU}(2)\)-generators \(J_x\) (\(x=1,2,3\)) in the holonomy group of the quaternionic Kähler manifold \(\mathscr {M}_{\textsc {qk}}\).

  19. 19.

    For string theory compactifications we should also require this latter scale to be negligible compared to the mass-scale of the string excitations (order \(1/\sqrt{\alpha '}\)).

  20. 20.

    We can relax this constraint by extending this representation to include the \(\mathbf{56}\) in (220). Consistency however would require the gauging of the scaling symmetry of the theory (which is never an off-shell symmetry), also called trombone symmetry [55, 56]. This however leads to gauged theories which do not have an action. We shall not discuss these gaugings here.

  21. 21.

    In the previous sections we have used, for the supergravity fields, notations which are different from those used in the literature of maximal supergravity (e.g. in [18]) in order to make contact with the literature of gauged \(N<8\) theories, in particular \(N=2\) ones [19]. Denoting by a hat the quantities in [18], the correspondence between the two notations is:

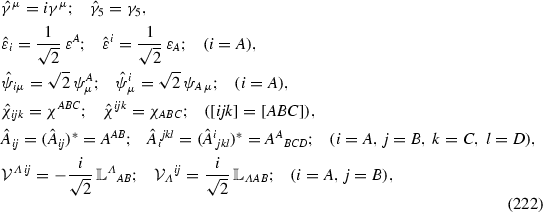
    figure e

    where in the last line the \(28\times 28\) blocks of \(\mathcal {V}_M{}^{\underline{N}}\) have been put in correspondence with those of \(\mathbb {L}^M{}_{\underline{N}}\). The factor \(\sqrt{2}\) originates from a different convention with the contraction of antisymmetric couples of \(\mathrm{SU}(8)\)-indices: \(\hat{V}_{ij}\hat{V}^{ij}=\frac{1}{2}\,V^{AB}\,V_{AB}\).

  22. 22.

    See Table 2 at the end of Sect. 4.

  23. 23.

    Here, for the sake of simplicity, we reabsorb the gauge coupling constant g into \(\varTheta \): \(g\,\varTheta \rightarrow \varTheta \).

  24. 24.

    These fields will also be described as 2-forms \(B_\alpha \equiv \frac{1}{2}\,B_{\mu \nu }\,dx^\mu \wedge dx^\nu \).

  25. 25.

    In our earlier discussion we showed that \(\mathcal {D}\mathcal {H}^M\,\varTheta _M{}^\alpha =\mathcal {D}F^M\,\varTheta _M{}^\alpha =0\). This is consistent with (278) since on-shell \(\mathcal {H}^M\varTheta _M{}^\alpha ={\mathcal {G}}^M\varTheta _M{}^\alpha \).

  26. 26.

    The Hodge dual \({}^*\omega \) of a generic q-form \(\omega \) is defined as:

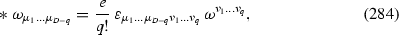
    figure f

    where \(\varepsilon _{01\dots D-1}=1\). One can easily verify that \({}^{**}\omega =(-)^{q(D-q)}\,(-)^{D-1}\,\omega \).

References

  1. O. Hohm, H. Samtleben, Exceptional field theory. II. E\(_{7(7)}\). Phys. Rev. D 89, 066017 (2014). arXiv:1312.4542 [hep-th]

    Article  ADS  Google Scholar 

  2. C. Hull, B. Zwiebach, Double field theory. JHEP 0909, 099 (2009). arXiv:0904.4664 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  3. C.M. Hull, P.K. Townsend, Unity of superstring dualities. Nucl. Phys. B 438, 109 (1995). arXiv:hep-th/9410167

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. B. de Wit, H. Nicolai, N \(=\) 8 Supergravity. Nucl. Phys. B 208, 323 (1982)

    Article  ADS  Google Scholar 

  5. B. de Wit, H. Samtleben, M. Trigiante, On Lagrangians and gaugings of maximal supergravities. Nucl. Phys. B 655, 93 (2003). arXiv:hep-th/0212239

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. B. de Wit, H. Samtleben, M. Trigiante, Maximal supergravity from IIB flux compactifications. Phys. Lett. B 583, 338 (2004). arXiv:hep-th/0311224

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. B. de Wit, H. Samtleben, Gauged maximal supergravities and hierarchies of non Abelian vector-tensor systems. Fortsch. Phys. 53, 442 (2005). arXiv:hep-th/0501243

    Article  ADS  MATH  Google Scholar 

  8. B. de Wit, H. Samtleben, M. Trigiante, Magnetic charges in local field theory. JHEP 0509, 016 (2005). arXiv:hep-th/0507289

    Article  MathSciNet  Google Scholar 

  9. C.M. Hull, Noncompact gaugings of N \(=8\) supergravity. Phys. Lett. B 142, 39 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  10. C.M. Hull, More gaugings of N \(=8\) supergravity. Phys. Lett. B 148, 297 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  11. M. Trigiante, Dual Gauged Supergravities (17th SIGRAV Conference Turin, September 4-7, Italy, 2006). arXiv:hep-th/0701218

    Google Scholar 

  12. H. Samtleben, Lectures on gauged supergravity and flux compactifications. Class. Quant. Grav. 25, 214002 (2008). arXiv:0808.4076 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. M. Grana, Flux compactifications in string theory: a comprehensive review. Phys. Rept. 423, 91 (2006). arXiv:hep-th/0509003

    Article  ADS  MathSciNet  Google Scholar 

  14. R. Blumenhagen, B. Kors, D. Lust, S. Stieberger, Four-dimensional string compactifications with D-Branes, orientifolds and fluxes. Phys. Rept. 445, 1 (2007). arXiv:hep-th/0610327

    Article  ADS  MathSciNet  Google Scholar 

  15. M.R. Douglas, S. Kachru, Flux compactification. Rev. Mod. Phys. 79, 733 (2007). arXiv:hep-th/0610102

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. F. Cordaro, P. Fre, L. Gualtieri, P. Termonia, M. Trigiante, N \(=\) 8 gaugings revisited: an exhaustive classification. Nucl. Phys. B 532, 245 (1998). arXiv:hep-th/9804056

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. H. Nicolai, H. Samtleben, Maximal gauged supergravity in three-dimensions. Phys. Rev. Lett. 86, 1686 (2001). arXiv:hep-th/0010076

    Article  ADS  MathSciNet  Google Scholar 

  18. B. de Wit, H. Samtleben, M. Trigiante, The maximal D \(=\) 4 supergravities. JHEP 0706, 049 (2007). arXiv:0705.2101 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  19. L. Andrianopoli, M. Bertolini, A. Ceresole, R. D’Auria, S. Ferrara, P. Fre, T. Magri, N \(=\) 2 supergravity and N \(=\) 2 super Yang-Mills theory on general scalar manifolds: symplectic covariance, gaugings and the momentum map. J. Geom. Phys. 23, 111 (1997). arXiv:hep-th/9605032

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. M.K. Gaillard, B. Zumino, Duality rotations for interacting fields. Nucl. Phys. B 193, 221 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  21. S. Ferrara, A. Marrani, E. Orazi, M. Trigiante, Dualities near the horizon. JHEP 1311, 056 (2013). arXiv:1305.2057 [hep-th]

    Article  ADS  Google Scholar 

  22. P.A.M. Dirac, Quantized singularities in the electromagnetic field. Proc. Roy. Soc. Lond. A 133, 60 (1931)

    Article  ADS  MATH  Google Scholar 

  23. J.S. Schwinger, Magnetic charge and quantum field theory. Phys. Rev. 144, 1087 (1966)

    Article  ADS  MathSciNet  Google Scholar 

  24. D. Zwanziger, Quantum field theory of particles with both electric and magnetic charges. Phys. Rev. 176, 1489 (1968)

    Article  ADS  Google Scholar 

  25. B. de Wit, P.G. Lauwers, A. Van Proeyen, Lagrangians of N \(=\) 2 supergravity—matter systems. Nucl. Phys. B 255, 569 (1985)

    Article  ADS  Google Scholar 

  26. P. Van Nieuwenhuizen, Supergravity. Phys. Rep. 68, 189 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  27. S. Ferrara L. Maiani, An introduction to supersymmetry breaking in extended supergravity, in 5th SILARG Symposium on Relativity, Supersymmetry and Cosmology (Bariloche, Argentina, January 4–11, 1985)

    Google Scholar 

  28. S. Cecotti, L. Girardello, M. Porrati, Constraints on partial superhiggs. Nucl. Phys. B 268, 295 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  29. R. D’Auria, S. Ferrara, On fermion masses, gradient flows and potential in supersymmetric theories. JHEP 0105, 034 (2001). arXiv:hep-th/0103153

    Article  MathSciNet  Google Scholar 

  30. J.M. Maldacena, The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 38, 1113 (1999) (Adv. Theor. Math. Phys. 2, 231 (1998)) arXiv:hep-th/9711200

  31. E. Cremmer, S. Ferrara, C. Kounnas, D.V. Nanopoulos, Naturally vanishing cosmological constant in N \(=\) 1 supergravity. Phys. Lett. B 133, 61 (1983)

    Article  ADS  MathSciNet  Google Scholar 

  32. J.R. Ellis, C. Kounnas, D.V. Nanopoulos, No scale supersymmetric guts. Nucl. Phys. B 247, 373 (1984)

    Article  ADS  Google Scholar 

  33. R. Barbieri, E. Cremmer, S. Ferrara, Flat and positive potentials in \(N=1\) supergravity. Phys. Lett. B 163, 143 (1985)

    Article  ADS  MathSciNet  Google Scholar 

  34. C. Angelantonj, S. Ferrara, M. Trigiante, New D \(=\) 4 gauged supergravities from N \(=\) 4 orientifolds with fluxes. JHEP 0310, 015 (2003). arXiv:hep-th/0306185

    Article  ADS  MathSciNet  Google Scholar 

  35. R. D’Auria, S. Ferrara, F. Gargiulo, M. Trigiante, S. Vaula, N \(=\) 4 supergravity Lagrangian for type IIB on T**6 / Z(2) in presence of fluxes and D3-branes. JHEP 0306, 045 (2003). hep-th/0303049

    Article  MathSciNet  Google Scholar 

  36. J. Scherk, J.H. Schwarz, Nucl. Phys. B 153, 61 (1979)

    Article  ADS  MathSciNet  Google Scholar 

  37. N. Kaloper, R.C. Myers, The odd story of massive supergravity. JHEP 9905, 010 (1999). hep-th/9901045

    Article  ADS  MathSciNet  MATH  Google Scholar 

  38. V. Mathai, J.M. Rosenberg, T duality for torus bundles with H fluxes via noncommutative topology. Commun. Math. Phys. 253, 705 (2004). hep-th/0401168

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. C.M. Hull, A geometry for non-geometric string backgrounds. JHEP 0510, 065 (2005). hep-th/0406102

    Article  ADS  MathSciNet  Google Scholar 

  40. J. Shelton, W. Taylor, B. Wecht, Nongeometric flux compactifications. JHEP 0510, 085 (2005). hep-th/0508133

    Article  ADS  MathSciNet  Google Scholar 

  41. N. Hitchin, Lectures on Generalized Geometry. arXiv:1008.0973 [math.DG]

  42. M. Gualtieri, Generalized Complex Geometry. arXiv:math/0401221 [math-dg]

  43. C.M. Hull, R.A. Reid-Edwards, Gauge symmetry, T-duality and doubled geometry. JHEP 0808, 043 (2008). arXiv:0711.4818 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  44. A. Dabholkar, C. Hull, Generalised T-duality and non-geometric backgrounds. JHEP 0605, 009 (2006). arXiv:hep-th/0512005

    Article  ADS  MathSciNet  Google Scholar 

  45. O. Hohm, C. Hull, B. Zwiebach, Generalized metric formulation of double field theory. JHEP 1008, 008 (2010). arXiv:1006.4823 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  46. C.M. Hull, Generalised geometry for M-theory. JHEP 0707, 079 (2007). arXiv:hep-th/0701203

    Article  ADS  MathSciNet  Google Scholar 

  47. P.P. Pacheco, D. Waldram, M-theory, exceptional generalised geometry and superpotentials. JHEP 0809, 123 (2008). arXiv:0804.1362 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  48. O. Hohm, H. Samtleben, Exceptional form of D \(=\) 11 supergravity. Phys. Rev. Lett. 111, 231601 (2013). arXiv:1308.1673 [hep-th]

    Article  ADS  Google Scholar 

  49. O. Hohm, H. Samtleben, Consistent Kaluza-Klein truncations via exceptional field theory. JHEP 1501, 131 (2015). arXiv:1410.8145 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  50. G. Dibitetto, A. Guarino, D. Roest, Charting the landscape of N \(=\) 4 flux compactifications. JHEP 1103, 137 (2011). arXiv:1102.0239 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  51. G. Dall’Agata, G. Inverso, On the vacua of N \(=\) 8 gauged supergravity in 4 dimensions. Nucl. Phys. B 859, 70 (2012). arXiv:1112.3345 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  52. G. Inverso, De Sitter Vacua in N \(=\) 8 Supergravity, MSc Thesis, Università di Padova, Italy, 14 July (2010)

    Google Scholar 

  53. E. Cremmer, B. Julia, The N \(=\) 8 supergravity theory. 1. The Lagrangian. Phys. Lett. B 80, 48 (1978)

    Article  ADS  Google Scholar 

  54. E. Cremmer, B. Julia, The SO(8) supergravity. Nucl. Phys. B 159, 141 (1979)

    Article  ADS  MathSciNet  Google Scholar 

  55. A. Le Diffon, H. Samtleben, Supergravities without an action: gauging the trombone. Nucl. Phys. B 811, 1 (2009). arXiv:0809.5180 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  56. A. Le Diffon, H. Samtleben, M. Trigiante, N \(=\) 8 supergravity with local scaling symmetry. JHEP 1104, 079 (2011). arXiv:1103.2785 [hep-th]

    Article  MathSciNet  MATH  Google Scholar 

  57. B. de Wit, H. Nicolai, The consistency of the S**7 truncation in D \(=\) 11 supergravity. Nucl. Phys. B 281, 211 (1987)

    Article  ADS  MathSciNet  Google Scholar 

  58. E. Cremmer, J. Scherk, J.H. Schwarz, Spontaneously broken N \(=\) 8 supergravity. Phys. Lett. B 84, 83 (1979)

    Article  ADS  Google Scholar 

  59. L. Andrianopoli, R. D’Auria, S. Ferrara, M.A. Lledo, Gauging of flat groups in four-dimensional supergravity. JHEP 0207, 010 (2002). arXiv:hep-th/0203206

    Article  ADS  MathSciNet  Google Scholar 

  60. G. Dall’Agata, G. Inverso, de Sitter vacua in N \(=\) 8 supergravity and slow-roll conditions. Phys. Lett. B 718, 1132 (2013). arXiv:1211.3414 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  61. G. Dall’Agata, G. Inverso, M. Trigiante, Evidence for a family of SO(8) gauged supergravity theories. Phys. Rev. Lett. 109, 201301 (2012). arXiv:1209.0760 [hep-th]

    Article  ADS  Google Scholar 

  62. G. Dall’Agata, G. Inverso, A. Marrani, Symplectic deformations of gauged maximal supergravity. JHEP 1407, 133 (2014). arXiv:1405.2437 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  63. A. Borghese, A. Guarino, D. Roest, All \(G_2\) invariant critical points of maximal supergravity. JHEP 1212, 108 (2012). arXiv:1209.3003 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  64. A. Borghese, G. Dibitetto, A. Guarino, D. Roest, O. Varela, The SU(3)-invariant sector of new maximal supergravity. JHEP 1303, 082 (2013)

    Article  ADS  MathSciNet  Google Scholar 

  65. A. Borghese, A. Guarino, D. Roest, Triality, periodicity and stability of SO(8) gauged supergravity. JHEP 1305, 107 (2013). arXiv:1302.6057 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  66. A. Gallerati, H. Samtleben, M. Trigiante, The \({\cal {N}}>2 \) supersymmetric AdS vacua in maximal supergravity. JHEP 1412, 174 (2014). arXiv:1410.0711 [hep-th]

  67. J. Tarrío, O. Varela, Electric/magnetic duality and RG flows in AdS\(_4\)/CFT\(_3\). JHEP 1401, 071 (2014). arXiv:1311.2933 [hep-th]

    Article  ADS  Google Scholar 

  68. Y. Pang, C.N. Pope, J. Rong, Holographic RG flow in a new \(SO(3)\times SO(3)\) sector of \(\omega \)-deformed \(SO(8)\) gauged \({\cal {N}}=8 \) supergravity. JHEP 1508, 122 (2015). arXiv:1506.04270 [hep-th]

  69. A. Anabalon, D. Astefanesei, Black holes in \(\omega \)-defomed gauged N \(=8\) supergravity. Phys. Lett. B 732, 137 (2014). arXiv:1311.7459 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  70. H. Lü, Y. Pang, C.N. Pope, An \(\omega \) deformation of gauged STU supergravity. JHEP 1404, 175 (2014). arXiv:1402.1994 [hep-th]

    Article  ADS  MathSciNet  MATH  Google Scholar 

  71. S.Q. Wu, S. Li, Thermodynamics of static Dyonic AdS black holes in the \(\omega \)-Deformed Kaluza-Klein gauged supergravity theory. Phys. Lett. B 746, 276 (2015). arXiv:1505.00117 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  72. K. Lee, C. Strickland-Constable, D. Waldram, New Gaugings and Non-geometry. arXiv:1506.03457 [hep-th]

  73. A. Guarino, D. L. Jafferis, O. Varela, String theory origin of dyonic N=8 Supergravity and Its Chern-Simons duals. Phys. Rev. Lett. 115(9), 091601 (2015) arXiv:1504.08009 [hep-th]

  74. B. de Wit, H. Samtleben, M. Trigiante, The maximal D \(=\) 5 supergravities. Nucl. Phys. B 716, 215 (2005). arXiv:hep-th/0412173

    Article  ADS  MathSciNet  MATH  Google Scholar 

  75. H. Samtleben, M. Weidner, The maximal D \(=\) 7 supergravities. Nucl. Phys. B 725, 383 (2005). arXiv:hep-th/0506237

  76. B. de Wit, H. Nicolai, H. Samtleben, Gauged supergravities, tensor hierarchies, and M-theory. JHEP 0802, 044 (2008). arXiv:0801.1294 [hep-th]

    Article  MathSciNet  Google Scholar 

  77. P. K. Townsend, in Gauge Field Theories: Theoretical Studies and Computer Simulations ed. by W. Garazynski (Harwood Academic Chur, New York 1981)

    Google Scholar 

  78. S. Cecotti, S. Ferrara, L. Girardello, Massive vector multiplets from superstrings. Nucl. Phys. B 294, 537 (1987)

    Article  ADS  Google Scholar 

  79. G. Dall’Agata, R. D’Auria, L. Sommovigo, S. Vaula, D \(=\) 4, N \(=\) 2 gauged supergravity in the presence of tensor multiplets. Nucl. Phys. B 682, 243 (2004). arXiv:hep-th/0312210

    Article  ADS  MathSciNet  MATH  Google Scholar 

  80. R. D’Auria, L. Sommovigo, S. Vaula, N \(=\) 2 supergravity Lagrangian coupled to tensor multiplets with electric and magnetic fluxes. JHEP 0411, 028 (2004). arXiv:hep-th/0409097

    Article  MathSciNet  Google Scholar 

  81. J. Louis, A. Micu, Type 2 theories compactified on Calabi-Yau three folds in the presence of background fluxes. Nucl. Phys. B 635, 395 (2002). arXiv:hep-th/0202168

    Article  ADS  MathSciNet  MATH  Google Scholar 

  82. E. Cremmer, B. Julia, H. Lu, C.N. Pope, Dualization of dualities. 1. Nucl. Phys. B 523, 73 (1998). arXiv:hep-th/9710119

    Article  ADS  MathSciNet  MATH  Google Scholar 

  83. Y. Tanii, Introduction to Supergravities in Diverse Dimensions. arXiv:hep-th/9802138

  84. M. Gunaydin, L.J. Romans, N.P. Warner, Compact and noncompact gauged supergravity theories in five-dimensions. Nucl. Phys. B 272, 598 (1986)

    Article  ADS  MathSciNet  Google Scholar 

  85. L. Andrianopoli, F. Cordaro, P. Fre’, L. Gualtieri, Nonsemisimple gaugings of D \(=\) 5 N \(=\) 8 supergravity and FDA.s. Class. Quant. Grav. 18, 395 (2001). arXiv:hep-th/0009048

    Article  ADS  MathSciNet  MATH  Google Scholar 

  86. E. Bergshoeff, H. Samtleben, E. Sezgin, The gaugings of maximal D \(=\) 6 supergravity. JHEP 0803, 068 (2008). arXiv:0712.4277 [hep-th]

    Article  ADS  MathSciNet  Google Scholar 

  87. M. Pernici, K. Pilch, P. van Nieuwenhuizen, Gauged maximally extended supergravity in seven-dimensions. Phys. Lett. B 143, 103 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  88. E. Bergshoeff, U. Gran, R. Linares, M. Nielsen, T. Ortin, D. Roest, The Bianchi classification of maximal D \(=\) 8 gauged supergravities. Class. Quant. Grav. 20, 3997 (2003). arXiv:hep-th/0306179

    Article  ADS  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department DISAT, Politecnico di Torino, Corso Duca Degli Abruzzi 24, 10129, Torino, Italy

    Antonio Gallerati & Mario Trigiante

Authors
  1. Antonio Gallerati
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mario Trigiante
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mario Trigiante .

Editor information

Editors and Affiliations

  1. Varian Physics Bldg., Stanford University, Stanford, California, USA

    Renata Kallosh

  2. Escola de Ciências & Tecnologia, Universidade Federal Rio Grande do Norte, Natal-RN, Brazil

    Emanuele Orazi

Rights and permissions

Reprints and permissions

Copyright information

© 2016 Springer International Publishing Switzerland

About this paper

Cite this paper

Gallerati, A., Trigiante, M. (2016). Introductory Lectures on Extended Supergravities and Gaugings. In: Kallosh, R., Orazi, E. (eds) Theoretical Frontiers in Black Holes and Cosmology. Springer Proceedings in Physics, vol 176. Springer, Cham. https://doi.org/10.1007/978-3-319-31352-8_2

Download citation

Publish with us

Policies and ethics

Search

Navigation