Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The spatial spread of infectious diseases has been observed many times in history. Most recent examples include the 2002–2003 SARS epidemic in Asia and the global spread of the 2009 pandemic influenza A(H1N1). The Middle East Respiratory Syndrome coronavirus (MERS-CoV) outbreak emerged in 2012, and West Africa is currently witnessing the extensive Ebola virus (EBOV) outbreak, that pose a global threat. There is an increasing interest in the mathematical modelling literature for the spread of epidemics between discrete geographical locations (patches, or cities). Such metapopulation models incorporate single or multiple species occupying multiple spatial patches that are connected by movement dependent or independent of disease status. Such models have been discussed for an array of infectious diseases including measles and influenza, by Arino and coauthors [2–5], Sattenspiel and coauthors [14, 15], Wang and coauthors [9, 13, 19, 20]. The work of Arino [1], and Arino and van den Driessche [6] provide a thorough review of the literature.

When considering intervention strategies for epidemic models , our attention is focused on the basic reproduction number \(\,\mathcal{R}_{0}\), which is the expected number of secondary cases generated by a typical infected host introduced into a susceptible population. This quantity serves as a threshold parameter for disease elimination ; if \(\,\mathcal{R}_{0} <1\) then the disease dies out when a small number of infected individuals is introduced whereas if \(\,\mathcal{R}_{0}> 1\) then the disease can persist in the population. The above mentioned works illustrate that in metapopulation models \(\,\mathcal{R}_{0}\) often arises as a complicated formula of the model parameters. Such models include multiple infected classes, and individuals’ movement makes it challenging to compute the number of new infections generated by an infected case, and to understand the dependence of \(\,\mathcal{R}_{0}\) on the movement rates. To calculate \(\,\mathcal{R}_{0}\) in metapopulation models, the next-generation method is used (see Diekmann et al. [7]).

The models in [4, 5, 14, 15] include residency patch, that is, these models keep track of the patch of origin of an individual as well as where an individual is at a given time (either as resident, or as visitor). There are many reasons why individuals should be distinguished in an epidemic model by their residential statuses; visitors and local residents may have very different contact rates and mixing patterns, but more significantly, these groups are different in their travel rates because in reality, a large part of outbound travels from a city are return trips. In the above works, the basic reproduction number was calculated and its dependence on the movement rates was studied numerically. Some complicated behavior of \(\,\mathcal{R}_{0}\) in these parameters was highlighted in [1, 2, 4]: numerical simulations suggest that when the infection is present in same patches but absent in others without movement, then travel with small rates can allow for disease persistence in the metapopulation although higher travel rates can drive the disease to extinction.

In this work we present a demographic SIRS epidemic metapopulation model in two cities, and analytically investigate the impact of individuals’ movement between the two cities on the disease dynamics. In each city we distinguish residents from visitors, and consider the general situation when individuals with different disease statuses and residential statuses have different movement rates. In our analysis we utilize the concept of the target reproduction number , developed by Shuai et al. in [16, 17]. This quantity measures the effort required to eliminate infectious diseases, when an intervention strategy is targeted at single entries or sets of such entries of a next-generation matrix . Focusing on the control of infected individuals’ movement between the two cities—an intervention strategy often applied in pandemic situations—we give conditions and describe how the travel rate of a specific group or some of these groups should be changed to prevent an outbreak.

2 Model Formulation

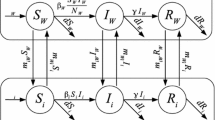
We formulate a dynamical model to describe the spread of an infectious disease among two cities. We divide the entire populations of the two cities into the disjoint classes S j m, I j m, R j m, j ∈ { 1, 2}, m ∈ { r, v}, where the letters S, I, and R represent the compartments of susceptible, infected, and recovered individuals, respectively. Lower index j ∈ { 1, 2} specifies the current city, upper index m ∈ { r, v} denotes the residential status of the individual in the current city (resident or visitor). An individual who is currently in city j and has residential status v, originally belongs to city k hence we say that this individual has origin in city k (k ∈ { 1, 2}, k ≠ j). Let S j m(t), I j m(t), R j m(t), j ∈ { 1, 2}, m ∈ { r, v} be the number of individuals belonging to S j m, I j m, R j m respectively, at time t. The transmission rate between a susceptible individual with residential status m and an infected individual with residential status n in region j ( j ∈ { 1, 2}, m, n ∈ { r, v}) is denoted by β j mn, and disease transmission is modelled by standard incidence. Model parameter γ j is the recovery rate of infected individuals in city j, and d j is the natural mortality rate of all individuals with origin in city j. Recovered individuals with residential status m in city j lose disease-induced immunity by rate θ j m. For the total population of residents and visitors currently being in city j we use the notations N j r and N j v, and let N j o denote the total population with origin in j. It holds that

$$\displaystyle{ \begin{array}{ll} N_{j}^{r}& = S_{j}^{r} + I_{j}^{r} + R_{j}^{r},\qquad N_{j}^{v} = S_{j}^{v} + I_{j}^{v} + R_{j}^{v}, \\ N_{j}^{o}& = S_{j}^{r} + I_{j}^{r} + R_{j}^{r} + S_{k}^{v} + I_{k}^{v} + R_{k}^{v},\quad k\neq j. \end{array} }$$

For the recruitment term Λ j into the susceptible resident population we assume that Λ j is a function of the populations N j r and N k v (k ≠ j), that is, the populations with origin in city j. We denote by m kj Sm, m kj Im, and m kj Rm the travel rate of susceptible, infected, and recovered individuals, respectively, with residential status m in city j travelling to city k. Based on the assumptions formulated above, we obtain the following system of differential equations for the disease transmission in city j:

$$\displaystyle{ \begin{array}{ll} \frac{\mathrm{d}S_{j}^{r}} {\mathrm{d}t} & =\varLambda _{j}(N_{j}^{r},N_{ k}^{v}) -\beta _{ j}^{rr} \frac{S_{j}^{r}I_{ j}^{r}} {N_{j}^{r}+N_{j}^{v}} -\beta _{j}^{rv} \frac{S_{j}^{r}I_{ j}^{v}} {N_{j}^{r}+N_{j}^{v}} - d_{j}S_{j}^{r} +\theta _{ j}^{r}R_{j}^{r} - m_{kj}^{Sr}S_{j}^{r} + m_{jk}^{Sv}S_{k}^{v}, \\ \frac{\mathrm{d}I_{j}^{r}} {\mathrm{d}t} & =\beta _{ j}^{rr} \frac{S_{j}^{r}I_{ j}^{r}} {N_{j}^{r}+N_{j}^{v}} +\beta _{ j}^{rv} \frac{S_{j}^{r}I_{ j}^{v}} {N_{j}^{r}+N_{j}^{v}} - (\gamma _{j} + d_{j})I_{j}^{r} - m_{ kj}^{Ir}I_{ j}^{r} + m_{ jk}^{Iv}I_{ k}^{v}, \\ \frac{\mathrm{d}R_{j}^{r}} {\mathrm{d}t} & =\gamma _{j}I_{j}^{r} - (\theta _{ j}^{r} + d_{ j})R_{j}^{r} - m_{ kj}^{Rr}R_{ j}^{r} + m_{ jk}^{Rv}R_{ k}^{v}, \\ \frac{\mathrm{d}S_{j}^{v}} {\mathrm{d}t} & = -\beta _{j}^{vr} \frac{S_{j}^{v}I_{ j}^{r}} {N_{j}^{r}+N_{j}^{v}} -\beta _{j}^{vv} \frac{S_{j}^{v}I_{ j}^{v}} {N_{j}^{r}+N_{j}^{v}} - d_{k}S_{j}^{v} +\theta _{ j}^{v}R_{ j}^{v} - m_{ kj}^{Sv}S_{ j}^{v} + m_{ jk}^{Sr}S_{ k}^{r}, \\ \frac{\mathrm{d}I_{j}^{v}} {\mathrm{d}t} & =\beta _{ j}^{vr} \frac{S_{j}^{v}I_{ j}^{r}} {N_{j}^{r}+N_{j}^{v}} +\beta _{ j}^{vv} \frac{S_{j}^{v}I_{ j}^{v}} {N_{j}^{r}+N_{j}^{v}} - (\gamma _{j} + d_{k})I_{j}^{v} - m_{ kj}^{Iv}I_{ j}^{v} + m_{ jk}^{Ir}I_{ k}^{r}, \\ \frac{\mathrm{d}R_{j}^{v}} {\mathrm{d}t} & =\gamma _{j}I_{j}^{v} - (\theta _{ j}^{v} + d_{ k})R_{j}^{r} - m_{ kj}^{Rv}R_{ j}^{v} + m_{ jk}^{Rr}R_{ k}^{r}.\end{array} }$$
(1)

Standard arguments from the theory of differential equations guarantee that the system (1) is well posed. The function forming the right hand side of the system is Lipschitz continuous, which implies the existence of a unique solution. The derivative of each system variable is nonnegative when the variable is zero, hence solutions remain nonnegative for nonnegative initial data. For the dynamics of the total population with origin in city j, we obtain the equation

$$\displaystyle{ \frac{\mathrm{d}N_{j}^{o}} {\mathrm{d}t} =\varLambda _{j}(N_{j}^{r},N_{ k}^{v}) - d_{ j}(N_{j}^{r} + N_{ k}^{v}),\quad k\neq j. }$$

If \(\varLambda _{j}(N_{j}^{r},N_{k}^{v}) = d_{j}(N_{j}^{r} + N_{k}^{v})\) then the population with origin in j is constant. For constant recruitment term Λ j it is easy to derive that \(\hat{N } _{j}^{o} =\varLambda _{j}/d_{j}\) gives the unique equilibrium of N j o. With fixed N 1 o and N 2 o it is obvious from nonnegativity that the solutions of the system (1) are bounded. The model is at an equilibrium if the time derivatives in the system (1) are zero. At a disease-free equilibrium it holds that \(I_{1}^{r} = I_{1}^{v} = I_{2}^{r} = I_{2}^{v} = 0\) that implies \(R_{1}^{r} = R_{1}^{v} = R_{2}^{r} = R_{2}^{v} = 0\). Thus at a DFE S 1 r, S 1 v, S 2 r, S 2 v satisfy

$$\displaystyle{ \begin{array}{rl} \varLambda _{1}(N_{1}^{r},N_{2}^{v}) - d_{1}S_{1}^{r} - m_{21}^{Sr}S_{1}^{r} + m_{12}^{Sv}S_{2}^{v}& = 0, \\ - d_{2}S_{1}^{v} - m_{21}^{Sv}S_{1}^{v} + m_{12}^{Sr}S_{2}^{r}& = 0, \\ \varLambda _{2}(N_{2}^{r},N_{1}^{v}) - d_{2}S_{2}^{r} - m_{12}^{Sr}S_{2}^{r} + m_{21}^{Sv}S_{1}^{v}& = 0, \\ - d_{1}S_{2}^{v} - m_{12}^{Sv}S_{2}^{v} + m_{21}^{Sr}S_{1}^{r}& = 0.\end{array} }$$

Hence if N 1 o and N 2 o are fixed then using that Λ 1 = d 1 N 1 o and Λ 2 = d 2 N 2 o, it follows that

$$\displaystyle{ \begin{array}{ll} \left [\begin{array}{*{10}c} S_{1}^{r} \\ S_{2}^{v} \end{array} \right ]& = \left [\begin{array}{*{10}c} d_{1} + m_{21}^{Sr}& -m_{12}^{Sv} \\ -m_{21}^{Sr} &d_{1} + m_{12}^{Sv} \end{array} \right ]^{-1}\left [\begin{array}{*{10}c} d_{1}N_{1}^{o} \\ 0 \end{array} \right ], \\ \left [\begin{array}{*{10}c} S_{2}^{r} \\ S_{1}^{v} \end{array} \right ]& = \left [\begin{array}{*{10}c} d_{2} + m_{12}^{Sr}& -m_{21}^{Sv} \\ -m_{12}^{Sr} &d_{2} + m_{21}^{Sv} \end{array} \right ]^{-1}\left [\begin{array}{*{10}c} d_{2}N_{2}^{o} \\ 0 \end{array} \right ]. \end{array} }$$

The following result is proved.

Proposition 1

Assume that the total populations with origin in city 1 and with origin in city 2 are constant. Then there is a unique DFE in the model (1) where

$$\displaystyle{ \begin{array}{ll} S_{j}^{r} & = \frac{(d_{j}+m_{jk}^{Sv})d_{ j}N_{j}^{o}} {(d_{j}+m_{kj}^{Sr})(d_{j}+m_{jk}^{Sv})-m_{jk}^{Sv}m_{kj}^{Sr}}, \\ S_{j}^{v}& = \frac{m_{jk}^{Sr}d_{ k}N_{k}^{o}} {(d_{k}+m_{jk}^{Sr})(d_{k}+m_{kj}^{Sv})-m_{kj}^{Sv}m_{jk}^{Sr}},\qquad j,k \in \{ 1,2\},k\neq j, \\ I_{j}^{r} & = I_{j}^{v} = 0,\;R_{j}^{r} = R_{j}^{v} = 0,\text{ and }N_{j}^{r} = S_{j}^{r},\;N_{j}^{v} = S_{j}^{v}.\end{array} }$$

For the stability of the DFE in the full model (1) we linearize the subsystem of (1) that consists of the equations for I 1 r, I 1 v, I 2 r, and I 2 v—the infected subsystem—about the DFE, and give the Jacobian J, as

$$\displaystyle\begin{array}{rcl} & J = B - G - M. & {}\\ & B = \left [\begin{array}{*{10}c} \frac{\beta _{1}^{rr}N_{ 1}^{r}} {N_{1}^{r}+N_{1}^{v}} & \frac{\beta _{1}^{rv}N_{ 1}^{r}} {N_{1}^{r}+N_{1}^{v}} & 0 & 0 \\ \frac{\beta _{1}^{vr}N_{ 1}^{v}} {N_{1}^{r}+N_{1}^{v}} & \frac{\beta _{1}^{vv}N_{ 1}^{v}} {N_{1}^{r}+N_{1}^{v}} & 0 & 0 \\ 0 & 0 & \frac{\beta _{2}^{rr}N_{ 2}^{r}} {N_{2}^{r}+N_{2}^{v}} & \frac{\beta _{2}^{rv}N_{ 2}^{r}} {N_{2}^{r}+N_{2}^{v}} \\ 0 & 0 & \frac{\beta _{2}^{vr}N_{ 2}^{v}} {N_{2}^{r}+N_{2}^{v}} & \frac{\beta _{2}^{vv}N_{ 2}^{v}} {N_{2}^{r}+N_{2}^{v}} \end{array} \right ],\;M = \left [\begin{array}{*{10}c} m_{21}^{Ir} & 0 & 0 &-m_{12}^{Iv} \\ 0 & m_{21}^{Iv} &-m_{12}^{Ir}& 0 \\ 0 &-m_{21}^{Iv}& m_{12}^{Ir} & 0 \\ -m_{21}^{Ir}& 0 & 0 & m_{12}^{Iv} \end{array} \right ],& {}\\ \end{array}$$

and \(G =\,\mathrm{ diag}(\gamma _{1} + d_{1},\gamma _{1} + d_{2},\gamma _{2} + d_{2},\gamma _{2} + d_{1}) =:\,\mathrm{ diag}(g_{1}^{r},g_{1}^{v},g_{2}^{r},g_{2}^{v})\). Let s(A) denote the maximum real part of all eigenvalues of any square matrix A, and ρ(A) denote the dominant eigenvalue of any square matrix A. We say that a square matrix A has the Z-sign pattern if all entries of A are nonpositive except possibly those in the diagonal. If A −1 ≥ 0 holds then A is a non-singular M-matrix (several definitions exist for M-matrices, see [8, Theorem 5.1]). By [18, Lemma 1] the stability of the DFE is determined by the eigenvalues of J; more precisely, the DFE is locally asymptotically stable if s(J) < 0, meaning that all eigenvalues have negative real part, and the DFE is unstable if s(J) > 0, when there is an eigenvalue with positive real part. The proof of the next proposition follows by similar arguments as those in the proof of [18, Theorem 2].

Proposition 2

Consider a splitting F − V of the Jacobian of the infected subsystem about the DFE, where F is a nonnegative matrix and V is a non-singular M-matrix. Then, it holds that s(J) < 0 if and only if ρ(FV −1 ) < 1, s(J) = 0 if and only if \(\rho (FV ^{-1}) = 1\) , and s(J) > 0 if and only if ρ(FV −1 ) > 1.

The stability of the DFE is often characterized through the basic reproduction number \(\,\mathcal{R}_{0}\), that is defined as the dominant eigenvalue of the next-generation matrix (NGM). The concept of the NGM was initially introduced by Diekmann et al. [7]. This matrix is computed as \(K_{0}:= F_{0}V _{0}^{-1}\), where F 0 equals B, the transmission matrix describing new infections, and V 0 is defined as G + M, the transition matrix for the transitions between and out of infected classes. F 0 and V 0 satisfy the conditions of Proposition 2, hence \(\,\mathcal{R}_{0} =\rho (K_{0}) =\rho (F_{0}V _{0}^{-1})\) is a threshold quantity for the stability of the DFE. We obtain the following corollary from Proposition 2.

Corollary 1

Consider a splitting F − V of the Jacobian of the infected subsystem about the DFE, where F is a nonnegative matrix and V is a non-singular M-matrix. Then, it holds that ρ(FV −1 ) < 1 if and only if \(\,\mathcal{R}_{0} <1\) , \(\rho (FV ^{-1}) = 1\) if and only if \(\,\mathcal{R}_{0} = 1\) , and ρ(FV −1 ) > 1 if and only if \(\,\mathcal{R}_{0}> 1\) .

With other words, for any splitting F − V of the Jacobian where F is nonnegative and V is a non-singular M-matrix, there arises an alternative NGM by FV −1; moreover, ρ(FV −1) and \(\,\mathcal{R}_{0}\) agree at the threshold value for the stability of the DFE. In the next section we will investigate the impact of movement on the disease dynamics by constructing some alternative next-generation matrices and utilizing the method of Shuai et al. [16] to measure the effort required to control the disease.

3 Main Results

Using the definition of G and the transmission matrix F 0, we introduce the quantities

$$\displaystyle{ \begin{array}{lcrlcr} \,\mathcal{R}_{1}^{r}& =&\frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}} {g_{1}^{r}(N_{1}^{r}+N_{1}^{v})},\quad &\,\mathcal{R}_{1}^{v}& =&\frac{\beta _{1}^{rv}N_{ 1}^{r}+\beta _{ 1}^{vv}N_{ 1}^{v}} {g_{1}^{v}(N_{1}^{r}+N_{1}^{v})}, \\ \,\mathcal{R}_{2}^{r}& =&\frac{\beta _{2}^{rr}N_{ 2}^{r}+\beta _{ 2}^{vr}N_{ 2}^{v}} {g_{2}^{r}(N_{2}^{r}+N_{2}^{v})},\quad &\,\mathcal{R}_{2}^{v}& =&\frac{\beta _{2}^{rv}N_{ 2}^{r}+\beta _{ 2}^{vv}N_{ 2}^{v}} {g_{2}^{v}(N_{2}^{r}+N_{2}^{v})}, \end{array} }$$

where \(\,\mathcal{R}_{j}^{m}\) denotes the expected number of new cases in city j when a single infected individual with residential status m who doesn’t travel is introduced into city j.

Consider the matrices \(F_{1} = B - M +\,\mathrm{ diag}(m_{21}^{Ir},m_{21}^{Iv},m_{12}^{Ir},m_{12}^{Iv})\) and \(V _{1} = G +\,\mathrm{ diag}(m_{21}^{Ir},m_{21}^{Iv},m_{12}^{Ir},m_{12}^{Iv})\). Then \(J = F_{1} - V _{1}\) gives another splitting of the Jacobian, moreover F 1 ≥ 0 and V 1 is a non-singular M-matrix. We obtain the following theorem.

Theorem 1

If \(\,\mathcal{R}_{1}^{r}> 1\) , \(\,\mathcal{R}_{1}^{v}> 1\) , \(\,\mathcal{R}_{2}^{r}> 1\) , and \(\,\mathcal{R}_{2}^{v}> 1\) then the DFE is unstable when the cities are isolated, and movement cannot stabilize the DFE. If the inequalities are reversed then the DFE is stable when the cities are isolated, and movement cannot destabilize the DFE.

Proof

Consider the splitting \(J = F_{1} - V _{1}\). As V 1 is a diagonal matrix, one easily computes the alternative NGM

$$\displaystyle{ K_{1} = F_{1}V _{1}^{-1} = \left [\begin{array}{*{10}c} \frac{\beta _{1}^{rr}N_{ 1}^{r}} {(m_{21}^{Ir}+g_{1}^{r})(N_{1}^{r}+N_{1}^{v})} & \frac{\beta _{1}^{rv}N_{ 1}^{r}} {(m_{21}^{Iv}+g_{1}^{v})(N_{1}^{r}+N_{1}^{v})} & 0 & \frac{m_{12}^{Iv}} {(m_{12}^{Iv}+g_{2}^{v})} \\ \frac{\beta _{1}^{vr}N_{ 1}^{v}} {(m_{21}^{Ir}+g_{1}^{r})(N_{1}^{r}+N_{1}^{v})} & \frac{\beta _{1}^{vv}N_{ 1}^{v}} {(m_{21}^{Iv}+g_{1}^{v})(N_{1}^{r}+N_{1}^{v})} & \frac{m_{12}^{Ir}} {(m_{12}^{Ir}+g_{2}^{r})} & 0 \\ 0 & \frac{m_{21}^{Iv}} {(m_{21}^{Iv}+g_{1}^{v})} & \frac{\beta _{2}^{rr}N_{ 2}^{r}} {(m_{12}^{Ir}+g_{2}^{r})(N_{2}^{r}+N_{2}^{v})} & \frac{\beta _{2}^{rv}N_{ 2}^{r}} {(m_{12}^{Iv}+g_{2}^{v})(N_{2}^{r}+N_{2}^{v})} \\ \frac{m_{21}^{Ir}} {(m_{21}^{Ir}+g_{1}^{r})} & 0 & \frac{\beta _{2}^{vr}N_{ 2}^{v}} {(m_{12}^{Ir}+g_{2}^{r})(N_{2}^{r}+N_{2}^{v})} & \frac{\beta _{2}^{vv}N_{ 2}^{v}} {(m_{12}^{Iv}+g_{2}^{v})(N_{2}^{r}+N_{2}^{v})} \end{array}\right ]. }$$

A standard result for nonnegative matrices (see, e.g., [12, Theorem 1.1]) says that the dominant eigenvalue of a nonnegative matrix is bounded below and above by the minimum and maximum of its column sums. We look at the column sums of K 1 to give upper and lower bounds on the dominant eigenvalue. The column sum in the first column is \(\frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}+m_{ 21}^{Ir}} {(m_{21}^{Ir}+g_{1}^{r})(N_{1}^{r}+N_{1}^{v})}\), and using basic calculus we derive that

$$\displaystyle{ \begin{array}{rlcr} 1 <\frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}+m_{ 21}^{Ir}} {(m_{21}^{Ir}+g_{1}^{r})(N_{1}^{r}+N_{1}^{v})} \leq \frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}} {g_{1}^{r}(N_{1}^{r}+N_{1}^{v})} & \qquad \text{ if }\;\frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}} {(N_{1}^{r}+N_{1}^{v})} - g_{1}^{r}> 0& \Leftrightarrow &\,\mathcal{R}_{ 1}^{r}> 1, \\ \\ \frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}} {g_{1}^{r}(N_{1}^{r}+N_{1}^{v})} \leq \frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}+m_{ 21}^{Ir}} {(m_{21}^{Ir}+g_{1}^{r})(N_{1}^{r}+N_{1}^{v})} <1&\qquad \text{ if }\;\frac{\beta _{1}^{rr}N_{ 1}^{r}+\beta _{ 1}^{vr}N_{ 1}^{v}} {(N_{1}^{r}+N_{1}^{v})} - g_{1}^{r} <0& \Leftrightarrow &\,\mathcal{R}_{ 1}^{r} <1. \end{array} }$$

Similar results follow for the second, third, and fourth columns. Thus if \(\,\mathcal{R}_{1}^{r}> 1\), \(\,\mathcal{R}_{1}^{v}> 1\), \(\,\mathcal{R}_{2}^{r}> 1\), and \(\,\mathcal{R}_{2}^{v}> 1\) hold then all column sums are greater than 1 for any m 21 Ir, m 21 Iv, m 12 Ir, and m 12 Iv, that implies by Proposition 2 that the dominant eigenvalue of K 1 is greater than 1 and the DFE is unstable. On the other hand, if the above inequalities are reversed then the column sums are less than 1 for any movement rates and the DFE is stable by ρ(K 1) < 1. □ 

Next, we investigate some cases when changing the movement rates of some groups can stabilize the DFE. We construct the matrix \(K_{2}:= F_{2}V _{2}^{-1}\), where F 2 is formed as we let \([F_{2}]_{1,1} = [F_{1}]_{1,1} - g_{1}^{r}\) and [F 2] i, j  = [F 1] i, j if (i, j) ≠ (1, 1), and \(V _{2} =\,\mathrm{ diag}(m_{21}^{Ir},g_{1}^{v} + m_{21}^{Iv},g_{2}^{r} + m_{12}^{Ir},g_{2}^{v} + m_{12}^{Iv})\). V 2 is a non-singular M-matrix and F 2 is nonnegative if \(\frac{\beta _{1}^{rr}N_{ 1}^{r}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{r}\). This condition is equivalent to when the number of new infections amongst residents of city 1 is less than 1, when an infected resident who doesn’t travel is introduced into city 1. The alternative NGM is computed as

$$\displaystyle{ K_{2}\,=\,F_{2}V _{2}^{-1}\,=\,\left [\begin{array}{*{10}c} \frac{\beta _{1}^{rr}N_{ 1}^{r}} {m_{21}^{Ir}(N_{1}^{r}+N_{1}^{v})} - \frac{g_{1}^{r}} {m_{21}^{Ir}} & \frac{\beta _{1}^{rv}N_{ 1}^{r}} {(m_{21}^{Iv}+g_{1}^{v})(N_{1}^{r}+N_{1}^{v})} & 0 & \frac{m_{12}^{Iv}} {(m_{12}^{Iv}+g_{2}^{v})} \\ \frac{\beta _{1}^{vr}N_{ 1}^{v}} {m_{21}^{Ir}(N_{1}^{r}+N_{1}^{v})} & \frac{\beta _{1}^{vv}N_{ 1}^{v}} {(m_{21}^{Iv}+g_{1}^{v})(N_{1}^{r}+N_{1}^{v})} & \frac{m_{12}^{Ir}} {(m_{12}^{Ir}+g_{2}^{r})} & 0 \\ 0 & \frac{m_{21}^{Iv}} {(m_{21}^{Iv}+g_{1}^{v})} & \frac{\beta _{2}^{rr}N_{ 2}^{r}} {(m_{12}^{Ir}+g_{2}^{r})(N_{2}^{r}+N_{2}^{v})} & \frac{\beta _{2}^{rv}N_{ 2}^{r}} {(m_{12}^{Iv}+g_{2}^{v})(N_{2}^{r}+N_{2}^{v})} \\ 1 & 0 & \frac{\beta _{2}^{vr}N_{ 2}^{v}} {(m_{12}^{Ir}+g_{2}^{r})(N_{2}^{r}+N_{2}^{v})} & \frac{\beta _{2}^{vv}N_{ 2}^{v}} {(m_{12}^{Iv}+g_{2}^{v})(N_{2}^{r}+N_{2}^{v})} \end{array}\right ], }$$

which is irreducible. Denote by L 2 the matrix that is formed by replacing [K 2]1, 1 and [K 2]2, 1 in K 2 by 0. Observe that K 2 converges to L 2 as m 21 Ir goes to infinity. We show that the disease can be eliminated by controlling only the travel rate of the residents of a single city.

Theorem 2

Assume that \(\,\mathcal{R}_{0}> 1\) , that is, the DFE is unstable. If \(\frac{\beta _{1}^{rr}N_{ 1}^{r}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{r}\) and ρ(L 2 ) < 1 then increasing m 21 Ir can stabilize the DFE. In particular, if \(\frac{\beta _{1}^{rr}N_{ 1}^{r}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{r}\) and \(\,\mathcal{R}_{1}^{v} <1\) , \(\,\mathcal{R}_{2}^{r} <1\) , and \(\,\mathcal{R}_{2}^{v} <1\) , then increasing m 21 Ir can stabilize the DFE.

Proof

We utilize some terminology and results from [16, 17]. Let S = { (1, 1), (2, 1)}, and define the 4 × 4 matrix K 2 S as [K 2 S] i, j  = [K 2] i, j if (i, j) ∈ S and 0 otherwise. Note that S identifies the set of elements in K 2 that depend on m 21 Ir, and K 2 S contains elements of K 2 that are subject to change when m 21 Ir is targeted. Following the terminology of [16] it is thus meaningful to refer to S as the target set and to K 2 S as the target matrix. Note that \(L_{2} = K_{2} - K_{2}^{S}\), hence the condition ρ(L 2) < 1 implies that ρ(K 2 − K 2 S) < 1, that is, the controllability condition holds and it is possible to stabilize the DFE by controlling only the elements in S [16].

We compute \(\mathcal{T}_{S} =\rho (K_{2}^{S}(I - K_{2} + K_{2}^{S})^{-1})\), the number referred to as the target reproduction number in [16]. Here I denotes the 4 × 4 identity matrix. Let \((m_{21}^{Ir})^{c} = m_{21}^{Ir}\mathcal{T}_{S}\), where we denote by (m 21 Ir)c the controlled travel rate of infected residents of city 1 travelling to city 2. It follows from Corollary 1 and [16, Theorem 2.1] by \(\,\mathcal{R}_{0}> 1\) that (m 21 Ir)c > m 21 Ir. The matrix K 2 c, constructed as we replace m 21 Ir in K 2 by (m 21 Ir)c, satisfies ρ(K 2 c) = 1 by [16, Theorem 2.2], which means that the disease can be eradicated by increasing m 21 Ir.

Note that the conditions \(\,\mathcal{R}_{1}^{v} <1\), \(\,\mathcal{R}_{2}^{r} <1\), and \(\,\mathcal{R}_{2}^{v} <1\) ensure that ρ(L 2) < 1. Indeed, it is easy to see that the column sums of the second, third, and fourth columns in L 2 are less than 1 for any travel rates, and the column sum in the first column is 1. We now show that 1 is not an eigenvalue of L 2, which together with [12, Theorem 1.1] implies that the dominant eigenvalue of L 2 is less than 1. Assume that 1 is an eigenvalue of L 2, and consider a left eigenvector v = [v 1, v 2, v 3, v 4] corresponding to 1. It holds that

$$\displaystyle{ \mathbf{v} \times L_{2} = 1 \times \mathbf{v}, }$$

and we deduce that

$$\displaystyle{ v_{4} = v_{1},\quad \max (v_{1},v_{2},v_{3})> v_{2},\quad \max (v_{2},v_{3},v_{4})> v_{3},\quad \max (v_{1},v_{3},v_{4})> v_{4}. }$$

From the fourth inequality and v 4 = v 1 it follows that v 3 > v 4, which together with the third inequality implies v 2 > v 3 > v 4, but v 1 > v 2 by the second inequality, a contradiction to v 1 = v 4. The proof is complete. □ 

To reveal the impact of visitors’ travel, a result analogous to Theorem 2 can be formulated. The proof of the following theorem follows by similar arguments to those in Theorem 2.

Theorem 3

Assume that \(\,\mathcal{R}_{0}> 1\) , that is, the DFE is unstable. If \(\frac{\beta _{1}^{vv}N_{ 1}^{v}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{v}\) , and \(\,\mathcal{R}_{1}^{r} <1\) , \(\,\mathcal{R}_{2}^{r} <1\) , and \(\,\mathcal{R}_{2}^{v} <1\) , then increasing m 21 Iv can stabilize the DFE.

Lastly, we give conditions under which controlling outbound travel from one city is sufficient for disease elimination. Consider two matrices F 3 and V 3, defined as \([F_{3}]_{1,1} = [F_{1}]_{1,1} - g_{1}^{r}\), \([F_{3}]_{2,2} = [F_{1}]_{2,2} - g_{1}^{v}\), and [F 3] i, j  = [F 1] i, j otherwise, and \(V _{3} =\,\mathrm{ diag}(m_{21}^{Ir},m_{21}^{Iv},g_{2}^{r} + m_{12}^{Ir},g_{2}^{v} + m_{12}^{Iv})\). V 3 is a non-singular M-matrix and F 3 is nonnegative if \(\frac{\beta _{1}^{vv}N_{ 1}^{v}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{v}\) and \(\frac{\beta _{1}^{rr}N_{ 1}^{r}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{r}\). The following theorem concerns about whether changing the movement rates of the current population of one city can lead to disease eradication.

Theorem 4

Assume that \(\,\mathcal{R}_{0}> 1\) , that is, the DFE is unstable. If \(\frac{\beta _{1}^{rr}N_{ 1}^{r}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{r}\) and \(\frac{\beta _{1}^{vv}N_{ 1}^{v}} {N_{1}^{r}+N_{1}^{v}}> g_{1}^{v}\) but \(\,\mathcal{R}_{2}^{r} <1\) and \(\,\mathcal{R}_{2}^{v} <1\) , then increasing m 21 Ir and m 21 Iv can stabilize the DFE.

Proof

The proof is similar to the proof of Theorem 2. We compute the alternative NGM

$$\displaystyle{ K_{3}\,=\,F_{3}V _{3}^{-1}\,=\,\left [\begin{array}{*{10}c} \frac{\beta _{1}^{rr}N_{ 1}^{r}} {m_{21}^{Ir}(N_{1}^{r}+N_{1}^{v})} - \frac{g_{1}^{r}} {m_{21}^{Ir}} & \frac{\beta _{1}^{rv}N_{ 1}^{r}} {m_{21}^{Iv}(N_{1}^{r}+N_{1}^{v})} & 0 & \frac{m_{12}^{Iv}} {(m_{12}^{Iv}+g_{2}^{v})} \\ \frac{\beta _{1}^{vr}N_{ 1}^{v}} {m_{21}^{Ir}(N_{1}^{r}+N_{1}^{v})} & \frac{\beta _{1}^{vv}N_{ 1}^{v}} {m_{21}^{Iv}(N_{1}^{r}+N_{1}^{v})} - \frac{g_{1}^{v}} {m_{21}^{Iv}} & \frac{m_{12}^{Ir}} {(m_{12}^{Ir}+g_{2}^{r})} & 0 \\ 0 & 1 & \frac{\beta _{2}^{rr}N_{ 2}^{r}} {(m_{12}^{Ir}+g_{2}^{r})(N_{2}^{r}+N_{2}^{v})} & \frac{\beta _{2}^{rv}N_{ 2}^{r}} {(m_{12}^{Iv}+g_{2}^{v})(N_{2}^{r}+N_{2}^{v})} \\ 1 & 0 & \frac{\beta _{2}^{vr}N_{ 2}^{v}} {(m_{12}^{Ir}+g_{2}^{r})(N_{2}^{r}+N_{2}^{v})} & \frac{\beta _{2}^{vv}N_{ 2}^{v}} {(m_{12}^{Iv}+g_{2}^{v})(N_{2}^{r}+N_{2}^{v})} \end{array}\right ], }$$

which is irreducible, and define the target set U by identifying the entries of K 3 that depend on m 21 Ir and/or m 21 Iv. We let U = { (1, 1), (1, 2), (2, 1), (2, 2)}, and define the 4 × 4 target matrix K 3 U as [K 3 U] i, j  = [K 3] i, j if (i, j) ∈ U and 0 otherwise. Note that ρ(K 3) > 1 holds by \(\,\mathcal{R}_{0}> 1\). However, the result in [12, Theorem 1.1] on the upper bound of the dominant eigenvalue implies that ρ(K 3 − K 3 U) ≤ 1.

Assume that \(\rho (K_{3} - K_{3}^{U}) = 1\), that is, 1 is an eigenvalue of K 3 − K 3 U. Then there is a left eigenvector v = [v 1, v 2, v 3, v 4] such that

$$\displaystyle{ \mathbf{v} \times (K_{3} - K_{3}^{U}) = 1 \times \mathbf{v} }$$

holds. We derive that

$$\displaystyle{ v_{4} = v_{1},\quad v_{3} = v_{2},\quad \max (v_{2},v_{3},v_{4})> v_{3},\quad \max (v_{1},v_{3},v_{4})> v_{4}, }$$

so v 4 > v 3 and v 3 > v 4 hold by the third and fourth inequalities, a contradiction. We showed that ρ(K 3 − K 3 U) < 1, which means that there is a potential to control m 21 Ir and m 21 Iv in a way such that the dominant eigenvalue of the controlled matrix drops below 1 (by decreasing targeted entries of K 3 to values close to 0). This condition also allows us to compute the target reproduction number \(\mathcal{T}_{U} =\rho (K_{3}^{U}(I - K_{3} + K_{3}^{U})^{-1})\).

By [16, Theorem 2.2], the controlled matrix K 3 c satisfies ρ(K 3 c) = 1 where K 3 c is formed by replacing [K 3] i, j by \([K_{3}]_{i,j}/\mathcal{T}_{U}\) if (i, j) ∈ U, that is achieved by replacing m 21 Ir by \((m_{21}^{Ir})^{c} = m_{21}^{Ir}\mathcal{T}_{U}\), and m 21 Iv by \((m_{21}^{Iv})^{c} = m_{21}^{Ir}\mathcal{T}_{U}\). Note that \(\mathcal{T}_{U}> 1\) by [16, Theorem 2.2], which means that the disease can be eradicated by increasing m 21 Ir and m 21 Iv. □ 

In the case of transmission coefficients equal for all populations present in a city, recovery rates equal for all populations and death rates equal for all populations, \(\,\mathcal{R}_{1}^{r}\) and \(\,\mathcal{R}_{1}^{v}\) reduce to \(\beta _{1}/(\gamma +d)\), and \(\,\mathcal{R}_{2}^{r}\) and \(\,\mathcal{R}_{2}^{v}\) reduce to \(\beta _{2}/(\gamma +d)\). Note that these quantities give the expected number of secondary infections generated by a single infected case in city 1 and city 2, respectively, in the absence of movement between the cities. Hence the local reproduction numbers in city 1 and city 2 can be defined as we consider our model without dispersal:

$$\displaystyle{ \,\mathcal{R}_{1}^{loc} = \frac{\beta _{1}} {\gamma +d},\qquad \,\mathcal{R}_{2}^{loc} = \frac{\beta _{2}} {\gamma +d}. }$$

We derive the following results from Theorems 1 and 4.

Corollary 2

Suppose that β 1 mn = β 1 and β 2 mn = β 2 for all m,n ∈{ r,v}, γ j = γ and d j = d for all j ∈{ 1,2}. Then, the DFE is unstable when the cities are isolated and \(\,\mathcal{R}_{1}^{loc}> 1\) , \(\,\mathcal{R}_{2}^{loc}> 1\) , and movement cannot stabilize the DFE. In the case when \(\,\mathcal{R}_{1}^{loc} <1\) and \(\,\mathcal{R}_{2}^{loc} <1\) , the DFE is stable when the cities are isolated, and movement cannot destabilize the DFE. If the DFE is unstable and \(\frac{\beta _{1}N_{1}^{r}} {N_{1}^{r}+N_{1}^{v}}> (\gamma +d)\) , \(\frac{\beta _{1}N_{1}^{v}} {N_{1}^{r}+N_{1}^{v}}> (\gamma +d)\) but \(\,\mathcal{R}_{2}^{loc} <1\) , then increasing the movement rates of individuals in city 1 can stabilize the DFE.

4 Discussion

A two-city compartmental epidemic model was considered to reveal the impact of population dispersal on disease persistence. This general SIRS model is applicable for an array of infectious diseases, and it can also be reduced to simpler models (SIS, SIR models) by setting parameters (or their inverses) to zero. In the model setup we distinguish local residents from temporary visitors in each city, that results in four infected classes in the model. We demonstrated that controlling the movement of one or two infected groups can be sufficient for preventing a disease outbreak. It was discussed in [11] that the role of different inflow rates of residents and visitors into a city is not necessarily significant in regards of the total epidemic burden, but it is of particular importance for pandemic preparedness, when it comes to assessing the risk for each group to import the infection to a disease-free city.

Modelling the spatial spread of diseases in metapopulations remains a complex task. This paper does not concern with models that include multiple species, hence more analysis is needed to quantify the effect of movement between patches in such models, which are useful in investigating vector-borne diseases and their control strategies. Combining some intervention measures—like the mutual control of dispersal rates and transmission rates—requires less effort for disease elimination, hence there is a potential to incorporate the results of this work into systematic risk assessment analyses, as described in [10].