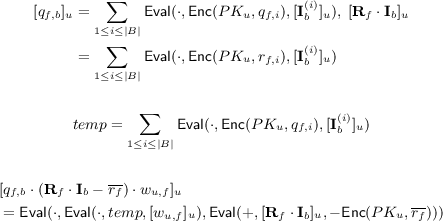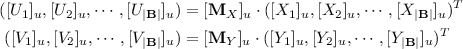Privacy-Preserving Context-Aware Recommender Systems: Analysis and New Solutions

Abstract

Nowadays, recommender systems have become an indispensable part of our daily life and provide personalized services for almost everything. However, nothing is for free – such systems have also upset the society with severe privacy concerns because they accumulate a lot of personal information in order to provide recommendations. In this work, we construct privacy-preserving recommendation protocols by incorporating cryptographic techniques and the inherent data characteristics in recommender systems. We first revisit the protocols by Jeckmans et al. and show a number of security issues. Then, we propose two privacy-preserving protocols, which compute predicted ratings for a user based on inputs from both the user’s friends and a set of randomly chosen strangers. A user has the flexibility to retrieve either a predicted rating for an unrated item or the Top-N unrated items. The proposed protocols prevent information leakage from both protocol executions and the protocol outputs. Finally, we use the well-known MovieLens 100k dataset to evaluate the performances for different parameter sizes.

This paper is an extended abstract of the IACR report [32].

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

As e-commerce websites began to develop, users were finding it very difficult to make the most appropriate choices from the immense variety of items (products and services) that these websites were offering. Take an online book store as an example, going through the lengthy book catalogue not only wastes a lot of time but also frequently overwhelms users and leads them to make poor decisions. As such, the availability of choices, instead of producing a benefit, started to decrease users’ well-being. Eventually, this need led to the development of recommender systems (or, recommendation systems). Informally, recommender systems are a subclass of information filtering systems that seek to predict the ‘rating’ or ‘preference’ that a user would give to an item (e.g. music, book, or movie) they had not yet considered, using a model built from the characteristics of items and/or users. Today, recommender systems play an important role in highly rated commercial websites such as Amazon, Facebook, Netflix, Yahoo, and YouTube. Netflix even awarded a million dollars prize to the team that first succeeded in improving substantially the performance of its recommender system. Besides these well-known examples, recommender systems can also be found in every corner of our daily life.

In order to compute recommendations, the service provider needs to collect a lot of personal data from its users, e.g. ratings, transaction history, and location. This makes recommender systems a double-edged sword. On one side users get better recommendations when they reveal more personal data, but on the flip side they sacrifice more privacy if they do so. Privacy issues in recommender systems have been surveyed in [3, 16, 28]. The most widely-recognized privacy concern is about the fact the service provider has full access to all users’ inputs (e.g. which items are rated and the corresponding ratings). Weinsberg et al. showed that what has been rated by a user can already breach his privacy [34]. The other less well-known yet equally serious privacy concern is that the outputs from a recommender system can also lead to privacy breaches against innocent users. Ten years ago, Kantarcioglu, Jin and Clifton expressed this concern for general data mining services [15]. Recently Calandrino et al. [6] showed inference attacks which allow an attacker with some auxiliary information to infer a user’s transactions from temporal changes in the public outputs of a recommender system. In practice, advanced recommender systems collect a lot of personal information other than ratings, and they cause more privacy concerns.

1.1 State-of-the-Art

Broadly speaking, existing privacy-protection solutions for recommender systems can be divided into two categories. One category is cryptographic solutions, which heavily rely on cryptographic primitives (e.g. homomorphic encryption, zero knowledge proof, threshold encryption, commitment, private information retrieval, and a variety of two-party or multi-party cryptographic protocols). For example, the solutions from [2, 7, 8, 11–14, 19, 23, 24, 27, 31, 36] fall into this category. More specifically, the solutions from [2, 7, 8, 11, 14, 19, 31] focus on distributed setting where every individual user is expected to participate in the recommendation computation, while those from [12, 13, 23, 24, 27, 36] focus on partitioned dataset, where several organizations wish to compute recommendations for their own users by joining their private dataset. These solutions typically assume semi-honest attackers and apply existing cryptographic primitives to secure the procedures in standard recommender protocols. This approach has two advantages: rigorous security guarantee in the sense of secure computation (namely, every user only learns the recommendation results and the server learns nothing) can be achieved, and there is no degradation in accuracy. The disadvantage lies in the fact that these solutions are all computation-intensive so that they become impractical when user/item populations get large.

The other category is data obfuscation based solutions, which mainly rely on adding noise to the original data or computation results to achieve privacy. The solutions from [4, 18, 20–22, 25, 26, 30, 35] fall into this category. These solutions usually do not incur complicated manipulations on the users’ inputs, so that they are much more efficient. The drawback is that they often lack rigorous privacy guarantees and downgrade the recommendation accuracy to some extent. With respect to privacy guarantees, an exception is the differential privacy based approach from [18] which does provide mathematically sound privacy notions. However, cryptographic primitives are required for all users to generate the accumulated data subjects (e.g. sums and covariance matrix).

1.2 Our Contribution

While most privacy-preserving solutions focus on recommender systems which only take into account users’ ratings as inputs, Jeckmans, Peter, and Hartel [13] moved a step further to propose privacy-preserving recommendation protocols for context-aware recommender systems, which include social relationships as part of the inputs to compute recommendations. Generally the protocols are referred to as the JPH protocols, and more specifically they are referred to as JPH online protocol and JPH offline protocol respectively. Interestingly, the JPH protocols make use of the recent advances in somewhat homomorphic encryption schemes [5]. In this paper, our contribution is three-fold.

Firstly, we analyze the JPH protocols and identify a number of security issues. Secondly, we revise the prediction computation formula from [13] by incorporating inputs from both friends and strangers. This change not only aligns the formula with standard recommender algorithms [17] but also enables us to avoid the cold start problem of the JPH protocols. Security wise, it helps us prevent potential information leakages through the outputs of friends. We then propose two privacy preserving protocols. One enables a user to check whether a specific unrated item might be of his interest, and the other returns the Top-N unrated items. Therefore, we provide more flexible choices for users to discover their interests in practice. Both protocols are secure against envisioned threats in our threat model. Thirdly, we analyze accuracy performances of the new protocols, and show that for some parameters the accuracy is even better than some other well-known recommendation protocols, e.g. those from [17].

1.3 Organization

The rest of this paper is organized as follows. In Sect. 2, we demonstrate the security issues with the JPH protocols. In Sect. 3, we propose our new formulation and trust assumptions for recommender systems. In Sect. 4, we present two protocols for single prediction and Top-N recommendations respectively. In Sect. 5, we present security and accuracy analysis for the proposed protocols. In Sect. 6, we conclude the paper.

2 Analysis of JPH Protocols

When X is a set, $x \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}X$ means that x is chosen from X uniformly at random, and |X| means the size of X. If $\chi$ is a distribution, then $s\leftarrow \chi$ means that s is sampled according to $\chi$. We use bold letter, such as $\mathbf {X}$, to denote a vector. Given two vector $\mathbf {X}$ and $\mathbf {Y}$, we use $\mathbf {X} \cdot \mathbf {Y}$ to denote their inner product. In a recommender system, the item set is denoted by $\mathbf {B} = (1, 2, \cdots , b, \cdots , |\mathbf {B}|)$, and a user x’s ratings are denoted by a vector $\mathbf {R}_x = (r_{x,1}, \cdots , r_{x,b}, \cdots , r_{x, |\mathbf {B}|})$. The rating value is often an integer from $\{0,1,2,3,4,5\}$. If item i has not been rated, then $r_{x,i}$ is set to be 0. With respect to $\mathbf {R}_x$, a binary vector $\mathbf {Q}_x =(q_{x,1}, \cdots , q_{x,b}, \cdots , q_{x, |\mathbf {B}|})$ is defined as follows: $q_{x,b} = 1$ iff $r_{x,b} \ne 0$ for every $1 \le b \le |\mathbf {B}|$. We use $\overline{r_x}$ to denote user x’s average rating, namely $\lceil \frac{\sum _{i \in \mathbf {B}}r_{x,i}}{\sum _{i \in \mathbf {B}}q_{x,i}}\rfloor$.

2.1 Preliminary of JPH Protocols

Let the active user, who wants to receive new recommendations, be denoted as user u. Let the friends of user u be denoted by $\mathbf {F}_u$. Every friend $f \in \mathbf {F}_u$ and user u assigns each other weights $w_{f, u}, w_{u,f}$ respectively, and these values can be regarded as the perceived importance to each other. Then, the predicted rating for an unrated item $b \in \mathbf {B}$ for user u is computed as follows.

$$\begin{aligned} p_{u,b}= & {} \frac{ \sum _{f \in \mathbf {F}_u}q_{f,b}\cdot r_{f,b}\cdot (\frac{w_{u,f}+w_{f,u}}{2})}{ \sum _{f \in \mathbf {F}_u}q_{f,b}\cdot (\frac{w_{u,f}+w_{f,u}}{2})}= \frac{ \sum _{f \in \mathbf {F}_u}r_{f,b}\cdot (w_{u,f}+w_{f,u})}{ \sum _{f \in \mathbf {F}_u}q_{f,b}\cdot (w_{u,f}+w_{f,u})} \end{aligned}$$

(1)

The JPH protocols [13] and the new protocols from this paper rely on the Brakerski-Vaikuntanathan SWHE Scheme [5], which is recapped in the Appendix. In [13], Jeckmans et al. did not explicitly explain their notation $[x]_u +y$ and $[x]_u \cdot y$. We assume these operations are as $[x]_u +y=\mathsf {Eval}^*(+,[x]_u, y)$ and $[x]_u \cdot y=\mathsf {Eval}^*(\cdot ,[x]_u, y)$. In any case, this assumption only affects the Insecurity against Semi-honest Server issue for the JPH online protocol. All other issues still exist even if this assumption is not true.

2.2 JPH Online Protocol

In the online scenario, the recommendation protocol is executed between the active user u, the server, and user u’s friends. In the initialization phase, user u generates a public/private key pair for the Brakerski-Vaikuntanathan SWHE scheme, and all his friends and the server obtain a valid copy of his public key. The protocol runs in two stages as described in Fig. 1.

Fig. 1.

JPH online protocol

It is worth noting that the friends only need to be involved in the first stage. We observe the following security issues.

• Hidden assumption. Jeckmans et al. [13] did not mention any assumption on the communication channel between users and the server. In fact, if the communication channel between any user f and the server does not provide confidentiality, then user u can obtain $[n_{f,b}]_u, \,\, [d_{f,b}]_u$ by passive eavesdropping. Then, user u can trivially recover $q_{f,b}$ and $r_{f,b}$.

• Insecurity against Semi-honest Server. With $[d_{f,b}]_u$, the server can trivially recover $q_{f,b}$, i.e. if $[d_{f,b}]_u=0$ then $q_{f,b}=0$; otherwise $q_{f,b}=1$. After recovering $q_{f,b}$, the server can trivially recover $r_{f,b}=\frac{[n_{f,b}]_u}{[d_{f,b}]_u}$. The root of the problem is the homomorphic operations have been done in the naive way, with $\mathsf {Eval}^*(\cdot ,,)$ and $\mathsf {Eval}^*(+,,)$.

• Encrypted Division Problems. The first concern is that it may not be able to determine the predicted rating $p_{u,b}$. As a toy example, let $t=7$. In this case, both $\lfloor \frac{2}{3}\rceil =1$ and $\lfloor \frac{3}{1}\rceil =3$ link to the index $2\cdot 3^{-1}=3 \cdot 1^{-1}=3 \mod 7$. If $p_{u,b}=3$, then user u will not be able to determine whether the predicted rating is $\lfloor \frac{2}{3}\rceil =1$ or $\lfloor \frac{3}{1}\rceil =3$. The second concern is that the representation of $p_{u,b}$ in the protocol may leak more information than the to-be predicted value $\lfloor \frac{n_b}{d_b}\rceil$. As an example, $\lfloor \frac{2}{3}\rceil =\lfloor \frac{3}{4}\rceil =1$. Clearly, giving $2\cdot 3^{-1}$ or $3\cdot 4^{-1}$ leaks more information than the to-be predicted value 1.

• Potential Information Leakage through Friends. For user u, his friends may not be friends with each other. For example, it may happen that some friend $f \in \mathbf {F}_u$ is not a friend of any other user from $\mathbf {F}_u$. Suppose that the users $\mathbf {F}_u\backslash f$ have learned the the value $p_{u,b}$ or some approximation of it (this is realistic as they are friends of user u). Then, they may be able to infer whether user f has rated the item b and the actual rating.

Besides the above security issues, there are some usability issues with the protocol as well. One issue is that, at the time of protocol execution, maybe only a few friends are online. In this case, the predicted rating may not be very accurate. It can also happen that $p_{u,b}$ cannot be computed, because none of user u’s friends has rated item b. This is the typical cold start problem in recommender systems [1]. The other issue is that the predicted rating needs to computed for every $b \in \mathbf {B}$ even if user u has already rated this item. Otherwise, user u may leak information to the server, e.g. which items have been rated. This not only leaks unnecessary information to user u, but also makes it very inefficient when user u only wants a prediction for a certain unrated item.

2.3 JPH Offline Protocol

In the offline scenario, the friends $\mathbf {F}_u$ need to delegate their data to the server to enable user u to run the recommendation protocol when they are offline. Inevitably, this leads to a more complex initialization phase. In this phase, both user u and the server generate their own public/private key pair for the Brakerski-Vaikuntanathan SWHE scheme and they hold a copy of the valid public key of each other. Moreover, every friend $f \in \mathbf {F}_u$ needs to pre-process $\mathbf {R}_f$, $\mathbf {Q}_f$, and $w_{f,u}$. The rating vector $\mathbf {R}_f$ is additively split into two sets $\mathbf {S}_f$ and $\mathbf {T}_f$. The splitting for every rating $r_{f,b}$ is straightforward, namely choose $r \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}\mathbb {Z}_t^*$ and set $s_{f,b}=r$ and $t_{f,b}=r_{f,b}-r \mod t$. Similarly, the weight $w_{f,u}$ is split into $x_{f,u}$ and $y_{f,u}$. It is assumed that $\mathbf {T}_f$ and $\mathbf {Q}_f$ will be delivered to user u through proxy re-encryption schemes. Running between user u and the server, the two-stage protocol is described in Fig. 2.

Fig. 2.

JPH offline protocol

This protocol has exactly the same encrypted division, potential information leakage through friends and usability issues, as stated in Sect. 2.2. In addition, we have the following new concerns.

• Explicit Information Disclosure. It is assumed that the $\mathbf {Q}_f$ values for all $f \in \mathbf {F}_u$ are obtained by user u in clear. This is a direct violation of these users’ privacy because it has shown that leaking what has been rated by a user can breach his privacy [34].

• Key Recovery Attacks against the Server. Chenal and Tang [9] have shown that given a certain number of decryption oracle queries an attacker can recover the private key of the Brakerski-Vaikuntanathan SWHE scheme. We show that user u can manipulate the protocol and recover the server’s private key $SK_u$. Before the attack, user u sets up a fake account $u'$ and a set of fake friends $\mathbf {F}_{u'}$ (e.g. through Sybil attacks [10]). The key recovery attack relies on multiple executions of the protocol, and it works as follows in each execution.

  • 1. User $u'$ chooses a carefully-chosen ciphertext c and replaces $[z_b+\xi _{1,b}]_s$ with c. He also sets $\xi _{1,b}=0$ for $[-\xi _{1,b}]_u$.

  • 2. When receiving $[p_{u',b}]_{u'}$, user $u'$ can recover the constant in $\mathsf {Dec}(SK_s, c)$ because he knows $a_b$ and $d_b^{-1}$ (note that user $u'$ forged all his friends $F_{u'}$).

  It is straightforward to verify that, if c is chosen according to the specifics in [9] then user $u'$ (and user u) can recover $SK_s$ in a polynomial number of executions. With $SK_s$, user u can recover the weights from his real friends in $\mathbf {F}_u$ and then infer their ratings. It is worth stressing that this attack does not violate the semi-honest assumption in [13].

3 New Formulation of Recommender System

3.1 Computing Predicted Ratings

In our solution, we compute the predicted rating for user u based on inputs from both his friends and some strangers for both accuracy and security reasons. In reality friends like and consume similar items, but it might happen that very few friends have rated the item b. If this happens, the predicated value from Eq. (1) may not be very accurate (cold start problem). In Sect. 2, we have shown that the private information of user u’s friends might be leaked through user u’s outputs. This is because the outputs are computed solely based on the inputs of user u’s friends. We hope that, by taking into account some randomly chosen strangers, we will mitigate both problems.

When factoring in the inputs from randomly chosen strangers, we will use the simple Bias From Mean (BFM) scheme for the purpose of simplicity. It is worth stressing that there are a lot of different choices for this task. Nevertheless, as to the accuracy, this scheme has similar performance to many other more sophisticated schemes, such as Slope One and Perason/Cosine similarity-based collaborative filtering schemes [17]. Let the stranger set be $\mathbf {T}_u$, the predicted value $p_{u,b}^{*}$ for an unrated item b is computed as follows.

$$\begin{aligned} \displaystyle p_{u,b}^{*}= & {} \overline{r_u} +\frac{ \sum _{t \in \mathbf {T}_u}q_{t,b}\cdot (r_{t,b}-\overline{r_t})}{ \sum _{t \in \mathbf {T}_u}q_{t,b}} \end{aligned}$$

(2)

When factoring in the inputs from the friends, we make two changes to Eq. (1) from Sect. 2.2. One is to only take into account the weight value from user u. This makes more sense because how important a friend means to user u is a very subjective matter for u only. Jeckmans et al. averaged the weights for the purpose of limiting information leakage [13]. The other is to compute the predication based on both u’s average rating and the weighted rating deviations from his friends. Let the friend set be $\mathbf {F}_u$, the predicted value $p_{u,b}^{**}$ for an unrated item b is computed as follows.

$$\begin{aligned} p_{u,b}^{**}= & {} \overline{r_u} + \frac{\sum _{f \in \mathbf {F}_u}q_{f,b}\cdot (r_{f,b} - \overline{r_f}) \cdot w_{u,f}}{ \sum _{f \in \mathbf {F}_u}q_{f,b}\cdot w_{u,f}} \end{aligned}$$

(3)

In practice, the similarity between friends means that they tend to prefer to similar items. However, this does not imply that they will assign very similar scores to the items. For example, a user Alice may be very mean and assign a score 3 to most of her favorite items while her friends may be very generous and assign a score 5 to their favorite items. Using the Eq. (1), we will likely generate a score 5 for an unrated item for Alice, who may just rate a score 3 for the item even if she likes it. In this regard, Eq. (3) is more appropriate because $\overline{r_u}$ reflects the user’s rating style and $\frac{\sum _{f \in \mathbf {F}_u}q_{f,b}\cdot (r_{f,b} - \overline{r_f}) \cdot w_{f,u}}{ \sum _{f \in \mathbf {F}_u}q_{f,b}\cdot w_{f,u}}$ reflects the user’s preference based on inputs from his friends.

Based on the inputs from the strangers and friends, a combined predicted value $p_{u,b}$ for an unrated item b can be computed as $p_{u,b}= \rho \cdot p_{u,b}^{*}+ (1-\rho )\cdot p_{u,b}^{**}$ for some $0 \le \rho \le 1$. Due to the fact that cryptographic primitives are normally designed for dealing with integers, we rephrase the formula as follows, where $\alpha , \beta$ are two integers.

$$\begin{aligned} p_{u,b}= & {} \frac{\beta }{\alpha +\beta } \cdot p_{u,b}^{*}+ \frac{\alpha }{\alpha +\beta }\cdot p_{u,b}^{**} \end{aligned}$$

(4)

3.2 Threat Model

As to communication, we assume all communications are mediated by the RS server and the communication channels are integrity and confidentiality protected. Instead of making a general semi-honest assumption on all participants, we distinguish the following.

• 1. Threat from Semi-honest RS Server. In the view of all users, the RS server will follow the protocol specification but it may try to infer their private information from openly collected transaction records.

• 2. Threat from a Semi-honest Friend. In the view of a user, none of his friends will collude with the RS server or another party to breach his privacy. We believe the social norm deters such colluding attacks, and the deterrence comes from the fact that once such a collusion is known to the victim user then the friendship may be jeopardized. Nevertheless, we still need to consider possible privacy threats in two scenarios.

  • In the view of $f \in \mathbf {F}_u$, user u may attempt to learn his private information when running the recommendation protocol. In the view of user u, his friend $f \in \mathbf {F}_u$ may also try to infer his information as well.

  • In the view of $f \in \mathbf {F}_u$, user u’s output (e.g. a new rated item and predicted rating value) may be leaked. If another party obtains such auxiliary information, then user f’s private information may be at risk. For example, the Potential Information Leakage through Friends security issue in Sect. 2.2 falls into this scenario.

• 3. Threat from Strangers. We consider the following two scenarios.

  • In the view of user u and his friends, a stranger may try to learn their private information.

  • In the view of a stranger, who is involved in the protocol execution of user u, user u may try to learn his private information.

4 New Privacy-Preserving Recommender Protocols

In this section, we propose two privacy-preserving protocols: one for the active user to learn the predicted rating for an unrated item, and the other is for the active user to learn Top-N unrated items. Both protocols share the same initialization phase.

In the initialization phase, user u generates a public/private key pair $(PK_u, SK_u)$ for the Brakerski-Vaikuntanathan SWHE scheme and sends $PK_u$ to the server. For the purpose of enabling strangers to validate his public key, user u asks his friends to certify his public key and puts the certification information on the server. In addition, user u assigns a weight $w_{u,f}$ to each of his friend $f \in \mathbf {F}_u$. All other users perform the same operations in this phase. Besides the user-specific parameters, the global system parameters should also be established in the initialization phase. Such parameters should include $\alpha , \beta$ which determine how a predicated rating value for user u is generated based on the inputs of friends and strangers, and they should also include the minimal sizes of friend set $\mathbf {F}_u$ and stranger set $\mathbf {T}_u$.

4.1 Recommendation Protocol for Single Prediction

When user u wants to figure out whether the predicted rating for an unrated item b is above a certain threshold $\tau$ in his mind, he initiates the protocol in Fig. 3. In more details, the protocol runs in three stages.

• 1. In the first stage, user u generates a binary vector $\mathbf {I}_b$, which only has 1 for the b-th element, and sends the ciphertext $[\mathbf {I}_b]_u=\mathsf {Enc}(PK_u,\mathbf {I}_b)$ to the server. The server first sends $PK_u$ to some randomly chosen strangers who are the friends of user u’s friends in the system. Such a user t can then validate $PK_u$ by checking whether their mutual friends have certified $PK_u$. After the server has successfully found a viable stranger set $\mathbf {T}_u$, it forwards $[\mathbf {I}_b]_u$ to every user in $\mathbf {T}_u$. With $PK_u$ and $(\mathbf {R}_t, \mathbf {Q}_t)$, user t can compute the following based on the homomorphic properties. For notation purpose, assume $[\mathbf {I}_b]_u = ([\mathbf {I}_b^{(1)}]_u, \cdots , [\mathbf {I}_b^{(|B|)}]_u)$.

  $$\begin{aligned}{}[q_{t,b}]_u&=\sum _{1 \le i \le |B|} \mathsf {Eval}(\cdot ,\mathsf {Enc}(PK_u,q_{t,i}),[\mathbf {I}_b^{(i)}]_u), \, [\mathbf {R}_t \cdot \mathbf {I}_b]_u\\&= \sum _{1 \le i \le |B|} \mathsf {Eval}(\cdot ,\mathsf {Enc}(PK_u,r_{t,i}), [\mathbf {I}_b^{(i)}]_u) \end{aligned}$$
  $$\begin{aligned} temp=\sum _{1 \le i \le |B|} \mathsf {Eval}(\cdot ,\mathsf {Enc}(PK_u,q_{t,i}),[\mathbf {I}_b^{(i)}]_u) \end{aligned}$$
  $$\begin{aligned}{}[q_{t,b} \cdot (\mathbf {R}_t \cdot \mathbf {I}_b - \overline{r_t})]_u=\mathsf {Eval}(\cdot , temp, \mathsf {Eval}(+, [\mathbf {R}_t \cdot \mathbf {I}_b]_u, - \mathsf {Enc}(PK_u,\overline{r_t}))) \end{aligned}$$

• 2. In the second stage, for every friend $f \in \mathbf {F}_u$, user u sends the encrypted weight $[w_{u,f}]_u=\mathsf {Enc}(PK_u,w_{u,f})$ to the server, which then forwards $[w_{u,f}]_u$ and $[\mathbf {I}_b]_u$ to user f. With $PK_u$, $[\mathbf {I}_b]_u$, $[w_{u,f}]_u$ and $(\mathbf {R}_f, \mathbf {Q}_f)$, user f can compute the following.

  

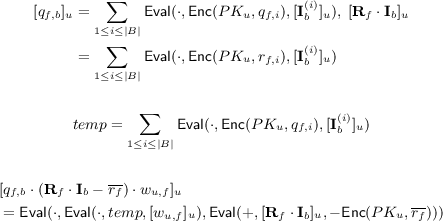
• 3. In the third stage, user u sends his encrypted average rating $[\overline{r_u}]_u= \mathsf {Enc}(PK_u,\overline{r_u})$ to the server. The server first computes $[n_T]_u,[d_T]_u,[n_F]_u,[d_F]_u$ as shown in Fig. 3, and then compute $[X]_u,[Y]_u$ as follows.

  $$\begin{aligned} temp_1= \mathsf {Eval}(\cdot ,\mathsf {Eval}(\cdot , \mathsf {Eval}(\cdot , [d_F]_u, [\overline{r_u}]_u), [d_T]_u), \mathsf {Enc}(PK_u,\alpha +\beta )) \end{aligned}$$
  $$\begin{aligned} temp_2 = \mathsf {Eval}(\cdot ,\mathsf {Eval}(\cdot , [n_T]_u, [d_F]_u), \mathsf {Enc}(PK_u,\beta )) \end{aligned}$$
  $$\begin{aligned} temp_3 = \mathsf {Eval}(\cdot ,\mathsf {Eval}(\cdot , [n_F]_u, [d_T]_u), \mathsf {Enc}(PK_u,\alpha )) \end{aligned}$$
  $$\begin{aligned}{}[X]_u = \mathsf {Eval}(+,\mathsf {Eval}(+, temp_1, temp_2), temp_3) \end{aligned}$$
  $$\begin{aligned}{}[Y]_u= \mathsf {Eval}(\cdot ,\mathsf {Eval}(\cdot , [d_F]_u, [d_T]_u), \mathsf {Enc}(PK_u, \alpha +\beta )) \end{aligned}$$

  Referring to Eqs. (2) and (3), we have $p_{u,b}^{*}=\overline{r_u} +\frac{n_T}{d_T}$ and $p_{u,b}^{**}=\overline{r_u} + \frac{n_F}{d_F}$. The ultimate prediction $p_{u,b}$ can be denoted as follows.

  $$\begin{aligned} p_{u,b}= & {} \frac{\beta }{\alpha +\beta } \cdot p_{u,b}^{*}+ \frac{\alpha }{\alpha +\beta }\cdot p_{u,b}^{**}= \frac{(\alpha + \beta ) \cdot d_T \cdot d_F \cdot \overline{r_u} + \beta \cdot n_T \cdot d_F + \alpha \cdot n_F \cdot d_T}{(\alpha + \beta ) \cdot d_T \cdot d_F}= \frac{X}{Y} \end{aligned}$$

  Due to the fact that all values are encrypted under $PK_u$, user u needs to run a comparison protocol $\mathsf {COM}$ with the server to learn whether $p_{u,b} \ge \tau$. Since $X, Y, \tau$ are integers, $\mathsf {COM}$ is indeed an encrypted integer comparison protocol: where user u holds the private key $sk_u$ and $\tau$, the server holds $[X]_u, [Y]_u$, and the protocol outputs a bit to user u indicating whether $X \ge \tau \cdot Y$. To this end, the protocol by Veugen [33] is the most efficient one.

Fig. 3.

Single prediction protocol

Fig. 4.

Top-N protocol

4.2 Recommendation Protocol for Top-N Items

When the active user u wants to figure out Top-N unrated items, he initiates the protocol in Fig. 4. In more details, the protocol runs in three stages.

• 1. In the first stage, the server sends $PK_u$ to some randomly chosen strangers who can then validate $PK_u$ as in the previous protocol. Suppose that the server has successfully found $\mathbf {T}_u$. With $PK_u$ and $(\mathbf {R}_t, \mathbf {Q}_t)$, user $t \in \mathbf {T}_u$ can compute $[q_{t,b} \cdot (r_{t,b} - \overline{r_t})]_u=\mathsf {Enc}(PK_u,q_{t,b} \cdot (r_{t,b} - \overline{r_t}))$ and $[q_{t,b}]_u=\mathsf {Enc}(PK_u,q_{t,b})$ for every $1 \le b \le |\mathbf {B}|$. All encrypted values are sent back to the server.

• 2. In the second stage, to every friend $f \in \mathbf {F}_u$, user u sends the encrypted weight $[w_{u,f}]_u=\mathsf {Enc}(PK_u,w_{u,f})$. With $PK_u$, $[w_{u,f}]_u$ and $(\mathbf {R}_f, \mathbf {Q}_f)$, user f can compute $[q_{f,b}]_u$ and

  $$\begin{aligned}{}[q_{f,b} \cdot (r_{f,b} - \overline{r_f}) \cdot w_{u,f}]_u=\mathsf {Eval}(\cdot , \mathsf {Enc}(PK_u,q_{f,b} \cdot (r_{f,b} - \overline{r_f})), [w_{u,f}]_u) \end{aligned}$$

  for every $1 \le b \le |\mathbf {B}|$. All encrypted values are sent back to the server.

• 3. In the third stage, user u generates two matrices $\mathbf {M}_X, \mathbf {M}_Y$ as follows: (1) generate a $|\mathbf {B}| \times |\mathbf {B}|$ identity matrix; (2) randomly permute the columns to obtain $\mathbf {M}_Y$; (3) to obtain $\mathbf {M}_X$, for every b, if item b has been rated then replace the element 1 in b-th column with 0.

  

  User u encrypts the matrices (element by element) and sends $[\mathbf {M}_X]_u, [\mathbf {M}_Y]_u$ to the server, which then proceeds as follows.

  • (a) The server first computes $[n_{T,b}]_u$, $[d_{T,b}]_u$, $[n_{F,b}]_u$, $[d_{F,b}]_u$, $[X_b]_u$, $[Y_b]_u$ for every $1 \le b \le |\mathbf {B}|$ as shown in Fig. 4, in the same way as in the previous protocol. Referring to Eq. (4), we see that $\overline{r_u}$ appears in $p_{u,b}$ for every b. For simplicity, we ignore this term when comparing the predictions for different unrated items. With this simplification, the prediction $p_{u,b}$ can be denoted as follows.

    $$\begin{aligned} p_{u,b}= & {} \frac{\beta }{\alpha +\beta } \cdot \frac{n_{T,b}}{d_{T,b}}+ \frac{\alpha }{\alpha +\beta }\cdot \frac{n_{F,b}}{d_{F,b}}= \frac{\beta \cdot n_{T,b} \cdot d_{F,b} + \alpha \cdot n_{F,b} \cdot d_{T,b}}{(\alpha + \beta ) \cdot d_{T,b} \cdot d_{F,b}}= \frac{X_b}{Y_b} \end{aligned}$$

  • (b) The server permutes the ciphertexts vector $(([X_1]_u, [Y_1]_u), ([X_2]_u, [Y_2]_u), \cdots , ([X_{|\mathbf {B}|}]_u, [Y_{|\mathbf {B}|}]_u))$ in an oblivious manner as follows.

    

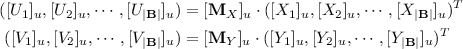
    The multiplication between the ciphertext matrix and ciphertext vector is done in the standard way, except that the multiplication between two elements is done with $\mathsf {Eval}(\cdot ,,)$ and the addition is done with $\mathsf {Eval}(+,,)$. Suppose item b has been rated before and $([X_b]_u, [Y_b]_u)$ is permuted to $([U_i]_u, [V_i]_u)$, then $U_i=0$ because the element 1 in b-th column has been set to 0.

  • (c) Based on some $\mathsf {COM}$ protocol, e.g. that used in the previous protocol, the server ranks $\frac{U_i}{V_i}$ $(1 \le i \le |\mathbf {B})|$ in the encrypted form using any standard ranking algorithm, where comparisons are done interactively with user u through the encrypted integer comparison protocol $\mathsf {COM}$.

  • (d) After the ranking, the server sends the “Top-N” indexes (e.g. the permuted Top-N indexes) to user u, who can then recover the real Top-N indexes.

The usage of matrix $\mathbf {M}_X$ in the random permutation of stage 3 guarantees that the rated items will all appear in the end of the list after ranking. As a result, the rated items will not appear in the recommended Top-N items.

5 Evaluating the Proposed Protocols

Parameters and Performances. The selection of the global parameters $\alpha , \beta$ and the sizes of $\mathbf {F}_u$ and $\mathbf {T}_u$ can affect the security, in particular when considering the threat from a semi-trusted friend. If $\frac{\alpha }{\alpha +\beta }$ gets larger or the size of $\mathbf {T}_u$ gets smaller, then the inputs from friends contribute more to the final outputs of user u. This will in turn make information reference attacks easier (for user u to infer the inputs of his friends). However, if $\frac{\alpha }{\alpha +\beta }$ gets smaller and $\mathbf {T}_u$ gets larger, then we will lose the motivation of explicitly distinguishing friends and strangers in computing recommendations, namely the accuracy of recommendations may get worse. How to choose these parameters will depend on the application scenarios and the overall distributions of users’ ratings.

In order to get some rough idea about how these parameters influence the accuracy of recommendation results. We choose the MovieLens 100k dataset¹ and define friends and strangers as follows. Given a user u, we first calculate the Cosine similarities with all other users and generate a neighborhood for user u. Then, we choose a certain number of users from the neighborhood as the friends, and randomly choose a certain number of users from the rest as strangers. For different parameters, the Mean Average Error (MAE) [29] of the proposed protocols is shown in Table 1. Note that lower MAE implies more accurate recommendations.

Table 1. MAE of experiments

From the numbers, it is clear that the more friends are involved the more accurate recommendation results user u will obtain (i.e. the MAE is lower). There is also a trend that the MAE becomes smaller when the contribution factor $\frac{\alpha }{\alpha +\beta }$ becomes larger. According to the accuracy results by Lemire and Maclachlan (in Table 1 of [17] where the values are MAE divided by 4), their smallest MAE is $0.752=0.188 \times 4$. From the above Table 1, we can easily get lower MAE when $|F_u| \ge 70$ by adjusting $\frac{\alpha }{\alpha +\beta }$.

Security Analysis. Informally, the protocols are secure based on two facts: (1) all inputs are first freshly encrypted and then used in the computations; (2) all computations (e.g. computing predictions and ranking) done by the server and other users are in the encrypted form. As to the single prediction protocol in Sect. 4.1, we have the following arguments.

• 1. Threat from Semi-honest RS Server. Given the $\mathsf {COM}$ protocol is secure (namely, the server does not learn anything in the process). Then the server learns nothing about any user’s private input information, e.g. $b, \tau , \mathbf {R}_u, \mathbf {Q}_u, \mathbf {R}_f, \mathbf {Q}_f, w_{u,f}, \mathbf {R}_t, \mathbf {Q}_t$ for all f and t, because every element is freshly encrypted in the computation and all left computations are done homomorphically. Moreover, the server learns nothing about $p_{u,b} \mathop {\ge }\limits ^{?} \tau$ based on the security of $\mathsf {COM}$.

• 2. Threat from a Semi-honest Friend. We consider two scenarios.

  • Informally, a friend f’s contribution to $p_{u,b}$ is protected by the inputs from users $\mathbf {F}_u\backslash f$ and the strangers $\mathbf {T}_u$. Given a randomly chosen unrated item for user u and a randomly chosen friend $f \in \mathbf {F}_u$, we perform a simple experiment to show how f’s input influences the predicted rating. We set $\frac{\alpha }{\alpha +\beta }=0.8$ and the $(|\mathbf {F}_u|,|\mathbf {T}_u|)=(30,10)$ in all tests, and choose strangers randomly in every test.

    Table 2. Influence of a single friend

    The results in Table 2 imply that a friend f’s contribution to user u’s output is obfuscated by the inputs from the stranger set. Simply from the output of user u, it is hard to infer user f’s input. Furthermore, it should be clear that the larger the friend set is the less information of a single friend will be inferred. With encryption, the friends learn nothing about user u.

  • For similar reasons, it will be hard for $\mathbf {F}_u\backslash f$ to infer user f’s data even if they learned user u’s output at the end of a protocol execution.

• 3. Threat from strangers. We consider the following two scenarios.

  • In the view of strangers, all values are encrypted under user u’s public key, so that they will not be able to derive any information about the inputs and outputs of user u and his friends.

  • For the strangers involved in a protocol execution, it does not leak much information for several reasons. Firstly, user u does not know which stranger is involved in the protocol execution. Secondly, the inputs of a group strangers are blended in the output to user u. We perform a simple experiment to show how strangers’ inputs influence the predicted ratings for user u. We set $\frac{\alpha }{\alpha +\beta }=0.8$ and the $(|\mathbf {F}_u|,|\mathbf {T}_u|)=(30,10)$. Table 3 shows the rating differences for 5 unrated items, depending on whether a stranger is involved in the computation or not. It is clear that very little information about a stranger can be inferred from user u’s outputs.

    Table 3. Influence of strangers

    Thirdly, the strangers are independently chosen in different protocol executions, so that it is difficult to leverage on the accumulated information.

Similar analysis applies to the Top-N protocol in Sect. 4.2. As to user u’s outputs, the matrices $[\mathbf {M}_X]_u, [\mathbf {M}_Y]_u$ randomly permuted the predictions so that the ranking does not leak any information about the Top-N items.

6 Conclusion

Recommender systems are complex in the sense that many users are involved and contributing to the outputs of each other. The privacy challenge is big because it is difficult to reach a realistic security model with efficient privacy-preserving protocols. This work, motivated by [13], tried to propose a realistic security model by leveraging on the similarity and trust between friends in digital communities. Compared to [13], we went a step further by introducing randomly selected strangers into the play and make it possible to protect users’ privacy even if their friends’ outputs are compromised. Moreover, we adjusted the recommendation formula and achieve better accuracy than some other well-known recommender protocols [17]. Following our work, many interesting topics remain open. One is to test our protocols on real dataset. Another is to implement the protocols and see how realistic the computational performances are. Another is to adjust the recommendation formula to reflect more advanced algorithms, such as Matrix Factorizations [19], which however will have different requirements on the involved user population. Another is to investigate stronger security models, e.g. assuming a malicious RS server. Yet another topic is to formally investigate the information leakages from the outputs. Our methodology, namely introducing randomly selected strangers, has some similarity with the differential privacy based approach [18]. A detailed comparative study will be very useful to understand their connections.

Appendix: Brakerski-Vaikuntanathan SWHE Scheme

Let $\lambda$ be the security parameter. The Brakerski-Vaikuntanathan public-key SWHE scheme [5] is parameterized by two primes $q, t \in \text {poly}(\lambda )\in \mathbb {N}$ where $t < q$, a degree n polynomial $f(x)\in \mathbb {Z}[x]$, two error distributions $\chi$ and $\chi '$ over the ring $R_q=\mathbb {Z}_q[x]/\langle f(x)\rangle$. The message space is $\mathcal {M}=\mathbf {R}_t=\mathbb {Z}_t[x]/\langle f(x)\rangle$. An additional parameter is $D \in \mathbb {N}$, namely the maximal degree of homomorphism allowed (and to the maximal ciphertext length). The parameters $n,f,q,t,\chi , \chi ', D$ are public.

• $\mathsf {Keygen}(\lambda )$: (1) sample $s, e_0\leftarrow \chi$ and $a_0\in R_q$; (2) compute $\mathbf {s}=(1,s,s^2,\ldots ,s^D)\in R_q^{D+1}$; (3) output $SK = \mathbf {s}$ and $PK=(a_0, b_0=a_0s+te_0)$.

• $\mathsf {Enc}(PK, m)$: (1) sample $v,e'\leftarrow \chi$ and $e''\leftarrow \chi '$; (2) compute $c_0=b_0v+te''+m$, $c_1=-(a_0v+te')$; (3) output $\mathbf {c}=(c_0,c_1)$.

• $\mathsf {Dec}(SK , \mathbf {c} =(c_0,\ldots ,c_D)\in R_q^{D+1})$: output $m=(\mathbf {c}\cdot \mathbf {s} \mod q) \mod t$.

Since the scheme is somewhat homomorphic, it provides an evaluation algorithm $\mathsf {Eval}$, which can multiply and add messages based on their ciphertexts only. For simplicity, we show how $\mathsf {Eval}$ works when the ciphertexts are freshly generated. Let $\mathbf {c}_{\alpha }=(c_{\alpha 0},c_{\alpha 1})$ and $\mathbf {c}_{\beta }=(c_{\beta 0},c_{\beta 1})$. Note that the multiplication operation will add an additional element for the ciphertext. This is why the $\mathsf {Dec}$ algorithm generally assumes the ciphertext to be a vector of $D+1$ elements (if the ciphertext has less elements, simply pad 0s).

$$\begin{aligned} \mathsf {Eval}(+, \mathbf {c}_{\alpha }, \mathbf {c}_{\beta })&= (c_{\alpha 0}+c_{\beta 0},c_{\alpha 1}+c_{\beta 1}). \,\, \mathsf {Eval}(\cdot , \mathbf {c}_{\alpha }, \mathbf {c}_{\beta })\\&= (c_{\alpha 0} \cdot c_{\beta 0}, c_{\alpha 0}\cdot c_{\beta 1}+c_{\alpha 1}\cdot c_{\beta 0}, c_{\alpha 1}\cdot c_{\beta 1}). \end{aligned}$$

When the evaluations are done to a ciphertext and a plaintext message, there is a simpler form for the evaluation algorithm, denoted as $\mathsf {Eval}^*$. This has been used in [13].

$$\begin{aligned} \mathsf {Eval}^*(+, \mathbf {c}_{\alpha }, m') = (c_{\alpha 0}+m',c_{\alpha 1}). \,\, \mathsf {Eval}^*(\cdot , \mathbf {c}_{\alpha }, m') = (c_{\alpha 0} \cdot m', c_{\alpha 1}\cdot m'). \end{aligned}$$

Throughout the paper, given a public/private key pair $(PK_u, SK_u)$ for some user u, we use $[m]_u$ to denote a ciphertext of the message m under public key $PK_u$. In comparison, $\mathsf {Enc}(PK_u, m)$ represents the probabilistic output of running $\mathsf {Enc}$ for the message m. When $\mathbf {m}$ is a vector of messages, we use $\mathsf {Enc}(PK_u, \mathbf {m})$ to denote the vector of ciphertexts, where encryption is done for each element independently. We use the notation $\sum _{1 \le i \le N}[m_i]_u$ to denote the result of sequentially applying $\mathsf {Eval}(+,,)$ to the cipheretxts.