Keywords

Introduction

Many of the most pressing and fundamental questions in biodiversity conservation require robust and sensible measures for quantifying and assessing changes in biodiversity. Many environmental and monitoring projects also require objective and meaningful similarity (or differentiation) measures to compare the diversities of multiple assemblages and their degree of complementarity in order to best conserve genetic, species, and ecosystem diversity . An enormous number of diversity measures and related similarity (or differentiation) indices have been proposed, not only in ecology but also in genetics, economics, information science, linguistics, physics, and social sciences, among others. See Magurran (2004) and Magurran and McGill (2011) for overviews.

In traditional species diversity measures, all species are considered to be equally different from each other; only species richness and abundances are involved. There are two general approaches: parametric and non-parametric (Magurran 2004). Parametric approaches assume a particular species abundance distribution (such as the lognormal or gamma) or a species rank abundance distribution (such as the negative binomial or log-series), and then use the parameters (e.g., Fisher’s alpha) of the distribution to quantify diversity. However, these methods often do not perform well and the results are un-interpretable unless the “true” species abundance distribution is known (Colwell and Coddington 1994; Chao 2005). The parametric model also does not permit meaningful comparison of assemblages with different abundance distributions. For example, a log-normal abundance model cannot be compared to an assemblage whose abundance distribution follows a gamma distribution. Non-parametric methods make no assumptions about the distributional form of the underlying species abundance distribution. The most widely used abundance-sensitive non-parametric measures have been the Shannon entropy and the Gini-Simpson index . These two measures, along with species richness were integrated into a class of measures called generalized entropies (Havrdra and Charvat 1967; Daróczy 1970; Patil and Taillie 1979; Tsallis 1988; Keylock 2005), which will be briefly reviewed in this chapter.

How to quantify abundance-based species diversity in an assemblage has been one of the most controversial issues in community ecology (e.g. Hurlbert 1971; Routledge 1979; Patil and Taillie 1982; Purvis and Hector 2000; Jost 2006, 2007; Jost et al. 2010). There have also been intense debates on the choice of diversity partitioning schemes; see Ellison (2010) and the Forum that follows it. Surprisingly, all authors in that forum achieved a consensus on the use of Hill number s , also called “effective number of species”, as the best choice to quantify abundance-based species diversity. Hill numbers are a mathematically unified family of diversity indices (differing among themselves only by a parameter q) that incorporate species richness and species relative abundances. They were first used in ecology by MacArthur (1965, 1972), developed by Hill (1973), and recently reintroduced to ecologists by Jost (2006, 2007).

Hill number s obey the replication principle or doubling property , an essential mathematical property that capture biologists’ notion of diversity (MacArthur 1965; Hill 1973). This property requires that if we have N equally diverse, equally large assemblages with no species in common, the diversity of the pooled assemblage must be N times the diversity of a single group. In other words, they are linear with respect to addition of equally-common species. We will review different versions of this property later. Classical diversity measures, such as Shannon entropy and the Gini-Simpson index , do not obey this principle and can lead to inconsistent or counter-intuitive interpretations, especially in conservation applications (Jost 2006, 2007). Hill numbers resolve many of the interpretational problems caused by classical diversity indices. Diversity measures that obey the replication principle yield self-consistent assessment in conservation applications, have intuitively-interpretable magnitudes, and can be meaningfully decomposed. In this chapter, Hill numbers are adopted as a general framework for quantifying and partitioning diversities.

Pielou (1975, p. 17) was the first to notice that traditional abundance-based species diversity measures could be broadened to include phylogenetic, functional, or other differences between species. We here concentrate on phylogenetic differences, though our framework can also be extended to functional traits (Tilman 2001; Petchey and Gaston 2002; Weiher 2011). For conservation purposes, an assemblage of phylogenetically divergent species is more diverse than an assemblage consisting of closely related species, all else being equal. Phylogenetic differences among species can be based directly on their evolutionary histories, either in the form of taxonomic classification or well-supported phylogenetic trees (Faith 1992; Warwick and Clarke 1995; McPeek and Miller 1996; Crozier 1997; Helmus et al. 2007; Webb 2000; Webb et al. 2002; Pavoine et al. 2010; Ives and Helmus 2010, 2011; Vellend et al. 2011; Cavender-Bares et al. 2009, 2012 among others). Three special issues in Ecology were devoted to integrating ecology and phylogenetics; see McPeek and Miller (1996), Webb et al. (2006), and Cavender-Bares et al. (2012) and papers in each issue. Phylogenetic diversity measures are especially relevant for conservation applications, since they quantify the amount of evolutionary history preserved by the assemblage; see Lean and MacLaurin (chapter “The Value of Phylogenetic Diversity ”).

The most widely used phylogenetic metric is Faith’s phylogenetic diversity (PD ) (Faith 1992) which is defined as the sum of the branch length s of a phylogenetic tree connecting all species in the target assemblage. As shown in Chao et al. (2010), Faith’s PD can be regarded as a phylogenetic generalization of species richness . The rarefaction formula for Faith’s PD was developed by Nipperess and Matsen (2013) and Nipperess (chapter “The Rarefaction of Phylogenetic Diversity : Formulation, Extension and Application”). Recently, Chao et al. (2015) derived an integrated sampling, rarefaction, and extrapolation methodology to compare Faith’s PD of a set of assemblages. Like species richness, Faith’s PD does not consider species abundances. For some conservation applications, the mere presence or absence of a species is all that matters, or all that can be determined from the available data. In those cases, Faith’s PD is a good measure of phylogenetic diversity. However, there are important advantages to incorporating abundance information into phylogenetic diversity measures for conservation. For example, some human impacts can result in the phylogenetic simplification of an ecosystem, reducing the population shares of phylogenetically distinct species relative to typical species. An abundance-based measure can catch this effect before it leads to actual extinctions.

Ecosystem simplification may be worthy of conservation concern even if it does not lead to extinctions of focal organisms. Often, the focal organisms for conservation represent a tiny fraction of the ecosystem’s biomass or richness . Each focal species will be tied to a web of non-focal species whose abundances are not usually monitored (e.g., insects). All else being equal, a more equitable distribution of the abundances of focal organisms will be able to support a more diverse, robust and stable set of non-focal species. Faith (chapter “Using Phylogenetic Dissimilarities Among Sites for Biodiversity Assessments and Conservation ”) rightly argues that phylogenetic diversity is a good proxy for functional diversity. Therefore an ecosystem with a more equitable distribution of abundance across phylogenetic lineages should also exhibit greater functional complexity (per interaction between individuals) than an ecosystem whose phylogenetically unusual elements are rare. If we have to prioritize such ecosystems, the more phylogenetically equitable one, which thoroughly integrates diverse lineages, should be preferred. In addition to being more resistant to lineage extinctions, a complex, well-integrated ecosystem may be worth preserving in and of itself, above and beyond its component species; conservation is not just about species. Evolution may take a different course in ecosystems whose members are constantly surprised by their interactions compared with an ecosystem whose interactors are highly predictable. These conservation goals – robustness against extinction of distinctive lineages, and preservation of well-integrated ecosystems with unique future option values – require phylogenetic diversity measures that incorporate species importance values.

Rao ’s quadratic entropy Q (Rao 1982), a generalization of the Gini-Simpson index , was the first diversity measure that accounts for both phylogeny and species abundances. The phylogenetic entropy H P (Allen et al. 2009) extends Shannon entropy to incorporate phylogenetic distance s among species. Since Shannon entropy and the Gini-Simpson index do not obey the replication principle , neither do their phylogenetic generalizations. These generalizations will therefore have the same interpretational problems as their parent measures; see Chao et al. (2010, their Supplementary Material) for examples.

Chao et al. (2010) extended Hill number s and related similarity measures to incorporate phylogeny. The new phylogenetic Hill numbers obey a generalized replication principle . Their measures were subsequently extended by Faith and Richards (2012) and Faith (2013). Both the original Hill numbers and their phylogenetic generalizations facilitate diversity decomposition (Jost 2007; Chiu et al. 2014). As with the original Hill numbers, both additive and multiplicative decompositions of phylogenetic Hill numbers lead to the same classes of similarity (or differentiation) measures. Hill numbers therefore provide a unified framework to quantify both abundance-based and phylogenetic diversity.

In this chapter, we first briefly review the classic abundance-based species diversity measures (section “Generalized Entropies”) and their phylogenetic generalizations (section “Phylogenetic generalized entropies”) for an assemblage. Then we focus on the framework of Hill number s (section “Hill numbers and the replication principle”), phylogenetic Hill numbers (section “Phylogenetic Hill numbers and related measures”) and related phylogenetic diversity measures. We also discuss the replication principle and its phylogenetic generalization (section “Replication principle for phylogenetic diversity measures”). For multiple assemblages, we review the diversity decomposition based on phylogenetic diversity measures (section “Decomposition of phylogenetic diversity measures”). The associated phylogenetic similarity and differentiation measures are then presented (section “Normalized phylogenetic similarity measures”). We use a real example for illustration (section “An example”). Our practical recommendations are provided in section “Conclusion”.

Classic Measures and Their Phylogenetic Generalizations

Generalized Entropies

The species richness of an assemblage is a simple count of the number of species present. It is the most intuitive and frequently used measure of biodiversity , and is a key metric in conservation biology (MacArthur and Wilson 1967; Hubbell 2001; Magurran 2004). However, it does not incorporate any information about the abundances of species, and it is a very hard number to estimate accurately from small samples (Colwell and Coddington 1994; Chao 2005; Gotelli and Colwell 2011).

Shannon entropy is a popular classical abundance-based diversity index and has been used in many disciplines. Shannon entropy is

$$ {H}_{Sh}=-{\displaystyle \sum}_{i=1}^S{p}_i \log {p}_i, $$
(1a)

where S is the number of species in the assemblage, and the ith species has relative abundance p i . Shannon entropy gives the uncertainty in the species identity of a randomly chosen individual in the assemblage. Another popular measure is the Gini-Simpson index ,

$$ {H}_{GS}=1-{\displaystyle \sum}_{i=1}^S{p}_i^2, $$
(1b)

which gives the probability that two randomly chosen individuals belong to different species. These two abundance-sensitive measures, along with species richness , can be united into a single family of generalized entropy :

$$ {}{}^qH=\left(1-{\displaystyle \sum}_{i=1}^S{p}_i^q\right)/\left(q-1\right). $$
(1c)

The parameter q determines the sensitivity of the measure to the relative frequencies of the species. When q = 0, q H becomes S − 1; When q tends to 1, q H tends to Shannon entropy . When q = 2, q H reduces to the Gini-Simpson index . This family was found many times in different disciplines (Havrdra and Charvat 1967; Daróczy 1970; Patil and Taillie 1979; Tsallis 1988; Keylock 2005). There are many other families of generalized entropies, notably the Rényi entropies (Rényi 1961).

Although the traditional abundance-sensitive generalized entropies and their special cases have been useful in many disciplines (e.g., see Magurran 2004), they do not behave in the same intuitive linear way as species richness . In ecosystems with high diversity , mass extinctions hardly affect their values (Jost 2010). They also lead to logical contradictions in conservation biology, because they do not measure a conserved quantity (e.g., under a given conservation plan, the proportion of “diversity” lost and the proportion preserved can both be 90 % or more); see Jost (2006, 2007) and Jost et al. (2010). Thus, changes in their magnitude cannot be properly compared or interpreted. Also, the main measure of similarity in the additive approach for traditional measures, the within-group or “ alpha” diversity divided by the total or “gamma” diversity, does not actually quantify the compositional similarity of the assemblages under study. This ratio can be arbitrarily close to unity (supposedly indicating high similarity) even when the assemblages being compared have no species in common. Finally, these measures each use different units (e.g., the Gini-Simpson index is a probability whereas Shannon entropy is in units of information), so they cannot be compared with each other. All these problems are consequences of their failure to satisfy the replication principle . Hill number s obey the replication principle and resolve all these problems; see section “Hill numbers and the replication principle”.

Phylogenetic Generalized Entropies

The classic measures reviewed in section “Generalized Entropies” were extended to incorporate phylogenetic distance between species. As mentioned in the Introduction and will be shown in section “Phylogenetic Hill numbers and related measures”, Faith’s PD can be regarded as a phylogenetic generalization of species richness .

Rao ’s quadratic entropy takes account of both phylogeny and species abundances (Rao 1982):

$$ Q={\displaystyle \sum}_{i,j}{d}_{ij}{p}_i{p}_j, $$
(2a)

where d ij denotes the phylogenetic distance (in years since divergence, number of DNA base changes, or other metric) between species i and j, and p i and p j denote the relative abundance of species i and j. This index measures the average phylogenetic distance between any two individuals randomly selected from the assemblage. Rao ’s Q represents a phylogenetic generalization of the Gini-Simpson index because in the special case of no phylogenetic structure (all species are equally related to one another), d ii  = 0 and d ij  = 1 (i ≠ j), it reduces to the Gini-Simpson index.

The phylogenetic entropy H P is a generalization of Shannon’s entropy to incorporate phylogenetic distance s among species (Allen et al. 2009):

$$ {H}_P=-{\displaystyle \sum}_i{L}_i{a}_i \log {a}_i $$
(2b)

where the summation is over all branches of a rooted phylogenetic tree, L i is the length of branch i, and a i denotes the summed relative abundance of all species descended from branch i.

For ultrametric trees, Faith’s PD , Allen et al.’s H P , and Rao ’s Q can be united into a single parametric family of phylogenetic generalized entropies (Pavoine et al. 2009):

$$ {}^qI=\left(T-{\displaystyle \sum}_{i\kern0.22em }{L}_i{a}_i^q\right)/\left(q-1\right). $$
(2c)

Here, L i and a i are defined in Eq. (2b) and T is the age of the root node of the tree. Then 0 I = Faith’s PD minus T; 1 I is identical to Allen et al.’s entropy H P given in Eq. (2b); and 2 I is identical to Rao ’s quadratic entropy Q given in Eq. (2a). In the special case that T = 1 (the tree height is normalized to unit length) and all branches have unit length, then the phylogenetic generalized entropy reduces to the classical generalized entropy defined in Eq. (1c), with species relative abundances {p 1, p 2, …, p S } as the tip-node abundances.

The abundance-sensitive (q > 0) phylogenetic generalized entropies provide useful information, but they do not obey the replication principle and thus have the same interpretational problems as their parent measures. This motivated Chao et al. (2010) to extend Hill number s to phylogenetic Hill numbers, which obey the replication principle; see section “Phylogenetic Hill numbers and related measures”.

Hill Numbers and Their Phylogenetic Generalizations

Hill Numbers and the Replication Principle

Pioneering work by Kimura and Crow (1964) in genetics and MacArthur (1965) in ecology showed that the Shannon and Gini-Simpson measures can be easily converted to “effective number of species” (i.e., the number of equally abundant species that are needed to give the same value of the diversity measure), which use the same units as species richness . Shannon entropy can be converted by taking its exponential, and the Gini-Simpson index can be converted by the formula 1/(1−H GS ). Hill (1973) integrated species richness and the converted Shannon and Gini-Simpson measures into a class of diversity measures called “ Hill number s ” of order q, or the “effective number of species”, defined as

$$ {}{}^qD={\left({\displaystyle \sum}_{i=1}^S{p}_i^q\right)}^{1/\left(1-q\right)},q\ge 0,q\ne 1. $$
(3a)

This measure is undefined for q = 1, but its limit as q tends to 1 exists and gives

$$ {}{}^1D=\underset{q\to 1}{ \lim }{}{}^qD= \exp \left(-{\displaystyle \sum}_{i=1}^S{p}_i \log {p}_i\right)= \exp \left({H}_{Sh}\right). $$
(3b)

The relationship between Hill number of order q (q ≠ 1) and the generalized entropy can be expressed as

$$ {}{}^qD={\left[1-\left(q-1\right)\left({}{}^qH\right)\right]}^{1/\left(1-q\right)}. $$
(3c)

When q = 0, the species abundances do not count at all and 0 D = S is obtained. When q = 1, the species are weighed in proportion to their frequencies, and the measure 1 D (in Eq. (3b)) can be interpreted as the effective number of common or “typical” species (i.e., species with typical abundances) in the assemblage. When q = 2, abundant species are favored and rare species are discounted; the measure 2 D becomes the inverse Simpson concentration. The measure 2 D can be interpreted as the effective number of dominant or very abundant species in the assemblage. In general, if q D = x, then the diversity of order q of this community is the same as that of an idealized reference community with x equally abundant species. All Hill number s are in units of “species”. It is thus possible to plot them on a single graph as a continuous function of the parameter q. This diversity profile characterizes the species-abundance distribution of an assemblage and provides complete information about its diversity. The steepness of its slope graphically illustrates the degree of dominance in the assemblage. An example is given in section “An example”.

Hill number s differ fundamentally from Shannon entropy and the Gini-Simpson index in that they obey the replication principle . Hill (1973) proved a weak version of the doubling property : if two completely distinct assemblages (i.e., no species in common) have identical relative abundance distributions, then the Hill number doubles if the assemblages are combined with equal weights. Chiu et al. (2014, their Appendix B) recently proved a strong version of the doubling property: if two completely distinct assemblages have identical Hill numbers of order q (relative abundance distributions may be different, unlike the weak version), then the Hill number of the same order doubles if the two assemblages are combined with equal weights. Species richness is a Hill number (with q = 0) and obeys both versions of the doubling property, but most other diversity indices do not obey even the weak version. Because Hill numbers obey this replication principle, changes in their magnitude have simple interpretations, and the ratio of alpha diversity to gamma diversity accurately reflects the compositional similarity of the communities. The replication principle is best known in economics, where it has long been recognized as an important property of concentration and diversity measures (Hannah and Kay 1977). In ecology, the doubling property has been extensively discussed by many authors (MacArthur 1965, 1972; Hill 1973; Whittaker 1972; Routledge 1979; Peet 1974; Jost 2006, 2007, 2009; Ricotta and Szeidl 2009; Jost et al. 2010) and has been extended to phylogenetic measures (Chao et al. 2010); see below.

Phylogenetic Hill Numbers and Related Measures

When the branch length s are proportional to divergence time, all branch tips are the same distance from the root (the first node). Such trees are called “ultrametric” trees. We first discuss the phylogenetic diversity measures for ultrametric trees. The phylogenetic Hill number s developed by Chao et al. (2010) for an ultrametric tree can be intuitively explained as the Hill number of a time-average of a tree’s generalized entropy over some evolutionary time interval of interest. Suppose the phylogenetic tree for an assemblage is calibrated to some relative or absolute timescale. We can slice this phylogenetic tree at any time t in the past; see the left panel of Fig. 1 (reproduced from Chao et al. 2010) for illustration and details about how to deal with shared lineages. The number of lineages at that time is the number of branch cuts, and the relative importance of each of these lineages for the present-day assemblage is the sum of the relative abundances of the branch’s descendants in the present-day assemblage. Using these relative importance values, we can calculate the generalized entropy of order q for the slice. The mean of these entropies, beginning at time –T (i.e., T years before present) and continuing until the present, is converted to a Hill number using Eq. (3c). This is the phylogenetic Hill number, which conveys information about the shape of the tree over the time interval of interest. Chao et al. (2010) symbolize it as \( {}{}^q\overline{D}\;(T) \), and also refer to it as the mean phylogenetic diversity of order q over T years (or simply the mean diversity for the interval [−T, 0]):

$$ {}{}^q\overline{D}\;(T)={\left\{{\displaystyle \sum}_{\kern0.22em i\in {B}_T}\frac{L_i}{T}\;{a}_i^q\right\}}^{1/\left(1-q\right)}=\frac{1}{T}{\left\{{\displaystyle \sum}_{\kern0.22em i\in {B}_T}{L}_i{\left(\frac{a_i}{T}\right)}^q\right\}}^{1/\left(1-q\right)},q\ge 0,q\ne 1; $$
(4a)
$$ {}{}^1\overline{D}\;(T)=\underset{q\to 1}{ \lim }{}{}^q\overline{D}\;(T)= \exp \left[-{\displaystyle \sum}_{i\in {B}_T}\frac{L_i}{T}{a}_i \log {a}_i\right], $$
(4b)

where B T is the set of all branches in the time interval [−T, 0], L i is the length of branch i in the set B T , and a i is the total relative abundance descended from branch i. The mean diversity \( {}{}^q\overline{D}\;(T) \) is interpreted as “the effective number of equally abundant and equally distinct lineages all with branch length s T during the time interval from T years ago to the present”. Here “equally distinct” also implies that the phylogenetic distance between any two species is T, so lineages are completely distinct (i.e., there are no shared branches).

Fig. 1
figure 1figure 1

(a) A hypothetical ultrametric rooted phylogenetic tree with four species. Three different slices corresponding to three different times are shown. For a fixed T (not restricted to the age of the root), the nodes divide the phylogenetic tree into segments 1, 2 and 3 with duration (length) T 1, T 2 and T 3, respectively. In any moment of segment 1, there are four species (i.e. four branches cut); in segment 2, there are three species; and in segment 3, there are two species. The mean species richness over the time interval [−T, 0] is \( \left({T}_1/T\right)\times 4+\left({T}_2/T\right)\times 3+\left({T}_3/T\right)\times 2 \). In any moment of segment 1, the species relative abundances (i.e. node abundances correspond to the four branches) are {p 1, p 2, p 3, p 4}; in segment 2, the species relative abundances are {g 1, g 2, g 3} = {p 1, p 2 + p 3, p 4}; in segment 3, the species relative abundances are {h 1, h 2} = {p 1 + p 2 + p 3, p 4}. (b) A hypothetical non-ultrametric tree. Let \( \overline{T} \) be the weighted (by species abundance) mean of the distances from root node to each of the terminal branch tips. \( \overline{T}=4\times 0.5+\left(3.5+2\right)\times 0.2+\left(1+2\right)\times 0.3=4 \). Note \( \overline{T} \) is also the weighted (by branch length ) total node abundance because \( \overline{T}=0.5\times 4+0.2\times 3.5+0.3\times 1+0.5\times 2=4 \). Conceptually, the ‘branch diversity ’ is defined for an assemblage of four branches: each has, respectively, relative abundance \( 0.5/\overline{T}=0.125 \), \( 0.2/\overline{T}=0.05 \), \( 0.3/\overline{T}=0.075 \) and \( 0.5/\overline{T}=0.125 \); and each has, respectively, weight (i.e. branch length) 4, 3.5, 1 and 2. This is equivalent to an assemblage with 10.5 equally weighted ‘branches’: there are four branches with relative abundance \( 0.5/\overline{T}=0.125 \); 3.5 branches with relative abundance \( 0.2/\overline{T}=0.05 \); one branch with relative abundance \( 0.3/\overline{T}=0.075 \) and two branches with relative abundance \( 0.5/\overline{T}=0.125 \) (This figure is reproduced from Fig. 1 of Chao et al. 2010)

Full size image

The phylogenetic Hill number s are invariant to the units used to measure branch length s. When all lineages are completely distinct, the measure \( {}{}^q\overline{D}\;(T) \) reduces to the Hill numbers \( {}^qD={\left({\displaystyle \sum}_i{a}_i^q\right)}^{1/\left(1-q\right)} \). This includes the special case that T tends to zero, i.e., the case that we ignore phylogeny and only consider the present-day community . This shows that the framework based on Hill numbers provides a unified approach to integrate abundances and phylogeny. Also, here we have a simple idealized reference tree to understand the value of \( {}{}^q\overline{D}\;(T)=z \) for an arbitrary tree: the mean phylogenetic diversity of the tree over the time period [−T, 0] is the same as the diversity of an idealized assemblage consisting of z equally abundant and equally distinct lineages all with branch length T.

For q = 0, when T is chosen as the age of the root node, we have \( {}{}^0\overline{D}\;(T)=\mathrm{Faith}'\mathrm{s}\;\mathrm{P}\mathrm{D}/T \), which can be interpreted as lineage richness . Faith’s PD can thus be regarded as a phylogenetic generalization of species richness. We can roughly interpret \( {}{}^1\overline{D}\;(T) \) as the effective number of common lineages, and \( {}{}^2\overline{D}\;(T) \) as the effective number of dominant lineages in the time period [−T, 0]. When T is chosen as the age of the root node, a simple relationship exists between phylogenetic entropy H P (Allen et al. 2009) and the measure \( {}{}^1\overline{D}\;(T) \):

$$ {}{}^1\overline{D}\;(T)= \exp \left({H}_P/T\right). $$
(4c)

For q = 2, when T is chosen as the age of the root node, there is a simple relationship between our measures and the widely used Rao ’s quadratic entropy Q (Chao et al. 2010):

$$ {}{}^2\overline{D}\;(T)=\frac{1}{1-Q/T}. $$
(4d)

The branch or phylogenetic diversity q PD(T) of order q during the time interval from T years ago to the present is defined as the product of \( {}{}^q\overline{D}\;(T) \) and T. It quantifies the amount of evolutionary history on the system over the interval [−T, 0], or “the effective total branch-length” (Chao et al. 2010):

$$ {}^qPD\;(T)=T\times {}{}^q\overline{D}(T)={\left\{{\displaystyle \sum}_{\kern0.22em i\in {B}_T}{L}_i{\left(\frac{a_i}{T}\right)}^q\right\}}^{1/\left(1-q\right)}. $$
(5a)
$$ {}{}^1PD\;(T)=\underset{q\to 1}{ \lim }{}{}^qPD\;(T)= \exp \left[-{\displaystyle \sum}_{i\in {B}_T}{L}_i\frac{a_i}{T} \log \left(\frac{a_i}{T}\right)\right]. $$
(5b)

If q = 0, and T is age of the root node, then 0 PD(T) reduces to Faith’s PD , regardless of branching pattern or abundances. As explained by Chao et al. (2010), we could imagine that all the branch segments in the interval [−T, 0] form a single assemblage with relative abundance set {a i /T; i∈B T }. In this assemblage, for each i there are L i “branches” with relative abundance a i /T. Then the Hill number of order q for this assemblage is exactly the branch diversity q PD(T) given in Eq. (5a). Dividing this Hill number by T, we obtain \( {}{}^q\overline{D}\;(T) \) given in Eq. (4a). Note in our framework that q PD(T) is truly a class of Hill numbers (“the effective number of lineage-years”), whereas \( {}{}^q\overline{D}\;(T) \) (“the effective number of lineages”) denotes a (generalized) mean of Hill numbers. See Faith and Richards (2012) and Faith (2013) for extensions of the measure q PD(T).

Unlike previous phylogenetic diversity measures developed in the literature, \( {}{}^q\overline{D}\;(T) \) and q PD(T) depend explicitly on two parameters, the abundance sensitivity parameter q and the time perspective (or time-depth) parameter T. The reasons we need this time-depth parameter and our suggestion to choose a perspective time are given as follows.

  1. 1.

    When we compare the phylogenetic diversities of several assemblages based on the measures \( {}{}^q\overline{D}\;(T) \) and q PD(T), all measures should refer to the same time periods to make meaningful comparisons. That is, the time-depth T should be kept as the same for all assemblages. Therefore, a parameter is required to specify the time-depth.

  2. 2.

    The choice of time perspective should reflect an investigator’s aims and facilitate comparisons with other studies. We suggest that at least two selected time perspectives should be included: T = 0, and T = the age of the root node of a phylogenetic tree connecting all species in the study. For the case of T = 0, the phylogeny is ignored and the diversity profile reduces to the profile in the present-day assemblage based on the ordinary Hill number s . If we choose T to be the age of the oldest node in the tree, we recover some of the standard measures of phylogenetic diversity (see Eqs. (4c) and (4d)).

  3. 3.

    As suggested in Chiu et al. (2014), other time perspectives can be selected, such as T = the age of the node at which the group of interest diverges from the rest of the species. This choice of T is independent of the species actually sampled, so it allows statistically robust comparisons across investigations and regions (unlike the conventional choice of T as the root node of the tree containing the species actually observed). This choice also provides an accurate measure of the proportion of a taxonomic group’s evolutionary history preserved in a given assemblage. Another choice is the time of the most recent common ancestor of all taxa alive today. Other choices may be made, depending on the purpose of an investigation. The formula in Chiu et al. (2014, p. 42) can be used to convert phylogenetic diversity from one temporal perspective to another.

To see how the measures vary with q and time perspective T, we recommend using two types of profiles to completely characterize phylogenetic tree information and species abundances as described below. See section “An example” for examples. (1) The first type of diversity profile is obtained by plotting q PD(T) or \( {}{}^q\overline{D}\;(T) \) as a function of order q as q varies from 0 to about 3 or 4 (beyond which there is usually little change), for some selected values of temporal perspective T. For this type of profile, q PD(T) and \( {}{}^q\overline{D}\;(T) \) have similar patterns as T is fixed, so it is sufficient to plot the profile only for one measure. (2) The second type of diversity profile is obtained by plotting q PD(T) and \( {}{}^q\overline{D}\;(T) \) as functions of T separately for q = 0, 1, and 2. This profile shows the effect of time-depth or evolution change on our diversity measures.

For the second type of profile, q PD(T) and \( {}{}^q\overline{D}\;(T) \) generally exhibit different patterns (the profile of \( {}{}^q\overline{D}\;(T) \) is decreasing with T whereas the profile of q PD(T) for q = 0 (Faith’s PD ) is always increasing, and for q > 0 is generally increasing up to a certain point, so the profiles for both measures are informative. The parameter q gives the sensitivity of the two measures to present-day species relative abundances. As in the ordinary Hill number s , the measures with q = 2 favor more abundant species, so they are useful in ecological studies to examine the phylogenetic relationships of the dominant species in a set of assemblages, or those examining functional diversity . The measures of q = 0 emphasizes rare species, so they are useful when abundance information is not necessarily relevant (e.g., when ecologists try to identify past episodes of differentiation, or for some conservation biology applications). The measures with q = 1 weigh species according to their frequencies and can be used in most applications when neither dominant nor rare species should be favored.

When the measure of evolutionary change is typically based on the number of nucleotide base changes at a selected locus, or the amount of functional or morphological differentiation from a common ancestor, the branches of the resulting tree will then be uneven, so the tree is non-ultrametric. In this case, Chao et al. (2010) showed that the time parameter T in all formulas should be replaced by the mean base change or mean branch length \( \overline{T}, \) the mean of the distances from the tree base to each of the terminal branch tips (i.e., the mean evolutionary change per species over the interval of interest). See the right panel of Fig. 1 for an illustrative example. Let \( {B}_{\overline{T}} \) denote the set of branches connecting all focal species, with mean branch length \( \overline{T}. \) Then we can express \( \overline{T} \) as \( \overline{T}={\displaystyle \sum}_{i\in {B}_{\overline{T}}}{L}_i{a}_i \). The diversity of a non-ultrametric tree with mean evolutionary change \( \overline{T} \) is the same as that of an ultrametric tree with time parameter \( \overline{T}. \) Therefore, the diversity formulas for a non-ultrametric tree are obtained by replacing T by \( \overline{T} \) in Eqs. (4a), (4b), (5a), and (5b). The resulting measures are denoted respectively as \( {}{}^q\overline{D}\;\left(\overline{T}\right) \), \( {}{}^1\overline{D}\;\left(\overline{T}\right) \), \( {}{}^qPD\;\left(\overline{T}\right) \) and \( {}{}^1PD\;\left(\overline{T}\right) \); see Chao et al. (2010) for details. When we compare the phylogenetic diversity based on the measures \( {}{}^q\overline{D}\;\left(\overline{T}\right) \) and \( {}{}^qPD\;\left(\overline{T}\right) \) for several non-ultrametric trees, all measures should refer to the same mean base change \( \overline{T} \) to make meaningful comparisons.

Replication Principle for Phylogenetic Diversity Measures

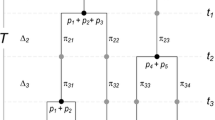
The replication principle was generalized to a phylogenetic version in Chao et al. (2010). Suppose there are N equally large and completely phylogenetically distinct assemblages (no shared lineages across assemblages, though lineages within an assemblage may be shared); see Fig. 2 (reproduced from Chiu et al. 2014) for an illustrative example. Suppose these assemblages have the same phylogenetic Hill number X. If these assemblages are pooled, then the pooled assemblages must have a phylogenetic Hill number N × X. In the proof of this replication principle, Chao et al. (2010) assumed that these N assemblages have the same mean branch length s. Here we relax this assumption and allow assemblages to have different mean branch lengths. (In the special case of ultrametric trees, this means that we allow different time perspectives for different assemblages.)

Suppose in assemblage k, the mean branch length is \( {\overline{T}}_k \), and the branch set is \( {B}_{{\overline{T}}_k,k} \) (we omit \( {\overline{T}}_k \) in the subscript and just use B k in the following proof for notational simplicity) with branch lengths {L ik ; i∈B k } and the corresponding nodes abundances {a ik ; i∈B k }, k = 1, 2, …, N. Assume that all assemblages have the same phylogenetic Hill number s \( {}{}^q\overline{D}\;\left({\overline{T}}_k\right)=X, \) implying \( {\displaystyle \sum}_{i\in {B}_k}{L}_{ik}\kern0.24em {a}_{ik}^q={X}^{1-q}{\overline{T}}_k \) for all k =1, 2, …, N. When the N trees are pooled with equal weight for each tree, each node abundance a ik in the pooled tree becomes a ik /N, and the mean branch length becomes \( \overline{T}=\left(1/N\right){\displaystyle \sum}_{k=1}^N{\overline{T}}_k \). Then the phylogenetic Hill number of order q for the pooled assemblage becomes

$$ \begin{array}{c}{}{}^q\overline{D}\;\left(\overline{T}\right)={\left\{{\displaystyle \sum}_{k=1}^N{\displaystyle \sum}_{i\in {B}_k}\frac{L_{ik}}{\overline{T}}{\left(\frac{a_{ik}}{N}\right)}^q\right\}}^{1/\left(1-q\right)}={\left\{\frac{1}{N^q}{\displaystyle \sum}_{k=1}^N\frac{1}{\overline{T}}{\displaystyle \sum}_{i\in {B}_k}{L}_{ik}{a}_{ik}^q\right\}}^{1/\left(1-q\right)}\\ {}={\left\{\frac{1}{N^q}{\displaystyle \sum}_{k=1}^N\frac{T_k}{\overline{T}}{X}^{1-q}\right\}}^{1/\left(1-q\right)}={\left\{{N}^{1-q}\times {X}^{1-q}\right\}}^{1/\left(1-q\right)}=N\times X.\end{array} $$
(6)

This proves a stronger version of the replication principle for phylogenetic Hill number s . Note the mean branch length in the pooled assemblage is the average of individual mean branch lengths. For example, if \( {}{}^q\overline{D}\left({\overline{T}}_1=2\right)={}{}^q\overline{D}\left({\overline{T}}_2=6\right)=10, \) then in an effective sense, there are ten lineages with mean branch length 2 in Assemblage 1 and there are ten lineages with mean branch length 6 in Assemblage 2. The replication principle implies that there are 20 lineages in the pooled tree with mean branch length 4. Since \( {}{}^qPD\;\left({\overline{T}}_k\right)={}{}^q\overline{D}\;\left({\overline{T}}_k\right)\times {\overline{T}}_k \), the replication principle for the phylogenetic diversity \( {}{}^qPD\;\left(\overline{T}\right) \) does need the assumption that all assemblages have the same mean branch lengths \( \left({\overline{T}}_1={\overline{T}}_2=\dots ={\overline{T}}_N\right) \). The proof is parallel and thus omitted.

Fig. 2
figure 2figure 2

Replication Principle for two completely phylogenetically distinct assemblages with totally different structures. Left panel: Assemblage 1 (black) includes three species with species relative abundances {p 11, p 21, p 31} for the three tips. Assemblage 2 (grey) includes four species with species relative abundances {p 12, p 22, p 32, p 42} for the four tips. The diversity of the pooled tree is double of that of each tree as long as the two assemblages are completely phylogenetically distinct as shown (no lineages shared between assemblages, though lineages within an assemblage may be shared) and have identical mean diversities (i.e., phylogenetic Hill number). Right panel: The same is valid for two completely phylogenetically distinct non-ultrametric assemblages (This figure is reproduced from Fig. 1of Chiu et al. 2014)

Full size image

Decomposition of Phylogenetic Diversity Measures

Decomposition of species richness and its phylogenetic analogues into within- and between-group (alpha and beta) components is widely used (Whittaker 1972; Faith et al. 2009). However, these take no notice of abundance differences between sites. Conservationists using these measures cannot distinguish a site whose species are equally abundant from a site with the same species but with a highly skewed abundance distribution whose most phylogenetically distinctive species are rare. The former site would be a better bet for conservation. These considerations, and others, motivate the development of decomposition theory for abundance-based phylogenetic diversity measures. The decomposition also leads to abundance-sensitive measures of phylogenetic similarity and complementarity.

When there are N assemblages, the phylogenetic Hill number s \( {}{}^q\overline{D}\;(T) \) (Eqs. 4a and 4b) and phylogenetic diversity q PD(T) (Eqs. 5a and 5b) of the pooled assemblage can be multiplicatively decomposed into independent alpha and beta components (Chiu et al. 2014). We briefly describe the decomposition of the measure \( {}{}^q\overline{D}\;(T) \) here for the ultrametric case, and only summarize the decomposition of the measure q PD(T). The extension to the non-ultrametric case for both measures is obtained by simply replacing all T in the formulas with the mean branch length \( \overline{T} \) of the pooled assemblage.

To begin the partitioning, a pooled tree is constructed for the N assemblages. Assume that there are S species in the present-day assemblage (i.e., there are S tip nodes). For any tip node i, let z ik denote any measure of species importance of the ith species in the kth assemblage, i = 1, 2, …, S, k = 1, 2, …, N. The measure z ik is referred to as “abundance” for simplicity, although it can be absolute abundances, relative abundances, incidence, biomasses, cover areas or any other importance measure. Define \( {z}_{+k}={\displaystyle \sum}_{i=1}^S{z}_{ik} \) (i.e., the “+” sign in z +k denotes a sum over the tip nodes only) as the current size of the kth assemblage. Let \( {z}_{++}={\displaystyle \sum}_{k=1}^N{z}_{+k} \) be the total abundance in the present-day pooled assemblage.

Now consider the phylogenetic tree in the time interval [−T, 0], and in the pooled assemblage define B T and L i as in section “Phylogenetic Hill numbers and related measures”. We extend the definition of z ik to include all nodes and their corresponding branches by defining z ik for all i∈B T as the total abundances descended from branch i. (Here the index i can correspond to both tip-node and internal node; if i is a tip-node, then z ik represents data of the current assemblage as defined in the preceding paragraph.) As shown in Fig. 2 of Chiu et al. (2014), the diversity for each individual assemblage can be computed from the pooled tree structure, and only the node abundances vary with assemblages.

In the pooled assemblage, the node abundance for branch i (i∈B T ) is \( {z}_{i+}={\displaystyle \sum}_{k=1}^N{z}_{ik} \) with branch relative abundance z i+/z ++, so the phylogenetic gamma diversity of order q can be calculated from Eq. (4a) as

$$ {}{}^q\overline{D}_{\gamma }(T)=\frac{1}{T}{\left\{{\displaystyle \sum}_{\kern0.22em i\in {B}_T}{L}_i{\left(\frac{z_{i+}/{z}_{++}}{T}\right)}^q\right\}}^{1/\left(1-q\right)},q\ge 0,q\ne 1. $$
(7a)

The limit when q approaches unity exists and is equal to

$$ {}{}^1\overline{D}_{\gamma }(T)=\underset{q\to 1}{ \lim }{}{}^q\overline{D}_{\gamma }(T)= \exp \left[-{\displaystyle \sum}_{i\in {B}_T}\frac{L_i}{T}\left(\frac{z_{i+}}{z_{++}}\right) \log \left(\frac{z_{i+}}{z_{++}}\right)\right]. $$
(7b)

The gamma diversity is the effective number of equally abundant and equally distinct lineages all with branch length s T in the pooled assemblage.

Chiu et al. (2014) derived the following phylogenetic alpha diversity for q ≥ 0 and q ≠ 1:

$$ {}{}^q\overline{D}_{\alpha }(T)=\frac{1}{TN}{\left\{{\displaystyle \sum}_{\kern0.22em i\in {B}_T}{L}_i{\displaystyle \sum}_{k=1}^N{\left(\frac{z_{ik}/{z}_{++}}{T}\right)}^q\right\}}^{1/\left(1-q\right)} $$
(8a)

For q = 1, we have

$$ {}{}^1\overline{D}_{\alpha }(T)=\underset{q\to 1}{ \lim }{}{}^q\overline{D}_{\alpha }(T)= \exp \left[-{\displaystyle \sum}_{i\in {B}_T}{L}_i{\displaystyle \sum}_{k=1}^N\frac{z_{ik}/{z}_{++}}{T} \log \frac{z_{ik}/{z}_{++}}{T}- \log (NT)\right] $$
(8b)

The alpha diversity is interpreted as the effective number of equally abundant and equally distinct lineages all with branch length s T in an individual assemblage. When normalized measures of species importance (like relative abundance or relative biomass) are used to quantify species importance, we have z ++ = N in Eqs. (8a) and (8b). The alpha formula then reduces to a generalized mean of the local diversities with the following property: if all assemblages have the same diversity X, the alpha diversity is also X (Jost 2007). For non-normalized measures of species importance, like absolute abundance or biomass, this property does not hold. This is because when species absolute abundances are compared, for example, a three-species assemblage with absolute abundances {2, 5, 8} will not be treated as identical as another three-species assemblage with absolute abundances {200, 500, 800}. However, these two assemblages are treated as identical when only relative abundances are compared.

Chiu et al. (2014) proved that the phylogenetic gamma Hill number (Eqs. 7a and 7b) is always greater than or equal to the phylogenetic alpha Hill number (Eqs. 8a and 8b) for all q ≥ 0 regardless of species abundances and tree structures. Based on a multiplicative partitioning, the phylogenetic beta diversity is the ratio of gamma diversity to alpha diversity :

$$ {}{}^q\overline{D}_{\beta }(T)=\frac{{}{}^q\overline{D}_{\gamma }(T)}{{}{}^q\overline{D}_{\alpha }(T)},\kern0.46em q\ge 0. $$
(9)

When the N assemblages are identical in species identities and species abundances, then \( {}{}^q\overline{D}_{\beta }(T)=1 \) for any T. When the N assemblages are completely phylogenetically distinct (no shared lineages), then \( {}{}^q\overline{D}_{\beta }(T)=N, \) no matter what the diversities or tree shapes of the assemblages. The measure \( {}{}^q\overline{D}_{\beta }(T) \) thus quantifies the effective number of completely phylogenetically distinct assemblages in the interval [−T, 0]. As proved by Chiu et al. (2014), the phylogenetic beta diversity \( {}{}^q\overline{D}_{\beta }(T) \) is always between unity and N for any given alpha value, implying alpha and beta components are unrelated (or independent) for both measures, \( {}{}^q\overline{D}\;(T) \) and q PD(T); see Chao et al. (2012) for a rigorous discussion of un-relatedness and independence of two measures. When all lineages in the pooled assemblage are completely distinct (no lineages shared) in the interval [−T, 0], the phylogenetic alpha, beta and gamma Hill number s reduce to those based on ordinary Hill numbers. This includes the limiting case in which T tends to zero, so that phylogeny is ignored.

Parallel decomposition can be made for the phylogenetic diversity q PD(T), and we summarize the following relations: \( {}{}^qP{D}_{\gamma }(T)={}{}^q\overline{D}_{\gamma }(T)\times T \) and \( {}{}^qP{D}_{\alpha }(T)={}{}^q\overline{D}_{\alpha }(T)\times T. \) Under a multiplicative partitioning scheme, we have \( {}{}^qP{D}_{\beta }(T)={}{}^qP{D}_{\gamma }(T)/{}{}^qP{D}_{\alpha }(T)={}{}^q\overline{D}_{\beta }(T) \), i.e., the beta components from partitioning the phylogenetic Hill number s \( {}{}^q\overline{D}\;(T) \) and phylogenetic diversity q PD(T) are identical, implying the interpretation and the corresponding similarity or differentiation measures (in the next section) are also identical. Thus, it is sufficient to focus only on the measure \( {}{}^q\overline{D}_{\beta }(T) \), which will be referred to as the phylogenetic beta diversity or beta component for simplicity.

For each of the two measures, \( {}{}^q\overline{D}\;(T) \) and q PD(T), alpha and gamma diversities obey the replication principle . Then the beta diversity formed by taking their ratio is replication-invariant (Chiu et al. 2014). That is, when assemblages are replicated, the beta diversity does not change. Therefore, when we pool equally-distinct sub-trees, such as pooling equally-ancient subfamilies, the beta diversity is unchanged by pooling the subfamilies if all subfamilies show the same beta diversity (“consistency in aggregation”).

We now give the phylogenetic beta diversities for the special cases of q = 0, 1 and 2.

  1. (a)

    When q = 0, we have \( {}{}^0\overline{D}_{\beta }(T)={L}_{\gamma }(T)/{L}_{\alpha }(T) \), where L γ(T) denotes the total branch length of the pooled tree (the gamma component of Faith’s PD ) and L α (T) denotes the average length of individual trees (the alpha component of Faith’s PD).

  2. (b)

    When q = 1, the phylogenetic beta diversity of order 1 is

    $$ {}{}^1\overline{D}_{\beta }(T)= \exp \left[\left({H}_{P,\gamma }-{H}_{P,\alpha}\right)/T+{\displaystyle \sum}_{k=1}^N\left(\frac{z_{+k}}{z_{++}}\right) \log \left(\frac{z_{+k}}{z_{++}}\right)+ \log N\right], $$
    (10a)

    where H P,γ and H P,α denote respectively the gamma and alpha phylogenetic entropy . When the species importance measure z ik represents the ith species relative abundance in the kth current-time assemblage, then \( {z}_{+k}=1,\kern0.24em {z}_{++}=N,\kern0.24em {z}_{+k}/{z}_{++}=1/N. \) In this special case, we have \( {}{}^1\overline{D}_{\beta }(T)= \exp \left[\left({H}_{P,\gamma }-{H}_{P,\alpha}\right)/T\right] \). Thus an additive decomposition for phylogenetic entropy H P holds (Pavoine et al. 2009; Mouchet and Mouillot 2011), as for ordinary Shannon entropy (Jost 2007).

  3. (c)

    When q = 2, the phylogenetic beta diversity can be expressed as

    $$ {}{}^2\overline{D}_{\beta }(T)=\frac{{\displaystyle \sum}_{i\in {B}_T}{L}_i{\displaystyle \sum}_{k=1}^N{z}_{ik}^2}{{\displaystyle \sum_{i\in {B}_T}^N{L}_i{z}_{i+}^2}}\;. $$

In the special case of \( {z}_{+k}=1,\kern0.24em {z}_{++}=N \), this phylogenetic beta diversity of order 2 can be linked to quadratic entropy as

$$ {}{}^2\overline{D}_{\beta }(T)={\left(1-{Q}_{\gamma }/T\right)}^{-1}/{\left(1-{Q}_{\alpha }/T\right)}^{-1}, $$
(10b)

where Q γ and Q α denote respectively the gamma and alpha quadratic entropy . The above formula is also applicable to non-ultrametric trees by replacing all T with \( \overline{T} \), the mean branch length in the pooled assemblage; see Chiu et al. (2014, Appendix C) for a proof.

Normalized Phylogenetic Similarity Measures

For traditional abundance-based diversity , the most commonly used similarity measures include N-assemblage generalizations of the Jaccard et al. (1966) and Morisita-Horn (Morisita 1959) measures. The latter three measures were integrated into a class of C qN measures by Chao et al. (2008). Jost (2006, 2007), Chao et al. (2008, 2012), and Chiu et al. (2014) have demonstrated that all the above measures are monotonic transformations of beta diversity based on the ordinary Hill number s . This is an advantage of using the framework of Hill numbers: a direct link exists between diversity and similarity (or differentiation) among assemblages.

Chiu et al. (2014) extended this framework by proposing four classes of similarity (or differentiation) measures that are monotonic functions of phylogenetic beta diversity . The basic idea is that the phylogenetic beta diversity , a ratio of gamma and alpha phylogenetic Hill number s , is independent of alpha and measures the pure differentiation among assemblages. The phylogenetic beta component always lies in the range [1, N] for any measures of species importance and all orders q ≥ 0. Since the range depends on N, the phylogenetic beta diversity cannot be used to compare phylogenetic differentiation among assemblages across multiple regions with different numbers of assemblages. To remove the dependence on N, several transformations can be used to transform the phylogenetic beta component onto [0, 1] to measure local overlap, regional overlap, homogeneity and turnover. We give a summary of these four transformations below and tabulate formulas and the relationship with previous measures in Table 1 for the two most important classes. The formulas for the special cases for q = 0, 1 and 2 are also displayed there.

  1. 1.

    A class of branch overlap measures from a local perspective:

    $$ {\overline{C}}_{qN}(T)=\frac{N^{1-q}-{\left[{}{}^q\overline{D}_{\beta }(T)\right]}^{1-q}}{N^{1-q}-1}. $$
    (11a)

    This gives the effective average proportion of shared branches in an individual assemblage. This class of similarity measures extends the C qN overlap measure derived in Chao et al. (2008) to a phylogenetic version. The corresponding differentiation measure \( 1-{\overline{C}}_{qN}(T) \) quantifies the effective average proportion of non-shared branches in an individual assemblage.

    1. (1a)

      For q = 0, this similarity measure is referred to as the “phylo-Sørensen ” N-assemblage overlap measure because for N = 2, it reduces to the measure PhyloSør (phylo-Sørensen) developed by Bryant et al. (2008) and Ferrier et al. (2007).

    2. (1b)

      For q = 1, this measure \( {\overline{C}}_{1N}(T) \) is called the “phylo-Horn ” N-assemblage overlap measure because it extends Horn (1966) two-assemblage measure to incorporate phylogenies for N assemblages.

    3. (1c)

      For q = 2, \( {\overline{C}}_{2N}(T) \) is called the “phylo-Morisita-Horn ” N-assemblage similarity measure because it extends Morisita-Horn measure (Morisita 1959) to incorporate phylogenies for N assemblages. The differentiation measure \( 1-{\overline{C}}_{2N}(T) \) when the species importance measure is relative abundances reduces to the measure proposed by de Bello et al. (2010). However, their measure is valid only for ultrametric trees (p. 7 of de Bello et al. 2010). Here, the measure can be applied to non-ultrametric trees to obtain

    $$ 1-{\overline{C}}_{2N}\left(\overline{T}\right)=\frac{1-\left[1/{}{}^2\overline{D}_{\beta}\left(\overline{T}\right)\right]}{1-1/N}=\frac{Q_{\gamma }-{Q}_{\alpha }}{\left(1-1/N\right)\left(\overline{T}-{Q}_{\alpha}\right)}, $$
    (11b)

    where Q γ and Q α are respectively gamma and alpha quadratic entropy , and \( \overline{T} \) is the mean branch length in the pooled assemblage. A general form for any species importance measure (including absolute abundances) is

    $$ 1-{\overline{C}}_{2N}\left(\overline{T}\right)=\frac{{\displaystyle \sum}_{i\in {B}_{\overline{T}}}{L}_i{\displaystyle \sum}_{m>k}^N{\left({z}_{im}-{z}_{ik}\right)}^2}{\left(N-1\right){\displaystyle \sum}_{i\in {B}_{\overline{T}}}{L}_i{\displaystyle \sum}_{k=1}^N{z}_{ik}^2}\;. $$
    (11c)

    The above expression shows that the similarity index \( {\overline{C}}_{2N}\left(\overline{T}\right) \), as in all other abundance-sensitive similarity measures, is unity if and only if \( {z}_{ij}={z}_{ik} \) (i.e., species importance measures are identical for any node i in the branch set and for any two assemblages j and k). This reveals that the similarity index \( {\overline{C}}_{2N}\left(\overline{T}\right) \) quantifies the node-by-node resemblance among the N abundance sets {z ik ; i∈B T̅}, k = 1, 2, …, N from a local perspective. See Fig. 2 of Chiu et al. (2014) for a simple example of the framework.

  2. 2.

    A class of branch overlap measures from a regional perspective:

    $$ {\overline{U}}_{qN}(T)=\frac{{\left[1/{}{}^q\overline{D}_{\beta }(T)\right]}^{1-q}-{\left(1/N\right)}^{1-q}}{1-{\left(1/N\right)}^{1-q}} $$
    (12a)

    This class of measures quantifies the effective proportion of shared branches in the pooled assemblage. The corresponding differentiation measure \( 1-{\overline{U}}_{qN}(T) \) quantifies the effective average proportion of non-shared branches in the pooled assemblage.

    1. (2a)

      For q = 0, this measure is called the “phylo-Jaccard ” N-assemblage measure because for N = 2 the measure \( 1-{\overline{U}}_{02}(T) \) reduces to the Jaccard-type UniFrac measure developed by Lozupone and Knight (2005) and the PD-dissimilarity measure developed by Faith et al. (2009).

    2. (2b)

      For q = 1, this measure is identical to the “phylo-Horn ” N-assemblage overlap measure \( {\overline{C}}_{1N}(T) \); see Table 1.

    3. (2c)

      For q = 2, we refer to the measure U̅ 2N (T) as a “phylo-regional-overlap ” measure. When the species importance measure is relative abundance, we have the following formula for non-ultrametric trees:

      $$ 1-{\overline{U}}_{2N}\left(\overline{T}\right)=\frac{N-{}{}^2\overline{D}_{\beta}\left(\overline{T}\right)}{N-1}=\frac{Q_{\gamma }-{Q}_{\alpha }}{\left(N-1\right)\left(\overline{T}-{Q}_{\gamma}\right)}, $$

      where \( \overline{T} \) denotes the mean branch length in the pooled assemblage. A general form for any species importance measure (including absolute abundances) is

      $$ 1-{\overline{U}}_{2N}\left(\overline{T}\right)=\frac{{\displaystyle \sum}_{i\in {B}_{\overline{T}}}{L}_i{\displaystyle \sum}_{m>k}^N{\left({z}_{im}-{z}_{ik}\right)}^2}{\left(N-1\right){\displaystyle \sum}_{i\in {B}_{\overline{T}}}{L}_i{z}_{i+}^2}\;. $$

    The numerator is the same as that in \( {\overline{C}}_{2N}\left(\overline{T}\right) \), revealing that the similarity index \( {\overline{U}}_{2N}\left(\overline{T}\right) \) also quantifies the node-by-node resemblance among the N abundance sets {z ik ; i∈B T̅ }, k = 1, 2, …, N; but here the denominator (for the purpose of normalization) is different and takes a regional perspective.

  3. 3.

    A class of phylogenetic homogeneity measures

    $$ {\overline{S}}_{qN}(T)=\frac{1/{}{}^q\overline{D}_{\beta }(T)-1/N}{1-1/N}. $$
    (12b)

    This measure is linear in the proportion of regional phylogenetic diversity contained in a typical assemblage.

    1. (3a)

      For q = 0, it reduces to the “phylo-Jaccard ” measure U̅ 0N (T), i.e., \( {\overline{S}}_{0N}(T)={\overline{U}}_{0N}(T) \).

    2. (3b)

      For q = 1, this measure does not reduce to the “phylo-Horn ” overlap measure.

    3. (3c)

      For q = 2, this measure is identical to \( {\overline{C}}_{2N}(T) \), the “phylo-Morisita-Horn ” similarity measure, i.e., \( {\overline{S}}_{2N}(T)={\overline{C}}_{2N}(T). \)

  4. 4.

    A class of measures of the complement of “phylogenetic turnover rate”:

    $$ {\overline{V}}_{qN}(T)=\frac{N-{}{}^q\overline{D}_{\beta }(T)}{N-1}=1-\frac{{}{}^q\overline{D}_{\beta }(T)-1}{N-1}. $$
    (12c)

    This measure in linear in the phylogenetic beta diversity and the corresponding differentiation measure \( \left[{}{}^q\overline{D}_{\beta }(T)-1\right]/\left(N-1\right) \) quantifies the relative branch turnover rate per assemblage.

    1. (4a)

      For q = 0, the measure \( {\overline{V}}_{0N}(T) \) is identical to the “phylo-Sørensen ” measure, i.e., \( {\overline{V}}_{0N}(T)={\overline{C}}_{0N}(T) \).

    2. (4b)

      For q = 1, this measure does not reduce to the “phylo-Horn ” overlap measure.

    3. (4c)

      For q = 2, this measure is identical to U̅ 2N (T), the “phylo-regional-overlap ” measure. That is, \( {\overline{V}}_{2N}(T)={\overline{U}}_{2N}(T) \).

As with the phylogenetic diversity measures, all the above similarity or differentiation measures are functions of two parameters: the sensitivity parameter q and the time perspective T. Thus, for each measure, we suggest using the two types of profiles described in section “Phylogenetic Hill numbers and related measures” for the two major similarity measures \( {\overline{C}}_{qN}(T) \) and U̅ qN (T) (or their complements) to convey complete information about the similarity or differentiation of a set of assemblages. An example showing the two types of profiles is given in section “An example”.

The lineage excess \( {}{}^q\overline{D}_{\gamma }(T)-{}{}^q\overline{D}_{\alpha }(T) \) and the phylogenetic diversity excess \( {}{}^qP{D}_{\gamma }(T)-{}{}^qP{D}_{\alpha }(T) \) can be interpreted as the effective number of regional lineages (or regional phylogenetic diversity) not contained in a typical local assemblage. However, they cannot be directly applied to compare the similarity or differentiation across multiple regions because both depend not only on the number of assemblages, but also on their corresponding alpha diversity . Following Chao et al. (2012) and Chiu et al. (2014, their Appendix D) proved that we can eliminate these dependences by using an appropriate normalization. After proper normalizations, the two measures lead to the same four classes of normalized similarity and differentiation measures as those obtained from the phylogenetic beta diversity . This is another advantage of using the framework of phylogenetic Hill number s . That is, a consensus can be achieved on phylogenetic similarity and differentiation measures, including N-assemblage phylogenetic generalizations of the classic Jaccard, Sørensen, Horn and Morisita-Horn measures, regardless of whether one prefers multiplicative or additive decompositions.

Table 1 Two major classes of phylogenetic similarity measures based on the transformations of phylogenetic beta diversity when species importance measures are incidences (for q = 0), relative abundances or absolute abundance (for q = 1 and 2). The corresponding differentiation measures are the one-complements of the similarity measures. When all lineages are completely distinct (this includes \( T\to 0 \), ignoring phylogeny), these phylogenetic measures reduce to the corresponding non-phylogenetic versions. All measures can also be applied to non-ultrametric trees if \( \overline{T} \) is substituted for T
Full size table

An Example

We apply the phylogenetic diversity measures and similarity (or differentiation) measures considered in this chapter to a real conservation biology case discussed by Pavoine et al. (2009), a heavily-fished assemblage of 52 rockfish species of the genus Sebastes collected for 20 years over three decades (1980–1986, 1993–1994, 1996, 1998–2007) from the Southern California Bight, USA. The phylogenetic tree for these 52 species was obtained from Hyde and Vetter (2007); see Fig. 3a. The age of the root for these species is around 7.9 million years (Myr).

Fig. 3
figure 3figure 3

(a) The phylogenetic tree of 52 rockfish species of the genus Sebastes (Hyde and Vetter 2007) and the species relative abundances in three assemblages: 1980s (Decade I), 1990s (Decade II) and 2000s (Decade III). The age of the root is T = 7.9 Myr. (b) A sub-tree contains only the dominant species (those with relative abundance >8 % in at least one assemblage), and these species are marked in figure (a). All six species are shared by the three assemblages and four of them diverged around 6 Myr ago (i.e., they have been in isolated lineages for 6 Myr) (See Pavoine et al. (2009) for details)

Full size image

We separate the data into three decades: 1980s, 1990s and 2000s, which will be referred to as Assemblages (and Decades) I, II and III respectively. Within each decade’s assemblage, species abundances are pooled. The species relative abundances for the three assemblages are shown in Fig. 3a. There were 48, 44 and 39 species in Decades I, II and III, respectively. (Note that each data point here is a mean of many years’ observations.) A sub-tree containing only the six dominant species (those with relative abundance >8 % in at least one assemblage) is shown in Fig. 3b. All six species are shared in the three assemblages and four of them have been in isolated lineages for 6 Myr.

As suggested in section “Phylogenetic Hill numbers and related measures”, we present for each assemblage two types of profiles. In Fig. 4a, we plot the measure \( {}{}^q\overline{D}\;(T) \) as a function of order q, 0 ≤ q ≤ 3, for two selected values of temporal perspectives: T = 0 (phylogeny is ignored) and T = 7.9 Myr (whole phylogenetic tree in Fig. 3a is considered). In Fig. 4b, we plot \( {}{}^q\overline{D}\;(T) \) and q PD(T) as functions of T separately for q = 0, 1, and 2 for 0 ≤ T ≤ 10.

Fig. 4
figure 4figure 4

(a) The first type of diversity profile plots \( {}{}^q\overline{D}\;(T) \) as a function of order q, 0 ≤ q ≤ 3, for two selected values of temporal perspectives: T = 0 (non-phylogenetic case) and T = 7.9 Myr (the age of the root of the phylogenetic tree in Fig. 3a). (b) The second type of diversity profile plots \( {}{}^q\overline{D}\;(T) \) (phylogenetic Hill number ) and q PD(T) (phylogenetic diversity) as functions of T, 0 ≤ T ≤ 10, separately for q = 0, 1 and 2

Full size image

Based on our phylogenetic diversity measures, all profiles in Fig. 4 reveal that the diversity in the most recent decade (Decade III) is the lowest among the three decades in the rockfish assemblage. This implies an appreciable loss of species (as shown in the first type of profile for T = 0), loss of lineages (as shown in the second type of profile based on the measure \( {}{}^q\overline{D}\;(T) \)), and loss of evolutionary history (as shown in the second type of profiles based on the measure q PD(T)) over the three decades.

When species/lineage abundances are discounted (q = 0 in the left panels of Fig. 4b), both lineage richness (based on the measure \( {}{}^0\overline{D}\;(T) \)) and total branch length s (based on the measure 0 PD(T), i.e., Faith’s PD ) exhibit the expected ordering: Decade I > Decade II > Decade III. When species/lineage abundances are counted (i.e. q = 1 and 2 in Fig. 4b), the profiles for Decades I and II cross because the assemblage of Decade II has more even abundant species than that of Decade I (see the first type of profiles for T = 0 and Fig. 3a, b). Note that if the time-depth is greater than 6 Myr (including the age of the root), then all the abundance-sensitive phylogenetic measures for the three assemblages are very close because most of the dominant species began to diverge around 6 Myr (Fig. 3b). This also explains the closeness of the three profiles in the first type of profile for T = 7.9 Myr (the right panel in Fig. 4a).

To illustrate the phylogenetic differentiation among assemblages, we focus on measuring the phylogenetic differentiation between any two decades for three pairs (i.e. Decades I vs. II, Decades I vs. III and Decades II vs. III). To see how the phylogenetic differentiation measures vary with the time perspective q and with the order T, we show two types of profiles for each of the two differentiation measures \( 1-{\overline{C}}_{qN}(T) \) and \( 1-{\overline{U}}_{qN}(T) \) in Figs. 5 and 6. In Fig. 5a, we present the first type of profile that plots the measure \( 1-{\overline{C}}_{qN}(T) \) as a function of q where q is in the range [0, 3] for two time perspectives: T = 0 (non-phylogenetic case) and T = 7.9 Myr (the age of the root node). In Fig. 5b, the same type of differentiation profile is shown for the other measure \( 1-{\overline{U}}_{qN}(T) \). Then in Fig. 6a, b, we present the second type of profile that shows the two measures as a function of temporal perspective T, 0 ≤ T ≤ 10, for q = 0, 1 and 2 separately.

Based on the two phylogenetic differentiation measures, all profiles in Figs. 5 and 6 show consistent patterns. When species/lineages abundances are discounted (q = 0), the differences among the differentiation measures of the three pairs of assemblages are not appreciable, as shown in the two left panels in Fig. 6 and in the initial point in each of profiles in Fig. 5. When species/lineages abundances are counted (q > 0), the compositional differentiation between Decades I vs. II is generally close to that between Decades I vs. III, and the differentiation between two recent decades (Decades II vs. III) is much lower than any of the other two pairs. This implies that the composition of species/lineage abundances has changed after 1990. Examining the relative abundances for those dominant species listed in Fig. 3b, we see that the most abundant species S. paucispinis (23 %) in Decade I became less abundant in both Decade II (9 %) and Decade III (11 %); the second most abundant species S. mystinus (11 %) in Decade I became quite rare in both Decade II (4 %) and Decade III (5 %). Also, the species S. miniatus in Decade I was rare, but it became the most dominant species in both Decade II (12 %) and Decade III (25 %). These compositional changes for dominant species help explain the above findings.

As the time perspective T becomes large, more dominant shared lineages are added to the two assemblages, implying the differentiation between any two assemblages should exhibit a non-increasing trend as T is increased. Our two differentiation measures for q > 0 in Fig. 6 show the expected decreasing trend, and the decline rates differ for q = 1 and q = 2. Based on Fig. 3b, we see that most of the dominant and isolated species began to diverge around 6 Myr ago. Thus, the two differentiation profiles for q = 1 and 2 start to decrease sharply around 6 Myr especially for order q = 2. Since the node abundances near roots (where the differentiation values are near zero) are relatively high and dominant in the whole tree, all values of the phylogenetic differentiation measures for T = 7.9 Myr (the first type of profile for T = 7.9 Myr in the right panel of Fig. 5) are substantially lower than their corresponding non-phylogenetic differentiation measure by comparing two figures (T = 0 and T = 7.9 Myr) in each row of Fig. 5. The two types of profiles (in Fig. 5a, b, and 6a, b) demonstrate that the two differentiation measures \( 1-{\overline{C}}_{qN}(T) \) and \( 1-{\overline{U}}_{qN}(T) \) can incorporate the differences in both tree structure and lineage abundances.

In summary, our phylogenetic diversity measures have shown an appreciable loss of species, lineage and evolutionary history in rockfish assemblage over time due to fishing pressure, and our phylogenetic differentiation measures show a pronounced change of species/lineages composition after 1990.

Fig. 5
figure 5figure 5

(a) Differentiation profiles of the measure \( 1-{\overline{C}}_{qN}(T) \) and (b) of the measure \( 1-{\overline{U}}_{qN}(T) \) as a function of order q, 0 ≤ q ≤ 3, for two specific time perspectives: T = 0 (left panels, corresponding to non-phylogenetic differentiation profiles), and T = 7.9 Myr (right panels, corresponding to the profiles for the age of the root node of the pooled phylogenetic tree in Fig. 3a) for three pairs of assemblages (I vs. II, I vs. III, and II vs. III)

Full size image
Fig. 6
figure 6figure 6

(a) Differentiation profiles of the measure \( 1-{\overline{C}}_{qN}(T) \) and (b) of the measure \( 1-{\overline{U}}_{qN}(T) \), as a function of the time perspective (or time-depth) T, 0 ≤ T ≤ 10, for q = 0 (left panel), q = 1 (middle panel), and q = 2 (right panel) for three pairs of assemblages. All measures are computed for the interval [−T, 0], where T varies from 0 to 10

Full size image

Conclusion

  1. 1.

    To quantify phylogenetic diversity of an assemblage, we suggest using two measures: (i) the phylogenetic Hill number \( {}{}^q\overline{D}\;(T) \) (Eqs. 4a and 4b) which measures the “the effective number of equally abundant and equally distinct lineages all with branch length s T”, and (ii) the phylogenetic or branch diversity q PD(T) (Eqs. 5a and 5b) which measures the “effective total lineage-length”, i.e., the total evolutionary history on an assemblage since time T. These two measures depend explicitly on two parameters, the abundance sensitivity parameter q and the time perspective (or time-depth) parameter T.

  2. 2.

    Two types of diversity profiles are recommended for considering species/branch abundances and phylogenetic information: (i) The first type of diversity profile is obtained by plotting q PD(T) or \( {}{}^q\overline{D}\;(T) \) as a function of order q, for some selected values of temporal perspective T including T = 0 (i.e., the non-phylogenetic profile based on the ordinary Hill number s ), and T = the age of the most basal node. See the upper panels of Fig. 4 for an example. It would be also informative to include T = the age of the divergence between the group under study and the rest of the tree. (ii) The second type of diversity profile is obtained by plotting q PD(T) and \( {}{}^q\overline{D}\;(T) \) as functions of T separately for q = 0, 1, and 2; see the middle and lower panels of Fig. 4 for an example. The second type of profile shows the effect of time-depth or evolution change on our diversity measures.

  3. 3.

    When there are multiple assemblages, the phylogenetic gamma Hill number is the effective number of equally abundant and equally distinct lineages in the pooled assemblage; the phylogenetic alpha Hill number is the effective number of equally abundant and equally distinct lineages per assemblage. Thus the phylogenetic beta Hill number, as the ratio of gamma and beta, is interpreted as “the number of phylogenetically completely distinct assemblages”. In this case, alpha and beta are unrelated (or independent). The difference of phylogenetic gamma and alpha Hill numbers is lineage excess, which is dependent on both alpha and gamma. The phylogenetic beta Hill number and lineage excess lead to the same classes of similarity and differentiation measures, listed in section “Normalized phylogenetic similarity measures”. See Table 1 for the two major classes of phylogenetic overlap measures, \( {\overline{C}}_{qN}(T) \) from a local perspective and U̅ qN (T) from a regional perspective.

  4. 4.

    To assess the phylogenetic resemblance or differentiation among assemblages, two types of similarity or differentiation profiles as those in Point 2 are suggested for the two major classes of measures, \( {\overline{C}}_{qN}(T) \) and U̅ qN (T) (Table 1); see Figs. 5 and 6 for examples.