Abstract
The PD phylogenetic diversity measure provides a measure of biodiversity that reflects variety at the level of features, among species or other taxa. PD is based on a simple model which assumes that shared ancestry explains shared features. PD provides a family of calculations that operate as if we were directly counting up features of taxa. PD-dissimilarity or phylogenetic beta diversity compares the branches/features represented by two different areas. We also can consider a companion model, which shifts the focus to shared habitat/environment among taxa as the explanation of shared features, including those features not explained by shared ancestry and PD. That model means that PD-dissimilarities, among sampled and unsampled sites, can be predicted using a regression method applied to distances in an environmental-gradients space. However, PD-based conservation planning requires more than the dissimilarities among all sites, in order to make decisions informed by gains and losses of branches/features. The companion model also suggests how to transform dissimilarities to provide these needed estimates. This ED (“Environmental Diversity”) method out-performs other suggested strategies for analysis of dissimilarities, including the Ferrier et al. method and the Arponen et al. method. The global biodiversity observation network (GEO BON) can use the ED method for inferences of biodiversity change that include loss of phylogenetic diversity.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
- Environmental diversity
- Phylogenetic beta diversity
- ED complementarity
- Conservation planning
- Biodiversity monitoring
Introduction
This book addresses important concepts, methods, and applications related to the role of evolutionary history in biodiversity conservation. In the chapter “The PD Phylogenetic Diversity Framework: Linking Evolutionary History to Feature Diversity for Biodiversity Conservation ” (Faith 2015a), I reviewed the reasons why we want to conserve evolutionary history. An important rationale is that the tree of life is a storehouse of variation among taxa, and so provides possible future benefits for humans (for discussion, see Faith et al. 2010). I also reviewed the justifications for a specific biodiversity measure. It interprets the degree of representation of evolutionary history as a phylogenetic measure of biodiversity, or “phylogenetic diversity ”. This measure of phylogenetic diversity, called “PD” (Faith 1992a, b) is justified as a useful biodiversity measure through its link to “feature diversity”. Feature diversity represents biodiversity “option values” – the term we use to refer to all those potential future benefits for humans – and so is well-justified as a target for biodiversity conservation. Forest et al. (2007) provide a good exemplar study, illustrating how PD links to feature diversity and to food, medicine, and other benefits to humans.
Faith (2002) summarised the link between evolutionary history, PD , and features as follows: “representation of “evolutionary history” (Faith 1994) encompassing processes of cladogenesis and anagenesis is assumed to provide representation of the feature diversity of organisms. Specifically, the phylogenetic diversity (PD) measure estimates the relative feature diversity of any nominated set of species by the sum of the lengths of all those phylogenetic branches spanned by the set…”
The calculation of the PD for a given subset of species (sampled from a phylogenetic tree) is quite simple. It is given by the minimum total length of all the phylogenetic branches required to connect all those species on the tree. However, calculation of PD is attempting something that is not all that simple – an inference of the relative feature diversity of that subset of species. The basis for this inference is an evolutionary model in which branch length s reflect evolutionary changes, and shared ancestry accounts for shared features (Faith 1992a, b). The model implies that PD, in effect, counts-up the relative number of features represented by a given subset of species (or other taxa, including populations within a species); any subset of species that has greater PD will be expected to have greater feature diversity.
In chapter “The PD Phylogenetic Diversity Framework: Linking Evolutionary History to Feature Diversity for Biodiversity Conservation ”, I described another important implication of the link to feature diversity : PD provides, not one single measure, but a set of calculations interpretable at the level of features of taxa. This helps guide the assessment of the phylogenetic diversity gains and losses from changing probabilities of extinction of species (or other taxa). This PD “calculus” also can help with the conservation problem addressed in this paper: assessing PD gains and losses when we gain or lose geographic areas. PD has long been integrated into conservation planning for areas (Walker and Faith 1994). However, the work so far has largely ignored the problem of geographic knowledge gaps; we do not know about the phylogenetic diversity represented in every area in a given region. Consequently, for conservation planning, we have to estimate or model these missing quantities, using spatial models incorporating predictive environmental variables.
One pathway for such predictions can take advantage of a part of the PD calculus called “PD-dissimilarities ” or “phylogenetic beta diversity ” (Fig. 1a; see also Lozupone and Knight 2005; Ferrier et al. 2007; Nipperess et al. 2010; Swenson 2011). PD-dissimilarities can be interpreted as compositional dissimilarities, based on the branches/features represented at the different sites (a site represents all branches that are ancestral to any of its member species). These calculations are “community -based” approaches in that they compare areas based on the set of elements (the community) found in each area . We can think of the standard compositional dissimilarity measures conventionally applied at the species level as simply re-caste at the level of features, through the PD model (Fig. 1a; for discussion, see Faith 2013).
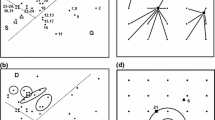
(a) A hypothetical phylogenetic tree with 5 taxa. Along the top, the presence of the taxa in two sites, j and k, is shown by + marks. The dashed-line branches indicate features only represented in j; hatched branches indicate features only represented in k; bold branches indicate features represented in both; the thin branch indicates features in neither. The presence absence version of Bray-Curtis type PD -dissimilarity between sites j and k counts the number of features in j, not k (length of dashed branches) plus the number of features in k, not j (length of hatched branches), divided by the sum of the total number of features found in each (length of dashed plus length of bold branches, plus length of hatched plus length of bold branches). Other PD-dissimilarity measures combine these counts in other ways. (b) A hypothetical environmental gradient (hollow-line) with positions of sites, j, k, and l. Suppose that positions of sites along this gradient reflect their features. Sites with a given feature are found in a corresponding part of the gradient. This clumping is called a “unimodal” response. Above the gradient is the hypothetical unimodal distribution of the branches and corresponding features/branches from 1a. Under the unimodal response model, the features in both j and k, for example, form the bold line segment. This unimodal relationship means that the Bray-Curtis type PD-dissimilarity has the most robust link to distances along environmental gradients (or in environmental space; for discussion, see Faith et al. 1987). For further information, also see Faith et al. (2009)
Spatial predictions can use a form of regression in which PD -dissimilarities between sites are explained and predicted by the known environmental distances between sites. Thus, we can predict the PD-dissimilarity between two un-sampled sites, given their environmental difference. Generalized dissimilarity modelling (GDM; Ferrier 2002; Ferrier et al. 2004, 2007; see also Faith and Ferrier 2002), an extension of matrix regression, is useful for these predictions. GDM realistically allows for a very general monotonic, curvilinear, relationship between increasing environmental distance and compositional dissimilarity. It is also robust in allowing for variation in the rate of compositional change at different positions along environmental gradients. GDM was developed for species-level dissimilarities, but has been extended to the prediction of PD-dissimilarities (Ferrier et al. 2007; Faith et al. 2009; Rosauer et al. 2013).
There are several ways to calculate a PD -dissimilarity (see Fig. 1a, b). The choice of the PD-dissimilarity measure for such analyses can be guided by another critical model, which makes additional assumptions about how features link to environmental variables. To understand the nature of this model, it is important to note that Faith (1992a, b; see also Faith 1996) was careful to point out that PD’s shared-ancestry/shared-features model provides a general prediction about feature diversity , but naturally does not apply to all possible features. This early work proposed that a companion model also can account for shared features, including those that are not explained by shared ancestry (e.g. those features that are convergent, arising independently on the phylogenetic tree). Here, a pattern among species describing shared habitat or environment explains shared branches/features (Fig. 1b; Faith 1989, 1996, 2015b; Faith et al. 2009). Figure 1b illustrates how shared habitat or environment explains shared features: the sites sharing particular branches or features form clumps or clusters in the environmental space (see also Fig. 2). I will refer to this as unimodal response (analogous the well-known unimodal response of species to environmental gradients; see e.g. Faith et al. 1987). This unimodal relationship (Fig. 1b) means that the Bray-Curtis type PD-dissimilarity has the most robust link to distances along environmental gradients (or in environmental space; for discussion, see Faith et al. 1987).
Bray-Curtis type PD -dissimilarities can be used in robust ordination methods to recover key gradients. A re-drawing of the gradient space from Rintala et al. (2008; see also Faith et al. 2009) for microbial communities in house dust and a microbial phylogenetic tree. Dots versus squares correspond to samples from two different buildings (for details of sampling see Rintala et al.). Arrows at the right side indicate major gradients revealed by the ordination. A sample locality represents the branch corresponding to a given family if the locality has one or more descendants of that branch. The two-dimensional space shows unimodal response for four branches (Acidaminococcaceae, Aerococcaceae, Enterobacteriaceae, Acetobacteraceae). For further information, see Faith et al. (2009)
This simple model arguably deserves to make a greater contribution towards our understanding of biodiversity methods. For example, an under-appreciation of this companion model has meant that some workers (Kelly et al. 2014) still naively characterise PD as intended to account for all features, including those convergently derived. Similarly, the role of this model in explaining habitat-driven feature diversity has been neglected in the development of functional trait diversity measures (discussed in Faith 2015b). In this paper, I discuss another good reason to consider this shared-habitat/shared-features model: it can fill a critical gap in our attempts to effectively use PD-dissimilarities for biodiversity assessments.
We can predict the Bray-Curtis type PD -dissimilarities from environmental distances using a GDM regression. However, this is a mixed blessing. We produce PD-dissimilarities for all pairs of sites, but a difficulty is that these dissimilarities do not directly tell us what we want to know for conservation planning – the total phylogenetic diversity represented by a given subset of areas, or the gain or loss in PD if an site is gained or lost. To fill this gap, we need to convert the pairwise dissimilarities into inferences about PD representation and/or gains and losses. I will show how the shared-habitat/shared-features model can guide this analysis.
While there are several natural candidate approaches for taking this extra analysis step (each extends methods applied to species-level dissimilarities ), surprisingly, there is no established, accepted method. One proposed approach, based on the unimodal response model, is the ED (“environmental diversity ”) method (defined below; see also Faith and Walker 1996a, b, c), which has for some time been linked to GDM and species-level dissimilarities (Faith and Ferrier 2002). Faith et al. (2009) proposed the application of ED to the predicted dissimilarities from phylogenetic GDM analyses, but there are no worked examples exploring this approach. Another attractive method, linked strongly to the GDM approach, is the Ferrier et al. (2004) index. This measure modifies the ED approach and has been applied for species-level dissimilarities. A closely related method is that of Arponen et al. (2008). Both of these have commonalities with ED, but the similarities and differences – and the strengths and weaknesses – among these alternative candidate measures has not been explored and documented (for related discussion, see Ferrier and Drielsma 2010).
Given this fundamental gap in building the complete toolbox of PD calculations for conservation, and given the lack of synthesis among candidate methods, this chapter will proceed as follows. I first show how the same model of shared-environment/shared-features that justifies the choice among possible PD-dissimilarity measures (Fig. 1a, b), also justifies the choice of the ED method. I then present a sample application of ED to PD-dissimilarities . I also present a simple graphical description of ED in the one dimensional case, which clarifies how ED estimates representation and gains and losses. I then use this graphical representation to reveal key properties of the alternative methods, suggesting critical weaknesses of the Ferrier et al. and Arponen et al. methods. I finish on a positive note, pointing to future work, including expanding the range of calculations useful for conservation assessment based on ED.
How the ED Method Converts PD -Dissimilarities to Estimates of Gains and Losses
“ED” refers to a specific family of “environmental diversity ” calculations (Faith and Walker 1996a, b, c; Faith 2003; Faith et al. 2003, 2004). ED typically uses an environmental gradients space, derived using species compositional dissimilarities and ordination methods (Faith and Walker 1996a, b, c). ED has been implemented as a surrogates strategy in biodiversity conservation-planning software that evaluates nominated sets of localities or finds best sites to add to an existing set. For example, ED provided the first integration of ‘costs’ into regional biodiversity planning based on comparing gains or ‘ED-complementarity’ values to marginal costs to facilitate trade-offs, balancing biodiversity conservation and other needs of society (Faith et al. 1996).
In order to understand the applicability of ED to PD -dissimilarities , we have to consider ED’s assumptions and then examine a simple example analysis. I referred above to unimodal response (Fig. 1b) and the shared-habitat/shared-features companion model to PD’s shared-ancestry/shared-features model. ED explicitly builds on this general unimodal response of species (or other elements) to environmental gradients (for background, see Austin 1985; Faith et al. 1987). ED’s environmental space typically is derived using compositional dissimilarities (including those estimated GDM) and ordination methods (for review, see Faith et al. 2004). The dissimilarities, the ordination methods and GDM all are relatively robust approaches under a general model of unimodal responses to environmental gradients (Fig. 1b; Faith et al. 1987; Faith and Walker 1996a; Ferrier et al. 2009).
The unimodal response model not only guides the inference of an environmental space using ordination methods (Faith et al. 1987), but also defines how ED methods should effectively sample that environmental space in order to capture biodiversity . ED is based on the idea that many different species (or other elements of biodiversity) respond to similar environmental gradients, and exhibit a general unimodal response at different positions along those gradients (Fig.1b). It follows that effective representation of these gradients (say, by a proposed set of protected areas) should deliver good representation of the various species or phylogenetic branches.
The assumption of a general unimodal response model directly leads to the use of p-median (and related) criteria for ED’s estimation of the number of species represented by a given set of localities in the environmental space or ordination. A p-median criterion is based on a sum of the distances in an environmental space. Each distance in this summation is that between a hypothetical point (‘demand point’) in the space and its nearest site (among all sites in some selected subset). The selected sites, for example, might be nominated protected-area localities. ED is defined based on this calculation. The ‘continuous’ version of ED refers to the case where the demand points are hypothetical points distributed uniformly throughout the continuous environmental space. Faith and Walker (1994, 1996a) demonstrated that, under a simple unimodal response model, species representation will be maximised by a selected set of sites if and only if it satisfies this continuous p-median criterion. Note that the ED score, because it counts un-represented species based on a sum of distances, is numerically small when the number of represented species is large (see example calculations below and in Faith and Walker 1996a). The ED surrogates approach therefore provides a rationale for interpreting high environmental diversity for a set of localities as implying high biodiversity for the set (see Beier and Albuquerque 2015).
I referred above to the p-median and related criteria. ED is not defined by any a priori choice of the p-median criterion . Instead, the various ED calculations emerge from the assumption of an underlying unimodal response model. In the simple case, unimodal response implies that features are effectively counted up when we apply calculations linked to the p-median; in other cases, the model implies calculations that are modifications of the simple p-median. Simple ED variants include weighting of demand points when species richness varies over the space (Faith and Walker 1996a; Faith et al. 2004), and creating an extended environmental space (‘extended polytope’; Faith and Walker 1994, 1996a, b; Faith et al. 2004; see also Hortal et al. 2009). These options modify the parameters used in calculating the p-median. In a later section, I will consider an ED variant that departs from p-median in order to capture expected diversity or persistence.
When extended to features and branches from a phylogeny, the unimodal response model supports an expectation that ED is compatible with Bray-Curtis type PD -dissimilarities . Does this unimodal model (as idealised in Fig. 1b) apply when the elements are branches or features? Certainly, this relationship can be expected, given that PD-dissimilarity operates as if it is a standard Bray Curtis dissimilarity, but applied to features, not species. The robust ordination of such dissimilarities should produce general unimodal responses, as in the species-level case (Faith et al. 1987).
PD and PD-dissimilarities are commonly applied to molecular phylogenetic trees and microbial community data; here, PD analyses overcome the typical absence of defined microbial species. However, there has not been any clear model linking branches to gradients in such studies. Faith et al. (2009) presented an example documenting unimodal response of branches based on a gradient space for microbial communities, sampled in house dust (Fig. 2; Rintala et al. 2008). In Fig. 2, arrows at the right side indicate major gradients revealed by the ordination of the PD-dissimilarities. The solid dots in the space indicate different communities or sample localities. A sample locality represents the branch corresponding to a given family if the locality has one or more descendants of that branch in the phylogeny (for details see Rintala et al. 2008; Faith et al. 2009).
For the ordination space of Rintala et al., Faith et al. (2009) showed that all but 3 of the 56 phylogenetic branches (corresponding to identified families) have a clear unimodal response in the gradients space. Here, a response was recorded as unimodal only if a simple shape could enclose all sample sites representing the given branch (and not include any other sites). This unimodal response for phylogenetic features or branches is a critical property: it provides theoretical justification for GDM on PD -dissimilarities and it accords with the assumptions of the ED (environmental diversity ) method.
Extending this example, I now will illustrate the application of the ED method to the PD -based environmental space of Rintala et al. (Fig. 3). In Fig. 3a, the space (from Fig. 2) is filled with ED “demand points”. In Fig. 3b, the ED value is calculated as the sum of the distances from each demand point to its nearest sample/site. In Fig. 3c, sample site x is assumed lost and ED is re-calculated. In Fig. 3d, alternatively, sample site y is lost and ED is re-calculated. We can see from the plots that the loss of sample x clearly results in a greater sum of distances. The loss of sample/site x would imply much greater loss of phylogenetic diversity compared to loss of sample/site y, as indicated by the amount of change in the sums of distances (Fig. 3c,d). This result corresponds to the intuition that sample x, in filling a larger gap in the space relative to sample y, is likely to uniquely represent more features.
ED analyses for the ordination space based on PD -dissimilarities , from Rintala et al. (Fig. 2). Black dots are samples as in Fig. 2 and two of the samples are labelled, x and y. Hollow dots are ED demand points. A small number of demand points, uniformly covering the range of samples in the space, are used here to illustrate the method. (a) Ordination space showing samples and demand points. (b) Line segments connect each demand point to its nearest sample, among all samples in a defined subset. The ED value is the sum of these distances. Here the subset includes all samples. (c) Sample site x is lost from the subset, and ED is re-calculated based on the new line segments. (d) Sample site y is lost and ED is re-calculated based on the new line segments
A Simple Graphical Description of ED for the Single Gradient Case
The example in Figs. 2 and 3 illustrated how sites or samples that fill a large gap in environmental space are likely to uniquely represent more branches or features. We can see why ED counts up branches or features by looking at a simple one-dimensional gradient and graphical representation of ED calculations, which illustrates the link from the counting-up property to ED calculations of gains and losses as sites are gained or lost.
Suppose we have an ordination with one gradient (say, a GDM transformation of a climate-related variable ; Fig. 4a). Demand points occur continuously along the gradient and define the centers of distribution for features or branches. These features are assumed to have a uniform distribution of range-extents along the gradient (Faith and Walker 1996a). Graphically, the height to the top of the gray area above any demand point (Fig. 4a) reflects the number of features centered at that point that are not overlapped by any of the selected sites; these would be features having a range-extent too small to overlap with the nearest site. This number corresponds to the demand point’s total contribution to the ED value; it indicates the total number of features at that demand point not covered by the selected sites. These demand point contributions form the triangle-shaped gray zones (Fig. 4a), whose total area equals the sum, over all demand points, of the distance from the demand point to its nearest selected site. In this single gradient case, ED is simply calculated as the sum of the triangular gray areas. This sum corresponds to the p-median value for the set of selected sites. This link from features to the p-median criterion nicely illustrates how ED counts-up features.
(a) A single environmental gradient (thick black line) and three selected sites (black dots). Each hypothetical branch/lineage, centred at a demand point, graphically is represented in the figure by a point above its demand point, at a vertical distance equal to one-half of its distribution extent on the gradient. Branch/lineage points in the figure are gray if no selected site overlaps with the range-extent of the branch/lineage. Branch/lineage ‘a’ would be captured by the middle site only, branch/lineage ‘b’ is not sampled by any sites as its extent is too small; it is therefore coloured gray. Branch/lineage ‘c’ is captured by two sites. The height to the top of the gray area above any demand point reflects the total number of branch/lineages centered at that point that are not overlapped by any selected sites. ED is the sum of the resulting triangular gray areas. When richness varies along the gradient, the corresponding weights on demand points can be interpreted as if we are calculating a volume when counting-up unrepresented branch/lineages to obtain the ED score. (b) If the hollow-circle site is added to the selected set indicated by the black dots, the ED value (number of branch/lineages not represented) will be reduced by the amount equal to the white-striped area. This ED-complementarity equals x*y/2, where x and y are distances from the hollow circle site to its left and right nearest neighbours. (c) Removal of the crossed-out site from the selected set (black dots) means that the ED index of number of branch/lineages not-represented increases by the amount equal to the dark-gray area. ED-complementarity again equals x*y/2, where x and y are distances from the crossed-out site to left and right neighbours. (d) A gradient and two selected sites (black dots), B and C, illustrating ED options. Branch/lineage extent along the gradient is assumed to not exceed some maximum value. Consequently, selected site, B, does not serve demand points along the gradient that are too far away to have any branch/lineages with extent less than or equal to the maximum value that at the same time overlap with B. All demand points further away contribute the maximum value to ED’s measure of number of branch/lineages not represented. The maximum-value line here is drawn extending across the gradient. The white area therefore represents the number of branch/lineages represented by the two selected sites, and the gray area corresponds to the number of branch/lineages not represented. The diagram also illustrates another ED option. The set of demand points on the right hand side is extended (beyond some initial gradient boundary shown by the tick mark) so that selection of site C on its own now would imply the capture of the same number of branch/lineages as selection of site B
The counting-up property is the basis for measures of ED-complementarity. An ED-complementarity value estimates the number of features gained (lost) when a site is added to (removed from) a set of selected sites (Fig. 4b, c). In this simple single-gradient case, the ED-complementarity of a site equals ½ times the product of its distances to its left and right nearest neighbours (Fig. 4b, c). These basic calculations can be modified by introduction of additional assumptions such as the maximum extent of features along the gradient (Fig. 4d).
The link from the basic unimodal response model to ED’s counting-up property provides a basis for comparing ED to other methods for transforming dissimilarities to estimates of degree of representation of biodiversity by subsets of sites. The graphical representation will be useful for these comparisons of methods.
Properties of the Ferrier et al. formula
Ferrier et al (2004) proposed a formula to convert pairwise dissimilarities into “an overall estimate of the proportion of species represented” (e.g. in a set of protected areas). Ferrier et al. predicted “the proportion of species represented (p)” as:
where n is the number of grid cells in a study area , ri is the relative richness of each cell and dij is the compositional dissimilarity between each pair of cells i and j. Further, the state of habitat in each cell (e.g., 1 = protected and 0 = unprotected) is given by sj. The power term, z, is interpreted as analogous to that in species-area curves (Ferrier et al. 2004).
Ferrier et al. (2004) drew on “principles of the “environmental diversity ” (ED) approach proposed originally by Faith and Walker (1996a) as a means of assessing the representativeness of protected areas within a continuous environmental or biological space.” Both p and ED intend to convert dissimilarities into a measure of representativeness (e.g., of a subset of sites), but the similarities and differences between the two methods have not been investigated. Allnutt et al. (2008) re-derived the Ferrier et al. measure, and noted the need for comparison with the existing ED method: “in contrast to the approach described here, under the ED method (Faith and Walker 1996a, b, c), the amount of biodiversity estimated to be retained would depend more on how spread out intact sites are in environmental space, and less on the proportion of habitat retained in any part of this space. Further work is necessary to compare these alternatives in detail.”
Allnutt et al. also noted a concern that was raised in my review of their paper, “Another existing approach to calculate the biodiversity retained, given GDM outputs and habitat state values, is the ED method (Faith and Walker 1996; see also Faith et al. 2004). A reviewer of this paper noted that the Ferrier et al. formula relies on the sum of the distances (or similarities) from any site to all the intact sites. A consequence is that selection of additional intact sites will have an attraction to any concentrations (in space) of sites – even allowing further, identical, intact sites to be selected in order to minimise this sum, rather than properly choosing a distant site as a new intact site. In contrast, the ED method sees the amount of biodiversity retained as dependent on how spread out the intact sites are in space. Future work may compare these alternatives.”
The graphical presentation of a one-dimensional gradient reveals a critical difference between the two methods. Suppose we have sites along a single environmental gradient as our environmental space (Fig. 5), and there are s sites at point a, two sites at point b and 1 site at point c. Suppose that one intact site is at point b, and an additional intact site can be located at point c or at point b. We can compare the two scenarios by calculating the numerator of the Ferrier et al. formula (the denominator does not vary). We let ri = 1 for convenience.
Application of the Ferrier et al. formula will select a duplicate intact site at point b (over a wide range of values of s and choice of distances between sites). Suppose, for example, that z = .25; s = 5; x = .4; y = .4. Then, selecting an additional site at point b provides a contribution towards p equal to 4.1, while selecting a site at point c provides a contribution towards p equal to only 3.8 (calculations available on request from the author). In contrast, ED would select the site at c, which does increase representation of biodiversity , under the general unimodal model.
It appears that the Ferrier et al. formula for p can over-estimate the amount of biodiversity that is represented. Put another way, if we started with all sites, the loss of the only site located at point c along the gradient is seen as less serious than the loss of a duplicate site at point b. This miss-estimation can have serious consequences for biodiversity conservation; for example, a country could wrongly receive credit for what is in fact a reduction in representation of biodiversity.
The Ferrier et al. index was recently applied and recommended by Zerger et al. (2013) as a strategy for building “continental biodiversity information capability”. Given the potential failure of this index to properly assess representativeness, and gains and losses, under our plausible general model, they perhaps incorrectly conclude that “The methodology described by Ferrier et al. (2004) and Allnutt et al. (2008) also allows estimation of the proportion of species expected to be retained in any defined region of interest”. While Zerger et al. refer to species-level analyses, this poor estimation of represented biodiversity will extend to the phylogenetic diversity case, given the direct correspondence of the species and PD /features calculations.
Maximization of Complementary Richness (MCR)
Similar problems arise for another method that has some similarities to ED. Arponen et al. (2008) introduced the ‘maximization of complementary richness ’ (MCR) method, described by the authors as the first “successful community -level strategy”. Arponen et al. developed their approach based on an assumption of unimodal responses for species centred at different positions in environmental space. It is logical, therefore, to assess whether their method succeeds in counting-up species or features under this unimodal model.
Arponen et al. did not report the similarities of MCR to the ED methods. Without proper comparisons and contrasts with ED, it remains unclear whether MCR offers advantages over the similar ED calculations. Their MCR method shares with ED several useful properties, including a similar unimodal model, an ordination space, variants of p-median, plus ED’s GDM and richness -weighting options (for discussion of ED options, see Faith and Walker 1994; Faith and Ferrier 2002; Faith et al. 2003, 2004).
Arponen et al. claimed that MCR has unique properties, but some of these in fact also are shared by ED. For example, Arponen et al. (2008, p. 1438) claimed MCR is “different from the previous use of ordinations”, because, in using richness weighting and GDM, it “accounts for gradients in species richness and non-constant turnover rates of community composition”. However, the existing ED framework already uses these options (see Faith et al. 2004). Further, MCR, like ED, uses points described as “demand” points, served by one or more selected sites. In fact, both methods seek to minimise the degree to which species at demand points are not covered by selected sites. Although Arponen et al. describe MCR as maximising a summation of ‘C i ’ values (and each C i value is to reflect the degree to which demand point i is covered by selected sites), each C i equals one minus a product term. Thus, MCR is minimising the sum of product terms, and so minimising the degree to which demand points are not covered by selected sites. This property again matches ED methods.
Similarities aside, there are critical differences between the two methods. Simple examples will highlight the fact that MCR does have some novel properties relative to ED – but these properties de-grade the counting-up property that surely is critical to any truly “successful community -level strategy”.
Novel properties of MCR’s basic selection criterion are well-revealed in the simple case where species richness is assumed equal at all sites. MCR then uses the product of a demand point’s dissimilarities to all selected sites, and seeks to minimise the sum, over demand points, of these products. Single-gradient scenarios (Fig. 6a) highlight weaknesses of this calculation. Suppose there are two candidate sites for selection, A and B. Selection depends on which site most reduces the MCR product score. Note that when a demand point becomes a selected site, it makes no contribution to the sum of products (as its distance to itself is 0, making its product contribution equal to 0). Selecting site A removes its large product (=.05 × 0.60 × 0.65 × 0.70 = 0.014) from the product sum (Fig. 6a). Also, it reduces the product score for non-selected sites (site B), with a reduction equal to (1–0.4) times the previous product value for B of (0.45 × 0.20 × 0.25 × 0.30 = 0.007), yielding a reduction of 0.004. Thus, selecting site A reduces the score by about 0.018 (0.014 + 0.004). In contrast, selecting site B implies removal of a product term equal to 0.007 (see above), and a reduction in the A product contribution of (1–0.4) times 0.0137 = 0.008. Thus, selecting site B reduces the MCR score by only 0.015, and MCR selects site A.
(a) A hypothetical gradient (for example, from GDM) with selected sites (solid circles), and two candidate sites for selection, A and B (hollow circles). Numbers along gradient are distances between sites. ED-complementarity of site B (areas with vertical stripes) is 0.045, while that for site A (areas with horizontal stripes) is only 0.015, reflecting its close proximity to an already-selected site. ED prefers site B, reflecting the greater count in number of branch/lineages gained. In contrast, MCR, to minimise its product score, selects site A. For MCR, selecting site B reduces the MCR product score by only 0.015, while selecting site A reduces the score by a higher value of about 0.018. For MCR, the greatest reduction in the product score implies the greatest branch/lineages gain, and so MCR prefers site A. For further information, see text. (b) Given two candidate sites (hollow circles) and already-selected sites (solid circles), MCR assigns a higher preference weight to site A, reflecting the large distance from A to the selected site at the other end of the gradient. ED identifies site B as the site that would fill the largest gap and provide the greatest gain in branch/lineages representation. (c) There are two candidate sites for selection, A and B (hollow circles). ED-complementarity values of A and B are shown by respective striped areas. Site B, selected by ED, provides more new branch/lineages. However, MCR cannot distinguish between the two sites
We also can ask whether site A or B is best to lose (smallest features loss), assuming all sites initially are protected. Loss of B would add a new term to the MCR product sum equal to 0.45 × 0.40 × 0.20 × 0.25 × 0.30 = 0.003. Loss of A would add a larger term (0.05 × 0.40 × 0.60 × 0.65 × 0.70 = 0.005). MCR prefers to retain site A and lose site B. MCR prefers site A over site B, whether adding or removing sites – yet this does not accord with MCR’s own model of random distributions of features in the environmental space.
ED correctly prefers site B, in accord with the unimodal model and counting-up property. ED-complementarity for the gain of site B (vertical striped area ; Fig. 6a) is 0.045, while that for site A (horizontal stripes) is only 0.015, reflecting the site’s close proximity to an already-selected site. The difference is 0.03, and is the same value when determining the best site to lose, illustrating how ED provides a consistent counting-up of features in comparing the two sites under different scenarios. Thus, site B, filling a large gap, is expected to contribute more features (Fig. 6a).
This example highlights general MCR weaknesses: a site can be wrongly preferred because MCR is misled by the site’s many large dissimilarities to other sites. Arponen et al. attempted to overcome one weakness of their core selection criterion – possible near-duplication of previously selected sites – by applying a down-weighting of those candidate sites close to already-selected sites. The weighting, equal to the product of the site’s dissimilarity to all selected sites, does not solve this problem. For example, a site very close to an already-selected site, nevertheless may receive higher weight because it is so far away from other selected sites (Fig. 6b).
MCR’s failure to identify gaps is exacerbated by its use of actual sites as demand points (so mimicking ‘discrete ED’; Faith and Walker 1996a). MCR consequently cannot take into account portions of the environmental space that do not have recorded sites. An example shows how ED, but not MCR, will give an edge site deserved priority (Fig. 6c), countering Arponen et al.’s claim that a particular advantage of MCR is that it gives priority to sites on the edge of environmental space.
ED succeeds, and MCR fails, in counting-up features under the basic unimodal model. While ED successfully has incorporated, in a consistent way, useful options relating to richness , extent of space, GDM, and other options, the MCR calculations degrade the counting-up of features. This contrast between MCR and ED has important implications for applications. Suppose we interpret the example (Fig. 6a) as a planning decision, in which the best site, A or B, will be removed from protection for non-conservation uses. MCR prefers to give away the site (B) implying a greater features loss. Thus, MCR would be a poor basis for the systematic conservation planning required to reduce rates of biodiversity loss; use of MCR in such conservation planning could inadvertently increase the rate of biodiversity loss. I conclude that MCR, like the Ferrier et al. method, will not provide an effective way to analyse PD -dissimilarities for assessments of PD representation and calculation of gains and losses.
Discussion
ED provides an effective strategy to analyse PD -dissimilarities among areas, and make inferences as if we are counting up branches or features. While well-justified through the link to feature diversity , application of ED to date has been frustrated by a lack of synthesis about alternative methods, including inconsistent use of names for methods and miss-representation of basic properties. Araújo et al. (2001, 2003, 2004), Hortal et al. (2009), and Arponen et al. (2008) all have incorrectly characterised “ED” as a method using only environmental data. Hortal et al. (2009) claimed to have evaluated the continuous ED method of Faith and Walker (1996a), but in fact used a quite different method (see Faith 2011). Recently, Beier and Albuquerque (2015) found strong support for ED as a biodiversity surrogate.
The comparison in this study of ED to other proposed methods helps to clarify key properties. ED, Ferrier et al.’s p, and the MCR method share important desirable properties for biodiversity assessment; they transform dissimilarities in order to infer useful information, including the amount of biodiversity represented by subsets of sites. All three methods are based to some degree on the idea of unimodal response. However, among these candidate approaches, ED seems to best reflect the plausible underlying model in which elements of biodiversity have general unimodal response to environmental space.
This chapter has attempted to provide some long-overdue comparisons among existing proposed methods, but it is important to note that more comparative evaluations are needed. In the interest of synthesis, I highlight several other methodological issues requiring study.
Hierarchical Clustering
Faith (2013) recently reviewed the prospects for another strategy, based on a hierarchical clustering of the PD -dissimilarities among sites or samples (including those predicted by GDM). Faith and Walker (1996a), in discussing dissimilarities defined at the species level, had argued that “a robust hierarchical clustering method designed for biotic distribution data, such as flexible-UPGMA with Bray-Curtis dissimilarities, is likely to produce a hierarchy where distances along branches between areas indeed reflect the relative number of species differences.” Faith (2013) suggested an extension of this idea: “This rationale extends to PD-dissimilarities in such a hierarchical clustering, distances along branches between samples reflect the relative difference in the PD of the samples. ….the PD method can be applied to a hierarchy of samples, just as it is applied to a hierarchy (phylogeny) of species. Various PD calculations can be applied to the hierarchies of sites/samples that are based on PD-dissimilarities among samples or sites.” Faith (2013) referred to this method as “PDh”, as it uses the PD calculus, but is applied to a samples/sites hierarchy. The PDh value for a subset of samples/sites indicates the PD of the subset. It is noteworthy that that the suggested hierarchical clustering approach for PDh is a method (Belbin et al. 1993) designed to be compatible with an environmental space and unimodal response.
Persistence Versus Representativeness
I argued above that Ferrier et al. perhaps inaccurately characterised their formula as estimating “the proportion of species represented”, and I questioned the conclusion of Zerger et al. (2013) that the method of Ferrier et al. (2004) and Allnutt et al. (2008) “allows estimation of the proportion of species expected to be retained in any defined region of interest,” These problems naturally extend from species-level to the features defined by PD -dissimilarities . Both Allnutt et al. (2008) and Ferrier et al. (2009) have suggested that the Ferrier et al. method contrasts with ED because it is intended to address expected persistence, and not just representation. While it seems doubtful that a measure that performs poorly in assessing representation will do well in assessing overall persistence, more work is needed to evaluate whether the Ferrier et al. method provides useful information about biodiversity persistence.
On a positive note, the persistence and the representation goals do not have to be addressed by different frameworks. One ED variant, departing from p-median, captures expected diversity or persistence in a “probabilistic ED” method:
…when we assign probabilities (of expected features persistence or ‘presence’) to sites … the p-median, which strictly depends on nearest neighbours, is relaxed, and the total estimated diversity now depends on summation over ordered nearest neighbours (Faith et al. 2004).
These probabilities form the analogue to the state or condition of habitat in each site j, given by sj, in the Ferrier et al. formula. Given the advantages of ED over p in the basic representation case, the “probabilistic ED” method deserves investigation as an alternative way to integrate state or condition of habitat in sites, for analysis of persistence.
Simulation Methods
These variants highlight the idea that the critical ingredient of the ED framework is unimodal response, reflecting the shared-habitat/shared-features model. Indeed, once we have an environmental space, under this model, we can simulate the sets of branches/features that would correspond, for example, to a nominated subset of sites. Faith et al. (2003) used this approach to map the distributions in geographic space of the hypothetical elements (species or features). This “biodiversity viability analysis” (BVA) uses this spatial information for each element for various biodiversity assessments. Thus, BVA translates information about any inferred element from ordination space to its implied distribution in geographic space (taking advantage of the link that environmental data for all areas provides from ordination space to geographic space). Mokany et al. (2011) provide a method that mimics the ED/BVA generation of hypothetical species (or other elements) based on unimodal response and related models. However, their method loses some useful information that BVA/ED derives from explicitly sampling from the environmental space under the unimodal response model. Further work is needed to evaluate these methods.
GEO BON
Future applications may require this full range of ED calculations. ED is one candidate biodiversity assessment strategy in a new global program for monitoring the status of biodiversity. The Group on Earth Observation s Biodiversity Observation Network (GEO BON; Andrefouet et al. 2008) has been developed as a mechanism for gathering and sharing observations regarding biodiversity change. GEO BON is to enhance cooperation among countries to understand changes in biodiversity by monitoring its state and trends. One monitoring strategy in GEO BON will use repeated observations, over time, of changes in the state or condition of sites (e.g., based on remote sensing data). These observations then are integrated with spatial biodiversity models that act as the ‘lens’ for inferences about the corresponding changes in biodiversity (Andrefouet et al. 2008; Faith et al. 2009; Ferrier 2011). The ED approach can provide such a biodiversity lens, using available environmental data, genetic, phylogenetic and species data covering multiple taxonomic groups, and GDM to include unsampled sites. In simple applications, ED complementarity values can be calculated when localities are judged as newly degraded (or newly protected). Alternatively, the estimates of condition from remote sensing may be interpreted as fractional species losses for localities, calling for methods such as probabilistic ED.
One of the GEO BON working groups is tasked with implementing these monitoring strategies to applications assessing change in phylogenetic diversity , over multiple taxonomic groups (including microbial diversity). ED methods applied to analyses of PD -dissimilarities (including those describing within-species genetic variation) appear to offer a robust flexible framework for assessments of biodiversity change at this important level of biodiversity.
References
Allnutt TF, Ferrier S, Manion G, Powell GVN, Ricketts TH, Fisher BL, Harper GJ et al (2008) A method for quantifying biodiversity loss and its application to a 50-year record of deforestation across Madagascar. Conserv Lett 1:173–181
Andrefouet S, Costello MJ et al (2008) The GEO biodiversity observation network: concept document. GEO – Group on Earth Observations, Geneva, http://www.earthobservations.com/documents/cop/bi_geobon/200811_geobon_concept_document.pdf
Araújo MB, Densham P, Lampinen R et al (2001) Would environmental diversity be a good surrogate for species diversity? Ecography 24:103–110
Araújo MB, Densham PJ, Humphries CJ (2003) Predicting species diversity with ED: the quest for evidence. Ecography 26:380–383
Araújo MB, Densham PJ, Williams PH (2004) Representing species in reserves from patterns of assemblage diversity. J Biogeogr 31:1037–1050
Arponen A, Moilanen A, Ferrier S (2008) A successful community-level strategy for conservation prioritization. J Appl Ecol 45:1436–1445
Austin MP (1985) Continuum concept, ordination methods, and niche theory. Ann Rev Ecol Syst 16:39–61
Beier P, Albuquerque F (2015) Environmental diversity is a reliable surrogate for species representation. Conserv Biol doi:10.1111/cobi.12508
Belbin L, Faith DP, Milligan G (1993) A comparison of two approaches to beta-flexible clustering. Multivar Behav Res 27:417–433
Faith DP (1989) Homoplasy as pattern: multivariate analysis of morphological convergence in Anseriformes. Cladistics 5:235–258
Faith DP (1992a) Conservation evaluation and phylogenetic diversity. Biol Conserv 61:1–10
Faith DP (1992b) Systematics and conservation: on predicting the feature diversity of subsets of taxa. Cladistics 8:361–373
Faith DP (1994) Phylogenetic pattern and the quantification of organismal biodiversity. Philos Trans R Soc Lond Ser B 345:45–58
Faith DP (1996) Conservation priorities and phylogenetic pattern. Conserv Biol 10:1286–1289
Faith DP (2002) The role of the phylogenetic diversity measure, PD, in bio-informatics: getting the definition right. Evol Bioinformatics Online 2006(2):1–7
Faith DP (2003) Environmental diversity (ED) as surrogate information for species-level biodiversity. Ecography 26:374–379
Faith DP (2011) Attempted tests of the surrogacy value of the ED environmental diversity measures highlight the need for corroboration assessment of surrogacy hypotheses. Ecol Indic 11:745–748
Faith DP (2013) Biodiversity and evolutionary history: useful extensions of the PD phylogenetic diversity assessment framework. Ann NY Acad Sci 1289:69–89
Faith DP (2015a) The PD phylogenetic diversity framework: linking evolutionary history to feature diversity for biodiversity conservation. In: Pellens R, Grandcolas R (eds) Biodiversity Conservation and Phylogenetic Systematics: preserving our evolutionary heritage in an extinction crisis. Springer, Dordrecht
Faith DP (2015b) Phylogenetic diversity, functional trait diversity and extinction: avoiding tipping points and worst-case losses from the tree of life. Proc Royal Soc London B 370:20140011
Faith DP, Ferrier S (2002) Linking beta diversity, environmental variation, and biodiversity assessment. Science [Online] 295:636 http://www.sciencemag.org/cgi/eletters/295/5555/636#504
Faith DP, Walker PA (1996a) Environmental diversity: on the best-possible use of surrogate data for assessing the relative biodiversity of sets of areas. Biodivers Conserv 5:399–415
Faith DP, Walker PA (1996b) Integrating conservation and development: effective trade-offs between biodiversity and cost in the selection of protected areas. Biodivers Conserv 5:431–446
Faith DP, Walker PA (1996c) Integrating conservation and development: incorporating vulnerability into biodiversity-assessment of areas. Biodivers Conserv 5:417–429
Faith DP, Minchin PR, Belbin L (1987) Compositional dissimilarity as a robust measure of ecological distance. Vegetation 69:57–68
Faith DP, Walker PA, Ive JR et al (1996) Integrating conservation and forestry production: exploring trade-offs between biodiversity and production in regional land-use assessment. For Ecol Manag 85:251–260
Faith DP, Carter G, Cassis G et al (2003) Complementarity, biodiversity viability analysis, and policy-based algorithms for conservation. Environ Sci Pol 6:311–328
Faith DP, Ferrier S, Walker PA (2004) The ED strategy: how species-level surrogates indicate general biodiversity patterns through an ‘environmental diversity’ perspective. J Biogeogr 31:1207–1217
Faith DP et al (2009) The cladistic basis for the phylogenetic diversity (PD) measure links evolutionary features to environmental gradients and supports broad applications of microbial ecology’s “phylogenetic beta diversity” framework. Int J Mol Sci 10:4723–4741
Faith DP, Magallón S, Hendry AP, Conti E, Yahara T, Donoghue MJ (2010) Evosystem services: an evolutionary perspective on the links between biodiversity and human-well-being. Curr Opin Environ Sustain 2:66–74
Ferrier S (2002) Mapping spatial pattern in biodiversity for regional conservation planning: where to from here? Syst Biol 51:331–363
Ferrier S (2011) Extracting more value from biodiversity change observations through integrated modelling. Bioscience 61:96–97
Ferrier S, Drielsma M (2010) Synthesis of pattern and process in biodiversity conservation assessment: a flexible whole-landscape modelling framework. Divers Distrib 16:386–402
Ferrier S, Powell GVN, Richardson KS et al (2004) Mapping more of terrestrial biodiversity for global conservation assessment. Biogeosciences 54:1101–1109
Ferrier S, Manion G, Elith J, Richardson KS (2007) Using generalized dissimilarity modelling to analyse and predict patterns of beta diversity in regional biodiversity assessment. Divers Distrib 13:252–264
Ferrier S, Faith DP, Arponen A, Drielsma M (2009) Community-level approaches to spatial conservation prioritisation. In: Moilanen A, Wilson KA, Possingham HP (eds) Systematic conservation planning. Oxford University Press, Oxford, pp 94–109
Forest F et al (2007) Preserving the evolutionary potential of floras in biodiversity hotspots. Nature 445:757–760
Hortal J, Araújo MB, Lobo JM (2009) Testing the effectiveness of discrete and continuous environmental diversity as a surrogate for species diversity. Ecol Indic 9:138–149
Kelly S, Grenyer R, Scotland RW (2014) Phylogenetic trees do not reliably predict feature diversity. Divers Distrib 20:600–612
Lozupone C, Knight R (2005) UniFrac: a new phylogenetic method for comparing microbial communities. Appl Environ Microbiol 71:8228–8235
Mokany K, Harwood TD, Overton JM, Barker GM, Ferrier S (2011) Ecol Lett 14:1043–1051
Nipperess DA, Faith DP, Barton K (2010) Resemblance in phylogenetic diversity among ecological assemblages. J Veg Sci 21:809–820
Rintala H et al (2008) Diversity and seasonal dynamics of bacterial community in indoor environment. BMC Microbiol 8:56
Rosauer D, Ferrier S, Williams KJ, Manion G, Keogh S, Laffan SW (2013) Phylogenetic generalised dissimilarity modelling: a new approach to analysing and predicting spatial turnover in the phylogenetic composition of communities. Ecography 37:21–32
Swenson NG (2011) Phylogenetic beta diversity metrics, trait evolution and inferring the functional beta diversity of communities. PLoS ONE 6(6):e21264. doi:10.1371/journal.pone.0021264
Walker PA, Faith DP (1994) DIVERSITY-PD: procedures for conservation evaluation based on phylogenetic diversity. Biodivers Lett 2:132–139
Zerger A, Williams KJ, Nicholls M, Belbin L, Harwood T, Bordas V, Ferrier S, Perkins G (2013) Biodiversity profiling: components of a continental biodiversity information capability, vol 2, Environmental Information Program Publication. Bureau of Meteorology, Canberra. 72 pp
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution-Noncommercial 2.5 License (http://creativecommons.org/licenses/by-nc/2.5/) which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Faith, D.P. (2016). Using Phylogenetic Dissimilarities Among Sites for Biodiversity Assessments and Conservation. In: Pellens, R., Grandcolas, P. (eds) Biodiversity Conservation and Phylogenetic Systematics. Topics in Biodiversity and Conservation, vol 14. Springer, Cham. https://doi.org/10.1007/978-3-319-22461-9_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-22461-9_7
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-22460-2
Online ISBN: 978-3-319-22461-9
eBook Packages: Biomedical and Life SciencesBiomedical and Life Sciences (R0)