Faster Algorithms for Quantitative Verification in Constant Treewidth Graphs

Abstract

We consider the core algorithmic problems related to verification of systems with respect to three classical quantitative properties, namely, the mean-payoff property, the ratio property, and the minimum initial credit for energy property. The algorithmic problem given a graph and a quantitative property asks to compute the optimal value (the infimum value over all traces) from every node of the graph. We consider graphs with constant treewidth, and it is well-known that the control-flow graphs of most programs have constant treewidth. Let n denote the number of nodes of a graph, m the number of edges (for constant treewidth graphs $m=O(n)$) and W the largest absolute value of the weights. Our main theoretical results are as follows. First, for constant treewidth graphs we present an algorithm that approximates the mean-payoff value within a multiplicative factor of $\epsilon$ in time $O(n \cdot \log (n/\epsilon ))$ and linear space, as compared to the classical algorithms that require quadratic time. Second, for the ratio property we present an algorithm that for constant treewidth graphs works in time $O(n \cdot \log (|a\cdot b|))=O(n\cdot \log (n\cdot W))$, when the output is $\frac{a}{b}$, as compared to the previously best known algorithm with running time $O(n^2 \cdot \log (n\cdot W))$. Third, for the minimum initial credit problem we show that (i) for general graphs the problem can be solved in $O(n^2\cdot m)$ time and the associated decision problem can be solved in $O(n\cdot m)$ time, improving the previous known $O(n^3\cdot m\cdot \log (n\cdot W))$ and $O(n^2 \cdot m)$ bounds, respectively; and (ii) for constant treewidth graphs we present an algorithm that requires $O(n\cdot \log n)$ time, improving the previous known $O(n^4 \cdot \log (n \cdot W))$ bound. We have implemented some of our algorithms and show that they present a significant speedup on standard benchmarks.

The research was partly supported by Austrian Science Fund (FWF) Grant No P23499- N23, FWF NFN Grant No S11407-N23 (RiSE/SHiNE), ERC Start grant (279307: Graph Games), and Microsoft faculty fellows award.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Boolean vs. Quantitative Verification. The traditional view of verification has been qualitative (Boolean) that classifies traces of a system as “correct" vs “incorrect". In the recent years, motivated by applications to analyze resource-constrained systems (such as embedded systems), there has been a huge interest to study quantitative properties of systems. A quantitative property assigns to each trace of a system a real-number that quantifies how good or bad the trace is, instead of classifying it as correct vs incorrect. For example, a Boolean property may require that every request is eventually granted, whereas a quantitative property for each trace can measure the average waiting time between requests and corresponding grants.

Variety of Results. Given the importance of quantitative verification, the traditional qualitative view of verification has been extended in several ways, such as, quantitative languages and quantitative automata for specification languages [15–17, 21, 27, 28, 44]; quantitative logics for specification languages [2, 9, 11]; quantitative synthesis for robust reactive systems [4, 5, 20]; a framework for quantitative abstraction refinement [13]; quantitative analysis of infinite-state systems [18, 23]; and model measuring (that extends model checking) [33], to name a few. The core algorithmic question for many of the above studies is a graph algorithmic problem that requires to analyze a graph wrt a quantitative property.

Important Quantitative Properties. The three quantitative properties that have been studied for their relevance in analysis of reactive systems are as follows. First, the mean-payoff property consists of a weight function that assigns to every transition an integer-valued weight and assigns to each trace the long-run average of the weights of the transitions of the trace. Second, the ratio property consists of two weight functions (one of which is a positive weight function) and assigns to each trace the ratio of the two mean-payoff properties (the denominator is wrt the positive function). The minimum initial credit for energy property consists of a weight function (like in the mean-payoff property) and assigns to each trace the minimum number to be added such that the partial sum of the weights for every prefix of the trace is non-negative. For example, the mean-payoff property is used for average waiting time, worst-case execution time analysis [13, 17, 18]; the ratio property is used in robustness analysis of systems [5]; and the minimum initial credit for energy for measuring resource consumptions [10].

Algorithmic Problems. Given a graph and a quantitative property, the value of a node is the infimum value of all traces that start at the respective node. The algorithmic problem (namely, the value problem) for analysis of quantitative properties consists of a graph and a quantitative property, and asks to compute either the exact value or an approximation of the value for every node in the graph. The algorithmic problems are at the heart of many applications, such as automata emptiness, model measuring, quantitative abstraction refinement, etc.

Treewidth of Graphs. A very well-known concept in graph theory is the notion of treewidth of a graph, which is a measure of how similar a graph is to a tree (a graph has treewidth 1 precisely if it is a tree) [40]. The treewidth of a graph is defined based on a tree decomposition of the graph [31], see Sect. 2 for a formal definition. Beyond the mathematical elegance of the treewidth property for graphs, there are many classes of graphs which arise in practice and have constant treewidth. The most important example is that the control flow graphs of goto-free programs for many programming languages are of constant treewidth [42], and it was also shown in [30] that typically all Java programs have constant treewidth. For many other applications see the surveys [6, 7]. The constant treewidth property of graphs has also played an important role in logic and verification; for example, MSO (Monadic Second Order logic) queries can be solved in polynomial time [24] (also in log-space [29]) for constant-treewidth graphs; parity games on graphs with constant treewidth can be solved in polynomial time [37]; and there exist faster algorithms for probabilistic models (like Markov decision processes) [14]. Moreover, recently it has been shown that the constant treewidth property is also useful for interprocedural analysis [18].

Previous Results and Our Contributions. In this work we consider general graphs and graphs with constant treewidth, and the algorithmic problems to compute the exact value or an approximation of the value for every node wrt to quantitative properties given as the mean-payoff, the ratio, or the minimum initial credit for energy. We first present the relevant previous results, and then our contributions.

Previous Results. We consider graphs with n nodes, m edges, and let W denote the largest absolute value of the weights. The running time of the algorithms is characterized by the number of arithmetic operations (i.e., each operation takes constant time); and the space is characterized by the maximum number of integers the algorithm stores. The classical algorithm for graphs with mean-payoff properties is the minimum mean-cycle problem of Karp [34], and the algorithm requires $O(n\cdot m)$ running time and $O(n^2)$ space. A different algorithm was proposed in [36] that requires $O(n\cdot m)$ running time and O(n) space. Orlin and Ahuja [38] gave an algorithm running in time $O(\sqrt{n}\cdot m\cdot \log (n\cdot W))$. For some special cases there exist faster approximation algorithms [19]. There is a straightforward reduction of the ratio problem to the mean-payoff problem. For computing the exact minimum ratio, the fastest known strongly polynomial time algorithm is Burns’ algorithm [12] running in time $O(n^2\cdot m)$. Also, there is an algorithm by Lawler [35] that uses $O(n\cdot m\cdot \log (n\cdot W))$ time. Many pseudopolynomial algorithms are known for the problem, with polynomial dependency on the numbers appearing in the weight function, see [26]. For the minimum initial credit for energy problem, the decision problem (i.e., is the energy required for node v at most c?) can be solved in $O(n^2\cdot m)$ time, leading to an $O(n^3\cdot m\cdot \log (n\cdot W))$ time algorithm for the minimum initial credit for energy problem [10]. All the above algorithms are for general graphs (without the constant-treewidth restriction).

Our Contributions. Our main contributions are as follows.

• 1. Finding the Mean-Payoff and Ratio Values in Constant-Treewidth Graphs. We present two results for constant treewidth graphs. First, for the exact computation we present an algorithm that requires $O(n\cdot \log (|a\cdot b|))$ time and O(n) space, where $\frac{a}{b}\ne 0$ is the (irreducible) ratio/mean-payoff of the output. If $\frac{a}{b}=0$, the algorithm uses O(n) time. Note that $\log (|a\cdot b|)\le 2\log (n\cdot W)$. We also present a space-efficient version of the algorithm that requires only $O(\log n)$ space. Second, we present an algorithm for finding an $\epsilon$-factor approximation of the mean-payoff value that requires $O(n\cdot \log (n/\epsilon ))$ time, as compared to the $O(n^{1.5}\cdot \log (n\cdot W))$ time solution of Orlin & Ahuja, and the $O(n^2)$ time solution of Karp (see Table 1).

• 2. Finding the Minimum Initial Credit in Graphs. We present two results. First, we consider the exact computation for general graphs, and present (i) an $O(n \cdot m)$ time algorithm for the decision problem (improving the previously known $O(n^2\cdot m)$ bound), and (ii) an $O(n^2\cdot m)$ time algorithm to compute value of all nodes (improving the previously known $O(n^3\cdot m \cdot \log (n\cdot W))$ bound). Finally, we consider the computation of the exact value for graphs with constant treewidth and present an algorithm that requires $O(n\cdot \log n)$ time (improving the previous known $O(n^4 \cdot \log (n\cdot W))$ bound) (see Table 2).

• 3. Experimental Results. We have implemented our algorithms for the minimum mean cycle and minimum initial credit problems and ran them on standard benchmarks (DaCapo suit [3] for the minimum mean cycle problem, and DIMACS challenges [1] for the minimum initial credit problem). For the minimum mean cycle problem, our results show that our algorithm has lower running time than all the classical polynomial-time algorithms. For the minimum initial credit problem, our algorithm provides a significant speedup over the existing method. Both improvements are demonstrated even on graphs of small/medium size. Note that our theoretical improvements (better asymptotic bounds) imply improvements for large graphs, and our improvements on medium sized graphs indicate that our algorithms have practical applicability with small constants.

Table 1. Time complexity of existing and our solutions for the minimum mean-cycle value and ratio-cycle value problem in constant treewidth weighted graphs with n nodes and largest absolute weight W, when the output is the (irreducible) fraction $\frac{a}{b}\ne 0$.

Table 2. Complexity of the existing and our solution for the minimum initial credit problem on weighted graphs of n nodes, m edges, and largest absolute weight W.

Technical Contributions. The key technical contributions of our work are as follows:

• 1. Mean-Payoff and Ratio Values in Constant-Treewidth Graphs. Given a graph with constant treewidth, let $c^{*}$ be the smallest weight of a simple cycle. First, we present a linear-time algorithm that computes $c^{*}$ exactly (if $c^{*}\ge 0$) or approximates $c^*$ within a polynomial factor (if $c^{*}<0$). Then, we show that if the minimum ratio value $\nu ^{*}$ is the irreducible fraction $\frac{a}{b}$, then $\nu ^{*}$ can be computed by evaluating $O(\log (|a\cdot b|))$ inequalities of the form $\nu ^{*} \ge \nu$. Each such inequality is evaluated by computing the smallest weight of a simple cycle in a modified graph. Finally, for $\epsilon$-approximating the value $\nu ^{*}$, we show that $O(\log (n/\epsilon ))$ such inequalities suffice.

• 2. Minimum Initial Credit Problem. We show that for general graphs, the decision problem can be solved with two applications of Bellman-Ford-type algorithms, and the value problem reduces to finding non-positive cycles in the graph, followed by one instance of the single-source shortest path problem. We then show how the invariants of the algorithm for the value problem on general graphs can be maintained by a particular graph traversal of the tree-decomposition for constant-treewidth graphs.

2 Definitions

Weighted Graphs. We consider finite weighted directed graphs $G=(V,E,\mathsf {wt}, \mathsf {wt}^{\prime })$ where V is the set of n nodes, $E\subseteq V\times V$ is the edge relation of m edges, $\mathsf {wt}:E \rightarrow \mathbb {Z}$ is a weight function that assigns an integer weight $\mathsf {wt}(e)$ to each edge $e\in E$, and $\mathsf {wt}^{\prime }:E\rightarrow \mathbb {N}^{+}$ is a weight function that assigns strictly positive integer weights. For technical simplicity, we assume that there exists at least one outgoing edge from every node. In certain cases where the function $\mathsf {wt}^{\prime }$ is irrelevant, we will consider weighted graphs $G=(V,E,\mathsf {wt})$, i.e., without the function $\mathsf {wt}^{\prime }$.

Finite and Infinite Paths. A finite path $P=(u_1,\dots , u_j)$, is a sequence of nodes $u_i\in V$ such that for all $1\le i<j$ we have $(u_i,u_{i+1})\in E$. The length of P is $|P|=j-1$. A single-node path has length 0. The path P is simple if there is no node repeated in P, and it is a cycle if $j>1$ and $u_1=u_j$. The path P is a simple cycle if P is a cycle and the sequence $(u_2,\dots u_j)$ is a simple path. The functions $\mathsf {wt}$ and $\mathsf {wt}^{\prime }$ naturally extend to paths, so that the weight of a path P with $|P|>0$ wrt the weight functions $\mathsf {wt}$ and $\mathsf {wt}^{\prime }$ is $\mathsf {wt}(P)=\sum _{1\le i<j} \mathsf {wt}(u_i,u_{i+1})$ and $\mathsf {wt}^{\prime }(P)=\sum _{1\le i<j} \mathsf {wt}^{\prime }(u_i,u_{i+1})$. The value of P is defined to be $\overline{\mathsf {wt}}(P)=\frac{\mathsf {wt}(P)}{\mathsf {wt}^{\prime }(P)}$. For the case where $|P|=0$, we define $\mathsf {wt}(P)=0$, and $\overline{\mathsf {wt}}(P)$ is undefined. An infinite path $\mathcal {P}=(u_1, u_2, \dots )$ of G is an infinite sequence of nodes such that every finite prefix P of $\mathcal {P}$ is a finite path of G. The functions $\mathsf {wt}$ and $\mathsf {wt}^{\prime }$ assign to $\mathcal {P}$ a value in $\mathbb {Z}\cup \{-\infty ,\infty \}$: we have $\mathsf {wt}(\mathcal {P})=\sum _i \mathsf {wt}(u_i,u_{i+1})$ and $\mathsf {wt}^{\prime }(\mathcal {P})=\infty$. For a (possibly infinite) path P, we use the notation $u\in P$ to denote that a node u appears in P, and $e\in P$ to denote that an edge e appears in P. Given a set $B\subseteq V$, we denote by $P\cap B$ the set of nodes of $B$ that appear in P. Given a finite path $P_1$ and a possibly infinite path $P_2$, we denote by $P_1\circ P_2$ the path resulting from the concatenation of $P_1$ and $P_2$.

Distances and Witness Paths. For nodes $u,v\in V$, we denote by $d(u,v)=\inf _{P:u\rightsquigarrow v} \mathsf {wt}(P)$ the distance from u to v. A finite path $P:u\rightsquigarrow v$ is a witness of the distance $d(u,v)$ if $\mathsf {wt}(P)=d(u,v)$. An infinite path $\mathcal {P}$ is a witness of the distance $d(u,v)$ if the following conditions hold:

• 1. $d(u,v)=\mathsf {wt}(\mathcal {P})=-\infty$, and

• 2. $\mathcal {P}$ starts from u, and v is reachable from every node of $\mathcal {P}$.

Note that $d(u,v)=\infty$ is not witnessed by any path.

Tree Decompositions. A tree-decomposition $\mathrm {Tree}(G)=(V_T, E_T)$ of G is a tree such that the following conditions hold:

• 1. $V_T=\{B_0,\dots , B_{n'-1}: \forall i~B_i\subseteq V\}$ and $\bigcup _{B_i\in V_T}B_i=V$ (every node is covered).

• 2. For all $(u,v)\in E$ there exists $B_i\in V_T$ such that $u,v\in B_i$ (every edge is covered).

• 3. For all i, j, k such that there is a bag $B_k$ that appears in the simple path $B_i\rightsquigarrow B_j$ in $\mathrm {Tree}(G)$, we have $B_i\cap B_j\subseteq B_k$ (every node appears in a contiguous subtree of $\mathrm {Tree}(G)$).

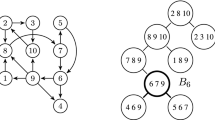
The sets $B_i$ which are nodes in $V_T$ are called bags. Conventionally, we call $B_0$ the root of $\mathrm {Tree}(G)$, and denote by $\mathsf {Lv}(B_i)$ the level of $B_i$ in $\mathrm {Tree}(G)$, with $\mathsf {Lv}(B_0)=0$. We say that $\mathrm {Tree}(G)$ is balanced if the maximum level is $\max _{B_i}\mathsf {Lv}(B_i)=O(\log n')$, and it is binary if every bag has at most two children bags. A bag $B$ is called the root bag of a node u if $B$ is the smallest-level bag that contains u, and we often use $B_u$ to refer to the root bag of u. The width of a tree-decomposition $\mathrm {Tree}(G)$ is the size of the largest bag minus 1. The treewidth of G is the smallest width among the widths of all possible tree decompositions of G.

Theorem 1

For every graph G with n nodes and constant treewidth, a balanced binary tree-decomposition $\mathrm {Tree}(G)$ of constant width and O(n) bags can be constructed in (1) O(n) time and space [8], (2) deterministic logspace (and hence polynomial time) [29].

In the sequel we consider only balanced and binary tree-decompositions of constant width and $n'=O(n)$ bags (and hence of height $O(\log n)$). Additionally, we assume that every bag is the root bag of at most one node. Obtaining this last property is straightforward, simply by replacing each bag $B$ which is the root of $k>1$ nodes $x_1,\dots x_k$ with a chain of bags $B_1, \dots , B_k=B$, where each $B_i$ is the parent of $B_{i+1}$, and $B_{i+1}=B_i\cup \{x_{i+1}\}$. Note that this keeps the tree binary and increases its height by at most a constant factor, hence the resulting tree is also balanced.

Throughout the paper, we follow the convention that the maximum and minimum of the empty set is $-\infty$ and $\infty$ respectively, i.e., $\max (\emptyset )=-\infty$ and $\min (\emptyset )=\infty$. Time complexity is measured in number of arithmetic and logical operations, and space complexity is measured in number of machine words. Given a graph G, we denote by $\mathcal {T}(G)$ and $\mathcal {S}(G)$ the time and space required for constructing a balanced, binary tree-decomposition $\mathrm {Tree}(G)$. We are interested in the following problems.

The Minimum Mean Cycle Problem [34]. Given a weighted directed graph $G=(V,E,\mathsf {wt})$, the minimum mean cycle problem asks to determine for each node u the mean value $\mu ^{*}(u)=\min _{C\in \mathcal {C}_u}\frac{\mathsf {wt}(C)}{|C|}$, where $\mathcal {C}_u$ is the set of simple cycles reachable from u in G. A cycle C with $\frac{\mathsf {wt}(C)}{|C|}=\mu ^{*}(u)$ is called a minimum mean cycle of u. For $0<\epsilon <1$, we say that a value $\mu$ is an $\epsilon$-approximation of the mean value $\mu ^{*}(u)$ if $|\mu -\mu ^{*}(u)|\le \epsilon \cdot |\mu ^{*}(u)|$.

The Minimum Ratio Cycle Problem [32]. Given a weighted directed graph $G=(V,E,\mathsf {wt}, \mathsf {wt}^{\prime })$, the minimum ratio cycle problem asks to determine for each node u the ratio value $\nu ^{*}(u)=\min _{C\in \mathcal {C}_u}\overline{\mathsf {wt}}(C)$, where $\overline{\mathsf {wt}}(C)=\frac{\mathsf {wt}(C)}{\mathsf {wt}^{\prime }(C)}$ and $\mathcal {C}_u$ is the set of simple cycles reachable from u in G. A cycle C with $\overline{\mathsf {wt}}(C)=\nu ^{*}_u$ is called a minimum ratio cycle of u. The minimum mean cycle problem follows as a special case of the minimum ratio cycle problem for $\mathsf {wt}^{\prime }(e)=1$ for each edge $e\in E$.

The Minimum Initial Credit Problem [10]. Given a weighted directed graph $G=(V,E,\mathsf {wt})$, the minimum initial credit value problem asks to determine for each node u the smallest energy value $\mathsf {E}(u)\in \mathbb {N}\cup \{\infty \}$ with the following property: there exists an infinite path $\mathcal {P}=(u_1, u_2\dots )$ with $u=u_1$, such that for every finite prefix P of $\mathcal {P}$ we have $\mathsf {E}(u)+\mathsf {wt}(P)\ge 0$. Conventionally, we let $\mathsf {E}(u)=\infty$ if no finite value exists. The associated decision problem asks given a node u and an initial credit $c\in \mathbb {N}$ whether $\mathsf {E}(u)\le c$.

3 Minimum Cycle

In this section we deal with a related graph problem, namely the detection of a minimum-weight simple cycle of a graph. In Sect. 4 we use our solution to this problem to obtain solutions for the minimum ratio and minimum mean cycle problems.

The Minimum Cycle Problem. Given a weighted graph $G=(V,E, \mathsf {wt})$, the minimum cycle problem asks to determine the weight $c^{*}$ of a minimum-weight simple cycle in G, i.e., $c^{*}=\min _{C\in \mathcal {C}} \mathsf {wt}(C)$, where $\mathcal {C}$ is the set of simple cycles in G.

We describe the algorithm $\mathsf {MinCycle}$ that operates on a tree-decomposition $\mathrm {Tree}(G)$ of an input graph G, and has the following properties.

• 1. If G has no negative cycles, then $\mathsf {MinCycle}$ returns the weight $c^{*}$ of a minimum-weight cycle in G.

• 2. If G has negative cycles, then $\mathsf {MinCycle}$ returns a value that is at most a polynomial (in n) factor smaller than $c^{*}$.

$\mathsf {U}$ -Shaped Paths. Following the recent work of [18], we define the important notion of $\mathsf {U}$-shaped paths in a tree-decomposition $\mathrm {Tree}(G)$. Given a bag $B$ and nodes $u,v\in B$, we say that a path $P:u\rightsquigarrow v$ is $\mathsf {U}$ -shaped in $B$, if one of the following conditions hold:

• 1. Either $|P|>1$ and $B$ is an ancestor of $B_w$ for all intermediate nodes $w\in P$,

• 2. or $|P|\le 1$ and $B$ is $B_u$ or $B_v$ (i.e., $B$ is the root bag of either u or v).

Informally, given a bag $B$, a $\mathsf {U}$-shaped path in $B$ is a path that traverses intermediate nodes that exist only in the subtree of $\mathrm {Tree}(G)$ rooted in $B$. The following remark follows from the definition of tree-decompositions, and states that every simple cycle C can be seen as a $\mathsf {U}$-shaped path P from the smallest-level node of C to itself. Consequently, we can determine the value $c^{*}$ by only considering $\mathsf {U}$-shaped paths in $\mathrm {Tree}(G)$.

Remark 1

Let $C=(u_1,\dots , u_k)$ be a simple cycle in G, and $u_j=\arg \min _{u_i\in C}\mathsf {Lv}(u_i)$. Then $P=(u_j, u_{j+1},\dots u_k, u_1,\dots , u_j)$ is a $\mathsf {U}$-shaped path in $B_{u_j}$, and $\mathsf {wt}(P)=\mathsf {wt}(C)$.

Informal Description of $\mathsf {MinCycle}$ . Based on $\mathsf {U}$-shaped paths, the work of [18] presented a method for computing algebraic path properties on tree-decompositions with constant width, where the weights of the edges come from a general semiring. Note that integer-valued weights are a special case of the tropical semiring. Our algorithm $\mathsf {MinCycle}$ is similar to the algorithm $\mathsf {Preprocess}$ from [18]. It consists of a depth-first traversal of $\mathrm {Tree}(G)$, and for each examined bag $B$ computes a local distance map $\mathsf {LD}_{B}:B\times B\rightarrow \mathbb {Z}\cup \{\infty \}$ such that for each $u,v\in B$, we have (i) $\mathsf {LD}_{B}(u,v)=\mathsf {wt}(P)$ for some path $P:u\rightsquigarrow v$, and (ii) $\mathsf {LD}_{B}\le \min _{P}\mathsf {wt}(P)$, where P are taken to be simple $u\rightsquigarrow v$ paths (or simple cycles) that are $\mathsf {U}$-shaped in $B$. This is achieved by traversing $\mathrm {Tree}(G)$ in post-order, and for each root bag $B_x$ of a node x, we update $\mathsf {LD}_{B_x}(u,v)$ with $\mathsf {LD}_{B_x}(u,x) + \mathsf {LD}_{B_x}(x,v)$ (i.e., we do path-shortening from node u to node v, by considering paths that go through x). See Fig. 1 for an illustration. At the end, $\mathsf {MinCycle}$ returns the smallest $\mathsf {LD}_{B_x}(x,x)$ it has found.

Fig. 1.

Path shortening in $\mathsf {MinCycle}$. When $B_x$ is examined, $\mathsf {LD}_{B_x}(u,v)$ is updated with the weight of the $\mathsf {U}$-shaped path $P=P_1\circ P_2$. The paths $P_1$ and $P_2$ are $\mathsf {U}$-shaped paths in the children bags $B_1$ and $B_2$ of $B_x$, and we have $\mathsf {LD}_{B_i}(u,x)=\mathsf {wt}(P_i)$.

The following lemma follows easily from [18, Lemma 2], and states that $\mathsf {LD}_{B}(u,v)$ is upper bounded by the smallest weight of a $\mathsf {U}$-shaped simple $u\rightsquigarrow v$ path in $B$.

Lemma 1

([18, Lemma 2]). For every examined bag $B$ and nodes $u,v\in B$, we have (1) $\mathsf {LD}_{B}(u,v)=\mathsf {wt}(P)$ for some path $P:u\rightsquigarrow v$ (and $\mathsf {LD}_{B}(u,v)=\infty$ if no such P exists), and (2) $\mathsf {LD}_{B}(u,v)\le \min _{P:u\rightsquigarrow v}\mathsf {wt}(P)$ where P ranges over $\mathsf {U}$-shaped simple paths and simple cycles in $B$.

Based on Lemma 1, we show that $\mathsf {MinCycle}$ returns $\min _{x}\mathsf {LD}_{B_x}(x,x)$, i.e., the weight of the smallest-weight $\mathsf {U}$-shaped (not necessarily simple) cycle $C:x\rightsquigarrow x$ it has discovered. The cycle C has polynomial (in n) length, thus $|\mathsf {wt}(C)|=|c^{*} |\cdot n^{O(1)}$, and C is necessarily simple if there are no negative cycles in G, in which case $\mathsf {wt}(C)=c^{*}$. We refer to the full version for a detailed analysis [22]. This leads to the following theorem.

Theorem 2

Let $G=(V,E,\mathsf {wt})$ be a weighted graph of n nodes with constant treewidth, and a balanced, binary tree-decomposition $\mathrm {Tree}(G)$ of G be given. Let $c^{*}$, be the smallest weight of a simple cycle in G. Algorithm $\mathsf {MinCycle}$ uses O(n) time and $O(\log n)$ additional space, and returns a value c such that:

• 1. If G has no negative cycles, then $c=c^{*}$.

• 2. If G has a negative cycle, then $c\le c^{*}$, and $|c|=|c^{*}|\cdot n^{O(1)}$.

4 The Minimum Ratio and Mean Cycle Problems

In the current section we present algorithms for solving the minimum ratio and mean cycle problems for weighted graphs $G=(V,E,\mathsf {wt}, \mathsf {wt}^{\prime })$ of constant treewidth.

Remark 2

If G is not strongly connected, we can compute its maximal strongly connected components (SCCs) in linear time [41], and use the algorithms of this section to compute the minimum cycle ratio $\nu ^{*}_i$ in every component $\mathcal {G}_i$. Afterwards, we assign the ratio values $\nu ^{*}(u)$ for all nodes u as follows. First, mark every SCC $\mathcal {G}_i$ with $M(\mathcal {G}_i)=\nu ^{*}_i$. Then, for every bottom SCC $\mathcal {G}_i$, (i) for every u in $\mathcal {G}_i$ assign $\nu ^{*}(u)=M(\mathcal {G}_i)$, (ii) for every neighbor SCC $\mathcal {G}_j$ of $\mathcal {G}_i$, mark $\mathcal {G}_j$ with $M(\mathcal {G}_j)=\min (M(\mathcal {G}_j), M(\mathcal {G}_i))$, (iii) remove $\mathcal {G}_i$ and repeat. Since these operations require linear time in total, they do not impact the time complexity. Therefore, we consider graphs G that are strongly connected, and we will speak about the minimum ratio $\nu ^{*}$ and mean $\mu ^{*}$ values of G.

Claim 1

Let $\nu ^{*}$ be the ratio value of G. Then $\nu ^{*}\ge \nu$ iff for every cycle C of G we have $\mathsf {wt}_{\nu }(C)\ge 0$, where $\mathsf {wt}_{\nu }(e)=\mathsf {wt}(e)-\mathsf {wt}^{\prime }(e)\cdot \nu$ for each edge $e\in E$.

Hence, given a tree-decomposition $\mathrm {Tree}(G)$, and a guess $\nu$ of the ratio value $\nu ^{*}$, we can evaluate whether $\nu ^{*}\ge \nu$ by executing algorithm $\mathsf {MinCycle}$ on input $G_{\nu }=(V,E,\mathsf {wt}_{\nu })$. By Item 2a of Theorem 2 and Claim 1 we have that the returned value c of $\mathsf {MinCycle}$ is $c\ge 0$ iff $\mathsf {wt}_{\nu }(C)\ge 0$ for all cycles C, iff $\nu ^{*}\ge \nu$ (and in fact $c=0$ iff $\nu ^{*} = \nu$).

4.1 Exact Solution

We now describe the method for determining the value $\nu ^{*}$ of G exactly. This is done by making various guesses $\nu$ such that $\nu ^{*}\ge \nu$ and testing for negative cycles in the graph $G_{\nu }=(V,E,\mathsf {wt}_{\nu })$. We first determine whether $\nu ^{*} = 0$, using Claim 1. In the remaining of this section we assume that $\nu ^{*}\ne 0$.

Solution Overview. Consider that $\nu ^{*}> 0$. First, we either find that $\nu ^{*}\in (0,1)$ (hence $\lfloor \nu ^{*}\rfloor =0$), or perform an exponential search of $O(\log \nu ^{*} )$ iterations to determine $j\in \mathbb {N}^+$ such that $\nu ^{*}\in [2^{j-1}, 2^{j}]$. In the latter case we perform a binary search of $O(\log \nu ^{*})$ iterations in the interval $[2^{j-1}, 2^{j}]$ to determine $\lfloor \nu ^{*}\rfloor$. Then we can write $\nu ^{*} = \lfloor \nu ^{*}\rfloor + x$, where $x<1$ is an irreducible fraction $\frac{a}{b}$. It has been shown [39] that such x can be determined by evaluating $O(\log b)$ inequalities of the form $x\ge \nu$. The case for $\nu ^{*}<0$ is handled similarly. We refer to the full version of the paper for a detailed description [22]. We thus obtain the following theorem, and by Theorem 1 the corollaries follow.

Theorem 3

Let $G=(V,E,\mathsf {wt}, \mathsf {wt}^{\prime })$ be a weighted graph of n nodes with constant treewidth, and $\lambda =\max _u |a_u\cdot b_u|$ such that $\nu ^{*}(u)$ is the irreducible fraction $\frac{a_u}{b_u}$. Let $\mathcal {T}(G)$ and $\mathcal {S}(G)$ denote the required time and space for constructing a balanced binary tree-decomposition $\mathrm {Tree}(G)$ of G with constant width. The minimum ratio cycle problem for G can be computed in (1) $O(\mathcal {T}(G)+n\cdot \log \lambda )$ time and $O(\mathcal {S}(G)+n)$ space; and (2) $O(\mathcal {S}(G)+\log n)$ space.

Corollary 1

Let $G=(V,E,\mathsf {wt}, \mathsf {wt}^{\prime })$ be a weighted graph of n nodes with constant treewidth, and $\lambda =\max _u |a_u\cdot b_u|$ such that $\nu ^{*}(u)$ is the irreducible fraction $\frac{a_u}{b_u}$. The minimum ratio value problem for G can be computed in (1) $O(n\cdot \log \lambda )$ time and O(n) space; and (2) $O(\log n)$ space.

Corollary 2

Let $G=(V,E,\mathsf {wt})$ be a weighted graph of n nodes with constant treewidth, and $\lambda = \max _u |\mu ^{*}(u)|$. The minimum mean value problem for G can be computed in (1) $O(n\cdot \log \lambda )$ time and O(n) space; and (2) $O(\log n)$ space.

4.2 Approximating the Minimum Mean Cycle

We now focus on the minimum mean cycle problem, and present a method for $\epsilon$-approximating the mean value $\mu ^{*}$ of G for any $0<\epsilon <1$ in $O(n\cdot \log (n/\epsilon ))$ time.

Approximate Solution in the Absence of Negative Cycles. We first consider graphs G that do not have negative cycles. Let C be a minimum weight simple cycle in G, and note that $\mu ^{*}\in [0,\mathsf {wt}(C)]$. Additionally, we have $\mathsf {wt}(C)\le n\cdot \mu ^{*}$. Consider a binary search in the interval $[0,\mathsf {wt}(C)]$, which in step i approximates $\mu ^{*}$ by the right endpoint $\mu _i$ of its current interval. The error is bounded by the length of the interval, hence $\mu _i-\mu ^{*}\le \mathsf {wt}(C)\cdot 2^{-i} \le n\cdot \mu ^{*}\cdot 2^{-i}$. To approximate within a factor $\epsilon$ it suffices to iterate for i steps, where $i\ge \log (n/\epsilon )$.

Approximate Solution in the Presence of Negative Cycles. We now turn our attention to $\epsilon$-approximating $\mu ^{*}$ in the presence of negative cycles in G. Let c be the value returned by $\mathsf {MinCycle}$ on input G. Item 2a of Theorem 2 guarantees that for the weight function $\mathsf {wt}_{-|c|}(e)=\mathsf {wt}(e)+|c|$, the graph $G_{-|c|}=(V,E,\mathsf {wt}_{-|c|})$ has no negative cycles (although it might still have negative edges). We show that $\mu ^{*}$ can be $\epsilon$-approximated by $\epsilon '$-approximating the value $\mu '^{*}$ of $G_{-|c|}$, for some $\epsilon '$ polynomially (in n) smaller than $\epsilon$ (i.e., $\epsilon '=\epsilon /n^{O(1)}$). We refer to the full version for a detailed description [22].

Theorem 4

Let $G=(V,E,\mathsf {wt})$ be a weighted graph of n nodes with constant treewidth. For any $0<\epsilon <1$, the minimum mean value problem can be $\epsilon$-approximated in $O(n\cdot \log (n/\epsilon ))$ time and O(n) space.

5 The Minimum Initial Credit Problem

In the current section we present algorithms for solving the minimum initial credit problem on weighted graphs $G=(V,E,\mathsf {wt})$. We first deal with arbitrary graphs, and provide an $O(n\cdot m)$ algorithm for the decision problem, and an $O(n^2\cdot m)$ algorithm for the value problem, improving the previously best upper bounds. Afterwards we adapt our approach to graphs of constant treewidth to obtain an $O(n\cdot \log n)$ algorithm.

Non-positive Minimum Initial Credit. For technical convenience we focus on a variant of the minimum initial credit problem, where energies are non-positive, and the goal is to keep partial sums of path prefixes non-positive. Formally, given a weighted graph $G=(V,E,\mathsf {wt})$, the non-positive minimum initial credit value problem asks to determine for each node u the largest energy value $\mathsf {E}(u)\in \mathbb {Z}_{\le 0}\cup \{-\infty \}$ with the following property: there exists an infinite path $\mathcal {P}=(u_1, u_2\dots )$ with $u=u_1$, such that for every finite prefix P of $\mathcal {P}$ we have $\mathsf {E}(u)+\mathsf {wt}(P)\le 0$. We let $\mathsf {E}(u)=-\infty$ if no finite such value exists. Hence, minimality is wrt the absolute value of the energy. The associated decision problem asks given a node u and an initial credit $c\in \mathbb {Z}_{\le 0}$ whether $\mathsf {E}(u)\ge c$.

We start with some definitions and claims that will give the intuition for the algorithms to follow. First, we define the minimum initial credit of a pair of nodes u, v, which is the energy to reach v from u (i.e., the energy is wrt a finite path).

Finite Minimum Initial Credit. For nodes $u,v\in V$, we denote by $\mathsf {E}_v(u)\in \mathbb {Z}_{\le 0}\cup \{-\infty \}$ the largest value with the following property: there exists a path $P:u\rightsquigarrow v$ such that for every prefix $P'$ of P we have $\mathsf {E}_v(u)+\mathsf {wt}(P')\le 0$. We let $\mathsf {E}_v(u)=-\infty$ if there is no path $u\rightsquigarrow v$. Note that for every pair of nodes $u,v\in V$, we have $\mathsf {E}(u)\ge \mathsf {E}_v(u)+\mathsf {E}(v)$.

Highest-Energy Nodes. Given a (possibly infinite) path P with $\mathsf {wt}(P)<\infty$, we say that a node $x\in P$ is a highest-energy node of P if there exists a highest-energy prefix $P_1$ of P ending in x such that for any prefix $P_2$ of P we have $\mathsf {wt}(P_1)\ge \mathsf {wt}(P_2)$. Note that since the weights are integers, for every pair of paths $P'_1$, $P'_2$, it is either $|\mathsf {wt}(P'_1)-\mathsf {wt}(P'_2)|=0$ or $|\mathsf {wt}(P'_1)-\mathsf {wt}(P'_2)|\ge 1$. Therefore the set $\{\mathsf {wt}(P_i)\}_i$ of weights of prefixes of P has a maximum, and thus a highest-energy node always exists when $\mathsf {wt}(P)<\infty$. The following properties are easy to verify:

• 1. If x is a highest-energy node in a path $P:u\rightsquigarrow v$, then $\mathsf {E}_v(x)=0$.

• 2. If x is a highest-energy node in an infinite path $\mathcal {P}$, then $\mathsf {E}(x)=0$.

Using the above properties we establish Claim 2, which is central to our algorithms.

Claim 2

For every $u\in V$, we have $\mathsf {E}(u)=\max _{v:\mathsf {E}(v)=0}\mathsf {E}_v(u)$.

5.1 The Decision Problem for General Graphs

Recall the decision problem: given a node u and an initial credit $c\in \mathbb {Z}_{\le 0}$, decide whether $\mathsf {E}(u)\ge c$. Our algorithm is based on Claim 3. The key idea is that $\mathsf {E}(u)\ge c$ iff there exists a witness path that reaches a non-positive cycle in less than n steps.

Claim 3

For every $u\in V$ and $c\in \mathbb {Z}_{\le 0}$, we have that $\mathsf {E}(u) \ge c$ iff there exists a simple cycle C such that (i) $\mathsf {wt}(C) \le 0$ and (ii) for every $v\in C$ we have that $\mathsf {E}_v(u) \ge c$, which is witnessed by a path $P_v:u\rightsquigarrow v$ with $|P_v|<n$.

Algorithm $\mathsf {DecisionEnergy}$. Claim 3 suggests a way to decide whether $\mathsf {E}(u) \ge c$. First, we start with energy c from u, and perform $n-1$ relaxation steps, similar to the Bellman-Ford algorithm, to discover the set $V_u^c$ of nodes that can be reached from u with initial credit c by a path of length at most $n-1$. Afterwards, we perform a Bellman-Ford computation on the subgraph $G\upharpoonright V_u^c$ induced by the set $V_u^c$. By Claim 3, we have that $\mathsf {E}(u) \ge c$ iff $G\upharpoonright V_u^c$ contains a non-positive cycle. We refer to the full version for a detailed description [22]. We thus obtain the following theorem.

Theorem 5

Let $G=(V,E,\mathsf {wt})$ be a weighted graph of n nodes and m edges. Let $u\in V$ be an initial node, and $c\in \mathbb {Z}_{\le 0}$ be an initial credit. The decision problem of whether $\mathsf {E}(u)\ge c$ can be solved in $O(n\cdot m)$ time and O(n) space.

5.2 The Value Problem for General Graphs

We now turn our attention to the value problem, where the task is to determine $\mathsf {E}(u)$ for every node u. The following claim reduces the finite minimum initial credit problem to reach a node v to the shortest-path problem, when all energies to reach v are negative.

Claim 4

If for all $w\in V\setminus \{v\}$ we have $\mathsf {E}_v(w)<0$, then for each $u\in V\setminus \{v\}$ we have $\mathsf {E}_v(u)=-d(u,v)$.

The rest of the section provides a $O(k\cdot n\cdot m)$ time solution, where $k=|X|+1$ is the number of 0-energy nodes (plus one). This solution is faster in graphs where $k=o(n)$. This is achieved by algorithm $\mathsf {ZeroEnergyNodes}$ for obtaining the set X fast.

Determining the 0-Energy Nodes. To determine the set of 0-energy nodes, we construct the graph $G_2=(V_2, E_2, \mathsf {wt}_2)$ with a fresh node $z\not \in V$ as follows:

• 1. The node set is $V_2=V\cup \{z\}$,

• 2. The edge set is $E_2=E\cup (\{z\}\times V)$,

• 3. The weight function $\mathsf {wt}_2:E_2\rightarrow \mathbb {Z}$ is $\mathsf {wt}_2(u,v) = \left\{ \begin{array}{ll} 0 &{} \text{ if } u=z \\ \mathsf {wt}(u,v) &{} \text{ otherwise } \end{array} \right.$

Note that for every $u\in V$, the energy $\mathsf {E}(u)$ is the same in G and $G_2$.

Algorithm $\mathsf {ZeroEnergyNodes}$. Algorithm $\mathsf {ZeroEnergyNodes}$ is used for obtaining the set X of all 0-energy nodes in $G_2$. Informally, the algorithm performs a sequence of modifications on a graph , initially identical to $G_2$. In each step, the algorithm executes a Bellman-Ford computation on the current graph with z as the source node, as long as a non-positive cycle C is discovered. For every such C, it determines a highest-energy node w of C, and modifies by replacing every incoming edge (x, w) with an edge (x, z) of the same weight, and then removing w. See Fig. 2 for an illustration.

Determining the Negative-Energy Nodes. Given the set X of 0-energy nodes, it remains to determine the energy of every other node $u\in V\setminus X$. Let be the modified graph of algorithm $\mathsf {ZeroEnergyNodes}$ after the set X has been computed. To compute the energy $\mathsf {E}(u)$ of each node $u\in V\setminus X$, it suffices to compute its distance to z in . This reduces to a single-source shortest path instance from z on with all edges reversed. Figure 2 illustrates the algorithms on an example. We refer to the full version of the paper for a detailed description [22]. We obtain the following theorem.

Fig. 2.

Solving the value problem using operations on the graph . Initially we examine , and a non-positive cycle is found (boldface edges) with highest-energy node x. Thus $\mathsf {E}(x)=0$, and we proceed with , to discover $\mathsf {E}(u)=0$. In all cycles are positive, and the energy of each remaining node is minus its distance to z.

Theorem 6

Let $G=(V,E,\mathsf {wt})$ be a weighted graph of n nodes and m edges, and $k=|\{v\in V: \mathsf {E}(v)=0\}|+1$. The minimum initial credit value problem for G can be solved in $O(k\cdot n\cdot m)$ time and O(n) space.

Corollary 3

Let $G=(V,E,\mathsf {wt})$ be a weighted graph of n nodes and m edges. The minimum initial credit value problem for G can be solved in $O( n^2\cdot m)$ time and O(n) space.

5.3 The Value Problem for Constant-Treewidth Graphs

We now turn our attention to the minimum initial credit value problem for constant-treewidth graphs $G=(V,E,\mathsf {wt})$. Note that in such graphs $m=O(n)$, thus Theorem 6 gives an $O(n^3)$ time solution as compared to the existing $O(n^4\cdot \log (n\cdot W))$ time solution. This section shows that we can do significantly better, namely reduce the time complexity to $O(n\cdot \log n)$. This is mainly achieved by algorithm $\mathsf {ZeroEnergyNodesTW}$ for computing the set X of 0-energy nodes fast in constant-treewidth graphs.

Extended $\varvec{+}$ and $\varvec{\min }$ Operators. Recall the graph $G_2=(V_2,E_2,\mathsf {wt}_2)$ from the last section. Given $\mathrm {Tree}(G)$, a balanced and binary tree-decomposition $\mathrm {Tree}(G_2)$ of $G_2$ with width increased by 1 can be easily constructed by (i) inserting z to every bag of $\mathrm {Tree}(G)$, and (ii) adding a new root bag that contains only z. Let $\mathcal {I}=\mathbb {Z}\times V\times \mathbb {Z}$. For a map $f:V_2\times V_2\rightarrow \mathbb {Z}$, define the map $g_{f}:V_2\times V_2\rightarrow \mathcal {I}$ as

$$ g_{f}(u,v) = \left\{ \begin{array}{ll} (f(u,v), u, 0) &{} ~~\text{ if } f(u,v)<0 \text{ or } v=z\\ (f(u,v), v, f(u,v)) &{} ~~\text{ otherwise } \\ \end{array} \right. $$

For triplets of elements $\alpha _1=(a_1,b_1, c_1),\alpha _2=(a_2,b_2, c_2)\in \mathcal {I}$, define the operations

• 1. $\varvec{\min }(\alpha _1,\alpha _2)=\alpha _i$ with $i=\arg \min _{j\in \{1,2\}}a_j$

• 2. $\alpha _1\varvec{+}\alpha _2 = (a_1+a_2, b, c)$, where $c=\max (c_1,a_1+c_2)$ and $b=b_1$ if $c=c_1$ else $b=b_2$.

In words, if f is a weight function, then $g_{f}(u,v)$ selects the weight of the edge (u, v), its highest-energy node (i.e., u if $f(u,v)<0$, and v otherwise, except when $v=z$), and the weight to reach that node from u. Recall that algorithm $\mathsf {MinCycle}$ from Sect. 3 traverses a tree-decomposition bottom-up, and for each encountered bag $B$ stores a map $\mathsf {LD}_{B}$ such that $\mathsf {LD}_{B}(u,v)$ is upper bounded by the weight of the shortest $\mathsf {U}$-shaped simple path $u\rightsquigarrow v$ (or simple cycle, if $u=v$). Our algorithm $\mathsf {ZeroEnergyNodesTW}$ for determining all 0-energy nodes is similar, but now $\mathsf {LD}_{B}$ stores triplets (a, b, c) where a is the weight of a $\mathsf {U}$-shaped path P, b is a highest-energy node of P, and c the weight of a highest-energy prefix of P. For triplets $\alpha _1=(a_1,b_1, c_1),\alpha _2=(a_2,b_2, c_2)\in \mathcal {I}$ corresponding to $\mathsf {U}$-shaped paths $P_1$, $P_2$, $\varvec{\min }(\alpha _1,\alpha _2)$ selects the path with the smallest weight, and $\alpha _1\varvec{+}\alpha _2$ determines the weight, a highest-energy node, and the weight of a highest-energy prefix of the path $P_1\circ P_2$ (see Fig. 3).

Fig. 3.

Illustration of the $\alpha _1\varvec{+}\alpha _2$ operation, corresponding to concatenating paths $P_1$ and $P_2$. The path $P_j^i$ denotes the i-th prefix of $P_j$. We have $P=P_1\circ P_2$, and the corresponding tripplet $\alpha =(a,b,c)$ denotes the weight a of P, its highest-energy node b, and the weight c of a highest-energy prefix.

Algorithm $\mathsf {ZeroEnergyNodesTW}$. The algorithm $\mathsf {ZeroEnergyNodesTW}$ for computing the set of 0-energy nodes in constant-treewidth graphs follows the same principle as $\mathsf {ZeroEnergyNodes}$ for general graphs. It stores a map of edge weights , and initially . The algorithm performs a bottom-up pass, and computes in each bag the local distance map $\mathsf {LD}_{B}:B\times B\rightarrow \mathcal {I}$ that captures $\mathsf {U}$-shaped $u\rightsquigarrow v$ paths, together with their highest-energy nodes (similar to algorithm $\mathsf {MinCycle}$ from Sect. 3). When a non-positive cycle C is found, the algorithm modifies the edges of a highest-energy node w of C and its incoming neighbors (similar to algorithm $\mathsf {ZeroEnergyNodes}$). These updates affect the distances between the remaining nodes, hence some local distance maps $\mathsf {LD}_{B}$ need to be corrected. We prove that each such edge modification only affects the local distance map of bags that appear in a path from a bag $B'$ to some ancestor $B''$ of $B'$. Instead of restarting the computation as in $\mathsf {ZeroEnergyNodes}$, the algorithm only updates those maps along the path $B'\rightsquigarrow B''$. We refer to the full version for a detailed description [22].

Theorem 7

Let $G=(V,E,\mathsf {wt})$ be a weighted graph of n nodes with constant treewidth. The minimum initial credit value problem for G can be solved in $O(n\cdot \log n)$ time and O(n) space.

6 Experimental Results

Here we report on preliminary experimental evaluation of our algorithms, and compare them to existing methods. Our algorithm for the minimum mean cycle problem provides improvement for constant-treewidth graphs, and has thus been evaluated on constant-treewidth graphs obtained from the control-flow graphs of programs. For the minimum initial credit problem, we have implemented our algorithm for arbitrary graphs, thus the benchmarks in this case are general graphs (i.e., not constant-treewidth graphs).

Minimum Mean Cycle. We have implemented our approximation algorithm for the minimum mean cycle problem, and we let the algorithm run for as many iterations until a minimum mean cycle was discovered, instead of terminating after $O(\log (n/\epsilon ))$ iterations required by Theorem 4. We have tested its performance in running time and space against six other minimum mean cycle algorithms from Table 3 in control-flow graphs of programs. The algorithms of Burns and Lawler solve the more general ratio cycle problem, and have been adapted to the mean cycle problem as in [26].

Table 3. Asymptotic complexity of compared minimum mean cycle algorithms.

The algorithms were executed on control-flow graphs of methods of programs from the DaCapo benchmark suit [3], obtained using the Soot framework [43]. For each benchmark we focused on graphs of at least 500 nodes. This supplied a set of medium sized graphs (between 500 and 1300 nodes), in which integer weights were assigned uniformly at random in the range $\{-10^3,\dots , 10^3\}$. Figure 4 shows the average time performance of the examined algorithms (bars that exceeded the maximum value in the y-axis have been truncated). Our algorithm has much smaller running time than each other algorithm, in almost all cases.

Fig. 4.

Average performance of minimum mean cycle algorithms.

Minimum Initial Credit. We have implemented our algorithm for the minimum initial credit problem on general graphs and evaluated its performance on a subset of benchmark weighted graphs from the DIMACS implementation challenges [1]. Our algorithm was tested against the existing method of [10], and an optimized version of that method. For each input graph we subtracted its minimum mean value $\mu ^{*}$ from the weight of each edge to ensure that at least one non-positive cycle exists (thus the energies are finite). Figure 5 depicts the running time of the algorithm of [10] (with and without optimizations) vs our algorithm. A timeout was forced at $10^{10} \mu s$. Our algorithm is orders of magnitude faster, and scales better than the existing method.

Fig. 5.

Comparison of running times for the minimum initial credit value problem.