Concept Synthesis Using Logic of Prototypes and Counterexamples: A Graded Consequence Approach

Abstract

This paper is a preliminary step towards proposing a scheme for synthesis of a concept out of a set of concepts focusing on the following aspects. The first is that the semantics of a set of simple (or independent) concepts would be understood in terms of its prototypes and counterexamples, where these instances of positive and negative cases may vary with the change of the context, i.e., a set of situations which works as a precursor of an information system. Secondly, based on the classification of a concept in terms of the situations where it strictly applies and where not, a degree of application of the concept to some new situation/world would be determined. This layer of reasoning is named as logic of prototypes and counterexamples. In the next layer the method of concept synthesis would be designed as a graded concept based on the already developed degree based approach for logic of prototypes and counterexamples.

1 Introduction

In our everyday decision making we face a few challenges. Some of them are, selecting relevant interpretations of the vague concepts involved in our daily communications, synthesis or analysis of new concepts in terms of the available (component) concepts, and deciding the applicability of a concept to a newly appeared situation based on some initial situations or worlds where the applicability of the concept of concern is known. So, while proposing the theory we would focus on the following issues; one is the semantics of the vague concepts, second is a general concept synthesis mechanism to generate compound (or dependent) concepts based on the simple (or independent) concepts, and the third is to allow open world scenario so that based on the available database decisions about the new situations/worlds/cases can be induced. Plenty of approaches concerning fuzzy sets, rough sets and their combinations are available [1, 6, 7, 13–20] to deal with the above mentioned aspects of human reasoning. Some of the theories [15, 19, 20] are used and verified against the real practical needs of automated decision support system.

We, in this paper, set a preliminary step to develop a theoretical background for a logic of prototypes and counterexamples, where a vague concept would be understood by clear positive and negative instances of its application. While developing the theory we would keep a room open for appearance of new cases, for which decisions regarding the applicability of a concept need to be taken. We would take a degree based approach to design the logic of prototypes and counterexamples based on the already developed notion of fuzzy approximation space [6]. Given this ground set-up, where concepts are understood in terms of their prototypes and counterexamples, interrelation between a set of (sub)concepts and a concept is defined as an application of graded consequence relation [2, 3]. Thus synthesis of a concept based on the interpretations of its component concepts is done in a graded approach. Drawing analogy from the real needs of a computer-aided decision support system, particularly in the field of health-care, we would try to explain why the theory, proposed in this paper, is worth exploring further.

2 Logic of Prototypes and Counterexamples

In this section we start with the notion of fuzzy approximation space as given in [6].

Definition 1

[6]. A fuzzy approximation space is defined as a pair ($U, R$) where $R$ is a fuzzy binary relation on $U$, i.e., $R: U \times U \mapsto [0, 1]$. The fuzzy lower and upper approximations $\underline{R}F, \overline{R}F: U \mapsto [0, 1]$ of a crisp or fuzzy subset $F$ of $U$ is defined as follows. $\underline{R}F(u)$ = $\inf _{v \in U}\{R(u, v) \rightarrow F(v)\}$ and $\overline{R}F(u)$ = $\sup _{v \in U}\{R(u, v) *F(v)\}$, where $*: [0, 1] \times [0, 1] \mapsto [0, 1]$ is a t-norm [12], and $\rightarrow : [0, 1] \times [0, 1] \mapsto [0, 1]$ is the S-implication [12] with respect to $*$ such that $a \rightarrow b$ = $1$ - $(a *(1$ - $b))$.

Let us start with an overview of the problem, a mathematical model of which would be our target to achieve under the name of ‘logic of prototypes and counterexamples’. Let we have a clinical record of $n$ number of patients’ details with respect to some $m$ number of parameters/attributes. These parameters might be some objective values of some clinical tests, called signs, or some subjective features experienced by the patients, called symptoms. With respect to the state of each patient, the values corresponding to all these parameters are converted, by some mean, to the values over a common scale, say $[0, 1]$. That is, if an $m$-tuple $\langle a_{1}, a_{2}, \ldots , a_{m}\rangle$ from $[0, 1]^{m}$ represents the rates of the $m$ parameters corresponding to a patient, then we say $\langle a_{1}, a_{2}, \ldots , a_{m}\rangle$ describes the state of a patient. Based on the rates assigned to all the parameters by each patient, i.e. a $m$-tuple of values $\langle a_{1}, a_{2}, \ldots , a_{m}\rangle$ from $[0, 1]^{m}$, which cases representing the states of the patients are how much similar or dissimilar may be anticipated. Now, one task is to make a tentative diagnosis about a patient whose measurement concerning the $m$-tuple of parameters appears to be new with respect to the database of the $n$ patients.

So, in the general set-up we start with a set $S$ of finitely many situations, say $\{s_{1}, s_{2}, \ldots , s_{n}\}$, and $P$ of finitely many parameters $\{p_{1}, p_{2}, \ldots , p_{m}\}$. Each $s_{i}$, $i$ = 1, 2, ...$n$, is considered to be a function $s_{i}: P \mapsto [0, 1]$. Let the consolidated data of each situation is stored in the form of a set $\{\langle s_{i}(p_{1}), s_{i}(p_{2}), \ldots , s_{i}(p_{m})\rangle : s_{i} \in S\}$, which is a subset of $[0, 1]^{m}$. Let $W \subseteq [0, 1]^{m}$ and $\{\langle s_{i}(p_{1}), s_{i}(p_{2}), \ldots , s_{i}(p_{m})\rangle : s_{i} \in S\} \subseteq W$. Each member of $W$ may be called a world. We now consider a fuzzy approximation space $\langle W, Sim\rangle$, where $Sim$ is a fuzzy similarity relation between worlds of $W$. That is, $Sim: W \times W \mapsto [0, 1]$, and we assume $Sim$ to satisfy the following properties.

• (i) $Sim(\upomega , \upomega )$ = 1 (reflexivity)

• (ii) $Sim(\upomega , \upomega ^{\prime })$ = $Sim(\upomega ^{\prime }, \upomega )$ (symmetry)

• (iii) $Sim(\upomega , \upomega ^{\prime }) *Sim(\upomega ^{\prime }, \upomega ^{\prime \prime }) \le Sim(\upomega , \upomega ^{\prime \prime })$ (transitivity)

Following [6], the fuzzy approximation space $\langle W, Sim\rangle$ is based on the unit interval $[0, 1]$ endowed with a t-norm $*$ and a S-implication operation $\rightarrow$, as mentioned in Definition 1. In Sect. 3, apart from $\rightarrow$ we would also require $\rightarrow _{*}$, the residuum operation with respect to $*$ in $[0, 1]$.

We now propose to represent any (vague) concept $\upalpha$ by a pair ($\upalpha ^{+}, \upalpha ^{-}$) consisting of the positive instances (prototypes) and negative instances (counterexamples) of $\upalpha$ respectively, where $\upalpha ^{+}, \upalpha ^{-} \subseteq W$ and $\upalpha ^{+} \cap \upalpha ^{-}$ = $\upphi$.

Definition 2

Given the fuzzy approximation space $\langle W, Sim\rangle$, and a concept $\upalpha$ represented by ($\upalpha ^{+}, \upalpha ^{-}$), the degree to which $\upalpha$ applies to a world $\upomega \in W$, denoted by $gr(\upomega \models \upalpha )$, is given by:

$$\begin{aligned}gr(\upomega \models \upalpha )&= 1 \text { if }\upomega \in {\upalpha }^{+},\\&= 0, \text { if } \upomega \in {\upalpha }^{-}, \text { and }\\&= \overline{Sim}{\upalpha }^{+}(\upomega ) *\lnot \overline{Sim}{\upalpha }^{-}(\upomega ), \text { otherwise.}\end{aligned}$$

The fuzzy upper approximations $\overline{Sim}\upalpha ^{+}$ and $\overline{Sim}\upalpha ^{-}$ are defined following the Definition 1, i.e., $\overline{Sim}\upalpha ^{+}(\upomega )$ = $\sup _{u \in W}Sim(\upomega , u) *\upalpha ^{+}(u)$ = $\sup _{u \in \upalpha ^{+}}Sim(\upomega , u)$. Similar is the case for $\overline{Sim}\upalpha ^{-}$. For further references we should also note that the fuzzy lower approximation is defined as $\underline{Sim}\upalpha ^{-}(\upomega )$ = $\inf _{u \in W}\{Sim(\upomega , u) \rightarrow \upalpha ^{-}(u)\}$ = 1 - $\inf _{u \notin \upalpha ^{-}}Sim(\upomega , u)$. The simplifications of $\overline{Sim}\upalpha ^{+}(\upomega )$ and $\underline{Sim}\upalpha ^{-}(\upomega )$ are done based on the properties of $*$, $\rightarrow$, and $\lnot$, where $a \rightarrow 1$ = 1, $a \rightarrow 0$ = $\lnot a$ = $1$ - $a$.

The third case given in the Definition 2 formalizes the idea that a concept $\upalpha$ applies to a newly appeared world $\upomega$ if $\upomega$ is similar to a world which lies in the possible zone of the positive instances of $\upalpha$ , and it is not that $\upomega$ is similar to a world which lies in the possible zone of the negative instances of $\upalpha$.

In the definition of $\models$, we have not specified the definition for $Sim$. $Sim$ may be interpreted in different ways. Sometimes $Sim$ is considered to be inversely proportional to a notion of distance. Here, we may think that given a set of prototypes and counterexamples of a property $\upalpha$, whether at a new situation/world $\upalpha$ applies or not, would depend on the arguments which go in favour of that the world qualifies $\upalpha$, as well as the arguments which go against; checking the above could be equivalent to check the degree of strength of the arguments which go in favour of considering the new world $\upomega$ to be similar to the set of positive instances of $\upalpha$, and the degree of strength of the arguments which go against for considering $\upomega$ similar to the worlds of $\upalpha ^{+}$. The arguments which go against considering $\upomega$ to be similar to the worlds of $\upalpha ^{+}$ can be counted as the same as the arguments which go in favour of considering $\upomega$ similar to the worlds of $\upalpha ^{-}$. So, $Sim$ would have some relations with the argument in favour and the argument against. For this paper we do not need to specify what do we really mean by the argument in favour and the argument against; let us just equate $\overline{Sim}\upalpha ^{+}(\upomega )$ = $D_{af}(\upomega , \upalpha )$, the degree of arguments in favour of $\upomega$ qualifies $\upalpha$ and $\overline{Sim}\upalpha ^{-}(\upomega )$ = $D_{ag}(\upomega , \upalpha )$, the degree of arguments against $\upomega$ qualifies $\upalpha$. So, given a concept $\upalpha$ and world $\upomega \notin \upalpha ^{+}, \upalpha ^{-}$, $gr(\upomega \models \upalpha )$ = $D_{af}(\upomega , \upalpha ) *\lnot D_{ag}(\upomega , \upalpha )$. That is, the underlying meaning is, a concept $\upalpha$ applies to a world $\upomega$ if we have arguments in favour of $\upomega$ qualifies $\upalpha$ and we do not have arguments against $\upomega$ qualifies $\upalpha$.

It is also to be noted, that when $D_{af}(\upomega , \upalpha )$ = $\sup _{u \in \upalpha ^{+}}Sim(\upomega , u)$ = $Sim(\upomega , \upomega ^{\prime })$ for some $\upomega ^{\prime } \in \upalpha ^{+}$, we say $D_{af}(\upomega , \upalpha )$ attains at $\upomega ^{\prime }$; i.e., the (highest) degree of argument in favour of $\upomega$ qualifies $\upalpha$ attains at $\upomega ^{\prime }$.

We now would like to explore the properties of the relation $\models$.

Theorem 1

(i) $gr(\upomega \models \upalpha )$ = 1 if $\upomega \in \upalpha ^{+}$.

(ii) If $\upalpha ^{+} \subseteq \upbeta ^{+}$ and $\upbeta ^{-} \subseteq \upalpha ^{-}$, then $gr(\upomega \models \upalpha ) \le gr(\upomega \models \upbeta )$.

(iii) For $\upomega \in \upalpha ^{+}$ and $\upomega ^{\prime } \in \upbeta ^{+}$ if $D_{af}(\upomega , \upbeta )$ attains at $\upomega ^{\prime }$ and $D_{ag}(\upomega , \upgamma )$ = 0,

then $gr(\upomega \models \upbeta ) *gr(\upomega ^{\prime } \models \upgamma ) \le gr(\upomega \models \upgamma )$.

Proof

(i) is obvious from the definition of $\models$.

(ii) $gr(\upomega \models \upalpha )$ = $\sup _{u \in \upalpha ^{+}}Sim(\upomega , u)$ $*$ $\lnot \sup _{u \in \upalpha ^{-}}Sim(\upomega , u)$

$\quad \quad \quad \le \sup _{u \in \upbeta ^{+}}Sim(\upomega , u) *\lnot \sup _{u \in \upalpha ^{-}}Sim(\upomega , u)$ [since $\upalpha ^{+} \subseteq \upbeta ^{+}$]    ...(a)

Since $\upbeta ^{-} \subseteq \upalpha ^{-}$, $\lnot \sup _{u \in \upalpha ^{-}}Sim(\upomega , u) \le \lnot \sup _{u \in \upbeta ^{-}}Sim(\upomega , u)$    ...(b)

Combining (a) and (b) we have, $gr(\upomega \models \upalpha ) \le gr(\upomega \models \upbeta )$.

(iii) Let for two concepts $\upalpha , \upbeta$, $\upomega \in \upalpha ^{+}$ and $\upomega ^{\prime } \in \upbeta ^{+}$. Let us consider another concept $\upgamma$.

$gr(\upomega \models \upbeta ) *gr(\upomega ^{\prime } \models \upgamma )$

= $[\sup _{u \in \upbeta ^{+}}Sim(\upomega , u) *\lnot \sup _{u \in \upbeta ^{-}}Sim(\upomega , u)]$

$*$ $[\sup _{v \in \upgamma ^{+}}Sim(\upomega ^{\prime }, v) *\lnot \sup _{v \in \upgamma ^{-}}Sim(\upomega ^{\prime }, v)]$

= $[\sup _{u \in \upbeta ^{+}}Sim(\upomega , u) *\sup _{v \in \upgamma ^{+}}Sim(\upomega ^{\prime }, v)]$

$*$ $[\lnot \sup _{u \in \upbeta ^{-}}Sim(\upomega , u) *\lnot \sup _{v \in \upgamma ^{-}}Sim(\upomega ^{\prime }, v)]$

$\le [\sup _{u \in \upbeta ^{+}}Sim(\upomega , u) *\sup _{v \in \upgamma ^{+}}Sim(\upomega ^{\prime }, v)]$

= $[Sim(\upomega , \upomega ^{\prime }) *\sup _{v \in \upgamma ^{+}}Sim(\upomega ^{\prime }, v)]$ [since $D_{af}(\upomega , \upbeta )$ attains at $\upomega ^{\prime }$]

= $\sup _{v \in \upgamma ^{+}}[Sim(\upomega , \upomega ^{\prime }) *Sim(\upomega ^{\prime }, v)]$ [by $a *\sup _{i}b_{i}$ = $\sup _{i}(a *b_{i})$]

$\le \sup _{v \in \upgamma ^{+}}Sim(\upomega , v) *\lnot \sup _{v \in \upalpha ^{-}}Sim(\upomega , v)$ [as $Sim$ is transitive and $D_{ag}(\upomega , \upgamma )$ = 0]

= $gr(\upomega \models \upgamma )$

A notion of logical consequence relation is usually supposed to be a relation between a set of sentences/propositions and a sentence. In model theoretic terms, we also talk about a model or a structure, which is a tuple consisting of the interpretations of the logical constants, predicates, and function symbols, satisfies a sentence. Here, the relation $\models$ is considered to be a binary relation between a world of $W$ and a concept. In that sense one may be skeptic about calling $\models$ a consequence relation or satisfaction relation. Nevertheless, it is to be noted that the above three properties of $\models$ seem to have some connection with our standard notion of logical consequence.

The first property of Theorem 1 ensures that any positive instance of a concept $\upalpha$ qualifies $\upalpha$; this clearly has similarity with the condition overlap of a logical consequence. Property (ii) of $\models$ ensures that if two concepts $\upalpha$ and $\upbeta$ are such that the positive instances of $\upalpha$ are the positive instances of $\upbeta$, and negative instances of $\upbeta$ are the negative instances of $\upalpha$, then if $\upomega$ qualifies $\upalpha$, $\upomega$ qualifies $\upbeta$ too. In ordinary context, where a concept applies and does not apply are complementary to each other we do only talk about positive instances of the concept. But in the context of vague concepts where the prototypes and the counterexamples of the concept do not exhaust the whole universe, (ii) may be considered similar to the monotonicity property of a logical consequence. The property (iii) is a variant version of the condition cut of a logical consequence. In the context of logic of prototypes and counterexamples, in order to claim that a world qualifies a concept we need to take care of both for and against arguments for such a claim. So, (iii) ensures that, if $\upomega$ , a positive instance of $\upalpha$ , qualifies $\upbeta$ by attaining the argument in favour at the world $\upomega ^{\prime }$ belonging to the positive instances of $\upbeta$ , then if $\upomega ^{\prime }$ qualifies $\upgamma$ and we do not have any argument against $\upomega$ qualifies $\upgamma$ , then $\upomega$ qualifies $\upgamma$.

Thus, the name ‘logic of prototypes and counterexamples’, for this particular system of reasoning about whether a concept applies to a world, justifies itself.

3 Concept Synthesis: An Application of Graded Consequence

In the previous section we have proposed a way to calculate the degree of applicability of a concept to a world from the available prototypes and counterexamples of the concept where it strictly applies and does not apply respectively. We also have observed that the relation $\models$ between a world and a concept satisfies some properties which might be viewed as properties similar to a notion of consequence. In this section we would make a step towards synthesis of compound concepts from a set of concepts. More specifically we would be interested in obtaining a grade to which a (compound) concept can be derived from a set of (sub)concepts. The idea is built as follows.

We start with $\mathcal {C}_{B}$, a set of basic concepts relevant for an arbitrarily fixed domain. We restrict $\mathcal {C}_{B}$ to be a finite set as in the field of application we indeed deal with a finite set of basic concepts in order to understand a bigger set of concepts, which again needs not be infinite for meeting our everyday purpose. Now for each $c_{b} \in \mathcal {C}_{B}$, we have ($c_{b}^{+}, c_{b}^{-}$) such that $c_{b}^{+}, c_{b}^{-} \subseteq W$ and $c_{b}^{+} \cap c_{b}^{-}$ = $\upphi$. Given the classification of concepts in terms of their prototypes and counterexamples, we induce a fuzzy relation $\models$ over $W \times \mathcal {C}_{B}$ mapping each pair from $W \times \mathcal {C}_{B}$ to $[0, 1]$. Let $\mathcal {C}$ be the set of all possible concepts over the same domain specified for $\mathcal {C}_{B}$, and $\mathcal {C}_{B} \subsetneqq \mathcal {C}$. As discussed in Sect. 2, the concepts are classified in terms of its prototypes and counterexamples based on a set of situations $S$. So, if $S$ changes the classification of the same concept may vary. That is, the subjective view of a concept is incorporated in the notion of classification of a concept in terms of its prototypes and counterexamples. Although interpretation of a vague concept and its interrelation with other concept are very much subjective in nature, there might be a universally accepted common view as well. So, we assume that $\mathcal {C}$ is endowed with an order relation $\subseteq _{k}$, may be called universal knowledge ordering of concepts, such that ($\mathcal {C}, \subseteq _{k}$) forms a poset. Informally the order relation $\subseteq _{k}$ is such that if it is commonly agreed that stomach infection is a subconcept of food poisoning, then the former is included in the latter under the relation $\subseteq _{k}$. We skip the definition of $\subseteq _{k}$ for the time being, as to proceed in this paper a formal definition of $\subseteq _{k}$ is not necessary. Each concept $c_{b} \in \mathcal {C}_{B}$ is independent in the sense that there is no $c_{b}^{\prime } \in \mathcal {C}_{B}$ such that $c_{b}^{\prime } \subseteq _{k} c_{b}$. We now extend the definition of $\models$ on $W \times \mathcal {C}$ in the following way.

Definition 3

$\models _{e}$ is a fuzzy relation from $W \times \mathcal {C}$ to $[0, 1]$ such that

$gr(\upomega \models _{e} c)$ = $gr(\upomega \models c)$ if $c \in \mathcal {C}_{B}$,

         = $\underline{\Sigma _{c^{\prime } \in C_{B}^{\prime }}gr(\upomega \models c^{\prime })}$, otherwise where $C_{B}^{\prime }$ = $\{c^{\prime } \in \mathcal {C}_{B}: c^{\prime } \subseteq _{k} c\}$.

                 $|C_{B}^{\prime }|$

The value of $gr(\upomega \models _{e} c)$ for $c \notin \mathcal {C}_{B}$ can be zero in two possible cases. One is when there is no concept in $\mathcal {C}_{B}$ which is a subconcept of $c$. The other case is when the concepts from $\mathcal {C}_{B}$, which are included in $c$, do not hold at the world $\upomega$, i.e., they hold to the degree 0 at $\upomega$.

Now we propose a method of derivation of a concept from a set of concepts, where the derivation is a matter of grade.

Definition 4

Given any collection of worlds $\{\upomega _{i}\}_{i \in I}$, taken from $W$, the fuzzy relation $\mid \approx$ over $P(\mathcal {C}) \times \mathcal {C}$, assuming values from $[0, 1]$, is defined as below.

$gr(\{c_{j}: j = 1, 2, \ldots , n\} \mid \approx c)$ = $\inf _{i \in I}[\inf _{j = 1}^{n}gr(\upomega _{i} \models _{e} c_{j}) \rightarrow _{*} gr(\upomega _{i} \models _{e} c)]$, where $\rightarrow _{*}$ is the residuum of $*$ in $[0, 1]$.

It is now easy to check that $\mid \approx$ is a graded consequence relation [3, 4], i.e., $\mid \approx$ satisfies the following properties.

• (GC1) If $c \in \{c_{j}: j = 1, 2, \ldots , n\}$ then $gr(\{c_{j}: j = 1, 2, \ldots , n\} \mid \approx c)$ = 1.

• (GC2) If $C_{1} \subseteq C_{2} (\in P(\mathcal {C}))$, then $gr(C_{1} \mid \approx c) \le gr(C_{2} \mid \approx c)$.

• (GC3) $\inf _{c^{\prime } \in C^{\prime }}gr(C \mid \approx c^{\prime }) *gr(C \cup C^{\prime } \mid \approx c) \le gr(C \mid \approx c)$.

As in the beginning of this section we have mentioned that for our daily purpose we do not need to deal with an infinite set of concepts over a fixed domain, we have proposed the definition of $\mid \approx$ for synthesis of a concept from a set of finite number of concepts. The definition can be easily considered for infinite case, for which one may be referred to the work of the theory of graded consequence [2, 3]. At this stage, again a similar point, as discussed at the end of Sect. 2, arises. The notion of graded consequence relation [2, 3] originally has been defined as a fuzzy relation between $P(F)$, the power set of all sentences over a language, to $F$, the set of all sentences. That is, according to the definition of graded consequence [3] $\mid \approx$ is a function from $P(F) \times F$ to some set of values; in particular the value set could be $[0, 1]$. Here, $\mid \approx$ maps every pair from $P(\mathcal {C}) \times \mathcal {C}$ to $[0, 1]$. Matching both the context from the mathematical perspective sounds well, though conceptually $\mid \approx$ in the present context is different from that of the context of [2–5].

Now question arises why at all we choose this way of synthesis of a concept from a set of concepts. First of all, this allows the concept synthesis method to exploit the so-far developed logical background of the theory of graded consequence [2–5, 8–11]. Theory of graded consequence gives a set-up where object language entities, which are here concepts, as well as the notion of deriving a concept from a set of concepts are of matter of grade. Besides, the theory of graded consequence allows the languages and the interpretations of different levels, like object, meta, and meta-meta levels, of a logical discourse to be distinctive. As a result, object level and meta-level of a logic may have different reasoning patterns and necessities. Like, here in the object level we have a graded relation $\models$ which has its own characteristics as mentioned in Theorem 1; the base algebraic structure for $\models$ is ($[0, 1], \wedge , \vee , *, \rightarrow$). In the next level, we have another relation $\mid \approx$ with its own characteristics, with respect to the algebraic structure ($[0, 1], \wedge , \vee , *, \rightarrow _{*}$). Dealing with vague concepts, it is quite natural to think that our mental process of synthesis of a vague concept from a set of vague concepts may not be crisp always, and it may need different layers of learning and synthesizing. So, the background of the theory of graded consequence might be advantageous for the theory of concept synthesis.

Let us check what else this definition of $\mid \approx$ can yield. We would try to explain a few natural expectations to a concept synthesis operation in the context of this definition.

• (1) Let $\{c_{j}: j = 1, 2, \ldots , n\}$ be such that $c_{j} \in \mathcal {C}_{B}$ and $c_{j} \subseteq _{k} c$ for $j$ = 1, ..., $n$. So, in accordance with the universal ordering $\subseteq _{k}$ between $c_{j}$’s and $c$, it is expected that $c$ can be derived from its subconcepts should have an affirmative answer. Below we present that the definition of $\mid \approx$ respects this natural demand in the following way.

  Let $\upomega _{i}$ be a world from the collection $\{\upomega _{i}\}_{i \in I}$, and $gr(\upomega _{i} \models _{e} c_{j})$ = $a_{ij}$ for $j$ = 1, 2, ..., $n$. Then by Definition 3, $gr(\upomega _{i} \models _{e} c)$ = $\frac{\Sigma _{j = 1}^{n}a_{ij}}{n}$. Now $\inf _{j}a_{ij} \le a_{ij}$ for $j$ = 1, 2, ..., $n$. So, $n(\inf _{j}a_{j}) \le \Sigma _{j = 1}^{n}a_{ij}$, i.e. $\inf _{j}a_{ij} \le \frac{\Sigma _{j = 1}^{n}a_{ij}}{n}$. Hence using property of $\rightarrow _{*}$ we have $gr(\{c_{j}: j = 1, 2, \ldots , n\} \mid \approx c)$ = 1.

• (2) Let us refer to the following quotation by Leslie Valiant [21], the 2010 Turing award winner. “A specific challenge is to build on the success of machine learning so as to cover broader issues in intelligence. This requires, in particular a reconcillation between two contradictory characteristics - the apparent logical nature of reasoning and the statistical nature of learning”.

  When at a world certain basic constituent properties of a compound concept hold, we often take a statistically average point of view to decide the applicability of the compound concept at that world. The Definition 3 in that way justifies itself. This may be referred to as statistical nature of learning of the applicability of a concept to a world. On the other way, when we need to check that whether a set of concepts $C$ yields a complex concept $c$, we need to be logical in our way of deriving conclusion. That is, we need to check that whether each of the available worlds satisfying each concept of $C$, also satisfies the concept $c$. The Definition 4 takes care of this logical reasoning part. Hence, this definition of concept synthesis is an attempt towards reconcillation of statistical nature of learning and logical nature of reasoning.

• (3) Let us think about some practical problems, and check how this proposed theory is dealing with those problems. In this regard, we would like to illucidate the idea by considering examples from the field of health-care system.

  Let $\{d_{1}, d_{2}, \ldots , d_{l}\}$ be the subconcepts of a disease $d$, and among them $d_{i_{1}}, \ldots , d_{i_{k}}$ for $1 \le i_{1} \le i_{k} \le l$ get only positive values at some world $\upomega _{i}$. Then the degree to which $d$ applies to the world must get decreased compare to the case when all of $d_{1}, \ldots d_{l}$ are tested positive. The Definition 3 shows that in the former case the value becomes $\frac{\Sigma _{j = 1}^{k}gr(\upomega _{i} \models _{e} d_{i_{j}})}{l}$, which is less than the value $\frac{\Sigma _{j = 1}^{l}gr(\upomega _{i} \models _{e} d_{i_{j}})}{l}$ for the latter case.

Let us assume that a new problem $d$ has emerged, and the medical domain knowledge does not have the information that which of the independent concepts of $\mathcal {C}_{B}$ are contained in $d$, in the sense of $\subseteq _{k}$. So, following the Definition 3 at all worlds the degree of applicability of $d$ would be 0. This reflects the problem that for a new concept there might not be any relevant information available according to the domain knowledge base; and there might not be also any statistical record available in favour of the concept as at each world the applicability of the concept gets nullified. In such a situation, based on experiences, one may still try to relate some known problems with the problem of concern, and want to check the relationship of a set of concepts $\{c_{1}, \ldots , c_{r}\}$ with the problem $d$. As $a \rightarrow _{*} 0$ is not necessarily $0$, that none of the worlds qualifies $d$ does not imply $gr(\{c_{1}, \ldots , c_{r}\} \mid \approx d)$ to be zero.

The example below gives an overview of the application of the proposed theory. We start with a database of finitely many patients, and a fragment of the concept ontology from the medical domain specifying a set of independent concepts ($C_{B}$), and their relations with other compound concepts of $C (\supseteq C_{B})$. From the database, positive and negative cases of each disease from $C_{B}$ are determined, and then diagnosis of a particular disease at some particular case/situation/world, which might be new, is determined following the Definitions 2 and 3; using this at the next level the degree of relatedness of a set of diseases from $C$ with a disease, say $d$, is computed following the Definition 4.

Example 1

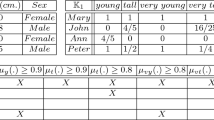
Let we have a clinical database of a set of situations, $S$ = $\{s_{1}, s_{2}, s_{3}, \ldots , s_{9}\}$ with respect to a set $P$ of parameters/attributes, consisting of temperature, blood-pressure, blood-tests, ecg, headache, sneezing, convulsion, vomiting, skin-rash, dizziness, stomach-upset, stomach pain. Sequentially let us call these parameters as $p_{1}, p_{2}, p_{3}, \ldots , p_{12}$. As $p_{1}, \ldots , p_{4}$ are determined by some objective values of some tests these are called signs; the rest are symptoms, determined by some subjective values as experienced by particular patients. Let $C_{B}$ = $\{Fev, Allergy, Stomach_{inf}, HBP, LBP, Vertigo, Unconsciousness\}$, and $C$ is the union of $C_{B}$ and $\{Fev_{c}, Fev_{v}, Stroke, Food$-$poisoning, Viral_{inf}, Peptic$-$ulcer\}$. The relations among the dependent and the independent concepts of $C$ are as follows. $Fev \subseteq _{k} Fev_{c}$; $Fev, \ Allergy \subseteq _{k} Fev_{v}$; $Fev, \ HBP, \ Vertigo, Unconsciousness \subseteq _{k} Stroke$; $Fev, \ Stomach_{inf} \subseteq _{k} Food$-$poisoning$; $Fev, Stomach_{inf}, \ Allergy \subseteq _{k} Viral_{inf}$; and $Stomach_{inf} \subseteq _{k} Peptic$-$ulcer$. $Fev_{c}$ and $Fev_{v}$ respectively stand for fever due to cold and viral fever. $HBP, LBP$, $Stomach_{inf}$, and $Viral_{inf}$ respectively stand for high blood pressure, low blood pressure, stomach infection and viral infection. Each $s_{i}$ is identified with its state given by $\langle s_{i}(p_{1}), s_{i}(p_{2}), s_{i}(p_{3}), \ldots , s_{i}(p_{12})\rangle \in [0, 1]^{12}$, and $W (\subseteq [0, 1]^{12})$ contains $\langle s_{i}(p_{1}), s_{i}(p_{2}), s_{i}(p_{3}), \ldots , s_{i}(p_{12})\rangle$ for each $s_{i}$. The tuple of values corresponding to each $s_{i}$, and the positive and negative cases of each disease from $C_{B}$ are given in the following table (Table 1). Let us use $d_{1}$ for $Fev$, $d_{2}$ for $Allergy$, $d_{3}$ for $Stomach_{inf}$, $d_{4}$ for $HBP$, $d_{5}$ for $LBP$, $d_{6}$ for $Vertigo$, and $d_{7}$ for $Unconsciousness$. For each $s_{i}$ if $d_{j}$ receives $+$, then $s_{i}$ is the positive case for $d_{j}$, and if it receives $-$, then $s_{i}$ is the negative case of $d_{j}$. Now as $s_{2} \in HBP^{+}, Vertigo^{+}, Unconsciousness^{+}$, following the concept ontology we may need to check $gr(s_{2} \models _{e} Stroke)$. Following the Definitions 2 and 3, $gr(s_{2} \models _{e} Stroke)$ = $\frac{3}{4} + \frac{1}{4}[\overline{Sim}_{Fev^{+}}(s_{2}) *\lnot \overline{Sim}_{Fev^{-}}(s_{2})]$. Also, as $s_{8} \in Vertigo^{+}, Unconsciousness^{+}$ verifying $gr(s_{8} \models _{e} Stroke)$ is natural too. In this case, as $s_{8} \in Fev^{-}, HBP^{-}$ $gr(s_{8} \models _{e} Stroke)$ turns out to be $\frac{1}{2}$.

Table 1. Patients data table

Let a new situation $s_{10}$, with the tuple $\langle .5, .5, .5, .5, .7, 0, .8, .5, .7, .8, .5, 0\rangle$ of values corresponding to the respective parameters, appear. The task is to make a diagnosis for $s_{10}$ based on the for and against arguments that which of the situations from $S$ are closely similar to $s_{10}$. Though for the progress of this paper it is not required to specify the exact formula for computing $Sim$, let us follow an intuitive reasoning for justifying the case for this example; formulation of the exact definition for $Sim$ is one of our future agendas. The tuple for $s_{10}$ indicates that both $p_{7}$ and $p_{10}$ are having the highest values. Also we can notice that $p_{7}, p_{10}$ have greater values at $s_{2}$ and $s_{8}$, both of which are the positive cases of $Vertigo$ and $Unconsciousness$. So, let us assume that $s_{10}$ is very similar to $s_{2}$ and $s_{8}$. The next prominent feature for $s_{10}$ is $p_{9}$. One can notice $p_{9}$ is most aggravated in the case of $s_{6}$, and so a close similarity between $s_{6}$ and $s_{10}$ may also be assumed. The diagnosis for the known cases shows, $s_{6}$ is the only positive case of $Allergy$. Now as from the concept ontology one can observe that $Vertigo, Unconsciousness \subseteq _{k} Stroke$ and $Allergy \subseteq _{k} Viral_{inf}$, finding out the degree of relationship among $\{Viral_{inf}, Vertigo, Unconsciousness\}$ and $Stroke$, i.e., $gr(\{Viral_{inf}, Vertigo, Unconsciousness\} \mid \approx Stroke)$ might be suggestive.

4 Future Directions

The study made in this paper is an initial step towards obtaining a concept systhesis method using finitely many observations about the prototypical cases and counterexamples of its component concepts. The newness of this approach, perhaps, lies in its way of proposing both satisfiability of a concept at a world, and determinning that a concept is synthesized out of a set of concepts as matters of grade, and allowing both the levels of $\models$ and $\mid \approx$ to have different logical characteristics. A few directions of further research are as follows. (i) How the theory of argumentation in favour of a claim, and against a claim can be incorporated in order to come to a decision that a situation $\upomega$ is similar to another situation $\upomega ^{\prime }$, or if some concept applies to $\upomega$, that also applies to $\upomega ^{\prime }$? (ii) What would be the properties of $\models _{e}$ when it would be extended on $P(W) \times \mathcal {C}$ with the standard set theoretic operations on $P(W)$? (iii) How to incorporate the views of a set of sets of situations, say $\{\upomega _{i}\}_{i \in I}$, $\{\upomega _{j}\}_{j \in J}$, ..., $\{\upomega _{l}\}_{l \in L}$, allowing exchange of views among different sets of situations in the process of concept synthesis?