Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Data and Hadron Mass Spectrum

1.1 Fits of Hadron Mass Spectrum

The number of known hadronic states more than tripled since Hagedorn performed his analysis of the shape of the mass spectrum, see Chap. 20 This provides an opportunity for an important cross-check of the Hagedorn analysis. I will now briefly describe the key new insights.

The Krakow group [1, 2] considered the integrated (‘accumulated’) spectrum

$$\displaystyle{ R(M) =\int _{ 0}^{M}\rho (m)dm }$$
(21.1)

and they also break the large set of hadron resonances into different classes, e.g. non-strange/strange hadrons, or mesons/baryons. While Hagedorn-type approach requires smoothing of the spectrum, adopting an effective Gaussian width for all hadrons, the integrated spectrum Eq. (21.1) allows one to address directly the step function arising from integrating the discrete hadron mass spectrum, i.e. avoiding the Hagedorn smoothing.

One could think that the Hagedorn smoothing process loses information that is now available in the new approach. However, it turns out that a greater information loss comes from the consideration of the integrated ‘signal’. This is seen in the results of Krakow group by noting that the fitted value of T H is strongly varying in dependence on supplementary hypotheses made about the procedure, with the value of T H changing by 100s MeV. This probably means that the integrated mass spectrum Eq. (21.1), aside of the physical parameter fit, also has other good fits. The likely cause of the T H instability is that these artifacts produce the best fit at an unphysical parameter set. This situation is not uncommon when considering any integrated signal function.

My own work [3, 4] has been more modest, an ‘almost’ redo of the original Hagedorn fit and is shown in Fig. 21.1. A comparison of the original Hagedorn fit, long dashed line in Fig. 21.1, with an analysis involving more than 5,000 hadron states; short dashed line suggests that results are highly compatible. However, there are a few caveats. The hadron mass spectrum that was fitted is

$$\displaystyle{ \rho (m) = c\, \frac{e^{m/T_{H}}} {(m_{0}^{2} + m^{2})^{a/2}} }$$
(21.2)

All three parameters T H , m 0, c are varied and find their best value. Hagedorn fixed m 0 = 0. 5 GeV as he was working in the limit m ≫ m 0, and this is clearly not the case as the mass spectrum available experimentally is limited to a range m < 1. 7 GeV. The introduction of a fitted value m 0 is necessary to improve the spectrum for low values of m.

Fig. 21.1
figure 1

Contemporary mass spectrum fit (short dashed) compared to 1968 fit of Hagedorn (long dashed): the case of power law scaling a = 3 is shown for parameters and also other values of a see Table 21.1

Full size image

The pre-exponential power value a = 2. 5 in Eq. (21.2) corresponds to Hagedorn’s original work, Eq. (20.6). However, several years later following further developments described below in Chap. 23, the value a = 3 was obtained. Moreover, a = 2. 5 leads to divergent energy density and excludes the phase transformation of HG to a new phase. Thus it must not be used considering existence of QGP.

The results shown in Fig. 21.1 are thus given for a = 3. The requirement that T H is a transformation temperature between phases favors larger values of a and thus a range a ∈ [2. 5–4] is presented in Table 21.1; fits obtained in 1994 were for a slightly smaller set of hadrons [4] than is available today. We see that as the pre-exponential power law a increases, the fitted value of T H decreases.

Table 21.1 Parameters of Eq. (21.2) fitted for a prescribed pre-exponential power a results from [4]. Note that the value of c for a = 2. 5 corresponds to \(c = 2.64 \times 10^{4}\,\mathrm{MeV}^{3/2}\) in excellent agreement to the value shown in Fig. 20.1
Full size table

1.2 The Value of the Power Index ‘a’

In the first Hagedorn mass spectrum paper Chap. 20, in Eq. (21.2) the values m 0 = 0. 5 GeV and the power index a = 2. 5 are assumed in the fit presented in Fig. 20.1. Upon the exact solution of the bootstrap equation it was recognized that the precise form of singularity that SBM condition generates requires a = 3, for references see Chap. 22, entries in Fig. 22.2, bottom left square and presentation of SBM, Eq. (23.12). A further requirement is imposed in order to assure that the Hagedorn Temperature is a phase transition temperature. For this to be true the energy density must remain finite when Δ T ≡ T − T H  → 0, and this requires a ≥ 7∕2, see Table 23.1 and comments below this table, as well as the discussion below Eq. (25.16). Inspection of the Table 23.1 shows that the condition a ≥ 7∕2 corresponds to T H  ≤ 151 MeV.

Given the extensive literature within the SBM context pointing at a = 3 and the phase transition studies which require a ≥ 7∕2, it is hard to understand why modern studies of the mass spectrum have all focused on a = 2. 5, a value which is obsolete. This assumption produces the highest value of T H but is inconsistent with the physics pictures that emerged in regard to SBM, and later of a phase transformation of HG to QGP.

Elaborate lattice-QCD numerical computations of QGP to HG transformation regime are available today [5–7]: the Hot-QCD collaboration [6] converged for 2 + 1 flavors towards T c  = 154 ± 9 MeV. One of the works of the Wuppertal-Budapest collaboration [8] suggests a low \(T_{c} \simeq 145\) MeV. However, this low value depends on the choice of the phase transformation tracking observable. The latest report of this group [7] mentions \(T_{c} \simeq 150\) MeV. All current lattice-QCD T H results are thus according to tabulation in Table 21.1 favoring a = 3. 5, which is the lowest value allowing for a finite energy density near HG phase boundary, see Table 23.1.

In the above Table 21.1, a value of a is not preferred experimentally: all fits shown are of comparable quality when all three model parameters T H , m 0, c are allowed to vary. If, however, a fixed value of m 0 is arbitrarily prescribed, as was done by Hagedorn who was compelled half a century ago by limited experimental information, the quality of the fit to the present day data will diminish. For example [9] fixes m 0 = 0. 5 GeV at a = 2. 5, i.e. Hagedorn’s 1968 parameter choices. Applying the Krakow group method approach, this fit produces with present day data T H  = 0. 174 GeV. We keep in mind that the assumed value of a is incompatible with SBM, while the assumption of a relatively small m 0 = 0. 5 GeV is forcing a relatively large value of T H .

2 Quarks and QCD

2.1 Lattice-QCD Trace Anomaly Constraint

Arguably, the most important recent step forward in regard to improving the Hagedorn mass spectrum analysis is the realization that one can infer important information about the hadron mass spectrum from lattice-QCD numerical results [10]. The lattice-QCD effort has a relatively easy numerical access to the trace anomaly of the energy-momentum tensor expressed in units of T 4, the so called ‘interaction measure’

$$\displaystyle{ I(T) = \frac{\epsilon -3P} {T^{4}}. }$$
(21.3)

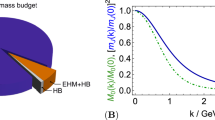
This quantity vanishes in scale invariant theory, for example for (effectively) massless and free gas of quarks and gluons. For interacting gas of quarks and gluons the QCD scale parameter generates a non-vanishing result, but asymptotic freedom implies that interaction effects decrease with increasing temperature of QGP. Accordingly, I(T), Eq. (21.3) is seen to decrease from a relatively high value achieved when quarks and gluons turn into hadrons, see the high T domain shown in Fig. 21.2. For low temperature, where we do not expect a deconfined quark-gluon phase, the rise of I(T) with T indicates that with increasing temperature more massive hadron states become relevant.

Fig. 21.2
figure 2

The comparison of interaction measure with hadron resonance gas, latest lattice-QCD results, after [7]

Full size image

At temperatures below QGP formation I(T), Eq. (21.3) is derived from the contribution of each hadron species folded into the hadron mass spectrum. In the Boltzmann limit Eq. (10.60) in [11] reads

$$\displaystyle{ I_{\mathrm{Boltz}}(T) =\int dm\rho (m)\frac{x^{3}} {2\pi ^{2}} K_{1}(x),\quad x = m/T, }$$
(21.4)

where the degeneracy g of each state of mass m is renamed ρ(m) and the continuous integral, rather than discrete sum, is introduced.

The Boltzmann limit is, however, not accurate as the power law expansion of the quantum distribution shows. Adopting Eq. (10.68) in [11], the result is

$$\displaystyle{ I_{Q}(T) =\int dm\rho (m)\sum _{n=1}^{\infty }\frac{(f)^{n+1}} {n} \frac{x^{3}} {2\pi ^{2}} K_{1}(nx),\quad x = m/T, }$$
(21.5)

where \(f = -/ + 1\mathrm{\ for\ Fermions/Bosons}\). The temperature domain of interest for us is T < 175 MeV. The presence of the relatively light boson, the pion, with a mass within this temperature domain means that we must include bosonic quantum corrections. While the results of [10] suggested the need for some additional undiscovered resonances, the comparison shown in [7], see Fig. 21.2, suggests that agreement between hadron resonance gas (HRG, dashed line in the figure) and current lattice-QCD results (uncertainty domains shown, techniques will not be discussed here) is achieved just with the known hadron set of states.

In the context of the search for a better understanding of the hadron mass spectrum and the determination of Hagedorn Temperature T H , the trace anomaly can fill a very important information gap. Given a parametrized mass spectrum shape, such as is Eq. (21.2), one must fit both, the experimental hadron mass spectrum, as well as the numerical lattice-QCD trace anomaly. Such a joint approach could produce a more unique phenomenological determination of both T H and favor a value for the pre-exponential power a.

2.2 Quark Bags and the Hadron Mass Spectrum

There are additional challenges arising from the prophetic work on the hadron mass spectrum by Hagedorn, Chap. 20 Hagedorn’s paper closes with remarks about the possibility that the multitude of quark bound states could relate to an exponential mass spectrum. This indeed is the case. Several quantitative implementations of this idea appeared in literature beginning in 1976 [12]. In 1981 Joe Kapusta [13] writes in his abstract: “A statistical evaluation of the mass spectrum in the (quark) bag model is made …(which) behaves asymptotically as \(\rho (m) \propto c\,m^{-3}exp(m/T_{H})\), …this model satisfies the strong bootstrap condition. …The thermodynamics of a system of such composite hadrons naively exhibits a maximum temperature T 0. However, …first-order phase transition to a gas of free elementary fields is found at a temperature T c  = 1. 05T H .”

This work has stimulated continued interest in evaluation of hadron mass spectrum based on quark bag model. However, given that the naive bag model is known to predict hadron states not found in experimental searches, this path cannot be trusted to produce in quantitative terms a result of phenomenological importance. Cohen and Krejcirik [14] criticizes also in this context the current widely accepted Hagedorn approach and Hagedorn Temperature. For reasons already described, and in particular in consideration of the loss of information for the integrated mass spectrum, we do not share in any of the views presented in this work.