Abstract
L’Hôpital met Bernoulli in November 1691 and almost immediately hired him as a tutor, to teach him the new calculus. In 1691–92, Bernoulli gave him lessons on the subject, including handwritten notes. Bernoulli kept copies of these notes for himself and long after the publication of the Analyse, he published the second part of these notes, on the integral calculus. However, his notes on the differential calculus, which form the basis of the first four chapters of l’Hôpital’s Analyse, remained unknown until a copy was discovered in Basel in 1922. These notes, originally written in Latin, appear here for the first time in English translation. When compared to the corresponding chapters of the Analyse, we see clearly that Bernoulli provided the major results and the structure for that portion of l’Hôpital’s book, but that l’Hôpital also contributed significantly, especially as a lucid expositor. This chapter contains the full text of Bernoulli’s lessons on the differential calculus, including reproductions of the hand drawn figures.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The manuscript employs the abbreviation “et in seqq.” here. Where possible, we will translate abbreviated Latin words with similarly abbreviated English words.
- 2.
The proof that follows is formatted like a sequence of calculations, with justifications in the right-hand column. It is perhaps easier to read the proof in this form: “multipl. x + e, supposing that e = dx, with a + 0, which is a plus nothing, because a is a determined quantity, which has no differential. The prod. is ax +ae, from which subtr. ax, leaving ae = a dx q.e.d.”
- 3.
This case of the Power Rule is given on p. 6, using the Product Rule.
- 4.
Compare to §5 on p. 4.
- 5.
In the expression that follows, the numerator consists of all twelve terms in the first four lines.
- 6.
The symbol □ is used to denote the square of the term that follows it.
- 7.
The symbol C is used to denote the cube of the term that follows it.
- 8.
The symbol QQ is used to denote the fourth power of the term that follows it.
- 9.
Compare the discussion that follows with L’Hôpital’s discussion of geometric and arithmetic progressions on p. 5. In this paragraph, Bernoulli denotes exponents with a left parenthesis in the superscript, perhaps as a form of emphasis. This notation is rarely used elsewhere in the Lectiones.
- 10.
Here and in the following the comma represents multiplication. In addition, we note that in Schafheitlin (1922), the term before the equal sign was given as ax + 2x dx.
- 11.
L’Hôpital gave this example on p. 8.
- 12.
L’Hôpital gave this example on p. 8.
- 13.
L’Hôpital gave a similar example on p. 8.
- 14.
Compare this to Example I, Part 1, on p. 13.
- 15.
Bernoulli wrote this proportional relationship as: a ⋅ 2y: : dy ⋅ dx.
- 16.
The relation dy: dx: : y: s, concerning the Differential Triangle, is given in Proposition I on p. 11.
- 17.
This is an abbreviation for Quod erit inveniendum; “which was to be found.”
- 18.
Compare what follows to the generalized parabola, where fractional exponents may be used, on p. 13.
- 19.
In Schafheitlin (1922) the denominator was given as a.
- 20.
In Schafheitlin (1922), the term 2ax was given as 2a.
- 21.
Compare this to the more general Example II on p. 13.
- 22.
Compare this to Example II, Part 2, on p. 13 and the more generalized Example III on p. 15.
- 23.
Compare this to §39 on p. 38.
- 24.
The notation that follows evidently signifies the progression of y-values.
- 25.
Compare this §18 on p. 18, which depends on a general proposition in §15.
- 26.
Compare this to §25 on p. 22, which depends on a more general proposition in §24.
- 27.
In Schafheitlin (1922), Schafheitlin suggests that we read this argument as: because ED = AB, \(\mathit{AG}: \mathit{GK} = \mathit{AB}: \mathit{BC} = \mathit{ED}: \mathit{BC} = \frac{\mathit{ED}} {\mathit{EF}} \cdot \frac{\mathit{EF}} {\mathit{BC}} = \frac{\mathit{DG}} {\mathit{GH}} \cdot \frac{\mathit{GF}} {\mathit{GC}}\) Bernoulli uses the rectangle symbol in analogy to the square: □ DGF represents the area of the rectangle DGF, i.e. the product of DG and GF.
- 28.
Compare this to §28 on p. 25, which depends on the more general proposition in §27.
- 29.
Compare this to §30 on p. 27, which depends on a more general proposition in §29.
- 30.
Compare this to §31 on p. 28.
- 31.
In Schafheitlin (1922), it is noted that in the manuscript this is erroneously given as IX.
- 32.
Compare this to §23 on p. 21, which depends on a more general proposition in §22.
- 33.
In other words, changes in radial distance are proportional to angular changes of the radius.
- 34.
There is no point K in Figure 11.13, although it presumably should be where the line AE intersects the circle DDCD.
- 35.
In other words, from the first proportion it follows that \(\mathit{FG} = \frac{\mathit{bx}\,\mathit{dx}} {a^{2}}\) and therefore from the second that \(\mathit{AE} = s = \frac{\mathit{bx}^{2}} {a^{2}}\).
- 36.
Compare this to the treatment of maximum and minimum beginning on p. 45.
- 37.
When D bisects BC, the volume of the solid is \(x\left (\frac{1} {2}(a - x)\right )^{2}\), so the quantity being maximized here is in fact a constant multiple of the volume, which achieves its maximum at the same value of x.
- 38.
In Schafheitlin (1922), the denominator of the second fraction was incorrectly given as \(\sqrt{2ax^{3 } - x^{4}}\). This was also repeated in the next line.
- 39.
The symbol
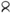 means + or −.
means + or −. - 40.
Compare to §59 on p. 54.
- 41.
Compare to §60 on p. 56.
- 42.
The Latin preposition in was used to mean the multiplication of the two factors. This will be consistently translated as “times.”
- 43.
I.e. the shortest twilight. Compare to §61 on p. 57.
- 44.
In Schafheitlin (1922) the following was written as kR.
- 45.
I.e., the supplement. In Schafheitlin (1922), the phrase ad duos rectos was misprinted as ad discos rectos.
- 46.
Compare this to Definition II given on p. 66.
- 47.
This is clarified in §66, Part 1. on p. 68.
- 48.
Compare this to §68 on p. 71.
- 49.
From this point onward, most occurrences □ , C, QQ (for square, cube, and fourth power) are followed by a colon. This is not meant to represent a proportion, but rather the application of the power to the expression that follows it.
- 50.
The letter C was missing in the figure in the manuscript.
- 51.
Compare this to §71 on p. 72.
- 52.
In Schafheitlin (1922), the differential dz was missing from the first term of the first numerator.
- 53.
Compare this to §72 on p. 74.
- 54.
In Schafheitlin (1922), the overline extended over the entire numerator.
- 55.
In Schafheitlin (1922), the minus sign before the az was omitted.
- 56.
In Schafheitlin (1922), the overline on the term z − a was omitted.
- 57.
In Schafheitlin (1922), every occurrence of dz in the numerator was written as dz 3.
- 58.
In Schafheitlin (1922), every occurrence of dz 3 in the numerator of the second fraction was written as dz.
- 59.
Compare this to §73 on p. 76.
References
Schafheitlin, Paul, “Johannis (I) Bernoullii Lectiones de calculo differentialium,” Verhandlungen der Naturforschenden Gesellschaft in Basel, 34, pp. 1–32.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Bradley, R.E., Petrilli, S.J., Sandifer, C.E. (2015). Bernoulli’s Lectiones de Calculo Differentialis . In: L’Hôpital's Analyse des infiniments petits. Science Networks. Historical Studies, vol 50. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-17115-9_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-17115-9_11
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-17114-2
Online ISBN: 978-3-319-17115-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


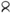 means + or −.
means + or −.