Abstract
Part I of Frege’s Grundgesetze is devoted to the “exposition [Darlegung]” of his formal system.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Baker [5] has considered, but finally rejected, the idea that Frege could also have ascribed this inappropriateness to himself, by referring to Sects. 9–10 of his [92]. My purpose here is not to describe the evolution of Frege’s views. I shall rather confine myself to considering his mature views, as they emerge from Grundgesetze or other contemporary works.
- 2.
Broadly speaking, a foundation of mathematics aims at a reorganisation of mathematics according to a suitable order. For Frege, such an order ought both to reflect an objective order of truths ([93], Sect. 2) and to provide mathematics, especially arithmetic and real analysis, with an epistemically sound basis (ibid., Sect. 3). For Lagrange, it should rather obey an ideal of purity (as I and my coauthor G. Ferraro have largely argued for in [89]).
- 3.
Cf. Sect. 3.1 of Chap. 3, below.
- 4.
A more comprehensive discussion is offered in [89].
- 5.
This is suggested by the complete title of the Théorie: ‘Théorie des fonctions analytiques contenant les principes du calcul différentiel [...] réduits à l’analyse algébrique des quantités finies’.
- 6.
For a discussion of Euler’s conception, I refer the reader to [152].
- 7.
As Lagrange uses it, the verb ‘to represent’ is not intended to indicate a relation between two distinct entities, one of which is taken to stand for the other under an appropriate respect. Expressions do not “represent” operations because they stand for them or present them afresh. They display at once these operations, their results, and the corresponding relations: ‘\(x^{2}\)’ displays, for example, the operation of taking the square, the quantity related to x according to this operation, and the relation between it and x.
- 8.
Though partial, this answer is not simple. It reveals a crucial feature that Lagrange’s program shares with any foundational reductionist program in mathematics: this program stipulates a new start for mathematics, without being free to forget what mathematics was before its advent. Hence, this start has both to be taken as primitive and to be so shaped as to allow a reformulation of what was there independently of it.
- 9.
Arguing for this is one of the main purpose of [89].
- 10.
Verification is easy. From (2.5) it follows:
$$\begin{aligned} z_{x}^{\prime }=y\varphi ^{\prime }\left( \frac{x}{y}\right) \frac{1}{y}=\varphi ^{\prime }\left( \frac{x}{y}\right) \qquad \mathrm {and}\qquad z_{y}^{\prime }=\varphi \left( \frac{x}{y}\right) - y\varphi ^{\prime } \left( \frac{x}{y}\right) \frac{x}{y^{2}}= \varphi \left( \frac{x}{y}\right) - \varphi ^{\prime } \left( \frac{x}{y}\right) \frac{x}{y} \end{aligned}$$Replacing in (2.3), one gets, then
$$\begin{aligned} y\varphi \left( \frac{x}{y}\right) +c +x\varphi ^{\prime } \left( \frac{x}{y}\right) =x\varphi ^{\prime }\left( \frac{x}{y}\right) +y\varphi \left( \frac{x}{y}\right) +c \end{aligned}$$.
- 11.
On these arguments and the mathematical discussion they were part of, cf.: [195], pp. 237–300; [117], pp. 1–21; [64]; [31], pp. 21–33; and [151], 256–264.
- 12.
For example in [207].
- 13.
Hintikka and Sandu’s theses have generated a sharp controversy: cf. [34, 62, 124], for example. This largely depended on their arguing that it is “unfortunate that philosophers habitually go to Frege”, since “Frege was far too myopic to be a fruitful source for concepts, idea and problems” ([129], p. 315). I shall not deal with this allegation, and confine myself to giving an account of Frege’s views in their historical context.
- 14.
An essentially different reaction was promoted by a group of British mathematicians including Woodhause, Babbage, and Peacock. Though their conceptions were highly influential in the history of logic, considering them is not relevant to my present purpose.
- 15.
A similar view had been endorsed by Ampère, almost twenty years earlier, in a memoir presented to the Institut des Sciences in 1803 and appearing in 1806 ([3], p. 496): “That which is termed a fact of analysis has always to be reduced to the metaphysical principles of this science if one wants to have a right idea of it. It is evident, indeed, that one has always to find the reasons for all the results obtained through calculation in the attentive examination of the conditions of any question, since the use of algebraic characters can add nothing to the ideas that they represent.”.
- 16.
Cf. [42], pp. 1–2, and [32], pp. 5–6:
First of all, we shall indicate what idea it seems appropriate to us to attach to the two words ‘number’ and ‘quantity’. We shall always take the denomination of numbers in the sense in which it is used in arithmetic, by making the numbers to arise from the absolute measure of magnitudes [grandeurs], and we shall only apply the denomination of quantities to real positive or negative quantities, i.e. to numbers preceded by the signs ‘\(+\)’ or ‘\(-\)’. Furthermore, we shall regard quantities as intended to express an increase or decrease, so that a given magnitude will simply be represented by a number, if one only means to compare it with another magnitude of the same species taken as a unity, and by the same number preceded by the sign ‘\(+\)’ or the sign ‘\(-\)’, if one considers it as to be used for increasing or decreasing a fixed magnitude of the same species [comme devant servir à l’accroissemment ou la diminuition d’une grandeur fixe de la même espèce]. [...] We shall call: the ‘numerical value’ of a quantity that number which forms its basis; ‘equal quantities’ those that have the same sign and the same numerical value; and ‘opposite quantities’ two quantities with the same numerical value affected by opposite signs.
- 17.
In Chap. 1 of this book, Benis Sinaceur argues that Dedekind’s logicism, if any, should not be assimilated to Frege’s. The previous remarks should be enough to confirm that this was also Frege’s conviction. These remarks fit, moreover, with another that Frege already makes in the Preface of the same Grundgesetze, also quoted by Benis Sinaceur, in Sect. 1.5.3 of Chap. 1, above ([97], Vorwort, p. VIII; [110]; p. VIII\(_{1}\)): “Mr Dedekind too is of the opinion that the theory of numbers is a part of logic; but his essay barely contributes to the confirmation of this opinion since his use of the expressions ‘system’ ‘a thing belongs to a thing’ are neither customary in logic nor reducible to something acknowledged as logical”. Frege’s point is then that the notions of set and set membership are not logical as such, but should rather be reduced to logical ones, which is just what Dedekind does not do. It follows that, for Frege, Dedekind’s view that “the unique and therefore absolutely indispensable foundation [...][for] the whole science of numbers” is “the ability of the mind to relate things to things, to let a thing correspond to a thing, or to represent a thing by a thing”, and that without this ability “no thinking is possible” ([49], p. VIII; [53], p. 14), do not coincide with the idea that “arithmetic belongs to logic”, as Stein maintains, by taking this last claim to be the same as the claim that “the principles of arithmetic are essentially involved in all thought” ([185], p. 246). The ability to which Dedekind refers is, indeed, a basic cognitive capacity, which, for Frege, does not pertains to logic at all.
- 18.
The same point is also made in “Über Begriff unf Gegenstand”, concerning concepts: [95], p. 193; [104], pp. 42–43.
- 19.
Cf. also [100], p. 665; [104], p. 115: “The peculiarity of functional signs, which we here called ‘unsaturatedness’, naturally has something answering to it in the functions themselves. They too may be called ‘unsaturated’, and in this way we mark them out as fundamentally different from numbers. Of course this is no definition; but likewise none is here possible. I must confine myself to hinting at what I have in mind by means of a metaphorical expression [bildlichen Ausdruck], and here I rely on the charitable discernment of the reader.” According to several scholars (cf., for instance: [44, 65]), the view that elucidation can convey ineffable content, and that this is an essential task for philosophy is Frege’s, and it manifests an important aspect of Frege’s influence on Wittgenstein (this view is often said to go back to [110], though Geach does not explicitly mention elucidation and limits himself to arguing that “Frege already held, and his philosophy of logic would oblige him to hold, that there are logical category-distinctions which will clearly show themselves in a well-constrcuted language, but which cannot properly be asserted in language”: ibid., p. 55). Usually, these scholars admit that Frege calls on different species of elucidation, and take the elucidation of “what is logically primitive” ([44], p. 182) to be the species in which ineffable content is conveyed, the prototypical example being the elucidation of the concept/object distinction. Despite this, it seems to me that if the notions of function and truth-value are taken for granted, the claim that concepts are first-level functions of one argument whose values are truth-values is fully unproblematic. The prototypical example of elucidation’s conveying ineffable content is rather that of the function/object distinction. The case of the elucidation of the notions of a concept and a relation also shows that, if the exposition of the Begriffsschrift is assimilated to elucidation, then elucidation is opposed to definition only if this last term is taken in a quite strict technical sense (which is proper to Frege), according to which it only refers to the explicit formal definitions admitted within the Begriffsschrift. In a broader sense, definitions, even explicit ones, can enter in an elucidation.
- 20.
The question whether the exposition that occupies part I of the Grundgsetze has or not a semantic extent—namely whether one can take it or not to provide “semantic justifications of axioms and rules” ([122], p. 365, where Heck is arguing for the affirmative, in contrast with what is argued by Ricketts [168])—is not fully relevant here. What seems to me relevant is that this semantic extent, if any, is quite different from that which would be involved in any discussion about the interpretation of a formal system, and, overall, that this exposition not only aims at showing that “the rules of the system are truth-preserving and that the axioms are true” ([122], p. 365), but also includes the elucidation of fundamental notions like those of an object, a function, a truth-value, a concept, and a relation (on this claim, cf. also [169], Sect. 6, esp. pp. 191–193). This elucidation is “required if one is to master the notation of [...][Frege’s] symbolism and properly understand its significance” ([44], p. 181), namely it is “necessary for explaining how Frege’s notation [i.e. his Begriffsschrift] is to be used in the expression of thoughts” ([201], pp. 251).
- 21.
Cf. footnote (17).
- 22.
Cf. also [99], p. 34; [109], p. 282: “It is clear that we cannot put down [hinstellen] a concept as independent, like an object; rather it can occur only in a connection. One may say that it can be distinguished within, but it cannot be separated from the context in which it occurs”.
- 23.
For example, in the same Sect. I.5, Frege argues that ‘\(2^{2}=4\)’ is a name of the True, and that the statement ‘
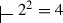 ’ asserts that the square of 2 is 4.
’ asserts that the square of 2 is 4. - 24.
Cf. footnote (4) of the Introduction.
- 25.
These definitions are informal insofar as they belong to the exposition of the Begriffsschrift, rather than to the Begriffsschrift, itself. Hence, they reduce to stipulations stated in the natural language, as clearly as possible (under the supposition that what is involved in them has been previously elucidated). This is, thus, another example of the fact that, if the exposition of the Begriffsschrift is assimilated to elucidation, the latter is not necessarily opposed to definition in the broad sense: cf. see the footnote (19).
- 26.
In fact, appropriate conventions relative to the “scope of the generality” have to be also made ([97], Sect. I.8 and I.17; [110], pp. 11\(_{1}\)–12\(_{1}\), 31\(_{1}\)). Here, I cannot enter into this matter, and merely observe that Frege’s use of Latin letters is such that generality cannot be expressed in the Begriffsschrift only through them: universal quantifiers are also necessary.
- 27.
Frege emphasises this fact by stipulating that a Latin letter for objects “indicates [andeute]” an object rather than refers to it ([97], Sect. I.17; [110], p. 31\(_{1}\)).
- 28.
That identity only applies to objects is a point that Frege makes on many occasions; he often argues as well that a “corresponding relation” applies to concepts or functions. But he does not use a fixed compact vocabulary for this purpose. In his review of Husserl’s Philosophie der Arithmetik ([98], p. 320; [109], p. 200), he argues that “coincidence [Zusammenfallen] in extension is a necessary and sufficient condition for the occurrence between concepts of the relation that corresponds to equality [Gleichheit] between objects” (I shall come back later to this claim, at p. 83), then remarks: “it should be noted in this connection that I’m using the word ‘equal [gleich]’ without further addition in the sense of ‘not different [nich verschieden]’, ‘coinciding [zusamenfallend]’, ‘identical [ identisch]’”. In “Ausführungen über Sinn und Bedeutung” ([106], vol. 1, pp. 132; [107], p. 122), he also argues that “the word ‘the same [derselbe]’ used to designate a relation between objects cannot properly be used to designate the corresponding relation between concepts”. Hence, speaking of sameness conditions for functions is not faithful to Frege’s parlance. Still, I use this expression for short, to speak of the conditions under which a certain function is this very function rather than some other one.
- 29.
In order to show that the paradox does not depend on the use of expressions like ‘the concept _’, Wright has stated it as follows ([206], pp. 74–77; for clarity, I adapt his argument to my setting; on this matter, cf. also [68], pp. 212 seq.): (i) the expression ‘That which is named by ‘\(\Phi \left( \xi \right) \)’ ’ is a singular term; (ii) hence, its reference, if any, is an object; (iii) the reference of ‘That which is named by ‘\(\Phi \left( \xi \right) \)’ ’ is that which is named by ‘\( \Phi \left( \xi \right) \)’; (iv) hence, that which is named by ‘\( \Phi \left( \xi \right) \)’ is an object. It follows that the problem cannot be solved by merely jettisoning expressions like ‘the concept _’.
- 30.
Some of these reasons have been offered in [174, 175]. For a critical discussion of them, cf. [170].
- 31.
I develop here a remark of Hintikka and Sandu ([129], p. 299: for Frege, “the extension of a concept can only be apprehended by our logical faculties starting out from the concept”.
- 32.
For simplicity, I only consider here first-level functions with one argument. It is easy to generalise Basic Law V to first-level functions with several arguments. But, if functions of higher-levels are considered, it is not perfectly clear what it would mean, for Frege, that these functions have the same or different value-ranges (on this matter, cf. [174], p. 32), and it would then be hard to allege that, in order to provide sameness conditions for these functions, it would be enough to stipulate that these conditions reduce to the identity conditions of the value-ranges of these functions.
- 33.
We find a similar claim already in “Über Begriff und Gegenstand” ([95], p. 198; [104], pp. 47–48): “We must say in brief, taking [...] ‘predicate’ in the linguistic sense: a concept is the reference of a predicate”.
- 34.
Frege even arrives at suggesting a special sign for this relation (to be used, of course, in the language of the exposition of the Begriffsschrift). Let \(\Phi \left( \xi \right) \) and \(\Psi \left( \xi \right) \) two concepts with the same extension. Frege suggests writing ‘
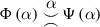 ’ arguing that this expresses the same thing as ‘
’ arguing that this expresses the same thing as ‘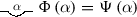 ’.
’. - 35.
That logic is concerned with truths about objects is, in my view, the distinctive mark of Frege’s extensionalist conception of logic (which he emphasises in “Ausführungen über Sinn und Bedeutung” by repeatedly observing that his remarks favour the “logician of extension against that of intension” ([106], vol. 1, p. 128 and 133–134; [107], p. 118 and 122–123). But this conception does not entail at all an extensionalist conception of functions.
- 36.
Cf. the quote from Sect. I.1 of Grundgesetze at the end of Sect. 2.4.2 below.
- 37.
I’m indebted to F. Schmitz for this account of the distinction between sense and reference of an f-name and the value-range of the corresponding function.
- 38.
In a letter to Husserl of October 30th–November 1st, 1906 ([106], vol. 2, pp. 101–105), Frege argues both that the thought expressed by a statement is what it has in common with any other equipollent [äequipollent] statement (ibid., p. 102) and that ‘if A then B’ and ‘it is not the case that A without B’ are equipollent (ibid., pp. 103–104). Insofar as the thought expressed by a statement is its sense, this means that these last statements have the same sense, so that also the f-names ‘if \(\xi \) then \(\zeta \)’ and ‘it is not the case that \(\xi \) without \(\zeta \)’ should have the same sense. This might appear to conflict with the view that two statements have different senses if one can “understand” both of them at the same time “while coherently taking different [epistemic] attitudes towards them”, that Evans has ascribed to Frege ([85], pp. 18–19). To solve this conflict, C. Penco has suggested distinguishing the semantic from the epistemic sense of a statement, arguing that the latter “could be represented by the different procedures through which each formula is given a truth condition” ([158], pp. 104–105). This suggests that ‘if \(\xi \) then \(\zeta \)’ and ‘it is not the case that \(\xi \) without \( \zeta \)’ have the same semantic sense but different epistemic senses, since these f-names are related to different procedures. Though Penco’s notion of the epistemic sense of a statement fits with my understanding of Frege’s notion of the sense of an f-name, it seems to me relevant to observe that, in the language of the Begriffsschrift, conjunction is expressed through implication and negation ([97], Sect. I.12), so that ‘\(\xi \) and \(\zeta \)’ is, by convention, a shortcut for ‘it is not the case that if \(\xi \) then non \(\zeta \)’. One could then argue that the previous statements have the same sense (without specification), since they correspond to the same procedure, so that one could also say (in the language of the exposition of the Begriffsschrift) that the f-names ‘it is not the case that \(\xi \) without \(\zeta \)’ and ‘if \(\xi \) then \(\zeta \)’ refer, once appropriately rendered, to the same function.
- 39.
The question has also been considered by Dummett, who has argued ([74], pp. 219–220) that “there is meagre evidence” for attributing to Frege the conception that his function-variables “range over the entire classical totality of [appropriate] functions”, and that “his formulation make it more likely that he thought of his function-variable as ranging over only those functions that could be referred to by functional expressions in his symbolism”.
- 40.
To understand what I mean by speaking of proper names or statements which are taken to result (rather than merely resulting) from saturating names of second-level functions with appropriate names of first-level functions, consider the example of a proper name like ‘\(\Phi (\Delta )\)’ or ‘\(\Psi (\Delta ,\Gamma )\)’. These can be either taken to result from saturating the names ‘\(\Phi (\xi )\)’ and ‘\(\Psi (\xi ,\zeta )\)’ of first-level functions with the proper names ‘\(\Delta \)’ and ‘\(\Gamma \)’, or taken to result from saturating the names ‘\(\varphi (\Delta )\)’ and ‘\(\psi (\Delta ,\Gamma )\)’ of second-level functions with these same names of first-level functions.
- 41.
The letter ‘\(\mu \)’ is here used here to hold a place empty for a second-level function with one argument, the index ‘\(\beta \)’ is used to make it clear that the arguments whose places are indicated by ‘\(\beta \)’, both in ‘\(\mathfrak {f}\left( \beta \right) \)’ and in ‘\(\Phi \left( \beta \right) \) ’, are bound, and ‘\(\Omega \)’ and ‘\(\Phi \)’ serve as schematic letters for functions of the second and first-level, respectively.
- 42.
This is enough evidence for concluding that, contrary to what Hintikka and Sandu seem to imply ([129], p. 311) Frege admitted the possibility of non-differentiable functions in real analysis (on this matter, cf. also [124], p. 41, and [36], pp. 90, 99–100).
- 43.
According to [62], pp. 142–145, the context of this passage suggests that Frege is here merely arguing for the possibility of extending the class of analytically representable functions so as “to include all functions of a particular class”: a quite common view among mathematicians of his time. Heck and Stanley ([124], p. 419–421) have considered, instead, that Frege’s only point, here, is that functions are unsaturated, which seems to me a quite implausible interpretation.
- 44.
This passage is also partially quoted in ([129], p. 312).
- 45.
More recently, Sandu has reiterated his and Hintikka’s major theses, and added that, for Frege, intensions have “logical primacy” over extensions ([173], pp. 241–243). To support this, Sandu argues that Ramsey’s efforts for reforming logicism [165] were manly motivated by an understanding of Frege’s and Russell’s conceptions about functions, which is close to that outlined in his joint paper with Hintikka. In opposition to this, Ramsey would have aimed to conciliate logicism with “the extensional attitude of the mathematics of his days (Cantorian set theory)”, and this resulted in his grasping of “the concept of arbitrary function in extension” ([173], pp. 238 and 250). This has convinced Demopoulos to reconsider the objections to Hintikka and Sandu’s theses advanced in a joint paper with Bell [62], and conclude that “Frege’s functions” should be distinguished from “arbitrary correspondences” i.e. arbitrary functions in set-theoretic sense ([61], especially p. 6).
- 46.
I agree then with Demopoulos, according to whom, “the interest of Hintikka and Sandu’s paper has less to do with standard versus nonstandard interpretations of second-order logic than with Frege’s concept of a function” ([61], p. 6).
- 47.
Despite their focusing on the question of whether Frege adopted the standard or a nonstandard interpretation of second-order logic, Hintikka and Sandu also suggest something like this when they claim ([129], p. 313) that “there is no niche in [...][Frege’s] world for [...][our] notion of an arbitrary function”, and that in Frege’s logic “there is no room for the idea of a arbitrary function-in-extension”.
- 48.
cf. see the footnote (13).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Benis-Sinaceur, H., Panza, M., Sandu, G. (2015). From Lagrange to Frege: Functions and Expressions. In: Functions and Generality of Logic. Logic, Epistemology, and the Unity of Science, vol 37. Springer, Cham. https://doi.org/10.1007/978-3-319-17109-8_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-17109-8_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-17108-1
Online ISBN: 978-3-319-17109-8
eBook Packages: Humanities, Social Sciences and LawPhilosophy and Religion (R0)


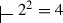 ’ asserts that the square of 2 is 4.
’ asserts that the square of 2 is 4.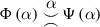 ’ arguing that this expresses the same thing as ‘
’ arguing that this expresses the same thing as ‘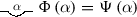 ’.
’.