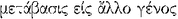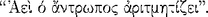Is Dedekind a Logicist? Why Does Such a Question Arise?

Benis-Sinaceur, Hourya; Panza, Marco; Sandu, Gabriel

doi:10.1007/978-3-319-17109-8_1

Hourya Benis-Sinaceur⁶,
Marco Panza⁶ &
Gabriel Sandu⁷

Part of the book series: Logic, Epistemology, and the Unity of Science ((LEUS,volume 37))

654 Accesses
13 Citations

Abstract

Logicism is generally presented as the philosophical thesis that arithmetic, and therefore all of mathematics, can be deduced from logic alone or can be reduced to logic.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Chapter: USD 29.95; Price excludes VAT (USA)

eBook: USD 39.99; Price excludes VAT (USA)

Softcover Book: USD 54.99; Price excludes VAT (USA)

Hardcover Book: USD 54.99; Price excludes VAT (USA)

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

1.
Boolos’ statement is more general (Boolos [23, pp. 216–217]): “Neither Frege nor Dedekind showed arithmetic to be part of logic. Nor did Russell. Nor did Zermelo or von Neumann. Nor did the author of Tractatus 6.02 or his follower Church. They merely shed light on it”.
2.
The name of this principle comes from Frege’s quoting, in [93] Sect. 63, Hume’s claim that “When two numbers are so combined as that the one has always an unit answering to every unit of the other, we pronounce them equal” (Treatise, Book I, Part iii, Sect. 1). Later, in Sect. 73, Frege argues that “the cardinal number which belongs to the concept F is identical with the cardinal number which belongs to the concept G if the concept F is equinumerous [gleichzähling] to the concept G” ([103], p. 80), which he tries, then, to prove. What is today usually called ‘Hume’s principle’ is the conjunction of this implication and the inverse one, which is formally (in the language of second-order logic) rendered as follows:
$$ \forall F,G\left[ \left( \#F=\#G\right) \Leftrightarrow F\thickapprox G \right] , $$
where ‘$F\thickapprox G$’ is a second-order formula expressing the existence of a one-to-one correspondence between the objects falling under F and those falling under G. Second-order logic$~+~$HP is called ‘Frege’s arithmetic’ or ‘FA’, for short. On the differences between Hume’s statement about numbers and Frege’s application to concepts cf. [191], who rightly points out that the definition of equinumerosity in terms of one-to-one correspondence is due to Cantor.
3.
What is proved is that HP has models with countable infinite domains.
4.
In Grundlagen, before trying to prove the if-direction of HP (cf. footnote (2), above), Frege claims to have reduced one-to-one correspondence to “purely logical relationships” ([93], Sect. 72: “Hiermit haben wir die beiderseits eindeutige Zuordnung auf rein logische Verhältnisse zurückgeführt”).
5.
For example, Gödel ([114], p. 127; my italics) writes that the vicious circle principle “makes impredicative definitions impossible and thereby destroys the derivation of mathematics from logic, effected by Dedekind and Frege, and a good deal of modern mathematics itself”.
6.
Before Burgess, also Parsons [153] and Heck [119] made the same claim.
7.
Burgess relies on the fact that from HP one can prove the existence of Dedekind infinite sets (a set A is Dedekind infinite when there is a bijection $\varphi $ from A onto a proper subset of A; for getting Dedekind infinite sets we need the infinity axiom $+$ an equivalent of the axiom of choice).
8.
I keep untranslated Dedekind’s terms ‘System’, which corresponds to our ‘set’, and ‘Abbildung’ (and cognates), which do not correspond to our mapping. Dedekind does not define an Abbildung by its graph as is defined a mapping in current set theory. The first translation made in [171, 209], namely ‘representation’, seems much better to me. In the light of Emmy Nœther’s developments and of Category Theory, the operation of representing a thing by a thing is a morphism.
9.
Cf. [171], p. 247: “It is a most remarkable fact that Dedekind’s previous assumptions suffice to demonstrate this theorem”.
10.
Cf. [49], Sect. 1, [53], p. 21: “A thing is completely determined by all that can be affirmed or thought concerning it. A thing a is the same as b (identical with b), and b the same as a, when all that can be thought concerning a can also be thought concerning b, and when all that is true of b can also be thought of a”.
11.
In Begriffsschrift, Frege rather uses the terms ‘Function’ and ‘Verfahren’ ([92], Sects. 24–31). ‘Abbilder’ occurs once (ibid., Sect. 13): “Diese Regeln und die Gesetze deren Abbilder sie sind, können in der Begriffsschrift deshalb nicht ausgedrückt werden, weil sie ihr zu Grunde liegen”.
12.
In Grundlagen, ‘Verfahren’ is replaced by ‘Beziehung’ ([93], Sect. 76ff.). Frege also uses ‘eindeutige Zuordnung’ (Sect. 62), ‘beiderseits eindeutige Zuordnung’ (Sect. 72) and ‘beiderseits eindeutige Beziehung’ (Sects. 78.5, 84) for expressing one-to-one relation, which is, in Dedekind’s terms, ‘ähnliche Abbildung’. For Frege (ibid., Sect. 70): “Der Beziehungsbegriff gehört also wie der einfache der reinen Logik an. Es kommt hier nicht der besondere Inhalt der Beziehung in Betracht, sondern allein die logische Form” (Sect. 70).
13.
On this matter, cf. Sect. 3.3 of Chap. 3, below.
14.
In 1877, Felix Klein writes to Dedekind ([67], p. 221): “Nothing that you have created in your solitary reflection went unheeded in the long term, everything decisive at its time has intervened in the development of mathematics, where it fructifies in a hundredfold way”.
15.
Tait translates ‘Abbildung’ by function: “I am very sympathetic with the view that the notion of function is a logical notion: a warrant for $\forall x\varphi \left( x\right) $ must be a function assigning to each b in the range of x a warrant to $\varphi \left( b\right) $, and a warrant for a proposition $A\rightarrow B$ is a function that assigns to each warrant of A a warrant of B. So the primitive truths of the logic of $\forall $ and $\rightarrow $ are truths about functions” ([190], p. 314).
16.
This view is presented in an unpublished paper, “On Dedekind logicism”, which the author wrote after his being aware of my own view. Ferreirós was so kind as to send a copy of his paper to me.
17.
Famously, the first of the three fundamental principles stated in Grundlagen goes as follows ([93], Einleitung, p. X; [103], p. xxii): “There must be a sharp separation of the psychological from the logical, the subjective from the objective”.
18.
As pointed out by Boolos ([23], p. 214), Frege’s proof that every natural number has a successor depends on the assumption that cardinal numbers are objects. And it is only if one supposes cardinal numbers not to be objects that HP looks analytic or obvious.
19.
Concerning Russell’s views cf., e.g., [24], [26], esp. p. 292.
20.
Cf. [97], Vorwort, p. XXVI, ([110], p. XVI$ _{1}$): “And so may this book, even if belatedly, contribute to a renaissance of logic.”
21.
Frege’s system has two connectives, negation and the conditional, six axioms, the universal quantifier introduced in Grundgesetze, Sect. 11, under the name ‘Generality’, with three more axioms, and two rules: explicitly modus ponens and, implicitly, rule of substitution. Relations between concepts are ruled by logical inference. In Ausführungen über Sinn und Bedeutung ([106], vol. 1, p. 128; [107], p. 118), Frege holds that all relations between concepts can be reduced to the “fundamental logical relation [...] of an object’s falling under a concept”, and adds that if an object falls under a concept, it falls under all concepts with the same extension, so that, “in relation to inference, and where the laws of logic are concerned, concepts differ only as so far their extensions are different”.
22.
Usually, concepts are taken to be predicates of judgements, like in Kant’s First Critic (Transcendental Analytic, I, Chap. 1), but Frege sees predicates as mathematical functions. By contrast, Dedekind does not consider the notion of judgement, because he does not tackle the question of the truth.
23.
On Frege’s notion of function, cf. Chap. 2 of the present book.
24.
The expression is used by Frege, e.g. in “Logik in der Mathematik” ([106], vol. 1, pp. 225–228; [107], pp. 208–211), possibly his lecture notes of a course attended by Carnap in the spring of 1914.
25.
Cf. [93], Sect. 46; [103], p. 59: “To throw light on the matter, it will help to consider number in the context of a judgement that brings its ordinary use.” Cf. also [106], vol. 1, “Zahl”, p. 284, [107], pp. 265: “What [...] is the number itself? [...] We may seek to discover something about the number itself from the use we make of numerals and number-words. Numerals and number-words are used, like names of objects, as proper names.” And again: “In arithmetic a number-word makes its appearance in the singular as a proper name of an object of this science; it is not accompanied by the indefinite article, but is saturated” ([106], vol. 1, “Aufzeichnungen für Ludwig Darmstaedter”, pp. 276; [104], pp. 256).
26.
In the preface of Grundgesetze, Frege stresses that in Dedekind Was Sind “nowhere [...] do we find a list of the logical or other laws he takes as basic ” ([103], Vorwort, p. VIII; [110], p. VIII$_{1}$).
27.
Symptomatically, Carnap does not refer to Zermelo’s way of avoiding the paradoxes.
28.
Gödel distinguishes between ‘tautological’ and ‘analytic’ and points out that the elementary theory of integers is demonstrably non-analytic as a consequence of his incompleteness theorem ([114], p. 139, footnote 46).
29.
Frege’s formulation is as follows ([92], Sect. 26; [125], p. 60): “If from the two propositions that every result of an application of the procedure f to x has property F and that property F is hereditary in the f-sequence, it can be inferred, whatever F may be, that y has property F, then I say: ‘y follows x in the f-sequence’, or ‘x precedes y in the f -sequence’”.
30.
Cf. also [93], Sect. 109; [103], pp. 118–119: “From all the preceding it thus emerged as a very probable conclusion that the truths of arithmetic are analytic and a priori; and we achieved an improvement of the view of Kant”.
31.
This expression does not belong to the vocabulary of Grundlagen.
32.
About Frege’s discussion of “Die schöpferischen Definitionen”, cf. [97], Sects. 139–147.
33.
Cf. [93], Sect. 109, [97], Sect. II.86–137, where Frege contrasts “die formale Arithmetik” (by Heine and Thomae) with “die inhaltliche Arithmetik”, and Sect. II.138–147, where he questions Dedekind’s, Hankel’s and Stolz’s definitions of real numbers. Cf. also the Frege-Hilbert correspondence in [105].
34.
Frege insists that this relation of subsumption is distinct from the relation of inclusion.
35.
In Grundlagen, Sect. 43, Frege criticises Schröder’s supposed assimilation of the number with a sign. Note that the term ‘Begriffsschrift’ is used by Frege to designate “the conceptual content [den begrifflichen Inhalt]” ([92], Sect. 3; [125], p. 12), which is independent from the peculiar statement which expresses it.
36.
Cf. the letter to Husserl of May, 25th, 1891 ([106], vol. 2, pp. 96–98), [96], and “Ausführungen über Sinn und Bedeutung” ([106], vol. 1, pp. 128–136; [107], p. 118–125).
37.
The Sinn of a statement is a thought; its Bedeutung is its truth-value. And judgement “could be characterised as a transition from a thought to a truth-value” (letter to Husserl of May, 25th, 1891: [106], vol. 2, p. 97; [108], p. 64).
38.
Also Frege employs the term ‘Begriffsbildung’ in his paper on Boole’s “logical calculus” ([106], vol. I, “Booles rechnende Logik und die Begriffsschrift”, p. 14). This term was common at that time, indeed. But while Dedekind aims at creating new specific mathematical concepts, Frege aims at showing the general logical method grounding the uniform process of concept formation.
39.
For a more refined distinction between language-logicism, consequence-logicism and truth-logicism, cf. [126]: Frege’s project was truth-logicism as far as mathematical truths can be proved merely “on the basis of general logic laws and definitions” (ibid., p. 206).
40.
Anyway, such a mapping cannot exist since arithmetic is undecidable ([23], p. 208).
41.
Boolos makes this remark in order to state that Russell advocates the definability thesis but not the provability thesis.
42.
This is Carnap’s biased rephrasing of Frege’s following statements: “In mathematics a mere moral conviction, supported by a mass of successful applications, is not good enough. Proof is now demanded for many things that formerly passed as self-evident. [...] In all directions the same ideals have be seen at work—rigour of proof, precise delimitations of extent of validity, and as a means to this, sharp definitions of concepts” ([93], Sect. 1; [103], p. 1). Nevertheless Frege assumes that abstract objects, such as thoughts or senses or numbers or mathematical truths, have a changeless existence, different from that of the real [wirklich] world and that of the inner world of an experiencing subject.
43.
Bynum ([37], p. 281) stresses that in Grundlagen “Frege did not consider the introduction of extensions to be necessary, and indeed he felt some discomfort in identifying them with numbers”. Bynum thinks that this discomfort pushed Frege to deal with that part of logic that is independent of set-theory, namely “fundamental logic”. Hodes ([132], pp. 143–144) points out the difficulty in interpreting Frege’s “Tagebucheintragungen über den Begriff der Zahl” , dated to March 23$\mathrm{th}$–25$\mathrm{th}$, 1924 ([106], vol. I, pp. 282–283; [107], pp. 263–264). According to Dummett ([74], p. 161), Frege’s early writings do not contain “a complete systematic theory of philosophical logic comparable to, and in competition with, that propounded by him from 1891 onwards”. Parsons [154] shows how Frege came to reject extensions as being really objects along with logicism.
44.
The claim that every arithmetic truth is a theorem of the system is abandoned because it clashes with Gödel’s first incompleteness theorem.
45.
Cf. ([93], Sect. 105; [103], p. 115): “In arithmetic we are not concerned with objects which we come to known as something alien from without through the medium of the senses, but with objects given directly to our reason and, as its nearest kin, utterly transparent to it”.
46.
Cf. [93], Sects. 13 and 64, [103], pp. 19–20 and 75: “In geometry [...] it is quite intelligible that general propositions should be derived from intuition”; “Everything geometrical must be given originally in intuition”.
47.
One may recall Aristotle’s refusal of “
”.
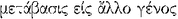
48.
Cf. [93], Sect. 19, [103], p. 255: “At this point I should like straight away to oppose the attempt to think of number geometrically, as a ratio between lengths or surfaces”.
49.
Cf. [97], Sect. II.157, [110], p. 155$_{2}$: “ [...] Darum ist es nicht möglich, das Gebiet der Anzahlen zu dem der reellen Zahlen zu erweitern; es sind eben ganz getrennte Gebiete”.
50.
Such identifications are very usual in mathematical practice, but the philosophical question about how to conceive of, e.g., the identity of the rational 2 and the real 2 gives still rise to subtle discussions.
51.
Cf. also [106], vol. I, “Neuen Versuch der Grundlegung der Arithmetik”, pp. 298–299; [107], pp. 278–279: “I have to abandon the view that arithmetic does not need to appeal to intuition either in its proofs, understanding by intuition the geometrical source of knowledge, that is, the source from which flow the axioms of geometry [...]. I distinguish the following sources of knowledge for mathematics and physics: (1) Sense perception; (2) The Geometrical Source of Knowledge; (3) The Logical Source of Knowledge. The last of these is involved when inferences are drawn, and thus is almost always involved. Yet it seems that this on its own cannot yield us any objects [...] [and] probably [...] cannot yield numbers either [...]”.
52.
In Grundlagen, Sect. 13, Frege holds that points, lines and plane are not individuated as are the numbers.
53.
Dedekind uses ‘Zahl’ or ‘natürliche Zahl’ to refer to finite ordinal numbers (Ordinalzahlen): [49], Definition 73; for ‘Anzahl’, he has the same use as Frege ([93], Sect. 4, footnote; cf. above, footnote (2) of the Introduction), since both use it to refer to cardinal numbers ([49], Definition 161).
54.
Of course, they don’t form the same structure, even though the totally ordered semi-ring of natural numbers is embedded in the totally ordered field of real numbers.
55.
Cf. also the following passage (idid.): “In speaking of arithmetic (algebra, analysis) as a part of logic I mean to imply that I consider the number-concept entirely independent of the conceptions or intuitions of space and time, that I consider it an immediate flow from the pure laws of pure thought [die reine Denkegesetze]”. Notice that Dedekind does not write “laws of logic”, but “laws of thought”.
56.
Cf. e.g. [47], Sect. I, [53], p. 2, (my italics): “I regard the whole of arithmetic as a necessary, or at least natural, consequence of the simplest arithmetic act, that of counting, and counting itself as nothing else than the successive creation of the infinite sequence of positive integers in which each individual is defined by the one immediately preceding [...]. The chain of these numbers forms in itself an exceedingly useful instrument for the human mind; it presents an inexhaustible wealth of remarkable laws obtained by the introduction of the four fundamental operations of arithmetic. Addition is the combination of any arbitrary repetition of the above-mentioned act into a singular act [...]”.
57.
In a famous letter to Bessel (of April 9, 1830), Gauss writes that “the number is a pure product of our mind” ([67], p. 40). And in a fragment dated to 1882, Dedekind maintains that “Analysis in its entirety is a necessary consequence of the thought as such” (ibid., p. 199).
58.
Remark also that Frege does not only avoid to emphasise the strict connection between defining numbers and defining operations on them, but considers the former as essentially independent of the latter. In the Vorwort of Grundgesetze, he feels no embarrass in observing that his “investigation”, namely that offered in the first volume of his treatise, “does not yet include the negative, fractional, irrational, and complex numbers, nor addition, multiplication, etc.” ([97], Vorwort, p. V; [110], p. V$_{1}$).
59.
Cf. [106], vol. I, “Erkenntnisquellen der Mathematik und der mathematischen Naturwissenschaften” p. 294, and “Zahlen und Arithmetik”, p. 297; [107], pp. 274 and 277.
60.
I shall come back in Sect. 1.5.1 to Dedekind’s and Frege’s different notions of a concept.
61.
Cf. [92], Vorwort, pp. III–IV; [125], p. 5: “The most reliable way of carrying out a proof, obviously, is to follow pure logic, a way that, disregarding the particular characteristics of objects, depends solely on those laws upon which all knowledge rests. [...] I first had to ascertain how far one could proceed in arithmetic by means of inferences alone, with the sole support of those laws of thought that transcend all particulars”. Cf. also [93], Vorwort, p. III, [103], p. XV: “Thought is in essentials the same everywhere: it is not true that there are different kinds of laws of thought to suit the different kinds of objects thought about”.
62.
Cf. [92], Sect. 23, [125], p. 55: “[...]pure thought irrespective of any content given by the senses or even by an intuition a priori, can, solely from the content that results from its own constitution, bring forth judgements that at first sight appear to be possible only on the basis of some intuition” (my italics). Cf. also [102], p. 74, [109], pp. 368–369: “Neither logic nor mathematics has the task of investigating minds and contents of consciousness owned by individual men. Their task could perhaps be represented rather as the investigation of the mind; of the mind, not of minds”. Dedekind would completely agree with this assertion.
63.
Cf. [93], Sect. 26, [103], p. 35: “What is objective [...] is what is subject to laws, what can be conceived and judged, what is expressible in words”.
64.
Cf. Dummett’s comments in [70], pp. 123–125.
65.
Cf. also [97], Sect. II.74, [110], p. 86$_{2}$: “We can distinguish physical from logical objects, by which of course no exhaustive classification is intended to be given. The former are in the proper sense actual; the latter not so, though no less objective because of that. While they cannot act on our senses, nonetheless they are graspable by our logical faculties. Such logical objects include our cardinal numbers; and it is probable that the remaining numbers also belong here”.
66.
Frege’s assertion that “the validity of Dedekind’s proofs [in Was sind, Sect. 66] rests on the assumption that thoughts obtain independently of our thinking” ([106], vol. I, “Logik”, p. 147, footnote; [107], p. 136) does not hold: Dedekind takes thoughts to be objective but not to obtain independently of our thinking. Actually, Dedekind’s number-realm ([49], Vorwort, p. VIII; [53], p. 14) does not exist independently of our thinking.
67.
Indeed, Stetigkeit shows that the Dedekindian “completeness” of the real numbers field implies logically its Cauchy’s completeness, once one defines a distance (a metric) on the field.
68.
Dedekind does not put an exclusive disjunction between logic and geometry, as does Frege in his early writings. He holds that the mathematical general concept of space differs from the Euclidean space, taken as intuitive until the nineteenth century, and from the physical sensible space.
69.
‘Numbers’ here does not merely refer to natural numbers; it rather refers to any kind of numbers.
70.
Cf. [97], Vorwort, pp. 15–16, [110], pp. XV$ _{1}$–XVI$_{1}$: “[...] being true is different from being taken to be true, be it by one, be it by many, be it by all, and is in no way reducible to it. It is no contradiction that something is true that is universally held to be false. By logical laws I do not understand psychological laws of taking to be true, but laws of being true”. Cf. also [106], vol. I, “Logik”, p. 158; and 146: “If a man holds something to be true [...] he thereby acknowledges that there is such a thing as something’s being true. But in that case it is surely probable that there will be laws of truth as well, and if there are, these must provide the norm for holding something to be true. And these will be the laws of logic proper ”. And again [102], p. 59, [109], p. 352: “ I assign to logic the task of discovering the laws of truth, not the laws of taking things to be true or of thinking”.
71.
The notions of a judgement and a concept are taken on from “the old logic” in general and, in particular, from Kant, but Frege’s notion of a concept is idiosyncratic and Frege’s way of connecting concepts and judgements with the notion of truth is totally new. More precisely, Frege holds that “the theory of concepts and of judgement is only preparatory to the theory of inference”, and that “the task of logic is to set up laws according to which a judgement is justified by others, irrespective of whether they are themselves true”; thus “ the laws of logic can guarantee the truth of a judgement only insofar as our original grounds for making it, reside in judgements that are true” ([106], vol. I, “17 Kernsäter zur Logik”, dated to 1906 or earlier, p. 175, sentences 14, 15, and 16; [107], p. 175). Boolos and Heck ([30], p. 333) point out that the following question may have occurred to Frege: “Can the notion of a truth of logic be explained otherwise than via the notion of provability?”. Insofar as he did not have the notion of interpretation, Frege could not have got the notion of logical consequence.
72.
The epigraph on the first-page of Was Sind is this:
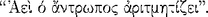
I discuss the matter in [56], pp. 101–113. It seems to me wrong to interpret the whole essay Was Sind as a “transcendental deduction” in Kant’s specific sense, as suggested by Mc Carty [145], or to cut radically any link between Kant and Dedekind, as suggested by Reck, instead (Reck 2003).
73.
A place where Dedekind expresses his permanent concern for rigour is his Letter to Weber of November 8, 1878, where he exhorts him to “not renounce to use logic” in secondary school ([55], vol. III, p. 485).
74.
Cf. [97], Vorwort, p. VII, [110], p. VII$_{1}$: “The gaplessness of the chains of inferences contrives to bring to light each axiom, each presupposition, hypothesis, or whatever one may want to call that on which a proof rests; and thus we gain a basis for an assessment of the epistemological nature of the proven law”. Frege discusses the nature of axioms in “Logik in der Mathematik”, [106], vol. I, pp. 221–222.
75.
I leave out of consideration Dummett’s remark, which Demopoulos renders as follows: “Frege’s basic approach [to numbers] would have been problematic even if no inconsistency had been discovered since there is an unacceptable circularity in Frege’s procedure: the abstraction principle which introduces the numbers contains an implicit first-order quantifier, so the numbers introduced on the left occur within the range of the variables bounded on the right in the explicit definition of one-one correspondence” ([60], p. 220).
76.
Cf. also [67], Appendix XXXI, and the letters to Lipschitz of June 6$\mathrm{th}$ and July 27$\mathrm{th}$, 1876 ([55], vol. III, pp. 468–479).
77.
Cf. [49], Vorwort, p. VII, [53], p. 14: “In science nothing capable of proof ought to be accepted without proof”. That’s the very first sentence of Was sind.
78.
Dedekind insists upon the fact that we must define in its entirety (up to an isomorphism) the domain of the real numbers in order to have the possibility to define in a general way the operations on it: otherwise how could we know that, e.g. the result c of the addition or of the multiplication of some two individual real numbers a and b is again a real number? Letter to Lipschitz, June 10, 1876 ([55], vol. III, pp. 462–474).
79.
Definitions are pervasively treated in [97], Sects. I.26-33, II.55–65 and in “Logik in der Mathematik” ([106], vol. I, pp. 219–270; [107], p. 201–250).
80.
Remember the third fundamental principle stated in Grundlagen: “never to lose sight of the distinction between concept and object” ([93], Einleitung, p. X; [103], p. XXII).
81.
Here is what Frege writes some line above: “Although it has already been announced many times that arithmetic is merely further developed logic, still this remains disputable as long as there occur transitions in the proofs which do not conform to acknowledged logical laws but rather seem to rest on intuitive knowledge. Only when these transitions are analysed into simple logical steps can one be convinced that nothing but logic forms the basis”.
82.
Frege means Dedekind’s definition of addition, multiplication, and so on.
83.
But this is only one first step; going further leads to construing the logical system lying at the bottom of mathematics.
84.
As noted by Dedekind, this simple statement involves infinity of S.
85.
We should not forget that Dedekind’s construct is based upon “a prior analysis of the sequence of natural numbers just as it presents itself in experience, so to speak, for our consideration” (Letter to Keferstein, February 27, 1890: [184], pp. 271–272; [125], p. 99). For a worthwile discussion of this matter, cf. [156], pp. 306–311.
86.
Frege recalls the Socratic aphorism: “The first prerequisite for learning [...] is [...] the knowledge that we do not know” ([93], Einleitung, p. III; [103], p. XV). Cf. also [106], vol. I, “Logik in der Mathematik”, p. 239; [107], p. 221.
87.
Cf. [106], vol. I, “Logik in der Mathematik”, pp. 234 and 262; [107], pp. 216 and 243; my italics: “Is that [...] a science which proves sentences without knowing what it proves?”; “Definitions must be given once and for all”.
88.
Frege summarises his method as follows ([106], vol. I, “Logik”, p. 154; [107], p. 143): “The first and most important task is to set out clearly what the objects to be investigated are. Only if we do this shall we be able to recognise the same as the same: in logic too such acts of recognition probably constitute the fundamental discoveries”.
89.
Cf. footnote (2), above.
90.
Cf., again, footnote (2), above.
91.
Cf. [27], p. 309. Also [153] displays some difficulties with the thesis that numbers are objects.
92.
Cf. the quote from the Nachwort of Grundgesetze, at the beginning of Sect. 1.4.3, below.
93.
This is one reason why “Dedekind would not have been happy with the suggestion that the existence of infinite systems be derived from Hume’s principle” ([23], p. 216).
94.
The following passage could be interpreted as conflicting with Frege’s ontological assumptions ([93], Sect.60; [103], pp. 72): “The self-subsistence which I am claiming for number is not to be taken to mean that a number-word designates something when removed from the context of a statements, but only to preclude the use of such words as predicates or attributes, which appreciably alters their meaning [Bedeutung]”. But for Dummett ([69], pp. 83, 81) the context principle is “a thesis about reference, not just about sense”, it is used “to justify regarding abstract terms as standing for genuine, objective objects”; and what conflicts with it is the doctrine that truth-values are objects.
95.
In retrospect Frege writes ([97], Vorwort, p. X; [110], p. X$_{1}$):

Previously I distinguished two components in that whose external form is a declarative statement [Behauptungssatz]: 1) the acknowledgement of truth [this is the definition of a judgement, given in Grundgesetze, Sect. I.5], 2) the content, which is acknowledged as true. The content I called ‘judgeable content [beurtheilbarer Inhalt]’. This now splits for me into what I call ‘thought’ and what I call ‘truth-value’. This is a consequence of the distinction between the sense and the reference [ Bedeutung] of a sign. In this instance, the thought is the sense of a statement and the truth-value is its reference. In addition, there is the acknowledgment that the truth-value is the True.
96.
Cf. [106], vol. I, “Meine grundlegeden logischen Einsichten” p. 272; [107], p. 252: “Work in logic just is, to a large extent, a struggle with the logical defects of language”.
97.
Cf. also also [106], vol. I, “Aufzeichnungen für Ludwig Dermstaedter”, p. 276, [107], p. 256: “In arithmetic a number-word makes its appearance in the singular as a proper name of an object of this science; it is not accompanied by the indefinite article, but is saturated”.
98.
Needless to say that ‘analytical’ in Kant’s conception conforms to Aristotle’s analysis of a proposition into subject and predicate (the predicate is contained in the subject). With the analysis into argument and function, Frege introduces a new sense of the adjective ‘analytical’ ([93], Sects. 3, 16–17). First, the analytical/synthetical, and a priori/ a posteriori distinctions “concern [...] not the content of the judgement, but the justification for making the judgement” (ibid., Sect. 3; [103], p. 3). Second, for Frege, analysis is a process similar to chemists’ decomposition; thus a truth resulting from an analysis (an analytical proposition) is a posteriori, at least in Kant’s sense. But, in mathematics, justification is “finding [...][a] proof and [...] following it up right back to the primitive truths” (ibid.,; [103], p. 4). Now, “if, in carrying out this process, we come only on general logical laws and on definitions, then the truth is an analytic one”, and “if [...][it] can be derived exclusively from general laws, which themselves neither need nor admit of proof, then the truth is a priori” (ibid.).
99.
Cf. [93], Sect. 17, where Frege expresses the innovative view that logic can provide us with substantive knowledge; if one can, writes Frege, show the inner link of arithmetic with logic, then “the prodigious development of arithmetical studies, with their multitudinous applications, will suffice to put an end to the widespread contempt of analytic judgements and to the legend of the sterility of pure logic” (ibid.; [103], p. 24). Cf. also [93], Sect. 91, [103], p. 104: “statements which extend our knowledge can have analytic judgements for their content”. Frege’s followers will dispute on the mathematical fruitfulness of logic: Poincaré and Wittgenstein will be against; Tarski, Abraham Robinson, Kreisel, Feferman, among others, will concretely show how logical analysis may be used as a tool for proving or discovering mathematical results.
100.
Cf. [55], Vol. III, “Über die Einführung neurer Funktionen in der Mathematik”, pp. 428–429 (my translation; Dedekind’s italics): “The chief task of any science is striving to ground the truth, [...] towards which one can but go farther [without being capable with our step-by-step understanding to attain it]. But science itself, which represents the course of human knowledge, is open to an infinite variety of presentations [Darstellungen][...] it may be framed into different systems, because as human work it is submitted to arbitrariness and affected by all the imperfections of the human intellectual powers”. By contrast, Frege thinks that the logical presentation of arithmetic is fundamentally unique.
101.
I think Dedekind would have agreed with Frege’s following remark: “What is known as the history of concepts is really a history either of our knowledge of concepts or of the meanings of words [Bedeutungen der Wörter]. Often it is only after immense intellectual effort, which may have continued over centuries, that humanity al lest succeeds in achieving knowledge of a concept in its pure form, in stripping off the irrelevant accretions which veil it from the eyes of the mind” ([93], Vorwort, p. VII; [103], p. XIX). But Dedekind does not consider that the history of knowledge is psychology of knowledge; knowing historically mathematical notions may lead to “stripping off the irrelevant accretions” and to throwing light on ignored aspects of them.
102.
It is noteworthy that neither in Grundlagen nor in Grundgesetze Frege criticises Dedekind’s way on grounds of psychologism. Dummett’s psychologistic reading of Dedekind ([74], Chap. 2, “Frege and the paradox of analysis”, p. 49) is very questionable.
103.
Frege is at odds with this dynamic view. Here is what he writes, instead ([106], vol. I, “Logik in der Mathematik” p. 261; [107], pp. 241–242): “We must always distinguish between history and system. In history we have development; a system is static. [...] what is once standing must remain, or else the whole system must be dismantled in order that a new one may be constructed”.
104.
On the relations between Frege and Thomae and between Frege and Hankel, cf. [46, 157].
105.
Cf. footnote (85), above.
106.
Something like the theorem proved here is lacking from the first draft ([67], Appendix LVI).
107.
Cf. [97], Sect. II.147 and II.157, respectively, [110], p. 149$_{2}$ and 155$_{2}$:

If there are logical objects at all—and the objects of arithmetic are such—then there must also be a means to grasp them, to recognise them. The basic law of logicd which permits the transformation of the generality of an equality into an equality serves for this purpose. Without such a means, a scientific foundation of arithmetic would be impossible. For us it serves the purposes that other mathematicians intend to achieve by the creation of new numbers. [...] In any case, our creation, if one wishes so to call it, is not unconstrained and arbitrary, but rather the way of proceeding, and its permissibility, is settled once and for all. And with this, all the difficulties and concerns that otherwise put into question the logical possibility of creation vanish; and by means of our value-ranges we may hope to achieve everything that these other approaches fall short of.

We have been reminded of our transformation of the generality of an equality into an equality of value-ranges that promises to accomplish what the creative definitions of other mathematicians are not capable of.

What Frege is evoking here is Basic Law five, which in a modern notation can be rephrased as follows:
$$ \left[ ValueRange\left( f\right) =ValueRange\left( g\right) \right] \Leftrightarrow \forall x\left[ f\left( x\right) =g\left( x\right) \right] . $$
Since this makes the generality of an equality (or identity), ‘$\forall x \left[ f\left( x\right) =g\left( x\right) \right] $’, equivalent to an equality (or identity) of value-ranges, ‘$\left[ ValueRange\left( f\right) =ValueRange\left( g\right) \right] $’. The generality is, of course, expressed by the universal quantifier.
108.
It has been remarked that, in Grundlagen, Frege makes no use of extensions once HP is derived (in Sect. 73). By contrast, extensions (or more generally value-ranges) are used throughout Grundgesetze. However [119] shows that they are eliminable except in the proof of HP.
109.
This is the essential reason why Frege does not have the notion of logical consequence, let us say from a set S of logical formulas to a logical formula A. He does not consider a formula under a range of interpretations.
110.
Cf., e.g., [74], Chap. 2, “Frege and the paradox of analysis”, pp. 17–52. Note in passing that Frege does not use the adjective ‘explicit’ to qualify explicit definitions (since, for him, any suitable definition is explicit).
111.
Cf. footnote (112), below.
112.
That’s the paradox of (logical) analysis, which results from an immediate insight and yields an axiom instead of giving an identity each member of which is a logical object. Regarding worries caused by the expression ‘ zerlegende Definition’, and its relations with “analytische Wahrheiten” and “analytische Grundsätzen”, which Frege deals with in Grundlagen ([93], Sects. 3–4)—where we do not find ‘analytische Definition’, but rather ‘Auflösung der Begriffe’, for ‘conceptual analysis’—, cf. [73], Chap. 2. Dummett renders ‘zerlegende Definition’ with ‘analytic definition’, in according with the translation of [107]. But, as rightly observed by Beaney ([6], p. 316, footnote 10), Frege’s zerlegende Definitionen are not analytisch in the Kantian sense. According to Beaney (ibid.), “where a definition is ‘analytic’, then it must be understood as either a ‘constructive definition’ or an ‘axiom’ ” (I suppose that he takes constructive definitions to include the definition of individual cardinal numbers in Grundlagen and Grundgesetze). But if “analytic” definitions may be “axioms”, the task remains to explain why Frege continues, as late as in 1914, to reject axioms as (implicit) definitions. After all, following Frege’s terminology, there are not only “logical concepts” and “logical objects”, but also “basic laws”, which might be taken as logical axioms.
113.
This last sentence occurs some pages earlier: [106], vol. I, “Logik in der Mathematics”, p. 206), [107], p. 206. Still, the truth of a statement that might count as an axiom is not relative. Compare with Dedekind’s view according to which “Drehen und Wenden der Definitionen, den aufgefundenen Gesetzen oder Wahrheiten zuliebe, in denen sie eine Rolle spielen, bildet die gröss te Kunst des Systematikers” ([55], vol. III, p. 430). Yet in mathematics this turning and shifting leaves no room for arbitrariness.
114.
A similar point is made few line below: “The effect of [...] logical analysis [...] will be precisely this—to articulate the sense clearly”.
115.
Cf. [153], for a discussion of this matter.
116.
Its aim or goal, not its essence, which is, rather, “the assertoric force with which a sentence is uttered” ([106], vol. I, “Meine grundlegenden logischen Einsichten”, p. 272; [107], pp. 252). The following quote, from the beginning of “Der Gedanke”, is even clearer ([102], pp. 58–59; [109], p. 351–352): “Just as ‘beautiful’ points the ways for aesthetics and ‘good’ for ethics, so do words like ‘true’ for logic. All sciences have truth as their goal; but logic is also concerned with it in a quite different way: it has much the same relation to truth as physics has to weight or heat. To discover truths is the task of all sciences; it falls to logic to discern the laws of truth. [...] I assign to logic the task of discovering the laws of truth, not the laws of taking things to be true or of thinking”.
117.
Cf. [106], vol. I, “17 Kernsätze zur Logik”, p. 189, sentence 7, [107], p. 174: “What true is, I hold to be indefinable”. Cf. also [106], vol. I, “Logik”, pp. 139–140, [107], pp. 128–129: a remarkable foreinsight of Tarski’s undefinability theorem.
118.
Cf. also [106], vol. I, “Logik”, p. 149; [107], p. 137: “The metaphors that underlie the expression we use when we speak of grasping a thought, of conceiving, laying hold of, seizing, understanding, of capere, percipere, comprehendere, intelligere, put the matter in essentially the right perspective. What is grasped, taken hold of, is already there and all we do is take possession of it”.
119.
Compare with Gödel’s more affirmative opinion about the axioms of set-theory, which “force themselves upon us as being true.” ([113], p. 268).
120.
That our current understanding of mathematical realism, which originates from Bolzano’s “Sätze an sich [16] and Frege’s “third realm”, does not fit with Plato’s account of the being of mathematical objects is soundly argued by Tait [189, 190] and McLarty [147], whose conclusion is that “Plato was not a mathematical Platonist” (ibid., p. 120). Hence my discriminant use of ‘realism’ and ‘Platonism’.
121.
Cf. [55], vol. III, p. 428: “Die weitere Entwicklung einer jeden Wissenschat immer wieder auf das System, durch welches man ihren Organismus zu erfassen sucht, neubildend zurück wirkt, ist nicht allein eine historische Tatsache, sondern beruht auch auf einer innern Notwendigkeit”.
122.
Cf. [55], vol. III, p. 428 (my italics): “Diese Vorlesung hat nicht etwa [...] die Einführung einer bestimmten Klasse neuer Funktionen in die Mathematik, sondern vielmehr die Art und Weise [my italics] zum Gegenstande, wie in der fortschreitenden Entwicklung [my italics] dieser Wissenschaft neue Funktionen, oder, wie man ebensowohl sagen kann, neue Operationen [Dedekind’s italics] zu der Kette der bisherigen hinzugefügt werden”.
123.
For a criticism of Frege’s twofold conception of sense, cf. [72], pp. 276–281.
124.
This makes Dedekind’s concepts close to middle ages universals (contrary to Boolos’ suggestion, in [29], p. 149, it’s not so easy to give the same ontological status to Plato’s Forms and to universals).
125.
Cf. the letters to Lipschitz of July 27, 1876 and to Weber of January 24, 1888 ([55], vol. III, pp. 474–479 and 488–490).
126.
Cf. [96], p. 35, [104], p. 65: “Judgements can be regarded as advances from a thought to a truth-value”, Cf. also [106], vol. I, “Ausführungen über Sinn und Bedeutung”, p. 133, [107], p. 122: “The laws of logic are first and foremost laws in the realm of Bedeutungen and only relate indirectly to sense”.
127.
Cf. [97], Nachwort, p. 253, [110], p. 253$_{2}$: “Even now, I do not see how arithmetic can be founded scientifically, how the numbers can be apprehended as logical objects and brought under consideration, if it is not—at least conditionally—permissible to pass from a concept to its extension”.
128.
A concept under which objects fall is a concept of first level, a concept under which concepts of first level fall is a concept of second level, etc.
129.
Cf. the third fundamental principle of Grundlagen: “Never to lose sight of the distinction between concept and object” ([93], Einleitung, p. X; [103], pp. XXII).
130.
Cf. [49], Sect. 73, [53], pp. 33–34) (Dedekind’s italics): “The relations or laws which are derived entirely from the conditions $\alpha $, $\beta $, $\gamma $, $\delta $ in (71) [cf. Sect. 1.4.1 above] and therefore are always the same in all ordered simply infinite systems, whatever names may happen to be given to the individual elements [...], form the first object of the science of numbers or arithmetic”.
131.
I do not want to say that a semantic point of view is absent in Dedekind’s work. What I take to be absent is a semantic theory, that is, a theory of truth. Likewise, I do not want to say that Dedekind has no syntactic views. What I want to say is that he has no syntactic theory, that is, no theory of inference.
132.
Cf. [74], Chap. 10, p. 235: “We can make no sense, for example, of the thesis that the content of a statement of number consists in predicating something of a concept unless we view the concept as being the reference of the concept-word”.
133.
Dummett ([74], Chap. 9, p. 215) distinguishes between thesis (T) that truth-values are the references [Bedeutungen] of statements and thesis (O) that truth-values are objects. According to him, (O) is “objectionable”, but (T) is not.
134.
Taking this time ‘concept’ in its common meaning, Frege writes similarly ([93], Sect. 48; [103], p. 61): “The concept has a power of collecting together far superior to the unifying power of synthetic apperception”.
135.
Beman’s English translation has ‘thought’ instead of ‘thinking’, but I take ‘thinking’ to be more appropriate here. Here is the German text: “Im folgenden verstehe ich unter einem Ding jeden Gegenstand unseres Denkens”. But notice that Denkens is not something subjective, for Dedekind, as it is for Frege. Then, in Sect. 2, Dedekind writes: “Ein [...] System S (oder ein Inbegriff, eine Mannigfaltigkeit, eine Gesamtheit) ist als Gegenstand unseres Denkens ebenfalls ein Ding”.
136.
Gödel thinks too that set-theoretical paradoxes are “a very serious problem, not for mathematics, however, but for logic and epistemology” ([113], p. 268, footnote 40). He also already points out the analogy between the “naïve” use of the concept of set, understood as the generating of unities out of manifolds, and Kant’s categories of pure understanding.
137.
The two letters have been published together as a single letter in [39], p. 443–447. Here what Cantor writes in the first of them ( ibid., p. 443): “Eine Vielheit kann nämlich so beschaffen sein, dass die Annahme eines ‘Zusammenseins’ aller ihrer Elemente auf einen Widerspruch führt, so das es unmöglich ist, die Vielheit al eine Einheit, als ein ‘fertiges Ding’ aufzufassen. Solche Vielheiten nenne ich absolut unendliche oder inkonsistente Vielheiten. Wie man sich leicht überzeugt, ist, z.B. der ‘Inbegriff alles Denkbaren’ eine solche Vielheit”. Cf. [155] for detailed comments. The request for a face-to-face discussion is included in the last part of the letter, which is omitted in the mentioned edition: cf. [67], p. 260.
138.
Parsons ([155], p. 526) uses modality in order to save the idea that any multiplicity of objects constitutes a set: “The idea that any available objects can be formed into a set is, I believe, correct, provided that it is expressed abstractly enough, so that ‘availability’ has neither the force of existence at a particular time nor of giveness to the human mind, and formation is not thought of as an action or Husserlian Akt. What we need to do is to replace the language of time and activity by the more bloodless language of potentiality and actuality”. By the way, Dedekind’s operation or activity of mind follows a Kantian line.
139.
I have mentioned above, in footnote 120, McLarty’s elaboration on the distinction between Plato’s original theories and our modern use of ‘Platonism’ and cognates, together with my discriminant use of ‘realism’ and ‘Platonism’.
140.
Cf. also [47], Sect. 1, [53], p. 2, (my italics): “I regard the whole of arithmetic as a necessary, or at least natural, consequence of the simplest arithmetic act, that of counting, and counting itself as nothing else than the successive creation of the infinite series of positive integers in which each individual is defined by the one immediately preceding; the simplest act is passing from an already-formed individual to the consecutive one to be formed. [...] Addition is the combination of any arbitrary repetition of the above-mentioned simplest act into a single act; from it in a similar way arises multiplication”.
141.
Parsons [156] discusses Tait’s view and offers a deep analysis of the notion of mathematical structure.
142.
Compare with Benacerraf’s view (advanced in [8]), according to which no set-theoretic representation should be taken as defining natural numbers. As I recalled above (42), Dedekind had written to Lipschitz that he did not want to invent some previously unknown irrational numbers. However, there is no contradiction between this early view (1876) and the one communicated to Weber in 1888, because the abstract elements of the theory of simple infinite sets—the “shadowy forms”—and the real numbers produced by cuts are not identical with the familiar numbers as they were commonly used.
143.
Cf., e.g., the note “Aus den Gruppen-Studien”, dated to 1855–58 ([55], vol. III, pp. 439–446), where Emmy Nœther found the germ of his own “Homomorphiesatzes” (ibid., p. 446; [149]), and the famous “Xth Supplément” to the second edition of Dirichlet’s lectures on the theory of numbers ([66], pp. 434–626), where Dedekind defines the field structure and develops his general theory of ideals using set-theoretical operations.
144.
The $\varphi $-chain of a singleton $\{e\}$, namely $\varphi _{0}\left( \{e\}\right) $, in Dedekind’s notation, is the intersection of all chains $K\subset S$ such that $\{e\}\subset K$ ($K\subset S$ is a $\varphi $-chain if $ \varphi (K)\subset K$).
145.
In short, the definition is as follows. Let the statement
- ‘n follows in the series of natural numbers directly after m’
mean the same as the statement
- ‘there exists a concept F, and an object x falling under it, such that the cardinal number belonging to the concept F is n and the cardinal number belonging to the concept $\ulcorner $falling under F but not identical with $x\urcorner $ is m’.
Let us say, for short, that n stands in the relation Succ with m if (and only if) n follows in the series of natural numbers directly after m (this notation is not Frege’s, which firstly gives his definitions for a generic $\varphi $-series, where $\varphi $ is a one-to-one correspondence whatsoever, then particularises them them by replacing ‘$ \varphi $-series’ with ‘series of natural numbers’). Let the statement
- ‘y follows in the series of natural numbers after x’
mean the same as the statement
- ‘if every object to which x stands in the relation Succ falls under the concept F, and if from the proposition that d falls under the concept F it follows universally, whatever d may be, that every object to which d stands in the relation Succ falls under the concept F, then y falls under the concept F, whatever concept F may be’.
(in modern terminology this provides a definition of the strong ancestral relation of Succ). Let, finally, the statement
- ‘n is a member of the series of natural numbers ending with a’
mean the same as the statement
- ‘a follows in the series of natural numbers after n or a is the same as n’.
146.
Cf. footnote (145), above.
147.
Cf. footnote (145), above.
148.
For the formal similarities between Dedekind’s chains and Frege’s following in a $\varphi $-sequence, cf., e.g. [63], pp. 140 and 141.
149.
Cf. also what Frege writes in Sect. 45 ([93], Sect. 45; [103], p. 58): “The terms ‘multitude’, ‘set’ and ‘plurality’, are unsuitable, owing to their vagueness, for use in defining number”. ‘Vagueness’ obviously means the same as ‘multivocity’.
150.
Translating ‘Folge’ by ‘consequence’, in accordance with our current usage, would be misleading since Frege actually deals with inference.
151.
For the logical similarity with the ancestral of a relation (defined as in footnote (145), above), and for setting on a par Dedekind’s introduction of the real numbers, as corresponding uniquely to cuts, and Frege’s introduction of extensions, as objects corresponding uniquely to concepts, cf. [25], pp. 249–254.
152.
Once again, Dedekind’s generality through Abbildung differs from Frege’s logical generality obtained by the ancestral of a relation.
153.
For the respective roles of Dedekind and Cantor in the emergence of this theory, cf. [90].
154.
Tarski [193] shows that the answer to the question: ‘Is mathematics reducible to logic?’ depends on the choice of the language. On the assumption of Tarski’s criterion of logicality, according to which logicality is set-theoretically defined through invariance under permutations of the domain of individuals, the answer is affirmative in Russell’s simple type theory, but negative in Zermelo’s first-order system. His paper prompted a rich discussion on the very nature of logic which is still open: Tarski’s criterion is accepted as a necessary but not sufficient condition for defining logicality in semantic terms [146], but it is criticised for reducing logic to set-theory [87].
155.
Gödel stands on the side of Frege: he distinguishes between sets or classes, on the one hand, and concepts, on the other hand, and aims too at establishing a “theory of concepts” ([114]; [113]; [199], pp. 297–299 and 309–312; [200], Chap. 8).
156.
But cf. also Dedekind’s use of the term ‘Systemlehre der Logic’ in a paper dating back to 1897, and mentioned by Ferreirós ([52], Sect. 4; [91], pp. 225–226).
157.
Dedekind highlights the inner link between his concept of cut and his concept of ideal, e.g. in the introduction of [48], on which cf. [67], pp. 65–72.
158.
Stein ([186], p. 247) rightly points out that Dedekind’s work is “quite free of the preoccupations with ‘ontology’ that so dominated Frege, and had so fascinated later philosophers”.

Author information

Authors and Affiliations

CNRS (IHPST, CNRS and University of Paris 1, Panthéon-Sorbonne, Paris, France
Hourya Benis-Sinaceur & Marco Panza
Department of Philosophy, University of Helsinki, Helsinki, Finland
Gabriel Sandu

Authors

Hourya Benis-Sinaceur
View author publications
You can also search for this author in PubMed Google Scholar
Marco Panza
View author publications
You can also search for this author in PubMed Google Scholar
Gabriel Sandu
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hourya Benis-Sinaceur .

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Benis-Sinaceur, H., Panza, M., Sandu, G. (2015). Is Dedekind a Logicist? Why Does Such a Question Arise?. In: Functions and Generality of Logic. Logic, Epistemology, and the Unity of Science, vol 37. Springer, Cham. https://doi.org/10.1007/978-3-319-17109-8_1

Download citation

DOI: https://doi.org/10.1007/978-3-319-17109-8_1
Published: 25 June 2015
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-17108-1
Online ISBN: 978-3-319-17109-8
eBook Packages: Humanities, Social Sciences and LawPhilosophy and Religion (R0)

Publish with us

Policies and ethics