Abstract
This paper addresses, from engineering point of view, issues in seismic risk assessment. It is more a discussion on the current practice, emphasizing on the multiple uncertainties and weaknesses of the existing methods and approaches, which make the final loss assessment a highly ambiguous problem. The paper is a modest effort to demonstrate that, despite the important progress made the last two decades or so, the common formulation of hazard/risk based on the sequential analyses of source (M, hypocenter), propagation (for one or few IM) and consequences (losses) has probably reached its limits. It contains so many uncertainties affecting seriously the final result, and the way that different communities involved, modellers and end users are approaching the problem is so scattered, that the seismological and engineering community should probably re-think a new or an alternative paradigm.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
3.1 Introduction
Seismic hazard and risk assessments are nowadays rather established sciences, in particular in the probabilistic formulation of hazard. Long-term hazard/risk assessments are the base for the definition of long-term actions for risk mitigation. However, several recent events raised questions about the reliability of such methods. The occurrence of relatively “unexpected” levels of hazard and loss (e.g., Emilia, Christchurch, Tohoku) and the continuous increase of hazard with time, basically due to the increase of seismic data, and the increase of exposure, make loss assessment a highly ambiguous problem.
Existing models present important discrepancies. Sometimes such discrepancies are only apparent, since we do not always compare two “compatible” values. There are several reasons for this. In general, it is usually statistically impossible to falsify one model only with one (or too few) datum. Whatever the value of probability for such an event is, a probability (interpreted as “expected annual frequency”) value greater than zero means that the occurrence of the event is possible, and we cannot know how much unlucky we have been. If the probability is interpreted as “degree of belief”, is instead in principle not testable. In addition, the assessments are often based on “average” values, knowing that the standard deviations are high. This is common practice, but this also means that such assessments should be compared to the average over multiple events, instead of one single specific event. However, we almost never have enough data to test long-term assessments. This is probably the main reason why different alternative models exist.
Another important reason why significant discrepancies are expected is the fact that we do know that many sources of uncertainties do exist in the whole chain from hazard to risk assessment. However, are we propagating accurately all the known uncertainties? Are we modelling the whole variability? The answer is that often it is difficult to define “credible” limits and constraints to the natural variability (aleatory uncertainty). One of the consequences is that the “reasonable” assessments are often based on “conservative” assumptions. However, conservative choices usually imply subjectivity and statistical biases, and such biases are, at best, only partially controlled. In engineering practice this is often the rule, but can this be generalized? And if yes, how can it be achieved? Epistemic uncertainty usually offers a solution to this point in order to constrain the limits of “subjective” and “reasonable” choices in the absence of rigorous rules. In this case, epistemic uncertainties are intended as the variability of results among different (but acceptable) models. But, are we really capable of effectively accounting for and propagating epistemic uncertainties? In modelling epistemic uncertainties, different alternative models are combined together, often arbitrarily, assuming that one true model exists and, judging this possibility, assigning a weight to each model based on the consensus on its assumptions. Here, two questions are raised. First, is the consensus a good metric? Are there any alternatives? How many? Second, does a “true” model exist? Can a model be only “partially” true, as different models are covering different “ranges” of applicability? To judge the “reliability” of one model, we should analyze its coherence with a “target behaviour” that we want to analyze, which is a-priori unknown and more important it is evolving with time. The model itself is a simplification of the reality, based on the definition of the main degrees of freedom that control such “target behaviour”.
In the definition of “target behaviour” and, consequently, in the selection of the appropriate “degrees of freedom”, several key questions remain open. First, are we capable of completely defining what the target of the hazard/risk assessments is? What is “reasonable”? For example, we tend to use the same approach at different spatiotemporal levels, which is probably wrong. Is the consideration of a “changing or moving target” acceptable by the community? Furthermore, do we really explore all the possible degrees of freedom to be accounted for? And if yes, are we able to do it accurately considering the eternal luck of good and well-focused data? Are we missing something? For example, in modelling fragility, several degrees of freedom are missing or over-simplified (e.g., aging effects, poor modelling including the absence of soil-structure interaction), while recent results show that this “degree of freedom” may play a relevant role to assess the actual vulnerability of a structure. More in general, the common formulation of hazard/risk is based on the sequential analyses of source (M, hypocenter), propagation (for one or few intensity measures) and consequences (impact/losses). Is this approach effective, or is it just an easy way to tackle the complexity of the nature, since it keeps the different disciplines (like geology, geophysics and structural engineering) separated? Regarding “existing models”, several attempts are ongoing to better constrain the analyses of epistemic uncertainties like critical re-analysis of the assessment of all the principal factors of hazard/risk analysis or proposal of alternative modelling approaches (e.g., Bayesian procedures instead of logic trees). All these follow the conventional path to go. Is this enough? Wouldn’t it be better to start criticizing the whole model? Do we need a change of the paradigm? Or maybe better, can we think of alternative paradigms? The general tendency is to complicate existent models, in order to obtain new results, which we should admit are sometimes better correlated with specific observations or example cases. Is this enough? Have we really deeply thought that in this way we may build “new” science over not consolidated roots? Maybe it is time to re-think these roots, in order to evaluate their stability in space, time and reliability.
The paper that follows is a modest effort to argue on these issues, unfortunately without offering any idea of the new paradigm.
3.2 Modelling, Models and Modellers
3.2.1 Epistemology of Models
Seismic hazard and risk assessments are made with models. The biggest problem of models is the fact that they are made by humans who have a limited knowledge of the problem and tend to shape or use their models in ways that mirror their own notion of which a desirable outcome would be. On the other hand, models are generally addressed to end users with different level of knowledge and perception of the uncertainties involved. Figure 3.1 gives a good picture of the way that different communities perceive “certainty”. It is called the “certainty trough”.
The certainty trough (after MacKenzie 1990)
In the certainty trough diagram, users are presented as either under-critical or over-critical, in contrast to producers, who have detailed understanding of the technology’s strengths and weaknesses. Model producers or modellers are a-priori aware of the uncertainties involved in their model. At least they should be. For end-users communities the situation is different. Experienced over-critical users are generally in better position to evaluate the accuracy of the model and its uncertainties, while the alienated under-critical users have the tendency to follow the “believe the brochures” concept. When this second category of end-users uses a model, the uncertainties are generally increased.
The present discussion focuses on the models and modellers and less on the end-users; however, the criticism will be more from the side of the end users.
All models are imperfect. Identifying model errors is difficult in the case of simulations of complex and poorly understood systems, particularly when the simulations extend to hundreds or thousands of years. Model uncertainties are a function of a multiplicity of factors (degrees of freedom). Among the most important are limited availability and quality of empirical-recorded data, the imperfect understanding of the processes being modelled and, finally, the poor modelling capacities. In the absence of well-constrained data, modellers often gauge any given model’s accuracy by comparing it with other models. However, the different models are generally based on the same set of data, equations and assumptions, so that agreement among them may indicate very little about their realism.
A good model is based on a wise balance of observation and measurement of accessible phenomena with informed judgment “theory”, and not in inconvenience. Modellers should be honestly aware of the uncertainties involved in their models and of how the end users could make use of them. They should take the models “seriously but not literally”, avoiding mixing up “qualitative realism” with “quantitative realism”. However, modellers typically identify the problem as users’ misuse of their model output, suggesting that the latter interpret the results too uncritically.
3.2.2 Data: Blessing or Curse
It is widely accepted that science, technology, and knowledge in general, are progressing with the accumulation of observation and data. However, it is equally true that without proper judgment, solid theoretical background and focus, an accumulation of data may fade out the problem and drive the scientist-modeller to a wrong direction. The question is how much aware of that is the modeller.
Une accumulation de faits n’est pas plus une science qu’un tas de pierres n’est une maison. Jules Henri Poincare
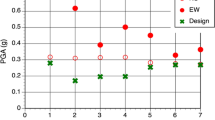
Historically the accumulation of seismic and strong motion data resulted in higher seismic hazard when seismic design motion is targeted. Typical example is the increase of the design Peak Ground Acceleration (PGA) value in Greece since 1956 and the even further increase recently proposed in SHARE (Giardini et al. 2013).
Data are used to propose models, for example Ground Motion Prediction Equations (GMPEs), or improve existing ones. There is a profound belief that more data lead to better models and deeper knowledge. This is not always true. The majority of recording stations worldwide are not located after proper selection of the site and in most cases the knowledge of the parameters affecting the recorded ground motion is poor and limited. Rather simple statistics and averaging, often of heterogeneous data, is usually the way to produce “a model” but not “the model”, which should describe the truth. A typical example is the research on the “sigma” on GMPEs. Important research efforts have been dedicated during the last two decades to improve “sigma” but in general it refuses to be improved, except for few cases of very well constrained conditions. Sometimes less data of excellent quality and well constrained in terms of all involved parameters, lead to better solutions and models. This is true in both engineering seismology and earthquake engineering. An abundant mass of poorly constrained and mindless produced data is actually a curse and probably it will strangle an honest and brave modeller. Unfortunately, this is often the case when one considers the whole chain from seismic hazard to risk assessment.
3.2.3 Modeller: Sisyphus or Prometheus
A successful parameterization requires understanding of the phenomena being parameterized, but such understanding is often lacking. For example, the influence of seismic rupture and wave propagation patterns in complex media are poorly known and poorly modelled.
When confronted with limited understanding of how the seismic pattern is, and engineering structures or human behaviours are, modellers seek to make their models comply with the expected earthquake generation, spatial distribution of ground motion and structural response. The adjustments may “save appearances” without integrating precise understanding of the causal relationships the models are intended to simulate.
Huge research in seismic risk consists of modifying a subset of variables in models developed elsewhere. This complicates clear-cut distinctions between users and producers of models. And even more important: there is no in depth criticism on the paradigm used (basic concepts). Practically no scientist single-handedly develops a complex risk model from bottom-up. He is closer to Sisyphus while sometimes he believes to be Prometheus.
Modellers are sometimes identified with their own models and become invested in their projections, which in turn can reduce sensitivity to their inaccuracy. Users are perhaps in the best position to identify model inaccuracies.
Model producers are not always willing or they are not always able to recognize weaknesses in their own models, contrary to what it is suggested by the certainty trough. They spend a lot of time working on something, and they are really trying to do their best at simulating what happens in the real world. It is easy to get caught up in it and start to believe that what happens in the model must be what happens in the real world. And often that is not true. The danger is that the modeller begins to lose some objectivity on the response of the model and starts to believe that the model really works like the real world and then he begins to take too seriously its response to a change in forcing.
Modellers often “trust” their models and sometimes they have some degree of “genuine confidence, maybe over-confidence” in their quantitative projections. It is not simply a “calculating seduction” but a “sincere act of faith”!
3.2.4 Models: Truth or Heuristic Machines
Models should be perceived as “heuristic” and not as “truth machines”. Unfortunately, very often modellers – keen to preserve the authority of their models – deliberately present and encourage interpretations of models as “truth machines” when speaking to external audiences and end users. They “oversell” their products because of potential funding considerations. Highest level of objectivity about a given technology should be found among those who produced it, and this is not always achieved.
3.3 Risk, Uncertainties and Decision-Making
Risk is uncertain by definition. The distinction between uncertainty and risk remains of fundamental importance today. The scientific and engineering communities do not unanimously accept the origins of the concept of uncertainty in risk studies. However, it is permanently criticized and subsequently it evolved into dominant models of decision making upon which the dominant risk-based theories of seismic risk assessment and policy-making were subsequently built.
The challenge is really important. Everything in our real world is formed and is working with risk and uncertainty. Multiple conventions deserve great attention as we seek to understand the preferences and strategies of economic and political actors. Within this chaotic and complicate world, risk assessment and policy-making is a real challenge.
Usually uncertainties (or variability) are classified in two categories: aleatory variability and epistemic uncertainty. Aleatory variability is the natural-intrinsic randomness in a phenomenon and a process. It is a result of our simplified modelling of a complex process parameterized by probability density functions. Epistemic uncertainty is considered as the scientific uncertainty in the simplified model of the process and is characterized by alternative models. Usually it is related to the lack of knowledge or the necessity to use simplified models to simulate the nature or the elements at risk.
Uncertainty is also related to the perception of the model developer or the user. Often these two distinctive terms of uncertainties are familiar to the model developers but not to the users for whom there is only one uncertainty seen in a scale “low” to “high”. A model developer probably believes that the two terms provide an unambiguous terminology. However this is not the case for the community of users. In most cases they cannot even understand it. So, they are often forced to “believe” the scientists, who have or should have the “authority” of the “truth”. At least the modellers should know better the limits of their model and the uncertainties involved and communicate them to the end-users.
A common practice to anticipate the epistemic uncertainty is through the use of the “logic tree” approach. Using this approach to overcome the lack of knowledge and the imperfection of the modelling is strongly based on subjectivity, regarding the credibility of each model, which is not a rigorous scientific method. It may be seen as a compromising method to smooth “fighting” among models and modellers. Moreover, a typical error is to put aleatory variability on some of the branches of the logic tree. The logic tree branches should be mainly relevant to the source characterization, the GMPE used and furthermore to the fragility curves used for the different structural typologies.
An important problem is then raised up. Is using many alternative models for each specific site and project a wrong or a wise approach? The question in its simplicity seems stupid and the answer obvious, but this is not true because more data usually lead to larger uncertainties.
For example, in a poorly known fault with few data and only one hazard study, there will be a single model and consequently 100 % credibility. In a very well known and studied fault, with many data, there will be probably several good or “acceptable” models and the user should be forced to attribute much lower credibility to each one of them, which leads to the absurd situation for the poorly known fault to have lower uncertainty than well known faults!
Over time additional hazard models are developed, but our estimates of the epistemic uncertainty have increased, not decreased, as additional data have been collected and new models have been developed!
Fragility curves on the other hand are based on simplified models (usually equivalent SDOF systems), which are an oversimplification of the real world and it is not known whether this oversimplification is on the conservative side. In any case, the scatter among different models is so high (Pitilakis et al. 2014a) that a logic tree approach should be recommended to treat the epistemic uncertainties related to the selection of the fragility curves. No such approach has been used so far. Moreover these curves, normally produced for simplified structures, are used to estimate physical damages and implicitly the associated losses for a whole city with a very heterogeneous fabric and typology of buildings. Then aleatory and epistemic uncertainties are merged.
At the end of the game there is always a pending question: How can we really differentiate the two sources of uncertainty?
Realizing the importance of all different sources of uncertainties characterizing each step of the long process from seismic hazard to risk assessment, including all possible consequences and impact, beyond physical damages, it is understood how difficult it is to derive a reliable global model covering the whole chain from hazard to risk. For the moment, scientists, engineers and policy makers are fighting with rather simple weapons, using simple paradigms. It is time to re-think the whole process merging their capacities and talents.
3.4 Taxonomy of Elements at Risk
The key assumption in the vulnerability assessment of buildings, infrastructures and lifelines is that structures and components of systems, having similar structural characteristics, and being in similar geotechnical conditions (e.g., a bridge of a given typology), are expected to perform in the same way for a given seismic excitation. Within this context, damage is directly related to the structural properties of the elements at risk. The hazard should be also related to the structure under study. Taxonomy and typology are thus fundamental descriptors of a system that are derived from the inventory of each element and system. Geometry, material properties, morphological features, age, seismic design level, anchorage of the equipment, soil conditions, and foundation details are among usual typology descriptors/parameters. Reinforced concrete (RC) buildings, masonry buildings, monuments, bridges, pipelines (gas, fuel, water, waste water), tunnels, road embankments, harbour facilities, road and railway networks, have their own specific set of typologies and different taxonomy.
The elements at risk are commonly categorized as populations, communities, built environment, natural environment, economic activities and services, which are under the threat of disaster in a given area (Alexander 2000). The main elements at risk, the damages of which affect the losses of all other elements, are the multiple components of the built environment with all kinds of structures and infrastructures. They are classified into four main categories: buildings, utility networks, transportation infrastructures and critical facilities. In each category, there are (or should be) several sets of fragility curves, that have been developed considering the taxonomy of each element and their typological characteristics. In that sense there are numerous typologies for reinforced concrete or masonry buildings, numerous typologies for bridges and numerous typologies for all other elements at risk of all systems exposed to seismic hazard.
The knowledge of the inventory of a specific structure in a region and the capability to create classes of structural types (for example with respect to material, geometry, design code level) are among the main challenges when carrying out a general seismic risk assessment for example at a city scale, where it is practically impossible to perform this assessment at building level. It is absolutely necessary to classify buildings, and other elements at risk, in “as much as possible” homogenous classes presenting more-or-less similar response characteristics to ground shaking. Thus, the derivation of appropriate fragility curves for any type of structure depends entirely on the creation of a reasonable taxonomy that is able to classify the different kinds of structures and infrastructures in any system exposed to seismic hazard.
The development of a homogenous taxonomy for all engineering elements at risk exposed to seismic hazard and the recommendation of adequate fragility functions for each one, considering also the European context, achieved in SYNER-G project (Pitilakis et al. 2014a), is a significant contribution to the reduction of seismic risk in Europe and worldwide.
3.5 Intensity Measures
A main issue related to the construction and use of fragility curves is the selection of appropriate earthquake Intensity Measures (IM) that characterize the strong ground motion and best correlate with the response of each element at risk, for example, building, pier bridge or pipeline. Several intensity measures of ground motion have been proposed, each one describing different characteristics of the motion, some of which may be more adverse for the structure or system under consideration. The use of a particular IM in seismic risk analysis should be guided by the extent to which the measure corresponds to damage to the components of a system or the system of systems. Optimum intensity measures are defined in terms of practicality, effectiveness, efficiency, sufficiency, robustness and computability (Cornell et al. 2002; Mackie and Stojadinovic 2003, 2005).
Practicality refers to the recognition that the IM has some direct correlation to known engineering quantities and that it “makes engineering sense” (Mackie and Stojadinovic 2005; Mehanny 2009). The practicality of an IM may be verified analytically via quantification of the dependence of the structural response on the physical properties of the IM such as energy, response of fundamental and higher modes, etc. It may also be verified numerically by the interpretation of the structure’s response under non-linear analysis using existing time histories.
Sufficiency describes the extent to which the IM is statistically independent of ground motion characteristics such as magnitude and distance (Padgett et al. 2008). A sufficient IM is the one that renders the structural demand measure conditionally independent of the earthquake scenario. This term is more complex and is often at odds with the need for computability of the IM. Sufficiency may be quantified via statistical analysis of the response of a structure for a given set of records.
The effectiveness of an IM is determined by its ability to evaluate its relation with an engineering demand parameter (EDP) in closed form (Mackie and Stojadinovic 2003), so that the mean annual frequency of a given decision variable exceeding a given limiting value (Mehanny 2009) can be determined analytically.
The most widely used quantitative measure from which an optimal IM can be obtained is efficiency. This refers to the total variability of an engineering demand parameter (EDP) for a given IM (Mackie and Stojadinovic 2003, 2005).
Robustness describes the efficiency trends of an IM-EDP pair across different structures, and therefore different fundamental period ranges (Mackie and Stojadinovic 2005; Mehanny 2009).
In general and in practice, IMs are grouped in two general classes: empirical intensity measures and instrumental intensity measures. With regards to the empirical IMs, different macroseismic intensity scales could be used to identify the observed effects of ground shaking over a limited area. In the instrumental IMs, which are by far more accurate and representative of the seismic intensity characteristics, the severity of ground shaking can be expressed as an analytical value measured by an instrument or computed by analysis of recorded accelerograms.
The selection of the intensity parameter is also related to the approach that is followed for the derivation of fragility curves and the typology of element at risk. The identification of the proper IM is determined from different constraints, which are first of all related to the adopted hazard model, but also to the element at risk under consideration and the availability of data and fragility functions for all different exposed assets.
Empirical fragility functions are usually expressed in terms of the macroseismic intensity defined according to different scales, namely EMS, MCS and MM. Analytical or hybrid fragility functions are, on the contrary, related to instrumental IMs, which are related to parameters of the ground motion (PGA, PGV, PGD) or of the structural response of an elastic SDOF system (spectral acceleration Sa or spectral displacement Sd for a given value of the period of vibration T). Sometimes integral IMs, which consider a specific integration of a motion parameter can be useful, for example Arias Intensity IA or a spectral value like the Housner Intensity IH. When the vulnerability of elements due to ground failure is examined (i.e., liquefaction, fault rupture, landslides) permanent ground deformation (PGD) is the most appropriate IM.
The selection of the most adequate and realistic IMs for every asset under consideration is still debated and a source of major uncertainties.
3.6 Fragility Curves and Vulnerability
The vulnerability of a structure is described in all engineering-relevant approaches using vulnerability and/or fragility functions. There are a number of definitions of vulnerability and fragility functions; one of these describes vulnerability functions as the probability of losses (such as social or economic losses) given a level of ground shaking, whereas fragility functions provide the probability of exceeding different limit states (such as physical damage or injury levels) given a level of ground shaking. Figure 3.2 shows examples of vulnerability and fragility functions. The former relates the level of ground shaking with the mean damage ratio (e.g., ratio of cost of repair to cost of replacement) and the latter relates the level of ground motion with the probability of exceeding the limit states. Vulnerability functions can be derived from fragility functions using consequence functions, which describe the probability of loss, conditional on the damage state.
Fragility curves constitute one of the key elements of seismic risk assessment and at the same time an important source of uncertainties. They relate the seismic intensity to the probability of reaching or exceeding a level of damage (e.g., minor, moderate, extensive, collapse) for the elements at risk. The level of shaking can be quantified using different earthquake intensity parameters, including peak ground acceleration/velocity/displacement, spectral acceleration, spectral velocity or spectral displacement. They are often described by a lognormal probability distribution function as in Eq. 3.1 although it is noted that this distribution may not always be the best fit.
where P f(·) denotes the probability of being at or exceeding a particular damage state, dsi, for a given seismic intensity level defined by the earthquake intensity measure, IM (e.g., peak ground acceleration, PGA), Φ is the standard cumulative probability function, IMmi is the median threshold value of the earthquake intensity measure IM required to cause the ith damage state and βtot is the total standard deviation. Therefore, the development of fragility curves according to Eq. 3.1 requires the definition of two parameters, IMmi and βtot.
There are several methods available in the literature to derive fragility functions for different elements exposed to seismic hazard and in particular to transient ground motion and permanent ground deformations due to ground failure. Conventionally, these methods are classified into four categories: empirical, expert elicitation, analytical and hybrid. All these approaches have their strengths and weaknesses. However, analytical methods, when properly validated with large-scale experimental data and observations from recent strong earthquakes, have become more popular in recent years. The main reason is the considerable improvement of computational tools, methods and skills, which allows comprehensive parametric studies covering many possible typologies to be undertaken. Another equally important reason is the better control of several of the associated uncertainties.
The two most popular methods to derive fragility (or vulnerability) curves for buildings and pier bridges are the capacity spectrum method (CSM) (ATC-40 and FEMA273/356) with its alternatives (e.g., Fajfar 1999), and the incremental dynamic analysis (IDA) (Vamvatsikos and Cornell 2002). Both have contributed significantly and marked the substantial progress observed the last two decades; however they are still simplifications of the physical problem and present several limitations and weaknesses. The former (CSM) is approximate in nature and is based on static loading, which ignores the higher modes of vibration and the frequency content of the ground motion. A thorough discussion on the pushover approach may be found in Krawinkler and Miranda (2004).
The latter (IDA) is now gaining in popularity because among other advantages it offers the possibility to select the most relevant to the structural response Engineering Demand Parameters (EDP) (inter-story drifts, component inelastic deformations, floor accelerations, hysteretic energy dissipation etc.). IDA is commonly used in probabilistic seismic assessment frameworks to produce estimates of the dynamic collapse capacity of global structural systems. With the IDA procedure the coupled soil-foundation-structure system is subjected to a suite of multiply scaled real ground motion records whose intensities are “ideally?” selected to cover the whole range from elasticity to global dynamic instability. The result is a set of curves (IDA curves) that show the EDP plotted against the IM used to control the increment of the ground motion amplitudes. Fragility curves for different damage states can be estimated through statistical analysis of the IDA results (pairs of EDP and IM) derived for a sufficiently large number of ground motions (normally 15–30). Among the weaknesses of the approach is the fact that scaling of the real records changes the amplitude of the IMs but keeps the frequency content the same throughout the inelastic IDA procedure. In summary both approaches introduce several important uncertainties, both aleatory and epistemic.
Among the most important latest developments in the field of fragility curves is the recent publication “SYNER-G: Typology Definition and Fragility Functions for Physical Elements at Seismic Risk”, Pitilakis K, Crowley H, Kaynia A (Eds) (2014a).
Several uncertainties are introduced in the process of constructing a set of fragility curves of a specific element at risk. They are associated to the parameters describing the fragility curves, the methodology applied, as well as to the selected damage states and the performance indicators (PI) of the element at risk. The uncertainties may again be categorized as aleatory and epistemic. However, in this case epistemic uncertainties are probably more pronounced, especially when analytical methods are used to derive the fragility curves.
In general, the uncertainty of the fragility parameters is estimated through the standard deviation, βtot that describes the total variability associated with each fragility curve. Three primary sources of uncertainty are usually considered, namely the definition of damage states, βDS, the response and resistance (capacity) of the element, βC, and the earthquake input motion (demand), βD. Damage state definition uncertainties are due to the fact that the thresholds of the damage indexes or parameters used to define damage states are not known. Capacity uncertainty reflects the variability of the properties of the structure as well as the fact that the modelling procedures are not perfect. Demand uncertainty reflects the fact that IM is not exactly sufficient, so different records of ground motion with equal IM may have different effects on the same structure (Selva et al. 2013). The total variability is modelled by the combination of the three contributors assuming that they are stochastically independent and log-normally distributed random variables, which is not always true.
Paolo Emilio Pinto (2014) in Pitilakis et al. (2014a) provides the general framework of the treatment of uncertainties in the derivation of the fragility functions. Further discussion on this issue is made in the last section of this paper.
3.7 Risk Assessment
3.7.1 Probabilistic, Deterministic and the Quest of Reasonable
In principle, the problem of seismic risk assessment and safety is probabilistic and several sources of uncertainties are involved. However, a full probabilistic approach is not applied throughout the whole process. For the seismic hazard the approach is usually probabilistic, at least partially. Deterministic approach, which is more appreciated by engineers, is also used. Structures are traditionally analyzed in a deterministic way with input motions estimated probabilistically. PSHA ground motion characteristics, determined for a selected return period (e.g., 500 or 1,000 years), are traditionally used as input for the deterministic analysis of a structure (e.g., seismic codes). On the other hand, fragility curves by definition represent the conditional probability of the failure of a structure or equipment at a given level of ground motion intensity measure, while seismic capacity of structures and components is usually estimated deterministically. Finally, damages and losses are estimated in a probabilistic way, mainly, if not exclusively, because of PSHA and fragility curves used. So in the whole process of risk assessment, probabilistic and deterministic approaches are used indifferently without knowing exactly what the impact of that is and how the involved uncertainties are treated and propagated.
In the hazard assessment the main debate is whether deterministic or probabilistic approach is more adequate and provides more reasonable results for engineering applications and in particular for the evaluation of the design ground motion. In the deterministic hazard approach, individual earthquake scenarios (i.e., Mw and location) are developed for each relevant seismic source and a specified ground motion probability level is selected (by tradition, it is usually either 0 or 1 standard deviation above the median). Given the magnitude, distance, and number of standard deviations, the ground motion is then computed for each earthquake scenario using one or several ground motion models (GMPEs) that are based on empirical data (records). Finally, the largest ground motion from any of the considered scenarios is used for the design.
Actually with this approach single values of the parameters (Mw, R, and ground motion parameters with a number of standard deviations) are estimated for each selected scenario. However, the final result regarding the ground shaking is probabilistic in the sense that the ground motion has a probability being exceeded given that the scenario earthquake occurred.
In the probabilistic approach all possible and relevant deterministic earthquake scenarios (e.g., all possible Mw and location combinations of physically possible earthquakes) are considered, as well as all possible ground motion probability levels with a range of the number of standard deviations above or below the median. The scenarios from the deterministic analyses are all included in the full set of scenarios from the probabilistic analysis. For each earthquake scenario, the ground motions are computed for each possible value of the number of standard deviations above or below the median ground motion. So the probabilistic analysis can be considered as a large number of deterministic analyses and the chance of failure is addressed by estimating the probability of exceeding the design ground motion.
The point where the two approaches are coinciding is practically the choice of the standard deviations. The deterministic approach traditionally uses at most one standard deviation above the median for the ground motion, but in the probabilistic approach, larger values of the number of standard deviations above the median ground motion are considered. As a result, the worst-case ground motions will be much larger than the 84th percentile deterministic ground motions.
Considering that in both deterministic and probabilistic approaches the design ground motions, (and in particular the largest ones), are controlled by the number of the standard deviations above the median, which usually are different in the two approaches, how can the design motion or the worst case scenario be estimated in a rigorous way?
If now we enter in the game the selection of standard deviations in all other stages of the risk assessment process, namely in the estimation of site effects, the ground motion variability, the fragility and capacity curves, without mentioning the necessary hypothesis regarding the intensity measures, performance indicators and damage states to be used, it is realized that the final result is highly uncertain.
At the end of the game the quest of soundness is still illusionary and what is reasonable is based on past experience and economic constraints considering engineering judgment and political decision. In other words we come back to the modeler’s “authority” and the loneliness and sometime desolation of the end-user in the decision making procedure.
3.7.2 Spatial Correlation
Ground motion variability and spatial correlation could be attributed to several reasons, i.e., fault rupture mechanism, complex geological features, local site conditions, azimuth and directivity effects, basin and topographic effects and induced phenomena like liquefaction and landslides. In practice most of these reasons are often poorly known and poorly modelled, introducing important uncertainties. The occurrence of earthquake scenarios (magnitude and location) and the occurrence of earthquake shaking at a site are related but they are not the same. Whether probabilistic or deterministic scenario is used, the ground motion at a site should be estimated considering the variability of ground motion. However in practice, and in particular in PSHA, this is not treated in a rigorous way, which leads to a systematic underestimation of the hazard (Bommer and Abrahamson 2006). PSHA should always consider ground motion variability otherwise in most cases it is incorrect (Abrahamson 2006).
With the present level of know-how for a single earthquake scenario representing the source and the magnitude of a single event, the estimation of the spatial variation of ground motion field is probably easier and in any case better controlled. In a PSHA, which considers many sources and magnitude scenarios to effectively sample the variability of seismogenic sources, the presently available models to account for spatial variability are more complicated and often lead to an underestimation of the ground motion at a given site, simply because all possible sources and magnitudes are considered in the analysis.
In conclusion it should not be forgotten that seismic hazard is not a tool to estimate a magnitude and a location but to evaluate the design motion for a specific structure at a given site. To achieve this goal more research efforts should be focused on better modelling of the spatial variability of ground motion considering all possible sources for that, knowing that there are a lot of uncertainties hidden in this game.
3.7.3 Site Effects
The important role of site effects in seismic hazard and risk assessment is now well accepted. Their modelling has been also improved in the last two decades.
In Eurocode 8 (CEN 2004) the influence of local site conditions is reflected with the shape of the PGA-normalized response spectra and the so-called “soil factor” S, which represents ground motion amplification with respect to outcrop conditions. As far as soil categorization is concerned, the main parameter used is Vs,30, i.e., the time-based average value of shear wave velocity in the upper 30 m of the soil profile, first proposed by Borcherdt and Glassmoyer (1992). Vs,30 has the advantage that it can be obtained easily and at relatively low cost, since the depth of 30 m is a typical depth of geotechnical investigations and sampling borings, and has definitely provided engineers with a quantitative parameter for site classification. The main and important weakness is that the single knowledge of the Vs profile at the upper 30 m cannot quantify properly the effects of the real impedance contrast, which is one of the main sources of the soil amplification, as for example in case of shallow (i.e., 15–20 m) loose soils on rock or deep soil profiles with variable stiffness and contrast. Quantifying site effects with the simple use of Vs,30 introduces important uncertainties in the estimated IM.
Pitilakis et al. (2012) used an extended strong motion database compiled in the framework of SHARE project (Giardini et al. 2013) to validate the spectral shapes proposed in EC8 and to estimate improved soil amplification factors for the existent soil classes of Eurocode 8 for a potential use in an EC8 update (Table 3.1). The soil factors were estimated using a logic tree approach to account for the epistemic uncertainties. The major differences in S factor values were found for soil category C. For soil classes D and E, due to the insufficient datasets, the S factors of EC8 remain unchanged with a prompt for site-specific ground response analyses.
In order to further improve design spectra and soil factors Pitilakis et al. (2013) proposed a new soil classification system that includes soil type, stratigraphy, thickness, stiffness and fundamental period of soil deposit (T0) and average shear wave velocity of the entire soil deposit (Vs,av). They compiled an important subset of the SHARE database, containing records from sites, which dispose a well-documented soil profile concerning dynamic properties and depth up to the “seismic” bedrock (Vs > 800 m/s). The soil classes of the new classification scheme are illustrated in comparison to EC8 soil classes in Fig. 3.3.
Simplified illustration of ground types according to (a) EC8 and (b) the new classification scheme of Pitilakis et al. (2013)
The proposed normalized acceleration response spectra were evaluated by fitting the general spectral equations of EC8 closer to the 84th percentile, in order to account as much as possible for the uncertainties associated with the nature of the problem. Figure 3.4 is a representative plot, illustrating the median, 16th and 84th percentiles, and the proposed design normalized acceleration spectra for soil sub-class C1. It is obvious that the selection of a different percentile would affect dramatically the proposed spectra and consequently the demand spectra, the performance points and the damages. While there is no rigorous argument why the median should be chosen, 84th percentile or close to this sounds more reasonable.
Normalized elastic acceleration response spectra for soil class C1 of the classification system of Pitilakis et al. (2013) for Type 2 seismicity (left) and Type 1 seismicity (right). Red lines represent the proposed spectra. The range of the 16th to 84th percentile is illustrated as a gray area
The proposed new elastic acceleration response spectra, normalized to the design ground acceleration at rock-site conditions PGArock, are illustrated in Fig. 3.5. Dividing the elastic response spectrum of each soil class with the corresponding response spectrum for rock, period-dependent amplification factors can be estimated.
Type 2 (left) and Type 1 (right) elastic acceleration response spectra for the classification system of Pitilakis et al. (2013)
3.7.4 Time Dependent Risk Assessment
Nature and earthquakes are unpredictable both in short and long term especially in case of extreme or “rare” events. Traditionally seismic hazard is estimated as time independent, which is probably not true. We all know that after a strong earthquake it is rather unlikely that another strong earthquake will happen in short time on the same fault. Exceptions like the sequence of Christchurch earthquakes in New Zealand or more recently in Cephalonia Island in Greece are rather exceptions that prove the general rule, if there is any.
Exposure is certainly varying with time, normally increasing. The vulnerability is also varying with time, increasing or decreasing (for example after mitigation countermeasures or post earthquake retrofitting have been undertaken). On the other hand aging effects and material degradation with time increase the vulnerability (Pitilakis et al. 2014b). Consequently the risk cannot be time independent. Figure 3.6 sketches the whole process.
Schematic illustration of time dependent seismic hazard, exposure, vulnerability and risk (After J. Douglas et al. in REAKT)
For the time being time dependent seismic hazard and risk assessment are in a very premature stage. However, even if in the near future rigorous models should be developed, the question still remains: is it realistic to imagine that time dependent hazard could be ever introduced in engineering practice and seismic codes? If it ever happens, it will have a profound political, societal and economic impact.
3.7.5 Performance Indicators and Resilience
In seismic risk assessment, the performance levels of a structure, for example a RC building belonging to a specific class, can be defined through damage thresholds called limit states. A limit state defines the boundary between two different damage conditions often referred to as damage states. Different damage criteria have been proposed depending on the typologies of elements at risk and the approach used for the derivation of fragility curves. The most common way to define earthquake consequences is a classification in terms of the following damage states: no damage; slight/minor; moderate; extensive; complete.
This qualitative approach requires an agreement on the meaning and the content of each damage state. The number of damage states is variable and is related to the functionality of the components and/or the repair duration and cost. In this way the total losses of the system (economic and functional) can be estimated.
Traditionally physical damages are related to the expected serviceability level of the component (i.e., fully or partially operational or inoperative) and the corresponding functionality (e.g., power availability for electric power substations, number of available traffic lanes for roads, flow or pressure level for water system). These correlations provide quantitative measures of the component’s performance, and can be applied for the definition of specific Performance Indicators (PIs). Therefore, the comparison of a demand with a capacity quantity, or the consequence of a mitigation action, or the accumulated consequences of all damages (the “impact”) can be evaluated. The restoration cost, when provided, is given as the percentage of the replacement cost. Downtime days to identify the elastic or the collapse limits are also purely qualitative and cannot be generalized for any structure type. These thresholds are qualitative and are given as general outline (Fig. 3.7). The user could modify them accordingly, considering the particular conditions of the structure, the network or component under study. The selection of any value of these thresholds inevitably introduces uncertainties, which are affecting the target performance and finally the estimation of damages and losses.
Conceptual relationship between seismic hazard intensity and structural performance (From Krawinkler and Miranda (2004), courtesy W. Holmes, G. Deierlein)
Methods for deriving fragility curves generally model the damage on a discrete damage scale. In empirical procedures, the scale is used in reconnaissance efforts to produce post-earthquake damage statistics and is rather subjective. In analytical procedures the scale is related to limit state mechanical properties that are described by appropriate indices, such as for example displacement capacity (e.g., inter-story drift) in the case of buildings or pier bridges. For other elements at risk the definition of the performance levels or limit states may be more vague and follow other criteria related, for example in the case of pipelines, to the limit strength characteristics of the material used in each typology.
The definition and consequently the selection of the damage thresholds, i.e., limit states, are among the main sources of uncertainties because they rely on rather subjective criteria. A considerable effort has been made in SYNER-G (Pitilakis et al. 2014a) to homogenize the criteria as much as possible.
Measuring seismic performance (risk) through economic losses and downtime (and business interruption), introduces the idea of measuring risk through a new more general concept: the resilience.
Resilience referring to a single element at risk or a system subjected to natural and/or manmade hazards usually goes towards its capability to recover its functionality after the occurrence of a disruptive event. It is affected by attributes of the system, namely robustness (for example residual functionality right after the disruptive event), rapidity (recovery rate), resourcefulness and redundancy (Fig. 3.8). It is also obvious that resilience has very strong societal, economic and political components, which amplify the uncertainties.
Schematic representation of seismic resilience concept (Bruneau et al. 2003)
Accepting the resilience to measure and quantify performance indicators and implicitly fragility and vulnerability, means that we introduce a new complicated world of uncertainties, in particular when from the resilience of a single asset e.g., a building, we integrate the risk in a whole city, with all its infrastructures, utility systems and economic activities.
3.7.6 Margin of Confidence or Conservatism?
The use of medians is traditionally considered as a reasonably conservative approach. Increased margin of confidence, i.e., 84th percentiles, is often viewed as over-conservatism. Conservatism and confidence are not actually reflecting the same thing in a probabilistic process. Figures 3.9 and 3.10 illustrate in a schematic example the estimated damages when using the median or median ±1 standard deviation (depending on which one is the more “conservative” or reasonable) in all steps of the assessment process of damages, from the estimation of UHS for rock and the soil amplification factors to the capacity curve and the fragility curves. The substantial differences observed in the estimated damages cannot be attributed to an increased margin of confidence or conservatism. Considering all relevant uncertainties, all assumptions are equally possible or at least “reasonable”. Who can really define in a scientifically rigorous way the threshold between conservatism and reasonable? Confidence is a highly subjective term varying among different end-users and model producers.
3.8 Damage Assessment: Subjectivity and Ineffectiveness in the Quest of the Reasonable
To further highlight the inevitable scatter in the current risk assessment of physical assets we use as example the seismic risk assessment and the damages of building stock in an urban area and in particular the city of Thessaloniki, Greece. Thessaloniki is the second largest city in Greece with about one million inhabitants. It has a long seismic history of devastating earthquakes, with the most recent one occurring in 1978 (Mw = 6.5, R = 25 km). Since then a lot of studies have been performed in the city to estimate the seismic hazard and to assess the seismic risk. Due to the very good knowledge of the different parameters, the city has been selected as pilot case study in several major research projects of the European Union (SYNER-G, SHARE, RISK-UE, LessLoss etc.)
3.8.1 Background Information and Data
The study area considered in the present application (Fig. 3.11) covers the central municipality of Thessaloniki. With a total population of 380,000 inhabitants and about 28,000 buildings of different typologies (mainly reinforced concrete), it is divided in 20 sub-city districts (SCD) (http://www.urbanaudit.org). Soil conditions are very well known (e.g., Anastasiadis et al. 2001). Figures 3.12 and 3.13 illustrate the classification of the study area based on the classification schemes of EC8 and Pitilakis et al. (2013) respectively. The probabilistic seismic hazard (PSHA) is estimated applying SHARE methodology (Giardini et al. 2013), with its rigorous treatment of aleatory and epistemic uncertainties. The PSHA with a 10 % probability of exceedance in 50 years and the associated UHS have been estimated for outcrop conditions. The estimated rock UHS has been then properly modified to account for soil conditions applying adequate period-dependent amplification factors. Three different amplification factors have been used: the current EC8 factors (Hazard 1), the improved ones (Pitilakis et al. 2012) (Hazard 2) and the new ones based on a more detailed soil classification scheme (Pitilakis et al. 2013) (Hazard 3) (see Sect. 3.7.3). Figure 3.14 presents the computed UHS for soil type C (or C1 according to the new classification scheme). Vulnerability is expressed through appropriate fragility curves for each building typology (Pitilakis et al. 2014a). Damages and associated probability of a building of a specific typology to exceed a specific damage state have been calculated with the Capacity Spectrum Method (Freeman 1998; Fajfar and Gaspersic 1996).
Map of the soil classes according to the new soil classification scheme proposed by Pitilakis et al. (2013) for Thessaloniki
SHARE rock UHS for Thessaloniki amplified with the current EC8 soil amplification factor for soil class C (CEN 2004), the improved EC8 soil amplification factor for soil class C (Pitilakis et al. 2012) and the soil amplification factors for soil class C1 of the classification system of Pitilakis et al. (2013). All spectra refer to a mean return period T = 475 years
The detailed building inventory for the city of Thessaloniki, which includes information about material, code level, number of storeys, structural type and volume for each building, allows a rigorous classification in different typologies according to SYNER-G classification and based on a Building Typologies Matrix representing practically all common RC building types in Greece (Kappos et al. 2006). The building inventory comprises 2,893 building blocks with 27,738 buildings, the majority of which (25,639) are reinforced concrete (RC) buildings. The buildings are classified based on their structural system, height and level of seismic design (Fig. 3.15). Regarding the structural system, both frames and frame-with-shear walls (dual) systems are included, with a further distinction based on the configuration of the infill walls. Regarding the height, three subclasses are considered (low-, medium- and high-rise). Finally, as far as the level of seismic design is concerned, four different levels are considered:
Classification of the RC buildings of the study area (Kappos et al. 2006). The first letter of each building type refers to the height of the building (L low, M medium, H high), while the second letter refers to the seismic code level of the building (N no, L low, M medium, H high)
-
No code (or pre-code): R/C buildings with very low level of seismic design and poor quality of detailing of critical elements.
-
Low code: R/C buildings with low level of seismic design.
-
Medium code: R/C buildings with medium level of seismic design (roughly corresponding to post-1980 seismic code and reasonable seismic detailing of R/C members).
-
High code: R/C buildings with enhanced level of seismic design and ductile seismic detailing of R/C members according to the new Greek Seismic Code (similar to Eurocode 8).
The fragility functions used (in terms of spectral displacement Sd) were derived though classical inelastic pushover analysis. Bilinear pushover curves were constructed for each building type, so that each curve is defined by its yield and ultimate capacity. Then they were transformed into capacity curves (expressing spectral acceleration versus spectral displacement). Fragility curves were finally derived from the corresponding capacity curves, by expressing the damage states in terms of displacements along the capacity curves (See Sect. 3.6 and in D’Ayala et al. 2012).
Each fragility curve is defined by a median value of spectral displacement and a standard deviation. Although the standard deviation of the curves is not constant, for the present application a standard deviation equal to 0.4 was assigned to all fragility curves, due to a limitation of the model used to perform the risk analyses. This hypothesis will be further discussed later in this section.
Five damage states were used in terms of Sd: DS1 (slight), DS2 (moderate), DS3 (substantial to heavy), DS4 (very heavy) and DS5 (collapse) (Table 3.2). According to this classification a spectral displacement of 2 cm or even lower can bring ordinary RC structures in the moderate (DS2) damage state, which is certainly a conservative assumption and in fact is penalizing, among other things, seismic risk assessment.
The physical damages of the buildings have been estimated using the open-source software EarthQuake Risk Model (EQRM http://sourceforge.net/projects/eqrm, Robinson et al. 2005), developed by Geoscience Australia. The software is based on the HAZUS methodology (FEMA and NIBS 1999; FEMA 2003) and has been properly modified so that it can be used for any region of the world (Crowley et al. 2010). The method is based on the Capacity Spectrum Method. The so called “performance points”, after properly adjusted to account for the elastic and hysteretic damping of each structure, have been overlaid with the relevant fragility curves in order to compute the damage probability in each of the different damage states and for each building type.
The method relies on two main parameters: The demand spectra (properly modified to account for the inelastic behaviour of the structure), which are driven from the hazard analysis, and the capacity curve. The latter is not user-defined and it is automatically estimated by the code using the building parameters supplied by the user. The capacity curve is defined by two points: the yield point (Sdy, Say) and the ultimate point (Sdu, Sdy) and is composed of three parts: a straight line to the yield point (representing elastic response of the building), a curved part from the yield point to the ultimate point expressed by an exponential function and a horizontal line starting from the ultimate point (Fig. 3.16). The yield point and ultimate point are defined in terms of the building parameters (Robinson et al. 2005) introducing inevitably several extra uncertainties, especially in case of existing buildings, designed and constructed several decades ago. In overall the following data are necessary to implement the Capacity Spectrum Method in EQRM: height of the building, natural elastic period, design strength coefficient, fraction of building weight participating in the first mode, fraction of the effective building height to building displacement, over-strength factors, ductility factor and damping degradation factors for each building or building class. All these introduce several uncertainties, which are difficult to be quantified in a rigorous way mainly because the uncertainties are mostly related to the difference between any real RC structure belonging in a certain typology and the idealized model.
Typical capacity curve in EQRM software, defined by the yield point (Sdy, Say) and the ultimate point (Sdu, Sdy) (Modified after Robinson et al. (2005))
3.8.2 Physical Damages and Losses
For each building type in each building block, the probabilities for slight, moderate, extensive and complete damage were calculated. These probabilities were then multiplied with the total floor area of the buildings of the specific building block that are classified to the specific building type in order to estimate for this building type the floor area, which will suffer each damage state. Repeating this for all building blocks which belong to the same sub-city district (SCD) and for all building types, the total floor area of each building type that will suffer each damage state in the specific SCD can be calculated (Fig. 3.17). The total percentages of damaged floor area per damage state for all SCD and for the three hazard analyses illustrated in the previous figures are given in Table 3.3.
The economic losses were estimated through the mean damage ratio (MDR) (Table 3.4), multiplying then this value with an estimated replacement cost of 1,000 €/m2 (Table 3.5).
3.8.3 Discussing the Differences
The observed differences in the damage assessment and losses are primarily attributed to the numerous uncertainties associated to the hazard models, to the way the uncertainties are treated and to the number of standard deviations accepted in each step of the analysis. Higher site amplification factors associated for example to median value plus one standard deviation, result in increasing building damages and consequently economic losses. The way inelastic demand spectra are estimated and the difference between computed UHS and a real earthquake records may also affect the final result (Fig. 3.18).
Despite the important influence of the hazard parameters, there are several other sources of uncertainties related mainly to the methods used. The effect of some of the most influencing parameters involved in the methodological chain of risk assessment will be further discussed for the most common building type (RC4.2ML) located in SCD 16. In particular the effect of the following parameters will be discussed:
-
Selection of the reduction factors for the inelastic demand spectra.
-
Effect of the duration of shaking.
-
Methodology for estimation of performance (EQRM versus N2).
-
Uncertainties in the fragility curves.
Reduction factors of the inelastic demand spectra
One of the main debated issues of CSM is the estimation of the inelastic demand spectrum for the estimation of the final performance of the structure. When buildings are subjected to ground shaking they do not remain elastic and dissipate hysteretic energy. Hence, the elastic demand curve should be appropriately reduced in order to incorporate the inelastic energy dissipation. Reduction of spectral values to account for the hysteretic damping associated with the inelastic behaviour of structures may be carried out using different techniques like the ATC-40 methodology, or inelastic design spectra and equivalent elastic over-damped spectra.
In the present study the ATC-40 methodology (ATC 1996) has been used combined with HAZUS methodology (FEMA and NIBS 1999; FEMA 2003). More specifically, damping-based spectral reduction factors were used assuming different reduction factors associated to different periods of the ground motion. According to this pioneer method the effective structural damping is the sum of the elastic damping and the hysteretic one. The hysteretic damping Bh is a function of the yield and ultimate points of the capacity curve (Eq. 3.2).
k is a degradation factor that defines the effective amount of hysteretic damping as a function of earthquake duration and energy-absorption capacity of the structure during cyclic earthquake load. This factor depends on the duration of the ground shaking while it is also a measure of the effectiveness of the hysteresis loops. When k factor is equal to unity, the hysteresis loops are full and stable. On the other hand when k factor is equal to 0.3 the hysteretic behaviour of the building is poor and the loop area is substantially reduced. It is evident that for a real structure the selection of the value of k is based on limited information, and hence practically introduces several uncontrollable uncertainties. In the present study a k factor equal to 0.333 is applied assuming moderate duration and poor hysteretic behaviour according to ATC-40 (ATC 1996).
Except from Newmark and Hall (1982) damping based spectral reduction factors, in the literature there are several other strength or spectral reduction factors one can use in order to estimate inelastic strength demands from elastic strength demands (Miranda and Bertero 1994). To illustrate the effect of the selection of different methods we compared the herein used inelastic displacement performance according to HAZUS (assuming k factor equal to 0.333 and 1), with other methods, namely those proposed by Newmark and Hall (1982) (as a function of ductility), Krawinkler and Nassar (1992), Vidic et al. (1994) and Miranda and Bertero (1994).
Applying the above methods for one building type (e.g., RC4.2ML) subjected to Hazard 3 (new soil classification and soil amplification factors according to Pitilakis et al. 2013), it is observed (Table 3.6) that the method used herein gives the highest displacements compared to all other methodologies (Fig. 3.19), a fact which further explains the over-predicted damages (Table 3.6).
Seismic risk (physical damages) in SCD16 for Hazard 3 and mean return period of 475 years in terms of the percentage of damage per damage state using (a) ATC-40 methodology combined with Hazus for k = 0.333 (b) ATC-40 methodology combined with Hazus for k = 1 (c) Newmark and Hall (1982) (d) Krawinkler and Nassar (1992) (e) Vidic et al. (1994) and (f) Miranda and Bertero (1994)
Duration of shaking
The effect of the duration of shaking is introduced through the k factor. It is supposed that the shorter the duration is, the higher the damping value should be. Applying this approach to the study case it is found that the effective damping for short earthquake duration is equal to 45 % while the effective damping for moderate earthquake duration is equal to 25 %. The differences are too high to underestimate the importance of the rigorous selection of this single parameter. Figure 3.20 presents the damages for SCD16 in terms of the percentage of damage per damage state considering short, moderate or long duration of the ground shaking.
EQRM versus N2 method (Fajfar 1999)
There are various methodologies that can be used for the vulnerability assessment and thus for building damage estimation (e.g., Capacity Spectrum Method, N2 Method). CSM (ATC-40 1996) that is also utilized in EQRM, evaluates the seismic performance of structures by comparing structural capacity with seismic demand curves. The key to this method is the reduction of 5 %-damped elastic response spectra of the ground motion to take into account the inelastic behaviour of the structure under consideration using appropriate damping based reduction factors. This is the main difference of EQRM methodology compared to “N2” method (Fajfar 1999, 2000), in which the inelastic demand spectrum is obtained from code-based elastic design spectra using ductility based reduction factors. The computed damages in SCD16 for Hazard 3 using EQRM and N2 methodology are depicted in Fig. 3.21. It is needless to comment on the differences.
Uncertainties in the Fragility Curves
Figure 3.22 shows the influence of beta (β) factor of the fragility curves. EQRM considers that beta factor is equal to 0.4. However the selection of a different, equally logical value, results in a very different damage level.
3.9 Conclusive Remarks
The main conclusion that one could make from this short and fragmented discussion is that we need a re-thinking of the whole analysis chain from hazard assessment to consequences and loss assessment. The uncertainties involved in every step of the process are too important, affecting the final result. Probably it is time to change the paradigm because so far we just use the same ideas and models trying to improve them (often making them very complex), not always satisfactorily. Considering the starting point of the various models and approaches and the huge efforts made so far, the progress globally is rather modest. More important is that in many cases the uncertainties are increased, not decreased, a fact that has a serious implication to the reliability and efficiency of the models regarding the assessment of the physical damages in particular in large scale e.g., city scale. Alienated end-users are more apt to serious mistakes and wrong decisions; wrong in the sense of extreme conservatism, high cost or unacceptable safety margins. It should be admitted, however, that our know-how has increased considerably and hence there is the necessary scientific maturity for a qualitative rebound towards a new global paradigm reducing partial and global uncertainties.
References
Abrahamson NA (2006) Seismic hazard assessment: problems with current practice and future developments. Proceedings of First European Conference on Earthquake Engineering and Seismology, Geneva, September 2006, p 17
Alexander D (2000) Confronting catastrophe: new perspectives on natural disasters. Oxford University Press, New York, p 282
Anastasiadis A, Raptakis D, Pitilakis K (2001) Thessaloniki’s detailed microzoning: subsurface structure as basis for site response analysis. Pure Appl Geophys 158:2597–2633
ATC-40 (1996) Seismic evaluation and retrofit of concrete buildings. Applied Technology Council, Redwood City
Bommer JJ, Abrahamson N (2006) Review article “Why do modern probabilistic seismic hazard analyses often lead to increased hazard estimates?”. Bull Seismol Soc Am 96:1967–1977. doi:10.1785/0120070018
Borcherdt RD, Glassmoyer G (1992) On the characteristics of local geology and their influence on ground motions generated by the Loma Prieta earthquake in the San Francisco Bay region, California. Bull Seismol Soc Am 82:603–641
Bruneau M, Chang S, Eguchi R, Lee G, O’Rourke T, Reinhorn A, Shinozuka M, Tierney K, Wallace W, Von Winterfelt D (2003) A framework to quantitatively assess and enhance the seismic resilience of communities. EERI Spectra J 19(4):733–752
CEN (European Committee for Standardization) (2004) Eurocode 8: Design of structures for earthquake resistance, Part 1: General rules, seismic actions and rules for buildings. EN 1998–1:2004. European Committee for Standardization, Brussels
Cornell CA, Jalayer F, Hamburger RO, Foutch DA (2002) Probabilistic basis for 2000 SAC/FEMA steel moment frame guidelines. J Struct Eng 128(4):26–533
Crowley H, Colombi M, Crempien J, Erduran E, Lopez M, Liu H, Mayfield M, Milanesi (2010) GEM1 Seismic Risk Report Part 1, GEM Technical Report, Pavia, Italy 2010–5
D’Ayala D, Kappos A, Crowley H, Antoniadis P, Colombi M, Kishali E, Panagopoulos G, Silva V (2012) Providing building vulnerability data and analytical fragility functions for PAGER, Final Technical Report, Oakland, California
Fajfar P (1999) Capacity spectrum method based on inelastic demand spectra. Earthq Eng Struct Dyn 28(9):979–993
Fajfar P (2000) A nonlinear analysis method for performance-based seismic design. Earthq Spectra 16(3):573–592
Fajfar P, Gaspersic P (1996) The N2 method for the seismic damage analysis for RC buildings. Earthq Eng Struct Dyn 25:23–67
FEMA, NIBS (1999) HAZUS99 User and technical manuals. Federal Emergency Management Agency Report: HAZUS 1999, Washington DC
FEMA (2003) HAZUS-MH Technical Manual. Federal Emergency Management Agency, Washington, DC
FEMA 273 (1996) NEHRP guidelines for the seismic rehabilitation of buildings — ballot version. U.S. Federal Emergency Management Agency, Washington, DC
FEMA 356 (2000) Prestandard and commentary for the seismic rehabilitation of buildings. U.S. Federal Emergency Management Agency, Washington, DC
Freeman SA (1998) The capacity spectrum method as a tool for seismic design. In: Proceedings of the 11th European Conference on Earthquake Engineering, Paris
Giardini D, Woessner J, Danciu L, Crowley H, Cotton F, Gruenthal G, Pinho R, Valensise G, Akkar S, Arvidsson R, Basili R, Cameelbeck T, Campos-Costa A, Douglas J, Demircioglu MB, Erdik M, Fonseca J. Glavatovic B, Lindholm C, Makropoulos K, Meletti F, Musson R, Pitilakis K, Sesetyan K, Stromeyer D, Stucchi M, Rovida A (2013) Seismic Hazard Harmonization in Europe (SHARE): Online Data Resource. doi:10.12686/SED-00000001-SHARE
Kappos AJ, Panagopoulos G, Penelis G (2006) A hybrid method for the vulnerability assessment of R/C and URM buildings. Bull Earthq Eng 4(4):391–413
Krawinkler H, Miranda E (2004) Performance-based earthquake engineering. In: Bozorgnia Y, Bertero VV (eds) Earthquake engineering: from engineering seismology to performance-based engineering, chapter 9. CRC Press, Boca Raton, pp 9.1–9.59
Krawinkler H, Nassar AA (1992) Seismic design based on ductility and cumulative damage demands and capacities. In: Fajfar P, Krawinkler H (eds) Nonlinear seismic analysis and design of 170 reinforced concrete buildings. Elsevier Applied Science, New York, pp 23–40
LessLoss (2007) Risk mitigation for earthquakes and landslides, Research Project, European Commission, GOCE-CT-2003-505448
MacKenzie D (1990) Inventing accuracy: a historical sociology of nuclear missle guidance. MIT Press, Cambridge
Mackie K, Stojadinovic B (2003) Seismic demands for performance-based design of bridges, PEER Report 2003/16. Pacific Earthquake Engineering Research Center, University of California, Berkeley
Mackie K, Stojadinovic B (2005) Fragility basis for California highway overpass bridge seismic decision making. Pacific Earthquake Engineering Research Center, University of California, Berkeley
Mehanny SSF (2009) A broad-range power-law form scalar-based seismic intensity measure. Eng Struct 31:1354–1368
Miranda E, Bertero V (1994) Evaluation of strength reduction factors for earthquake-resistant design. Earthq Spectra 10(2):357–379
Newmark NM, Hall WJ (1982) Earthquake spectra and design. Earthquake Engineering Research Institute, EERI, Berkeley
Padgett JE, Nielson BG, DesRoches R (2008) Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq Eng Struct Dyn 37:711–725
Pinto PE (2014) Modeling and propagation of uncertainties. In: Pitilakis K, Crowley H, Kaynia A (eds) SYNER-G: typology definition and fragility functions for physical elements at seismic risk, vol 27, Geotechnical, geological and earthquake engineering. Springer, Dordrecht. ISBN 978-94-007-7872-6
Pitilakis K, Riga E, Anastasiadis A (2012) Design spectra and amplification factors for Eurocode 8. Bull Earthq Eng 10:1377–1400. doi:10.1007/s10518-012-9367-6
Pitilakis K, Riga E, Anastasiadis A (2013) New code site classification, amplification factors and normalized response spectra based on a worldwide ground-motion database. Bull Earthq Eng 11(4):925–966. doi:10.1007/s10518-013-9429-4
Pitilakis K, Crowley H, Kaynia A (eds) (2014a) SYNER-G: typology definition and fragility functions for physical elements at seismic risk, vol 27, Geotechnical, geological and earthquake engineering. Springer, Dordrecht. ISBN 978-94-007-7872-6
Pitilakis K, Karapetrou ST, Fotopoulou SD (2014b) Consideration of aging and SSI effects on seismic vulnerability assessment of RC buildings. Bull Earthq Eng. doi:10.1007/s10518-013-9575-8
REAKT (2014) Strategies and tools for real time earthquake and risk reduction. Research Project, European Commission, Theme: ENV.2011.1.3.1-1, Grant agreement: 282862. http://www.reaktproject.eu
RISK-UE (2004) An advanced approach to earthquake risk scenarios with applications to different European towns. Research Project, European Commission, DG ΧΙI2001-2004, CEC: EVK4-CT-2000-00014
Robinson D, Fulford G, Dhu T (2005) EQRM: Geoscience Australia’s earthquake risk model technical manual Version 3.0. Geoscience Australia Record 2005/01
Selva J, Argyroudis S, Pitilakis K (2013) Impact on loss/risk assessments of inter-model variability in vulnerability analysis. Nat Hazards 67(2):723–746. doi:10.1007/s11069-013-0616-z
SHARE (2013) Seismic Hazard Harmonization in Europe. Research Project, European Commission, ENV.2008.1.3.1.1, Grant agreement: 226769. www.share-eu.org
SYNER-G (2013) Systemic seismic vulnerability and risk analysis for buildings, lifeline networks and infrastructures safety gain. Research Project, European Commission, ENV-2009-1-244061
Vamvatsikos D, Cornell CA (2002) Incremental dynamic analysis. Earthq Eng Struct Dyn 31:491–514
Vidic T, Fajfar P, Fischinger M (1994) Consistent inelastic design spectra: strength and displacement. Earthq Eng Struct Dyn 23:507–521
Acknowledgments
Special acknowledgment to Dr Jacopo Selva, Dr Sotiris Argyroudis and Professor Theodoros Chatzigogos for several breakthrough discussions we had on the nature and the practical treatment of uncertainties. Also to Dr Zafeiria Roumelioti, Dr Stavroula Fotopoulou and my PhD students Evi Riga, Anna Karatzetzou and Sotiria Karapetrou for helping me in preparing this lecture and paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution Noncommercial License, which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Copyright information
© 2015 The Author(s)
About this chapter
Cite this chapter
Pitilakis, K. (2015). Earthquake Risk Assessment: Certitudes, Fallacies, Uncertainties and the Quest for Soundness. In: Ansal, A. (eds) Perspectives on European Earthquake Engineering and Seismology. Geotechnical, Geological and Earthquake Engineering, vol 39. Springer, Cham. https://doi.org/10.1007/978-3-319-16964-4_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-16964-4_3
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-16963-7
Online ISBN: 978-3-319-16964-4
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)