Abstract
In seismic hazard evaluation and risk mitigation, there are many random and epistemic uncertainties. On the another hand, the researches in this area as part of knowledge are with rest, that is, the results are with interpretable questions with open answers. The knowledge cannot be exhausted by results. The authors developed in last time the concept of “Nonlinear Seismology – The Seismology of the XXI Century” (Marmureanu et al. Nonlinear seismology-the seismology of XXI century. In: Modern seismology perspectives, vol 105. Springer, New York, pp 49–70, 2005).
The leading question is: how many cities, villages, metropolitan areas, etc., in seismic regions are constructed on rock? Most of them are located on soil deposits. A soil is of basic type sand or gravel (termed coarse soils), silt or clay (termed fine soils), etc. Strong ground accelerations from large earthquakes can produce a nonlinear response in shallow soils. This can be studied by comparing surface and borehole seismic records for earthquakes of different sizes. When a nonlinear site response is present, then the shaking from large earthquakes cannot be predicted by simple scaling of records from small earthquakes (Shearer, Introduction to seismology, 2nd edn. Cambridge University Press, Cambridge, 2009). Nonlinear amplification at sediments sites appears to be more pervasive than seismologists used to think…Any attempt at seismic zonation must take into account the local site condition and this nonlinear amplification (Aki, Tectonophysics 218:93–111, 1993).
The difficulty for seismologists is to demonstrate the nonlinear site effects, these being overshadowed by the overall patterns of shock generation and propagation. In other words, the seismological detection of the nonlinear site effects requires a simultaneous understanding/knowledge of earthquake source, propagation path, and local geological site conditions. To see the actual influence of nonlinearity of the whole system (seismic source-path propagation-local geological structure), the authors used to study the free field response spectra which are the last in this chain and are taken into account in seismic design of all structures. Soils from the local geological structure at the recording site exhibit a strong nonlinear behavior under cyclic loading conditions and although they have many common mechanical properties, the use of different models to describe their seismic behavior is required.
The studies made by the authors in this chapter show that using real spectral amplification factors (SAF), amplifications showing local effects, have values which differ totally from those of crustal earthquakes. The spectral amplifications highlight strong nonlinear response of soil composed of fractured limestone, limestone with clay, marl, sands, clay, etc., and these amplifications are strongly dependent of earthquake magnitude and nature of soils from site. Finally, these amplifiers are compared to those from Regulatory Guide 1.60 of the U. S. Atomic Energy Commission (Design response spectra for seismic design of nuclear power plants. Regulatory Guide 1.60. Rev. 1, Washington, D.C., 1973) which can be used only for crustal earthquakes and not for deep and strong Vrancea earthquakes from Romania. The study of the nonlinear behavior of soils during strong earthquakes may clarify uncertainties in ground motion prediction equations used by probabilistic and classical deterministic seismic hazard analysis.
Moto: The nonlinear seismology is the rule, The linear seismology is the exception. Paraphrasing Tullio Levi-Civita
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
17.1 Introduction
The Vrancea seismogenic zone denotes a peculiar source of seismic hazard, which represents a major concern in Europe, especially to neighboring regions from Bulgaria, Serbia, Republic of Moldova, etc. The strong seismic events that can occur in this area can generate the most destructive effects in Romania, and may seriously affect high-risk man-made structures such as nuclear power plants (Cernavoda, Kosloduj, etc.), chemical plants, large dams, and pipelines located within a wide area from Central Europe to Moscow.
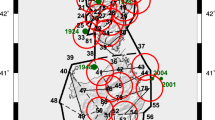
Earthquakes in the Carpathian–Pannonian region are confined to the crust, except the Vrancea zone, where earthquakes with focal depth down to 200 km occur. For example, the ruptured area migrated from 140 to 180 km (November 10, 1940 earthquake, M w = 7.7), from 90 to 110 km (March 4, 1977 earthquake, M w = 7.4), from 130 to 150 km (August 30, 1986 earthquake, M w = 7.1), and from 70 to 90 km (May 30, 1990 earthquake, M w = 6.9) depth. The depth interval between 110 and 130 km remains not ruptured since October 26, 1802, when it was the strongest earthquake occurred in this part of Central Europe. The magnitude is assumed to be M W = 7.9–8.0 and this depth interval is a natural candidate for the next strong Vrancea event (Fig. 17.1).
Bucharest City is located in Moesian Platform. From geological point of view, above Cretaceous and Miocene deposits (isobaths around 1,400 m depth), a Pliocene shallow water deposit (~700 m thick) was settled. The surface geology consists mainly of Quaternary alluvial deposits, later covered by loess. In the extra-Carpathian area, there are thick soil deposits (Buzau: 4.5 km; Bucharest: 0.55–1.4 km; etc.) (Mandrescu et al. 2008). There are large fundamental periods (T, s) for soils in all extra-Carpathian area. Nonlinear amplification at sediments sites appears to be more pervasive than seismologists used to think…Any attempt at seismic zonation must take into account the local site condition and this nonlinear amplification (Aki, Tectonophysics 218:93–111, 1993).
This basic material characteristic shall be taken into account when we are evaluating the seismic response of soil deposits or earth structures. The model of linear elastic response of the Earth to earthquakes has been almost universally used in seismology to model teleseismic, weak, and also strong earthquakes.
For teleseismic and weak ground motions, there is no reason to doubt that this model is acceptable, but for strong ground motions, particularly when are recorded on soils, the consequences of nonlinear soil behavior have to be seriously considered.
Soils exhibit a strong nonlinear behavior under cyclic loading conditions. In the elastic zone, soil particles do not slide relative to each other under a small stress increment and the stiffness is at its maximum. The stiffness begins to decrease from the linear elastic value as the applied strains or stresses increase, and the deformation moves into the nonlinear elastic zone (Fig. 17.2).
Stiffness degradation curve in terms of shear modulus G and Young’s modulus E: stiffness plotted against logarithm of typical strain levels observed during construction of typical geotechnical structures (Marmureanu et al. 2013)
Stress and strain states are not enough to determine the mechanical behavior of soils. It is necessary, in addition, to model the relation between stresses and deformations by using specific constitutive laws to soils. Currently, there are no constitutive laws to describe all real mechanical behaviors of deformable materials like soils. From mechanical behavior point of view, there are two main groups of essential importance: sands and clays. Although these soils have many common mechanical properties, they require the use of different models to describe the differences in their seismic behavior. Soils are simple materials with memory: sands are “rate-independent” type and clays are “rate-dependent” ones, terms used in deformable body mechanics. However, the complexity of these “simple” models exceeds the possibility of solving and requires the use of simplifying assumptions or conditions that are restricting the loading conditions, which makes additional permissible assumptions. Sands typically have low rheological properties and can be shaped with an acceptable linear elastic model (Borcherdt 2009) by using Boltzmann’s formulation of the constitutive relation between stresses and strains. Clays which frequently present significant changes over time can be shaped by a nonlinear viscoelastic model.
17.2 Quantitative Evidence of Nonlinear Behavior of Soils
Laboratory tests made by using Hardin or Drnevich resonant columns consistently show the decreasing of dynamic torsion function (G) and increasing of torsion damping function (D%) with shear strains (γ%) induced by strong earthquakes; G = G(γ), respectively, D% = D%(γ); therefore, nonlinear viscoelastic constitutive laws are required (Fig. 17.2). The strong dependence of response on strain amplitude (Figs. 17.3, 17.4, 17.5, 17.6, and 17.7) with earthquake magnitude becomes a standard assumption in evaluation of Vrancea strong earthquake effects on urban environment.
The absolute values of the variation of dynamic torsion modulus function (G, daN/cm2) and torsion damping function (D %) of specific strain (γ %) for marl samples obtained in Hardin and Drnevich resonant columns from NIEP (USA patent), Laboratory of Earthquake Engineering (Marmureanu et al. 2010)
The normalized values of the variation of dynamic torsion modulus function (G, daN/cm2) and torsion damping function (D %) of specific strain (γ %) for sand and gravel samples with normal humidity obtained in Hardin and Drnevich resonant columns from NIEP (USA patent) (Marmureanu et al. 2010)
Nonlinear relation between dynamic torsion modulus (G, daN/cm2) and shear-strain (γ%) experimental data from Hardin and Drnevich resonant columns from NIEP (USA patent). Normalized values for limestone, gritstone, marl, clay+gravel, sand, and clay (Marmureanu et al. 2010)
Nonlinear relation between torsion damping function (D%) and shear-strain (γ%) experimental data from Hardin and Drnevich resonant columns from NIEP (USA patent). Normalized values for limestone, gritstone, marl, clay+gravel, sand, and clay (Marmureanu et al. 2010)
Dependence of dynamic torsion modulus function (G, daN/cm2) and torsion damping function (D%) with shear strains γ% and frequency ω. For frequencies between 1 and 10 Hz, shear modulus (G) and damping ratio are constant in this main field used in engineering (Bratosin 2002; Marmureanu et al. 2005, 2010, 2013)
The dependence of dynamic torsion modulus function (G, daN/cm2) and torsion damping function (D%) with shear stains (γ%) and frequency ω are given. In Fig. 17.7 one can observe the constant values of G(γ) and D(γ) between 1 and 10 Hz, the domain used in civil engineering structures design.
The analysis of several resonant column tests shows a major weight of the strain level on modulus and damping values and a minor influence of the frequency values between 1 and 10 Hz (Marmureanu et al. 2005, 2010). Therefore, for practical purposes, we can consider these functions as constants in terms of frequency ω at least between 1 and 10 Hz. This hypothesis involves only the independence of ω of these soil functions and not of the soil response.
For smaller deep Vrancea earthquakes (M W = 6.1), the strains are smaller and we are in the left-hand side of Fig. 17.4; for strong earthquakes (M W = 7.2), the strains are larger and we are in the right-hand-side of Fig. 17.4 with large damping. Consequently the responses of a system of nonlinear viscoelastic materials (clays, marls, gravel, sands, etc.) subjected, for example, to vertically traveling shear waves are far away from being linear and generating large discrepancies. In this case, the SH wave vertical propagation equation is (Marmureanu et al. 2005, 2010):
where G(daN/cm2) is the dynamic torsion modulus function and D(%) is the torsion damping function; both of them are functions of shear strains (γ %) induced by strong earthquakes, frequency (ω), confining pressure (σ), depth (h), temperature (t o), void ratio (v), etc., that is:
G = G(γ, ω, σ, h, t, v,…) and D = D(γ, ω, σ, h, t, v,…). If we accept a strain-history of forms (harmonic and stationary): γ(t) = γo exp (−iωt) and from Fig. 17.7, where for frequencies ω between 1 and 10 Hz, shear modulus (G) and damping ratio (D) are constant in this main field used in engineering, then G(γ) an D(γ) will depend only of shear strain (γ%) developed during of strong Vrancea earthquakes (Marmureanu et al. 2013).
17.2.1 Spectral Amplification Factors (SAF) Dependence of Magnitude
Currently, there are no constitutive laws to describe all real mechanical behaviors of deformable materials like soils. In order to make quantitative evidence of large nonlinear effects, the authors introduced and developed after 2005 (Marmureanu et al. 2005) the concept of nonlinear spectral amplification factor (SAF). SAF is the ratio between maximum spectral absolute acceleration S max a , relative velocity S max v , relative displacement S max d from response spectra for a fraction of critical damping (β,%) and peak values of acceleration (a max ), velocity (v max ), and displacement (d max ), respectively. From processed strong motion records, one can compute \( \left(\mathrm{S}\mathrm{A}\mathrm{F}\right)\mathrm{a}={S}_a^{max}/{a}_{max} \); \( \left(\mathrm{S}\mathrm{A}\mathrm{F}\right)\mathrm{v}={S}_v^{max}/{v}_{max} \); \( \left(\mathrm{S}\mathrm{A}\mathrm{F}\right)\mathrm{d}={S}_d^{max}/{d}_{max} \).
The analysis was conducted for last strong and deep Vrancea earthquakes (March 04, 1977: M W = 7.4 and h = 94 km; August 30, 1986: M W = 7.1 and h = 134.4 km; May 30 1990: M W = 6.9 and h = 90.9 km; May 31, 1990: M W = 6.4 and h = 86.9 km). The spectral amplification factors decrease with increasing the magnitudes of deep strong Vrancea earthquakes and these values are far of that given by Regulatory Guide 1.60 of the U. S. Atomic Energy Commission and accepted by IAEA Vienna (Cioflan et al. 2011; Marmureanu et al. 2013; U.S. Atomic Energy Commission 1973).
A characteristic of the nonlinearity is a systematic decrease in variability of peak ground accelerations with increasing earthquake magnitude. For example, for the last Vrancea earthquakes, in extra-Carpathian area, spectral amplification factor (SAF) decreases from 5.89 (M W = 6.4) to 5.16 (M W = 6.9) and to 4.04 (M W = 7.1) at Bacau Seismic Station. The amplification factors decrease as the earthquake magnitude increases. This is consistent with our data which confirm that the ground accelerations tend to decrease as earthquake magnitude increases. As the excitation level increases, the response spectrum is larger for the linear case than for the nonlinear one. The analysis for a site indicates that the effect of nonlinearity is large and peak ground acceleration is 45.7 % smaller assuming that response of soil to earthquake with M W = 6.4 is still in elastic domain and then the possibility to compare to it (an example is in Table 17.1).
At Bucharest-Panduri Seismic Station (Table 17.2) and Fig. 17.8, close to borehole 172, for horizontal components and β = 5 % damping, the values of the SAF for accelerations are 3.29 for August 30, 1986 Vrancea earthquake (M W = 7.1); 4.49 for May 30, 1990 (M W = 6.9); and 4.98 for May 31, 1990 (M W = 6.4). The effect of nonlinearity is large and peak ground accelerations is 51.3 smaller assuming that the response of soil to Vrancea earthquake on May 31, 1990 (M W = 6.4) is still in elastic domain and then we have the possibility to compare to it (Tables 17.3 and 17.4, Figs. 17.9).
Geological structure under Bucharest. Isobars are generally oriented East to West with slope of 8 % down from South to North. In the same direction, the thickness of layers becomes larger (Mandrescu et al. 2008)
Acceleration response spectra for Bucharest-INCERC Seismic Station, NS components and the effects of nonlinearity of soil (cross-hatched areas) for last strong Vrancea earthquakes: March 04, 1977; August 30, 1986; and May 30, 1990. The fundamental periods (T, s) are not the same for the three earthquakes (β = 5 %) (Marmureanu et al. 2005)
On the other hand, from Table 17.5 and Fig. 17.10 we can see that there is a strong nonlinear dependence of the spectral amplification factors on earthquake magnitude (Mar. 1996) for other seismic stations on Romanian territory on extra-Carpathian area (Iasi, Focsani, Bucharest-NIEP, Bucharest-INCERC, etc.). In brackets are the values from Regulatory Guide 1.60 of the U. S. Atomic Commission and IAEA Vienna (U.S. Atomic Energy Commission 1973).
The spectral amplification factors (SAF) and, in fact, the nonlinearity, are functions of Vrancea earthquake magnitude. The amplification factors decrease as the magnitude increases (Fig. 17.11) for all the extra-Carpathian area.
17.3 The Implications of Soil Nonlinearity During Strong Earthquakes in PSHA
In seismic hazard evaluation and risk mitigation, there were many random and epistemic uncertainties. The main ones are in step “ground motion evaluation.” Probabilistic or deterministic seismic hazard analysis (PSHA/DSHA) are commonly used in engineering, nuclear power plants, bridges, military objectives, dams, etc. (Fig. 17.12). Ground motion characteristics at a site, conditional on a given earthquake, can be estimated in several ways, which depend on the earthquake source characteristics available. If peak motion characteristics have been estimated (depth, magnitude, seismic moment, time, etc.), then the response spectrum can be derived via spectral amplification factors (SAF). Empirical ground motion equation characteristics are the oldest estimates in seismic hazard analysis, dating from the 1960s and they typically have the following type of form:
Basic steps in probabilistic (PSHA) – left and deterministic (DSHA) – right seismic hazard analysis (Marmureanu et al. 2010)
where A is ground motion amplitude, which can be a peak motion parameter or spectral amplitude; c o is a constant; f(m), f(r) are functions of magnitude and distance; ε is a random variable taking on a specific value for each observation. As can be observed the nonlinear behaviors of soils are not included in GMPE. It is important to understand the strengths and weaknesses of one equation versus another. One is never sure of having the “correct” functional form of a ground motion equation.
Linear stress–strain theory is generally valid at the low strains typical of most seismic waves. Strong ground accelerations from large earthquakes can produce a nonlinear response in shallow soils. This can be studied by using many ways. When a nonlinear site response is present, then the shaking from large earthquakes cannot be predicted by simple scaling of records from small earthquakes (Shearer 2009).
The fundamental understanding about both uncertainties in ground motion comes from the large scatter in observations, even when they are normalized by magnitude, distance, and other parameters.
Seismic hazard P (A > a) as a function of soil level of movement is given in probabilistic seismic hazard analysis by:
where s – number of seismic sources; ln(a)−g(m, r) = attenuation low; σ – standard deviation; Σ – summation over sources; ν i – annual average frequency; f R(r|m) – probability density function of the distances from the site; f M(m) – probability density function of magnitude (M); λ(a) – the annual probability of exceedance of peak ground acceleration at the site by considering a Poissonian process.
It was developed from mathematical statistics (Benjamin and Cornell 1970) under four fundamental assumptions (Cornell 1968, 1971; Marmureanu et al. 2010, 2013):
-
1.
The constant in time is an average occurrence rate of earthquakes.
-
2.
Equal likelihood of earthquake occurrence along a line or over an areal source: in fact a single point source.
-
3.
Variability of ground motion at a site is independent.
-
4.
Poisson (or “memory-less”) behavior of earthquake occurrences.
In the case of Fukushima Nuclear Power Plant, deterministic hazard assessment methods were used for the original design, but Japanese authorities recently moved to probabilistic assessment methods and the resulted probability of exceedance of the design basis acceleration was expected to be 10-4-10-6(Klϋgel 2014). The design basis seismic data were exceeded during the March 11, 2011, earthquake (M = 9.0) at Fukushima NPP as shown in (Klϋgel 2014). Ignoring their own information from historical events caused a violation of the deterministic hazard analysis principles!
What is wrong with traditional PSHA or DSHA?
-
(a)
A Poisson process is a stochastic process. This Poissonian process implies that the occurrence of events/earthquakes is independent of time and space. The nature of earthquake occurrence is not Poissonian! Earthquake occurrence is characterized by a self-exciting behavior and a self-correcting behavior
-
(b)
Ground motion prediction equations. The empirical equations represent far field approximations (symmetric isotropic wave propagation). The so-called aleatory variability (ε) is just the error of this assumption – source of diffusivity making the Khinchine (Хинчин) (Хинчин 1926) theorem valid (superposition of stochastic processes with none of them dominating converges asymptotically to a resulting Poissonian process):
Also, ergodic assumption(s) – pooling of world wide data → supports the lognormal assumption because of the central limit theorem. There are ground motion uncertainties: aleatory uncertainties in random effects and epistemic uncertainties in knowledge.
The fundamental understanding about both uncertainties in ground motion comes from the large scatter in observations, even when they are normalized by magnitude, distance, and other parameters. One is never sure of having the “correct” functional form of a ground motion equation and the nonlinear behavior of soil to strong earthquakes is still unknown to many structural designers.
17.4 Conclusions
The authors developed in last time the concept of “Nonlinear Seismology – The Seismology of the XXI Century”(Marmureanu et al. 2005). The difficulty for seismologists and structural engineers to demonstrate the nonlinear effects of the site lies in the difficulty of separating the effects of the source from the effects of the path between sources to free field of site (Grecu et al. 2007). To see the actual influence of nonlinearity of the whole system (seismic source – path propagation – local geological structure) the authors used to study the spectral amplification factors (SAF) from response spectra because they are the last in this chain and, of course, that they are the ones who are taken into account in seismic design of structures.
There is a strong dependence of the spectral amplification factors (SAF) with earthquake magnitude. At the same seismic station, for example at Bacau NIEP Seismic Station, horizontal components and 5 % damping, the values of the SAF for accelerations are 4.0443 for August 30,1986 Vrancea earthquake (M W = 7.1); 5.1649 for May 30, 1990 (M W = 7.9); and 5.8942 for May 31, 1990 (M W = 6.4). Also, for Bucharest-Panduri Seismic Station the values are 3.29, 4.49, and 4.98 (Tables 17.1 and 17.2) by considering linear behavior of soils during Vrancea earthquake on May 31, 1990 with magnitude M W = 6.4. A characteristic of the nonlinearity is a systematic decrease in variability of peak ground acceleration with increasing earthquake magnitude.
The spectral amplification factors for last three strong and deep Vrancea earthquakes for NPP Cernavoda site are larger than the values given by Regulatory Guide 1.60 of the U. S. Atomic Energy Commission, IAEA Vienna-through Safety Series No. 5-SG-S1, and the values used by AECL-Canada in 1978 (U.S. Atomic Energy Commission 1973).
It is essential for seismologists and engineers to understand seismic hazard and risk, as well as the science behind them. PSHA emphasizes the probability, which depends on the statistical models, whereas NDSHA emphasizes the ground motion, which depends on the physical models.
This knowledge can be very fruitfully used by civil engineers in the design of new seismic resistant constructions and in the reinforcement of the existing built environment, and, therefore, supply a particularly powerful tool for the prevention aspects of Civil Protection.
References
Aki A (1993) Local site effects on weak and strong ground motion. Tectonophysics 218:93–111
Benjamin JR, Cornell CA (1970) Probability, statistics and decision for civil engineers. McGraw-Hill, New York
Borcherdt RD (2009) Viscoelastic waves in layered media. Cambridge University Press, Cambridge/New York, 350 pp. ISBN 978-0521898539
Bratosin D (2002) Soil dynamics elements. Romanian Academy Publishing House, Bucharest, p 136
Cioflan CO, Marmureanu A, Marmureanu G (2011) The quantitative evidence of the soil nonlinear behavior during of strong Vrancea earthquakes in real/nonlinear seismology. Rom Rep Phys 63:839–851
Cornell CA (1968) Engineering seismic risk analysis. Bull Seismol Soc Am 58(5):1583–1606
Cornell CA (1971) Probabilistic analysis of damage to structures under seismic loads. In: Howells
Grecu B, Radulian M, Mandrescu N, Panza GF (2007) H/V spectral ratios technique application in the city of Bucharest: can we get rid of source effect? J Seismol Earthq Eng 9(1–2):1–4
Klϋgel JU (2014) Lessons not yet learned from the Fukushima disaster. EGU, 27 April 2014, ISSO, Vienna
Mandrescu N, Radulian M, Marmureanu GH, Ionescu C (2008) Integrate research of the geological, geophysical and seismological data for local response evaluation in bucharest urban area. Romanian Academy Publishing House, Bucuresti, p 134
Mărmureanu GH, Mişicu M, Cioflan CO, Balan FS, Apostol BF (2005) Nonlinear seismology-the Seismology of the XXI century. Lecture notes of earth sciences, perspective in modern seismology, vol 105. Springer, Heidelberg, pp 47–68
Marmureanu GH, Cioflan CO, Marmureanu A (2010) Researches on local seismic hazard (microzonation) of Bucharest metropolitan area. Microzoning maps accelerations, fundamental periods and intensities for maximum Vrancea earthquake magnitude of 7.5 on Richter scale. Tehnopress Publishing, Iasi, p 472 (in Romanian). ISBN 978-974-702-809-9
Marmureanu G, Cioflan CO, Marmureanu A (2013) Nonlinear seismology a reality. The quantitative data. EGU, 22–27 Apr 2012, Section NH4, vol 65. Published in Romanian Reports in Physics, Vienna, pp 512–523
Shearer PM (2009) Introduction to seismology, 2nd edn. Cambridge University Press, Cambridge. ISBN 978-0-521-70842-5
U.S. Atomic Energy Commission (1973) Design response spectra for seismic design of nuclear power plants. Regulatory Guide 1.60. Rev. 1, Washington, D.C.
Хинчин (1926) Идеи интуиционизма и борьба за предмет в современной математике. Вестник Коммунистическая Академ 16:184–192
Acknowledgments
This work is performed in the frame of the National Romanian Plan for Research, Development and Innovation, NII, Partnership Program; Project “Bridging the gap between seismology and earthquake engineering. From the seismicity of Romania towards refined implementation of seismic action of European Norm EN 1998–1 in earthquake resistant design of buildings” (BIGSEES), Contract nr. 72/2012–2016.
This work was supported partially by a grant of the Romanian National Authority for Scientific Research, CNCS – UEFISCDI, project number PN-II-RU-TE-2012-3-0215.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution Noncommercial License, which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Copyright information
© 2015 The Author(s)
About this chapter
Cite this chapter
Marmureanu, G., Cioflan, C.O., Marmureanu, A., Ionescu, C., Manea, E.F. (2015). Bridging the Gap Between Nonlinear Seismology as Reality and Earthquake Engineering. In: Ansal, A. (eds) Perspectives on European Earthquake Engineering and Seismology. Geotechnical, Geological and Earthquake Engineering, vol 39. Springer, Cham. https://doi.org/10.1007/978-3-319-16964-4_17
Download citation
DOI: https://doi.org/10.1007/978-3-319-16964-4_17
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-16963-7
Online ISBN: 978-3-319-16964-4
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)