Abstract
The chapter deals with the analysis of Quantum Communications systems in the presence of thermal noise, sometimes called background noise, neglected in the previous chapter. This is achieved by passing from pure states to mixed states, described by density operators. Consequently, the analysis and especially the optimization become very difficult. For binary Quantum Communications systems the optimization is based again on Helstrom’s theory, whereas for multilevel systems the numerical optimization is used, and especially the square root measurement (SRM), which is suboptimal but gives a good approximation of the performance. The SRM technique is applied to the most popular Quantum Communications systems (QAM, PSK, and PPM) seen in the previous chapter in the absence of thermal noise. We will find that, also in the presence of thermal noise, Quantum Communications systems perform better than the classical counterparts.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
More specifically, letting \(\alpha =x+\mathrm{i}y\), the integration must be interpreted in the form
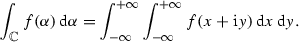
- 2.
In Sect. 5.7 the factor of a density operator was denoted by \(\gamma \), but here this symbol denotes the complex number determining the density operator \(\rho (\gamma )\). Thus, in this chapter the factor is denoted by \(\beta \).
References
G. Cariolaro, G. Pierobon, Performance of quantum data transmission systems in the presence of thermal noise. IEEE Trans. Commun. 58(2), 623–630 (2010)
G. Cariolaro, G. Pierobon, Theory of quantum pulse position modulation and related numerical problems. IEEE Trans. Commun. 58(4), 1213–1222 (2010)
R.J. Glauber, The quantum theory of optical coherence. Phys. Rev. 130, 2529–2539 (1963)
C.W. Helstrom, J.W.S. Liu, J.P. Gordon, Quantum-mechanical communication theory. Proc. IEEE 58(10), 1578–1598 (1970)
C.W. Helstrom, Quantum Detection and Estimation Theory. Mathematics in Science and Engineering, vol. 123. Academic Press, New York (1976)
V. Vilnrotter and C. W. Lau, Quantum detection of binary and ternary signals in the presence of thermal noise fields. NASA, Technical Report, February (2003). Interplanetary Network Progress (IPN) Progress Report 42–152
J. Shapiro, Quantum noise and excess noise in optical homodyne and heterodyne receivers. Quantum Electron. IEEE J. 21(3), 237–250 (1985)
S. J. Dolinar, J. Hamkins, B. Moiston, and V. Vilnrotter, Optical modulation and coding, in H. Hemmati, ed. Deep Space Optical Communications, Wiley (2006)
G. Cariolaro, R. Corvaja, G. Pierobon, Compression of pure and mixed states in quantum detection, in Global Telecommunications Conference (GLOBECOM, (2011) IEEE. December 2011, 1–5 (2011)
A. Assalini, G. Cariolaro, G. Pierobon, Efficient optimal minimum error discrimination of symmetric quantum states. Phys. Rev. A 81, 012315 (2010)
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Alternative Discretization
An alternative discretization of a Glauber density operator is based on the subdivision of the integration region in (8.8) into a finite number \(K\) of regions of the complex plane, namely,
In such a way, one gets the discrete approximation of the density operator
where
and \(|\alpha _{k}\rangle \) are the Glauber coherent states with complex parameter \(\alpha _{k}\in A_{k}\). This integral gives the probability of the state \(|\alpha _k\rangle \)
The normalization of the probability is verified because the volume determined by the Gaussian profile is unitary
To arrive at a finite form, the Glauber states in (8.76) are approximated by a finite number \(N\) of terms, that is,
Partition strategy. The partition of the complex plane \(\mathbb {C}\) into the regions \(A_k\) can be done in several ways. The strategy that will be considered here is:
-
(1)
partition \(\mathbb {C}\) into a finite number \(L\) circular rings centered on the nominal state \(|\gamma \rangle \)
$$ D_i=\left\{ r_{i-1}^2\le |\alpha -\gamma |^2<r_i^2\right\} , \qquad i=1,2,\ldots ,L $$with \(r_0 = 0\) and \(r_{L}=\infty \).
-
(2)
subdivide the \(i\)th ring into \(k_i\) equal parts
$$ A_{ip}=\left\{ \frac{2\pi }{k_i}\,(p-1)\le \arg (\alpha -\gamma )<\frac{2\pi }{k_i}\,p \right\} , \qquad p=1,2,\ldots ,k_i $$where for convenience we use the double subscript \(ip\) instead of \(k\),
-
(3)
choose the state \(|\alpha _{ip}\rangle \), with \( \alpha _{ip}\) given by the barycenter of the region \(A_{ip}\),
-
(4)
assume the condition that the states are equally likely.
With such a procedure the number of states is \( K=k_1+\cdots k_L \) and the volume determined by the ring \(D_i\) results in
which is subdivided into \(k_i\) equal parts, so that the equal probability condition is
By imposing such a condition, the radii of the circular rings can be evaluated by the recurrence
letting \(r_0 = 0\) and \(r_{L}=\infty \).
Finally, the barycentric radius of the ring \(D_i\) results in
where erf is the error function. In such a way, the coherent state \(|\alpha _{ip}\rangle \) is identified by the complex number
The number of states in this approximation of the density operator is given by the total number of subdivisions \(K=k_1+\cdots +k_L\).
Example 8.5
We consider two examples of subdivision shown in Fig. 8.26. In both cases the subdivision is into \(L=4\) rings and the inner ring is not subdivided and is associated to the nominal state \(|\gamma \rangle \). In the first example, the 3 outer rings are subdivided into 5 parts, and we get \(K=16\) global subdivisions, while in the second example they are respectively subdivided into 5 , 7 and 9 parts with \(K=22\) global subdivisions.
We complete the evaluation in the first subdivision, assuming
With \(N=11\) we find the matrix
As done in Example 8.19, we perform the factorization choosing the accuracy 0.001 to neglect the very small eigenvalues. In such a way we get the \(11\times 4\) factor
The comparison with the results of Example 8.19 shows that the numerical values are very close (the difference is of the same order of magnitude as the chosen accuracy) .
1.2 Proof of Proposition 8.2 on Factorization
We exploit the rule of mixed products (ordinary products and Kronecker’s products) seen in Sect. 2.13, Eq. (2.104). For example, for \(K=4\) and \(i=2\) this rule yields
from which
and it is evident how the general result (8.65) can be obtained.
1.3 Simultaneous Diagonalization of \(S\) and \(T\)
We outline a procedure for finding the simultaneous diagonalization (8.72) starting from an arbitrary EID \(S=U_S\,\varLambda \,U_S^*\) of the symmetry and using the commutativity \(\textit{TS}=\textit{ST}\).
- (1):
-
We assume that, possibly after a reordering, the multiple eigenvalues in \(\varLambda \) occur contiguously on the main diagonal. Then \(\varLambda \) has the block diagonal form
$$\begin{aligned} \varLambda = \mathrm {diag}[\lambda _1I_1,\ldots ,\lambda _kI_k] \end{aligned}$$(8.80)where \(\lambda _i\) are the distinct eigenvalues of \(S\) and \(I_i\) are identity matrices of size given by the multiplicity of \(\lambda _i\).
- (2):
-
Since \(S\) commutes with \(T\), it follows \(U_S\varLambda U_S^*T= TU_S\varLambda U_S^*\) and \(\varLambda U_S^*TU_S= U_S^*TU_S\varLambda \), so that \(\varLambda \) commutes with \( V=U_S^*TU_S\).
- (3):
-
Partition the matrix \(V=[\,V_{ij}\,]\) according to the partition (8.80) of \(\varLambda \). Then, from \(\varLambda V=V\varLambda \) we get \(\lambda _iV_{ij}=\lambda _jV_{ij}\) and \(V_{ij}\) does not vanish only if \(i=j\). One concludes that \(V\) is block diagonal, \(V=\mathrm {diag}[V_1,\ldots ,V_k]\), with blocks \(V_i\) of the same order as \(I_i\) in (8.80).
- (4):
-
Since \(V\) is PSD, each block \(V_i\) is PSD. Then, we perform the EID of the blocks \(V_i=X_i\varSigma _i^2X_i^*\) and we get the diagonalization \(V=X\varSigma ^2 X^*\) with \(\varSigma ^2=\mathrm {diag}[\varSigma _1^2\ldots ,\varSigma _k^2]\) and \(X=\mathrm {diag}[X_1,\ldots ,X_k]\).
- (5):
-
By reversing the previous unitary transformations we get the diagonalization \( T=U_SVU_S^*=U_SX\varSigma ^2X^*U_S^* \) and, remembering that \(X_iX_i^*=I_i\), the simultaneous diagonalization \( S=U_S\varLambda U_S^*=U_SX\varLambda X^*U_S^*\;. \) Thus, we get (8.72) with \(U=U_S\,X\).
Note that \(SU_S=U_S\varLambda \) and \(U_S^*S=\varLambda U_S^*\) (see point 1). Then
$$ V=U_S^*TU_S=\sum _{k=0}^{m-1}U_S^*S^k\rho _0(S^*)^kU_S =\sum _{k=0}^{m-1}\varLambda ^kU_S^*\rho _0U_S\varLambda ^{-k}\;. $$Since \(V\) and \(\varLambda \) are block–diagonal
$$\begin{aligned} V_i=\sum _{k=0}^{m-1}\lambda _k^iI_i(U_S^*\rho _0U_S)_{ii} \lambda _k^{-i}I_i=(U_S^*\rho _0U_S)_{ii} \end{aligned}$$(8.81)and the block \(V_i\) coincides with the \(i\)th diagonal block of \(U_S^*\rho _0U_S\).
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Cariolaro, G. (2015). Quantum Communications Systems with Thermal Noise. In: Quantum Communications. Signals and Communication Technology. Springer, Cham. https://doi.org/10.1007/978-3-319-15600-2_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-15600-2_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-15599-9
Online ISBN: 978-3-319-15600-2
eBook Packages: EngineeringEngineering (R0)