Differential Cryptanalysis of SipHash

Abstract

SipHash is an ARX based message authentication code developed by Aumasson and Bernstein. SipHash was designed to be fast on short messages. Already, a lot of implementations and applications for SipHash exist, whereas the cryptanalysis of SipHash lacks behind. In this paper, we provide the first published third-party cryptanalysis of SipHash regarding differential cryptanalysis. We use existing automatic tools to find differential characteristics for SipHash. To improve the quality of the results, we propose several extensions for these tools to find differential characteristics. For instance, to get a good probability estimation for differential characteristics in SipHash, we generalize the concepts presented by Mouha et al. and Velichkov et al. to calculate the probability of ARX functions. Our results are a characteristic for SipHash-2-4 with a probability of $2^{-236.3}$ and a distinguisher for the Finalization of SipHash-2-4 with practical complexity. Even though our results do not pose any threat to the security of SipHash-2-4, they significantly improve the results of the designers and give new insights in the security of SipHash-2-4.

1 Introduction

A message authentication code (MAC) is a cryptographic primitive, which is used to ensure the integrity and the origin of messages. Normally, a MAC takes a secret key $K$ and a message $M$ as input and produces a fixed size tag $T$. A receiver of such a message-tag-pair verifies the authenticity of the message by simply recalculating the tag $T$ for the message and compare it with the received one. If the two tags are the same, the origin of the message and its integrity are ensured.

SipHash [1] was proposed by Aumasson and Bernstein due to the lack of MACs, which are fast on short inputs. Aumasson and Bernstein suggest two main fields of application for SipHash. The first application is as replacement for non-cryptographic hash functions used in hash-tables and the second application is to authenticate network traffic. The need for a fast MAC used in hash-tables arises from the existence of a denial-of-service attack called “hash flooding” [1]. This attack uses the fact, that is easy to find collisions for non-cryptographic hash functions. With the help of these collision producing inputs, an attacker is able to degenerate hash-tables to e.g. linked lists. Such a degeneration increases the time to perform operations like searching and inserting elements drastically and can lead to denial of service attacks.

So far, SipHash is already implemented in many applications. For example, SipHash is used as hash() in Python on all major platforms, in the dnschache instances of OpenDNS resolvers and in the hash-table implementation of Ruby. Besides these mentioned applications, other applications and dozens of third-party implementations of SipHash can be found on the SipHash website¹.

In this paper, we provide the first external security analysis regarding differential cryptanalysis. To find differential characteristics, we adapt techniques originally developed for the analysis of hash functions to SipHash. Using differential cryptanalysis to find collisions for hash functions has become very popular since the attacks on MD5 and SHA-1 by Wang et al. [15, 16]. As a result, a number of automated tools have been developed to aid cryptographers in their search for valid characteristics [6–8]. For hash functions, the probability of a characteristic does not play an important role since message modification can be used to improve the probability and create collisions. However, this is not possible for keyed primitives like MACs. Therefore, we have to modify existing search tools to take the probability of a characteristic into account. With the help of these modified tools, we are able to improve the quality of the results for SipHash.

In cryptographic primitives consisting solely out of modular additions, rotations and xors (like SipHash), only the modular addition might contribute to the probability of a differential characteristic, if xor differences are considered for representation. A method to calculate the exact differential probability of modular additions is presented by Mouha et al. [9]. In constructions like SipHash, modular additions, rotations and xors interact together. Hence, the characteristic uses many intermediate values of the single rounds and is therefore divided into many small sections. To get a more exact prediction of the probability for the characteristic, it would be nice to calculate the probability of subfunctions combining modular additions, rotations and xors. Therefore, we introduce the concept of cyclic S-functions. This concept is a generalization of the work done by Mouha et al. [9] and Velichkov et al. [13] for generalized conditions [3]. Although all the basic concepts needed to create cyclic S-functions are already included in the work of Velichkov et al. [13], we do not think that the generalization to generalized conditions is trivial, since we have not seen a single use of it. Cyclic S-functions will help analysts and designers of ARX based cryptographic primitives to provide closer bounds for the probability of differential characteristics.

With the help of the extended search strategies and the probability calculation, we are able to find the first published collision producing characteristics for SipHash-1-x and SipHash-2-x (see Table 1). The characteristic for SipHash-2-x is also the best known characteristic for SipHash-2-4. Moreover, we are able to present a distinguisher for the Finalization (4 SipRounds) of SipHash-2-4.

Table 1. Best found characteristics.

The paper starts with a description of SipHash in Sect. 2. The following Sect. 3 explains the basic concepts and strategies used by us to search for differential characteristics. Section 4 deals with improvements of automatic search techniques to find suitable characteristics for SipHash. Finally, the most significant differential characteristics for SipHash found by us are presented in Sect. 5. Further results on SipHash are given in Appendix A.

2 Description of SipHash

SipHash is a cryptographic MAC consisting solely of modular additions, rotations and xors (ARX). SipHash has an internal state size of 256 bits, uses a 128-bit key and produces a 64-bit tag. The process of authenticating a single message can be split into three stages: Initialization, Compression and Finalization.

• Initialization. The internal state $V$ of SipHash consists of the four 64-bit words $V_a$, $V_b$, $V_c$ and $V_d$. The initial value consists of the ASCII representation of the string “somepseudorandomlygeneratedbytes” and is written to the internal state first. Then, the 128-bit key $K=K_1\mathop {\Vert }K_0$ is xored to the state words $V_a\mathop {\Vert }V_b\mathop {\Vert }V_c\mathop {\Vert }V_d = V_a\mathop {\Vert }V_b\mathop {\Vert }V_c\mathop {\Vert }V_d \oplus K_0\mathop {\Vert }K_1\mathop {\Vert }K_0\mathop {\Vert }K_1$.

• Compression. The message $M$ is padded with as many zeros as needed to reach multiple block length minus 1 byte. Then, one byte, which encodes the length of the message modulo 256 is added to get a multiple of the block length. Afterwards, the message is split into $t$ 8-byte blocks $M_1$ to $M_{t}$. The blocks $M_i$ are in little-endian encoding. For each block $M_i$, starting with block $M_1$, the following is performed. The block $M_i$ is xored to $V_d$. After that the SipRound function is performed $c$ times on the internal state. Then the block $M_i$ is xored to $V_a$.

• Finalization. After all message blocks have been processed, the constant $\text {ff}_{16}$ is xored to $V_c$. Subsequently, $d$ iterations of SipRound are performed. Finally, $V_a \oplus V_b \oplus V_c \oplus V_d$ is used as the MAC value $h_K = \text {SipHash-c-d}(K,M)$.

As shown above, SipHash is parameterizable using $c$ SipRounds in the Compression and $d$ SipRounds in the Finalization. Such a specific instantiation of SipHash is called SipHash-c-d. Aumasson and Bernstein propose two specific versions for use, which are SipHash-2-4 and SipHash-4-8.

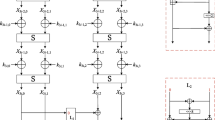
Next, we describe one SipRound. As SipHash is an ARX based MAC, the SipRound network shown in Fig. 1 consists only of modular additions, xors and rotations. Every operation is an operation on 64-bit.

Fig. 1.

One SipRound [1].

Now, we will discuss our naming scheme for the different variables involved in SipHash. In Fig. 1 one SipRound is shown. We will indicate a specific bit of a word by $V_{a,m,r}[i]$, where $i=\{0,...,63\}$ denotes the specific bit position of a word, $m$ denotes the message block index, and $r$ denotes the specific SipRound. Hence, to process the first message block, the input to the first SipRound is denoted by $V_{a,1,1}$, the intermediate variables by $A_{a,1,1}$, and the output by $V_{a,1,2}$. Words, which take part in the Finalization, are indicated with $m=f$.

3 Automatic Search for Differential Characteristics

For the search for differential characteristics, we have used an automatic search tool. To make use of such a tool, several key aspects have to be considered.

• The representation of the differential characteristic (Sect. 3.1).

• The description of the cryptographic primitive to perform propagation (Sect. 3.2).

• The used search strategy to search for characteristics (Sect. 3.3).

3.1 Generalized Conditions

We use generalized (one-bit) conditions introduced by De Cannière and Rechberger [3] to represent the differential characteristics within the automatic search tool. With the help of the 16 generalized conditions, we are able to express every possible condition on a pair of bits. For instance the generalized condition x denotes unequal values, - denotes equal values and ? denotes that every value for a pair of bits is possible.

In addition, we also use generalized two-bit conditions [6]. Using these conditions, every possible combination of a pair of two bits $\left| \varDelta x, \varDelta y \right|$ can be represented. In the most general form, these two bits can be any two bits of a characteristic. In our case, such two-bit conditions are used to describe differential information on carries, when computing the probability using cyclic S-functions.

3.2 Propagation of Conditions

Single conditions of a differential characteristic are connected via functions (additions, rotations, xors). Thus, the concrete value of a single condition affects other conditions. To be more precise, the information that certain values on a condition are allowed may lead to the effect, that certain values on other conditions are impossible. Therefore, we are able to remove impossible values on those conditions to refine their values. We can say that information propagates.

Within the automatic search tool, we do this propagation in a bitsliced manner like it is shown in [7]. This means, that we split the functions into single bitslices and brute force them by trying all possible combinations allowed by the generalized conditions. In this way, we are able to remove impossible combinations.

For the performance of the whole search for characteristics, it is crucial to find a suitable “size” of the subfunctions of a specific cryptographic primitive, which are used to perform propagation. The “size” of such a subfunction determines how many different conditions are involved during brute forcing a single bitslice. On one hand, “big” functions (many conditions involved in one bitslice) make the propagation slower. On the other hand, the amount of information that propagates is usually enhanced by using a few “big” subfunctions instead of many “small” ones. Generalized conditions are not able to represent every information that is gathered during propagation(mainly due to effects regarding the carry of the modular addition) [6]. So we loose information between single subfunctions. Usually, less information is lost if the subfunctions are “bigger”. In fact, finding a good trade-off between speed and quality of propagation is not trivial.

3.3 Basic Search Strategy

For analyzing unkeyed primitives, especially when trying to find collisions for hash functions, the following search method, as used by Mendel et al. [7] has turned out to be a viable strategy.

• Find a good starting point for the search.

• Search for a good characteristic.

• Use message modification to find a colliding message pair.

The starting point describes the target problem to be solved and a good starting point can greatly reduce the complexity of a search. In the start characteristic, bits where no differences are allowed are represented by the condition - and bits where the characteristic may contain differences are represented by ?.

The search algorithm refines the conditions represented by a ? to - and x to get a valid differential characteristic in the end. An example of a search strategy can be found in [7]. Here, the search algorithm is split in three main parts:

• Decision (Guessing). In the guessing phase, a bit is selected, which condition is refined. This bit can be selected randomly or according to a heuristic.

• Deduction (Propagation). In this stage, the effects of the previous guess on other conditions is determined (see Sect. 3.2).

• Backtracking (Correction). If a contradiction is determined during the deduction stage the contradiction is tried to be resolved in this stage. A way to do this is to jump back to earlier stages of the search until the contradiction can be resolved.

There exist several message modification techniques [5, 12, 14]. The one used by us (in Appendix A) is refining a valid characteristic further until the colliding message pair is fixed [7]. For keyed primitives like SipHash, message modification to enhance the probability is usually out of reach, since the key is unknown. Hence, we need to stop the search at the characteristic and need an adapted search algorithm to find characteristics, which have a high probability.

4 Improvements in the Automatic Search for SipHash

We have used existing automatic search tools to analyze SipHash. Those tools use the search strategy describe in Sect. 3.3. This strategy has been developed to find collisions for hash functions. It turns out that this strategy is unsuitable for keyed primitives like MACs. Therefore, we extend the search strategy to the greedy strategy described in Sect. 4.1. This greedy strategy uses information on the probability of characteristics, or on the impact of one guess during the search for characteristics. We have created all the results of Sect. 5 with the help of this greedy strategy. To get closer bounds on the probability of the characteristic, we generalize the concepts presented by Mouha et al. [9] and Velichkov et al. [13] to cyclic S-functions (Sect. 4.2).

Another important point in the automatic search for differential characteristics is the representation of the cryptographic primitives within the search tool. We have evaluated dozens of different descriptions and present the most suitable in Sect. 4.3.

4.1 Extended Search Strategy

Our search strategy extends the strategy used in [7]. The search algorithm of Sect. 3.3 is split in three main parts decision (guessing), deduction (propagation), and backtracking (correction). We have extended this strategy to perform greedy searches using quality criteria like the probability. In short, we perform the guessing and propagation phase several times on the same characteristic. After that, we evaluate the resulting characteristics and take the characteristic with the best probability. Then, the next iteration of the search starts. The upcoming algorithm describes the search in more detail:

Let $U$ be a set of bits with condition ? in the current characteristic $A$. In $H$ we store all characteristics, which have been visited during the search. $L$ is a set of candidate characteristics for $A$. $n$ is the number of guesses. $B_\mathtt{- }$ and $B_\mathtt{x }$ are characteristics.

Preparation

• 1. Generate $U$ from $A$. Clear $L$. Set $i$ to 0.

Decision (Guessing)

• 2. Pick a bit from $U$.

• 3. Restrict this bit in $A$ to - to get $B_\mathtt{- }$ and to x to get $B_\mathtt{x }$.

Deduction (Propagation)

• 4. Perform propagation on $B_\mathtt{- }$ and $B_\mathtt{x }$.

• 5. If $B_\mathtt{- }$ and $B_\mathtt{x }$ are inconsistent, mark bit as critical and go to Step 13, else continue.

• 6. If $B_\mathtt{- }$ is not inconsistent and not in $H$, add it to $L$. Do the same for $B_\mathtt{x }$.

• 7. Increment $i$.

• 8. If $i$ equals $n$, continue with Evaluation. Else go to Step 2.

Evaluation

• 9. Set $A$ to the characteristic with the highest probability in $L$.

• 10. Add $A$ to $H$.

• 11. If there are no ? in $A$, output $A$. Then set $A$ to a characteristic of $H$.

• 12. Continue with Step 1.

Backtracking (Correction)

• 13. Jump back until the critical bit can be resolved.

• 14. Continue with Step 1.

To generate the set $U$, we use the following variables of SipHash $A_a$, $A_c$, $V_a$, and $V_c$. Except for $V_{a,m,1}$, $V_{c,m,1}$, $V_{a,f,1}$, and $V_{c,f,1}$, since they are only connected via an xor to their predecessors, or are even the same variable. We guess solely on those variables, since a guess on them always affects the probability of the differential characteristic. Experiments have shown that setting the number of guesses $n$ to $25$ leads to the best results.

Due to performance reasons, we store hash values of characteristics in $H$. In addition, we maintain a second list $H^*$. In this list, we store the next best characteristics of $L$ according to a certain heuristic. The characteristics of $H^*$ are also used for backtracking. If a characteristic is found and $U$ is empty, we take a characteristic out of $H^*$ instead of $H$ in Step 11. After a while, we perform a soft restart, where everything is set to the initial values (also $H^*$ is cleared) except for $H$.

This search strategy turns out to be good if we search for high probability characteristics, which do not lead to collisions. When searching for colliding characteristics, we have to adapt the given algorithm and perform a best impact strategy similar to Eichlseder et al. [4].

The best impact strategy differs in the following points from the strategy described above. In the best impact strategy, we do not calculate the characteristic $B_\mathtt{x }$. Instead of taking the probability of $B_\mathtt{- }$ as a quality criterion for the selection, we use the variant of $B_\mathtt{- }$ of the candidate list $L$, where the most information propagates. As a figure of merit for the amount of information that propagates, we take the number of conditions with value ?, which have changed their value due to the propagation.

This best impact strategy has several advantages. The first one lies in the fact that mostly guesses will be made, which have a big impact on the characteristic. This ensures that no guesses are made, where nothing propagates. Such guesses often imply additional restrictions on the characteristic, which are not necessary. In addition, the big impact criterion also leads to rather sparse characteristics, which usually have a better probability than dense ones.

4.2 Calculating the Probability Using Cyclic S-Functions

In this section, we show a method to extend the use of S-functions [9] by introducing state mapping functions $m_i$ and making the relationship between the states cyclic. For instance such cyclic states occur if rotations work together with modular additions. Velichkov et al. showed in [13] how to calculate the additive differential probability of ARX based functions. The method of cyclic S-functions is closely related to the methods shown in [13].

Concept of Cyclic S-Functions. According to Mouha et al. [9], a state function (S-function) is a function, where the output $s[i]$ can be computed using only the input bits $a_1[i]$, $a_2[i]$,... $a_k[i]$ and the finite state $S[i-1]$. This computation also leads to a next state $S[i]$. An example of such an S-function is the modular addition $a + b = s$. In ARX systems, we can discover the same behavior as for additions, except that the first state $S[0]$ depends on the outcome of the last operation and is therefore related to $S[n]$. We picture this relation by introducing so called state mapping functions $m_i$ and making the state cyclic as it is shown in Fig. 2. The state mapping function $m_i$ is a function, which maps distinct state values of $S_o[i]$ to $S_i[i]$. It is possible and often the case that more values of $S_o[i]$ map to the same value of $S_i[i]$. If $m_i$ is the identity function, then the states $S_o[i]$ and $S_i[i]$ are the same state and we only write $S[i]$ in this case.

Fig. 2.

Concept of cyclic S-functions.

Note that every classic S-function can be transformed into a cyclic S-function by defining every $m_i$ as the identity function except for $m_n$. The function $m_n$ maps every value of $S_o[n]$ to the state $S_i[0] = 0$.

To give an example, we describe the function $((a+b)\lll 1) + c =s_b$ with the help of S-functions. In this example, we use 4-bit words. We picture the system as it is shown in Fig. 3. The carry $c_a$ and $c_b$ serve as state $S$ together. They can be considered as a two-bit condition $|c_a, c_b|$. The black vertical lines in Fig. 3 mark transitions, where the state mapping function $m_i$ is not the identity function. As $c_a[0]$ and $c_b[0]$ can only be 0, the state mapping functions perform the following mapping for any value $v_a$ of $c_a$ and $v_b$ of $c_b$:

• $S_o[1] \Rightarrow S_i[1]: \left| v_a, v_b\right| \Rightarrow \left| 0, v_b\right|$

• $S_o[4] \Rightarrow S_i[0]: \left| v_a, v_b\right| \Rightarrow \left| v_a, 0\right|$.

So the states in case of the system in Fig. 3 are:

Fig. 3.

Rewritten system to do $((a+b)\lll 1) + c =s_b$ in one step.

For a word length of $n$ and a general rotation to the left by $r$, the state is $S[i] = \left| c_a[(i-r)\mod n], c_b[i]\right|$, except for states, where $m_i$ is not the identity function. These are the states $S_o[r] = \left| c_a[n], c_b[r]\right|$, $S_i[r] = \left| c_a[0], c_b[r]\right|$, $S_o[n] = \left| c_a[n-r], c_b[n]\right|$ and $S_i[0] = \left| c_a[n-r], c_b[0]\right|$. The realization of additions with multiple rotations in between leads to more mapping functions $m_i$, which are not the identity function. Using additions with more inputs leads to bigger carries and bigger states.

Using Graphs for Description. Similar to S-functions [9], we can build a graph representing the respective cyclic S-function. The vertices in the graph stand for the single distinct states and the circles in the graph represent valid solutions. Such a graph can be used to either propagate conditions, or to calculate the differential probability. An illustrative example for propagation and the probability calculation can be found in Appendix B.

The whole cyclic graph consists of subgraphs $i$. Each subgraph $i$ consists of vertices representing $S_i[i-1]$, and $S_o[i]$ and single edges connecting them. So each subgraph represents a single bitslice of the whole function. For the system in Fig. 3, the edges of each subgraph are calculated by trying every possible pair of input bits for $a[((i-r-1)\mod n) + 1]$, $b[((i-r-1)\mod n) + 1]$ and $c[i]$, which is given by their generalized conditions and using every possible carry of the set of $S_i[i-1]$ to get an output $s_b[i]$ and a carry which belongs to $S_o[i]$. If the output is valid (with respect to the generalized conditions, which describe the possible values for $s_b$), an edge can be drawn from the respective value of the input vertex of $S_i[i-1]$ to the output vertex belonging to $S_o[i]$. Such a subgraph can be created for every bitslice.

Now, we have to form a graph out of these subgraphs. Subgraphs connected over a state mapping function $m_i$, which is the identity, stay the same. There exist two ways for connecting subgraphs $i$ and $i+1$, which are separated by a state mapping function. Either the edges of graph $i$ can be redrawn, so that they follow the mapping from $S_o[i]$ to $S_i[i]$, or the edges of graph $i+1$ can be redrawn so that they follow the inverse mapping from $S_i[i]$ to $S_o[i]$. We call the so gathered set of subgraphs “transformed subgraphs”. After all subgraphs are connected, we can read out the valid input output combinations. These combinations are minimal circles in the directed graph. Since we are aware of the size of the minimal circles and of the shape of the graph, we can transform the search for those circle in a search for paths.

Probability Calculation Using Matrix Multiplication. To calculate the differential probability, we only need to divide the number of valid minimal circles of the graph by the number of total possible combinations of the input. The number of valid minimal circles can be calculated with the help of matrix multiplications. Similar to S-functions [9], we have to calculate the biadjacency matrix $A[i] = [x_{kj}]$ for each “transformed subgraph”. $x_{kj}$ stands for the number of edges, which connect vertex $j$ of the group $S_i[i-1]$ with vertex $k$ of the group $S_i[i]$. We define the $1 \times N$ matrices $L_i$ and the $N \times 1$ matrices $C_i$.

Here, $N$ is the number of distinct states of $S[i]$. As $S_i[n]$ (this is $S_o[n]$ after applying the mapping) and $S_i[0]$ are in fact the same states, we can calculate the number of circles by summing up all paths which lead from a vertex in $S_i[0]$ to the same vertex in $S_i[n]$:

$$\begin{aligned} \#Circles = \sum ^{n}_{i = 1}\left( L_i \cdot A[n] \cdot \cdot \cdot A[2] \cdot A[1] \cdot C_i\right) \end{aligned}$$

(1)

The formula shown above basically sums the numbers in the diagonal of the resulting matrix when all $A[i]$ are multiplied together. This sum divided by all possible input combinations gives us the exact differential probability of one step.

We consider the presented method based on cyclic S-functions to be equivalent to brute force and therefore to be optimal. The equivalence is only given if the words of the input and the output are independent of each other. For example, if the same input is used twice in the same function $f$, we do not have the required independence. Such a case is the calculation of $s = a + (a\lll 10)$.

Probability Calculation of SipHash. To calculate the probability of SipHash we group two subsequent additions together, considering also the intermediate outputs. In contrast to the propagation (Sect. 4.3), we do not do this overlapping, since we would calculate the probability twice. So we get two subfunctions per SipRound to calculate the probability (2). In the case of SipHash, we also consider the intermediate values of the additions, but they are omitted in the formulas.

$$\begin{aligned} \begin{aligned} V_{a,m,r+1}&= ((V_{a,m,r} + V_{b,m,r}) \lll 32) + A_{d,m,r} \\ V_{c,m,r+1}&= (V_{c,m,r} + V_{d,m,r} + A_{b,m,r}) \lll 32 \end{aligned} \end{aligned}$$

(2)

In addition, we also consider the differential probability introduced by xors. Since we use generalized conditions, xors might contribute to the probability as well. To calculate the differential probability connected with xors, a simple bitsliced approach is used.

4.3 Bitsliced Description of SipHash

For SipHash, we have evaluated dozens of different descriptions. Because of several searches and other evaluations, we have chosen the following description. We combine every two subsequent two input modular additions to one subfunction, regardless if they are separated by a rotation. The resulting subfunctions overlap each other. This means, that every two input addition as shown in Fig. 1 takes part in two subfunctions. This results in the following subfunctions (the intermediate output is also considered, but not given in the formulas):

$$\begin{aligned} V_{a,m,r+1}&= ((V_{a,m,r} + V_{b,m,r}) \lll 32) + A_{d,m,r} \\ V_{c,m,r+1}&= (V_{c,m,r} + V_{d,m,r} + A_{b,m,r}) \lll 32 \\ A_{a,m,r+1}&= (A_{a,m,r} \lll 32) + A_{d,m,r} + V_{b,m,r+1}\\ A_{c,m,r+1}&= ((A_{c,m,r} + A_{b,m,r}) \lll 32) + V_{d,m,r+1} \end{aligned}$$

The xor operations are represented using only three variables (two inputs). We do this, since there is no information loss due to the representation capability of the generalized conditions.

5 Results

In this section, we give some results using the presented search strategies and the new probability calculation. At first, we start with characteristics, which lead to internal collisions. This type of characteristic can be used to create forgeries as described in [10, 11]. To improve this attack, characteristics are needed, which have a probability higher than $2^{-128}$ (in the case of SipHash). Otherwise, a birthday attack should be preferred to find collisions. We are able to present characteristics that lead to an internal collision for SipHash-1-x ($2^{-167}$) and SipHash-2-x ($2^{-236.3}$). The characteristic for SipHash-2-x is also the best published characteristic for full SipHash-2-4.

The last part of this section deals with a characteristic for the Finalization of SipHash-2-4. This characteristic has a considerable high probability of $2^{-35}$. Due to this high probability, this characteristic can be used as a distinguisher for the Finalization.

5.1 Colliding Characteristics for SipHash-1-x and SipHash-2-x

First, we want to start with an internal collision producing characteristic for SipHash-1-x. We have achieved the best result with the biggest impact strategy by using a starting point consisting of 7 message blocks. The bits of the first message block, the key, and the last state values are set to -. The rest of the characteristic is set to ?. We introduce one difference in a random way by picking a bit out of all $A_a$, $A_c$, $V_a$, and $V_c$. This strategy results in a characteristic with an estimated probability of $2^{-169}$. The characteristic leads to an internal collision within 3 message blocks.

In the second stage of the search, we fix the values of the 3 message blocks to the values found before and set the internal state variables to ?. By using the so gotten starting point, we perform a high probability greedy search. This high probability greedy search results in the characteristic given in Table 2. This characteristic has an estimated probability of $2^{-167}$.

Table 2. Characteristic for SipHash-1-x, which leads to an internal collision (probability $2^{-167}$).

Next, we handle the search for a characteristic, which results in an internal collision for SipHash-2-x. The collision with the best probability has been found by setting only the bits of one Compression iteration (including the corresponding message block) to ? and everything else to -. The difference is introduced in the most significant bit of the message block. The best characteristic we have found using this starting point and the best impact strategy has an estimated probability of $2^{-238.9}$. In a second stage, we use the value for the message block of this found characteristic to perform a high probability greedy search. With this method, we are able to get the characteristic of Table 3. This characteristic has an estimated probability of $2^{-236.3}$.

Table 3. Characteristic for SipHash-2-x, which leads to an internal collision (probability of $2^{-236.3}$). This is also the best characteristic for SipHash-2-4.

Although both characteristics do not have a probability higher than $2^{-128}$, they are the best collision producing characteristics published for SipHash so far. Especially the characteristic for SipHash-1-x (Table 2) is not far away from the bound of $2^{-128}$, where it gets useful in an attack. Moreover, the characteristic for SipHash-2-x (Table 3) is the best published characteristic for full SipHash-2-4, with a probability of $2^{-236.3}$. The previous best published characteristic for SipHash-2-4 has a probability of $2^{-498}$ [1]. Nevertheless, SipHash-2-4 still has a huge security margin.

5.2 Characteristic for Finalization of SipHash-2-4

Now, we want to present a distinguisher for the full four SipRound Finalization of SipHash-2-4. For this result, we have used the greedy search algorithm presented in Sect. 4 considering solely the probability. With the help of this algorithm, we have found the distinguisher shown in Table 4. By using this characteristic, four rounds of the Finalization can be distinguished from a pseudo-random function with a complexity of $2^{35}$.

Table 4. Distinguisher for 4 finalization rounds (probability $2^{-35}$).

Considering this new result, we are able to distinguish both building blocks of SipHash-2-4, the Compression and the Finalization from idealized versions (It is already shown in [1] that two rounds of the Compression are distinguishable). However, these two results do not endanger the full SipHash-2-4 function, which is still indistinguishable from a pseudo-random function.

6 Conclusion

This work deals with the differential cryptanalysis of SipHash. To be able to find good results, we had to introduce new search strategies. Those search strategies extend previously published strategies, which have solely been used in the search for collisions for hash functions. With the new presented concepts, also attacks on other primitives like MACs, block-ciphers and stream-ciphers are within reach.

Furthermore, we generalized the concept of S-functions to the concept of cyclic S-functions. With the help of cyclic S-functions, cryptanalysts will be able to get more exact results regarding the probability of differential characteristics for ARX based primitives.

With these new methods, we were able to improve upon the existing results on SipHash. Our results include the first published characteristics resulting in internal collisions, the first published distinguisher for the Finalization of SipHash and the best published characteristic for full SipHash-2-4.

Future work includes to apply the greedy search strategies to other ARX based primitives. Such cryptographic primitives may be for instance block ciphers or authenticated encryption schemes. Also, the further improvement of the used automatic search tools is part of future work.

Appendices

A Results Without Secret Key

In this section, we present results for SipHash without considering the secret key. This allows us to create semi-free-start collisions for the Compression as well as an internal collision using chosen related keys. Despite the fact that these attacks do not lie within the specified use of SipHash, the following results give at least some insight in the strength of the MAC. In addition, the existence of the semi-free-start collisions are a strong indicator that the characteristics given in Tables 2 and 3 are valid and that the estimated probability is at least somewhat realistic.

With the help of the characteristic of Table 2, we can produce a semi-free-start collision. Furthermore, we are able to fix the value of $V_{a,i,1}$ and $V_{b,i,1}$ to 0 in advance of the search. The values for the semi-free-start collision are given in Table 5. The message pair can be created out of the characteristic in seconds. However, we cannot state a time it takes to create the characteristic, since the best characteristic out of many searches has been selected.

Table 5. Message pair and state values for semi-free-start collision for SipHash-1-x using three message blocks.

The same can be done for SipHash-2-x by using the characteristic of Table 3. Here, we are able to produce the semi-free-start collision for SipHash-2-x shown in Table 6 within 10 s. Due to the rather low probability of $2^{-236.3}$ of the characteristic given in Table 3, we are not able to fix any values in advance of a search for a semi-free-start collision.

Table 6. Message pair and state values for semi-free-start collision for SipHash-2-x using one message block.

Table 7. Message pair, key, state values after internal collision, and MAC value (SipHash-2-4) for internal collision of SipHash-2-x using chosen related keys and a fixed IV.

Now, we want to present internal collision using chosen related keys for SipHash-2-4. For the creation of the best found characteristic for a Compression consisting of 2 SipRounds per iteration, we use a starting point, where we place the difference in the most significant bit of the first message. The rest of the message, as well as the key can be chosen completely free. The best characteristic we have found by using the impact oriented strategy has an estimated probability of $2^{-169}$. By using this characteristic, we are able to create the pairs in Table 7. To be easier to verify, we have included the MAC value for SipHash-2-4. In addition, we give the state after the collision happens in the first message block. Again, we cannot state the time it takes to create the characteristic, because it is the best characteristic out of many searches. The collision producing message and key pair can be created within seconds out of the characteristic.

B An Example for Cyclic S-Functions

In this section, we want to clarify the use of cyclic S-functions with the help of an example. We use $((a+b)\lll 1) + c =s_b$ (Fig. 3) as cyclic S-function. Throughout this example, we use the following values for inputs and outputs.

$$\begin{aligned} a = \mathtt{1x11 } \quad b = \mathtt{AEn5 } \quad c = \mathtt{15nx } \quad s_{b} = \mathtt{11Ax } \end{aligned}$$

(3)

Before we start an explanation how to calculate the probability, we first show how the propagation is done by using the graph shown in Fig. 4. To represent the graph in Fig. 4 clearly, we use information, which can be gathered using a bitslice propagation to narrow the value for the carries and therefore decrease the amount of edges and vertices in the graph. This precomputation is only done to produce a graph with few edges. The concept also works if this bitslice precomputation is omitted.

Now, we want to describe the concept of propagation by looking at first at the state mapping. Performing a state mapping function for doing addition with rotations in between is in principle merging a set of vertices together. After this merging, some edges, which have led to separated vertices, may lead to the same vertex. In case of the example in Fig. 4 this means that the vertices $\left| u,n\right|$ and $\left| 1,n\right|$ of $S_o[1]$ are mapped both on vertex $\left| 0, n\right|$ of $S_i[1]$. Vertex $\left| 1,0\right|$ of $S_o[1]$ is mapped on vertex $\left| 0,0\right|$ of $S_i[1]$. The vertex $\left| u, n\right|$ of $S_o[4]$ is mapped on vertex $\left| u, 0\right|$ of $S_i[0]$, vertex $\left| 1, 0\right|$ of $S_o[4]$ is mapped on vertex $\left| 1, 0\right|$ of $S_i[0]$ and vertex $\left| n, n\right|$ of $S_o[4]$ is mapped on vertex $\left| n, 0\right|$ of $S_i[0]$. The vertices of $S_i[0]$ and $S_o[4]$ are in fact the same. Therefore, we can reduce the problem of finding circles to the problem of finding paths from a vertex $\left| v, 0\right|$ of state $S_i[0]$ to the in fact same vertex $\left| v, 0\right|$ of state $S_i[4]$ (this is $S_o[4]$ after applying the mapping), where $v$ stands for any value of a state. Edges, which do not belong to a path can be deleted. These are the dashed edges in Fig. 4. So we get following values after propagation:

$$\begin{aligned} a = \mathtt{1u11 } \quad b = \mathtt{AAn5 } \quad c = \mathtt{15nn } \quad s_{b} = \mathtt{11Au } \end{aligned}$$

(4)

Note that that this result is optimal with respect to the limited representation capability of generalized conditions (The graph of Fig. 4 shows that in fact only two valid solutions exist).

Fig. 4.

Graph for $((a+b)\lll 1) + c =s_b$. States of the same color can be considered as equivalent (except for the black ones). The values on the edges represent $a[i]$, $b[i]$, $c[i]$ and $s_b[i]$.

Now we show, how the probability calculation is done. Because of space constraints, we only give the biadjacency matrix $A[1]$ (5) out of the set of transformed subgraphs. The matrix $A[1]$ corresponds to the rightmost subgraph shown in Fig. 4.

(5)

After doing matrix multiplication and adding the elements of the diagonal together, we get two valid circles in the graph (1). This result can also be verified by looking at the graph of Fig. 4. The number of valid solutions divided by all possible input combinations gives us the exact differential probability of this subfunction. Here, we have to distinguish if we consider the input values given before (3) or after propagation (4). In the case of (3), we have $96$ possible input pairs resulting in a probability of $2^{-5.58}$. For (4), we only have $16$ possible input pairs and get a probability of $2^{-3}$. Both results are exact.