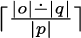Skip to main content
SpringerLink
Log in

Certification of Nontermination Proofs Using Strategies and Nonlooping Derivations

  • Conference paper
  • First Online:
Verified Software: Theories, Tools and Experiments (VSTTE 2014)

Part of the book series: Lecture Notes in Computer Science ((LNPSE,volume 8471))

Abstract

The development of sophisticated termination criteria for term rewrite systems has led to powerful and complex tools that produce (non)termination proofs automatically. While many techniques to establish termination have already been formalized—thereby allowing to certify such proofs—this is not the case for nontermination. In particular, the proof checker  was so far limited to (innermost) loops. In this paper we present an Isabelle/HOL formalization of an extended repertoire of nontermination techniques. First, we formalized techniques for nonlooping nontermination. Second, the available strategies include (an extended version of) forbidden patterns, which cover in particular outermost and context-sensitive rewriting. Finally, a mechanism to support partial nontermination proofs further extends the applicability of our proof checker.

This research was supported by the Austrian Science Fund (FWF): P22767 and I963.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    In the literature (e.g., in [7]) a nonterminating DP problem is also called infinite. This is the reason why in  this property is defined as infinite-dpp.

  2. 2.

    More precisely, \(n_0\) can be set to \(0\) if \(p=\varepsilon \) and to

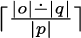
    figure b

    otherwise.

  3. 3.

    Rules (i)–(iv) in [22, Definition 5], which are omitted here for brevity.

References

  1. Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theoret. Comput. Sci. 236, 133–178 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  2. Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)

    Google Scholar 

  3. Blanqui, F., Koprowski, A.: \({\sf CoLoR}\): a \({\sf Coq}\) library on well-founded rewrite relations and its application to the automated verification of termination certificates. Math. Struct. Comput. Sci. 4, 827–859 (2011)

    Article  MathSciNet  Google Scholar 

  4. Contejean, E., Courtieu, P., Forest, J., Pons, O., Urbain, X.: Automated certified proofs with \({\sf CiME3}\). In: Proceedings of the RTA ’11. LIPIcs, vol. 10, pp. 21–30 (2011)

    Google Scholar 

  5. Emmes, F., Enger, T., Giesl, J.: Proving non-looping non-termination automatically. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS(LNAI), vol. 7364, pp. 225–240. Springer, Heidelberg (2012)

    Chapter  Google Scholar 

  6. Giesl, J., Schneider-Kamp, P., Thiemann, R.: \({\sf AProVE 1.2}\): automatic termination proofs in the dependency pair framework. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 281–286. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  7. Giesl, J., Thiemann, R., Schneider-Kamp, P., Falke, S.: Mechanizing and improving dependency pairs. J. Autom. Reason. 37(3), 155–203 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  8. Gramlich, B.: Abstract relations between restricted termination and confluence properties of rewrite systems. Fund. Inform. 24, 3–23 (1995)

    MathSciNet  MATH  Google Scholar 

  9. Gramlich, B., Schernhammer, F.: Extending context-sensitivity in term rewriting. In: Proceedings of the WRS ’09. EPTCS, vol. 15, pp. 56–68 (2010)

    Google Scholar 

  10. Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) FLOPS 2010. LNCS, vol. 6009, pp. 103–117. Springer, Heidelberg (2010)

    Chapter  Google Scholar 

  11. Huffman, B., Kunčar, O.: Lifting and transfer: a modular design for quotients in Isabelle/HOL. In: Gonthier, G., Norrish, M. (eds.) CPP 2013. LNCS, vol. 8307, pp. 131–146. Springer, Heidelberg (2013)

    Chapter  Google Scholar 

  12. Korp, M., Sternagel, C., Zankl, H., Middeldorp, A.: Tyrolean termination tool 2. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 295–304. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  13. Krauss, A.: Partial and nested recursive function definitions in higher-order logic. J. Autom. Reason. 44(4), 303–336 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  14. Krauss, A.: Recursive definitions of monadic functions. In: Proceedings of the PAR ’10. EPTCS, vol. 43, pp. 1–13 (2010)

    Google Scholar 

  15. Lucas, S.: Context-sensitive computations in functional and functional logic programs. J. Funct. Logic Program. 1, 1–61 (1998)

    Google Scholar 

  16. Nipkow, T., Paulson, L.C., Wenzel, M. (eds.): Isabelle/HOL. LNCS, vol. 2283. Springer, Heidelberg (2002)

    MATH  Google Scholar 

  17. Oppelt, M.: Automatische Erkennung von Ableitungsmustern in nichtterminierenden Wortersetzungssystemen. Diploma thesis, HTWK Leipzik, Germany (2008)

    Google Scholar 

  18. Sternagel, C., Thiemann, R.: Formalizing Knuth-Bendix orders and Knuth-Bendix completion. In: Proceedings of the RTA ’13. LIPIcs, vol. 21, pp. 287–302 (2013)

    Google Scholar 

  19. Thiemann, R.: Mutually recursive partial functions. Arch. Formal Proofs, February 2014. Formal Proof Development. http://afp.sf.net/entries/Partial_Function_MR.shtml

  20. Thiemann, R., Giesl, J., Schneider-Kamp, P.: Deciding innermost loops. In: Voronkov, A. (ed.) RTA 2008. LNCS, vol. 5117, pp. 366–380. Springer, Heidelberg (2008)

    Chapter  Google Scholar 

  21. Thiemann, R., Sternagel, C.: Certification of termination proofs using \({\sf CeTA}\). In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 452–468. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  22. Thiemann, R., Sternagel, C.: Loops under strategies. In: Treinen, R. (ed.) RTA 2009. LNCS, vol. 5595, pp. 17–31. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  23. Sternagel, C., Thiemann, R.: Certification of nontermination proofs. In: Beringer, L., Felty, A. (eds.) ITP 2012. LNCS, vol. 7406, pp. 266–282. Springer, Heidelberg (2012)

    Chapter  Google Scholar 

  24. Thiemann, R., Sternagel, C., Giesl, J., Schneider-Kamp, P.: Loops under strategies ... continued. In: Proceedings of the IWS ’10, vol. 44, pp. 51–65 (2010)

    Google Scholar 

Download references

Acknowledgments

The authors are listed in alphabetical order regardless of individual contributions or seniority.

Author information

Authors and Affiliations

  1. Institute of Computer Science, University of Innsbruck, Innsbruck, Austria

    Julian Nagele, René Thiemann & Sarah Winkler

Authors
  1. Julian Nagele
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. René Thiemann
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sarah Winkler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to René Thiemann .

Editor information

Editors and Affiliations

  1. NASA Ames Research Center, Mountain View, USA

    Dimitra Giannakopoulou

  2. University of Oxford, Oxford, United Kingdom

    Daniel Kroening

Rights and permissions

Reprints and permissions

Copyright information

© 2014 Springer International Publishing Switzerland

About this paper

Cite this paper

Nagele, J., Thiemann, R., Winkler, S. (2014). Certification of Nontermination Proofs Using Strategies and Nonlooping Derivations. In: Giannakopoulou, D., Kroening, D. (eds) Verified Software: Theories, Tools and Experiments. VSTTE 2014. Lecture Notes in Computer Science(), vol 8471. Springer, Cham. https://doi.org/10.1007/978-3-319-12154-3_14

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-12154-3_14

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-12153-6

  • Online ISBN: 978-3-319-12154-3

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation