Abstract
The purpose of this note is to show that the normalization theorem can be proved for first order Peano arithmetic by adapting to natural deduction the method used in Gentzen’s second consistency proof. Gentzen explained the intuitive idea behind his proof by informally arguing for the possibility of a normalization theorem of natural deduction, but what he actually proved was a special case of the Hauptsatz for a sequent calculus formalization of arithmetic. To transfer Gentzen’s method to natural deduction, I shall assign his ordinals to notations for natural deductions that use an explicit operation of substitution. The idea is first worked out for predicate logic. The main problems reside there and consist in finding a normalization strategy that harmonizes with the ordinal assignment. The result for predicate logic is then extended to arithmetic without effort, and thereby full normalization of natural deductions in first order arithmetic is achieved.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
- 2.
- 3.
- 4.
It has recently been revealed that Gentzen was not only aware of the possibility of such a theorem, but that, in an early draft of his dissertation (found in Bernays’ archive, see [27]), he also stated and proved the theorem for intuitionistic logic, essentially in the way it was later proved (Prawitz [20]—the independent proof by Raggio [21] is a little different).
- 5.
- 6.
- 7.
This presumption is supported by what has been found in Gentzen’s Nachlass by Jan von Plato. It turns out that at an early stage of the work on his dissertation, Gentzen had expected to obtain the consistency of arithmetic directly from a normalization theorem for natural deduction. When that failed, he restricted his dissertation essentially to predicate logic, and then proved the consistency of arithmetic along other lines. But it is clear that he did not abandon his original idea. A witness to this is even found in his plans for a book on the foundations of mathematics. In a notebook concerned with these plans, he writes: “to assimilate the proof of the hillock theorem to the proof of consistency” (translation by von Plato); “the hillock theorem” is here Gentzen’s name for the normalization theorem of natural deduction (“der Hügelsatz” in German—but in other contexts often “der Gipfelsatz”).
- 8.
If we choose ⊥ , &, ⊃ , and ∀ as logical constants, the normalization theorem for classical logic even takes a simpler form than for intuitionistic logic [20].
- 9.
This question has been raised by several people, but has remained unanswered. Recently, Kanckos [10, 11] showed that a closed natural deduction of ⊥ in a system for Heyting arithmetic would reduce to normal form by using vectors from Howard [8], instead of Gentzen’s ordinal assignment. For my own part, I outlined an approach to a positive answer in lectures at Stockholm University 1979, a conference at Oxford 1980, and one at Siena 1984, and, in more detail, in (professor Ettore Casari’s Saturday) seminars at Università degli Studi di Firenze 1991. The approach was not brought to a conclusion at these times, but agreed with the present solution in being built on the idea of adding an operation of explicit substitution.
- 10.
Von Plato [28] has also drawn attention to the key position of this operation (under the name composition) when comparing natural deductions and sequent calculus derivations.
- 11.
After finishing this paper, I have found that Gentzen planned to organize the book mentioned in footnote 7 in the same way, first treating predicate logic using a finite version of his ordinal assignment and then extending the result to arithmetic using transfinite ordinals.
- 12.
Examples of such systems, essentially like classical sequent calculi, are found in, for instance, Schütte [25] and Tait [26]. The latter considers not only inference rules with infinitely many premisses but also infinitely long sentences. Martin-Löf [14] develops an intuitionistic system of natural deduction of that kind.
- 13.
An alternative is to enrich the infinitary system with information allowing one to extract a finitary normal derivation from the normalized infinitary one, as was first outlined by Mints [15]. This general idea has later been worked out in more detail and in different ways by Buchholz [3] and Mints [18]. Another alternative is presented by Mints [16], who defines other reductions and another ordinal assignment.
- 14.
The better known bound is credited to Schütte [25], who noted that the analogue to the fact stated in Sect. 2.2.1 holds for his infinitary system mentioned in footnote 12; the length n is then in general a transfinite ordinal. The statement in Sect. 2.2.1 was proved for Gentzen’s intuitionistic system of natural deduction by Pereira [19]. Cellucci [4] establishes several results concerning how the length of natural deduction increases by normalization, including negative results on how much the upper bound can be improved.
- 15.
As long as there is no line under Π that separates it from A, the deduction Π is taken to include A. We can choose either to make explicit that Π has A as its end-formula by writing
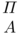
—sometimes written Π∕A to keep it on one line—or leave that out, writing just Π (in the same way as we may indicate the free occurrences of x in a formula A by writing A(x) but may also leave that implicit, writing just A). A linear notation for the result of substituting Π∕A for the assumptions [A] in Σ is: \(\Pi /[A]/\Sigma \).
- 16.
Such a definition of potential maximum formula could be given by using ideas presented by Sanz [22].
- 17.
In the sequent calculus for predicate logic, the level lines are determined by the actual cuts. An inference line is a level line if and only if it is the inference line of a cut such that all cuts further down have lower degree than that cut; the degree of a cut being defined as the degree of its cut formula. Since maximum formulas are what correspond to cut formulas, one could expect that the level lines in natural deduction should be similarly determined by the actual maximum formulas, but this would lead to an entirely wrong notion.
- 18.
A similar result was proved for the sequent calculus for predicate logic by Pereira [19].
- 19.
A fact noted and used by Scarpellini [23].
- 20.
I first learned about adding such a substitution notation to the language of predicate logic in 1960 from Ettore Casari, who studied it in his doctoral thesis at the University of Münster.
- 21.
When using induction over the degree of the maximum formulas (Sect. 2.1) instead of the Gentzen measure, there is of course no need to move the new substitution in this way.
- 22.
However, there would be no harm in adding 1 to n or to 2j(n) in this case too. There is also an option in the original definition of the Gentzen measure (Sect. 2.3): when assigning a value to a formula immediately below a level line, it is possible to avoid the addition of 1 to 2j(n).
- 23.
In Gentzen’s consistency proof, the logical constants are ¬, &, ∨, ∀, and ∃. The possibility that several formulas occur in the succedent is essential there, why the proof does not easily extend to intuitionistic logic. To include ⊃ is of course essential in natural deduction.
- 24.
Martin-Löf’s [13] proof of the normalization theorem has two similar main cases, and in this respect, the main strategy of my proof is the same as his.
- 25.
This is a recurring theme in the verifications. An inference containing a level line may also disappear without being replaced by any new inference, as is the case with the simplifications (section 4.2.3), which is a special case of the one above. Gentzen [6, p. 41], [7, pp. 281–282] deals at length with the same phenomenon that occurs when eliminating a cut. It may also happen that an inference line that was a level line in a deduction \(\mathcal{D}\) ceases to be a level line in a reduction \(\mathcal{D}^{{\ast}}\) of \(\mathcal{D}\), although the inference remains the same. This may, for instance, be the case when some elimination inferences are excepted from being counted as critical, as in Sects. 2.3 and 6.4. If the jump of the level line was j, then for the formulas A immediately above the line it holds again that \(G_{\mathcal{D}^{{\ast}}}(A) \leq 2_{j}(G_{\mathcal{D}}(A))\). But since the line is not a level line in \(\mathcal{D}^{{\ast}}\), it holds for the formula B immediately below the line that \(G_{\mathcal{D}^{{\ast}}}(B) \leq (G_{\mathcal{D}}(B))\).
- 26.
In the proofs of the normalization theorems, I have not paid attention to their status as consistency proofs, but now the statement that Gentzen measure goes down in a reduction sequence, from which it follows by transfinite induction that it must terminate, has the simple form that Gentzen required of a statement proved by induction in a consistency proof.
References
M. Abadi, L. Cardelli, P.-L. Curien, J.-J. Levy, Explicit Substitutions. J. Funct. Program. 1, 375–416 (1991)
P. Bernays, On the original Gentzen consistency proof for number theory, in Intuitionism and Proof Theory, ed. by J. Myhill et al. (North-Holland, Amsterdam, 1980), pp. 409–417
W. Buchholz, Explaining Gentzen’s consistency proof within an infinitary proof theory, in Computational logic and proof theory, KGC 1997, ed. by G. Gottlob et al., Lecture Notes in Computer Science, vol. 1289 (Springer, Berlin, 1997)
C. Cellucci, Proof theory and complexity. Synthese 62, 173–189 (1985)
G. Gentzen, Untersuchungen über das logische Schließen, Math. Z. 39, 176–210, 405–431 (1934–1935)
G. Gentzen, Neue Fassung des Widerspruchsfreiheitsbeweises für die reine Zahlentheorie, Forschungen zur Logik und zur der exakten Wissenschaften. Neue Folge, Heft 4 (Hirzel, Leipzig, 1938), pp. 19–44
G. Gentzen, in The Collected Papers of Gerhard Gentzen, ed. by M.E. Szabo (North-Holland, Amsterdam, 1969)
W.A. Howard, Assignments of ordinals to terms for primitive recursive functionals of finite type, in Intuitionism and Proof Theory, ed. by J. Myhill et al. (North-Holland, Amsterdam, 1970), pp. 443–458
H. Jervell, A normal form in first order arithmetic, in Proceedings of the Second Scandinavian Logic Symposium, ed. by J.E. Fenstad (North Holland, Amsterdam, 1971), pp. 93–108
A. Kanckos, Consistency of Heyting arithmetic in natural deduction. Math. Log. Q. 56, 611–624 (2010)
A. Kanckos, A possible and necessary consistency proof, in Philosophical Studies from the University of Helsinki (University of Helsinki, Helsinki, 2011)
D. Leivant, Strong normalization for arithmetic (variations on a theme of Prawitz), in Proof Theory Symposium Kiel 1974, ed. by A. Dold et al., Lecture Notes in Mathematics, vol. 500 (Springer, Berlin, 1975), pp. 182–197
P. Martin-Löf, Hauptsatz for the intuitionistic theory of iterated inductive definitions, in Proceedings of the Second Scandinavian Logic Symposium, ed. by J.E. Fenstad (North Holland, Amsterdam, 1971), pp. 179–216
P. Martin-Löf, Infinite terms and a system of natural deduction. Compos. Math. 2, 92–103 (1972)
G. Mints, Normalization of finite terms and derivations via infinite ones, in V. International Congress for LMPS, Abstracts of Papers, 1975, pp. 215–219 (reprinted in [17, pp. 73–76])
G. Mints, A new reduction sequence for arithmetic (in Russian), in Zapiski nauchnyh seminarov LOMI, vol. 88 (1979), pp. 106–130 (translated in [17, pp. 77–96])
G. Mints, Selected Papers in Proof Theory (Bibliopilis and North-Holland, Napoli, 1992)
G. Mints, Reduction of finite and infinite derivations. Ann. Pure Appl. Log. 104, 167–188 (2000)
L.C. Pereira, On the estimation of the length of normal derivations, in Philosophical Studies, vol. 4 (Akademilitteratur, Stockholm, 1982)
D. Prawitz, Natural Deduction. A Proof-Theoretical Study (Almqvist & Wicksell, Uppsala, 1965) (Reprinted: Dover Publications, Mineola, 2006)
A. Raggio, Gentzen’s Hauptsatz for the systems NI and NK. Log. Anal. 30, 91–100 (1965)
W.C. Sanz, Big bound, in Natural Deduction, Rio 2001, mimeographed abstracts of invited talks, PUC, Rio de Janeiro, 2001
B. Scarpellini, Applications of Gentzen’s second consistency proof. Math. Ann. 181, 325–354 (1969)
K. Schütte, Beweistheorie (Springer, Berlin, 1960)
K. Schütte, Beweistheoretische Erfassung der unendlichen Induktion in der Zahlentheorie. Math. Ann. 122, 369–389 (1951)
W. Tait, Normal derivability in classical logic, in The Syntax and Semantics of Infinitary Languages, ed. by J. Barwise, Lecture Notes of Mathematics, vol. 72 (Springer, Berlin, 1968), pp. 204–236
J. von Plato, Gentzen’s proof of normalization for intuitionistic natural deduction. Bull. Symb. Log. 14, 240–257 (2008)
J. von Plato, Talk at Workshop on Proof Theory and Constructivism, 2012, Helsinki, 23 March 2012
Acknowledgements
Per Martin-Löf encouraged me to make investigations that led to the addition of Sect. 6 to a first version of this paper. Luiz Carlos Pereira and Michael Hahn made valuable comments after reading manuscripts at different stages and pointed out a deficiency in an earlier version of the proof. Sama Agahi made the figures that are inserted in the text. I am grateful to all of them.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Prawitz, D. (2015). A Note on How to Extend Gentzen’s Second Consistency Proof to a Proof of Normalization for First Order Arithmetic. In: Kahle, R., Rathjen, M. (eds) Gentzen's Centenary. Springer, Cham. https://doi.org/10.1007/978-3-319-10103-3_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-10103-3_6
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-10102-6
Online ISBN: 978-3-319-10103-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)