Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Gravitational Waves and Degrees of Freedom

1.1 Polarizations

One of the genuine predictions of General Relativity is the existence of a graviton or massless spin-2 field under the Poincaré group which mediates the gravitational force. The existence of this particle implies the presence of Gravitational Waves (GWs). Whilst advanced LIGO and other interferometer [1] are expected to be on the edge of discovering GWs, the indirect detection of GWs has been confirmed for forty years via the spin-down of binary pulsars and particularly the Hulse Taylor pulsar [2]. The spin-down is in perfect agreement with the emission of gravitational radiation and the prediction that in GR gravitational waves have two polarizations. Nevertheless this does not necessarily rule out the existence of additional polarizations which could be screened for instance via the Vainshtein mechanism see [3] and [4].

In modified theories of gravity GWs could have up to four additional polarizations: two ‘vector’ polarizations which mix the longitudinal and the transverse directions, as well as two ‘scalar’ polarizations, one of each being a conformal or breathing mode and the other one a purely longitudinal mode as depicted in Fig. 5.1.

Fig. 5.1
figure 1

Polarizations of Gravitational Waves in General Relativity and potential additional polarizations in modified gravity. From [6]

Full size image

These last four polarizations are absent in GR. However in theories of modified gravity one could in principle excite them. For instance in massive gravity the graviton is instead seen as a massive spin-2 field. In four dimensions, a massive spin-s fields is known to propagate 2s + 1 dofs (degrees of freedom), so a massive spin-2 field should propagate five dofs.

At the same time, massive gravity breaks diffeomorphism invariance, corresponding to four symmetries in four dimensions. This means that we expect massive gravity to propagate four dofs more than in GR, this would correspond to the four additional polarizations depicted in Fig. 5.1. This corresponds to one additional polarization compared to what a massive spin-2 field should have. If present, this additional fourth new polarization is always pathological and enters as a ghost, now commonly known as the Boulware–Deser (BD) ghost [5]. This BD ghost correspond to the last polarization depicted in Fig. 5.1, namely the longitudinal scalar mode. So for a theory of massive gravity to be free of the BD ghost it should only have at most the three first additional polarizations of Fig. 5.1 and should not excite the last one. In what follows we explain why the presence of a BD ghost would always invalidate the theory and then proceed by constructing explicit models of massive gravity which are free from this pathology. We refer to [6] for a recent review on massive gravity.

1.2 Implications of the BD Ghost

To understand the implications of the BD ghost, we consider a simple but representative example of how this ghost can present itself. Let us consider a free scalar field ϕ with kinetic termFootnote 1 \(-1/2(\partial \phi )^{2}\). For definiteness, one way the BD ghost can manifest itself is via a new operator of the form \((\square \phi )^{3}\) arising at a scale Λ,

$$\displaystyle\begin{array}{rcl} \mathcal{L} = -\frac{1} {2}(\partial \phi )^{2} + \frac{1} {6\varLambda ^{5}}(\square \phi )^{3}\,.& &{}\end{array}$$
(5.1)

Considering the fluctuations about a non-trivial background \(\phi =\phi _{0}+\delta \phi\), with say \(\phi _{0} =\varLambda ^{3}/8B_{0}\eta _{\mu \nu }x^{\mu }x^{\nu }\), the Lagrangian for the fluctuations is

$$\displaystyle\begin{array}{rcl} \mathcal{L} = -\frac{1} {2}\delta \phi \left (1 + \frac{B_{0}} {\varLambda ^{2}} \square \right )\square \delta \phi \,.& &{}\end{array}$$
(5.2)

The associated propagator has two poles signaling the presence of two dofs

$$\displaystyle\begin{array}{rcl} \mathcal{G} = \frac{1} {\left (1 + \frac{B_{0}} {\varLambda ^{2}} \square \right )\square } = \frac{1} {\square }- \frac{1} {\square +\varLambda ^{2}/B_{0}^{2}}\,.& &{}\end{array}$$
(5.3)

The pole at zero mass represents the standard degree of freedom associated with ϕ, but we see a new pole with (tachyonic) mass square Λ 2∕B 0 2 which always enters with the wrong sign. So the new degree of freedom at Λ∕B 0 is a ghost.

We emphasize that a ghost represents a degree of freedom with the wrong sign kinetic term and should be distinguished from a tachyon which corresponds to a degree of freedom with the wrong sign mass term or an instability in the potential. For a tachyon the scale of the instability is governed by the mass of the mode and we can thus survive with small mass tachyonic modes as the time scale of the instability is long compared to other process that may be taking place. For a ghost on the other hand, the scale associated with the instability is the momentum of the field and so the instability scale is always at least of the order of the cutoff of the theory. This implies that if a ghost is present at a scale μ then one cannot trust the theory beyond the scale μ. In the case of the BD ghost, the ghost enters at the background dependent scale Λ∕B 0. By choosing an arbitrarily large background B 0, one can brings the scale at which the theory breaks down arbitrarily low, which would mean that one can never trust this theory, neither at the classical level nor at the quantum level. New physics has to enter at the cutoff scale or at the scale Λ∕B 0 to help making sense of the theory. This is distinct from having a low strong coupling scale where classical predictions break down at that scale but not the quantum ones. New physics does not need to enter at the strong coupling scale.

To summarize, a ghost leads to an arbitrarily fast instability already at the classical level and signals the fact that the theory cannot be trusted neither classically nor quantum mechanically at and above the mass of the ghost. However as we shall see below the Vainshtein mechanism relies crucially on classical configurations at the low scale Λ. It is therefore essential to be able to trust the theory at the scale at which the first interactions enter (i.e., at the strong coupling scale). To get some intuition on how to obtain a ghost-free theory of massive gravity and other modifications of gravity a useful tool is to rely on a higher dimensional theory of gravity. In some cases this higher-dimensional theory is merely a ‘mathematical trick’ but it will show to provide useful insights.

2 Consistent Modifications of Gravity From Extra Dimensions

One of the most straight-forward way to derive a sensible and theoretical consistency theory of modified gravity is to start with General Relativity in higher dimensions. Higher dimensional gravity is known to lead to consistent high energy modifications of gravity. Here we shall focus on infrared (IR) modifications and see how it can lead to different interconnected models like Galileon theories of DGP and massive gravity which behave as Galileons in some limit. In the rest of this contribution we will use the notation that y represents the fifth extra dimension and x μ are the 4d space-time coordinates. The 5d coordinates are given by \(\{x^{\alpha }\}_{\alpha =0}^{4} =\{ x^{\mu },y\}\).

2.1 DBI–Galileon

2.1.1 Five-Dimensional Minkowski

Starting with five dimensional GR, we can consider all the Lovelock invariants namely a cosmological constant (CC), a five dimensional scalar curvature R (5) and a Gauss-Bonnet (GB) invariant \(\mathcal{L}_{\mathrm{GB}}\). The presence of a cosmological constant leads to a non-flat maximally symmetric 5d spacetime (AdS) and will be mentioned in what follows. To start with we stick to a flat Minkowski 5d spacetime \(\,\mathrm{d}s^{2} =\,\mathrm{ d}y^{2} +\eta _{\mu \nu }\,\mathrm{d}x^{\mu }\,\mathrm{d}x^{\nu }\) and set the CC to zero. In order to recover 4d gravity in some regime we consider a probe brane located at y = π(x μ) and consider the boundary terms induced by the Lovelock invariants. The scalar curvature leads to an extrinsic boundary term K on the brane and the GB to a related term K GB. Furthermore induced on the brane one can consider a tension or a 4d CC λ and a 4d induced scalar curvature R (4). If the brane is localized at y = π(x μ), the induced metric on the brane is \(g_{\mu \nu } =\eta _{\mu \nu } + \partial _{\mu }\pi \partial _{\nu }\pi\) leading to what will represent a disformal coupling to matter. In the weak field limit, these invariants lead to a generalized Galileon-DBI set of interactions in 4d [7],

$$\displaystyle\begin{array}{rcl} \begin{array}{cccclcl} \mathrm{5d} & & \mathrm{4d} & & & &\mathrm{DBI - Galileon} \\ \hline \\ & & \lambda & \rightarrow &\mathcal{L}_{2} & \sim &-\lambda \sqrt{1 - (\partial \pi )^{2}} \\ R^{(5)} & \rightarrow & K & \rightarrow &\mathcal{L}_{3} & \sim &(\partial _{\mu }\pi \partial _{\nu }\pi \varPi ^{\mu \nu })/(1 - (\partial \pi )^{2}) \\ & & R^{(4)} & \rightarrow &\mathcal{L}_{4} & \sim &\left ([\varPi ]^{2} - [\varPi ]^{2}\right )/\sqrt{1 - (\partial \pi )^{2}} + \cdots \\ \mathcal{L}_{\mathrm{GB}} & \rightarrow &K_{\mathrm{GB}} & \rightarrow &\mathcal{L}_{5} & \sim &\left ([\varPi ]^{2} - 3[\varPi ][\varPi ^{2}] + 2[\varPi ^{3}]\right )/(1 - (\partial \pi )^{2}) + \cdots \,,\end{array} & &{}\end{array}$$
(5.4)

where here and in what follows \(\varPi _{\mu \nu } = \partial _{\mu }\partial _{\nu }\pi\) and square brackets represent the trace of a tensor with respect to η μ ν , [Π] = η μ ν Π μ ν , etc. In the weak field limit, these invariants lead to the Galileon terms on the brane [8]

$$\displaystyle\begin{array}{rcl} \begin{array}{lcl} L_{2} & =&\left (\partial \pi \right )^{2} \\ L_{3} & =&\left (\partial \pi \right )^{2}[\varPi ] \\ L_{4} & =&\left (\partial \pi \right )^{2}\left ([\varPi ]^{2} - [\varPi ^{2}]\right ) \\ L_{5} & =&\left (\partial \pi \right )^{2}\left ([\varPi ]^{3} - 3[\varPi ][\varPi ^{2}] + 2[\varPi ^{3}]\right )\,.\end{array} & &{}\end{array}$$
(5.5)

This is a finite set of interactions and the fact that these terms be it in their exact form (5.4) or in their weak field limit (5.5) derive from Lovelock invariants in five dimensions ensures that they are ghost free. Furthermore Poincaré invariance in five dimensions leads to the following four-dimensional global symmetry [7]

$$\displaystyle\begin{array}{rcl} \pi \rightarrow \pi +c + v_{\mu }x^{\mu } +\pi v^{\mu }\partial _{\mu }\pi \,,& &{}\end{array}$$
(5.6)

for the interactions (5.4) and the Galilean symmetry for the Galileon interactions (5.5)

$$\displaystyle\begin{array}{rcl} \pi \rightarrow \pi +c + v_{\mu }x^{\mu }\,.& &{}\end{array}$$
(5.7)

In addition they also satisfy a non-renormalization theorem [9] which means that the coefficient governing any of these interactions can be set to any desired value without the loops of the field itself destabilizing it.

2.1.2 Curved Five Dimensions

As mentioned previously, one can also consider a CC in five dimensions, leading to 5d AdS rather than Minkowski. Since this is still a maximally symmetric spacetime, there is an equivalent to the symmetries presented in (5.6) or (5.7) for Minkowski, simply involving the AdS curvature [7]. The results sets of interactions are a Galileon generalization of the warped DBI and satisfy the same properties as previously namely the absence of ghost and radiative stability.

One can also extend the setup to arbitrary matter in five dimensions leading to an arbitrary five dimensional metric q μ ν . The induced metric on the brane is then \(g_{\mu \nu } = q_{\mu \nu } + \partial _{\mu }\pi \partial _{\nu }\pi\) and the resulting Galileon field π leaves on a curved metric q μ ν . This leads to the covariant set of Galileon interactions first proposed in [10] which remains free of ghost but does satisfy the Galileon symmetry nor a generalized one. The reason is clear: the five dimensional spacetime is no longer maximally symmetric and there is therefore no reason to expect any resulting global symmetry.

These Galileon scalar fields can play an important role on cosmological scales (for instance they can be a good candidate for dark energy) and yet remain frozen on short distance scales thanks to a Vainshtein mechanism. Before describing this mechanism in Sect. 5.5 (see also other contributions), we show how theories of modified gravity are derived from extra dimensions.

2.2 Massive Gravity

2.2.1 Infinite Extra Dimension: DGP

If one is to start with five dimensional gravity to derive theories of IR modifications of gravity one first needs to confine gravity in four dimensions. This can be performed in two ways: Either by compactifying the extra dimension, which is performed in Sects. 5.2.2.2 and 5.3 or by considering an large (even infinite) extra dimension and inducing a four-dimensional curvature on a four-dimensional brane. This is the idea behind the DGP (Dvali–Gabadadze–Porrati) model where we start with five-dimensional gravity with a five-dimensional Planck scale M 5 and induce a four-dimensional curvature with Planck scale M Pl in four dimensions [11]. The effective Friedman equation on the brane is then [12]

$$\displaystyle\begin{array}{rcl} M_{\mathrm{Pl}}^{2}H^{2} \pm M_{ 5}^{3}H =\rho \,,& &{}\end{array}$$
(5.8)

where H is the Hubble parameter and ρ the energy density of fields localized on the four-dimensional brane. This modified Friedman equation has lead to a wealth of new directions for testing cosmology.

The brane-bending mode on the brane behaves as a cubic Galileon [9], given by \(\mathcal{L}_{3}\) in (5.5). From a four-dimensional view point, the graviton is effectively massive and at the linearized level it satisfies (symbolically) the following equation

$$\displaystyle\begin{array}{rcl} \left (\square - m\sqrt{-\square }\right )h_{\mu \nu } = M_{\mathrm{Pl}}^{-1}T_{\mu \nu }\,,& &{}\end{array}$$
(5.9)

where \(m = M_{5}^{3}/M_{\mathrm{Pl}}^{2}\) and the effective mass of the graviton is momentum-dependent m eff 2(k) = mk. So rather than having a fixed pole at the scale m, the propagator has rather a resonance. In this sense DGP is a model of ‘soft-massive gravity’.

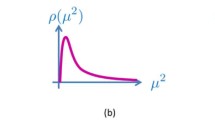
For DGP, the peak of the spectral distribution still occurs at zero mass as can be seen in Fig. 5.2. However extensions of DGP to higher dimensions (known as Cascading gravity [13–15]) can lead to a peak in the spectral representation as depicted in Fig. 5.2 and are possibly closer to models of a hard mass graviton. In what follows, we discuss an alternative way to derive a theory of massive gravity from five dimensional GR, via Kaluza–Klein reduction or deconstruction.

Fig. 5.2
figure 2

Spectral representation of different models. (a) DGP, (b) higher-dimensional cascading gravity and (c) multi-gravity. Bi-gravity is the special case of multi-gravity with one massless mode and one massive mode. Massive gravity is the special case where only one massive mode couples to the rest of the standard model and the other modes decouple. (a) and (b) are models of soft massive gravity where the graviton mass can be thought of as a resonance. From [6]

Full size image

2.2.2 Compact Extra Dimension

An alternative to the DGP model and its extensions is to consider a compact extra dimension of size R. A Kaluza-Klein decomposition (discretization in the momentum along the extra dimension) leads to a massless mode and an infinite tower of massive Kaluza-Klein modes, with mass gap \(m = 1/R\). Rather than performing a Kaluza-Klein decomposition, one can also consider a deconstruction of the extra dimension which is a discretization of the extra dimension directly in real space rather than in momentum. Rather than considering a smooth extra dimension 0 < y < R, we replace that direction by a series of N points y n . In the large N limit one should in principle recover 5d GR but as we shall see below this does not occur in some special gauge choices.

The deconstruction framework will be explained in more detail below and as we shall see, for a finite number of site N one obtains a four-dimensional theory of N interacting gravitons (multi-gravity), with one massless graviton and N − 1 massive ones. Moreover this theory is identical to a truncated Kaluza-Klein decomposition after a non-trivial field redefinition.

As we have seen before, in the case of an infinite extra dimension à la DGP, we obtain a theory of gravity where the graviton acquires a soft mass or resonance. In the case of a compact extra dimension, the deconstruction framework leads to a finite number N of discrete graviton(s) with mass ∼ n∕R as can be seen from the spectral representation in Fig. 5.2.

In both cases starting from five-dimensional GR ensures (to some extendFootnote 2) a consistent resulting four-dimensional theory of modified gravity. Indeed a massless graviton in 5d propagates 5 dofs which is precisely the right number of dofs that a massive spin-2 field should propagate in 4d without the BD pathology discussed in Sect. 5.1.2. In what follows we thus proceed by showing how 5d gravity can lead to a consistent theory of 4d massive gravity free of the BD ghost.

3 Deconstruction and Massive Gravity

We now present how to deconstruct 5d GR and recover 4d multi-gravity. We will then specialize to bi-gravity and to massive gravity as special cases. We follow the formalism derived in [17].

Starting with 5d gravity in the Einstein–Cartan form, the 5d metric is given by

$$\displaystyle\begin{array}{rcl} g_{\alpha \beta }(x,y) = e_{\alpha }^{A}(x,y)e_{\beta }^{B}(x,y)\eta _{\mathit{ AB}}\,.& &{}\end{array}$$
(5.10)

The connection is set of the torsionless condition,

$$\displaystyle\begin{array}{rcl} \omega _{\alpha }^{\mathit{AB}} = \frac{1} {2}e_{\alpha }^{C}\left (O^{\mathit{AB}}_{ C} - O_{C}^{\mathit{AB}} - {O^B}_{ C}^{A}\right )\,,& &{}\end{array}$$
(5.11)

with \(O^{\mathit{AB}}_{C} = 2e^{A\alpha }e^{B\beta }\partial _{[\alpha }e_{\beta ]C}\). The 5d curvature 2-form is then

$$\displaystyle\begin{array}{rcl} \mathcal{R}^{\mathit{AB}} =\,\mathrm{ d}\omega ^{\mathit{AB}} +\omega ^{A}_{ C} \wedge \omega ^{\mathit{CB}}\,.& &{}\end{array}$$
(5.12)

The 5d Einstein-Hilbert action is then

$$\displaystyle\begin{array}{rcl} S_{\mathrm{EH}}^{(5)}& =& \frac{M_{5}^{3}} {2} \int \,\mathrm{d}^{4}x\,\mathrm{d}y\sqrt{-g}R^{(5)}[g]{}\end{array}$$
(5.13)
$$\displaystyle\begin{array}{rcl} & =& \frac{M_{5}^{3}} {2 \times 3!}\int \varepsilon _{\mathit{ABCDE}}\mathcal{R}^{\mathit{AB}} \wedge e^{C} \wedge e^{D} \wedge e^{E}\,.{}\end{array}$$
(5.14)

Before we proceed with discretizing this action we first briefly discuss the gauge choice we use.

3.1 Gauge-Fixing

The theory has 5 spacetime symmetries associated with 5d diffeomorphism invariance. In addition in the veilbein language there are 10 Lorentz symmetries. As a result one can make 15 gauge choices. We chose the following conditions on the vielbein and the connection

$$\displaystyle\begin{array}{rcl} \begin{array}{lll} e_{y}^{a} = 0,\ e_{\mu }^{5} = 0,\ e_{y}^{5} = 1&\longrightarrow &9\ \mathrm{gauge\ fixing} \\ \omega _{y}^{\mathit{ab}} = e^{\mu [a}\partial _{y}e_{\mu }^{b]} = 0 &\longrightarrow &6\ \mathrm{gauge\ fixing}\,,\end{array} & &{}\end{array}$$
(5.15)

which fully fixes all the gauge freedom. The condition on the vielbein implies \(e^{A} = \left (e_{\mu }^{a}\,\mathrm{d}x^{\mu },\,\mathrm{d}y\right )\) and the condition on the connection implies the symmetric vielbein condition. Interestingly this condition ensures that the theory can be written back in terms of the metric. Here it appears as a simple consequence of our gauge choice. In the metric language this gauge choice implies that the lapse is unity and the shift vanishes, \(\,\mathrm{d}s^{2} =\,\mathrm{ d}y^{2} + g_{\mu \nu }(x,y)\,\mathrm{d}x^{\mu }\,\mathrm{d}x^{\nu }\). We now proceed with discretizing 5d GR in this gauge.

3.2 From 5d Gravity to 4d Multi-Gravity

In the gauge chosen previously, 5d GR can be written as

$$\displaystyle\begin{array}{rcl} S_{\mathrm{EH}}^{(5)}& =& \frac{M_{5}^{3}} {2} \int \,\mathrm{d}^{4}x\,\mathrm{d}y\sqrt{-g}\left (R^{(4)}[g] + [K]^{2} - [K^{2}]\right )\,,{}\end{array}$$
(5.16)

where K is the extrinsic curvature, in the metric language

$$\displaystyle\begin{array}{rcl} K_{\mu \nu } = \frac{1} {2}g^{\mu \alpha }(x,y)\partial _{y}g_{\alpha \nu }(x,y)\,.& &{}\end{array}$$
(5.17)

We now discretize the extra dimension as follows:

$$\displaystyle\begin{array}{rcl} & & y\longrightarrow y_{n} \\ & & e_{A}^{a}(x,y)\longrightarrow {e_ n}_{A}^{a}(x) \\ & & g_{\mu \nu }(x,y) =\eta _{ab}e_{\mu }^{a}(x,y)e_{\nu }^{b}(x,y)\longrightarrow g_{\mu \nu }^{(n)}(x) =\eta _{ ab}e_{n}{}_{\mu }^{a}(x)e_{ n}{}_{\nu }^{b}(x)\quad \\ & & \partial _{y}e(x,y)\longrightarrow m\left (e_{n+1}(x) - e_{n}(x)\right )\,, {}\end{array}$$
(5.18)

with \(m = N/R\). Applying this discretization procedure on the extrinsic curvature,

$$\displaystyle\begin{array}{rcl} K_{\,\,\nu }^{\mu } \sim g^{\mu \alpha }\partial _{y}g_{\alpha \nu } \sim e^{-1}\partial _{ y}e\,,& &{}\end{array}$$
(5.19)

and using the symmetric vielbein condition we obtain

$$\displaystyle\begin{array}{rcl} K_{\,\,\nu }^{\mu } \rightarrow me_{n}^{-1}\left (e_{ n+1} - e_{n}\right )& =& -m\left (\delta _{\,\,\nu }^{\mu } -\sqrt{\left (g^{(n) } \right ) ^{\mu \alpha } g_{\alpha \nu }^{(n+1)}}\right ) \\ & \equiv & -m\mathcal{K}_{\,\,\nu }^{\mu }[g^{(n)},g^{(n+1)}] \equiv -m\mathcal{K}_{ n,n+1}{}_{\,\,\nu }^{\mu }\,.{}\end{array}$$
(5.20)

Using this expression into the 5d Einstein-Hilbert action (5.16) we obtain [17]

$$\displaystyle\begin{array}{rcl} \mathcal{L}& =& M_{5}^{3}\int \,\mathrm{d}y\left (R^{(4)}[g] + [K]^{2} - [K^{2}]\right ){}\end{array}$$
(5.21)
$$\displaystyle\begin{array}{rcl} & \rightarrow & \frac{M_{5}^{3}} {m} \sum _{n=1}^{N}\left (R_{ n}^{(4)} + m^{2}\left ([\mathcal{K}_{ n,n+1}]^{2} - [\mathcal{K}_{ n,n+1}^{2}]\right )\right )\,.{}\end{array}$$
(5.22)

This is a 4d theory of multi-gravity as presented in [18] with the specific interactions governed by \(\mathcal{K}_{n,m}\) derived in [19, 20]. The 4d fundamental Planck scale is then given by \(M_{\mathrm{Pl}}^{2} = M_{5}^{3}/(mN) = M_{5}^{3}R\).

3.3 Generalized Mass Term

The multi-gravity theory derived previously has only one of the possible sets of allowed interactions derived in [19, 20]. In the previous derivation we have applied the most straightforward discretization procedure but there is some freedom on how one wishes to define a field or its derivative at a point. To see the most general discretization procedure it is convenient to return to the vielbein language where rather than using

$$\displaystyle\begin{array}{rcl} e^{a} \rightarrow e_{ n}^{a}\,,& &{}\end{array}$$
(5.23)

we may use the more general procedure

$$\displaystyle\begin{array}{rcl} e^{a} \rightarrow \left (we_{ n}^{a} + (1 - w)e_{ n+1}^{a}\right )\,.& &{}\end{array}$$
(5.24)

The mass term then gets generalized to

$$\displaystyle\begin{array}{rcl} \sqrt{ -g}\left ([K]^{2} - [K^{2}]\right )& =& \varepsilon _{\mathit{ abcd}}e^{a} \wedge e^{b} \wedge \partial _{ y}e^{c} \wedge \partial _{ y}e^{d} \\ & \rightarrow & m^{2}\varepsilon _{ \mathit{abcd}}\left (w_{1}e_{n}^{a} + (1 - w_{ 1})e_{n+1}^{a}\right ) \wedge \left (w_{ 2}e_{n}^{b} + (1 - w_{ 2})e_{n+1}^{b}\right ) \\ & & \wedge \left (e_{n}^{c} - e_{ n+1}^{c}\right ) \wedge \left (e_{ n}^{d} - e_{ n+1}^{d}\right ) \\ & \equiv & m^{2}\sqrt{-g}\left (\mathcal{L}_{ 2}(\mathcal{K}) + (w_{1} + w_{2})\mathcal{L}_{3}(\mathcal{K}) + w_{1}w_{2}\mathcal{L}_{4}(\mathcal{K})\right )\,, {}\end{array}$$
(5.25)

where we recover the ghost-free interaction terms L 2, 3, 4 first derived in [20] (sometimes known as ‘dRGT’ mass terms or interactions),

$$\displaystyle\begin{array}{rcl} 2\mathcal{L}_{2}[\mathcal{K}]& =& \varepsilon ^{abcd}\varepsilon _{ a'b'cd}\mathcal{K}_{a}^{a'}\mathcal{K}_{ b}^{b'}{}\end{array}$$
(5.26)
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{3}[\mathcal{K}]& =& \varepsilon ^{abcd}\varepsilon _{ a'b'c'd}\mathcal{K}_{a}^{a'}\mathcal{K}_{ b}^{b'}\mathcal{K}_{ c}^{c'}{}\end{array}$$
(5.27)
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{4}[\mathcal{K}]& =& \varepsilon ^{abcd}\varepsilon _{ a'b'c'd'}\mathcal{K}_{a}^{a'}\mathcal{K}_{ b}^{b'}\mathcal{K}_{ c}^{c'}\mathcal{K}_{ d}^{d'}\,,{}\end{array}$$
(5.28)

or equivalently,

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{2}[\mathcal{K}]& =& \left ([\mathcal{K}^{2}] - [\mathcal{K}]^{2}\right ){}\end{array}$$
(5.29)
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{3}[\mathcal{K}]& =& \left ([\mathcal{K}]^{2} - 3[\mathcal{K}][\mathcal{K}^{2}] + 2[\mathcal{K}^{3}]\right ){}\end{array}$$
(5.30)
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{4}[\mathcal{K}]& =& \left ([\mathcal{K}]^{4} - 6[\mathcal{K}^{2}][\mathcal{K}]^{2} + 3[\mathcal{K}^{2}]^{2} + 8[\mathcal{K}][\mathcal{K}^{3}] - 6[\mathcal{K}^{4}]\right )\,.\quad {}\end{array}$$
(5.31)

This structure is very similar to that of the Galileons [8] and as we shall see they are indeed very closely related and are the essence of the absence of BD ghost.

3.4 Strong Coupling Scale

This theory of multi-gravity has one massless mode with 2 dofs and (N − 1) massive modes with 5 dofs each, meaning that there is no BD ghost for any mode. The lightest mode has a mass \(m_{1} = 1/R = m/N\), while the heaviest mode has a mass set by m ∼ Nm 1 (in the large N limit.)

The strong coupling scale for this theory (the scale at which the lowest interactions arise) is the same as for a normal (ghost-free) theory of massive gravity and is given by de Rham and Gabadadze [19]

$$\displaystyle\begin{array}{rcl} \varLambda = (M_{\mathrm{Pl}}m_{1}^{2})^{1/3}\,,& &{}\end{array}$$
(5.32)

where m 1 is the mass of the lightest mode. Interestingly in what should be the continuum limit R → ∞ or m 1 → 0 the degree of freedom that interact at the scale Λ (namely the helicity-0 mode of the lightest mode), as well as all the other helicity-0 modes entirely decouple in that limit. This means that in this specific theory, we do not recover 5d GR in the limit R → ∞ or m 1 → 0 but rather N decoupled massless spin-2 fields, (N − 1) decoupled spin-0 fields and (N − 1) decoupled spin-1 fields. This decoupling is ensured by the low strong coupling scale (5.32) and is responsible for the Vainshtein mechanism [3] and the absence of vDVZ (van Dam–Veltman–Zakharov) discontinuity in the massless limit [21, 22]. In this sense the strong coupling scale (5.32) is a desirable (and even required) feature of the theory if one would like to be able to consider it as a truncated theory in its own right.

There is an alternative to the low strong coupling scale (5.32) which implies choosing a different gauge choice that what was performed here. If instead we keep the lapse dynamical, the presence of low strong coupling scale is avoided but at the price of introducing a ghost at the scale of the heaviest mode. This means that the truncated theory is not consistent, and one should keep an infinite number of modes or work at energy scales well below the mass of the heaviest mode. In that case one recovers 5d GR in the continuum limit R → ∞ or m 1 → 0.

3.5 Bi-Gravity

Focusing on a discretization with two sites only with respective metrics g μ ν and f μ ν , we obtain the following bi-gravity theory [23] with the same ghost-free interactions [20]

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{g,f}& =& M_{g}^{2}\sqrt{-g}R[g] + M_{ f}^{2}\sqrt{-f}R[f]{}\end{array}$$
(5.33)
$$\displaystyle\begin{array}{rcl} & +& m^{2}M_{ f}M_{g}\sqrt{-g}\sum _{n=0}^{4}\alpha _{ n}\mathcal{L}_{n}\left (\mathcal{K}[g,f]\right )\,,{}\end{array}$$
(5.34)

with

$$\displaystyle\begin{array}{rcl} \mathcal{K}_{\,\,\nu }^{\mu }[g,f] =\delta _{ \,\,\nu }^{\mu } -\left (\sqrt{g^{-1 } f}\right )_{\,\,\nu }^{\mu }\,.& &{}\end{array}$$
(5.35)

In the absence of the interaction governed by m, this would the theory of two non-interactive massless spin-2 fields bearing 2 × 2 = 4 dofs. This theory would have two copies of diffeomorphism invariance.

Including the interaction breaks one copy of diffeomorphism invariance which excites three new dofs in the theory leading to a total of \(4 + 3 = 7\) dofs, which is the correct counting for one massless mode and one massive mode which carry a total of \(2 + 5 = 7\) dofs without any BD ghost.

It is sometimes stated that unlike massive gravity bi-gravity does not break diffeomorphism invariance. This statement is quite incorrect, just like massive gravity, bi-gravity breaks one copy of diffeomorphism invariance and just like in massive gravity four Stückelberg fields (only three of which are independent) should be included in bi-gravity to restore that homeomorphism invariance.

3.6 Massive Gravity

We can now easily see how to obtain a theory of massive gravity and a decoupled massless spin-2 field out of massive gravity.Footnote 3 From simplicity let us imagine that no matter couples directly to the metric f μ ν (such a coupling does not affect the argument it simply allows to generalize massive gravity on arbitrary reference metrics [24]) and we set \(\alpha _{0} =\alpha _{1} = 0\). In that case it is useful to split the metric f μ ν as follows

$$\displaystyle\begin{array}{rcl} f_{\mu \nu } =\eta _{\mu \nu } + \frac{1} {M_{f}}\chi _{\mu \nu }\,.& &{}\end{array}$$
(5.36)

Taking the scaling limit M f  → ∞ while keeping χ μ ν fixed does not change the number of dofs in the theory but simply decouples some of them. In this limit, we obtain a theory of massive gravity and a decoupled massless-spin-2 field,

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{M_{f}\rightarrow \infty }& =& M_{g}^{2}\sqrt{-g}\left (R[g] + m^{2}\sum _{ n=2}^{4}\alpha _{ n}\mathcal{L}_{n}(\mathcal{K}[g,\eta ])\right ) \\ & & -\frac{1} {2}\chi ^{\mu \nu }\hat{\mathcal{E}}_{\mu \nu }^{\alpha \beta }\chi _{\alpha \beta }\,, {}\end{array}$$
(5.37)

where \(\hat{\mathcal{E}}\) is the Lichnerowicz operator which is the healthy linearized kinetic term for a massless spin-2 field. Notice that the second line is exact to all orders in χ, so the massless sector of the theory is not interacting at all, not even with itself. Nevertheless it still carries the two standard dofs of a massless spin-2 field, and the massive graviton carried in g μ ν carries five dofs, leading once again to the same number of dofs as any other healthy bi-gravity theory.

As already mentioned, one could generalize this procedure to allow for a non-trivial background metric, \(f_{\mu \nu } =\bar{ f}_{\mu \nu } + \frac{1} {M_{f}}\chi _{\mu \nu }\) before taking the limit M f  → ∞. In that case, the resulting theory is massive gravity on the reference metric \(\bar{f}_{\mu \nu }\) and a decoupled non-interacting massless spin-2 field.

The fact that this theory emerges from 5d GR which carries the correct number of dofs for a massive graviton is suggestive that the theory of massive gravity we have derived here does not suffer from the BD ghost. We shall prove this more explicitly in what follows working both in the ADM language and in the decoupling limit.

4 Absence of Boulware–Deser Ghost

4.1 ADM Language

The presence of a BD ghost in a large class of massive gravity theories was originally presented in the ADM language [5]. Starting with the ADM decomposition,

$$\displaystyle\begin{array}{rcl} \,\mathrm{d}s^{2} = -N_{ 0}^{2}\,\mathrm{d}t^{2} +\gamma _{\mathit{ ij}}\left (\,\mathrm{d}x^{i} + N^{i}\,\mathrm{d}t\right )\left (\,\mathrm{d}x^{j} + N^{j}\,\mathrm{d}t\right )\,,& &{}\end{array}$$
(5.38)

GR is special in that both the lapse and the shift are Lagrange multipliers, propagating 4 first class constraints. This means that the phase space has a priori 6 × 2 dofs in γ ij and its conjugate momentum but 8 of them are removed by the 4 first class constraints, leading to a total of 4 = 2 × 2 dofs in phase space or 2 dofs in field space which is the correct counting for GR (leading to the two first polarizations presented in Fig. 5.1.)

Now focusing on massive gravity (without the decoupled linearized massless spin-2 field), neither the lapse nor the shift remain linear. A priori this means that one looses four first class constraints, and one is left with a priori 6 degrees of freedom in γ ij in field space, which would correspond to the five expected dofs and an additional sixth BD ghost, which as we have seen would always signal a disaster (see Sect. 5.4.)

However this naive estimation does not account from the fact that not all the shift and lapse are necessarily independent. As first explained in [19] and then carried out in [20], the real criteria for determining the number of degrees of freedom in field space in d spacetime dimensions is

$$\displaystyle\begin{array}{rcl} \#\ \mathrm{field\ space\ dof} = \frac{1} {2}d(d - 1) - (d -\mathrm{ rank}\left (L\right ))\,,& &{}\end{array}$$
(5.39)

where the Hessian L μ ν is given by the second derivative of the potential \(\mathcal{U} = \sqrt{-g}\sum _{n}\alpha _{n}\mathcal{L}_{n}\),

$$\displaystyle\begin{array}{rcl} L_{\mu \nu } = \frac{\partial ^{2}\mathcal{U}} {\partial N^{\mu }\partial N^{\nu }}\,.& &{}\end{array}$$
(5.40)

In d = 2 dimensions, it was shown in [20] that the rank of L was 1 and so the number of physical dofs in 2 dimensions is zero, as it should be for a healthy spin-2 field without BD pathology. The counting carries through to any number of dimensions and in d = 4 is was shown in [19] for special cases and then in [25] in all generality that rankL = 3, for the special form of the potential given in (5.37) and so in the theory given in (5.37) has only 5 and not 6 dofs in the massive spin-2 field. This theory is thus free of the BD ghost.

4.2 Decoupling Limit

The theory of multi-gravity presented previously breaks (N − 1) copies of diffeomorphism invariance. To restore them one can introduce (N − 1) Stückelberg fields. The same counting remains for bi-gravity and massive gravity. In what follows we shall focus on the case of massive gravity bearing in mind that the same derivation follows for bi- and multi-gravity as well as for New Massive Gravity (NMG) [26].

When formulating the theory of massive gravity, we made use of a reference metric \(\bar{f}_{\mu \nu }\) which can be chosen to be Minkowski or other. We focus the discussion on a Minkowski reference metric \(\bar{f}_{\mu \nu } =\eta _{\mu \nu }\) but the essence of the argument remains the same for other reference metrics. See for instance [27] for the decoupling limit of a de Sitter reference metric. The existence of a reference metric breaks diff invariance, but it can be restored by introducing four Stückelberg fields ϕ a which transform as scalar under local diffs

$$\displaystyle\begin{array}{rcl} \eta _{\mu \nu } \rightarrow \tilde{\eta }_{\mu \nu } = \partial _{\mu }\phi ^{a}\partial _{\nu }\phi ^{b}\eta _{ ab}\,,& &{}\end{array}$$
(5.41)

where \(\tilde{\eta }_{\mu \nu }\) now transforms as a tensor under local diffs. Even if in bi-gravity the two metrics are dynamical it does not change the fact that the interaction between the two metrics breaks one copy of diff and the theory is not fully diff invariant unless the same four Stückelberg fields are introduced. The same remain valid for NMG and multi-gravity.

We can further split the Stückelberg fields into a helicity-0 and -1 modes:

$$\displaystyle\begin{array}{rcl} \phi ^{a} = x^{a} + \frac{1} {mM_{\mathrm{Pl}}}A^{a} + \frac{1} {m^{2}M_{\mathrm{Pl}}}\eta ^{\mathit{ab}}\partial _{ b}\pi \,,& &{}\end{array}$$
(5.42)

where the scales are introduced for later convenience and in what follows we only focus on the helicity-0 mode π. The full decoupling limit including the vector A a was derived in [28].

Using the expression (5.41) into (5.35) with \(f_{\mu \nu } \rightarrow \tilde{\eta }_{\mu \nu }\), we see directly that

$$\displaystyle\begin{array}{rcl} \mathcal{K}_{\,\,\nu }^{\mu } = \frac{1} {m^{2}M_{\mathrm{Pl}}}\eta ^{\mu \alpha }\varPi _{ \alpha \nu } + \mathcal{O}\left ( \frac{1} {M_{\mathrm{Pl}}}h\right )\,,& &{}\end{array}$$
(5.43)

where we write the metric g μ ν as

$$\displaystyle\begin{array}{rcl} g_{\mu \nu } =\eta _{\mu \nu } + \frac{1} {M_{\mathrm{Pl}}}h_{\mu \nu }\,.& &{}\end{array}$$
(5.44)

We now take the decoupling limit where M Pl → ∞ and m → 0 while keeping the scale \(\varLambda = (m^{2}M_{\mathrm{Pl}})^{1/3}\) fixed. Clearly in this decoupling limit \(\mathcal{K}\rightarrow \varPi\) and the mass terms for massive gravity given in ((5.26)–(5.28)) or equivalently ((5.29)–(5.31)) reduce to total derivatives. As a result to zeroth order in h∕M Pl the theory has no ghost.

We now proceed to first order in h∕M Pl, to that order the mass term becomes

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\mathrm{mGR}}& =& M_{\mathrm{Pl}}^{2}\sqrt{-g}\left (\frac{1} {2}R + m^{2}\left (\mathcal{L}_{ 2}[\mathcal{K}] +\alpha _{3}\mathcal{L}_{3}[\mathcal{K}] +\alpha _{4}\mathcal{L}_{4}[\mathcal{K}]\right )\right ){}\end{array}$$
(5.45)
$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\mathrm{mGR}}^{\mathrm{(dec)}}& =& -\frac{1} {2}h^{\mu \nu }\hat{\mathcal{E}}_{\mu \nu }^{\alpha \beta }h_{\alpha \beta } - h^{\mu \nu }\left (X_{\mu \nu }^{(1)} + \frac{1 + 3\alpha _{3}} {\varLambda ^{3}} X_{\mu \nu }^{(2)} + \frac{\alpha _{3} + 4\alpha _{4}} {\varLambda ^{6}} X_{\mu \nu }^{(3)}\right )\!,\qquad \ {}\end{array}$$
(5.46)

where as \(\hat{\mathcal{E}}\) is the Lichnerowicz operator and

$$\displaystyle\begin{array}{rcl} X^{(1)}{}_{ \mu '}^{\mu }& =& \varepsilon ^{\mu \nu \alpha \beta }\varepsilon _{\mu '\nu '\alpha \beta }\varPi _{\nu '}^{\nu }{}\end{array}$$
(5.47)
$$\displaystyle\begin{array}{rcl} X^{(2)}{}_{ \mu '}^{\mu }& =& \varepsilon ^{\mu \nu \alpha \beta }\varepsilon _{\mu '\nu '\alpha '\beta }\varPi _{\nu '}^{\nu }\varPi _{\alpha '}^{\alpha }{}\end{array}$$
(5.48)
$$\displaystyle\begin{array}{rcl} X^{(3)}{}_{ \mu '}^{\mu }& =& \varepsilon ^{\mu \nu \alpha \beta }\varepsilon _{\mu '\nu '\alpha '\beta '}\varPi _{\nu '}^{\nu }\varPi _{\alpha '}^{\alpha }\varPi _{\beta '}^{\beta }\,.{}\end{array}$$
(5.49)

This set of tensors satisfies some remarkable properties: First they are identically conserved. Second they share a similar structure as Galileon interactions and are indeed closely related. Third, they trivially satisfy the Galileon symmetry by construction (and this already at the level of the Lagrangian unlike Galileon interactions). Finally and most importantly, these interactions can be proven to have no ghost. The reason for that is that their respective equations of motion never bear more than two derivatives and the X 00 bears no time derivative, while X 0i carries at most a single time derivative.

The helicity-0 and -2 modes can be ‘semi-diagonalized’ by performing a field redefinition,

$$\displaystyle\begin{array}{rcl} h_{\mu \nu } =\bar{ h}_{\mu \nu } +\pi \eta _{\mu \nu } + \frac{1 + 3\alpha _{3}} {\varLambda ^{3}} \partial _{\mu }\pi \partial _{\nu }\pi \,,& &{}\end{array}$$
(5.50)

leading to a Galileon theory

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\mathrm{mGR}}^{\mathrm{(dec)}}& =& -\frac{1} {2}\bar{h}^{\mu \nu }\hat{\mathcal{E}}_{\mu \nu }^{\alpha \beta }\bar{h}_{\alpha \beta } +\sum _{ n=2}^{5} \frac{c_{n}} {\varLambda ^{3(n-2)}}\mathcal{L}_{\mathrm{Gal}}^{(n)} + \frac{\alpha _{3} + 4\alpha _{4}} {\varLambda ^{6}} \bar{h}^{\mu \nu }X_{\mu \nu }^{(3)}\,,\quad {}\end{array}$$
(5.51)

where \(\mathcal{L}_{\mathrm{Gal}}^{(n)}\) are the Galileon Lagrangian, \(\mathcal{L}_{\mathrm{Gal}}^{(n)} =\pi X^{(n-1)}{}_{\mu }^{\mu }\) and the c n are dimensionless coefficients related to the α n . We see that when \(\alpha _{3} + 4\alpha _{4} = 0\), the helicity-2 and -0 modes fully decouple in this limit and the interactions for the helicity-0 mode are pure Galileon interactions. The only two differences with a standard Galileon model is that it only has one free parameter (namely α 3) and the coupling to matter includes a disformal contribution

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\mathrm{matter}} = \frac{1} {M_{\mathrm{Pl}}}h_{\mu \nu }T^{\mu \nu } = \frac{1} {M_{\mathrm{Pl}}}\bar{h}_{\mu \nu }T^{\mu \nu } + \frac{1} {M_{\mathrm{Pl}}}\pi T \frac{1 + 3\alpha _{3}} {M_{\mathrm{Pl}}\varLambda ^{3}} \partial _{\mu }\pi \partial _{\nu }\pi T^{\mu \nu }\,,\quad \ & &{}\end{array}$$
(5.52)

which can lead to specific observational signatures as the field now also couple to radiation.

In [29, 30] the BD ghost was connected to the existence of an Ostrogradsky instability in the decoupling limit. The fact the decoupling limit of this theory is a Galileon which is known to be free of Ostrogradsky instability was therefore the first indication that the theory was in fact free of the BD ghost. As explained earlier this was later confirmed by a multitude of independent studies.

In what follows we will introduce the Vainshtein mechanism using the cubic Galileon as a toy model and discuss the existence of superluminalities.

5 Vainshtein Mechanism

The essence of the Vainshtein mechanism, and its subtleties is already manifest in the cubic Galileon

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\mathrm{cub}} = -\frac{1} {2}(\partial \pi )^{2} + \frac{1} {\varLambda ^{3}} (\partial \pi )^{2}\square \pi + \frac{1} {M_{\mathrm{Pl}}}\pi T\,.& &{}\end{array}$$
(5.53)

In the absence of the cubic interaction, the field π would always couple to matter with gravitational strength and would be incompatible with observations. In what follows we show how the cubic interaction at the low scale Λ ≪ M Pl is key in screening this scalar field.

5.1 Redressed Coupling

Let us consider a macroscopic source \(\bar{T}\) and smaller perturbations on top of it, \(T =\bar{ T} +\delta T\). Similarly we may split the field as the configuration \(\bar{\pi }\) soured by \(\bar{T}\) and its fluctuations \(\pi =\bar{\pi } +\delta \pi\). For definiteness we consider a constant source \(\bar{T}\) although the argument is relatively unaffected by the precise form of source, so long as there is a regime where \(\bar{T} \gg M_{\mathrm{Pl}}\varLambda ^{3}\). The background configuration is then given by

$$\displaystyle\begin{array}{rcl} & & \bar{\pi }= -\varLambda ^{3}Ax^{2}{}\end{array}$$
(5.54)
$$\displaystyle\begin{array}{rcl} \mathrm{with}\quad & & A = -\frac{1} {24}\left (1 -\left (1 + \frac{6\bar{T}} {M_{\mathrm{Pl}}\varLambda ^{3}}\right )^{1/2}\right ) \simeq \frac{1} {4\sqrt{6}}\sqrt{ \frac{\bar{T}} {M_{\mathrm{Pl}}\varLambda ^{3}}} \gg 1\,,{}\end{array}$$
(5.55)
$$\displaystyle\begin{array}{rcl} \mathrm{so}\quad & & \bar{\varPi }\sim \partial ^{2}\bar{\pi } \sim \varLambda ^{3}A \gg \varLambda ^{3}{}\end{array}$$
(5.56)

On top of these background configuration, the effective Lagrangian for the fluctuations is

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\delta \pi } = -\frac{Z} {2} (\partial \delta \pi )^{2} + \frac{1} {\varLambda ^{3}} (\partial \delta \pi )^{2}\square \delta \pi + \frac{1} {M_{\mathrm{Pl}}}\delta \pi \delta T\,,& &{}\end{array}$$
(5.57)

with

$$\displaystyle\begin{array}{rcl} Z = 1 + 24A\,.& &{}\end{array}$$
(5.58)

When \(\bar{T} \gg M_{\mathrm{Pl}}\varLambda ^{3}\) then A ≫ 1 and it follows that Z ≫ 1. Next we canonically normalize the field,

$$\displaystyle\begin{array}{rcl} \delta \pi = Z^{-1/2}\delta \hat{\pi }\,,& &{}\end{array}$$
(5.59)

so that the properly canonically normalized field sees the effective Lagrangian

$$\displaystyle\begin{array}{rcl} \mathcal{L}_{\delta \hat{\pi }} = -\frac{1} {2}(\partial \delta \hat{\pi })^{2} + \frac{1} {\varLambda _{\star }^{3}}(\partial \delta \hat{\pi })^{2}\square \delta \hat{\pi } + \frac{1} {M_{\mathrm{Pl}}\sqrt{Z}}\delta \hat{\pi }\delta T\,,& &{}\end{array}$$
(5.60)

with the new ‘redressed’ scale \(\varLambda _{{\ast}} =\varLambda Z^{1/2} \gg \varLambda\). As a result on the background of the source T 0 the field is no longer strongly coupled at the scale Λ but rather at the much scale Λ ∗. Notice that at no point do we consider the scale Λ or Λ ∗ to be the cutoff, as it would simply not make sense to have a cutoff which is background dependent unless some very peculiar mixing with high energy physics occurs. Instead Λ (resp. Λ ∗) are the scales at which tree-level unitarity breaks down. This scale differs from the cutoff which is the scale at which new physics enters (see [31] for other examples in physics where the strong coupling scale which dictates the breakdown of tree-level unitarity is distinct from the cutoff scale at which new physics enters.)

Moreover we see that the coupling to matter occurs at the new scale \(M_{\mathrm{Pl}}\sqrt{Z} \gg M_{\mathrm{Pl}}\). This means that in the vicinity of large sources T 0 (for instance the Sun), the coupling to other sources (for instance the planets of the solar system) is very much suppressed. This is precisely how the Vainshtein mechanism succeeds at screening the field π. In what follows we will show how this Vainshtein mechanism comes at the price of allowing superluminal classical velocities. After reviewing a simple example we shall see why the presence of these superluminalities do not imply acausality.

5.2 Superluminalities

5.2.1 Classical Superluminalities

Similarly as seen previously, if we split the field into a background configuration \(\bar{\pi }\) and a fluctuation δ π, with \(\bar{\varPi }_{\mu \nu } = \partial _{\mu }\partial _{\nu }\bar{\pi } \gg \varLambda ^{3}\) (by that we mean, that at least some of the eigenvalues of \(\bar{\varPi }_{\mu \nu }\) are larger than Λ 3), then the fluctuations δ π see the effective second order Lagrangian

$$\displaystyle\begin{array}{rcl} \mathcal{L}^{(2)} = -\frac{1} {2}Z^{\mu \nu }\partial _{\mu }\delta \pi \partial _{\nu }\delta \pi \,,& &{}\end{array}$$
(5.61)

with the effective metric

$$\displaystyle\begin{array}{rcl} Z^{\mu \nu } =\eta ^{\mu \nu } + \frac{4} {\varLambda ^{3}} \left (\bar{\varPi }^{\mu \nu } - [\bar{\varPi }]\eta ^{\mu \nu }\right )\,.& &{}\end{array}$$
(5.62)

Now without loss of generality, at any point x one can perform a global Lorentz transformation to a frame where Z  ν μ is diagonal. In that frame the speed of propagation along the direction x 1 is

$$\displaystyle\begin{array}{rcl} c_{s,1}^{2} = \frac{Z_{\,1}^{1}} {Z_{\,0}^{0}} = \frac{1 -\frac{4} {\varLambda ^{3}} \left (\bar{\varPi }_{\,0}^{0} +\bar{\varPi }_{ \,2}^{2} +\bar{\varPi }_{ \,3}^{3}\right )} {1 -\frac{4} {\varLambda ^{3}} \left (\bar{\varPi }_{\,1}^{1} +\bar{\varPi }_{ \,2}^{2} +\bar{\varPi }_{ \,3}^{3}\right )}\,.& &{}\end{array}$$
(5.63)

As a result, the field δ π propagates with superluminal classical (group and phase) velocity along the direction x 1 for any configuration admitting \(\bar{\varPi }_{\,0}^{0} >\bar{\varPi }_{ \,1}^{1}\) at least at one point. This is easily achieved, at least locally, for instance considering a plane wave \(\bar{\pi }= F(x^{1} - t)\) which satisfies the background equations of motion in the absence of any source. Then the fluctuations travel with classical superluminal group and phase velocity as soon as F″ > 0 [32, 33].

5.2.2 Front Velocity and Causality

The existence of these classical superluminalities has been the object of much concern and claims connecting them to acausality have been made. However it is important to emphasize that causality is not determined from the classical group or phase velocity but rather from the front velocity which is the high frequency limit of the phase velocity. As a consequence quantum corrections ought to be included in order to compute the front velocity and before any claims may be made on the causality of the theory. This is especially important in the context of these theories since we have seen that the strong coupling scale, or scale at which tree-level calculations can no longer be trusted depend on the background. As a result the tree-level (or classical) calculation presented above of the front velocity are only valid at low energy and break down precisely in the regime where one would want to connect it with causality. Consequently there has been so far no evidence that massive gravity or other theories that exhibit the Vainshtein mechanism are causal or acausal.

5.2.3 Galileon Duality

To emphasize further how the notion of classical group or front velocity can be misleading we perform a coordinate and field redefinition to specific example of quintic Galileon. Consider the following quintic Galileon [33],

$$\displaystyle\begin{array}{rcl} S_{\mathrm{quintic}} =\int \,\mathrm{ d}^{4}x\left (-\frac{1} {12}\mathcal{L}_{\mathrm{Gal}}^{(2)} + \frac{1} {6\varLambda ^{3}}\mathcal{L}_{\mathrm{Gal}}^{(3)} - \frac{1} {8\varLambda ^{6}}\mathcal{L}_{\mathrm{Gal}}^{(4)} + \frac{1} {30\varLambda ^{9}}\mathcal{L}_{\mathrm{Gal}}^{(5)}\right ),\qquad & &{}\end{array}$$
(5.64)

where the Galileon Lagrangian are given below Eq. (5.51). The same analysis as for the cubic Galileon applies here and similarly it is straightforward to find exact solutions in the absence of matter which exhibits superluminal propagation along any direction for the field fluctuation δ π.

Now performing the following combined field and coordinate transformation

$$\displaystyle\begin{array}{rcl} x^{\mu }& \rightarrow & \tilde{x}^{\mu } = x^{\mu } + \frac{1} {\varLambda ^{3}} \partial \pi (x){}\end{array}$$
(5.65)
$$\displaystyle\begin{array}{rcl} \pi (x)& \rightarrow & \rho (\tilde{x}) =\pi (x) + \frac{1} {\varLambda ^{3}} (\partial \pi (x))^{2}\,,{}\end{array}$$
(5.66)

the quintic Galileon theory introduced in (5.64) simplifies to a free theory for ρ [33]

$$\displaystyle\begin{array}{rcl} S_{\mathrm{quintic}} \rightarrow \tilde{ S} =\int \,\mathrm{ d}^{4}x\left (-\frac{1} {2}\left (\partial \rho \right )^{2}\right )\,,& &{}\end{array}$$
(5.67)

which can never exhibit any superluminalities and is manifestly causal. This does not mean that the causal structure between the two representations is different, quite the opposite the causal structure is the same but is distinct from the notion of superluminalities. This comes to show how the notion of classical superluminality can be misleading and one ought to keep track of the front velocity (with in this case its full quantum corrections) in order to infer whether or not the theory is causal.

6 Summary and Outlook

In this proceedings we have reviewed how to derive consistent and ghost-free four-dimensional theories of massive gravity using five-dimensional General Relativity as our starting point. In the case of an infinite extra dimension, gravity may be localized in four dimensions by inducing a four-dimensional Einstein Hilbert term on a four-dimensional brane. Depending on the setup, this leads to a general DBI-Galileon model or to a soft theory of massive gravity known as DGP. Alternatively for finite size-extra dimensions, a discretization of this extra dimension (either in real space or in Fourier space) leads to a ghost-free theory of massive gravity (sometimes known as dRGT) provided the discretization is performed in the vielbein formalism. Galileons are ubiquitous to all these theories of massive gravity and provide a simple way to understand the Vainshtein mechanism whereby the helicity-0 mode of the graviton is screened in the vicinity of large matter sources. This Vainshtein mechanism is also shown to come hand in hand with classical superluminalities. While superluminalities in the front velocity would indeed imply acausality superluminal classical group and front velocities do not have the same implications and have been observed in nature. In order to comment on the causality of the theory it is therefore essential to find a prescription which allows us to compute the front velocity with all its quantum corrections. This is where the Vainshtein mechanism and its implementation at the quantum level could come in useful.