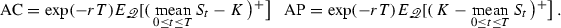Bid-Ask Spread for Exotic Options under Conic Finance

Abstract

This paper puts the concepts of model and calibration risks into the perspective of bid and ask pricing and marketed cash-flows which originate from the conic finance theory. Different asset pricing models calibrated to liquidly traded derivatives by making use of various plausible calibration methodologies lead to different risk-neutral measures which can be seen as the test measures used to assess the (un)acceptability of risks.

1 Introduction

The publication of the pioneering work of Black and Scholes in 1973 sparked off an unprecedented boom in the derivative market, paving the way for the use of financial models for pricing financial instruments and hedging financial positions. Since the late 1970s, incited by the emergence of a liquid market for plain-vanilla options, a multitude of option pricing models has seen the day, in an attempt to mimic the stylized facts of empirical returns and implied volatility surfaces. The need for such advanced pricing models, ranging from stochastic volatility models to models with jumps and many more, has even been intensified after Black Monday, which evidenced the inability of the classical Black–Scholes model to explain the intrinsic smiling nature of implied volatility. The following wide panoply of models has inescapably given rise to what is commonly referred to as model uncertainty or, by malapropism, model risk. The ambiguity in question is the Knightian uncertainty as defined by Knight [17], i.e., the uncertainty about the true process generating the data, as opposed to the notion of risk dealing with the uncertainty on the future scenario of a given stochastic process. This relatively new kind of “risk” has significantly increased this last decade due to the rapid growth of the derivative market and has led in some instances to colossal losses caused by the misvaluation of derivative instruments. Recently, the financial community has shown an accrued interest in the assessment of model and parameter uncertainty (see, for instance, Morini [19]). In particular, the Basel Committee on Banking Supervision [2] has issued a directive to compel financial institutions to take into account the uncertainty of the model valuation in the mark-to-model valuation of exotic products. Cont [6] set up the theoretical basis of a quantitative framework built upon coherent or convex risk measures and aimed at assessing model uncertainty by a worst-case approach.¹ Addressing the question from a more practical angle, Schoutens et al. [22] illustrated on real market data how models fitting the option surface equally well can lead to significantly different results once used to price exotic instruments or to hedge a financial position.

Another source of risk for the price of exotics originates from the choice of the procedure used to calibrate a specific model on the market reality. Indeed, although the standard approach consists of solving the so-called inverse problem, i.e., quoting Cont [7], of finding the parameters for which the value of benchmark instruments, computed in the model, corresponds to their market prices, alternative procedures have seen the day. The ability of the model to replicate the current market situation could rather be specified in terms of the distribution goodness of fit or in terms of moments of the asset log-returns as proposed by Eriksson et al. [9] and Guillaume and Schoutens [12]. In practice, even solving the inverse problem requires making a choice among several equally suitable alternatives. Indeed, matching perfectly the whole set of liquidly traded instruments is typically not plausible such that one looks for an “optimal” match, i.e., for the parameter set which replicates as well as possible the market price of a set of benchmark instruments. Put another way, we minimize the distance between the model and the market prices of those standard instruments. Hence, the calibration exercise first requires not only the definition of the concept of a distance and its metric but also the specification of the benchmark instruments. Benchmark instruments usually refer to liquidly traded instruments. In equity markets, it is a common practice to select liquid European vanilla options. But even with such a precise specification, several equally plausible selections can arise. We could for instance select out-of-the-money options with a positive bid price, following the methodology used by the Chicago Board Options Exchange (CBOE [4]) to compute the VIX volatility index, or select out-of-the-money options with a positive trading volume, or ... Besides, practitioners sometimes resort to time series or market quotes to fix some of the parameters beforehand, allowing for a greater stability of the calibrated parameters over time. In particular, the recent emergence of a liquid market for volatility derivatives has made this methodology possible to calibrate stochastic volatility models. Such an alternative has been investigated in Guillaume and Schoutens [11] under the Heston stochastic volatility model, where the spot variance and the long-run variance are inferred from the spot value of the VIX volatility index and from the VIX option price surface, respectively. Another example is Brockhaus and Long [3] (see also Guillaume and Schoutens [13]) who propose to choose the spot variance, the long-run variance, and the mean reverting rate of the Heston stochastic volatility model in order to replicate as well as possible the term structure of model-free variance swap prices, i.e., of the return expected future total variance. Regarding the specification of the distance metric, several alternatives can be found in the literature. The discrepancy could be defined as relative, absolute, or in the least-square sense differences and expressed in terms of price or implied volatility. Detlefsen and Härdle [8] introduced the concept of calibration risk (or should we say calibration uncertainty) arising from the different (plausible) specifications of the objective function we want to minimize. Later, Guillaume and Schoutens [10] and Guillaume and Schoutens [11] extended the concept of calibration risk to include not only the choice of the functional but also the calibration methodology and illustrated it under the Heston stochastic volatility model.

In order to measure the impact of model or parameter ambiguity on the price of structured products, several alternatives have been proposed in the financial literature. Cont [6] proposed the so-called worst-case approach where the impact of model uncertainty on the value of a claim is measured by the difference between the supremum and infimum of the expected claim price over all pricing models consistent with the market quote of a set of benchmark instruments (see also Hamida and Cont [16]). Gupta and Reisinger [14] adopted a Bayesian approach allowing for a distribution of exotic prices resulting directly from the posterior distribution of the parameter set obtained by updating a plausible prior distribution using a set of liquidly traded instruments (see also Gupta et al. [15]). Another methodology allowing for a distribution of exotic prices, but based on risk-capturing functionals has recently been proposed by Bannör and Scherer [1]. This method differs from the Bayesian approach since the distribution of the parameter set is constructed explicitly by allocating a higher probability to parameter sets leading to a lower discrepancy between the model and market prices of a set of benchmark instruments. Whereas the Bayesian approach requires a parametric family of models and is consequently appropriate to assess parameter uncertainty, the two alternative proxies (i.e., the worst-case and the risk-capturing functionals approaches) can be considered to quantify the ambiguity resulting from a broader set of models with different intrinsic characteristics. These three approaches share the characteristic that the plausibility of any pricing measure $\fancyscript{Q}$ is assessed by considering the average distance between the model and market prices, either by allocating a probability weight to each measure $\fancyscript{Q}$ which is proportional to this distance or by selecting the measures $\fancyscript{Q}$ for which the distance falls within the average bid-ask spread. Hence, the resulting measure of uncertainty implicitly depends on the metric chosen to express this average distance. We will adopt a somewhat different methodology, although similar to the ones above-mentioned. We start from a set of plausible calibration procedures and we consider the resulting risk-neutral probability measures (i.e., the optimal parameter sets) as the test measures used to assess the (un)acceptability of any zero cost cash-flow $X$. In other words, these pricing measures can be seen as the ones defining the cone of acceptable cash-flows; where $X$ is acceptable or marketed, denoted by $X \in \fancyscript{A}$, if its expectation under any of the test measures $\fancyscript{Q}$ is nonnegative:

$$ X \in \fancyscript{A} \Leftrightarrow E_{\fancyscript{Q}}[X] \ge 0 \; \forall \fancyscript{Q} \in \fancyscript{M}. $$

This allows us to define the cone of marketed cash-flows in a market-consistent way rather than parametrically in terms of some family of concave distortion functions as proposed by Cherny and Madan [5]. We can even play with the minimum proportion $p$ of model prices included within their bid-ask spread in order to change the amplitude of the cone of acceptability by requiring that at least $\lceil p M \rceil$ model prices are within their market spread for $\fancyscript{Q}$ to be included in the set of test measures $\fancyscript{M}$:

$$ \fancyscript{Q} \in \fancyscript{M} \Leftrightarrow \# \left\{ \widehat{P}^{\fancyscript{Q}}_i \in [b_i, a_i], i = 1, \ldots , M\right\} \ge \lceil p M \rceil , $$

where $\widehat{P}^{\fancyscript{Q}}_i, \, a_i, \, b_i, \ i=1,\dots , M$ denote the model price under the pricing measure $\fancyscript{Q}$, the quoted ask price, and the quoted bid price of the $M$ benchmark instruments, respectively. The higher the proportion, the smaller the set of test measures $\fancyscript{M}$ and hence, the wider the cone of acceptability. We opt for a threshold expressed as a percentage rather than as an average distance since we want our specification to be free of any distance metric. Indeed, the set $\fancyscript{M}$ will be built by considering different objective functions (expressed as price or implied volatility differences, as absolute, relative, or in the least-square sense differences, ...) such that we do not want to favor any of these metrics, to the detriment of the others. The impact of model or parameter uncertainty on the price of exotic (i.e., illiquid) instruments is then assessed by adopting a worst-case approach as in Cont [6]:

$$\begin{aligned} s(p) = \max \limits _{\fancyscript{Q} \in \fancyscript{M}} \left\{ {\mathrm{EP}}^{\fancyscript{Q}}\right\} - \min \limits _{\fancyscript{Q} \in \fancyscript{M}} \left\{ {\mathrm{EP}}^{\fancyscript{Q}}\right\} , \end{aligned}$$

(1)

provided that $\fancyscript{M} \ne \emptyset$; where ${\mathrm{EP}}^{\fancyscript{Q}}$ denotes the exotic price under the pricing measure $\fancyscript{Q}$. The model uncertainty can thus be quantified by the bid-ask spread of illiquid products. Indeed, the cash-flow of selling a claim with payoff $X$ at time $T$ at its ask price is acceptable for the market if $E_{\fancyscript{Q}}[a- \exp (-rT)X] \ge 0, \forall \fancyscript{Q} \in \fancyscript{M}$, i.e., if $a \ge \exp (-rT) \max \limits _{\fancyscript{Q} \in \fancyscript{M}} \left\{ E_{\fancyscript{Q}}[X]\right\}$. For the sake of competitiveness, the ask price is set at the minimum value, i.e.,

$$ a = \exp (-rT) \max \limits _{\fancyscript{Q} \in \fancyscript{M}} \left\{ E_{\fancyscript{Q}}[X]\right\} . $$

Similarly, the cash-flow of buying a claim with payoff $X$ at time $T$ at its bid price is acceptable for the market if $E_{\fancyscript{Q}}[-b +\exp (-rT)X] \ge 0, \forall \fancyscript{Q} \in \fancyscript{M}$, i.e., taking the maximum possible value for competitiveness reasons

$$ b = \exp (-rT) \min \limits _{\fancyscript{Q} \in \fancyscript{M}} \left\{ E_{\fancyscript{Q}}[X]\right\} . $$

The impact of model uncertainty can be expressed as a function of the severity of the percentage threshold $p$. We note that decreasing the threshold ultimately boils down to considering a thinner set of benchmark instruments since the model price has to fall within the market bid-ask spread for a smaller number of calibration instruments in order for a pricing measure to be selected. In particular, such a relaxation typically results in the “elimination” of the most illiquid calibration instruments, i.e., deep out-of-the-money options in the case of equity markets (see Fig. 2).

For the numerical study, we consider the Variance Gamma (VG) model of Madan et al. [18] only, although the methodology can be equivalently used to assess calibration or/and model uncertainty. The calibration instrument set consists of liquid out-of-the-money options: moving away from the forward price, we select put and call options with a positive bid price and with a strike lower and higher than the forward price, respectively, and this until we encounter two successive options with zero bid. Denoting by $P_i = \frac{a_i + b_i}{2}$ the mid-price of option $i$ and by $\sigma _i$ its implied volatility, the set of measures $\fancyscript{M}$ results from the following specifications for the objective function we minimize (i.e., for the distance and its metric):

• 1. Root-mean square error (RMSE)

  • a. price specification

    $$ {\mathrm{RMSE}} = \sqrt{\sum \limits _{i=1}^M \omega _i \left( P_i - \widehat{P}_i\right) ^2} $$

  • b. implied volatility specification

    $$ {\mathrm{RMSE}}^{\sigma } = \sqrt{\sum \limits _{i=1}^M \omega _i \left( \sigma _i - \widehat{\sigma }_i\right) ^2} $$

• 2. Average relative percentage error (ARPE)

  • a. price specification

    $$ {\mathrm{ARPE}} = \sum \limits _{i=1}^M \omega _i \frac{\left| P_i - \widehat{P}_i\right| }{P_i} $$

  • b. implied volatility specification

    $$ {\mathrm{ARPE}}^{\sigma } = \sum \limits _{i=1}^M \omega _i \frac{\left| \sigma _i - \widehat{\sigma }_i\right| }{\sigma _i} $$

• 3. Average absolute error (APE)

  • a. price specification

    $$ {\mathrm{APE}} = \frac{1}{\bar{P}} \sum \limits _{i=1}^M \omega _i \left| P_i - \widehat{P}_i\right| $$

  • b. implied volatility specification

    $$ {\mathrm{APE}}^{\sigma } = \frac{1}{\bar{\sigma }} \sum \limits _{i=1}^M \omega _i \left| \sigma _i - \widehat{\sigma }_i\right| , $$

    where $\bar{P}$ and $\bar{\sigma }$ denote the average option price and the average implied volatility, respectively.

Each of these six objective functions can again be subdivided into an unweighted functional for which the weight $\omega _i = \omega = \frac{1}{M} \ \forall i$ and a weighted functional for which the weight $\omega _i$ is proportional to the trading volume of option $i$. We furthermore consider the possibility of adding an extra penalty term to the objective function in order to force the model prices to lie within their market bid-ask spread. Besides these standard specifications (in terms of the price or the implied volatility of the calibration instruments), we consider the so-called moment matching market implied calibration proposed by Guillaume and Schoutens [12] and which consists in matching the moments of the asset log-return which are inferred from the implied volatility surface. As the VG model is fully characterized by three parameters, we consider three standardized moments, namely the variance, the skewness, and the kurtosis. Since as shown by Guillaume and Schoutens [12], the variance can always be perfectly matched, we either allocate the same weight to the matching of the skewness and the kurtosis or we match uppermost the lower moment, i.e., the skewness. This leads to a total of 26 plausible calibration procedures, each of them leading to a test measure $\fancyscript{Q} \in \fancyscript{M}$ provided that the proportion of model prices falling within their market bid-ask spread is at least equal to the threshold $p$.

Fig. 1

Maximum proportion $\pi$ of option prices replicated within their bid-ask spread (upper) and option bid-ask spreads (below)

2 Exotic Bid-Ask Spread

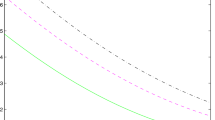
For the numerical study, we consider daily S&P 500 option surfaces for a timespan ranging from October 2008 to October 2009, including ,therefore, the recent credit crunch². We calibrate the VG model daily on the quoted (liquid) maturity which is the closest to the reference maturity of three months. Note that we only consider maturities for which the total trading volume of out-of-the-money options exceeds 1,000 contracts which allows to avoid the extreme situation of an undetermined calibration problem where the number of parameters to calibrate is higher than the number of benchmark instruments. This also ensures that the number of option prices is large enough (and so the strike range wide and refined enough) to guarantee a sufficient precision for the derived market implied moments. For each of the trading days included in the sample period, we successively perform the 26 calibration methodologies, which leads to 26 optimal parameter sets. We then select those for which the proportion of model prices falling within their market bid-ask spread is at least $p$. The higher the threshold $p$, the fewer the test measures $\fancyscript{Q} \in \fancyscript{M}$ and hence, the thinner the exotic bid-ask spreads. Figure 1 shows the highest proportion $\pi$ of option prices replicated within their bid-ask spread for the 26 above-mentioned calibration procedures:

$$\begin{aligned} \pi = \frac{1}{M} \max \limits _{\fancyscript{Q}} \# \left\{ \widehat{P}^{\fancyscript{Q}}_i \in [b_i, a_i], i = 1, \ldots , M\right\} . \end{aligned}$$

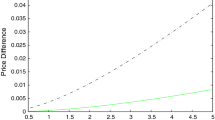
If $\pi < p$, then $\fancyscript{M}$ is an empty set and there does not exist exotic spread for that particular threshold $p$ as defined by (1). Hence, when selecting the proportion threshold $p$, we should keep in mind the trade-off between the in-spread precision and the number of test measures. Indeed, the higher the proportion, the higher the precision but the fewer the measures selected as test measure, which can in turn lead to an underestimation of the calibration uncertainty measured as the exotic bid-ask spreads. From Fig. 1, we observe that $\pi$ is significantly higher during the heart of the recent credit crunch, i.e., from the beginning of the sample period until mid 2009. This can easily be explained by the typically wider bid-ask spreads observed during market distress periods. Indeed, as shown on the lower panel of Fig. 1, the quoted spread for at-the-money, in-the-money ($K = 0.75 \, S_0$), and out-of-the-money ($K = 1.25 \, S_0$) options has significantly shrunk after the troubled period of October 2008–July 2009.

Fig. 2

Number of options for which the model price falls within the quoted bid-ask spread

Figure 2 shows the number of vanilla options whose model price falls within the quoted bid-ask spread as a function of the option moneyness for four of the calibration procedures under investigation, namely the weighted and unweighted RMSE price and implied volatility specifications without penalty term. To assess the impact of moneyness on the model ability to replicate option prices within their bid-ask spread, we split the strike range into 21 classes: $\frac{K}{S_0} < 0.5, \ 0.5 \le \frac{K}{S_0} < 0.55, \ 0.55 \le \frac{K}{S_0} < 0.6, \ldots , 1.45 \le \frac{K}{S_0} < 1.5$, and $\frac{K}{S_0} > 1.5$. We clearly see that, at least for the price specifications, option prices falling outside their quoted bid-ask spread are mainly observed for deep out-of-the-money calls and puts. This trend is even more marked and present in the implied volatility specifications when we add a penalty term in the objective function to constraint the model price within the market spread. Hence, increasing the proportion threshold $p$ mainly boils down to limit the set of calibration instruments to close to the money vanilla options.

In order to illustrate the impact of parameter uncertainty on the bid-ask spread of exotics, we consider the following path dependent options (with a maturity of $T = 3$ months):

• 1. Asian option

  The payoff of Asian options depends on the arithmetic average of the stock price from the emission to the maturity date of the option. The fair price of the Asian call and put options with maturity $T$ is given by

  

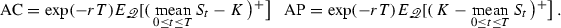
• 2. Lookback call option

  The payoff of lookback call and put options corresponds to the call and put vanilla payoff where the strike is taken equal to the lowest and highest levels the stock has reached during the option lifetime, respectively. The fair price of the lookback call and put with maturity $T$ is given by

  $$ {\mathrm{LC}} = \exp (- r T)E_{\fancyscript{Q}} \left[ (S_T - m^S_T)^{+}\right] \quad {\mathrm{LP}} = \exp (- r T)E_{\fancyscript{Q}} \left[ (M^S_T - S_T)^{+}\right] , $$

  respectively, where $m^X_t$ and $M_X^t$ denote the minimum and maximum processes of the process $X = \left\{ X_t , 0 \le t \le T \right\}$, respectively:

  $$ m^X_t = \inf \left\{ X_s , 0 \le s \le t\right\} \quad M^X_t = \sup \left\{ X_s , 0 \le s \le t\right\} . $$

• 3. Barrier call option

  The payoff of a one-touch barrier option depends on whether the underlying stock price reaches the barrier $H$ during the lifetime of the option. We illustrate the findings by looking at the up-and-in call and the down-and-in put price:

  $$ {\mathrm{UIBC}} = \exp (- r T)E_{\fancyscript{Q}} \left[ (S_T - K)^{+} \mathbf 1 \left( M^S_T \ge H\right) \right] $$
  $$ {\mathrm{DIBP}} = \exp (- r T)E_{\fancyscript{Q}} \left[ (K - S_T)^{+} \mathbf 1 \left( m^S_T \le H\right) \right] . $$

• 4. Cliquet option

  The payoff of a cliquet option depends on the sum of the stock returns over a series of consecutive time periods; each local performance being first floored and/or capped. Moreover, the final sum is usually further floored and/or capped to guarantee a minimum and/or maximum overall payoff such that cliquet options protect investors against downside risk while allowing them for significant upside potential. The Cliquet we consider has a fair price given by

  $$ {\mathrm{Cliquet}} = \exp (- r T)E_{\fancyscript{Q}} \left[ \max \left( 0,\sum _{i=1}^N \min \left( {\mathrm{cap}}, \max \left( {\mathrm{floor}}, \frac{S_{t_i} - S_{t_{i-1}}}{S_{t_{i-1}}}\right) \right) \right) \right] . $$

Fig. 3

Evolution of exotic bid and ask prices through time

Fig. 4

Evolution of exotic relative bid-ask spreads (in absolute value) through time

For sake of comparison, we also price a 3 months at-the-money call option. Note that this option does not generally belong to the set of benchmark instruments since, most of the time, we can not observe a market quote for the option with the exact same maturity and moneyness.

The path dependent nature of exotic options requires the use of the Monte Carlo procedure to simulate sample paths of the underlying index. The stock price process

$$ S_t = \frac{S_0 \exp ((r-q) t + X_t)}{E_{\fancyscript{Q}}[\exp (X_t)]}, \quad X \sim VG(\sigma , \nu , \theta ) $$

is discretized by using a first order Euler scheme (for more details on the simulation, see Schoutens [21]). The (standard) Monte Carlo simulation is performed by considering one million scenarios and 252 trading days a year.

The bid and ask prices and the relative bid-ask spread (dollar bid-ask spread expressed as a proportion of the mid-price) of different exotic options are shown on Figs. 3 and 4, respectively, and this for a proportion threshold $p$ equal to 0.5, 0.75, and 0.9. For sake of comparison, Fig. 5 shows the same results but for the 3 months at-the-money call option. The figures clearly indicate that the impact of parameter uncertainty is much more marked for path-dependent derivatives than for (non-quoted) vanilla options. Indeed, the relative bid-ask spread is of a magnitude order at least 10 times higher for the Asian call, lookback call, barrier call, and cliquet than for the vanilla call option. Besides, we observe that a far above average call relative spread does not necessarily imply a far above average percentage spread for path dependent options. In order to assess the consistency of our findings, we have reproduced the Monte Carlo simulation 400 times for one fixed quoting day (namely October, 1, 2008) with different sets of sample paths and computed the option relative spreads for each simulation. Figure 6 shows the resultant histogram for each relative spread and clearly brings out the consistency of the results: the relative spread is far more significant for the exotic options than for the vanilla options whatever the set of sample paths considered. The consistency of the Monte Carlo study is besides guaranteed by the fact that we used the same set of sample paths to price each option. Table 1 which shows the average price, standard deviation, and relative spread (across the 400 Monte Carlo simulations) for the price weighted RMSE functional confirms that the exotic bid-ask spreads are due to the nature of the exotic options rather than to the intrinsic uncertainty of Monte Carlo simulations. Indeed, the Monte Carlo relative spread given in Table 1 is significantly smaller than the option spread depicted on Fig. 6, and this for each exotic option. Table 2 shows the average of the relative spread over the whole period under investigation, and this for the different options under consideration. We clearly observe that the threshold $p$ impacts more severely the spread of the path-dependent options. Indeed, decreasing $p$ leads to a sharper increase of the relative bid-ask spread for the exotic options than for the European call and put options. Besides, the calibration risk is predominant for the up-and-in barrier call option and, to a smaller extent, for the Asian options. Table 3 shows the 95 % quantile of relative bid-ask spreads. We clearly see that in terms of extreme events, the more risky options are the up-and-in barrier call option and the lookback options. By way of conclusion, our findings clearly illustrate the impact of the calibration methodology on the price of exotic options, suggesting that risk managers should take into account calibration uncertainty when assessing the safety margin.

Fig. 5

Evolution of vanilla bid and ask prices and relative bid-ask spread (in absolute value) through time

Fig. 6

Relative bid-ask spreads (in absolute value) for different Monte Carlo simulations

Table 1 Monte Carlo precision

Table 2 Average relative bid-ask spreads (in %)

Table 3 95 % quantile of relative bid-ask spreads (in %)

3 Conclusion

This paper sets the theoretical foundation of a new framework aimed at assessing the impact of calibration uncertainty. The main advantage of the proposed methodology resides in its metric-free nature since the selection of test measures does not depend on any specified distance. Besides, the paper links the concept of uncertainty and the recently developed conic finance theory by defining the test measures used to construct the cone of acceptable cash-flows as the pricing measures resulting from any plausible calibration methodology such that model and parameter uncertainties are naturally measured as bid-ask spreads. The numerical study has highlighted the significant impact of parameter uncertainty for a wide range of path-dependent options under the popular VG model.