Reducing Surrender Incentives Through Fee Structure in Variable Annuities

Abstract

In this chapter, we study the effect of the fee structure of a variable annuity on the embedded surrender option. We compare the standard fee structure offered in the industry (fees set as a fixed percentage of the variable annuity account) with periodic fees set as a fixed, deterministic amount. Surrender charges are also taken into account. Under fairly general conditions on the premium payments, surrender charges and fee schedules, we identify the situation when it is never optimal for the policyholder to surrender. Solving partial differential equations using finite difference methods, we present numerical examples that highlight the effect of a combination of surrender charges and deterministic fees in reducing the value of the surrender option and raising the optimal surrender boundary.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A variable annuity (VA) is a unit-linked insurance product, which guarantees a certain amount at some future dates. Usually, the policyholder pays an initial premium for the contract. This premium is invested in a mutual fund chosen by the policyholder. There are different kinds of VAs defined by the type of guarantees embedded in the contract (for more details see Hardy [9]). In this paper, we focus on a variable annuity contract that pays the maximum of the mutual fund value and a guaranteed amount at maturity. This type of VA is referred to as a guaranteed minimum accumulation benefit (GMAB) (see Bauer et al. [1]).

Typically, the fee that covers the management of the VA and embedded financial guarantees is set as a constant percentage of the VA account and withdrawn directly from it at regular intervals. When the account value is high, the financial guarantee is worth very little, but the fee is still being paid as the same percentage. Thus, it represents an incentive for the policyholder to surrender the contract and take the amount accumulated in the account. Such surrenders represent an important risk for VA issuers as the expenses linked to the sale of the policy are typically reimbursed through the fees collected throughout the duration of the contract. As exposed by Kling et al. [11], unexpected surrenders also compromise the efficiency of dynamic hedging strategies.

There are various ways to reduce the incentive to surrender a VA contract with guarantees. For example, insurance companies usually impose surrender charges, which reduce the amount available at surrender. Milevsky and Salisbury [13] argue that these charges are necessary for VA contracts to be both hedgeable and marketable. The design of VA benefits can also discourage policyholders from surrendering. Kling et al. [11] discuss for example the impact of ratchet options (possibility to reset the maturity guarantee as the fund value increases) to convince policyholders to keep the VA alive. Yet another way to reduce the incentive to surrender can be to modify the way fees are paid from the VA account. As explained above, the typical constant percentage fee structure leads to a mismatch between the fee paid and the value of the financial guarantee, which can discourage the policyholder from staying in the contract.¹ By reducing the fee paid when the value of the financial guarantee is low, it is possible to reduce the value of the real option to surrender embedded in a VA. The new fee structure can take different forms. For example, Bernard et al. [2] suggest to set a certain account value above which no fee will be paid. This is shown to modify the rational policyholder’s surrender incentive. In this paper, we explore another fee structure so that part of (or all) the fee is paid as a deterministic periodic amount. The intuition behind this fee structure is that the amount will represent a lower percentage of the account value as the value of the financial guarantee decreases. This will affect the surrender incentive, and reduce the additional value created by the possibility to surrender the contract.

To explore the effect of the deterministic fee amount on the surrender incentive, we consider a VA with a simple GMAB. We assume that the total fee withdrawn from the VA account throughout the term of the contract is set as the sum of a fixed percentage $c$ of the account value, and a deterministic, pre-determined amount $p_t$ at time $t$ (in other words, the deterministic amount does not need to be constant).² Our paper constitutes a significant extension of the results obtained on the optimal surrender strategy for a fee set as a fixed percentage of the fund [4], since the deterministic fee structure increases the complexity of the dynamics of the VA account value. For this reason, we need to resort to PDE methods to obtain the optimal surrender strategy when a portion of the fee is set as a deterministic amount. This paper also extends the work done on state-dependent fee structures, since Bernard et al. [2] do not quantify the reduction in the surrender incentive resulting from the new fee structure.

Throughout the paper, our main goal is to investigate the impact of the deterministic fee amount on the value of the surrender option. In Sect. 2, we describe the model and the VA contract. Section 3 introduces a theoretical result and discusses the valuation of the surrender option. Numerical examples are presented in Sects. 4 and 5 concludes.

2 Assumptions and Model

Consider a market with a bank account yielding a constant risk-free rate $r$ and an index evolving as in the Black-Scholes model so that

$$ \frac{\mathrm{{d}}S_t}{S_t}=r\mathrm{{d}}t+\sigma \mathrm{{d}}W_t, $$

under the risk-neutral measure $\mathbb {Q}$, where $\sigma >0$ is the constant instantaneous volatility of the index. Let $\fancyscript{F}_t$ be the natural filtration associated with the Brownian motion $W_t$.

In this paper, we use a Black-Scholes setting since its simplicity allows us to compute prices explicitly, and thus to study the surrender incentive precisely. More realistic market models could be considered, but resorting to Monte Carlo methods or more advanced numerical methods would be required. Since the focus of this paper is on the surrender incentive, we believe that the Black-Scholes model’s approximation of market dynamics is sufficient to provide insight on the effect of the deterministic amount fee structure.

2.1 Variable Annuity

We consider a VA contract with an underlying fund fully invested in the index $S$. At time $t$, we assume that the fee paid is the sum of a constant percentage $c\ge 0$ of the account value and a deterministic amount $p_t$. Setting $p_t=0$, we will find back the results commonly used in the literature with the fee being only paid as a percentage of the fund (see for example [4]).

The motivation to study periodic deterministic fees is that the surrender incentives when the fees are paid as a fixed percentage of the fund are larger than when the fees are set as a deterministic amount. This will be illustrated via numerical examples in Sect. 4.

We further assume that the investment of the policyholder is $P_0$ at time 0, and that regular additional premiums $a_t$ are paid at time $t$. Additional contributions are common in variable annuities but they are regularly neglected in the literature and most academic research focuses on the single premium case as it is simpler. When additional contributions can be made to the account throughout time, VAs are called Flexible Premiums Variable Annuities (FPVAs). Chi and Lin [7] provide examples of such VAs where the policyholder is given the choice between a single premium and a periodic monthly payment in addition to some initial lump sum. Analytical formulae for the value of such contracts can be found in [8, 10]. In the first part of this chapter, we show how flexible premium payments influence the surrender value.

We assume that all premiums paid at 0 and at later times $t$ are invested in the fund. All fees (percentage or fixed fees) are taken from the fund. We need to model the dynamics of the fund. Our approach is inspired by Chi and Lin [7]. For the sake of simplicity, we assume that all cash flows happen in continuous time, so that a fixed payment of $A$ at time 1 (say, end of the year) is similar to a payment made continuously over the interval $[0,1]$. Due to the presence of a risk-free rate $r$, an amount paid at time $T$ equal to $A$ is equivalent to an instantaneous contribution of $a_t~\mathrm{{d}}t$ at any time $t\in (0,1]$ so that the annual amount paid per year is $A=\int _0^1 a_t e^{r(1-t)} \mathrm{{d}}t$. By abuse of notation, if $a_t$ is constant over the year, we will write that $a_t$ is the annual rate of contribution per year (although there is no compounding effect).

Specifically, the dynamics of the fund can be written as follows

$$ \mathrm{{d}}F_t=(r-c)F_t \mathrm{{d}}t+\sigma F_t \mathrm{{d}}W_t+a_t \mathrm{{d}}t-p_t \mathrm{{d}}t $$

with $F_0=P_0$, and where $F_t$ denotes the value of the fund at time $t$, $a_t$ is the annual rate of contributions, $c$ is the annual rate of fees, and $p_t$ is the annual amount of fee to pay for the options. Similarly as [7] it is straightforward to show that

$$ F_t=F_0e^{(r-c-\frac{\sigma ^2}{2})t+\sigma W_t}+\int \limits _0^t (a_s-p_s)e^{(r-c-\frac{\sigma ^2}{2})(t-s)+\sigma (W_t-W_s)} \mathrm{{d}}s, \ \quad t\ge 0, $$

that is

$$\begin{aligned} F_t=S_te^{-ct}+\int \limits _0^t (a_s-p_s)e^{-c(t-s)}\frac{S_t}{S_s} \mathrm{{d}}s, \end{aligned}$$

(1)

in particular $P_0=F_0=S_0$. To simplify the notation, we will write

$$\begin{aligned} F_t=S_te^{-ct}+\int \limits _0^t b_se^{-c(t-s)}\frac{S_t}{S_s} \mathrm{{d}}s, \end{aligned}$$

(2)

where $b_s=a_s-p_s$ can take values in $\mathbb {R}$. While in the case of regular contributions, $b_s$ is typically positive, it can also be negative, for example in the single premium case, or if the regular premiums are very low. We will split $b_s$ into contributions $a_s$ and deterministic fees $p_s$ when it is needed for the interpretation of the results.

This formulation can be seen as an extension of the case studied in [7], where it is assumed that a constant contribution parameter $a_t=a$ for all $t$ and there is no periodic fees, so that $p_t=0$. It is clear from (2) that the fund value becomes path-dependent and involves a continuous arithmetic average. Without loss of generality, let $F_0=S_0$.

2.2 Benefits

We assume that there is a guaranteed minimum accumulation rate $g<r$ on all the contributions of the policyholder until time $t$ so that the accumulated guaranteed benefit $G_t$ at time $t$ has dynamics

$$ \mathrm{{d}}G_t=gG_t\mathrm{{d}}t +a_t \mathrm{{d}}t $$

where $G_0=P_0$ at time $0$. Thus, at time $t$ the guaranteed amount $G_t$ can be expressed as

$$ G_t=P_0e^{gt}+\int \limits _0^ta_se^{g(t-s)}\mathrm{{d}}s. $$

When the annual rate of contribution is constant ($a_t=a$), the guaranteed value can be simplified to

$$ G_t=P_0e^{gt}+a\left( \frac{e^{gt}-1}{g}1\!\!1_{\{g>0\}}+t1\!\!1_{\{g=0\}}\right) . $$

Chi and Lin [7] develop techniques to price and hedge the guarantee at time $t$. Using their numerical approach it is possible to estimate the fair fee for the European VA (Proposition 3 in their paper).

As in [4, 13], we assume that the policyholder has the option to surrender the policy at any time $t$ and to receive a surrender benefit at surrender time equal to

$$ (1-\kappa _t)F_{t} $$

where $\kappa _t$ is a penalty percentage charged for surrendering at time $t$. As presented for instance in [3, 13] or [15], a standard surrender penalty is decreasing over time. Typical VAs sold in the US have a surrender charge period. In general, the maximum surrender charge is around 8 % of the account value and decreases during the surrender charge period. A typical example is New York Life’s Premier Variable Annuity [14], for which the surrender charge starts at 8 % in the first contract year, decreases by 1 % per year to reach 2 % in year 7. From year 8 on, there is no penalty on surrender. In another example, “the surrender charge is 7 % during the first Contract Year and decreases by 1 % each subsequent Contract Year. No surrender charge is deducted for surrenders occurring in Contract Years 8 and later” [17].

3 Valuation of the Surrender Option

In this section, we discuss the valuation of the variable annuity contract with maturity benefit and surrender option.³ We first present a sufficient condition to eliminate the possibility of optimal surrender. We then explain how we evaluate the value of the surrender option using partial differential equations (PDEs). We consider a variable annuity contract with maturity benefit only, which can be surrendered. We choose to ignore the death benefits that are typically added to that type of contract since our goal is to analyze the effect of the fee structure on the value of the surrender option.

3.1 Notation and Optimal Surrender Decision

We denote by $\upsilon (t,F_t)$ and $V(t,F_t)$ the value of the contract without and with surrender option, respectively. In this paper, we ignore death benefits and assume that the policyholder survives to maturity.⁴ Thus, the value of the contract without the surrender option is simply the risk-neutral expectation of the payoff at maturity, conditional on the filtration up to time $t$.

$$\begin{aligned} \upsilon (t,F_t)=E[e^{-r(T-t)}\max (G_T,F_T)|\fancyscript{F}_t] \end{aligned}$$

(3)

We assume that the difference between the value of the maturity benefit and the full contract is only attributable to the surrender option, which we denote by $e(t,F_t)$. Then, we have the following decomposition.

$$\begin{aligned} V(t,F_t)=\upsilon (t,F_t)+e(t,F_t) \end{aligned}$$

(4)

The value of the contract with surrender option is calculated assuming that the policyholder surrenders optimally. This means that the contract is surrendered as soon as its value drops below the value of the surrender benefit. To express the total value of the variable annuity contract, we must introduce further notation. We denote by $\fancyscript{T}_t$ the set of all stopping times $\tau$ greater than $t$ and bounded by $T$. Then, we can express the continuation value of the VA contract as

$$\begin{aligned} V^*(t,F_t)=\sup _{\tau \,\in \, \fancyscript{T}_t} E[e^{-r(\tau -t)}\psi (\tau ,F_{\tau })], \end{aligned}$$

where

$$\begin{aligned} \psi (t,x)= {\left\{ \begin{array}{ll} (1-\kappa _t)x, &{}\quad \mathrm{if } ~t \in (0,T)\\ \max (G_T,x), &{}\quad \mathrm{if } ~t=T \end{array}\right. } \end{aligned}$$

is the payoff of the contract at surrender or maturity. Finally, we let $\fancyscript{S}_t$ be the optimal surrender region at time $t\in [0,T]$. The optimal surrender region is given by the fund values for which the surrender benefit is worth more than the VA contract if the policyholder continues to hold it for at least a small amount of time. Mathematically speaking, it is defined by

$$\begin{aligned} \fancyscript{S}_t=\{F_t : V^*(t,F_t) \leqslant \psi (t,F_t)\}. \end{aligned}$$

The complement of the optimal surrender region $\fancyscript{S}_t$ will be referred to as the continuation region. We also define $B_t$, the optimal surrender boundary at time $t$, by

$$\begin{aligned} B_t=\inf _{F_t \,\in \, [0,\infty )}\{F_t \in \fancyscript{S}_t\}. \end{aligned}$$

3.2 Theoretical Result on Optimal Surrender Behavior

According to (2) the account value $F_t$ can be written as follows at time $t$

$$ F_t=e^{-ct}S_{t}+\int \limits _0^t b_se^{-c(t-s)}\frac{S_t}{S_s} \mathrm{{d}}s, \quad \ t \geqslant 0, $$

and at time $t+\mathrm{{d}}t$, it is equal to

$$ F_{t+\mathrm{{d}}t}=e^{-c(t+\mathrm{{d}}t)}S_{t+\mathrm{{d}}t}+\int \limits _0^{t+\mathrm{{d}}t} b_se^{-c(t+\mathrm{{d}}t-s)}\frac{S_{t+\mathrm{{d}}t}}{S_s} \mathrm{{d}}s. $$

Proposition 3.1

(Sufficient condition for no surrender) For a fixed time $t\in [0,T]$, a sufficient condition to eliminate the surrender incentive at time ‘$t$’ is given by

$$\begin{aligned} (\kappa ^\prime _t+(1-\kappa _t)c)F_t< b_t(1-\kappa _t), \end{aligned}$$

(5)

where $\kappa ^\prime _t={\partial \kappa _t}/{\partial t}$. Here, are some special cases of interest:

• When $a_t=p_t=0$ (no periodic investment, no periodic fee) and $\kappa _t=1-e^{-\kappa (T-t)}$ (situation considered by [4]) then $b_t=0$ and (5) becomes

  $$\kappa >c.$$

• When $a_t=0$ (no periodic investment, i.e., a single lump sum paid at time 0), then $b_t=-p_t\le 0.$ Assume that $p_t>0$ so that $b_t<0$ thus

  • If $\kappa ^\prime _t+(1-\kappa _t)c>0$ (for example if $\kappa$ is constant), then the condition can never be satisfied and no conclusion can be drawn.

  • If $\kappa ^\prime _t+(1-\kappa _t)c<0$ then it is not optimal to surrender when

    $$ F_t>\frac{-p_t(1-\kappa _t)}{\kappa ^\prime _t+(1-\kappa _t)c}. $$

• When $\kappa _t=\kappa$ and $b_t=b$ are constant over time, condition (5) can be rewritten as

  $$ F_t<\frac{b(1-\kappa )}{c(1-\kappa )}=\frac{b}{c}. $$

Remark 3.1

Proposition 3.1 shows that in the absence of periodic fees and investment, an insurer can easily ensure that it is never optimal to surrender by choosing a surrender charge equal to $1-e^{-\kappa t}$ at time $t$, with a penalty parameter $\kappa$ higher than the percentage fee $c$. Proposition 3.1 shows that it is also possible to eliminate the surrender incentive when there are periodic fees and investment opportunities, but the conditions are more complicated.

Proof

Consider a time $t$ at which it is optimal to surrender. This implies that for any time interval of length $\mathrm{{d}}t>0$, it is better to surrender at time $t$ than to wait until time $t+\mathrm{{d}}t$. In other words, the surrender benefit at time $t$ must be at least equal to the expected discounted value of the contract at time $t+\mathrm{{d}}t$, and in particular larger than the surrender benefit at time $t+\mathrm{{d}}t$. Thus

$$ (1-\kappa _t)F_t\ge E[e^{-r\mathrm{{d}}t}(1-\kappa _{t+\mathrm{{d}}t})F_{t+\mathrm{{d}}t}\ |\fancyscript{F}_t] $$

Using the martingale property for the discounted stock price $S_t$ and the independence of increments for the Brownian motion, we know that $E[S_{t+\mathrm{{d}}t}e^{-r\mathrm{{d}}t}]=S_t$ and $E\left[ \left. \frac{S_{t+\mathrm{{d}}t}}{S_t}\right| \fancyscript{F}_t\right] =E\left[ \frac{S_{t+\mathrm{{d}}t}}{S_t}\right] =e^{r\mathrm{{d}}t}$ thus

$$\begin{aligned} E[e^{-r\mathrm{{d}}t}F_{t+\mathrm{{d}}t}|\fancyscript{F}_t]&=e^{-c(t+\mathrm{{d}}t)}S_t+\int \limits _0^{t} b_se^{-c(t+\mathrm{{d}}t-s)}\frac{S_{t}}{S_s} \mathrm{{d}}s\nonumber \\&\quad +\int \limits _t^{t+\mathrm{{d}}t} b_se^{-c(t+\mathrm{{d}}t-s)}e^{-r\mathrm{{d}}t}E\left[ \frac{S_{t+\mathrm{{d}}t}}{S_s}\right] \mathrm{{d}}s,\nonumber \\&=e^{-c(t+\mathrm{{d}}t)}S_t+\int \limits _0^{t} b_se^{-c(t+\mathrm{{d}}t-s)}\frac{S_{t}}{S_s} \mathrm{{d}}s+\int \limits _t^{t+\mathrm{{d}}t} b_se^{-c(t+\mathrm{{d}}t-s)} \mathrm{{d}}s,\nonumber \\&=e^{-c\mathrm{{d}}t}F_{t}+e^{-c\mathrm{{d}}t}\int \limits _t^{t+\mathrm{{d}}t} b_se^{-c(t-s)} \mathrm{{d}}s. \end{aligned}$$

(6)

Thus

$$ (1-\kappa _t)F_t\ge (1-\kappa _{t+\mathrm{{d}}t})\left( e^{-c\mathrm{{d}}t}F_{t}+e^{-c\mathrm{{d}}t}\int \limits _t^{t+\mathrm{{d}}t} b_se^{-c(t-s)} \mathrm{{d}}s\right) $$

We then use $\kappa _{t+\mathrm{{d}}t}=\kappa _t+\kappa ^\prime _t \mathrm{{d}}t+o(\mathrm{{d}}t)$, $e^{-c\mathrm{{d}}t} = 1-c\mathrm{{d}}t+o(\mathrm{{d}}t)$ and $\int _t^{t+\mathrm{{d}}t} b_se^{-c(t-s)} \mathrm{{d}}s = b_t \mathrm{{d}}t+o(\mathrm{{d}}t)$ to obtain

$$\begin{aligned} (1-\kappa _t)F_t\ge (1-\kappa _t-\kappa ^\prime _t \mathrm{{d}}t)\left( (1-c\mathrm{{d}}t)F_{t}+(1-c\mathrm{{d}}t) b_t\mathrm{{d}}t\right) +{j}(\mathrm{{d}}t), \end{aligned}$$

which can be further simplified into

$$\begin{aligned} (\kappa ^\prime _t+(1-\kappa _t)c)F_t\mathrm{{d}}t\ge b_t(1-\kappa _t)\mathrm{{d}}t+{j}(\mathrm{{d}}t). \end{aligned}$$

(7)

where the function ${j}(\mathrm{{d}}t)$ is $o(\mathrm{{d}}t)$. Since this holds for any $\mathrm{{d}}t>0$, we can divide (7) by $\mathrm{{d}}t$ and take the limit as $\mathrm{{d}}t\rightarrow 0$. Then, we get that if it is optimal to surrender the contract at time $t$, then

$$(\kappa ^\prime _t+(1-\kappa _t)c)F_t \ge b_t(1-\kappa _t).$$

It follows that if $(\kappa ^\prime _t+(1-\kappa _t)c)F_t < b_t(1-\kappa _t)$, it is not optimal to surrender the contract at $t$.   $\square$

3.3 Valuation of the Surrender Option Using PDEs

To evaluate the surrender option $e(t,F_t)$, we subtract the value of the maturity benefit from the value of the VA contract. These values can be compared to American and European options, respectively, since the guarantee in the former is only triggered when the contract expires, while the latter can be exercised at any time before maturity.

From now on, we assume that the deterministic fee $p_t$ is constant over time, so that $p_t=p$ for any time $t$. We also assume that the policyholder makes no contribution after the initial premium (so that $a_t=0$ for any $t$).

It is well-known⁵ that the value of a European contingent claim on the fund value $F_t$ follows the following PDE:

$$\begin{aligned} \frac{\partial \upsilon }{\partial t}+\frac{1}{2}\frac{\partial ^2 \upsilon }{\partial F^2_t}F^2_t \sigma ^2 + \frac{\partial \upsilon }{\partial F_t} (F_t(r-c)-p)-r\upsilon =0. \end{aligned}$$

(8)

Note that Eq. (8) is very similar to the Black-Scholes equation for a contingent claim on a stock that pays dividends (here, the constant fee $c$ represents the dividends), with the addition of the term $\frac{\partial {\upsilon }}{\partial {F_t}}p$ resulting from the presence of a deterministic fee. Since it represents the contract described in Sect. 2, Eq. (8) is subject to the following conditions:

$$\begin{aligned} \upsilon (T,F_T)&=\max (G_T,F_T)\\ \lim _{F_t \rightarrow 0} \upsilon (t,F_t)&=G_T e^{-r(T-t)}. \end{aligned}$$

The last condition results from the fact that when the fund value is very low, the guarantee is certain to be triggered. When $F_t\rightarrow \infty$, the problem is unbounded. However, we have the following asymptotic behavior:

$$\begin{aligned} \lim _{F_t \rightarrow \infty } \upsilon (t,F_t)=E_t[F_T e^{-r(T-t)}], \end{aligned}$$

(9)

which stems from the value of the guarantee approaching 0 for very high fund values. We will use this asymptotic result to solve the PDE numerically, when truncating the grid of values for $F_t$. The expectation in (9) is easily calculated and is given in the proof of Proposition 3.1.

As it is the case for the American put option,⁶ the VA contract with surrender option gives rise to a free boundary problem. In the continuation region, $V^*(t,F_t)$ follows Eq. (8), the same equation as for the contract without surrender option. However, in the optimal surrender region, the value of the contract with surrender is the value of the surrender benefit:

$$\begin{aligned} V^*(t,F_t)=\psi (t,F_t), \quad t \in [0,T], F_t \in \fancyscript{S}_t. \end{aligned}$$

(10)

For the contract with surrender, the PDE to solve is thus subject to the following conditions:

$$\begin{aligned} V^*(T,F_T)&=\max (G_T,F_T)\\ \lim _{F_t \rightarrow 0} V^*(t,F_t)&=G_T e^{-r(T-t)}\\ \lim _{F_t \rightarrow B_t} V^*(t,F_t)&=\psi (t,B_t).\\ \lim _{F_t \rightarrow B_t} \frac{\partial }{\partial F_t} V^*(t,F_t)&=1-\kappa _t. \end{aligned}$$

For any time $t \in [0,T]$, the value of the VA with surrender is given by

$$ V(t,F_t)=\max (V^*(t,F_t),\psi (t,F_t)). $$

This free boundary problem is solved in Sect. 4 using numerical methods.

4 Numerical Example

To price the VA using a PDE approach, we modify Eq. (8) to express it in terms of $x_t=\log F_t$. We discretize the resulting equation over a rectangular grid with time steps $\mathrm{{d}}t=0.0001$ ($\mathrm{{d}}t=0.0002$ for $T=15$) and $\mathrm{{d}}x=\sigma \sqrt{3\mathrm{{d}}t}$ (following suggestions by Racicot and Théoret [16]), from $0$ to $T$ in $t$ and from $0$ to $\log 450$ in $x$. We use an explicit scheme with central difference in $x$ and in $x^2$.

Throughout this section, we assume that the contract is priced so that only the maturity benefit is covered. In other words, we set $c$ and $p$ such that

$$\begin{aligned} P_0=\upsilon (t,F_t), \end{aligned}$$

(11)

where $P_0$ denotes the initial premium paid by the policyholder. In this section, when the fee is set in the manner, we call it the fair fee, even if it does not cover the full value of the contract. We set the fee in this manner to calculate the value added by the possibility to surrender.

4.1 Numerical Results

We now consider variable annuities with the maturity benefit described in Sect. 2. We assume that the initial premium $P_0=100$, that there are no periodic premium ($a_s=a=0$), that the deterministic fee is constant ($p_t=p$) and that the guaranteed roll-up rate is $g=0$. We further assume that the surrender charge, if any, is of the form $\kappa _t=1-e^{\kappa (T-t)}$, and that $r=0.03$ and $\sigma =0.2$.

For contracts with and without surrender charge and with maturity 5, 10 and 15 years, the results are presented in Table 1. In each case, the fee levels $c$ and $p$ are chosen such that $P_0=\upsilon (t,F_t)$. As a percentage of the initial premium, the fair fee when it is paid as a deterministic amount is higher than the fair constant percentage fee. In fact, for high fund values, the deterministic fee is lower than the amount paid when the fee is set as a constant percentage. But when the fund value is low, the deterministic fee represents a larger proportion of the fund compared to the constant percentage fee. This higher proportion drags the fund value down and increases the option value. The effect of each fee structure on the amount collected by the insurer can explain the difference between the fair fixed percentage and deterministic fees.

Table 1 Value of the surrender option in 5-, 10- and 15-year variable annuity contracts for various fee structures and surrender charges

The results in Table 1 show that when the fee is set as a fixed amount, the value of the surrender option is always lower than when the fee is expressed as a percentage of the fund. When a mix of both types of fees is applied, the value of the surrender option decreases as the fee set as a percentage of the fund decreases. When the fee is deterministic, a lower percentage of the fund is paid out when the fund value is high. Consequently, the fee paid by the policyholder is lower when the guarantee is worth less, reducing the surrender incentive. This explains why the value of the surrender option is lower for deterministic fees. This result can be observed both with and without surrender charges. However, surrender charges decrease the value of the surrender option, as expected. The effect of using a deterministic amount fee, instead of a fixed percentage, is even more noticeable when a surrender charge is added. A lower surrender option value means that the possibility to surrender adds less value to the contract. In other words, if the contract is priced assuming that policyholders do not surrender, unexpected surrenders will result in a smaller loss, on average.

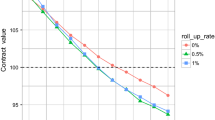
Figure 1 shows the optimal surrender boundaries for the fee structures presented in Table 1 for 10-year contracts. As expected, the optimal boundaries are higher when there is a surrender charge. Those charges are put in place in part to discourage policyholders from surrendering early. The boundaries are also less sensitive to the fee structure when there is a surrender charge. In fact, when there is a surrender charge, setting the fee as a fixed amount leads to a higher optimal boundary during most of the contract. This highlights the advantage of the fixed amount fee structure combined with surrender charges. Without those charges, the fixed fee amount could lead to more surrenders. We also note that the limiting case $p=0$ corresponds to the situation when fees are paid as a percentage of the fund. The optimal boundary obtained using the PDE approach in this paper coincides with the optimal boundary derived in [4] by solving an integral equation numerically.

Fig. 1

Optimal surrender boundary when $T=10$

Fig. 2

Optimal surrender boundary when $T=15$

Table 1 also shows the effect of the maturity combined with the fee structure on the surrender option. For all maturities, setting the fee as a fixed amount instead of a fixed percentage has a significant effect on the value of the surrender option. This effect is amplified for longer maturities. As for the 10-year contract, combining the fixed amount fee with a surrender charge further reduces the value of the surrender option, especially when $T=15$. The optimal surrender boundaries for different fee structures when $T=15$ are presented in Fig. 2. For longer maturities such as this one, the combination of surrender charges and deterministic fee raises the surrender boundary more significantly.

In all cases, the decrease in the value of the surrender option caused by the combination of a deterministic amount fee and a surrender charge is significant. In our example with a 15-year contract, moving from a fee entirely set as a fixed percentage to a fee set as a deterministic amount reduces the value of the surrender option by over 85 %. This is surprising since the shift in the optimal surrender boundary is not as significant (as can be observed in Figs. 1 and 2). A possible explanation for the sharp decrease in the surrender option value is that the fee income lost when a policyholder surrenders when the account value is high is less important, relatively to the value of the guarantee, than in the constant percentage fee case.

5 Concluding Remarks

In this chapter, the maturity guarantee fees are paid during the term of the contract as a series of deterministic amounts instead of a percentage of the fund, which is more common in the industry. We give a sufficient condition that allows the elimination of optimal surrender incentives for variable annuity contracts with fairly general fee structures. We also show how deterministic fees and surrender charges affect the value of the surrender option and the optimal surrender boundary. In particular, we highlight the efficiency of combining deterministic fees and exponential surrender charges in decreasing the value of the surrender option. In fact, although the optimal surrender boundary remains at a similar level, a fee set as a deterministic amount reduces the value of the surrender option, which makes the contract less risky for the insurer. This result also suggests that the state-dependent fee suggested in [2] could also be efficient in reducing the optimal surrender incentive. Future work could focus on more general payouts (see for example [12] for ratchet and lookback options [4] for Asian benefits) in more general market models, and include death benefits.