RF Cavities

Abstract

This introduction and Sect. 4.1 are based on the article “Ferrite cavities” [2] published in CERN Report CERN-2011-007 under the CC BY 3.0 Attribution License (http://creativecommons.org/licenses/by/3.0/). The original content (http://cds.cern.ch/record/1411778/files/p299.pdf) has been modified slightly.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

This introduction and Sect. 4.1 are based on the article “Ferrite cavities” [2] published in CERN Report CERN-2011-007 under the CC BY 3.0 Attribution License (http://creativecommons.org/licenses/by/3.0/). The original content (http://cds.cern.ch/record/1411778/files/p299.pdf) has been modified slightly.

The revolution frequency of charged particles in synchrotrons or storage rings is usually lower than 10 MHz. Even if we consider comparatively small synchrotrons (e.g., like HIT/HICAT in Heidelberg, Germany, or CNAO in Pavia, Italy, with about 20–25 m diameter, both used for tumor therapy), the revolution time will be greater than 200 ns, since the particles cannot reach the speed of light. Since according to Eq. (1.4),

$$\displaystyle{f_{\mathrm{RF}} = h \cdot f_{\mathrm{R}},}$$

the RF frequency is an integer multiple of the revolution frequency, the RF frequency will typically be lower than 10 MHz if only small harmonic numbers h are desired. For such an operating frequency, the spatial dimensions of a conventional RF resonator would be far too large to be used in a synchrotron. One possibility for solving this problem is to reduce the wavelength by filling the cavity with magnetic material. This is the basic idea of ferrite-loaded cavities (cf. [1]). Furthermore, this type of cavity offers a simple means to modify the resonant frequency in a wide range (typically up to a factor of 10) and in a comparatively short time (typically at least 10 ms cycle time). Therefore, ferrite cavities are suitable for ramped operation in a synchrotron. The possibility of adjusting the resonant frequency of a cavity to the desired operating frequency is called tuning.

Due to the low operating frequencies, the transit-time factor (cf. Sect. 4.3) of traditional ferrite-loaded cavities is almost 1 and is therefore not of interest.

If a synchrotron is operated at comparatively high harmonic numbers, the RF frequency will reach values that can be realized as resonant frequencies of classical RF resonators (typically 300 MHz or higher). Furthermore, if the particles are already relativistic (i.e., β_R ≈ 1) when they are injected into the synchrotron,¹ there is no need to make the cavity tunable to different resonant frequencies. In this case, the use of classical resonators is possible.

Many accelerating cavities of this classical type may be regarded as modifications and/or combinations of the so-called pillbox cavity [3, 4]. The pillbox cavity is the simplest type of resonator that can be used for particle acceleration. It will be discussed in Sect. 4.4.

4.1 Ferrite-Loaded Cavities

The main purpose of this section is to derive the general lumped element circuit for cavities and to discuss the main properties of RF cavities in synchrotrons and storage rings. Furthermore, some specifics that are typical for ferrite-loaded cavities are discussed.

We will see that a ferrite-loaded cavity may be regarded as roughly a transformer whose primary coil consists of only one winding fed by an RF power source in which the beam acts as the secondary coil. Consequently, some conclusions that are valid for transformers are also valid here. For example, the cavity will not work properly if the frequency is too low, because the reactance (product of inductance and angular frequency) will be too small in comparison with the ohmic parts, thereby decreasing the transformation ratio. If the frequency becomes too large, flux leakage and distributed effects will become important, so that a simple magnetoquasistatic analysis is no longer possible. Hence, an optimum operating frequency range can be specified for a ferrite-loaded cavity, similar to that of a transformer, taking the material properties and the geometry into account. For our analysis, which begins in Sect. 4.1.2, it is assumed without further notice that the considered frequency belongs to this optimum frequency range.

4.1.1 Permeability of Magnetic Materials

In this section, all calculations are based on permeability quantities μ for which

$$\displaystyle{\mu =\mu _{\mathrm{r}}\mu _{0}}$$

holds. In material specifications, the relative permeability μ_r is given, which means that we have to multiply by μ₀ to obtain μ. This comment is also valid for the incremental/differential permeability introduced below.

In RF cavities, only so-called soft magnetic materials that have a narrow hysteresis loop are of interest, since their losses are comparatively low (in contrast to hard magnetic materials, which are used for permanent magnets.²)

Figure 4.1 shows the hysteresis loop of a ferromagnetic material. It is well known that the hysteresis loop leads to a residual inductionB_r if no magnetizing field H is present and that some coercive magnetizing fieldH_c is needed to set the induction B to zero.

Fig. 4.1

Hysteresis loop

Let us now assume that some cycles of the large hysteresis loop have already passed and that H is currently increasing. We now stop to increase the magnetizing field H in the upper right-hand part of the diagram. Then H is decreased by a much smaller amount $2 \cdot \Delta H$, then increased again by that amount $2 \cdot \Delta H$, and so forth.³ As the diagram shows, this procedure will lead to a much smaller hysteresis loop whereby B changes by $2 \cdot \Delta B$. We may therefore define a differential or incremental permeability⁴

$$\displaystyle{\fbox{$\mu _{\Delta } = \frac{\Delta B} {\Delta H},$}}$$

which describes the slope of the local hysteresis loop. It is this quantity $\mu _{\Delta }$ that is relevant for RF applications. One can see that $\mu _{\Delta }$ can be decreased by increasing the DC component of H. Since H is generated by currents, one speaks of a bias current that is applied in order to shift the operating point to higher inductions B, leading to a lower differential permeability $\mu _{\Delta }$.

If no biasing is applied, the maximum $\mu _{\Delta }$ is obtained, which is typically of order a few hundred or a few thousand times μ₀.

The hysteresis loop and the AC permeability of ferromagnetic materials can be described in a phenomenological way by the so-called Preisach model, which is explained in the literature (cf. [5]). Unfortunately, the material properties are even more complicated, since they are also frequency-dependent. One usually uses the complex permeability

$$\displaystyle{ \fbox{$\underline{\mu } =\mu _{ \mathrm{s}}^{{\prime}}- j\mu _{\mathrm{ s}}^{{\prime\prime}}$} }$$

(4.1)

in order to describe losses (hysteresis loss, eddy current loss, and residual loss). The parameters $\mu _{\mathrm{s}}^{{\prime}}$ and $\mu _{\mathrm{s}}^{{\prime\prime}}$ are frequency-dependent. In the following, we will assume that the complex permeability $\underline{\mu }$ describes the material behavior in rapidly alternating fields as the above-mentioned real quantity $\mu _{\Delta }$ does when a biasing field H_bias is present. However, we will omit the index $\Delta$ for the sake of simplicity.

4.1.2 Magnetoquasistatic Analysis of a Ferrite Cavity

Figure 4.2 shows the main elements of a ferrite-loaded cavity. The beam pipe is interrupted by a ceramic gap. This gap ensures that the beam pipe may still be evacuated, but it allows a voltage V_gap to be induced in the longitudinal direction. Several magnetic ring cores are mounted in a concentric way around the beam and beam pipe (five ring cores are drawn here as an example). The whole cavity is surrounded by a metallic housing, which is connected to the beam pipe.

Fig. 4.2

Simplified 3D sketch of a ferrite-loaded cavity

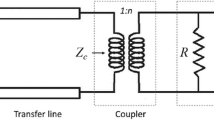
Figure 4.3 shows a cross section through the cavity. The dotted line represents the beam, which is located in the middle of a metallic beam pipe (for analyzing the influence of the beam current, this dotted line is regarded as a part of a circuit that closes outside the cavity, but this is not relevant for understanding the basic operational principle). The ceramic gap has a parasitic capacitance, but additional lumped-element capacitors are usually connected in parallel, leading to the overall capacitance C. Starting at the generator port located at the bottom of the figure, an inductive coupling loop surrounds the ring core stack. This loop was not shown in Fig. 4.2.

Fig. 4.3

Simplified model of a ferrite cavity

Please note that due to the cross-section approach, we obtain a wire model of the cavity with two wires representing the cavity housing. This is sufficient for practical analysis, but one should keep in mind that in reality, the currents are distributed.

In the following, we will represent voltages, currents, field, and flux quantities as phasors, i.e., complex amplitudes/peak values for a given frequency $f =\omega /2\pi$. In this case, for a quantity X in the time domain, we write $\underline{\hat{X}}$ for the phasor in the frequency domain. The function X(t) can be reconstructed by means of the complex function

$$\displaystyle{\underline{X} = \underline{\hat{X}}e^{j\omega t}}$$

according to

$$\displaystyle{X(t) =\mathrm{ Re}\{\underline{X}\} =\mathrm{ Re}\{\underline{\hat{X}}e^{j\omega t}\}.}$$

Let us consider a contour that surrounds the lower left ring core stack. Based on Maxwell’s second equation in the time domain (Faraday’s law),

$$\displaystyle{\oint _{\partial A}\vec{E} \cdot \mathrm{ d}\vec{r} = -\int _{A}\dot{\vec{B}} \cdot \mathrm{ d}\vec{A},}$$

we obtain

$$\displaystyle{ \underline{\hat{V }}_{\mathrm{gen}} = +j\omega \underline{\hat{\Phi }}_{\mathrm{m,tot}} }$$

(4.2)

in the frequency domain. If we now use the complete lower cavity half as the integration path, we obtain

$$\displaystyle{\underline{\hat{V }}_{\mathrm{gap}} = +j\omega \underline{\hat{\Phi }}_{\mathrm{m,tot}}.}$$

Hence we obtain

$$\displaystyle{ \underline{\hat{V }}_{\mathrm{gap}} = \underline{\hat{V }}_{\mathrm{gen}}. }$$

(4.3)

Here we assumed that the stray field B in the air region is negligible in comparison with the field inside the ring cores (due to their high permeability). Finally, we consider the beam current contour:

$$\displaystyle{\underline{\hat{V }}_{\mathrm{beam}} = +j\omega \underline{\hat{\Phi }}_{\mathrm{m,tot}} = \underline{\hat{V }}_{\mathrm{gap}}.}$$

For negligible displacement current, we have Maxwell’s first equation (Ampère’s law)

$$\displaystyle{\oint _{\partial A}\vec{H} \cdot \mathrm{ d}\vec{r} =\int _{A}\vec{J} \cdot \mathrm{ d}\vec{A}.}$$

We use a concentric circle with radius ρ around the beam as integration path:

$$\displaystyle{ H\;2\pi \rho = I_{\mathrm{tot}}. }$$

(4.4)

In the frequency domain, this leads to

$$\displaystyle{ \underline{\hat{B}} =\underline{\mu } \frac{\underline{\hat{I}}_{\mathrm{tot}}} {2\pi \rho } }$$

(4.5)

with

$$\displaystyle{ \underline{\hat{I}}_{\mathrm{tot}} = \underline{\hat{I}}_{\mathrm{gen}} -\underline{\hat{I}}_{C} -\underline{\hat{I}}_{\mathrm{beam}}. }$$

(4.6)

For the flux through a single ring core, we get

$$\displaystyle{\underline{\hat{\Phi }}_{\mathrm{m,1}} =\int \underline{\hat{\vec{B}}} \cdot \mathrm{ d}\vec{A} = d_{\mathrm{core}}\;\int _{r_{\mathrm{i}}}^{r_{\mathrm{o}} }\underline{\hat{B}}\;\mathrm{d}\rho = \frac{d_{\mathrm{core}}\underline{\mu }\underline{\hat{I}}_{\mathrm{tot}}} {2\pi } \;\ln \frac{r_{\mathrm{o}}} {r_{\mathrm{i}}}.}$$

With the complex permeability

$$\displaystyle{\underline{\mu }=\mu _{ \mathrm{s}}^{{\prime}}- j\mu _{\mathrm{ s}}^{{\prime\prime}}}$$

and assuming that N ring cores are present, we obtain

$$\displaystyle{\underline{\hat{V }}_{\mathrm{gap}} = j\omega \underline{\hat{\Phi }}_{\mathrm{m,tot}} = j\omega N\;\underline{\hat{\Phi }}_{\mathrm{m,1}} = j\omega \frac{\mathit{Nd}_{\mathrm{core}}(\mu _{\mathrm{s}}^{{\prime}}- j\mu _{\mathrm{s}}^{{\prime\prime}})\underline{\hat{I}}_{\mathrm{tot}}} {2\pi } \;\ln \frac{r_{\mathrm{o}}} {r_{\mathrm{i}}}.}$$

Therefore, we obtain

$$\displaystyle{ \underline{\hat{V }}_{\mathrm{gap}} = \underline{\hat{I}}_{\mathrm{tot}}(j\omega L_{\mathrm{s}} + R_{\mathrm{s}}) = \underline{\hat{I}}_{\mathrm{tot}}Z_{\mathrm{s}} }$$

(4.7)

if

$$\displaystyle{ Z_{\mathrm{s}} = \frac{1} {Y _{\mathrm{s}}} = j\omega L_{\mathrm{s}} + R_{\mathrm{s}}, }$$

(4.8)

$$\displaystyle{\fbox{$L_{\mathrm{s}} = \frac{\mathit{Nd}_{\mathrm{core}}\mu _{\mathrm{s}}^{{\prime}}} {2\pi } \;\ln \frac{r_{\mathrm{o}}} {r_{\mathrm{i}}},$}}$$

$$\displaystyle{ \fbox{$R_{\mathrm{s}} =\omega \frac{\mathit{Nd}_{\mathrm{core}}\mu _{\mathrm{s}}^{{\prime\prime}}} {2\pi } \;\ln \frac{r_{\mathrm{o}}} {r_{\mathrm{i}}} =\omega \frac{\mu _{\mathrm{s}}^{{\prime\prime}}} {\mu _{\mathrm{s}}^{{\prime}}} L_{\mathrm{s}} = \frac{\omega L_{\mathrm{s}}} {Q},$} }$$

(4.9)

are defined. Here,

$$\displaystyle{ Q = \frac{\mu _{\mathrm{s}}^{{\prime}}} {\mu _{\mathrm{s}}^{{\prime\prime}}} = \frac{1} {\tan \delta _{\mu }} }$$

(4.10)

is the quality factor (or Q factor) of the ring core material. Using Eq. (4.6), we obtain

$$\displaystyle\begin{array}{rcl} & \underline{\hat{V }}_{\mathrm{gap}}Y _{\mathrm{s}} = \underline{\hat{I}}_{\mathrm{tot}} = \underline{\hat{I}}_{\mathrm{gen}} -\underline{\hat{I}}_{\mathrm{beam}} -\underline{\hat{V }}_{\mathrm{gap}}\;j\omega C & \\ & \Rightarrow \fbox{$\underline{\hat{V }}_{\mathrm{gap}} = \frac{\underline{\hat{I}}_{\mathrm{gen}} -\underline{\hat{I}}_{\mathrm{beam}}} {Y _{\mathrm{s}} + j\omega C} = Z_{\mathrm{tot}}(\underline{\hat{I}}_{\mathrm{gen}} -\underline{\hat{I}}_{\mathrm{beam}}).$}&{}\end{array}$$

(4.11)

This equation corresponds to the equivalent circuit shown in Fig. 4.4. In the last step, we defined

$$\displaystyle{Y _{\mathrm{tot}} = \frac{1} {Z_{\mathrm{tot}}} = Y _{\mathrm{s}} + j\omega C.}$$

In the literature, one often finds a different version of Eq. (4.11), in which $\underline{\hat{I}}_{\mathrm{beam}}$ has the same sign as $\underline{\hat{I}}_{\mathrm{gen}}$. This corresponds to both currents having the same direction (flowing into the circuits in Figs. 4.4 and 4.5). In any case, one has to make sure that the correct phase between beam current and gap voltage is established.

Fig. 4.4

Series equivalent circuit

Fig. 4.5

Parallel equivalent circuit

In Chap. 3, we studied the stationary case, whereby the gap voltage is given by

$$\displaystyle{V _{\mathrm{gap}}(t) =\hat{ V }_{\mathrm{gap}}\sin (\omega _{\mathrm{RF}}t)}$$

and the bunches are located at $t = 0,\pm T_{\mathrm{RF}},\pm 2T_{\mathrm{RF}},\ldots$ (operation with positively charged particles below transition energy). Therefore, the fundamental harmonic of the beam current will be proportional to cos(ω_RFt), which corresponds to a 90^∘ phase shift between V_gap and I_beam. For low beam currents and for a cavity that is tuned to resonance, the phase of the gap voltage is equal to the phase of the generator current. For higher beam currents, however, not only the generator current, but also the beam current will have an influence on the gap voltage due to the beam impedanceZ_tot, as can be seen in Eq. (4.11) and in Fig. 4.4. This phenomenon is called beam loading.

4.1.3 Parallel and Series Lumped Element Circuit

In the vicinity of the resonant frequency, it is possible to convert the lumped element circuit shown in Fig. 4.4 into a parallel circuit as shown in Fig. 4.5. The admittances of both circuits will be assumed equal:

$$\displaystyle{Y _{\mathrm{tot}} = j\omega C + \frac{1} {R_{\mathrm{s}} + j\omega L_{\mathrm{s}}} = j\omega C + \frac{1} {R_{\mathrm{p}}} + \frac{1} {j\omega L_{\mathrm{p}}}}$$

$$\displaystyle{\Rightarrow \frac{R_{\mathrm{s}} - j\omega L_{\mathrm{s}}} {R_{\mathrm{s}}^{2} + (\omega L_{\mathrm{s}})^{2}} = \frac{1} {R_{\mathrm{p}}} + \frac{1} {j\omega L_{\mathrm{p}}}.}$$

A comparison of the real and imaginary part yields

For the inverse relation, we modify the first equation according to

$$\displaystyle{(\omega L_{\mathrm{s}})^{2} = R_{\mathrm{ s}}(R_{\mathrm{p}} - R_{\mathrm{s}})}$$

and use this result in the second equation:

$$\displaystyle\begin{array}{rcl} & \omega L_{\mathrm{p}}\sqrt{R_{\mathrm{s} } (R_{\mathrm{p} } - R_{\mathrm{s} } )} = R_{\mathrm{s}}R_{\mathrm{p}} & {}\\ & \Rightarrow (\omega L_{\mathrm{p}})^{2}(R_{\mathrm{p}} - R_{\mathrm{s}}) = R_{\mathrm{s}}R_{\mathrm{p}}^{2} & {}\\ & \Rightarrow \fbox{$R_{\mathrm{s}} = \frac{(\omega L_{\mathrm{p}})^{2}} {R_{\mathrm{p}}^{2} + (\omega L_{\mathrm{p}})^{2}}R_{\mathrm{p}}.$}& {}\\ \end{array}$$

Equations (4.12) and (4.13) directly provide

$$\displaystyle{ R_{\mathrm{p}}R_{\mathrm{s}} = (\omega L_{\mathrm{p}})(\omega L_{\mathrm{s}}), }$$

(4.14)

which leads to

$$\displaystyle{\fbox{$\omega L_{\mathrm{s}} = \frac{R_{\mathrm{p}}} {\omega L_{\mathrm{p}}} R_{\mathrm{s}} = \frac{R_{\mathrm{p}}^{2}} {R_{\mathrm{p}}^{2} + (\omega L_{\mathrm{p}})^{2}}\omega L_{\mathrm{p}}.$}}$$

Since it is suitable to use both types of lumped element circuit, it is also convenient to define the complex permeability $\underline{\mu }$ in a parallel form:

$$\displaystyle{ \fbox{$\frac{1} {\underline{\mu }} = \frac{1} {\mu _{\mathrm{p}}^{{\prime}}} + j \frac{1} {\mu _{\mathrm{p}}^{{\prime\prime}}}.$} }$$

(4.15)

This is an alternative representation of the series form shown in Eq. (4.1), which leads to

$$\displaystyle{\frac{1} {\underline{\mu }} = \frac{\mu _{\mathrm{s}}^{{\prime}} + j\mu _{\mathrm{s}}^{{\prime\prime}}} {\mu _{\mathrm{s}}^{{\prime^{2}}} + \mu _{\mathrm{s}}^{{\prime\prime^{2}}}}.}$$

Comparing the real and imaginary parts of the last two equations, we obtain

$$\displaystyle{ \mu _{\mathrm{p}}^{{\prime}} = \frac{\mu _{\mathrm{s}}^{{\prime^{2}}} + \mu _{\mathrm{ s}}^{{\prime\prime^{2}}}} {\mu _{\mathrm{s}}^{{\prime}}}, }$$

(4.16)

$$\displaystyle{ \mu _{\mathrm{p}}^{{\prime\prime}} = \frac{\mu _{\mathrm{s}}^{{\prime^{2}}} + \mu _{\mathrm{ s}}^{{\prime\prime^{2}}}} {\mu _{\mathrm{s}}^{{\prime\prime}}}. }$$

(4.17)

These two equations lead to

$$\displaystyle{\mu _{\mathrm{p}}^{{\prime}}\mu _{ \mathrm{s}}^{{\prime}} =\mu _{ \mathrm{ p}}^{{\prime\prime}}\mu _{ \mathrm{s}}^{{\prime\prime}}.}$$

Putting this together with Eqs. (4.9), (4.10), and (4.14), we conclude that

$$\displaystyle{ \fbox{$Q = \frac{\mu _{\mathrm{s}}^{{\prime}}} {\mu _{\mathrm{s}}^{{\prime\prime}}} = \frac{\omega L_{\mathrm{s}}} {R_{\mathrm{s}}} = \frac{R_{\mathrm{p}}} {\omega L_{\mathrm{p}}} = \frac{\mu _{\mathrm{p}}^{{\prime\prime}}} {\mu _{\mathrm{p}}^{{\prime}}}.$} }$$

(4.18)

With these expressions, we may write Eqs. (4.16) and (4.17) in the form

$$\displaystyle{ \fbox{$\mu _{\mathrm{p}}^{{\prime}} =\mu _{ \mathrm{ s}}^{{\prime}}\left (1 + \frac{1} {Q^{2}}\right ),$} }$$

(4.19)

$$\displaystyle{ \fbox{$\mu _{\mathrm{p}}^{{\prime\prime}} =\mu _{ \mathrm{ s}}^{{\prime\prime}}\left (1 + Q^{2}\right ).$} }$$

(4.20)

If we use Eq. (4.18),

$$\displaystyle{Q = \frac{\omega L_{\mathrm{s}}} {R_{\mathrm{s}}},}$$

we may rewrite Eqs. (4.12) and (4.13) in the form

By combining Eqs. (4.21) and (4.9), we obtain

$$\displaystyle{R_{\mathrm{p}} = (1 + Q^{2})\omega \frac{\mathit{Nd}_{\mathrm{core}}\mu _{\mathrm{s}}^{{\prime\prime}}} {2\pi } \;\ln \frac{r_{\mathrm{o}}} {r_{\mathrm{i}}}.}$$

With the help of Eqs. (4.18) and (4.19), we obtain

$$\displaystyle{\mu _{\mathrm{s}}^{{\prime\prime}} = \frac{\mu _{\mathrm{s}}^{{\prime}}} {Q} = \frac{\mu _{\mathrm{p}}^{{\prime}}} {Q + \frac{1} {Q}} = \frac{\mu _{\mathrm{p}}^{{\prime}}Q} {1 + Q^{2}}.}$$

The last two equations lead to

$$\displaystyle{R_{\mathrm{p}} =\omega \frac{\mathit{Nd}_{\mathrm{core}}\mu _{\mathrm{p}}^{{\prime}}Q} {2\pi } \;\ln \frac{r_{\mathrm{o}}} {r_{\mathrm{i}}} = \mathit{Nd}_{\mathrm{core}}\mu _{\mathrm{p}}^{{\prime}}\mathit{Q f }\;\ln \frac{r_{\mathrm{o}}} {r_{\mathrm{i}}}.}$$

This shows that R_p is proportional to the product $\mu _{\mathrm{p}}^{{\prime}}\mathit{Q f }$, which is a material property. The other parameters refer to the geometry. Therefore, the manufacturers of ferrite cores sometimes specify the $\boldsymbol{\mu }_{\mathrm{r}}\mathbf{Qf}$product (for the sake of simplicity, we define $\mu _{\mathrm{r}}:=\mu _{ \mathrm{p,r}}^{{\prime}}$).⁵

For Q ≥ 5, we may use the approximations

$$\displaystyle{ R_{\mathrm{p}} \approx R_{\mathrm{s}}\;Q^{2},\mbox{ }L_{\mathrm{ p}} \approx L_{\mathrm{s}},\mbox{ }\mu _{\mathrm{p}}^{{\prime}}\approx \mu _{\mathrm{ s}}^{{\prime}},\mbox{ }\mu _{\mathrm{ p}}^{{\prime\prime}}\approx \mu _{\mathrm{ s}}^{{\prime\prime}}\;Q^{2}, }$$

(4.23)

which then have an error of less than 4%.

4.1.4 Frequency Dependence of Material Properties

As an example, the frequency dependence of the permeability is shown in Figs. 4.6 and 4.7 for the special ferrite material Ferroxcube 4, assuming small magnetic RF fields without biasing. All the data presented for this material are taken from [6]. It is obvious that the behavior depends significantly on the choice of the material. Without biasing, a constant $\mu _{\mathrm{s}}^{{\prime}} \approx \mu _{\mathrm{p}}^{{\prime}}$ may be assumed only up to a certain frequency (see Fig. 4.6). With increasing frequency from 0, the Q factor will decrease (compare Figs. 4.6 and 4.7). Figure 4.8 shows the resulting frequency dependence of the μ_rQf product.

Fig. 4.6

$\mu _{\mathrm{s,r}}^{{\prime}}$ versus frequency for three different types of ferrite material (1: Ferroxcube 4A, 2: Ferroxcube 4C, 3: Ferroxcube 4E). Data taken from [6]

Fig. 4.7

$\mu _{\mathrm{s,r}}^{{\prime\prime}}$ versus frequency for three different types of ferrite material (1: Ferroxcube 4A, 2: Ferroxcube 4C, 3: Ferroxcube 4E). Data taken from [6]

Fig. 4.8

$\mu _{\mathrm{s,r}}^{{\prime}}\mathit{Qf }$ product versus frequency for three different types of ferrite material (1: Ferroxcube 4A, 2: Ferroxcube 4C, 3: Ferroxcube 4E). Please note that $\mu _{\mathrm{r}}:=\mu _{ \mathrm{p,r}}^{{\prime}}\approx \mu _{\mathrm{s,r}}^{{\prime}}$ holds, due to Eq. (4.23). No bias field is present, and small magnetic RF field amplitudes are assumed. Data taken from [6]

If the magnetic RF field is increased, both Q and μ_rQf will decrease in comparison with the diagrams in Figs. 4.6, 4.7, and 4.8. The effective incremental permeability μ_r will increase for rising magnetic RF fields, as one can see by interpreting Fig. 4.1. Therefore, it is important to consider the material properties under realistic operating conditions (the maximum RF B-field is usually of order $10\ldots 20\,\mathrm{mT}$).

If biasing is applied, the μ_rQf curve shown in Fig. 4.8 will be shifted to the lower right-hand side; this effect may approximately compensate the increase in μ_rQf with frequency [6]. Therefore, the μ_rQf product may sometimes be regarded as approximately a constant if biasing is used to keep the cavity at resonance for all frequencies under consideration.

4.1.5 Quality Factor of the Cavity

The quality factor of the equivalent circuit shown in Fig. 4.5 is obtained if the resonant (angular) frequency

$$\displaystyle{\fbox{$\omega _{\mathrm{res}} = 2\pi f_{\mathrm{res}} = \frac{1} {\sqrt{L_{\mathrm{p} } C}}$}}$$

is inserted into Eq. (4.18):

$$\displaystyle{\fbox{$Q_{\mathrm{p}} = R_{\mathrm{p}}\sqrt{ \frac{C} {L_{\mathrm{p}}}}.$}}$$

In general, all parameters $\mu _{s}^{{\prime}}$, $\mu _{s}^{{\prime\prime}}$, $\mu _{p}^{{\prime}}$, $\mu _{p}^{{\prime\prime}}$, R_s, L_s, R_p, L_p, Q, and Q_p are frequency-dependent. It depends on the material whether the parallel or the series lumped element circuit is the better representation in the sense that its parameters may be regarded as approximately constant in the relevant operating range. In the following, we will use the parallel representation.

We briefly show that Q_p is in fact the quality factor defined by

$$\displaystyle{Q_{\mathrm{p}} =\omega \frac{\overline{W}_{\mathrm{tot}}} {\overline{P}_{\mathrm{loss}}},}$$

where $\overline{W}_{\mathrm{tot}}$ is the stored energy and $\overline{P}_{\mathrm{loss}}$ is the power loss (both time-averaged):

$$\displaystyle{ \fbox{$\overline{P}_{\mathrm{loss}} = \frac{\vert \underline{\hat{V }}_{\mathrm{gap}}\vert ^{2}} {2R_{\mathrm{p}}},$} }$$

(4.24)

$$\displaystyle{\overline{W}_{\mathrm{el}} = \frac{1} {4}\;C\;\vert \underline{\hat{V }}_{\mathrm{gap}}\vert ^{2},}$$

$$\displaystyle{\overline{W}_{\mathrm{magn}} = \frac{1} {4}\;L_{\mathrm{p}}\;\vert \underline{\hat{I}}_{L}\vert ^{2} = \frac{1} {4}\;L_{\mathrm{p}}\;\frac{\vert \underline{\hat{V }}_{\mathrm{gap}}\vert ^{2}} {\omega ^{2}L_{\mathrm{p}}^{2}} = \frac{\vert \underline{\hat{V }}_{\mathrm{gap}}\vert ^{2}} {4\omega ^{2}L_{\mathrm{p}}}.}$$

At resonance, we have $\overline{W}_{\mathrm{el}} = \overline{W}_{\mathrm{magn}}$, which leads to

$$\displaystyle{Q_{\mathrm{p}} = 2\omega \frac{\overline{W}_{\mathrm{el}}} {\overline{P}_{\mathrm{loss}}} = 2\omega \frac{R_{\mathrm{p}}C} {2} = R_{\mathrm{p}}\sqrt{ \frac{C} {L_{\mathrm{p}}}},}$$

as expected. The parallel resistor R_p defined by Eq. (4.24) is sometimes called a shunt impedance. Please note that different definitions for shunt impedance exist in the literature. Sometimes, especially in the LINAC community, the shunt impedance is defined as twice R_p (cf. [7]).

4.1.6 Impedance of the Cavity

The impedance of the cavity

$$\displaystyle{Z_{\mathrm{tot}} = \frac{1} { \frac{1} {R_{\mathrm{p}}} + j\left (\omega C - \frac{1} {\omega L_{\mathrm{p}}} \right )} = \frac{\sqrt{\frac{L_{\mathrm{p} } } {C}} } { \frac{1} {R_{\mathrm{p}}} \sqrt{\frac{L_{\mathrm{p} } } {C}} + j\left (\omega \sqrt{L_{\mathrm{p} } C} - \frac{1} {\omega \sqrt{L_{\mathrm{p} } C}}\right )}}$$

may be written as

$$\displaystyle\begin{array}{rcl} & Z_{\mathrm{tot}} = \frac{\frac{R_{\mathrm{p}}} {Q_{\mathrm{p}}} } { \frac{1} {Q_{\mathrm{p}}} +j\left ( \frac{\omega }{\omega _{ \mathrm{res}}} -\frac{\omega _{\mathrm{res}}} {\omega } \right )} & \\ & \Rightarrow \fbox{$Z_{\mathrm{tot}} = \frac{R_{\mathrm{p}}} {1 + j\;Q_{\mathrm{p}}\left ( \frac{\omega }{\omega _{\mathrm{ res}}} -\frac{\omega _{\mathrm{res}}} {\omega } \right )}.$}&{}\end{array}$$

(4.25)

The Laplace transformation yields

$$\displaystyle{ Z_{\mathrm{tot}}(s) = \frac{R_{\mathrm{p}}} {1 + s\frac{Q_{\mathrm{p}}} {\omega _{\mathrm{res}}} + \frac{Q_{\mathrm{p}}\omega _{\mathrm{res}}} {s} } = \frac{R_{\mathrm{p}} \frac{\omega _{\mathrm{res}}} {Q_{\mathrm{p}}} s} {s \frac{\omega _{\mathrm{res}}} {Q_{\mathrm{p}}} + s^{2} +\omega _{ \mathrm{res}}^{2}}, }$$

(4.26)

which may be found in the literature (cf. [8, 9]) in the form

$$\displaystyle{Z_{\mathrm{tot}}(s) = \frac{2R_{\mathrm{p}}\sigma \;s} {s^{2} + 2\sigma s +\omega _{ \mathrm{res}}^{2}}}$$

if

$$\displaystyle{\sigma = \frac{\omega _{\mathrm{res}}} {2Q_{\mathrm{p}}}}$$

is defined.

We now determine the 3-dB bandwidth⁶ of the cavity. The corresponding corner frequencies are reached if the absolute value of the impedance is $1/\sqrt{2}$ of the maximum value R_p. Equation (4.25) shows that this is fulfilled for

$$\displaystyle\begin{array}{rcl} & \frac{\omega }{\omega _{\mathrm{ res}}} -\frac{\omega _{\mathrm{res}}} {\omega } = \pm \frac{1} {Q_{\mathrm{p}}} \mbox{ } \Rightarrow \omega ^{2} \mp \omega \frac{\omega _{\mathrm{res}}} {Q_{\mathrm{p}}} -\omega _{\mathrm{res}}^{2} = 0 & {}\\ & \Rightarrow \omega = \pm \frac{\omega _{\mathrm{res}}} {2Q_{\mathrm{p}}} \pm \sqrt{ \frac{\omega _{\mathrm{res } }^{2 }} {4Q_{\mathrm{p}}^{2}} +\omega _{ \mathrm{res}}^{2}} = \pm \frac{\omega _{\mathrm{res}}} {2Q_{\mathrm{p}}} \pm \omega _{\mathrm{res}}\sqrt{1 + \frac{1} {4Q_{\mathrm{p}}^{2}}}.& {}\\ \end{array}$$

The absolute value of the second expression is always larger than that of the first expression. Since ω must be positive, one obtains

$$\displaystyle{\omega =\omega _{\mathrm{res}}\sqrt{1 + \frac{1} {4Q_{\mathrm{p}}^{2}}} \pm \frac{\omega _{\mathrm{res}}} {2Q_{\mathrm{p}}}.}$$

This obviously leads to the 3-dB bandwidth

$$\displaystyle{\Delta \omega _{\mathrm{3dB}} = \frac{\omega _{\mathrm{res}}} {Q_{\mathrm{p}}}\mbox{ } \Rightarrow \fbox{$Q_{\mathrm{p}} = \frac{\omega _{\mathrm{res}}} {\Delta \omega _{\mathrm{3dB}}} = \frac{f_{\mathrm{res}}} {\Delta f_{\mathrm{3dB}}}.$}}$$

4.1.7 Length of the Cavity

In the previous sections, we assumed that the ferrite ring cores can be regarded as lumped-element inductors and resistors. This is, of course, true only if the cavity is short in comparison with the wavelength.

As an alternative to the transformer model introduced above, one may therefore use a coaxial transmission line model. For example, the section of the cavity that is located on the left side of the ceramic gap in Fig. 4.3 may be interpreted as a coaxial line that is homogeneous in the longitudinal direction and that has a short circuit at the left end. The cross section consists of the magnetic material of the ring cores, air between the ring cores and the beam pipe, and air between the ring cores and the cavity housing. This is, of course, an idealization, since cooling disks, conductors, and other air regions are neglected. Taking the SIS18 cavity at GSI as an example, the ring cores have μ_r = 28 at an operating frequency of 2. 5 MHz. The ring cores have a relative dielectric constant of 10–15, but this is reduced to an effective value of ε_r,eff = 1. 8, since the ring cores do not fill the full cavity cross section. These values lead to a wavelength of λ = 16. 9 m. Since 64 ring cores with a thickness of 25 mm are used, the effective length of the magnetic material is 1. 6 m = 0. 095 λ (which corresponds to a phase of 34^∘). In this case, the transmission line model leads to deviations of less than 10% with respect to the lumped-element model. The transmission line model also shows that the above-mentioned estimation for the wavelength is too pessimistic; it leads to λ = 24 m, which corresponds to a cavity length of only 24^∘.

This type of model makes it understandable why the ferrite cavity is sometimes referred to as a shortened quarter-wavelength resonator.

Of course, one may also use more detailed models in which subsections of the cavity are modeled as lumped elements. In that case, computer simulations can be performed to calculate the overall impedance. If one is interested in resonances that may occur at higher operating frequencies, one should perform full electromagnetic simulations.

In any case, one should always remember that some parameters are difficult to determine, especially the permeability of the ring core material under different operating conditions. This uncertainty may lead to larger errors than simplifications of the model. Measurements of full-size ring cores in the requested operating range are inevitable when a new cavity is developed. Also, parameter tolerances due to the manufacturing process have to be taken into account.

In general, one should note that the total length and the dimensions of the cross section of the ferrite cavity are not determined by the wavelength as for a conventional RF cavity. For example, the SIS18 ferrite cavity has a length of 3 m flange to flange, although only 1. 6 m is filled with magnetic material. This provides space for the ceramic gap, the cooling disks, and further devices such as the bias current bars. In order to avoid resonances at higher frequencies, one should not waste too much space, but there is no exact size of the cavity housing that results from the electromagnetic analysis.

4.1.8 Differential Equation and Cavity Filling Time

The equivalent circuit shown in Fig. 4.5 was derived in the frequency domain. As long as no parasitic resonances occur, this equivalent circuit may be generalized. Therefore, we may also analyze it in the time domain (allowing slow changes of L_p with time):

$$\displaystyle\begin{array}{rcl} & I_{C} = C \cdot \frac{\mathrm{d}V _{\mathrm{gap}}} {\mathrm{d}t} \mbox{, }V _{\mathrm{gap}} = L_{\mathrm{p}} \cdot \frac{\mathrm{d}I_{L}} {\mathrm{d}t} \mbox{, }V _{\mathrm{gap}} = (I_{\mathrm{gen}} - I_{L} - I_{C} - I_{\mathrm{beam}})\;R_{\mathrm{p}}& \\ & \Rightarrow I_{L} = -\frac{V _{\mathrm{gap}}} {R_{\mathrm{p}}} + I_{\mathrm{gen}} - I_{C} - I_{\mathrm{beam}} &{}\end{array}$$

(4.27)

$$\displaystyle\begin{array}{rcl} & \Rightarrow V _{\mathrm{gap}} = L_{\mathrm{p}}\left (- \frac{1} {R_{\mathrm{p}}} \frac{\mathrm{d}V _{\mathrm{gap}}} {\mathrm{d}t} + \frac{\mathrm{d}} {\mathrm{d}t}(I_{\mathrm{gen}} - I_{\mathrm{beam}}) - C\frac{\mathrm{d}^{2}V _{\mathrm{ gap}}} {\mathrm{d}t^{2}} \right ) & \\ & \Rightarrow L_{\mathrm{p}}C\;\ddot{V }_{\mathrm{gap}} + \frac{L_{\mathrm{p}}} {R_{\mathrm{p}}} \;\dot{V }_{\mathrm{gap}} + V _{\mathrm{gap}} = L_{\mathrm{p}} \frac{\mathrm{d}} {\mathrm{d}t}(I_{\mathrm{gen}} - I_{\mathrm{beam}}) & \\ & \Rightarrow \fbox{$\ddot{V }_{\mathrm{gap}} + \frac{2} {\tau } \;\dot{V }_{\mathrm{gap}} +\omega _{ \mathrm{res}}^{2}V _{\mathrm{ gap}} = \frac{1} {C} \frac{\mathrm{d}} {\mathrm{d}t}(I_{\mathrm{gen}} - I_{\mathrm{beam}}).$}&{}\end{array}$$

(4.28)

Here we used the definition

$$\displaystyle{\fbox{$\tau = 2R_{\mathrm{p}}C.$}}$$

The product R_pC is also present in the expression for the quality factor:

$$\displaystyle\begin{array}{rcl} & Q_{\mathrm{p}} = R_{\mathrm{p}}\sqrt{ \frac{C} {L_{\mathrm{p}}}} = \frac{R_{\mathrm{p}}C} {\sqrt{L_{\mathrm{p} } C}} = \frac{1} {2}\tau \omega _{\mathrm{res}}& {}\\ & \Rightarrow \fbox{$\tau = \frac{2Q_{\mathrm{p}}} {\omega _{\mathrm{res}}} = \frac{Q_{\mathrm{p}}} {\pi f_{\mathrm{res}}}.$} & {}\\ \end{array}$$

Under the assumption $\omega _{\mathrm{res}} > \frac{1} {\tau }$ ($Q_{\mathrm{p}} > \frac{1} {2}$), the approach $V _{\mathrm{gap}} = V _{0}e^{\alpha t}$ (with a complex constant α) for the homogeneous solution of Eq. (4.28) actually leads to

$$\displaystyle{\alpha = -\frac{1} {\tau } \pm j\omega _{\mathrm{d}}}$$

with exponential decay time τ and oscillation frequency

$$\displaystyle{\omega _{\mathrm{d}} =\omega _{\mathrm{res}}\sqrt{1 - \frac{1} {(\tau \omega _{\mathrm{res}})^{2}}} =\omega _{\mathrm{res}}\sqrt{1 - \frac{1} {4Q_{\mathrm{p}}^{2}}}.}$$

This leads to ω_d ≈ ω_res even for moderately high Q_p > 2 (error less than 4%). Sometimes, the resonant frequency ω_res is called the undamped natural frequency, whereas ω_d is called the damped natural frequency.

The time τ is the time constant for the cavity, which also determines the cavity filling time. Furthermore, the time constant τ is relevant for amplitude and phase jumps of the cavity (see, e.g., [10] and Appendices A.12.1 and A.12.2). We will visualize this fact in Sect. 4.2.

Sometimes, especially in the LINAC community, the cavity filling time is defined as Q_p∕ω_res (one-half of our definition; cf. [7]) in order to specify the energy decay instead of the field strength or voltage decay.

4.1.9 Power Amplifier

Up to now, the Q factor of the cavity has been called Q_p. What we have not mentioned is that the Q factor of the cavity itself is the so-called unloaded Q factor. From now on, this unloaded Q factor will be denoted by Q_p,0. In accordance with this, the parallel resistor will be denoted by R_p,0. The reason for this is the following: An RF power amplifier that feeds the cavity may often be represented by a voltage-controlled current source (e.g., in the case of a tetrode amplifier as discussed in Chap. 6). The impedance of this current source will be connected in parallel to the equivalent circuit, thereby reducing the ohmic part R_p according to R_p = R_p,0 | | R_gen (see Sect. 4.1.12). Therefore, the loaded Q factorQ_p will usually be reduced in comparison with the unloaded Q factor Q_p,0. Also, the cavity filling time will be reduced due to the impedance of the power amplifier.

The formulas that were derived for the parallel equivalent circuit are valid for both cases, the cavity alone and the combination of cavity and amplifier. This is why they were based on R_p.

It must be emphasized that for ferrite cavities, $50\,\Omega$ impedance matching is not necessarily used in general. The cavity impedance is usually on the order of a few hundred ohms or a few kilohms. Therefore, it is often more suitable to connect the tetrode amplifier directly to the cavity. Impedance matching is not mandatory if the amplifier is located close to the cavity. Short cables have to be used, since they contribute to the overall impedance/capacitance. Cavity and RF power amplifier must be considered as one unit; they cannot be developed individually, since that the impedance curves of the cavity and the power amplifier influence each other.

4.1.10 Cooling

Both the power amplifier and the ferrite ring cores need active cooling. Of course, the Curie temperature of the ferrite material (typically > 100 ^∘C) must never be reached. Depending on the operating conditions (e.g., CW or pulsed operation), forced air cooling may be sufficient or water cooling may be required. Cooling disks between the ferrite cores may be used. In this case, one has to ensure that the thermal contact between cooling disks and ferrite cores is good.

4.1.11 Cavity Tuning

We already mentioned in Sect. 4.1.1 that a DC bias current may be used to decrease $\mu _{\Delta }$, which results in a higher resonant frequency. This is one possible way to realize cavity tuning. Strictly speaking, one deals with a quasi-DC bias current, since the resonant frequency must be modified during a synchrotron machine cycle if it is to equal the variable RF frequency. Such a tuning of the resonant frequency f_res to the RF frequency f_RF is usually desirable, since the large Z_tot makes it possible to generate large voltages with moderate RF power consumption.

Sometimes, the operating frequency range is small enough in comparison with the bandwidth of the cavity that no tuning is required.

If tuning is required, one has at least two possibilities to realize it:

• 1. Bias current tuning

• 2. Capacitive tuning

The latter may be realized by a variable capacitor (see, e.g., [11, 12]) whose capacitance may be varied by a stepping motor. This mechanical adjustment, however, is possible only if the resonant frequency is not changed from machine cycle to machine cycle or even within one machine cycle.

In the case of bias current tuning, one has two different choices, namely perpendicular biasing (also called transverse biasing) and parallel biasing (also called longitudinal biasing). Also, a mixture of both is possible [13]. The terms parallel and perpendicular refer to the orientation of the DC field H_bias in comparison with the RF field H.

Parallel biasing is simple to realize. One adds bias current loops, which may in principle be located in the same way as the inductive coupling loop shown in Fig. 4.3. If only a few loops are present, current bars with large cross sections are needed to withstand the bias current of several hundred amps. The required DC current may, of course, be reduced if the number N_bias of loops is increased accordingly (keeping the ampere-turns constant). This increase in the number of bias current windings may be limited by resonances. On the other hand, a minimum number of current loops is usually applied to guarantee a certain amount of symmetry, which leads to a more homogeneous flux in the ring cores.

Perpendicular biasing is more complicated to realize; it requires more space between the ring cores, and the permeability range is smaller than for parallel biasing. The main reason for using perpendicular biasing is that lower losses can be reached (see, e.g., [14]). One can also avoid the so-called Q-loss effect or high loss effect. The Q-loss effect often occurs when parallel biasing is applied and if the bias current is constant or varies only slowly. After a few milliseconds, one observes that the induced voltage breaks down by a certain amount even though the same amount of RF power is still applied (see, e.g., [15, 16]). For perpendicular biasing, the Q-loss effect was not observed. The Q-loss effect is not fully understood. However, there are strong indications that it may be caused by mechanical resonances of the ring cores induced by magnetostriction effects [17]. It is possible to suppress the Q-loss effect by mechanical damping. For example, in some types of ferrite cavities, the ring cores are embedded in a sealing compound [18], which should damp mechanical oscillations. Not only the Q-loss effect but also further anomalous loss effects have been observed [15].

When the influence of biasing is described, one usually defines an average bias field H_bias for the ring cores. For this purpose, one may use the magnetic field

$$\displaystyle{H_{\mathrm{bias}} = \frac{N_{\mathrm{bias}}I_{\mathrm{bias}}} {2\pi \bar{r}} }$$

located at the mean radius

$$\displaystyle{\bar{r} = \sqrt{r_{\mathrm{i} } r_{\mathrm{o}}}.}$$

Of course, this choice is somewhat arbitrary from a theoretical point of view, but it is based on practical experience.

A combination of bias current tuning and capacitive tuning has also been applied to extend the frequency range [19].

4.1.12 Resonant Frequency Control

A method that has traditionally been applied to decide whether a ferrite-loaded cavity is at resonance is the measurement of the phase of the gap voltage and of the phase of the control grid voltage (in case of a tetrode power amplifier, cf. Chap. 6).

At first glance, it seems to be clear that the cavity is at resonance if and only if the cavity impedance is purely resistive, i.e., if the inductance of the lumped element (parallel) circuit exactly compensates the capacitance (see Fig. 4.5). Therefore, it is obvious that the generator current and the gap voltage must be in phase for the cavity operating at resonance.

In order to analyze this fact in detail, however, one should be aware that a tube amplifier also contributes to the overall cavity impedance. It is not only the ohmic output impedance that will contribute to the overall impedance of the cavity, but also the capacitance of the tetrode and its circuitry (and also some inductances). As shown in Fig. 4.9, we may use a model [20] in which the tetrode power amplifier is represented as a voltage-controlled current source with an internal resistor R_gen in parallel. The capacitance of the power amplifier is represented by a capacitor C_gen (if necessary, C_gen may be frequency-dependent to include the effect of parasitic inductances). The cavity without the power amplifier is shown on the right side of the circuit. It consists of R_p,0, L_p, and C₀. Now it becomes obvious that the resonant frequency of the overall system is

$$\displaystyle{\omega _{\mathrm{res}} = \frac{1} {\sqrt{L_{\mathrm{p} } (C_{0 } + C_{\mathrm{gen } } )}}.}$$

If the cavity is tuned to resonance, it is not the current I_cav that is in phase with the gap voltage V_gap, but the current I_gen. This current I_gen cannot be measured, however, since it may be regarded as an internal current of the tetrode. Fortunately, the control grid voltage V_g1 of the tetrode is usually in phase with the internal current I_gen (cf. Chap. 6). Therefore, a resonant frequency control loop may compare the phase of V_g1 with the phase of V_gap. If both are in phase (or 180^∘ out of phase, depending on the chosen orientation of the voltages), the whole cavity system consisting of generator and cavity will be at resonance. One typically uses a phase detector, which provides the phase difference between V_g1 and V_gap. This output signal is then used by a closed-loop controller (cf. Chap. 7) to modify the bias current of the ferrite cavity so that I_gen and V_g1 are in phase with V_gap, as desired.

Fig. 4.9

Equivalent circuit of RF generator and cavity

It must be emphasized that the equivalent circuit in Fig. 4.5 and the related formulas are still valid. We just have to interpret the circuit in a slightly different way. If we compare it with Fig. 4.9, it becomes obvious that $C = C_{\mathrm{gen}} + C_{0}$ is the total capacitance of generator and cavity, and $R_{\mathrm{p}} = R_{\mathrm{p,0}}\vert \vert R_{\mathrm{gen}} = \frac{R_{\mathrm{p,0}}R_{\mathrm{gen}}} {R_{\mathrm{p,0}}+R_{\mathrm{gen}}}$ also includes both contributions.

Sometimes, it is desired to operate the cavity not at resonance but slightly off-resonance. In this case, one may choose a target value that differs from zero (or 180^∘, respectively) for the phase difference.

Completely detuning the cavity may be a choice to deactivate the cavity without having a high beam impedance. Then, of course, no gap voltage is produced, so that the closed-loop control system will not work. However, one may modify the bias current in an open-loop mode in this case.

4.1.13 Further Complications

We already mentioned that the effective differential permeability depends on the hysteresis behavior of the material, i.e., on the history of bias and RF currents. It was also mentioned that due to the spatial dimensions of the cavity, we have to deal with ranges between lumped-element circuits and distributed elements. The anomalous loss effects are a third complication. There are further points that make the situation even more complicated in practice:

• If no biasing is applied, the maximum of the magnetic field is present at the inner radius r_i. One has to ensure that the maximum ratings of the material are not exceeded.

• Bias currents lead to an ρ⁻¹ dependency of the induced magnetic field H_bias. Therefore, biasing is more effective in the inner parts of the ring cores than in the outer parts, resulting in a $\mu _{\Delta }$ that increases with ρ. According to Eq. (4.5), this will modify the ρ⁻¹ dependency of the magnetic RF field. As a result, the dependence on ρ may be much weaker than without a bias field.

• The permeability depends not only on the frequency, on the magnetic RF field, and on the biasing. It is also temperature-dependent.

• Depending on the thickness of the ferrite cores, on the conductivity of the ferrite, on the material losses, and on the operating frequency, the magnetic field may decay from the surface to the inner regions, reducing the effective volume.

• At higher operating frequencies with strong bias currents, the differential permeability will be rather low. This means that the magnetic flux will no longer be guided perfectly by the ring cores. The fringe fields in the air regions will be more important, and resonances may occur.

4.1.14 Cavity Configurations

A comparison of different types of ferrite cavities can be found in [21–23]. We summarize a few aspects here that lead to different solutions.

• Instead of using only one stack of ferrite ring cores and only one ceramic gap, as shown in Fig. 4.3, one may also use more sections with ferrites (e.g., one gap with half the ring cores on the left side and the other half on the right side of the gap, for reasons of symmetry) or more gaps. Sometimes, the ceramic gaps belong to different independent cavity cells, which may be coupled by copper bars (e.g., by connecting them in parallel). Connections of this type must be short to allow operation at high frequencies.

• One configuration that is often used is a cavity consisting of only one ceramic gap and two ferrite stacks on each side. Figure-eight windings surround these two ferrite stacks (see, e.g., [24]). With respect to the magnetic RF field, this leads to the same magnetic flux in both stacks. In this way, an RF power amplifier that feeds only one of the two cavity halves will indirectly supply the other cavity half as well. This corresponds to a 1:2 transformation ratio. Hence, the beam will see four times the impedance compared with the amplifier load. Therefore, the same RF input power will lead to higher gap voltages (but also to a higher beam impedance). The transformation law may be derived by an analysis that is similar to that in Sect. 4.1.2.

• Instead of the inductive coupling shown in Fig. 4.3, one may also use capacitive coupling if the power amplifier is connected to the gap via capacitors. If a tetrode power amplifier is used, one still has to provide it with a high anode voltage. Therefore, an external inductor (choke coil) is necessary, which allows the DC anode current but blocks the RF current from the DC power supply. Often a combination of capacitive and inductive coupling is used (e.g., to influence parasitic resonances). The coupling elements will contribute to the equivalent circuit.

• Another possibility is inductive coupling of individual ring cores. This leads to lower impedances, which ideally allow a 50-$\Omega$ impedance matching to a standard solid-state RF power amplifier (see, e.g., [25]).

• If a small relative tuning range is required, it is not necessary to use biasing for the ferrite ring cores inside the cavity. One may use external tuners (see, e.g., [26, 27]), which can be connected to the gap. For external tuners, both parallel and perpendicular biasing may be applied [28].

No general strategy can be defined for how a new cavity is to be designed. Many compromises have to be found. A certain minimum capacitance is given by the gap capacitance and the parasitic capacitances. In order to reach the upper limit of the frequency range, a certain minimum inductance has to be realized. If biasing is used, this minimum inductance must be reached using the maximum bias current, but the effective permeability should still be high enough to reduce stray fields. Also, the lower frequency limit should be reachable with a minimum but nonzero bias current. There is a maximum RF field B_RF,max (about 15 mT), which should not be exceeded for the ring cores. This imposes a lower limit on the number of ring cores. The required tuning range in combination with the overall capacitance will also restrict the number of ring cores. As mentioned above, the amplifier design should be taken into account from the very beginning, especially with respect to the impedance. The maximum beam impedance that is tolerable is defined by beam dynamics considerations. This impedance budget also defines the power that is required. If more ring cores can be used, the impedance of the cavity will increase, and the power loss will decrease for a given gap voltage.

4.1.15 The GSI Ferrite Cavities in SIS18

As an example for a ferrite cavity, we summarize the main facts about GSI’s SIS18 ferrite cavities (see Figs. 4.10 and 4.11). Two identical ferrite cavities are located in the synchrotron SIS18.

Fig. 4.10

SIS18 ferrite cavity. Photography: GSI Helmholtzzentrum für Schwerionenforschung GmbH, T. Winnefeld

Fig. 4.11

Gap area of the SIS18 ferrite cavity. Photography: GSI Helmholtzzentrum für Schwerionenforschung GmbH, T. Winnefeld

The material Ferroxcube FXC 8C12m is used for the ferrite ring cores. In total, N = 64 ring cores are used per cavity. Each core has the following dimensions:

$$\displaystyle{d_{\mathrm{o}} = 2\;r_{\mathrm{o}} = 498\,\mathrm{mm}\mbox{, }d_{\mathrm{i}} = 2\;r_{\mathrm{i}} = 270\,\mathrm{mm}\mbox{, }d_{\mathrm{core}} = 25\,\mathrm{mm},}$$

$$\displaystyle{\bar{r} = \sqrt{r_{\mathrm{i} } r_{\mathrm{o}}} = 183\,\mathrm{mm}.}$$

For biasing,

$$\displaystyle{N_{\mathrm{bias}} = 6}$$

figure-eight copper windings are present. The total capacitance amounts to

$$\displaystyle{C = 740\,\mathrm{pF},}$$

including the gap, the gap capacitors, the cooling disks, and other parasitic capacitances. The maximum voltage that is reached under normal operating conditions is $\hat{V }_{\mathrm{gap}} = 16\,\mathrm{kV}$.

Table 4.1 Equivalent circuit parameters for SIS18 ferrite cavities (without influence of tetrode amplifiers)

Table 4.1 shows the main parameters for three different frequencies. All these values are consistent with the formulas presented in this book. It is obvious that both $\mu _{\mathrm{p,r}}^{{\prime}}\mathit{Qf }$ and R_p do not vary strongly with frequency, justifying the parallel equivalent circuit. This compensation effect was mentioned at the end of Sect. 4.1.4.

All the parameters mentioned here refer to the beam side of the cavity. The cavity is driven by an RF amplifier coupled to only one of two ferrite core stacks (consisting of 32 ring cores each). The two ring core stacks are coupled by the bias windings. Therefore, a transformation ratio of 1: 2 is present from amplifier to beam. This means that the amplifier has to drive a load of about $R_{\mathrm{p,0}}/4 \approx 1.1\ \mathrm{k}\Omega$. For a full amplitude of $\hat{V }_{\mathrm{gap}} = 16\,\mathrm{kV}$ at f = 5 MHz, the power loss in the cavity amounts to 31 kW.

The SIS18 cavity is supplied by a single-ended tetrode power amplifier using a combination of inductive and capacitive coupling.

It has to be emphasized that the values in Table 4.1 do not contain the amplifier influence. Depending on the operating point of the tetrode, R_p will be reduced significantly in comparison with R_p,0, and all related parameters vary accordingly.

4.1.16 Further Practical Considerations

For measuring the gap voltage, one needs a gap voltage divider in order to decrease the high-voltage RF to a safer level. This can be done by capacitive voltage dividers. Gap relays are used to short-circuit the gap if the cavity is temporarily unused. This reduces the beam impedance, which may be harmful for beam stability. If cycle-by-cycle switching is needed, semiconductor switches may be used as gap switches instead of vacuum relays. Another possibility to temporarily reduce the beam impedance is to detune the cavity.

The capacitance/impedance of the gap periphery devices must be considered when the overall capacitance C and the other elements in the equivalent circuit are calculated. Also, further parasitic elements may be present.

On the one hand, the cavity dimensions should be as small as possible, since space in synchrotrons and storage rings is valuable and since undesired resonances may be avoided. On the other hand, certain minimum distances have to be kept in order to prevent high-voltage sparkovers. For reasons of EMC (electromagnetic compatibility), RF seals are often used between conducting metal parts of the cavity housing to reduce electromagnetic emission.

In order to satisfy high vacuum requirements, it may be necessary to allow a bakeout of the vacuum chamber. This can be realized by integrating a heating jacket that surrounds the beam pipe. It has to be guaranteed that the ring cores are not damaged by heating and that safety distances (for RF purposes and high-voltage requirements) are kept.

If the cavity is used in a radiation environment, the radiation hardness of all materials is an important topic.

4.1.17 Magnetic Materials

A large variety of magnetic materials is available. Nickel-zinc (NiZn) ferrites may be regarded as the traditional standard material for ferrite-loaded cavities. At least the following material properties are of interest for material selection, and they may differ significantly for different types of material:

• permeability

• magnetic losses

• saturation induction (typically 200–300 mT for NiZn ferrites)

• maximum RF inductions (typically 10–20 mT for NiZn ferrites)

• relative dielectric constant (on the order of 10–15 for NiZn ferrites but, e.g., very high for MnZn ferrites) and dielectric losses (usually negligible for typical NiZn applications)

• maximum operating temperature, thermal conductivity, and temperature dependence in general

• magnetostriction

• specific resistance (very high for NiZn ferrites, very low for MnZn ferrites)

In order to determine the RF properties under realistic operating conditions (large magnetic flux, biasing), thorough reproducible measurements in a fixed test setup are inevitable.

Amorphous and nanocrystalline magnetic alloy (MA) materials have been used to build very compact cavities that are based on similar principles as the classical ferrite cavities (see, e.g., [12, 23, 29–31]). These materials allow a higher induction and have a very high permeability. This means that a smaller number of ring cores is needed for the same inductance. MA materials typically have lower Q factors than those of ferrite materials. Low Q factors have the advantage that frequency tuning is often not necessary and that it is possible to generate signal forms including higher harmonics instead of pure sine signals (cf. Sect. 5.5.1). MA cavities are especially of interest for pulsed operation at high field gradients. If a low Q-factor is not desired, it is also possible to increase it by cutting the MA ring cores.

Microwave garnet ferrites have been used at frequencies in the range 40–60 MHz in connection with perpendicular biasing, since they provide comparatively low losses (see, e.g., [32–34]).

4.2 Cavity Excitation

In Sect. 4.1.8, we derived the differential equation (4.28) that is obtained for the standard lumped element circuit of the cavity shown in Fig. 4.5. This is valid for several types of cavities.

We already mentioned that the cavity time constant τ determines how the cavity reacts to excitations, i.e., changes in the generator current and the beam current.

In Appendix A.12.1, a solution (A.65) of the ODE (4.28) is derived for a special excitation, namely that the sinusoidal generator current is switched on.

We now evaluate this solution for a specific case. Consider the following parameters as an example:

$$\displaystyle{R_{\mathrm{p}} = 2\,\mathrm{k}\Omega \mbox{, }C = 500\,\mathrm{pF}\mbox{, }L_{\mathrm{p}} = 50.66\,\mu \mathrm{H}.}$$

This leads to

$$\displaystyle{Q_{\mathrm{p}} \approx 6.28\mbox{, }\tau = 2\,\mu \mathrm{s}}$$

and a resonant frequency of 1 MHz. The impedance is shown in Fig. 4.12.

Fig. 4.12

Impedance of the cavity versus frequency

Figures 4.13, 4.14, 4.15, 4.16, 4.17, and 4.18 show what happens if the cavity is excited with a current

$$\displaystyle{I_{\mathrm{gen}}(t) =\hat{ I}_{\mathrm{gen}}\;\sin (\omega t)}$$

that is switched on at t = 0 with an amplitude of $\hat{I}_{\mathrm{gen}} = 5\,\mathrm{A}$.

Fig. 4.13

Excitation with f = 0.1 MHz

Fig. 4.14

Excitation with f = 0. 5 MHz

Fig. 4.15

Excitation with f = 0. 9 MHz

Fig. 4.16

Excitation with f = 1 MHz

Fig. 4.17

Excitation with f = 1. 1 MHz

Fig. 4.18

Excitation with f = 10 MHz

If the excitation frequency differs much from the resonant frequency of the cavity, the cavity first tries to oscillate with the resonant frequency. After a while, this transient behavior ends, and the cavity oscillates with the excitation frequency. However, no significant voltage is obtained.

If the excitation frequency is close to the resonant frequency, one sees some overshoot before the stationary conditions are reached.

If the cavity is excited with its resonant frequency, the maximum voltage is achieved for a given current. The time constant τ is clearly visible.

4.3 Transit Time Factor

In the simplest case, the longitudinal component of the electric field may be regarded as constant in the ceramic gap, and it has a harmonic shape:

$$\displaystyle{E(t) =\hat{ E}\;\cos (\omega _{\mathrm{RF}}t).}$$

We now consider a particle that passes the center of the gap at z = 0 exactly at the time t = 0, when the electric field is at its crest.

The particle then experiences the voltage

$$\displaystyle{V =\int _{ -\Delta l_{\mathrm{gap}}/2}^{+\Delta l_{\mathrm{gap}}/2}E\;\mathrm{d}z =\int _{ -\Delta t_{\mathrm{gap}}/2}^{+\Delta t_{\mathrm{gap}}/2}E(t)\;u_{\mathrm{ R}}\;\mathrm{d}t.}$$

Here we assume that the percentage of change in the particle velocity is small enough that one may simply write

$$\displaystyle{u_{\mathrm{R}} = \frac{z} {t} = \frac{\Delta l_{\mathrm{gap}}} {\Delta t_{\mathrm{gap}}}.}$$

The quantity $\Delta t_{\mathrm{gap}}$ denotes the time of flight through the gap. In this way, we obtain

$$\displaystyle\begin{array}{rcl} & & V = u_{\mathrm{R}}\hat{E}\;\int _{-\Delta t_{\mathrm{gap}}/2}^{+\Delta t_{\mathrm{gap}}/2}\cos (\omega _{\mathrm{ RF}}t)\;\mathrm{d}t = 2u_{\mathrm{R}}\hat{E}\left [\frac{\sin (\omega _{\mathrm{RF}}t)} {\omega _{\mathrm{RF}}} \right ]_{0}^{\Delta t_{\mathrm{gap}}/2} {}\\ & & \qquad \qquad \qquad \qquad \qquad \quad \qquad \qquad = 2u_{\mathrm{R}}\hat{E}\frac{\sin (\omega _{\mathrm{RF}}\Delta t_{\mathrm{gap}}/2)} {\omega _{\mathrm{RF}}} {}\\ & & \Rightarrow V = \Delta l_{\mathrm{gap}}\hat{E}\;\frac{\sin (\omega _{\mathrm{RF}}\Delta t_{\mathrm{gap}}/2)} {\omega _{\mathrm{RF}}\Delta t_{\mathrm{gap}}/2}. {}\\ \end{array}$$

If the time of flight is, according to

$$\displaystyle{\Delta t_{\mathrm{gap}} \ll T_{\mathrm{RF}} \Leftrightarrow \omega _{\mathrm{RF}}\Delta t_{\mathrm{gap}} \ll 2\pi,}$$

small in comparison with the RF period, it follows that

$$\displaystyle{V \rightarrow V _{0} = \Delta l_{\mathrm{gap}}\hat{E}.}$$

If this is not the case, one obtains

$$\displaystyle{V = V _{0} \cdot f_{\mathrm{T}},}$$

where f_T denotes the transit time factor

$$\displaystyle{f_{\mathrm{T}} =\mathrm{ si}\left (\omega _{\mathrm{RF}}\Delta t_{\mathrm{gap}}/2\right ) =\mathrm{ si}\left (\frac{\omega _{\mathrm{RF}}\Delta l_{\mathrm{gap}}} {2u_{\mathrm{R}}} \right ).}$$

In a synchrotron,

$$\displaystyle{\omega _{\mathrm{RF}} = h \frac{2\pi } {T_{\mathrm{R}}}}$$

and

$$\displaystyle{u_{\mathrm{R}} = \frac{l_{\mathrm{R}}} {T_{\mathrm{R}}}}$$

are valid, so that

$$\displaystyle{f_{\mathrm{T}} =\mathrm{ si}\left (\frac{\pi h\Delta l_{\mathrm{gap}}} {l_{\mathrm{R}}} \right )}$$

is obtained.

In the synchrotron SIS18 at GSI, the gap length $\Delta l_{\mathrm{gap}}$ of the ferrite cavities amounts to about 0. 1 m, the circumference of the synchrotron is l_R = 216 m, and the maximum harmonic number is 4. This leads to

$$\displaystyle{f_{\mathrm{T}} \approx 0.999994,}$$

so that the transit time effect is not at all relevant.

The situation is different in a linear accelerator, in which a gap length of 10 cm may have a significant effect. In the linear accelerator UNILAC at GSI, β = 0. 15 is reached at an RF frequency of 108 MHz, so that

$$\displaystyle{f_{\mathrm{T}} \approx 0.9079}$$

holds.

The transit time factor that was derived here should be regarded as only a rule of thumb to check whether the transit time effect is relevant. The formula was based on the following drastic simplifications:

• The arrival time was chosen in such a way that the particle experiences the maximum field strength.

• The field was assumed to be homogeneous in the longitudinal direction.

• The relative change in the particle velocity inside the gap was assumed to be small.

4.4 Pillbox Cavity

The pillbox cavity may be regarded as the fundamental cavity type, especially in linear accelerators. Other accelerating structures may often be considered as a modification or combination of pillbox cavities. Therefore, the pillbox cavity is analyzed in this section. The notation used here is close to that used in [35, 36].

Firstly, we discuss the TE modes and the TM modes in circular waveguides (perfectly conducting hollow cylinder). In both cases, a field solution for the pillbox cavity will afterward be generated by introducing ideally conducting end plates.

4.4.1 TM Modes

We begin with the equations for the vector potential (2.50) and the scalar potential (2.51). Since we are interested in only time-harmonic solutions, phasors will be used—even though we do not mark⁷ them specifically as phasors in this section:

$$\displaystyle\begin{array}{rcl} \Delta \vec{A} + \frac{\omega ^{2}} {c^{2}}\;\vec{A}& =& -\mu \vec{J}, {}\\ \Delta \Phi + \frac{\omega ^{2}} {c^{2}}\;\Phi & =& -\frac{\rho _{q}} {\epsilon }. {}\\ \end{array}$$

The inside of the cavity is evacuated and is therefore free of charges and free of currents. Hence, we are looking for solutions of the vector Helmholtz equation

$$\displaystyle{\Delta \vec{A} + k^{2}\;\vec{A} = 0}$$

and the scalar Helmholtz equation

$$\displaystyle{\Delta \Phi + k^{2}\;\Phi = 0}$$

with

$$\displaystyle{k = \frac{\omega } {c_{0}},}$$

which are coupled by the Lorenz gauge condition (2.49)

$$\displaystyle{ \mathrm{div}\;\vec{A} = -j\omega \mu _{0}\epsilon _{0}\Phi. }$$

(4.29)

As we will see, nontrivial solutions are still possible if

$$\displaystyle{ \vec{A} = A_{z}^{E}\vec{e}_{ z} }$$

(4.30)

is assumed. This leads to the following equation:

$$\displaystyle{ \Delta A_{z}^{E} + k^{2}\;A_{ z}^{E} = 0. }$$

(4.31)

According to Eqs. (2.47) and (2.48), the fields can be derived from the vector potential by means of

$$\displaystyle{ \vec{B} =\mathrm{ curl}\;\vec{A} =\vec{ e}_{\rho }\frac{1} {\rho } \frac{\partial A_{z}^{E}} {\partial \varphi } -\vec{ e}_{\varphi }\frac{\partial A_{z}^{E}} {\partial \rho } }$$

(4.32)

and

$$\displaystyle{\vec{E} = -j\omega \vec{A} -\mathrm{ grad}\;\Phi = -j\omega \vec{A} - \frac{1} {-j\omega \mu _{0}\epsilon _{0}}\;\mathrm{grad}\;\mathrm{div}\;\vec{A} = -j\omega \vec{A} + \frac{c_{0}^{2}} {j\omega } \;\mathrm{grad}\;\mathrm{div}\;\vec{A}.}$$

Here, Eq. (4.29) was used. For $\vec{A} = A_{z}^{E}\vec{e}_{z}$, we have

$$\displaystyle{\mathrm{div}\;\vec{A} = \frac{\partial A_{z}^{E}} {\partial z} }$$

and

$$\displaystyle{\mathrm{grad}\;\mathrm{div}\;\vec{A} =\vec{ e}_{\rho }\;\frac{\partial ^{2}A_{z}^{E}} {\partial \rho \partial z} +\vec{ e}_{\varphi }\;\frac{1} {\rho } \;\frac{\partial ^{2}A_{z}^{E}} {\partial \varphi \partial z} +\vec{ e}_{z}\;\frac{\partial ^{2}A_{z}^{E}} {\partial z^{2}},}$$

so that

$$\displaystyle{ \vec{E} = \frac{c_{0}^{2}} {j\omega } \left [\vec{e}_{\rho }\;\frac{\partial ^{2}A_{z}^{E}} {\partial \rho \partial z} +\vec{ e}_{\varphi }\;\frac{1} {\rho } \;\frac{\partial ^{2}A_{z}^{E}} {\partial \varphi \partial z} +\vec{ e}_{z}\;\left (\frac{\partial ^{2}A_{z}^{E}} {\partial z^{2}} + \frac{\omega ^{2}} {c_{0}^{2}}\;A_{z}^{E}\right )\right ] }$$

(4.33)

is the result. Equations (4.32) and (4.33) were obtained by expressing the curl, div, and grad operators in cylindrical coordinates. The first result shows that our assumption (4.30) for the vector potential implies that there are no longitudinal components of the magnetic field. We will therefore get transverse magnetic (TM) waves, which are also called E waves. This explains why we called the longitudinal component of the vector potential $A_{z}^{E}$. In cylindrical coordinates, Eq. (4.31) can be written as

$$\displaystyle{\frac{\partial ^{2}A_{z}^{E}} {\partial \rho ^{2}} + \frac{1} {\rho } \frac{\partial A_{z}^{E}} {\partial \rho } + \frac{1} {\rho ^{2}} \frac{\partial ^{2}A_{z}^{E}} {\partial \varphi ^{2}} + \frac{\partial ^{2}A_{z}^{E}} {\partial z^{2}} + k^{2}A_{ z}^{E} = 0.}$$

We solve this equation by inserting the separation ansatz (cf. [36])

$$\displaystyle{A_{z}^{E} = A_{ 0}(\rho,\varphi )A_{3}(z).}$$

After division by $A_{z}^{E}$, one gets

$$\displaystyle{\left ( \frac{1} {A_{0}}\;\frac{\partial ^{2}A_{0}} {\partial \rho ^{2}} + \frac{1} {\rho } \frac{1} {A_{0}}\;\frac{\partial A_{0}} {\partial \rho } + \frac{1} {\rho ^{2}} \frac{1} {A_{0}}\;\frac{\partial ^{2}A_{0}} {\partial \varphi ^{2}} \right ) + \frac{1} {A_{3}}\;\frac{\partial ^{2}A_{3}} {\partial z^{2}} + k^{2} = 0.}$$

It is obvious that the first term in parentheses may depend only on ρ and $\varphi$, and the second term only on z. Since the last term, k², however, does not depend on any of these coordinates, the two terms must be constant:

$$\displaystyle\begin{array}{rcl} \frac{1} {A_{0}}\;\frac{\partial ^{2}A_{0}} {\partial \rho ^{2}} + \frac{1} {\rho } \frac{1} {A_{0}}\;\frac{\partial A_{0}} {\partial \rho } + \frac{1} {\rho ^{2}} \frac{1} {A_{0}}\;\frac{\partial ^{2}A_{0}} {\partial \varphi ^{2}} & =& -C_{0}, {}\\ \frac{1} {A_{3}}\;\frac{\partial ^{2}A_{3}} {\partial z^{2}} & =& -C_{3}, {}\\ C_{0} + C_{3}& =& k^{2}. {}\\ \end{array}$$

If we multiply the first equation by ρ², we get

$$\displaystyle{\left (\rho ^{2} \frac{1} {A_{0}}\;\frac{\partial ^{2}A_{0}} {\partial \rho ^{2}} +\rho \frac{1} {A_{0}}\;\frac{\partial A_{0}} {\partial \rho } + C_{0}\rho ^{2}\right ) + \frac{1} {A_{0}}\;\frac{\partial ^{2}A_{0}} {\partial \varphi ^{2}} = 0.}$$

We insert the separation ansatz

$$\displaystyle{A_{0} = A_{1}(\rho )\;A_{2}(\varphi )}$$

and obtain

$$\displaystyle{\left (\rho ^{2} \frac{1} {A_{1}}\;\frac{\partial ^{2}A_{1}} {\partial \rho ^{2}} +\rho \frac{1} {A_{1}}\;\frac{\partial A_{1}} {\partial \rho } + C_{0}\rho ^{2}\right ) + \frac{1} {A_{2}}\;\frac{\partial ^{2}A_{2}} {\partial \varphi ^{2}} = 0.}$$

The first term in parentheses may depend only on ρ, whereas the second term may depend only on $\varphi$. Therefore, they must both be constant:

$$\displaystyle\begin{array}{rcl} \rho ^{2} \frac{1} {A_{1}}\;\frac{\partial ^{2}A_{1}} {\partial \rho ^{2}} +\rho \frac{1} {A_{1}}\;\frac{\partial A_{1}} {\partial \rho } + C_{0}\rho ^{2}& =& C_{ 1}, {}\\ \frac{1} {A_{2}}\;\frac{\partial ^{2}A_{2}} {\partial \varphi ^{2}} & =& -C_{1}. {}\\ \end{array}$$

The three ordinary differential equations may be rewritten in the following form:

$$\displaystyle\begin{array}{rcl} \rho ^{2}\frac{\mathrm{d}^{2}A_{ 1}} {\mathrm{d}\rho ^{2}} +\rho \; \frac{\mathrm{d}A_{1}} {\mathrm{d}\rho } + (C_{0}\rho ^{2} - C_{ 1})A_{1}& =& 0,{}\end{array}$$

(4.34)

$$\displaystyle\begin{array}{rcl} \frac{\mathrm{d}^{2}A_{2}} {\mathrm{d}\varphi ^{2}} + C_{1}A_{2}& =& 0,{}\end{array}$$

(4.35)

$$\displaystyle\begin{array}{rcl} \frac{\mathrm{d}^{2}A_{3}} {\mathrm{d}z^{2}} + C_{3}A_{3}& =& 0,{}\end{array}$$

(4.36)

$$\displaystyle\begin{array}{rcl} C_{0} + C_{3} = k^{2}.& &{}\end{array}$$

(4.37)

For real constants C₁, C₃ > 0, the last two differential equations describe a harmonic oscillator, so that the solutions

$$\displaystyle{ A_{3} = A_{31}\;\cos (\sqrt{C_{3}}z) + A_{32}\;\sin (\sqrt{C_{3}}z) }$$

(4.38)

and

$$\displaystyle{ A_{2} = A_{21}\;\cos (\sqrt{C_{1}}\varphi ) + A_{22}\;\sin (\sqrt{C_{1}}\varphi ) }$$

(4.39)

are obvious.⁸ In the first equation (4.34), the substitution $\tilde{\rho }= \sqrt{C_{0}}\rho$ leads to

$$\displaystyle{\tilde{\rho }^{2}\frac{\mathrm{d}^{2}A_{ 1}} {\mathrm{d}\tilde{\rho }^{2}} +\tilde{\rho }\; \frac{\mathrm{d}A_{1}} {\mathrm{d}\tilde{\rho }} + (\tilde{\rho }^{2} - C_{ 1})A_{1} = 0.}$$

This is equivalent to Bessel’s differential equation

$$\displaystyle{ \fbox{$x^{2} \frac{\mathrm{d}^{2}y} {\mathrm{d}x^{2}} + x\frac{\mathrm{d}y} {\mathrm{d}x} + (x^{2} - m^{2})y = 0,$} }$$

(4.40)

where we define

$$\displaystyle{m = \sqrt{C_{1}}.}$$

A set of solutions is given by the Bessel functions of the first kind J_m(x) and Bessel functions of the second kind Y_m(x) (also called Neumann functions N_m(x))—see Table A.2 on p. 415 and Figs. A.17 and A.18. In our case, we get

$$\displaystyle{A_{1} = A_{11}\mathrm{J}_{m}(\sqrt{C_{0}}\rho ) + A_{12}\mathrm{Y}_{m}(\sqrt{C_{0}}\rho ).}$$

Since the field components and $A_{z}^{E}$ must not change if integer multiples of 2π are added to $\varphi$, the restriction $m \in \{ 0,1,2,\ldots \}$ must be valid, as Eq. (4.39) shows. Negative m do not lead to new degrees of freedom ($\mathrm{J}_{-m} = (-1)^{m}\mathrm{J}_{m}$, $\mathrm{Y}_{-m} = (-1)^{m}\mathrm{Y}_{m}$) and can therefore be excluded. Because Y_m(x) has a pole at x = 0, which would lead to singularities of the field components at ρ = 0, it cannot correspond to a physical solution. Hence, we omit the last term. The total solution is therefore given by

$$\displaystyle{A_{z}^{E}=\,\mathrm{J}_{ m}(\!\sqrt{C_{0}}\rho )\left [A_{21}\;\cos (m\varphi )+A_{22}\;\sin (m\varphi )\right ]\left [\!A_{31}\;\cos (\sqrt{C_{3}}z)+A_{32}\;\sin (\sqrt{C_{3}}z)\!\right ]\!.}$$

We finally define $K = \sqrt{C_{0}}$ and $k_{z} = \sqrt{C_{3}}$, so that

$$\displaystyle{A_{z}^{E} =\mathrm{ J}_{ m}(K\rho )\left [A_{21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ]\left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ]}$$

with

$$\displaystyle{K^{2} + k_{ z}^{2} = k^{2}}$$

is valid. According to Eqs. (4.33) and (4.32), this leads to the following field components:

$$\displaystyle\begin{array}{rcl} E_{\rho }& =& \frac{c_{0}^{2}} {j\omega } \;\frac{\partial ^{2}A_{z}^{E}} {\partial \rho \partial z} = \\ & =& \frac{c_{0}^{2}} {j\omega } \;Kk_{z}\;\mathrm{J}_{m}^{{\prime}}(K\rho )\left [A_{ 21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ] \\ & & \times \left [-A_{31}\;\sin (k_{z}z) + A_{32}\;\cos (k_{z}z)\right ], {}\end{array}$$

(4.41)

$$\displaystyle\begin{array}{rcl} E_{\varphi }& =& \frac{c_{0}^{2}} {j\omega } \;\frac{1} {\rho } \;\frac{\partial ^{2}A_{z}^{E}} {\partial \varphi \partial z} = \\ & =& \frac{c_{0}^{2}} {j\omega } \;\frac{m} {\rho } \;k_{z}\mathrm{J}_{m}(K\rho )\left [-A_{21}\;\sin (m\varphi ) + A_{22}\;\cos (m\varphi )\right ] \\ & & \times \left [-A_{31}\;\sin (k_{z}z) + A_{32}\;\cos (k_{z}z)\right ], {}\end{array}$$

(4.42)

$$\displaystyle\begin{array}{rcl} E_{z}& =& \frac{c_{0}^{2}} {j\omega } (k^{2} - k_{ z}^{2})A_{ z}^{E} = \\ & =& \frac{c_{0}^{2}} {j\omega } \;K^{2}\;\mathrm{J}_{ m}(K\rho )\left [A_{21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ] \\ & & \times \left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ], {}\end{array}$$

(4.43)

$$\displaystyle\begin{array}{rcl} B_{\rho }& =& \frac{1} {\rho } \frac{\partial A_{z}^{E}} {\partial \varphi } = \\ & =& \frac{m} {\rho } \;\mathrm{J}_{m}(K\rho )\left [-A_{21}\;\sin (m\varphi ) + A_{22}\;\cos (m\varphi )\right ] \\ & & \times \left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ], {}\end{array}$$

(4.44)

$$\displaystyle\begin{array}{rcl} B_{\varphi }& =& -\frac{\partial A_{z}^{E}} {\partial \rho } = \\ & =& -K\;\mathrm{J}_{m}^{{\prime}}(K\rho )\left [A_{ 21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ] \\ & & \times \left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ], {}\end{array}$$

(4.45)

$$\displaystyle\begin{array}{rcl} B_{z}& =& 0.{}\end{array}$$

(4.46)

At the conducting surface at ρ = r_pillbox, the tangential components of the electric field (i.e., $E_{\varphi }$, E_z) and the normal component of the magnetic field (i.e., B_ρ) must vanish.⁹This leads to the condition

$$\displaystyle{\mathrm{J}_{m}(\mathit{Kr}_{\mathrm{pillbox}}) = 0.}$$

The zeros of J_m(x) with x > 0 will be denoted by j_mn, where $n \in \{ 1,2,3,\ldots \}$. Selecting n therefore determines K according to

$$\displaystyle{K = \frac{j_{\mathit{mn}}} {r_{\mathrm{pillbox}}}.}$$

In conclusion, the field pattern of a TM mode is determined by the two numbers m and n. Therefore, one writes TM_mn or E_mn to specify the modes in a circular waveguide. The propagation constant for such a mode is given by

$$\displaystyle{k_{z} = \sqrt{k^{2 } - K^{2}}.}$$

It is obvious that a minimum (angular) frequency ω = ω_c is needed if k_z is to be real, which means that the wave is propagating. This cutoff frequency of the TM mode under consideration is given by k = K, which is equivalent to

$$\displaystyle{\omega _{\mathrm{c}} = c_{0} \frac{j_{\mathit{mn}}} {r_{\mathrm{pillbox}}}.}$$

A pillbox cavity corresponds to a circular waveguide with additional conducting walls at z = 0 and z = l_pillbox. Since E_ρ and $E_{\varphi }$ must be zero at z = 0, one then selects A₃₂ = 0. Because one has to satisfy $E_{\rho } = E_{\varphi } = 0$ at z = l_pillbox in addition, the condition

$$\displaystyle{k_{z}l_{\mathrm{pillbox}} = p\pi }$$

must hold. For characterizing the modes in a resonator, we therefore have to introduce a third number $p \in \{ 0,1,2,\ldots \}$. If the three numbers m, n, and p are fixed, then K and k_z are fixed as well, and the equation

$$\displaystyle{ \frac{\omega } {c_{0}} = k = \sqrt{k_{z }^{2 } + K^{2}}}$$

determines the resonant frequency $f_{\mathrm{res}} = \frac{\omega _{\mathrm{res}}} {2\pi } = \frac{\omega } {2\pi }$. In a cavity with perfectly conducting walls, electromagnetic fields may exist only at these discrete resonant frequencies (eigenvalue problem). The corresponding modes are denoted by TM_mnp or E_mnp.

4.4.2 TE Modes

The solutions derived in the previous section are based on the assumption that the inside of the waveguide or the cavity is evacuated. Therefore, the Maxwell’s equations that had to be solved reduce to

$$\displaystyle\begin{array}{rcl} \mathrm{curl}\;\vec{H}& =& j\omega \epsilon _{0}\;\vec{E},{}\end{array}$$

(4.47)

$$\displaystyle\begin{array}{rcl} \mathrm{curl}\;\vec{E}& =& -j\omega \mu _{0}\;\vec{H},{}\end{array}$$

(4.48)

$$\displaystyle\begin{array}{rcl} \mathrm{div}\;\vec{B}& =& 0,{}\end{array}$$

(4.49)

$$\displaystyle\begin{array}{rcl} \mathrm{div}\;\vec{D}& =& 0.{}\end{array}$$

(4.50)

The general approach to deriving the vector potential is based on the equation

$$\displaystyle{\mathrm{div}\;\vec{B} = 0,}$$

so that

$$\displaystyle{\vec{B} =\mathrm{ curl}\;\vec{A}}$$

was required above. Now we see that in the special case that the waveguide is evacuated, we can alternatively satisfy

$$\displaystyle{\mathrm{div}\;\vec{D} = 0}$$

by defining

$$\displaystyle{ \vec{D} =\mathrm{ curl}\;\vec{A}. }$$

(4.51)

If we insert this into Eq. (4.47), we get

$$\displaystyle{\mathrm{curl}\left (\vec{H} - j\omega \;\vec{A}\right ) = 0,}$$

which may be satisfied if the scalar potential $\Phi$ is defined according to

$$\displaystyle{ \vec{H} - j\omega \;\vec{A} =\mathrm{ grad}\;\Phi \mbox{ } \Rightarrow \vec{ H} = j\omega \;\vec{A} +\mathrm{ grad}\;\Phi. }$$

(4.52)

The expressions for $\vec{D}$ and $\vec{H}$ are now inserted into Eq. (4.48):

$$\displaystyle\begin{array}{rcl} & \mathrm{curl}\;\mathrm{curl}\;\vec{A} = -j\omega \mu _{0}\epsilon _{0}\left (j\omega \;\vec{A} +\mathrm{ grad}\;\Phi \right ) & {}\\ & \Rightarrow \mathrm{ grad}\;\mathrm{div}\;\vec{A} - \Delta \vec{A} = \frac{\omega ^{2}} {c_{0}^{2}} \;\vec{A} - j \frac{\omega } {c_{ 0}^{2}} \;\mathrm{grad}\;\Phi & {}\\ & \Rightarrow \Delta \vec{A} + k^{2}\vec{A} =\mathrm{ grad}\left (\mathrm{div}\;\vec{A} + j \frac{\omega } {c_{ 0}^{2}} \;\Phi \right ). & {}\\ \end{array}$$

By means of the gauge condition

$$\displaystyle{ \mathrm{div}\;\vec{A} = -j \frac{\omega } {c_{0}^{2}}\;\Phi, }$$

(4.53)

this leads to the vector Helmholtz equation

$$\displaystyle{\Delta \vec{A} + k^{2}\vec{A} = 0.}$$

Our new ansatz for the vector potential obviously leads to the same equations to be solved as in the previous section. However, in this case, the curl of the vector potential now determines the electric field instead of the magnetic one. One therefore speaks of TE waves instead of TM waves.

We now determine the field components of the TE waves (also called H waves) in the same way as those for the TM waves (also known as E waves). Therefore,

$$\displaystyle{ \vec{A} = A_{z}^{H}\vec{e}_{ z} }$$

(4.54)

is assumed. This leads to the following equation:

$$\displaystyle{ \Delta A_{z}^{H} + k^{2}\;A_{ z}^{H} = 0. }$$

(4.55)

According to Eqs. (4.51) and (4.52), the fields can be derived from the vector potential by means of

$$\displaystyle{ \vec{D} =\mathrm{ curl}\;\vec{A} =\vec{ e}_{\rho }\frac{1} {\rho } \frac{\partial A_{z}^{H}} {\partial \varphi } -\vec{ e}_{\varphi }\frac{\partial A_{z}^{H}} {\partial \rho } }$$

(4.56)

and

$$\displaystyle{\vec{H} = j\omega \vec{A} +\mathrm{ grad}\;\Phi = j\omega \vec{A} -\frac{c_{0}^{2}} {j\omega } \;\mathrm{grad}\;\mathrm{div}\;\vec{A}.}$$

Here, Eq. (4.53) was used. For $\vec{A} = A_{z}^{H}\vec{e}_{z}$, we have

$$\displaystyle{\mathrm{div}\;\vec{A} = \frac{\partial A_{z}^{H}} {\partial z} }$$

and

$$\displaystyle{\mathrm{grad}\;\mathrm{div}\;\vec{A} =\vec{ e}_{\rho }\;\frac{\partial ^{2}A_{z}^{H}} {\partial \rho \partial z} +\vec{ e}_{\varphi }\;\frac{1} {\rho } \;\frac{\partial ^{2}A_{z}^{H}} {\partial \varphi \partial z} +\vec{ e}_{z}\;\frac{\partial ^{2}A_{z}^{H}} {\partial z^{2}},}$$

so that

$$\displaystyle{ \vec{H} = -\frac{c_{0}^{2}} {j\omega } \left [\vec{e}_{\rho }\;\frac{\partial ^{2}A_{z}^{H}} {\partial \rho \partial z} +\vec{ e}_{\varphi }\;\frac{1} {\rho } \;\frac{\partial ^{2}A_{z}^{H}} {\partial \varphi \partial z} +\vec{ e}_{z}\;\left (\frac{\partial ^{2}A_{z}^{H}} {\partial z^{2}} + \frac{\omega ^{2}} {c_{0}^{2}}\;A_{z}^{H}\right )\right ] }$$

(4.57)

is the result. Equations (4.56) and (4.57) were obtained by expressing the curl, div, and grad operators in cylindrical coordinates. The first result shows that our assumption (4.54) for the vector potential implies that there are no longitudinal components of the electric field. We will therefore get transverse electric (TE) waves. This explains why we called the longitudinal component of the vector potential $A_{z}^{H}$.

Since the Helmholtz equation (4.55) is still identical to that of the E mode derivation (4.31), the same separation ansatz may be used as in the previous section.

The total solution is therefore given by

$$\displaystyle{A_{z}^{H} =\mathrm{ J}_{ m}(K\rho )\left [A_{21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ]\left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ]}$$

with

$$\displaystyle{K^{2} + k_{ z}^{2} = k^{2}.}$$

According to Eqs. (4.56) and (4.57), this leads to the following field components:

$$\displaystyle\begin{array}{rcl} D_{\rho }& =& \frac{1} {\rho } \frac{\partial A_{z}^{H}} {\partial \varphi } = \frac{m} {\rho } \;\mathrm{J}_{m}(K\rho )\left [-A_{21}\;\sin (m\varphi ) + A_{22}\;\cos (m\varphi )\right ] {}\\ & & \qquad \qquad \ \times \left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ], {}\\ D_{\varphi }& =& -\frac{\partial A_{z}^{H}} {\partial \rho } = -K\;\mathrm{J}_{m}^{{\prime}}(K\rho )\left [A_{ 21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ] {}\\ & & \qquad \qquad \ \times \left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ], {}\\ D_{z}& =& 0, {}\\ H_{\rho }& =& -\frac{c_{0}^{2}} {j\omega } \;\frac{\partial ^{2}A_{z}^{H}} {\partial \rho \partial z} = {}\\ & =& -\frac{c_{0}^{2}} {j\omega } \;Kk_{z}\;\mathrm{J}_{m}^{{\prime}}(K\rho )\left [A_{ 21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ] {}\\ & & \times \left [-A_{31}\;\sin (k_{z}z) + A_{32}\;\cos (k_{z}z)\right ], {}\\ H_{\varphi }& =& -\frac{c_{0}^{2}} {j\omega } \;\frac{1} {\rho } \;\frac{\partial ^{2}A_{z}^{H}} {\partial \varphi \partial z} = {}\\ & =& -\frac{c_{0}^{2}} {j\omega } \;\frac{m} {\rho } \;k_{z}\mathrm{J}_{m}(K\rho )\left [-A_{21}\;\sin (m\varphi ) + A_{22}\;\cos (m\varphi )\right ] {}\\ & & \times \left [-A_{31}\;\sin (k_{z}z) + A_{32}\;\cos (k_{z}z)\right ], {}\\ H_{z}& =& -\frac{c_{0}^{2}} {j\omega } (k^{2} - k_{ z}^{2})A_{ z}^{H} = {}\\ & =& -\frac{c_{0}^{2}} {j\omega } \;K^{2}\;\mathrm{J}_{ m}(K\rho )\left [A_{21}\;\cos (m\varphi ) + A_{22}\;\sin (m\varphi )\right ] {}\\ & & \times \left [A_{31}\;\cos (k_{z}z) + A_{32}\;\sin (k_{z}z)\right ]. {}\\ \end{array}$$

At the conducting surface at ρ = r_pillbox, the tangential component of the electric field (i.e., $E_{\varphi }$ and hence also $D_{\varphi }$) and the normal component of the magnetic field (i.e., B_ρ and hence also H_ρ) must vanish. This leads to the condition

$$\displaystyle{\mathrm{J}_{m}^{{\prime}}(\mathit{Kr}_{\mathrm{ pillbox}}) = 0.}$$

The zeros of $\mathrm{J}_{m}^{{\prime}}(x)$ with x > 0 will be denoted by $j_{\mathit{mn}}^{{\prime}}$, where $n \in \{ 1,2,3,\ldots \}$. Selecting n therefore determines K according to

$$\displaystyle{K = \frac{j_{\mathit{mn}}^{{\prime}}} {r_{\mathrm{pillbox}}}.}$$

In conclusion, the field pattern of a TE mode is determined by the two numbers m and n. Therefore, one writes TE_mn or H_mn to specify the modes in a circular waveguide. The propagation constant for such a mode is given by

$$\displaystyle{k_{z} = \sqrt{k^{2 } - K^{2}}.}$$

It is obvious that a minimum (angular) frequency ω = ω_c is needed if k_z is to be real, which means that the wave is propagating. This frequency is given by k = K, which is equivalent to

$$\displaystyle{\omega _{\mathrm{c}} = c_{0} \frac{j_{\mathit{mn}}^{{\prime}}} {r_{\mathrm{pillbox}}}.}$$

We again introduce end plates at z = 0 and z = l_pillbox in order to convert the waveguide into a pillbox cavity. Since D_ρ and $D_{\varphi }$ must be zero at z = 0, one then selects A₃₁ = 0. Because one has to satisfy $D_{\rho } = D_{\varphi } = 0$ at z = l_pillbox in addition, the condition

$$\displaystyle{k_{z}l_{\mathrm{pillbox}} = p\pi }$$

must hold ($p \in \{ 1,2,\ldots \}$). Please note that p = 0 is not an option for TE modes, since all field components disappear in that case. If the three numbers m, n, and p are fixed, K and k_z are fixed as well, and the equation

$$\displaystyle{ \frac{\omega } {c_{0}} = k = \sqrt{k_{z }^{2 } + K^{2}}}$$

determines the resonant frequency. The corresponding modes are denoted by TE_mnp and H_mnp.

According to Table 4.2 on p. 145, $j_{11}^{{\prime}}$ is smaller than j₀₁. Hence, the dominant mode in the circular waveguide, i.e., the mode with the lowest cutoff frequency, is the TE₁₁ mode.

Table 4.2 Zeros j_mn of the Bessel function J_m(x) and zeros $j_{\mathit{mn}}^{{\prime}}$ of its derivative $\mathrm{J}_{m}^{{\prime}}(x)$; values taken from [37]

Since the TE modes do not have any longitudinal component of the electric field, they cannot be used for acceleration in a pillbox cavity. Therefore, in a pillbox cavity, the mode TM₀₁₀ is usually used for acceleration. In this case, the TM₀₁₀ mode should also be the dominant mode. Therefore, one has to exclude the situation in which the resonant frequency of the TE₁₁₁ mode is lower. For the TE₁₁₁ mode, we have

$$\displaystyle{k^{2} = \frac{\omega _{\mathrm{res}}^{2}} {c_{0}^{2}} = k_{z}^{2} + K^{2}}$$

with

$$\displaystyle{k_{z} = \frac{\pi } {l_{\mathrm{pillbox}}},\mbox{ }K = \frac{j_{11}^{{\prime}}} {r_{\mathrm{pillbox}}}.}$$

For the TM₀₁₀ mode,

$$\displaystyle{k = K = \frac{j_{01}} {r_{\mathrm{pillbox}}}}$$

is valid. Therefore we require

$$\displaystyle{\left ( \frac{\pi } {l_{\mathrm{pillbox}}}\right )^{2} + \left ( \frac{j_{11}^{{\prime}}} {r_{\mathrm{pillbox}}}\right )^{2} > \left ( \frac{j_{01}} {r_{\mathrm{pillbox}}}\right )^{2},}$$

$$\displaystyle{\frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} > \frac{1} {\pi } \sqrt{j_{01 }^{2 } - j^{{\prime2}}{}_{11}} \approx 0.49.}$$

Roughly speaking, the length of the cavity must therefore be smaller than the diameter.

4.4.3 Energy Considerations for the TM₀₁₀ Mode

As mentioned above, the mode that is used for acceleration is the TM₀₁₀ mode. For this mode,

$$\displaystyle{m = 0,\mbox{ }n = 1,\mbox{ }p = 0\mbox{ } \Rightarrow k_{z} = 0\mbox{ } \Rightarrow K = k = \frac{\omega } {c_{0}}}$$

is valid.

Equations (4.41)–(4.46) then reduce to

$$\displaystyle{ E_{z} = \frac{c_{0}^{2}} {j\omega } \;K^{2}\;\mathrm{J}_{ 0}(K\rho )\;A_{21}\;A_{31} = -j\omega \;A_{0}\;\mathrm{J}_{0}(K\rho ), }$$

(4.58)

$$\displaystyle{ B_{\varphi } = -K\;\mathrm{J}_{0}^{{\prime}}(K\rho )\;A_{ 21}\;A_{31} = -A_{0}\;K\;\mathrm{J}_{0}^{{\prime}}(K\rho ). }$$

(4.59)

Here we defined A₀ = A₂₁ A₃₁ as a new constant. The voltage that is generated along the z-axis is

$$\displaystyle{ \hat{V } = \left \vert \int _{0}^{l_{\mathrm{pillbox}} }E_{z}(\rho = 0)\;\mathrm{d}z\right \vert =\omega \; \vert A_{0}\vert \;\mathrm{J}_{0}(0)\;l_{\mathrm{pillbox}} =\omega \; \vert A_{0}\vert \;l_{\mathrm{pillbox}}, }$$

(4.60)

where J₀(0) = 1 was used.

4.4.3.1 Electric Energy

We now calculate the total time-averaged electric energy in the cavity:

$$\displaystyle\begin{array}{rcl} \overline{W}_{\mathrm{el}}& =& \frac{1} {4}\mathrm{Re}\left \{\int \vec{D}^{{\ast}}\cdot \vec{ E}\;\mathrm{d}V \right \} = {}\\ & =& \frac{1} {4}\epsilon _{0}\int _{0}^{l_{\mathrm{pillbox}} }\int _{0}^{r_{\mathrm{pillbox}} }\int _{0}^{2\pi }\vert E_{ z}\vert ^{2}\rho \;\mathrm{d}\varphi \;\mathrm{d}\rho \;\mathrm{d}z=\frac{2\pi } {4}l_{\mathrm{pillbox}}\epsilon _{0}\int _{0}^{r_{\mathrm{pillbox}} }\vert E_{z}\vert ^{2}\rho \;\mathrm{d}\rho = {}\\ & =& \frac{\pi } {2}l_{\mathrm{pillbox}}\epsilon _{0}\omega ^{2}\vert A_{ 0}\vert ^{2}\int _{ 0}^{r_{\mathrm{pillbox}} }\mathrm{J}_{0}^{2}(K\rho )\;\rho \;\mathrm{d}\rho. {}\\ \end{array}$$

According to Gradshteyn [38, Sect. 5.5, formula 5.54-2],

$$\displaystyle\begin{array}{rcl} & \fbox{$\int \mathrm{J}_{m}^{2}(K\rho )\;\rho \;\mathrm{d}\rho = \frac{\rho ^{2}} {2}\left \{\mathrm{J}_{m}^{2}(K\rho ) -\mathrm{ J}_{ m-1}(K\rho )\;\mathrm{J}_{m+1}(K\rho )\right \}$}& {}\\ & \Rightarrow \int \mathrm{ J}_{0}^{2}(K\rho )\;\rho \;\mathrm{d}\rho = \frac{\rho ^{2}} {2}\left \{\mathrm{J}_{0}^{2}(K\rho ) -\mathrm{ J}_{ -1}(K\rho )\;\mathrm{J}_{1}(K\rho )\right \} & {}\\ \end{array}$$

is valid. Due to Eq. (A.72), Table A.2 on p. 415, we have

$$\displaystyle{\mathrm{J}_{-m}(z) = (-1)^{m}\mathrm{J}_{ m}(z)\mbox{ } \Rightarrow \mathrm{ J}_{-1}(z) = -\mathrm{J}_{1}(z),}$$

so that

$$\displaystyle{\int \mathrm{J}_{0}^{2}(K\rho )\;\rho \;\mathrm{d}\rho = \frac{\rho ^{2}} {2}\left \{\mathrm{J}_{0}^{2}(K\rho ) +\mathrm{ J}_{ 1}^{2}(K\rho )\right \}}$$

holds. In our case, the upper integration limit is r_pillbox, which leads to the argument $K\rho = Kr_{\mathrm{pillbox}} = j_{01}$. Therefore, we obtain

$$\displaystyle{\int _{0}^{r_{\mathrm{pillbox}} }\mathrm{J}_{0}^{2}(K\rho )\;\rho \;\mathrm{d}\rho = \frac{r_{\mathrm{pillbox}}^{2}} {2} \;\mathrm{J}_{1}^{2}(j_{ 01}).}$$

This leads to

$$\displaystyle{ \overline{W}_{\mathrm{el}} = \frac{\pi } {4}l_{\mathrm{pillbox}}r_{\mathrm{pillbox}}^{2}\epsilon _{ 0}\omega ^{2}\vert A_{ 0}\vert ^{2}\;\mathrm{J}_{ 1}^{2}(j_{ 01}) = \frac{\pi } {4} \frac{r_{\mathrm{pillbox}}^{2}} {l_{\mathrm{pillbox}}} \epsilon _{0}\hat{V }^{2}\;\mathrm{J}_{ 1}^{2}(j_{ 01}). }$$

(4.61)

In the last step, Eq. (4.60) was used.

4.4.3.2 Magnetic Energy

For the sake of completeness, we now check that the stored (time-averaged) magnetic energy equals the electric energy stored in the cavity:

$$\displaystyle\begin{array}{rcl} \overline{W}_{\mathrm{magn}}& =& \frac{1} {4}\mathrm{Re}\left \{\int \vec{H}^{{\ast}}\cdot \vec{ B}\;\mathrm{d}V \right \} = {}\\ & =& \frac{1} {4\mu _{0}}\int _{0}^{l_{\mathrm{pillbox}} }\int _{0}^{r_{\mathrm{pillbox}} }\int _{0}^{2\pi }\vert B_{\varphi }\vert ^{2}\rho \;\mathrm{d}\varphi \;\mathrm{d}\rho \;\mathrm{d}z=\frac{2\pi l_{\mathrm{pillbox}}} {4\mu _{0}} \!\int _{0}^{r_{\mathrm{pillbox}} }\vert B_{\varphi }\vert ^{2}\rho \;\mathrm{d}\rho = {}\\ & =& \frac{\pi } {2} \frac{l_{\mathrm{pillbox}}} {\mu _{0}} K^{2}\vert A_{ 0}\vert ^{2}\int _{ 0}^{r_{\mathrm{pillbox}} }J^{{\prime2}}{}_{ 0}(K\rho )\;\rho \;\mathrm{d}\rho. {}\\ \end{array}$$

According to Table A.2 on p. 415, Eq. (A.77),

$$\displaystyle{\mathrm{J}_{0}^{{\prime}}(z) = -\mathrm{J}_{ 1}(z),}$$

is valid, which leads to

$$\displaystyle{\overline{W}_{\mathrm{magn}} = \frac{\pi } {2} \frac{l_{\mathrm{pillbox}}} {\mu _{0}} K^{2}\vert A_{ 0}\vert ^{2}\int _{ 0}^{r_{\mathrm{pillbox}} }\mathrm{J}_{1}^{2}(K\rho )\;\rho \;\mathrm{d}\rho.}$$

We may again apply formula 5.54-2 in [38]:

$$\displaystyle{\int \mathrm{J}_{1}^{2}(K\rho )\;\rho \;\mathrm{d}\rho = \frac{\rho ^{2}} {2}\left \{\mathrm{J}_{1}^{2}(K\rho ) -\mathrm{ J}_{ 0}(K\rho )\;\mathrm{J}_{2}(K\rho )\right \}.}$$

One gets

$$\displaystyle{ \int _{0}^{r_{\mathrm{pillbox}} }\mathrm{J}_{1}^{2}(K\rho )\;\rho \;\mathrm{d}\rho = \frac{r_{\mathrm{pillbox}}^{2}} {2} \;\mathrm{J}_{1}^{2}(j_{ 01}). }$$

(4.62)

This leads to

$$\displaystyle\begin{array}{rcl} \overline{W}_{\mathrm{magn}}& =& \frac{\pi } {4} \frac{l_{\mathrm{pillbox}}r_{\mathrm{pillbox}}^{2}} {\mu _{0}} K^{2}\vert A_{ 0}\vert ^{2}\;\mathrm{J}_{ 1}^{2}(j_{ 01}) {}\\ & =& \frac{\pi } {4} \frac{l_{\mathrm{pillbox}}r_{\mathrm{pillbox}}^{2}} {\mu _{0}} \frac{\omega ^{2}} {c_{0}^{2}}\vert A_{0}\vert ^{2}\;\mathrm{J}_{ 1}^{2}(j_{ 01}) = \frac{\pi } {4} \frac{r_{\mathrm{pillbox}}^{2}} {l_{\mathrm{pillbox}}} \epsilon _{0}\hat{V }^{2}\;\mathrm{J}_{ 1}^{2}(j_{ 01}), {}\\ \end{array}$$

which verifies $\overline{W}_{\mathrm{el}} = \overline{W}_{\mathrm{magn}}$ after comparison with Eq. (4.61). In the last step, Eq. (4.60) was used.

4.4.3.3 Power Loss

According to the power loss method, the (time-averaged) losses in the conductor (conductivity κ) can be calculated approximately by

$$\displaystyle{\fbox{$\overline{P}_{\mathrm{loss}} = \frac{R_{\mathrm{surf}}} {2} \int \vert H_{t}\vert ^{2}\;\mathrm{d}A.$}}$$

Here

$$\displaystyle{\fbox{$R_{\mathrm{surf}} = \frac{1} {\kappa \delta } $}}$$

denotes the surface resistivity with skin depth

$$\displaystyle{\fbox{$\delta = \sqrt{\frac{2} {\omega \mu \kappa }}.$}}$$

In the scope of the power loss method, one assumes that the fields outside the conductor (i.e., inside the cavity) do not change significantly if the ideal conductors are replaced by real ones with sufficiently high κ. Therefore, the tangential field H_t according to our solution (4.59) in the previous section can be used. For the cylindrical surface at ρ = r_pillbox, we therefore have

$$\displaystyle{H_{t} = H_{\varphi }(\rho = r_{\mathrm{pillbox}}) = -A_{0}\;\frac{K} {\mu _{0}} \;\mathrm{J}_{0}^{{\prime}}(\mathit{Kr}_{\mathrm{ pillbox}}) = A_{0}\;\frac{K} {\mu _{0}} \;\mathrm{J}_{1}(j_{01}),}$$

which leads to

$$\displaystyle\begin{array}{rcl} \overline{P}_{\mathrm{loss,1}}& =& \frac{R_{\mathrm{surf}}} {2} \;2\pi r_{\mathrm{pillbox}}l_{\mathrm{pillbox}}\;\vert A_{0}\vert ^{2}\;\frac{K^{2}} {\mu _{0}^{2}} \;\mathrm{J}_{1}^{2}(j_{ 01}) = {}\\ & =& \pi R_{\mathrm{surf}}\frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} \;\hat{V }^{2}\;\frac{\epsilon _{0}} {\mu _{0}}\;\mathrm{J}_{1}^{2}(j_{ 01}) =\pi \frac{R_{\mathrm{surf}}} {Z_{0}^{2}} \frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} \;\hat{V }^{2}\;\mathrm{J}_{ 1}^{2}(j_{ 01}). {}\\ \end{array}$$

Here

$$\displaystyle{\fbox{$Z_{0} = \sqrt{\frac{\mu _{0 } } {\epsilon _{0}}} \approx 376.73\;\Omega $}}$$

denotes the impedance of free space.

For each of the two end plates of the pillbox cavity, one obtains

$$\displaystyle\begin{array}{rcl} \overline{P}_{\mathrm{loss,2}}& =& \frac{R_{\mathrm{surf}}} {2} \int _{0}^{r_{\mathrm{pillbox}} }\int _{0}^{2\pi }\vert H_{\varphi }\vert ^{2}\rho \;\mathrm{d}\varphi \;\mathrm{d}\rho = {}\\ & =& \frac{R_{\mathrm{surf}}} {2\mu _{0}^{2}} 2\pi \vert A_{0}\vert ^{2}K^{2}\int _{ 0}^{r_{\mathrm{pillbox}} }\mathrm{J}^{{\prime2}}\!\!_{ 0}(K\rho )\;\rho \;\mathrm{d}\rho = {}\\ & =& \pi R_{\mathrm{surf}}\frac{\epsilon _{0}} {\mu _{0}}\vert A_{0}\vert ^{2}\omega ^{2}\int _{ 0}^{r_{\mathrm{pillbox}} }\mathrm{J}_{1}^{2}(K\rho )\;\rho \;\mathrm{d}\rho. {}\\ \end{array}$$

Here we may use the result (4.62) and Eq. (4.60) again:

$$\displaystyle{\overline{P}_{\mathrm{loss,2}} = \frac{\pi } {2} \frac{R_{\mathrm{surf}}} {Z_{0}^{2}} \hat{V }^{2}\frac{r_{\mathrm{pillbox}}^{2}} {l_{\mathrm{pillbox}}^{2}} \;\mathrm{J}_{1}^{2}(j_{ 01}).}$$

Since two end plates are present, the total power loss is

$$\displaystyle{ \overline{P}_{\mathrm{loss}} = \overline{P}_{\mathrm{loss,1}} + 2\;\overline{P}_{\mathrm{loss,2}} =\pi \frac{R_{\mathrm{surf}}} {Z_{0}^{2}} \;\hat{V }^{2}\;\mathrm{J}_{ 1}^{2}(j_{ 01})\left (\frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} + \frac{r_{\mathrm{pillbox}}^{2}} {l_{\mathrm{pillbox}}^{2}} \right ). }$$

(4.63)

This leads to the Q factor

$$\displaystyle\begin{array}{rcl} Q_{\mathrm{p,0}}& =& \omega _{\mathrm{res}}\frac{\overline{W}_{\mathrm{total}}} {\overline{P}_{\mathrm{loss}}} =\omega _{\mathrm{res}}\frac{2\overline{W}_{\mathrm{el}}} {\overline{P}_{\mathrm{loss}}} {}\\ & =& \omega _{\mathrm{res}} \frac{ \frac{\pi } {2} \frac{r_{\mathrm{pillbox}}^{2}} {l_{\mathrm{pillbox}}} \epsilon _{0}\hat{V }^{2}\;\mathrm{J}_{1}^{2}(j_{01})} {\pi \frac{R_{\mathrm{surf}}} {Z_{0}^{2}} \;\hat{V }^{2}\;\mathrm{J}_{1}^{2}(j_{01})\left (\frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} + \frac{r_{\mathrm{pillbox}}^{2}} {l_{\mathrm{pillbox}}^{2}} \right )} = \frac{\omega _{\mathrm{res}}r_{\mathrm{pillbox}}\mu _{0}} {2R_{\mathrm{surf}}\;\left (1 + \frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} \right )}. {}\\ \end{array}$$

Due to

$$\displaystyle{ \fbox{$\omega _{\mathrm{res}} = c_{0} \frac{j_{01}} {r_{\mathrm{pillbox}}},$} }$$

(4.64)

this may also be written as

$$\displaystyle{ \fbox{$Q_{\mathrm{p,0}} = \frac{c_{0}\mu _{0}j_{01}} {2R_{\mathrm{surf}}\;\left (1 + \frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} \right )} = \frac{Z_{0}j_{01}} {2R_{\mathrm{surf}}\;\left (1 + \frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} \right )} = \frac{r_{\mathrm{pillbox}}} {\delta } \; \frac{1} {1 + \frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} }.$} }$$

(4.65)

Equation (4.63) leads directly to the shunt impedance

$$\displaystyle{ \fbox{$R_{\mathrm{p,0}} = \frac{\hat{V }^{2}} {2\;\overline{P}_{\mathrm{loss}}} = \frac{Z_{0}^{2}} {2\pi R_{\mathrm{surf}}\;\mathrm{J}_{1}^{2}(j_{01})\frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} \left (1 + \frac{r_{\mathrm{pillbox}}} {l_{\mathrm{pillbox}}} \right )}$} }$$

(4.66)

with

$$\displaystyle{j_{01} \approx 2.40483\mbox{ and }\mathrm{J}_{1}(j_{01}) \approx 0.51915.}$$

Again we have to emphasize that the shunt impedance is often defined with an additional factor of 2. Furthermore, the transit time factor may be included in the definition of the shunt impedance (cf. [39, 40] or [41, vol. II, Sect. 6.1.4]).

4.4.4 Practical Considerations

In order to calculate the losses of the pillbox cavity, we introduced a transition from ideal conductors to realistic conductors with finite conductivity. The cavity with ideal conductors does not have any losses at all. Therefore, Q → ∞ and R_p,0 → ∞ are valid. According to Eqs. (4.65) and (4.66), this result is also obtained for κ → ∞, δ = 0, R_surf = 0.

In the case of a lossless cavity, fields are present only for specific resonant frequencies. If losses are present, this discrete spectrum of resonant frequencies is transformed into a continuous one. The resonant frequencies correspond to local maxima of the absolute value of the impedance; each resonance has a finite bandwidth in the frequency domain (according to the Q factor of that specific mode). At the fundamental resonance, one therefore usually describes the pillbox cavity with the same lumped element circuit (parameters ω_res, Q_p,0, R_p,0, Eq. (4.25), Fig. 4.5) that was obtained previously for the ferrite cavity.

In the analytical calculations above, we completely neglected the beam pipe, the beam itself, and coupling elements. The beam pipe of course has a smaller diameter than the cavity, but it still allows undesired higher-order modes (HOM) to propagate. Of course, the presence of the beam pipe also modifies the solutions obtained above. The beam itself is sometimes modeled as an RF current; it induces fields inside the cavity (beam loading) that may act back on the beam.

Coupling elements are needed both to excite the fields inside the cavity and to measure them. These coupling elements (e.g., small coupling loops) are usually designed in such a way that they can be connected to waveguides or transmission lines with a specific impedance (e.g. $50\,\Omega$).

Instead of the unmodified pillbox cavity, one often uses rounded geometries. Several individual cavities may be combined into a larger structure in order to supply it with only one RF power source.

A cooling system is required to keep the lossy parts at constant temperature. This is especially important for high Q factors, since temperature changes may otherwise lead to significant drifts of the resonant frequency.

Since an unmodified pillbox cavity cannot be tuned in real time, i.e., since its resonant frequency cannot be changed during operation, it is suitable only for synchrotrons that work with a fixed RF frequency. This is, for example, possible if ultrarelativistic electrons are accelerated where $\beta \approx 1$ is valid. Of course, tuning is at least necessary during the commissioning phase of a cavity. Due to tolerances, the desired resonant frequency will usually not be hit after manufacture. Therefore, possibilities to slightly modify the geometry must be offered. For this purpose, plungers may, for example, be moved during normal operation in LINAC structures.

4.4.5 Example

As an example, we consider an 805-MHz pillbox cavity [42, 43]. The geometric dimensions are

$$\displaystyle{r_{\mathrm{pillbox}} = 0.1562\,\mathrm{m},\mbox{ }l_{\mathrm{pillbox}} = 0.0519\,\mathrm{m},\mbox{ }r_{\mathrm{pillbox}}/l_{\mathrm{pillbox}} = 3.0096.}$$

This leads to a theoretical resonant frequency of

$$\displaystyle{f_{\mathrm{res}} = \frac{c_{0}j_{01}} {2\pi r_{\mathrm{pillbox}}} = 734.6\,\mathrm{MHz}.}$$

In reality, the modifications of the ideal pillbox cavity (e.g., rounded edges, beam pipe, coupling elements, etc.) lead to the above-mentioned resonant frequency of 805 MHz. At this frequency, one gets

$$\displaystyle{\delta = 2.3292\,\mu \mathrm{m},\mbox{ }R_{\mathrm{surf}} = 7.40225\,\mathrm{m}\Omega }$$

if one assumes a conductivity of 5. 8 ⋅ 10⁷ S∕m (copper). With Eq. (4.65), this leads to

$$\displaystyle{Q_{\mathrm{p,0}} = 15262,}$$

which is close to the measured value of Q_p,0 = 15080 [43]. According to Eq. (4.66), one obtains

$$\displaystyle{R_{\mathrm{p,0}} = 943\,\mathrm{k}\Omega,\mbox{ } \Rightarrow R_{\mathrm{p,0}}/l_{\mathrm{pillbox}} = 18.18\,\mathrm{M}\Omega /\mathrm{m}.}$$

The design value in [42, 43] corresponds to $19\,\mathrm{M}\Omega /\mathrm{m}$, since the definition of the shunt impedance differs by a factor of 2 from our circuit definition and since the transit time factor is included in [43] (but not in [42]).