Seismic Analysis and Design of Bridges with an Emphasis to Eurocode Standards

Abstract

Bridges are quite different from buildings regarding their dimensions, structural systems and in general regarding their seismic response. Thus the specialized standards for their seismic design are needed. One of them is Eurocode 8/2 standard (EC8/2), which considerably improved the design practice. It is well organized, practically oriented and designer friendly.

In Slovenia it has been used for years. Some experiences, obtained during its application in practice are presented. Four issues are addressed: (1) the correlation between pre-yielding stiffness and strength of structures as well as the reduction of the seismic forces and equal displacement rule, (2) the application of the nonlinear static (pushover) methods of analysis, (3) the estimation of the shear strength of RC columns, and (4) the protection of the longitudinal reinforcement in RC columns against buckling.

It was concluded that pre-yielding stiffness and strength of structures are strongly correlated. The pre-yielding stiffness is different for different levels of selected strength. This does not negate the equal displacement rule. The EC8/2 is one of the rare standards that explicitly recognized the quite important correlation between chosen strength of structures and corresponding pre-yielding effective stiffness. Accordingly, the equal displacement rule is presented in a modified way. Different interpretations of this rule are discussed in the paper.

The EC8/2 introduced the nonlinear static pushover methods into the design practice. The way of their use is examined in the paper. Specifics in the application of the single mode pushover methods and the scope of their applicability are discussed. Some of the alternative methods are briefly overviewed.

It was found that EC8/2 provisions related to the estimation of the shear strength of some typical bridge columns can be quite conservative. Some of the alternative methods are presented and discussed on the example of the experimentally investigated columns. It is concluded that the estimation of the shear strength, in general, is far from being solved and it demands further investigations.

It was also found that some requirements of EC8/2 related to the prevention of buckling of the longitudinal reinforcement in RC columns are not interpreted in an appropriate way; thus their corrections are needed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

6.1 Introduction

Bridges are specific structures whose structural concept is mostly related to functionality. They give the impression of being rather simple structures whose seismic response could be easily predicted. Therefore, in the past, a little attention was paid to their seismic design. Usually, the design methodologies, developed primarily for the analysis and design of buildings were also uncritically applied to bridges. In many cases this approach was/is inappropriate, since the structural system of bridges, dimensions, and their seismic response, in general, is considerably different from buildings.

The need for special consideration, which is adjusted to specific properties of bridges, has been recognized and the practice has been changed. An example of this good practice is the Eurocode standard, which comprises a part Eurocode 8/2 (CEN 2005a) – EC8/2 that regulates the seismic design of bridges.

This standard includes many modern design principles of the seismic engineering, which were usually not taken into account in the design practice in the past, and very often they are not taken into account even in the nowadays practice. In some countries, e.g. in Slovenia, it has been used for many years. In the beginning, the pre-standard version of EC8/2 (CEN 1994) was applied. Although the early applications were unofficial, most of the bridges built on the main highways in Slovenia were designed taking into account its requirements. For the last 6 years it has been used as an official standard in Slovenia.

Based on the experiences obtained during its application, it can be concluded that EC8/2 definitely considerably improved the seismic design of bridges. It is well organized, practically oriented and designer friendly.

In this paper some of the experiences, obtained when applying the standard in the practice and a critical overview of some of its requirements are presented. They are listed in the next paragraphs.

• 1. The reduction of the seismic forces and equal displacement rule are well known and they are regularly used in the design practice. Nevertheless, sometimes they are applied, neglecting the correlation between the strength of the structure and corresponding pre-yielding effective stiffness (initial effective stiffness). As a consequence some researchers and designers expressed their doubts about this basic principle of the seismic engineering. Following the previous discussion about these issues, and solutions that are proposed in EC8/2, the problem of the correlated strength (reduction of forces) and equivalent initial stiffness is examined in Sect. 6.2.

• 2. Seismic load is the strongest load that threatened the bridge in the seismically prone areas. Accordingly, many structures can be exposed to significant plastic deformations and its response can be significantly nonlinear. Nevertheless, the elastic linear methods are usually used for their analysis.

  In bridges, which are supported by piers having very different stiffness and strength, a considerable redistribution of the effects of the seismic load in the transverse direction of the bridge is usually observed comparing to the results of the linear analysis. Consequently, the nonlinear methods are needed in such cases, since the linear methods cannot estimate the response realistically. This was recognized by the EC8/2 standard as well. In bridges, where the significant redistribution of the seismic effects is expected, the nonlinear analysis is suggested as an option to estimate their seismic response more realistically.

  As an alternative to the nonlinear dynamic analysis, which is still too demanding for the everyday design, a simplified nonlinear pushover method, N2 method (Fajfar and Fischinger 1987) is included to the EC8/2. This method was primarily developed for the analysis of buildings. Therefore some important modifications are needed when it is applied to bridges. They are discussed in Sect. 6.3. Moreover, the limitations of the method are analyzed and possible alternatives are briefly presented.

• 3. It has been observed that EC8/2 requirements related to the estimation of the shear strength can be quite conservative for some typical types of bridge columns (e.g. hollow box columns). Namely, the contribution of the concrete to the shear strength should be quite often neglected even if the displacement demand is relatively low. Since this contribution can be as large as the half of the total shear strength of a column, quite a large shear reinforcement could be required if this contribution is not taken into account.

  It should be noted that according to the organization of the Eurocode standards, this subject is primarily related to Eurocode 2 standard, EC2 (CEN 2004a), where the procedure for estimation of the shear strength is defined. However, these already conservative requirements of EC2 are in some cases additionally tightened by EC8/2, which sometimes additionally reduces the already low level of the shear strength defined in EC2. This issue is discussed in Sect. 6.4.

• 4. The ductility capacity of the column (bridge) strongly depends on the ability of its lateral reinforcement to sustain the buckling of the longitudinal flexural reinforcement and to ensure the adequate confinement of the concrete core. These two functions of lateral reinforcement were in the past designs in many cases neglected, and are not considered even in some new designs. This can lead to undesirable brittle types of failure and irreparable types of damage. In EC8/2 a special attention is devoted to these problems. However, some provisions require certain modifications, which are discussed in Sect. 6.5.

6.2 The Strength and the Effective Stiffness – The Equal Displacement Rule

According to EC8/2 bridges can be designed so that their behaviour under the design seismic action is either ductile or limited ductile/essentially elastic. The type of the response depends on the chosen global behaviour factor. It defines the global level of the reduction of forces that would be obtained in the structure, which responds to the seismic load elastically and have the same effective pre-yielding stiffness as the analysed structure. In EC8/2 the limited ductile and ductile response corresponds to the behaviour factor of 1.5 and 3, respectively.

When the larger reduction of forces (larger behaviour factor) is chosen, the larger global ductility capacity of the analysed structure is required, since the displacement demand in a structure, which respond to the seismic load elastically and the corresponding structure with the reduced strength and the same pre-yielding stiffness and mass are in general approximately the same. This is so called equal displacement rule, which is more strictly speaking, applicable to structures with medium and long periods of vibrations.

This basic principle of the seismic engineering is usually illustrated with the idealized force-displacement diagram presented in Fig. 6.1a. The larger reduction of the force means that the smaller strength and the larger ductility capacity of the structure should be provided. In this presentation the pre-yielding stiffness is independent of the level of the force reduction (strength). For the reasons explained in the next paragraphs, this presentation is applicable only to different structures with the same effective pre-yielding stiffness and different strengths.

Fig. 6.1

Different interpretations of the equal displacement rule. (a) Traditional interpretation of the equal displacement rule. (b) The equal displacement rule, where the correlation between the strength and the stiffness is taken into account. (c) Interpretation of the equal displacement rule in EC8/2

In general it cannot be applied to one structure with the same geometry of structural components and different levels of the provided strength. For this case, the equal displacement rule can be presented in a different way, as it is illustrated in Fig. 6.1b for medium and long period structures. It is assumed that the yield displacements are approximately the same; regardless of the strength (explanation is provided later in this section). For the sake of simplicity the rule is presented for the case of a simple cantilever. For more complex structure it is discussed later in this section.

In Fig. 6.1b three types of response (three levels of force reduction) are examined: (1) The essentially elastic response (presented with black line), (2) limited ductile (presented with red line) and (3) ductile response (presented with blue line). The F_e1, F_e2 and F_e3 represent the elastic forces, which correspond to certain effective pre-yielding stiffness that is correlated with the chosen strength (reduction of forces or chosen behaviour factor). Forces F_y2 and F_y3 are reduced forces. They are defined as it is proposed in EC8/2 reducing the force F_e1 by factors 1.5 and 3. Thus, F_y2 is 1.5 and F_y3 is 3 times smaller than F_e1, respectively. Seismic displacements corresponding to three examined types of response are denoted as D₁, D₂ and D₃ respectively. Corresponding yielding displacements are denoted as D_y1, D_y2 and D_y3.

Contrary to the interpretation in Fig. 6.1a, where the effective pre-yielding stiffness is independent of the level of the force reduction, in the interpretation, presented in Fig. 6.1b, this stiffness varies based on the chosen level of strength or the chosen level of the force reduction. Moreover, the seismic displacements D₁–D₃ as well as the elastic forces F_e1–F_e3 are not the same (as in Fig. 6.1a) and are, in general, also dependent on the chosen reduction of forces.

A superficial analysis of the diagrams, presented in Fig. 6.1b, can lead to a conclusion that equal displacement rule is invalid. This opinion is recently often expressed by different researchers. However, the precise examination of the presented diagrams confirms that equal displacement rule is not doubtful. The seismic displacements D₁–D₃ are still the same as those that characterize the corresponding elastic response, calculated taking into account the adequate (corresponding) effective pre-yielding stiffness. The ratio of the seismic displacements and yield displacements are still approximately the same as the corresponding level of the force reduction. Note that actual global reduction of forces is somewhat smaller than 1.5 and 3, since the corresponding elastic forces F_e2 and F_e3 are also smaller than F_e1, which was used to select the reduced strength F_y2 and F_y3.

In other words, the equal displacements rule is valid, but it should be adequately interpreted, taking into account the correlation between the strength of the structure and the corresponding pre-yielding stiffness as well as the corresponding reduced demand. It is applicable for each level of the chosen strength individually. This is illustrated in Fig. 6.1b.

The strong correlation between the strength and effective pre-yielding stiffness is crucial for the proper interpretation of Fig. 6.1b. Therefore it is analysed in more details in the next paragraphs. For the sake of clarity, this relationship is analysed on the example of simple cantilever column (presented in Fig. 6.2a). It is assumed that the strength of the column is chosen and that it is expressed in term of the force F_y.

Fig. 6.2

The cantilever column

The selected level of force can be resisted providing an appropriate bending moment resistance at the bottom of the cantilever M_y = F_y × h. In this expression M_y is the bending moment corresponding to yielding of the cantilever, h represents its height and F_y the force that should be resisted (chosen strength).

For the sake of simplicity, let’s assume that the response of the analysed structure is perfectly elasto-plastic (there is no strain hardening after yielding). This means that the moment M_y represents also the bending moment capacity that corresponds to the chosen level of force reduction.

Moment M_y can be further correlated with the yield curvature Φ_y using the simple expression:

$$ {\Phi}_y=\frac{M_y}{E{ I}_{eff}} $$

(6.1)

where E is the modulus of elasticity and I_eff the effective moment of inertia of the bottom most critical cross-section. The yield curvature depends first of all on the yield strain of the reinforcement and the effective depth of the cross-section. The variations of the axial force and the corresponding variation of the yield moment have only slight influence to the value of the yield curvature. This is documented on the example, presented in Fig. 6.3. More examples can be found elsewhere (e.g. Priestley et al. 2007).

Fig. 6.3

Moment – curvature relationship of one cross section for different levels of axial forces

Considering a small variation of the yield curvature, it is evident from Eq. (6.1) that the variations of the yield moment (bending moment capacity) has considerable influence only to the effective moment of the inertia I_eff. Consequently it has also considerable influence to the effective pre-yielding stiffness. Since the curvature Φ_y is almost independent of the level of the yield moment, the effective pre-yielding stiffness and yield moment are explicitly correlated. In other words, the effective stiffness cannot be randomly chosen, when the yield moment (strength) is selected and vice versa. In general, the effective stiffness varies proportionally to the strength. This is illustrated in Fig. 6.1b.

As it was mentioned before, the seismic displacements corresponding to different strength levels are not equal (displacements D₁–D₃ in Fig. 6.1b). Instead, the yield displacements (displacements D_y1–D_y3 in Fig. 6.1b) are quite similar and almost independent of the strength (taking into account that the yield curvature is not strongly correlated with the strength).

In more complex structures the relationship between global effective pre-yielding stiffness and the strength is not so straightforward. In general, iterations are needed, particularly when the bridge is analysed in the transverse direction and when the analysed structure is irregular, supported by columns of different heights and strengths. However, the conclusions, presented above are in general essentially the same. The effective stiffness and strength are correlated, and the effective stiffness varies proportionally to the variations of the strength.

This is illustrated in Fig. 6.4, where the response of a bridge, supported by two columns of different strength and stiffness is analysed in its longitudinal direction. For each column a force-displacement relationship is defined (red dashed lines in Fig. 6.4a). The total stiffness of the structure can be obtained summing the stiffness of both columns. Thus, the total force-displacement diagram can be determined summing the forces in both structural components (bold solid red line in Fig. 6.4a). The effective pre-yielding stiffness of the whole structure can be defined taking into account equal energy rule (bold dashed red line in Fig. 6.4a). This stiffness defines the equivalent period of the structure, which further influences the seismic displacements (see red lines in Fig. 6.4d).

Fig. 6.4

Equal displacement rule in the case of bridge, supported by two columns

When the strength of both components is decreased, the effective stiffness is also decreased. This is illustrated in Fig. 6.4b, where the equivalent stiffness (bold blue dashed line) is defined in the same way as it was explained on the example, presented in Fig. 6.4a. Both cases are compared in Fig. 6.4c, where it is evident that reduction of strength also means the reduction of the effective stiffness. It can be concluded that the strength and the stiffness are strongly correlated also in more complex structures. In other words, if the strength of the structure is chosen, the stiffness of single components and the global stiffness cannot be randomly selected and vice versa.

The seismic displacements of the analysed bridge can be estimated using the equal displacement rule presented in Fig. 6.4d. The presentation of this rule is essentially the same as in the simple cantilever structure. The yield displacements are almost independent of the strength. Contrary, the seismic displacements significantly vary depending on the pre-yielding stiffness and the chosen strength.

As it was mentioned earlier, the correlation between stiffness, strength, and seismic displacement demand is more complex than in the simple cantilever beam. The equivalent pre-yielding stiffness is not a simple sum of the pre-yielding stiffness of single components (as it is illustrated in Fig. 6.4a, b). In general iterations are needed.

The correlation between the effective per-yielding stiffness and the strength is recognized in the standard EC8/2 (see Fig. 6.1c). The interpretation of the equal displacement rule is similar to that presented in Fig. 6.1b, with an important difference. The strength of all structures exhibiting the elastic response is presented to be the same (forces F_e1, F_e2 and F_e3).

Taking into account the EC8 acceleration spectrum, it can be concluded that in many medium and long period structures, the elastic forces determined in this way are overestimated. Consequently the seismic displacements are also overestimated. This means that an additional safety is introduced to the design. Taking into account the complexity of the response (e.g. the redistribution of the seismic effects in the nonlinear range) and considering that standard EC8/2 does not require explicit examination of the available displacement ductility capacity (it is ensured by special detailing rules) this additional safety is feasible. It should be noted that in the case of highly irregular structures, where in the nonlinear range the considerable redistribution of seismic effects between the single components can occur, the examination of the seismic response using the nonlinear methods (see next Section) is highly recommended.

The elastic forces F_e1, F_e2 and F_e3 could be the same for certain short period structure with periods suited to the resonant region of spectrum. However, in this region the seismic displacement defined using the equal displacement rule should be modified (increased).

6.3 The Nonlinear Static Pushover Analysis

The EC8/2 standard recognized the need for more reliable estimation of the highly nonlinear seismic response of bridges. It introduced the nonlinear methods into the design practice: (a) the most refined nonlinear response-history analysis (NRHA), as well as (b) simplified nonlinear pushover based method – N2 method.

In most of the cases, the most refined NRHA is still quite complex to be used in the everyday design. It requires a lot of experiences regarding the modelling of the dynamic response of structures and an appropriate modelling of the seismic loading as well. The specialized software is needed. Thus, to simplify the nonlinear analysis and to make it more regulated, different simplified nonlinear methods can be used. There are many variations of different simplified nonlinear methods proposed, mostly for the analysis of buildings. They can be divided regarding the influence of the higher modes and variability of the important mode shapes based on the different levels of the seismic load.

The simplest methods assume that the response is governed by one predominant mode, which does not essentially change when the seismic load is changed. These methods can be characterized as the single-mode non-adaptive methods.

The next more complex group of methods takes into account the influence of the higher modes, but still suppose that these modes are essentially independent of the seismic intensity. These are so called multimode non-adaptive pushover methods.

The more complex methods take into account the influence of the higher modes as well as their changes based on the seismic intensity. These are so called multimode adaptive methods.

The accuracy of these methods depends on many parameters. A comprehensive analysis of these parameters as well as the list of different pushover methods can be found in FEMA-440 (2005). This document is related mostly to buildings. More specialized information about the application of different pushover methods for the analysis of bridges can be found in Kappos et al. (2012).

In this paper the single-mode non-adaptive method, which is included into EC8/2 (and to Eurocode 8/1 – CEN 2004b) the N2 method (Fajfar 1999) is analysed first. As it was mentioned before, it was developed primarily for the analysis of buildings. When it is applied to bridges it can be used in the unmodified way only when the analysis is performed in the longitudinal direction. In the transverse direction, the structural system of bridges and consequently their response is considerably different from buildings. Therefore some modifications of the method are needed. They are described in Sect. 6.3.1.

Since the N2 method is simplified, it has certain limitations. They are presented in Sect. 6.3.2 and illustrated with the appropriate numerical examples. Section 6.3.3 includes a brief overview of two alternative methods: multimode non-adaptive MPA method (Chopra and Goel 2002), and multimode adaptive IRSA (Aydinoğlu 2003) method, which can be used when the N2 method is not suitable for the analysis. Others can be found e.g. in Kappos et al. (2012) or FEMA-440 (2005).

6.3.1 Specifics of the N2 Method When Applied to the Analysis of Bridges

The N2 method was initially proposed and developed for the design of buildings (Fajfar and Fischinger 1987; Fajfar 1999). Later it has been subsequently improved and generalized. It has been applied for special types of buildings like infilled frames (Dolšek and Fajfar 2005) and for 3D analysis (Fajfar et al. 2005). First applications for bridges were published in mid-90s (Fajfar et al. 1997).

The name N2 method describes its basic features. N stands for the nonlinear analysis, and 2 for the two models and two types of analysis: (1) nonlinear static analysis of the actual multi-degree-of-freedom model (MDOF model) of the structure and (2) nonlinear dynamic analysis of corresponding simplified single-degree-of-freedom model (SDOF model). The nonlinear static analysis is used to define the basic effective properties of the structure, such as e.g. effective stiffness, which are further needed to define an equivalent SDOF model, used for the nonlinear dynamic analysis.

It has been realized (i.e. Isakovic and Fischinger 2006), that in the application of the N2 method as well as all other similar procedures, which were originally developed for buildings, one should take into account special properties of the bridge structural system. Before these specifics are described, let us overview the basic steps of the method, first (see Fig. 6.5):

• 1. First, the multi-degree-of-freedom (MDOF) model of structure is defined.

• 2. The MDOF model is subjected to the lateral static (inertial) load, which is gradually increased and the displacement of the superstructure is monitored (pushover analysis is performed),

• 3. Based on the analysis performed in the second step, the force-displacement relationship is defined (the relationship total base shear versus displacement at the chosen position is defined; pushover curve is constructed),

• 4. The relationship determined in the third step is used to define an equivalent SDOF model of the structure, which is further used for the nonlinear dynamic analysis,

• 5. The nonlinear dynamic analysis is performed using the nonlinear response spectra that can be defined based on the standard elastic acceleration spectra.

• 6. The result of the nonlinear dynamic analysis is the maximum displacement of the bridge at the chosen position, corresponding to the certain seismic intensity.

• 7. Considering the maximum displacement, defined by the nonlinear dynamic analysis, the MDOF model is pushed again with forces defined in the 2nd step and different aspects of the bridge response is analysed

The modifications of the N2 method, which are needed when it is applied to bridges, are related to:

• 1. The distribution of the lateral forces along the superstructure (see 2nd step above)

• 2. The choice of the reference point on the structure where the displacements are monitored in order to obtain the force-displacement relationship (see 3rd step),

• 3. Idealization of the force-displacement curve, and calculation of yielding force F_y* and yielding displacement D_y* (see 4th step).

Fig. 6.5

The scheme of the N2 method

6.3.1.1 Distribution of the Lateral Load

In the 2nd step of the N2 method (see Sect. 6.3.1) the MDOF model of the structure is subjected to the static lateral load (inertial forces). The distribution of the inertial forces (lateral load) should be assumed before the nonlinear static analysis is performed. In the Annex H (informative annex) of Standard EC8/2 two possible distributions are proposed: (a) distribution proportional to the 1st mode of the bridge in the elastic range, and (b) uniform distribution (see Figs. 6.6a, b and 6.7a, b). The first distribution can be defined based on the simple modal analysis with some of the standard programs for elastic modal analysis.

Fig. 6.6

Distributions of the lateral load, appropriate for bridges that are pinned at the abutments

Fig. 6.7

Distributions of the lateral load, appropriate for bridges with roller supports at the abutments

In the previous research (Isakovic and Fischinger 2006), it was found that the parabolic distribution (Fig. 6.6c) was appropriate for bridges that were pinned at the abutments. This distribution is simpler to define than that proportional to the first mode. Using the parabolic distribution, in many bridges the response can be estimated better than in the case of the uniform distribution. For more details see Isakovic et al. (2008a) and Kappos et al. (2012).

6.3.1.2 The Choice of the Reference Point

One of the crucial steps in the application of the N2 method is the static nonlinear analysis of the MDOF system. Based on this analysis the force-displacement relationship is determined, which is further used to define the properties of the equivalent SDOF system.

The force-displacement relationship is determined observing changes of displacement at the certain position in the structure (reference point) due to the gradual increase of the lateral load. The top of buildings is typically selected as the reference point, since at this position the maximum displacement is typically observed in the majority of cases. In bridges this choice is not so straightforward.

In EC8/2 the centre of the mass of the deformed deck is proposed as the reference point. An alternative solution could be the top of a certain column. However, in irregular bridges both of these solutions could be inadequate.

In highly irregular bridges the influence of higher modes is typically large and variation of mode shapes is substantial (especially if the structure is torsionally sensitive). Consequently, the station of maximum displacement varies and it depends on the intensity of the load. This can quite complicate the construction of the pushover curve. The question arises, which point is the reference point. The authors of the paper believe that the pushover curve should be constructed using the maximum displacement of the superstructure regardless its position, since the maximum displacement is a measure of stiffness of the superstructure. In other words the station of the reference point is not always constant throughout the analysis.

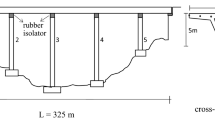
Let’s analyse the response of the viaduct V213P, presented in Fig. 6.8. Considering displacements at the top of three different columns, three very different pushover curves were obtained (curves 1–3 in Fig. 6.9a). Consequently, very different stiffness of the equivalent SDOF model was obtained, resulting in very different estimation of dynamic properties of equivalent SDOF system and significantly different displacements of the structure (see curves 1–3 in Fig. 6.9c). One can conclude that the pushover curve corresponding to the column with maximum displacement at the top should be evidently used. This is true so far this is the station of the maximum displacement of the superstructure, too. The station of maximum displacement of the superstructure in viaduct V213P does not coincide with the position of any column. Moreover it changes depending on the level of the load. Therefore, the corresponding pushover curve (see curve 4 in Fig. 6.9b) does not coincide with any of the pushover curves constructed based on the displacements monitored at the top of some column. Consequently, the corresponding displacements of the viaduct also differ from those, calculated using the top of the columns as the reference points (see Fig. 6.9c).

Fig. 6.8

An example of a highly irregular bridge

Fig. 6.9

Pushover curves, and displacement envelopes, obtained based on different reference points

The analysed viaduct is highly irregular structure, where the mode shapes, their importance and ratios are changing depending on the seismic intensity. When the seismic load is low and the structure respond elastically the maximum displacement is above the right column. When the load is increased the position of the maximum displacement gradually moves toward the centre of the bridge. Station of the maximum displacement gradually shifts for about 40 m (20 % of the bridge length). Thus, the maximum displacement occurs at the centre of mass only at stronger seismic intensities.

The reason for such behaviour is a significant variation of shape, order and importance of modes. The authors believe that the proper pushover curve is the lowest possible one (bold line in Fig. 6.9d), corresponding to the current maximum displacement of the superstructure.

6.3.1.3 Idealization of the Pushover Curve, Target Displacement

Idealization of the base shear-displacement relationship is one of the basic steps of the N2 method, since it significantly influences the stiffness of the equivalent SDOF model and the value of the maximum displacement. When this stiffness is not adequately estimated, the actual and estimated maximum displacement can be significantly different (Isakovic and Fischinger 2006; Isakovic et al. 2008a).

Elasto-plastic idealisation is typically used. This solution is also proposed in EC8/2. However, in viaducts, which are pinned at the abutments, this idealization can be inappropriate, since an underestimated equivalent stiffness of the SDOF system, and overestimated maximum displacement (see Fig. 6.10) can be obtained. Namely, in bridges with pinned abutments where the elastic response of the superstructure is expected, the pushover curve exhibits considerable strain hardening slope, which should be properly taken into account. This is illustrated in Fig. 6.10.

Fig. 6.10

Idealization of the pushover curve. (a) Bridges pinned at the abutments. (b) Bridges with roller supports at the abutments

The force-displacement relationship is usually idealized using the equal energy principle of idealized and actual curve. Since the energy depends on the reached maximum displacement, which is not known at the moment of the idealization, the authors’ opinion is that iterations are necessary. In the majority of cases, only one iteration is needed.

In the annex H of the EC8/2 it is proposed that the maximum displacement is estimated using the results of the elastic analysis. This solution is very convenient at the first glance. However, to estimate these displacements properly, the pre-yielding effective stiffness of the whole structure corresponding to a certain level of the seismic load should be also defined. That means that (more) iterations are also needed (see Sect. 6.2).

6.3.2 Applicability of the N2 Method

The N2 method is a typical single mode non-adaptive pushover method. Although it is appropriate for the analysis of many bridges, it has certain limitations. Since it is single-mode method, it can take into account the predominant influence of only one vibration mode. Therefore, it is appropriate for the analysis of bridges, where the influence of the higher modes is not very important. This is the case where the effective mass of the predominant mode exceeds 80 % of the total mass.

The method is non-adaptive, which means that it cannot take into account significant variations of the predominant mode of vibration. Therefore, it is suitable for the analysis of bridges where the predominant mode does not significantly change.

The N2 method can be efficiently used for the estimation of the seismic response of the majority of the short and medium length bridges. An example of the good estimation of the bridge seismic response is presented in Fig. 6.11, where the displacements calculated by the N2 method and NRHA are compared. The response of the presented bridge is influenced by one predominant mode, which does not considerably change with the seismic intensity.

Fig. 6.11

In bridges, where the response is influenced by one predominant mode, the response is estimated very well by the N2 method

In short bridges and bridges of medium length, the accuracy of the N2 method can depend on the seismic intensity. Usually the higher intensity means better accuracy.

The example of such bridge is presented in Fig. 6.8. In the elastic range the response is influenced by two modes (Fig. 6.8). Consequently, the results of the N2 method (see dashed line in Fig. 6.12a) does not agree very well with the results of the nonlinear response-history analysis – NRHA (see solid line in Fig. 6.12a). However, when the seismic intensity is increased, the response is influenced by only one predominant mode. Consequently, the results of the N2 method agree better with the results of the nonlinear response-history analysis (see Fig. 6.12b).

Fig. 6.12

The accuracy of the N2 method in some bridges depends on the seismic intensity

However, this is not a rule. There are certain types of bridges, reported in Isakovic and Fischinger (2011) where the accuracy of the method decreases with the intensity of the seismic load.

The N2 method is, in general, less accurate in the case of long bridges. It was found (Isakovic et al. 2008a) that in long bridges (e.g. the length is over 500 m), due to the large flexibility of the superstructure (due to the large length), the response is very often significantly influenced by higher modes even if they are supported by relatively flexible columns. For the analysis of such bridges multimode pushover methods can be used (see next subsection) or they can be analysed by the nonlinear response-history analysis.

Let us summarize the previous findings. The N2 method can be used in bridges where:

• (a) The stiffness of the superstructure is large comparing to that of the columns. In such bridges the superstructure governs the response. This is typical for viaducts which are not too long and which are not supported by very short columns.

• (b) The stiffness of the columns does not change abruptly. Namely, if a bridge is supported by columns of very different heights, each column tends to move in its natural mode. Therefore, when the superstructure is not stiff enough to control the overall response, the response is considerably influenced by higher modes.

More details about the applicability of the N2 method can be found elsewhere (Isakovic and Fischinger 2006; Isakovic et al 2008a).

6.3.3 Alternative Pushover Methods of Analysis

When the higher modes have an important role in the response of a bridge, two solutions are available: (a) the multimode pushover methods can be employed, or (b) the NRHA is performed. The choice depends again on the complexity of the bridge, experiences, available software, etc. It is worthy to note that the more refined methods demand also the more refined analysis tools. As it has been mentioned before different multimode pushover methods are available. Here, two of them: (a) non-adaptive MPA and (b) adaptive IRSA are briefly summarized.

6.3.3.1 The MPA Method

The MPA method has been developed by Chopra and Goel (2002). Later it has been modified by the authors (Goel and Chopra 2005) and other researchers, e.g. (Paraskeva et al. 2006; Paraskeva and Kappos 2009), who have been focused on the seismic response of bridges. It is simplified nonlinear pushover method, which can take into account the influence of the higher modes to the seismic response of structures.

In the MPA method the number of pushover analyses depends on the number of the important modes of vibration. Each analysis is preformed taking into account the lateral load proportional to corresponding elastic mode shape. The calculation procedure is similar to that described in Sect. 6.3.1. It is repeated taking into account each important mode, separately. Then the contributions of individual modes are combined using the SRSS or CQC combination rule.

One of the differences between the N2 method and the MPA method is related to the choice of the reference point. In the MPA, the displacements can be monitored anywhere along the superstructure, so far the mode shapes do not considerably change, because in the MPA method the shape factor is taken into account. However, when the mode shapes considerably depends on the load intensity, the appropriate choice of the monitoring point is as important as in the N2 method (Isakovic and Fischinger 2006). In such cases the ratio of displacements along the superstructure is variable and the constant shape factor used in the method cannot take into account these changes. Therefore, in such bridges it is recommended to consider the maximum displacement of the superstructure at its current (variable) position (as it is proposed for the N2 method – see the comment in Sect. 6.3.1). The results of the MPA can be considerably improved taking into account modifications proposed by Paraskeva et al. (2006) and Paraskeva and Kappos (2009).

The analysis with the MPA method is reasonable when the higher modes have considerable influence to the response of the bridge (when N2 method is less accurate), e.g. in very long bridges (e.g. when the length of the bridge is 500 m or more). In such bridges the influence of the higher modes is usually important, particularly when they are supported by short (very stiff) columns. The accuracy is good when the mode shapes do not considerably depend on the seismic intensity.

An example is presented in Fig. 6.13. The displacements of the bridge calculated by the MPA and the NRHA method are compared for two seismic intensity levels. The match between the MPA and NRHA is quite good, particularly for the weak seismic intensity, since the mode shapes are close to the initial mode shapes corresponding to the elastic range. For the strong earthquake, the results of the MPA and NRHA method still agree well, since the mode shapes do not considerably change comparing to the elastic range.

Fig. 6.13

In long bridges with common pier configuration, the accuracy of the MPA (dotted line) is very well (results of the NRHA are presented with the solid line)

If the modes of vibrations are variable, then the MPA method is not feasible enough, like in the bridge presented in Fig. 6.14. In such cases adaptive methods can be employed, or the NRHA preformed.

Fig. 6.14

Response of the experimentally tested bridge, where the modes of vibration changes depending on the seismic intensity

6.3.3.2 The IRSA Method

The IRSA method, proposed by Aydinoğlu (2003) is multimode adaptive pushover method. This means that it takes into account changes of the dynamic properties of the structure each time when the new plastic hinge is formed. Changes of both, modal shapes and the corresponding participation factors are considered each time the dynamic properties of the structure are changed. Contrary to the MPA method, all changes in the structure are coupled. Since it can take into account the changes of the mode shapes it can describe the response of the bridge, presented in Fig. 6.14, more accurately then both previously presented methods.

Since the method is more complex than the other two, the details will be skipped. They can be found in Aydinoğlu (2003), Kappos et al. (2012), and Isakovic et al. (2008a), as well as the appropriate numerical examples. It is worthy to note, that in spite of the complexity this method is not universal and cannot always replace the NRHA, particularly in the most complex bridges, similar to the one, presented in Fig. 6.15.

Fig. 6.15

The response of the highly irregular viaduct obtained by MPA (dotted line), IRSA (dashed) and NRHA (solid lines)

6.4 The Shear Strength of RC Columns

According to the EC8/2 the shear demand in RC columns is defined using the capacity design procedure. It should be less or equal to the shear capacity. In EC8/2 the shear capacity of RC columns is estimated based on the requirements of the standard EC2. According to this standard the contribution of the concrete without shear reinforcement (including the beneficial contribution of the compression stresses) should be neglected in all cases where the demand exceeds this value.

In EC8/2 the value of the shear strength, estimated in this way, is additionally reduced. In bridges, designed as limited ductile structures, it is recommended to reduce the shear strength by factor of 1.25. In ductile structures this reduction depends on the expected value of the shear demand corresponding to the elastic response and the shear demand defined based on the capacity design. The reduction factor is in a range between 1 and 1.25. When the shear resistance of the plastic hinges in ductile structures is estimated, the angle between the concrete compression strut and the main tension chord shall be assumed to be equal to 45°.

In general, the requirements of EC2 are adjusted to structural components of buildings, which have quite different dimensions of bridge columns. Consequently, different mechanisms that contribute to the shear strength, can have different importance than those in bridge columns. Due to the larger dimensions of bridge columns, the contribution of the concrete to the total shear strength can be quite important. Thus the approach, defined in EC2, can result in a quite conservative design. It is worthy to note that certain level of the conservatism is certainly needed for the shear design (since the type of the failure is brittle and the damage is difficult to repair), however the excessive conservatism can result in a very large required amount of the shear reinforcement, which is difficult to construct. Some balance between safety and feasibility is reasonable to achieve.

The classical truss analogy, where the angle between the compression strut and the tension reinforcement is assumed to be 45° seems to be reasonable, particularly for the case of the seismic (reversible) load and relatively low values of the shear span ratios of columns, where the shear response is particularly critical. This actually ensures the maximum amount of the shear reinforcement corresponding to certain truss configuration.

In addition to this requirement the contribution of the concrete without shear reinforcement and beneficial contribution of the compression stresses to the shear strength are neglected usually at quite low levels of the displacement demand. This can result in a quite conservative design, increasing the required shear reinforcement in some types of bridge columns to a quite large amount.

An example of such column is presented in Fig. 6.16. This is a hollow box column, which was experimentally tested in a scale 1:4. The basic properties of the column are presented in Fig. 6.16. More details can be found in Isakovic et al. (2008b) and Elnashai et al. (2011). The column was tested cyclically until the combined shear-flexural failure was achieved. The appearance of the specimen after the experiment is presented in Fig. 6.17b. The shear strength of the investigated column was 390 kN. In this particular case the EC8/2 requirement related to the angle between the compression strut and tension reinforcement was confirmed. It was 45°.

Fig. 6.16

The 1:4 scale model of the experimentally investigated column (Reinforcement type A: longitudinal reinforcement 90ϕ6 mm (f_y = 324 MPa), transverse reinforcement ϕ4 mm/5 cm (f_y = 240 MPa). Reinforcement type C: longitudinal reinforcement 90ϕ3.4 mm (f_y = 240 MPa), transverse reinforcement ϕ2.5 mm/5 cm (f_y = 265 MPa))

Fig. 6.17

(a) Casting of the tested column. (b) Combined shear-flexural failure of the tested column

Taking into account the requirements of the EC2, considerably smaller value of 171 kN of the shear strength was obtained (see line 1 in Fig. 6.18). Note that all safety factors, defined in EC2, were excluded (e.g. the material safety factors for steel and concrete) since the actual shear strength was investigated. According to the requirements of the standard only the contribution of the shear reinforcement was taken into account, since the demand exceeded the sum of the contributions of the concrete without shear reinforcement and the contribution of the compression stresses. In the investigated column, however, these mechanisms contributed almost half of the total shear strength, 147 kN.

Fig. 6.18

Estimated value of the shear strength using different procedures compared to the experiment

When all important mechanisms were taken into account, the estimated value of the total shear strength was increased to 318 kN. This value was still smaller than the experimentally observed strength (see line 2 in Fig. 6.18).

Since the actual and estimated strength were quite different, other procedures available in the literature and other standards were also employed. The UCBS procedure (Priestley et al. 1994) as well as the procedure included in the Eurocode 8/3 standard (CEN 2005b; Biskinis et al. 2004) was considered. Both of them predicted the shear strength of the investigated column quite well (see Fig. 6.18). Contrary to the EC2 standard, these methods define the shear strength based on the displacement ductility demand. Larger values of the shear strength correspond to smaller value of displacement demand. This approach reflects the actual response more realistically, since the reduction of the contribution of the concrete to the shear strength is gradual. In EC2 it is neglected at very small displacement demand. Thus the reduction of the shear strength is abrupt.

Consequently, the difference in the design of the column where the demand exceeds the contribution of the concrete by say 10 % and that where this contribution can be taken into account, can be unacceptably large. For example in the investigated case the difference in the amount of the shear reinforcement would be about 50 %. Therefore, it is feasible to make this transition more gradual like in the other two methods.

Further analysis of the estimated values of the shear strength, presented in Fig. 6.18, showed that EC2 approaches the other two methods in the region of large displacement demands. This is another indication that shear design in EC2 can be quite conservative.

Since the low value of shear strength was defined also for the lower displacement demand, completely misleading conclusions about the type of the failure and the corresponding displacement was obtained in the investigated case. According to the EC2 the failure of the investigated column would be pure shear corresponding to the unrealistically small displacement demand of about 3 mm (the measured displacement at the moment of the failure was about four times larger – 12 mm).

The previous discussion clearly shows that some modifications of the shear design, required in EC2, are needed. However, before any modifications are accepted, additional specialized studies, adjusted to bridge columns are needed. The alternative methods, presented in the previous paragraphs might be a suitable solution; however note that the differences between these two methods can be also quite large (at the region of the small displacement demand – see Fig. 6.18) indicating that the problem of shear is still not adequately investigated and solved. Similar conclusions can be found elsewhere in the literature (e.g. Calvi et al. 2005).

6.5 The Buckling of the Longitudinal Bars and Confinement of the Core of Cross-Sections

The lateral reinforcement has an important role in the protection of columns (bridge) against different types of brittle failure. Beside the prevention of brittle shear failure (discussed in the previous section), it should be designed to prevent also other possible types of brittle failure; to prevent buckling of the longitudinal reinforcement and also to ensure the adequate confinement of the concrete core preventing its deterioration due to the excessive lateral tensile stresses. Both functions considerably influence the ductility capacity of columns (structure). Although they are correlated, they still have to be addressed separately, since it is not always the case that these types of failure occur at the same moment.

The requirements of EC8/2, related to the confinement of the concrete core, seem to be reasonable. The minimum requirements are stringent than those included into the standard EC8/1, where the seismic design of buildings is addressed. This is, however, reasonable, since the columns have the crucial role in the seismic response of bridges, and they are typically loaded by considerable compression stresses, which reduce their ductility capacity. In general the structural system of bridges is less redundant and robust than that of buildings. Taking into account the mentioned characteristics it can be concluded that requirements related to the confinement of the concrete core are reasonable.

Several requirements of EC8/2, related to the protection of the flexural reinforcement against buckling, define the necessary amount of the lateral reinforcement, maximum distance of the lateral bars along the column as well as the maximum distance between the tie legs. These requirements prevent the two types of failure: (a) the limited maximum distance of lateral bars prevents the buckling of the longitudinal bars between two consecutive ties, and (b) the minimum amount of the lateral reinforcement prevents the buckling of the longitudinal bars between several ties.

All the requirements included into EC8/2 are known from the literature (e.g. Priestley et al. 1997). However, the one, which defines the minimum amount of transverse ties (Eq. 6.10 in the EC8/2) is misinterpreted. This requirement was defined based on the experimental investigations. An explanation can be found e.g. in Priestley et al. (1997). In the original formula the spacing of the ties in the vertical direction of column is employed. Instead of this spacing, in EC8/2 the transverse (horizontal) spacing of the tie legs in the plane of the cross-section is addressed. Thus, the use of the formula in EC8/2 should be corrected.

Detailing of the transverse reinforcement is extremely important when the buckling of the longitudinal bars is addressed. The ties should be properly shaped with 135° hooks. Ties with 90° degree hooks usually cannot prevent buckling of the longitudinal bars, even if the proper amount of lateral reinforcement is provided. Standard EC8/2 allows cross-ties that have 90° degree hook on one side and 135° at the other side of the tie, as long as the axial force does not exceed 30 % of the characteristic compression strength of the concrete. It is the authors’ opinion that 90° degree hooks should not be allowed at all, regardless of the level of the axial force.

This is illustrated on the example of the typical I shape column, presented in Fig. 6.19. This is the 1:4 scale model of the column, where the lateral reinforcement fulfilled the EC8/2 requirements related to the shear strength, but the amount was insufficient considering the confinement and the buckling of the longitudinal bars. Additionally the ties were shaped according to some solutions applied in the practice, using the 90° overlapped hooks. The compression stresses due to the permanent load were relatively small (11 % of the characteristic compression strength). The column was tested cyclically until the failure occurred.

Fig. 6.19

(a) Cross-section of the tested column, (b) The shape of the outer ties, (c) The reinforcement of the specimen

A brittle failure was obtained (see Fig. 6.20). After the spalling of the cover concrete, some of the improperly shaped ties with 90° degree hooks were opened, and could not support the longitudinal bars properly. Consequently the buckling of these bars between two consecutive ties as well as between more ties was observed. This was also the consequence of the insufficient amount of the lateral reinforcement. The failure was sudden, without any additional ductility capacity.

Fig. 6.20

A brittle failure was obtained due to the buckling of the longitudinal bars

6.6 Conclusions and Final Remarks

During many years of use of the Eurocode 8/2 standard it was found that this standard considerably improved the seismic design of bridges, since it introduced many modern principles of the seismic engineering into design practice. This is modern standard, which is well organized, practically oriented and designer friendly.

In this paper some of the experiences, obtained when applying the standard in the practice and a critical overview of some of its requirements are presented. First the two topics related to the analysis of bridges were addressed: (a) the relationship between the pre-yielding stiffness and strength of structures as well as the application of the equal displacement rule, and (b) the nonlinear static analysis.

It was concluded that pre-yielding stiffness and strength of structures are strongly correlated. The pre-yielding stiffness is different for different levels of the selected strength. This does not negate the equal displacement rule.

The interpretation of the equal displacement rule included to the EC8/2 was compared with some different options. It has been found that certain conservatism in estimation of the seismic displacements is introduced. This conservatism has been found reasonable since the standard does not require explicit control of the displacement ductility capacity of structures. This can be particularly important in highly irregular structures, where in the nonlinear range considerable redistributions of the seismic effects can occur, and the results of the elastic analyses can be only a rough approximation of the actual response.

In general, for highly irregular structures it is strongly recommended to examine the seismic response using the nonlinear procedures. This is recognized by EC8/2 as well. It introduced the most refined nonlinear response history analysis as well as the simplified nonlinear procedures into the design practice. In the paper some issues related to the application of the single mode pushover method are discussed. The important differences between bridges and buildings related to the application of this method are analysed: (a) distribution of the lateral load, (b) the choice of the reference point and (c) the idealization of the pushover curve. Some alternatives to the procedures, defined in the standard, are proposed. The applicability of the single mode pushover methods is also briefly addressed. It was concluded that this type of methods is applicable mainly to short and medium length bridges, where the response is predominantly influenced by one invariant mode of vibration. In other cases the multimode pushover methods or the nonlinear response history analysis is recommended.

The second part of the paper is devoted to the shear and ductility capacity of RC columns. In EC8/2 the displacement ductility capacity of structures is ensured with proper structural detailing, which prevents the undesirable brittle types of failure. The brittle shear failure is prevented by a requirement that the shear strength of structural components should be at least equal to the shear demand determined based on the capacity design procedure. The shear capacity of RC columns is determined based on the requirements of the EC2. This capacity is in some cases reduced.

The procedure that is used to define the shear strength of columns can be quite conservative, since the contribution of the concrete to the shear strength is very often neglected at quite small displacement demand. In some bridge columns almost half of the total shear strength is neglected in this way. The comparison with some other procedures, available in the literature, also confirmed that the provisions of the EC2 can be quite conservative. The result can be a large required amount of transverse reinforcement, which is difficult to construct.

It has been concluded that the contribution of the concrete to the shear strength should be reduced gradually. It has been also found that the problem of the shear capacity in general is not adequately solved and that it requires further investigations. This is particularly applicable to bridge columns, since the available data are limited comparing to the structural elements in buildings.

The brittle failure due to the insufficient confinement of the concrete core is in EC8/2 prevented by proper detailing of the transverse reinforcement in columns. The required minimum amount of the transverse confinement reinforcement is larger than that in e.g. EC8/1. This was found feasible, since columns have the crucial role in the seismic response of bridges, and they are typically loaded by considerable compression stresses, which reduce their ductility capacity. It should be also noted that the bridge structures are in general less redundant than buildings.

The transverse reinforcement that protects the longitudinal reinforcement of columns against buckling is also addressed in EC8/2. The requirement related to the minimum amount of this reinforcement is, however, misinterpreted and should be corrected according to the results presented in the literature.