Abstract
Several performance measures are being used in modern seismic engineering applications, suggesting that seismic performance could be classified a number of ways. This paper reviews a range of performance measures currently being adopted and then proposes a new seismic performance classification framework based on expected annual losses (EAL). The motivation for an EAL-based performance framework stems from the observation that, in addition to limiting lives lost during earthquakes, changes are needed to improve the resilience of our societies, and it is proposed that increased resilience in developed countries could be achieved by limiting monetary losses. In order to set suitable preliminary values of EAL for performance classification, values of EAL reported in the literature are reviewed. Uncertainties in current EAL estimates are discussed and then an EAL-based seismic performance classification framework is proposed. The proposal is made that the EAL should be computed on a storey-by-storey basis in recognition that EAL for different storeys of a building could vary significantly and also recognizing that a single building may have multiple owners.
A number of tools for the estimation of EAL are reviewed in this paper and the argument is made that simplified methods for the prediction of EAL are required as engineers transition to this new performance parameter. In order to illustrate the potential value of an EAL-based classification scheme, a three storey RC frame building is examined using a simplified displacement-based loss assessment procedure and performance classifications are made for three different retrofit options. The results show that even if only limited non-structural interventions are made to the case study, the EAL could be significantly reduced. It is also argued that overall, such a performance classification, coupled with some form of government or insurance-driven incentive scheme, may provide an effective means of reducing the risk, and increasing the resilience, of our societies.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
11.1 Introduction
Looking back at how the subject of earthquake engineering has developed, we have observed what went wrong in earthquakes, learnt from these events and subsequently developed an engineering approach (building codes, analysis tools and construction techniques) that one could argue provides our communities with an acceptable level of seismic risk. However, as communities develop, it is also apparent that the definition of what is an acceptable level of risk changes. Some 40 years ago, it would appear that the intention of seismic design and retrofit was solely to ensure that the probability of loss of life during an earthquake was acceptably low. However, following earthquakes such as the Northridge earthquake in 1994 and the more recent 2011 Christchurch earthquake, it is becoming increasingly clear that the protection of lives is not enough. Financial losses associated with repair, disruption to businesses and the time lost to clean up and reinstate services and activities, are just a number of important factors that need to be considered in a modern definition of seismic risk, and which are already entering into performance-based earthquake engineering procedures, as will be discussed shortly.
Another means of considering performance and risk is to focus on disaster resilience. Also here, as has been discussed by experts in the field (e.g. Comerio 2012), even if the number of lives lost in an earthquake are low, individuals and communities cannot return to their normal way-of-life unless they have jobs and housing, and if the community services (transport systems, schools, hospitals, banks, businesses and governments) are functioning properly. The best means of quantifying resilience is arguably still to be identified, with various resilience indicators in the literature (see Comerio 2012). However, it is clear that an engineering approach that focusses solely on the concept of life-safety will not ensure resilient communities.
With the above points in mind, this paper will review modern measures of performance and propose a new performance classification scheme that is based only on expected monetary losses. It will be argued that, whilst the important issue of life safety should not be forgotten, a monetary loss-based performance scheme could offer an effective means of reducing risk and increasing resilience, provided that it is used together with suitable government incentive schemes to motivate retrofit and improvements.
11.2 Modern Measures of Performance
Performance measures offer engineers a means of quantifying and communicating risk. As explained in the introduction, until recently the main concern for seismic engineers was the risk of loss of life. However, since the nineties (and arguably before that time in some parts of the world where serviceability limit state checks were in place since the seventies), a need for additional performance measures has arisen, in response to the need to reduce other risks posed by earthquakes, including the high repair costs and disruption (loss of time and social upset) that earthquakes can cause. In response to this there have been a series of initiatives (SEAOC 1995; ATC 2011a) aimed at developing performance-based earthquake engineering (PBEE) approaches. The most refined PBEE procedure currently available appears to be the framework developed for the PEER PBEE methodology (Porter 2003) which offers engineers a means of quantifying performance measures of deaths, dollars and downtime (the “3 D’s”) by following the approach outlined in Fig. 11.1. Referring to Fig. 11.1, the PEER PBEE framework consists of defining the facility type and location followed by four analysis stages: hazard analysis, structural analysis, damage analysis and loss (decision) analysis.
The four stages allow for each aspect of the seismic assessment to be treated in a probabilistic manner where inherent uncertainties are incorporated within a given stage and carried through to subsequent stages of the assessment process. In order to better illustrate how this is performed, a mathematical relationship in the form of a triple integral is shown in (11.1). Notably, the terms in (11.1) are displayed for the calculation of consequences from damage across all seismic intensities, yet a similar form is applicable to other consequences or decision variables (DV).
The terms λ[x|y] and p[x|y] represent the mean annual occurrence rate and probability density of x given y. The design, D, represents the structure and site to be assessed, where all building details are specific to D and site hazard characteristics are addressed in order to obtain the occurrence relationship of a given intensity measure, λ[IM]. Site hazard is typically defined by a Probabilistic Seismic Hazard Analysis (PSHA) which allows for the site hazard to be related to an IM of interest (e.g. 1st mode spectral acceleration, Sa(T1)) via proper selection of accelerograms for input into the structural analysis stage. The structural analysis stage is perhaps the most familiar to the engineering community where a model of the structure is developed in order to run nonlinear time history analyses (NLTH) to obtain likely response quantities; defined here as engineering demand parameters (EDPs). The output of the structural analysis stage results in probabilistic distributions of EDPs such as inter-storey drift and floor acceleration that are associated with a given level of seismic intensity, p[EDP|IM]. These EDPs are then used to estimate the damage of various assemblies within a building within the damage analysis stage. The relationship between structural response (EDP) and a given damage measure (DM) is represented by fragility functions (cumulative distribution of p[DM|EDP]) that are assigned to various components within the building (e.g. columns, partitions and ceilings). Each set of DMs for a given component are sufficiently separated to represent distinct methods and extent of repair; with each DM having an associated decision variable distribution (p[DV|DM]), in this case repair cost, associated with it. Remaining consistent with the formulation of (11.1), the final result of the triple integral would represent the mean annual occurrence of repair cost for the given building and site, λ[DV|D].
The previous description of the PEER PBEE methodology represents only one metric of performance (annualized repair cost due to damage), yet the seismic performance can consider numerous sources of loss (e.g. the 3 D’s) expressed in a variety of metrics. These metrics can be annualized, such as expected annual loss (EAL), to allow losses to be treated as an expense within cash flow analysis (Porter et al. 2004), based on a given intensity such as that corresponding to a design level event, or based on a given scenario possibly recreating a previous or anticipated event of known magnitude and distance (ATC 2011a). Further, loss metrics can be expressed based on input from decision makers such as the annual or 50 year probability that losses will exceed a given value, such as probable maximum loss (PML).
The PEER framework for performance assessment is attractive since it is quite clear and very flexible, noting that no restrictions are imposed on the approach used to quantify hazard, to undertake the structural analysis, relate EDPs to losses and other performance measures. To this extent, it is also apparent that the results of a performance-assessment conducted using the PEER PBEE procedure will currently lead to quite different measures of performance depending on the assumptions made in applying the procedure and the risk parameters of interest. The following sub-sections review considerations currently made when estimating life-safety, monetary losses and downtime, and identify some of the factors that will affect their quantification.
11.2.1 Life-Safety and Probability of Collapse
The inherent risk of a structure to collapse and subsequently endanger lives has been the primary concern of earthquake engineering since the earliest seismic provisions were adopted. Further, the ongoing efforts within the field of seismic design over the past four decades have made great strides in controlling the collapse risk of structures. However, only until recently have advances in computing power, experimental testing and engineering seismology allowed analysts to quantify life safety and collapse risks probabilistically. Conceptually, the estimation of the likelihood of loss-of-life is explained by three basic requirements: (i) determine the ways in which a structure can endanger life, (ii) relate critical structural conditions to the likelihood of the seismic hazard producing them and (iii) establish an estimate of the number of lives exposed to the dangerous conditions. However, numerous factors challenge the estimation of collapse probability and consequential risk of loss-of-life.
Rather intuitively, a majority of fatalities occur when at least a portion of a structure collapses (Hengjiam et al. 2003). However, although small in comparison, there are still a number of fatalities that can be attributed to the damage of non-structural elements (e.g. masonry partitions, large equipment, failed exteriors) or building contents (e.g. furniture) (Durkin and Thiel 1992; Stojanovski and Dong 1994; Hengjiam et al. 2003). Alternatively, as non-structural damage may not be a significant source of fatalities, resulting injuries may be substantial (Porter et al. 2006) which leads to another, at least viable, consideration in seismic risk assessment. Further discussion of life and injury risks associated with non-structural hazards is omitted for the sake of brevity, yet it is noted that this source of risk has received wide attention in recent years (Charleson 2007; ICC-ES 2010; FEMA 2011).
Given the complexity of the physical interactions of a building at imminent collapse, the first major challenge lies within capturing these complexities in a reliable manner within mathematical models for computer simulations of earthquake demands. For more modern (ductile) structures, current seismic provisions mandate that certain strength hierarchy be followed (e.g. SCWB ratio, flexure-controlled members) to ensure a ductile response and indirectly force a sidesway or global collapse mechanism. Although numerous methods and tools have been made available for the modelling of structural members, as a result of countless experimental campaigns (Ibarra et al. 2005; Berry et al. 2004; Lignos 2013; Lignos and Krawinkler 2011; among others) the intricacy associated with even a “ductile” collapse mode require that numerous uncertainties must be accounted for. In light of state-of-the-art assessment methods such as the PEER PBEE methodology, the probability of global collapse of a structure is addressed with a collapse fragility function (typically a cumulative lognormal distribution) requiring that the median collapse intensity be estimated and the corresponding dispersion to represent uncertainty. Estimation of the median collapse intensity can be performed by various methods (ATC 2011a; FEMA 2009; Mohammadjavad et al. 2013; Vamvatsikos and Cornell 2006). The collapse dispersion must address uncertainty involved in both demand (record-to-record) and capacity (modelling) with the former requiring a large number of time history simulations (e.g. IDA, Vamvatsikos and Cornell 2002) or reliable approximation (Perus et al. 2013). The latter source of uncertainty is typically benchmarked through parametric studies (e.g. Haselton and Deierlein 2007) and then adjusted based on the judgment of the analyst in terms of level of knowledge of the structure (e.g. details, materials, construction quality) adequacy of the structural model (ATC 2011a; FEMA 2009).
When dealing with older structures that lack strength hierarchy provisions and proper detailing, numerous additional modes of failure can be expected (e.g. joint failure, shear failure, punching shear of slab-column connections) other than a global sidesway collapse. This combined with current limitations of modelling and simulation capabilities (Liel and Deierlein 2008) requires that the collapse probability become a two staged problem. Initially the probability of a sidesway collapse is estimated using methods similar to ductile structures, and then a subsequent assessment must be made with simulations that did not produce collapse in order to estimate the probability of brittle or non-simulated modes of failure. Taking the shear failure of a column as an example, the expected deformation capacity of the column corresponding to a brittle shear failure would be estimated based on structural properties (e.g. material, axial load, detailing) and available experimental data in order obtain a fragility function similar to that used to estimate global collapse (Aslani and Miranda 2005). Further, the influence of joint deterioration could be captured in the structural model (Altoonash 2004; Pampanin et al. 2003) which would affect the expected structural deformation and subsequently influence the likelihood of a brittle collapse mode.
An additional challenge of estimating the collapse risk of a structure lies within associating a given structural demand to a proper representation of seismic hazard in order to convey collapse risk. As current assessment methods rely heavily on NLTH analysis, accelerograms must be selected to represent the expected seismic demands. Although numerous factors must be considered with record selection in general (e.g. Baker and Cornell 2006a; Iervolino et al. 2006; Kalkan and Kunnath 2006), the use of accelerograms in collapse studies becomes an even more daunting task as recorded data from very large events is just as rare as the events that produce them; with the recent improvements in seismic design producing structures that are expected to have median collapse intensities on the order of 2–3 times that expected for the 2 % in 50 year probability of exceedence intensity which typically corresponds to the maximum credible earthquake (Haselton and Deierlein 2007). As such, the proper treatment of the uncertainty associated with these rare events is critical when conducting collapse assessments. A very important characteristic of very rare ground motions is that of spectral shape; an importance that is a result of structural analysts’ use of first-mode spectral acceleration as an intensity measure in collapse assessments. Briefly, spectral shape for rare ground motions (e.g. 2 % in 50 year intensity) must be properly considered because they can significantly differ from the corresponding uniform hazard (UHS) or design spectra (Baker and Cornell 2006b). The main issue relating to the prediction of collapse is that rare ground motions have a much longer return period, TR, (e.g. 2,475 years) compared to the return period of the events that cause them (e.g. 150–500 years in the Western U.S.) requiring that this rarity be accounted for (FEMA 2009). This is typically done with an epsilon factor, ε, that relates the number of standard deviations above (or below) a median hazard spectrum for a given TR and structural period (Baker and Cornell 2006b). Although this concept is not the most recent development, it is deemed important in the context of collapse assessment where failing to incorporate some procedure to consider epsilon (i.e. Haselton et al. 2011) has lead to collapse capacities to be underestimated by 30–80 % (FEMA 2009).
In order to estimate the number of fatalities due to the collapse of a structure, the type of failure mode must be considered with respect to how many building occupants will be exposed to dangerous or lethal conditions. This has been quantified previously as a collapsed volume ratio (CVR) expressed as a percentage of the building that completely collapses in previous efforts to estimate life safety risk; where reconnaissance data has shown it to be a good indicator of the level of fatalities within a structure (Coburn et al. 1992; Yeo and Cornell 2003). The uncertainties in estimating this parameter are even more difficult that assessing the collapse probability due to the lack of data on the subject and typically must rely on judgment. To illustrate the different considerations for estimating CVR the assumptions made by Liel and Deierlein (2008) in the assessment of reinforced concrete (RC) frame buildings are used as an example.
The data in Tables 11.1 and 11.2 illustrate how the CVR is estimated provided that a global side-sway collapse is expected. The initial CVR is estimated via NLTH analysis in terms of the number of stories involved in the collapse mechanism which can vary significantly depending on the number of stories and expected ductility of the building as shown in Table 11.1. Additionally, the likelihood of a side-sway collapse causing a complete collapse of every storey (i.e. pancake collapse) must also be estimated. An example set of values for the likelihood of a pancake collapse provided that side-sway collapse occurs is presented in Table 11.2.
Notably, the values are based on judgment, yet reflect two basic principles: i) ductile structures have a higher deformation capacity which could involve more stories in the collapse mechanism and ii) taller structures are more susceptible to secondary effects (e.g. P-delta) as shown with respect to the expected ductility and height of the building in Table 11.2 (Liel and Deierlein 2008).
When collapse is conditioned on a local brittle failure (e.g. shear) the fact that a soft-storey mechanism involving only one storey initially may lead to subsequent failure of additional stories (i.e. progressive collapse) must also be considered. The event tree shown in Fig. 11.2 shows how different modes of collapse may lead to different estimations of the collapsed volume ratio (CVR).
Example of an event tree to determine the collapsed volume ratio of a structure conditioned on either a global or local collapse for the estimation of fatalities (Adapted from Liel and Deierlein 2008)
Once the likely percentage of the building that has collapsed in estimated, the fatality probability is calculated by estimating the number of lives expected within that area of the building. This is currently achieved by attributing a population model to the structure. Population models vary according to the use or occupancy of the building. Two examples are provided in Fig. 11.3 for a commercial office building and a healthcare facility (e.g. hospital). The figure shows that it is likely that the office building will be vacant overnight and the occupancy is drastically reduced on the weekend. Conversely, the hospital model expects a minimum of 2 people per 1,000 ft2 (93 m2) at all times and only a small reduction in population on the weekend. Notably the population models represent expected values and additional uncertainty may be incorporated as well as additional time frames for population variation (e.g. monthly).
Illustration of different population models used for life safety assessment: (a) commercial office, (b) healthcare facility (Values taken from ATC 2011b)
Although the probability of the loss-of-life may be estimated, it may be in the decision-makers best interest to also estimate the economic impact of the expected life safety risk of a structure or facility. Attributing a price to human life comes with both moral and economic challenges, yet this is usually necessary in order to compare the benefits of allocating monetary resources to protect public welfare; both by municipalities and decision makers within the private sector. This is typically done by estimating the value of a statistical life, VSL (FHWA 1994; Mrozek and Taylor 2002). Values can depend on the amount an industry is willing to pay to preserve life safety for a particular type of risk (Liel and Deierlein 2008) or even considering a life quality index based on a country’s gross domestic product (per capita) and life expectancy (Rackwitz 2004).
11.2.2 Direct Monetary Losses
The calculation of seismic losses can have numerous sources as previously mentioned (e.g. the 3 D’s). However, it is useful to make a distinction between the types of losses based on how they may affect decision making. The term direct loss is typically attributed to monetary loss from repair costs due to damage and full replacement costs in the case of a structural collapse (Mitrani-Reiser 2007; Welch et al. 2014). The remaining losses associated with other sources of loss are termed indirect losses herein. It is noted that the damage of building contents (e.g. furniture, office equipment) can also be a significant source of direct loss (Comerio et al. 2001), yet the current discussion will be limited to only the structure and its non-structural components.
The calculation of direct losses due to repair costs requires that (ideally) each damageable component within a building has a specific damage fragility and consequence function attributed to it in order to transition from structural response to damage and then repair cost in line with the progression shown in Fig. 11.1. A sample set of fragility and consequence functions are shown in Figs. 11.4 and 11.5 for a ductile interior RC beam-column joint. Figure 11.4 illustrates that as inter-storey drift ratio (IDR) increases the likelihood of each successive (more damaging) damage state also increases; where an IDR of 5.0 % will return that almost certainly the element has significant cracking and spalling and there is a 50 % probability that the element has suffered severe damage.
Sample fragility function (left) and damage state parameters (right) for a modern interior RC beam-column joint (Values taken from ATC 2011b)
Repair costs for various damage states of a modern interior RC beam-column joint: (a) significant cracking, (b) spalling and (c) severe damage (Values in 2011 USD from ATC 2011b)
To estimate the repair cost associated with a given damage state, the corresponding consequence function (Fig. 11.5) is used. Notably, Fig. 11.5 displays the mean estimated repair cost (solid line) as well as the plus and minus one standard deviation bounds (dashed lines) which highlights the uncertainty associated with estimating repair costs following a seismic event. Further, the cost functions relate the unit repair cost to the total number of units to be repaired, showing a reduction in unit cost as the total increases which represents the reduction in labor required (e.g. set-up time, transport of materials) to repair numerous elements in the same building. Further, the availability of materials and human resources may fluctuate significantly, yet these types of factors will be discussed more thoroughly in the following section.
Aside from the need for additional experimental testing in order to produce more reliable and component-specific fragility and consequence functions, the next greatest challenge in estimating repair costs could be the appropriate consideration of the damageable assemblies within a building. Since structural elements are of manageable quantities within a structure the largest source of this difficulty is rooted in repairs associated with non-structural elements. Although a vast range of components complete a fully functional facility it is not only their quantities that make non-structural elements a critical part of estimating direct losses due to repair costs.
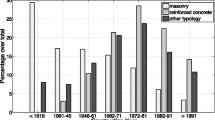
The importance of non-structural damage in direct loss assessment is mostly derived from the fact that non-structural elements comprise a significant portion (or majority) of the total construction costs of a building (see Fig. 11.6a) and many non-structural elements are damaged at seismic intensities much lower than structural elements. This importance is reflected in the tremendous losses associated with non-structural damage in previous seismic events (Miranda et al. 2012; Filiatrault et al. 2001; Reitherman and Sabol 1995).
(a) Summary of relative value of non-structural elements for three different occupancies, (b) Relative contribution of different non-structural element classes for a given building and (c) Example EDP sensitivity of non-structural elements within a building (Values from Taghavi and Miranda 2003)
In order to incorporate non-structural elements into a comprehensive loss framework, the various types of non-structural components that compose the inventory of a building (Fig. 11.6b) must be assigned engineering demand parameter (EDP) sensitivity. Typical sensitivities are (but are not limited to) inter-storey drift ratio (IDR) and peak floor acceleration (PFA). Additionally, many components within the building may not be affected by building response and are only treated as a loss in the event of collapse; these components are typically termed “rugged”. An example sensitivity distribution is shown in Fig. 11.6c.
There are numerous ways in which this discretization of non-structural elements can be carried out. First, there is the component-based (or assembly-based) approach where the damageable assemblies are identified and assigned fragility and consequence functions based on available information (Mitrani-Reiser 2007; Porter et al. 2001). Additionally recent studies (Ramirez and Miranda 2009, 2012; Welch et al. 2012) have also implemented a storey-based loss model developed by Ramirez and Miranda (2009) which combines the likely structural and non-structural inventory into a set of engineering demand parameter to decision variable functions (EDP-DV). The two loss modelling aproaches differ significantly and each has its own inherent benefits and drawbacks.
The component-based model is advantageous in that it allows the actual component inventory to be represented (e.g. 12 beams/floor, 600 m2 of ceiling/floor) whereas the storey-based model relies on relative inventories based on construction estimating documents. The storey-based approach is advantageous not only due to its simplicity (provided that EDP-DV functions have been constructed) but also eliminates the need to select the type and number of damageable assemblies. This can lead to repair costs that may or may not reflect the total damaged inventory, yet other component-based studies (Krawinkler 2005) have used “generic” fragility functions in order to consider components that do not have available fragilities based on experimental results. Further, the storey-based model avoids allocating repair cost to an element that must also be repaired in order to repair another or “double counting”; with the simplest example being the replacement of partition walls in order access structural members for repair, where considered separately the partition cost could be counted twice. However, this problem can be overcome by careful formulation of a component-based model which would indeed consider the building most accurately if formulated properly.
The allocation of direct losses based on collapse typically attribute the building replacement cost to the probability of collapse for a given intensity. However, there are a number of additional factors that may be considered when estimating direct losses due to collapse. The influence of residual displacements can significantly affect loss estimates (Ramirez and Miranda 2012) and their consideration could prove critical to accurately represent post-event conditions; based on previous reconnaissance where significant residual drifts can render a structure a complete loss without actually collapsing (Mahin and Bertero 1981; Rosenbluth and Meli 1986; Anderson and Fillipou 1995). Additonally, the direct loss based on collapse assumes a total loss in monetary terms, yet it may be difficult to properly consider expected increases in cost due to demolition before new construction can begin or even the increased cost to tear down a building that has experienced excessive residual deformation.
11.2.3 Indirect Losses and Downtime
The third and final source of seismic loss is downtime. The estimation of downtime is perhaps the most difficult to achieve of all of the 3 D’s. Predominately since this metric not only involves the numerous considerations that have been discussed thus far, but because it depends on many additional external factors; not only involving a structure experiencing an earthquake, but an entire region or community.
The basic contributions to downtime following a seismic event can be broken up into two components: rational and irrational downtime as defined by Comerio (2006). Rational downtime represents the time needed to repair damage of replace a building. Irrational downtime includes a number of factors including financing and human resources, as well as economic and regulatory uncertainty (Comerio 2006).
The concept of estimating rational downtime is quite similar to the manner in which repair costs are estimated. Using the previous example of an RC beam-column joint, as sample set of expected repair times are shown for three damage states in Fig. 11.7.
Repair times for various damage states of a modern interior RC beam-column joint: (a) significant cracking, (b) spalling and (c) severe damage (Values from ATC 2011b)
The figure shows that the estimated repair time is proportional to the level of damage for the component which is logical. However, noting that the ranges defined by the standard deviation bands (dashed lines) are giving estimates differing by a factor of two which highlights the large uncertainty involved with repair time estimation. Further, considering an entire building requiring repair, these uncertainties would be expected to exacerbate. For the repair of an entire facility, the rational component of downtime relating to mean repair time is a function of: building size (e.g. number of floors, plan area), the number of different trades that are involved (e.g. electrician, drywall installer/finisher) and, similar to the component level, the number of assemblies and the extent of damage. The downtime associated with the number of trades involved also contributes to what is termed change of trade delay where certain tradesman will not be able to access the building until others have completed their tasks. This type of delay can vary significantly depending on the repair scheme adopted (Mitrani-Reiser 2007; Beck et al. 1999). Repair schemes vary in efficiency between the lower bound of a slow-track scheme where all trades are performed in series to a fast-track scheme where (ideally) all trades are performed in parallel. A summary of the rational components of downtime is shown in Fig. 11.8.
The various contributions of irrational downtime are very difficult to estimate. Economic factors such as municipal buildings waiting for a decision on government funding or private facilities negotiating a loan for repairs could vary significantly depending on individuals and the condition of the surrounding area. Similarly, another component of the irrational downtime would be, upon acquisition of funds, the delay for the start up of construction which could involve the development of drawings and repair schemes, bidding for construction, and various levels of engineering assessments; factors that would greatly depend on the relationship of the owner with the engineers, architects and contractors (Comerio 2006). The various components of downtime are summarized in Fig. 11.8.
The outcome of initial engineering inspections has been the primary metric for the estimation of downtime in recent loss assessment studies (Mitrani-Reiser 2007). The procedure for carrying out post-earthquake inspections typically implements a “tagging” system by which buildings can be quickly identified with a commonly adopted green, yellow and red system such as the ATC-20 guidelines (ATC 2005) where:
-
Green signifies that the building is “inspected” and occupancy is permitted (bearing in mind that the use of the word permitted here would suggest that the undamaged building was deemed safe),
-
Yellow represents the presence of some hazard within the building and receives a “restricted use” placard typically with notes describing the risks and extent of entry and
-
Red represents the case of a clear hazard to human life and returns an “unsafe” placard that prohibits any re-entry or occupation of the building.
In order to quantify downtime, Mitrani-Reiser (2007) developed a “virtual inspector” algorithm which simulates the engineering inspection process. As an example of the differences in downtime due to engineering inspection outcomes, Mitrani-Reiser (2007) assumed that the mobilization time associated with a green, yellow and red tag were 10 days, 1 month, and 6 months respectively. Notably, when considering a building that is damaged beyond repair, a downtime of 38 months was attributed. Further, although some estimations must be made in order to quantify downtime, it is mentioned that the time associated with a yellow tag can vary significantly as the purpose of the yellow tag is to provide more in depth inspections to arrive at a final decision of a red tag or possible repair requirements before the issuance of a green tag.
Despite the difficulties in its estimation, downtime following a seismic event can be orders of magnitude in importance above all other sources of seismic loss depending on the scenario. For example, some lease agreements for commercial real estate in seismic areas, such as California, include a window period (typically 270 days) in which building owners must repair damages to avoid a break of the lease agreement (Comerio 2006). Similarly, tenants of the same commercial real estate may be losing valuable clients or contracts for every week or even day they are out of operation. This would be a similar case for industrial buildings that produce a certain product or provide a service. Although building repair is different than business recovery (Chang and Falit-Baiamonte 2002), property owners and tenants will likely be forced to compete within the same pool of (possibly scarce) services and resources which could significantly affect resulting downtime. The concept of “demand surge” for human resources and materials to restore an entire city (or region) facing these types of dilemmas becomes much more apparent.
In light of the importance of downtime, as well as the other sources of seismic loss, mitigation of this risk may be a cumbersome task, yet even small reductions in seismic risk in terms of direct losses or life-safety could translate into tremendous benefits when considering the indirect loss associated with downtime.
11.3 Proposal to Use EAL for Seismic Performance Classification
This section proposes a performance-classification scheme that is based on direct expected annual monetary losses (EAL), with no consideration of life safety or indirect losses. The motivation for the classification scheme is first provided, some limitations with the EAL performance measure are discussed and then a tentative classification framework is proposed.
11.3.1 Motivation for EAL-Based Performance Classification
At first it might appear that a good performance classification scheme should be all-encompassing, considering life-safety, monetary losses and downtime, as well as the other factors considered in the definition of community resilience. However, it is argued here that best performance classification parameter really depends on the intended use of the classification scheme. In this paper it is proposed that an EAL-based performance classification can provide suitable means of motivating retrofit measures that help build community resilience and reduce losses and downtime due to earthquakes. It is argued that the issue of life-safety should be separately addressed by code-requirements; buildings should satisfy minimum requirements for what regards the probability of loss of life, but that these do not form the basis of a performance-classification scheme.
This concept of separating life safety from EAL performance could be considered somewhat analogous to the way that the performance of washing machines and refrigerators is currently quantified; the energy performance rating scheme gives us an idea of the performance of the fridge (or washing machine) in terms of running-costs (energy use) but does not provide any indication of the likelihood that the machine will break down or not. Instead, we tend to rely on brand-names and guarantees to ensure that the likelihood of breakdown is not too high. The benefit of the establishment of the energy-rating performance scheme for home appliances is that it is saving our communities (as well as the individual) money and energy (which is a sustainable initiative important for the environment). In the context of earthquake engineering, such savings are vital as they could help reduce household and business disruption and social impacts of earthquakes. Even though the 2011 Christchurch earthquakes (and other events in modern engineered societies) only caused limited loss of life, the upheaval on the community has been extensive and has taken a long time to recover from. Fortunately, in the case of Christchurch a large proportion of the damage was insured and therefore recovery is easier but it is still taking a long time and the earthquake has clearly caused widespread upset. In other parts of the world, such as Italy, the majority of homeowners and many businesses don’t have earthquake insurance and therefore the government either steps in or the local community suffers hugely (or both).
In order to be effective, it is also argued that a performance classification index needs to be coupled with some sort of incentive scheme. In the case of home-appliances the benefit of energy-efficiency to homeowners is clear and immediate. In the case of low-risk building solutions the benefit of improved performance may only become apparent after an intense earthquake event, which has a low probability of occurrence and may never in fact occur during the building owner’s lifetime. As such, it is considered that government incentive schemes could provide the suitable motivation to building owners and this could consist of tax-rebates, discounted bank loans or even subsidized building materials. Another possibility is to engage the insurance industry more effectively, ensuring that insurance premiums can be tailored according to the building-specific seismic risk, rather than generic fragility functions for broad building typologies. However, this will require more dialogue with insurance companies who ideally would have some input in defining final performance-classification schemes such as those defined shortly in this paper.
11.3.2 Observed Trends in Expected Annual Loss Estimates
As the implementation of advanced loss assessments is still somewhat rare in the current literature, the results of the PEER benchmark study on modern RC moment-resisting frame (MRF) buildings is the largest source of building-specific loss data currently available. The EAL for thirty 2003 International Building Code (IBC) conforming RC MRF buildings was estimated using two different loss model formulations. Taking the same site hazard and structural analysis as input, the buildings were assessed using a storey-based loss model by Ramirez and Miranda (2009) and a component-based MDLA (Matlab Damage and Loss Analysis) toolbox (Mitrani-Reiser 2007; Beck et al. 2002) reported within Ramirez et al. (2012). The buildings range from one to twenty stories and consider either space-frame or perimeter-frame lateral load systems. Buildings also consider a variety of foundation modelling assumptions (e.g. pinned, fixed, grade beams modelled). The EAL results are shown for the two different loss models in Fig. 11.9. The figure shows that code conforming RC MRF designs have EAL values between 0.5 % and 1.5 % of replacement cost which is a plausible initial benchmark for standard buildings designed to modern seismic codes. Notably, the one story building with higher EAL was treated as an outlier.
The figure also shows a general trend of decreasing EAL with story height. This is quite easily explained by the concentration of damage in only a few stories of taller, more expensive, buildings. Conversely, shorter buildings will have a larger percentage of its stories damaged which can result in larger losses in terms of the percentage of replacement cost. This relationship with height may need to be considered before making further assumptions of generalized EAL values for code conforming buildings. However, the range of 0.5–1.5 % is supported by the previous results for variations of modern 4-storey RC MRF frames reported by Haselton et al. (2008) who found EAL in the range of 0.55–1.07 % of replacement cost.
As part of a continuing effort, Liel and Deierlein (2008) essentially extended the previous benchmark study to include non-ductile structures. The study examines eight different non-ductile 1967 IBC conforming RC MRF designs and compares them with the equivalent 2003 IBC designs that were discussed in the previous section. The buildings consist of perimeter and space frame designs ranging from two to twelve stories. The EAL results are shown in Table 11.3 in comparison with the corresponding 2003 IBC conforming design from other PEER studies.
The table shows that the EAL values range from 1.6 % to 5.2 % with an average of 2.5 % of replacement cost for non-ductile RC frame buildings. These values suggest that a possible “non-ductile” range of EAL could be 1.5–3.0 %. However, the resulting values show an even stronger dependence on height which suggests that EAL classification ranges should distinguish between low-rise (say 1–4 stories), mid-rise (5–12) and high rise (>12 stories) in order to consider this difference, yet furture research is needed to confirm these trends.
The study by Krawinkler (2005) on the Van Nuys hotel building, which is a 7-storey RC perimeter frame building located in California, is an additional case study involving non-ductile structures. The structure was constructed in 1966 in the San Fernando Valley and can be confidently labeled as a “non-ductile” structure based on the witnessed performance in the 1971 San Fernando and 1994 Northridge events; the latter of which causing brittle shear failures of columns and beam column joints (Trifunac and Hao 2001). As Krawinkler (2005) estimated an EAL of 2.2 % of the replacement cost ($198,000 of $9 M replacement in 2002 USD), the generalization of non-ductile buildings having an expected annual loss on the order of 1.5–3 % is supported. However, additional work with this case study building has shown different results and this will be discussed along with other concerning points about generalizing EAL values to classify seismic risk categories.
11.3.3 Uncertainties with Expected Annual Loss Estimates
A number of inherent difficulties in implementing expected annual loss (EAL) as a seismic risk classification metric are addressed in this section. It is shown that even while using a normalized loss value (e.g. percentage of replacement cost) there are still various aspects of the loss estimation procedure that must, ideally, also be “normalized” before EAL could be expected to give reliable results for various structural typologies.
General trends, thus far, have shown expected annual loss (EAL) to be on the order of 0.5–1.5 % of replacement cost for 2003 IBC conforming MRF buildings (Haselton et al. 2008; Liel and Deierlein 2008; Ramirez and Miranda 2009) and non-ductile RC MRF buildings exhibiting EAL values on the order of 1.5–3.0 % of the replacement cost (Liel and Deierlein 2008). However, the manner in which the replacement cost of these structures has been calculated has been somewhat controlled (typically with the current version of the RS Means estimating manual at the time the study was conducted). Liel and Deierlein (2008) point out that the replacement cost estimates using RS Means (Balboni 2007) are expected to be at least 25 % lower than the actual cost of construction and that total project costs can be underestimated by as much as $200/ft2 (2006 USD). Further, Liel and Deierlein (2008) state that these discrepancies from actual repair costs can still produce unbiased loss estimates provided that both replacement cost (e.g. entire structure) and repair costs (e.g. non-structural damage) are calculated using the same estimating reference (e.g. RS Means). The implications that deviation from this caveat can have on obtaining consistent EAL estimates to classify the seismic risk of a structure are illustrated with a previous case study performed on base isolated buildings.
The work of Sayani (2009) implemented the PEER PBEE methodology on two variations of a three storey steel moment frame building located in Southern California: (i) a typical special moment-resisting frame (SMRF) and (ii) an isolated ordinary moment-resisting frame building (IMRF). The buildings are designed to modern U.S. seismic code provisions, assume typical office occupancy and consider similar non-structural typologies and fragilities as studies that have been previously discussed (e.g. Mitrani-Reiser 2007; Beck et al. 2002). Assuming similar site hazard (e.g. Los Angeles area), the reported values of EAL were 0.134 % and 0.194 % of replacement cost for the IMRF and SMRF respectively; assuming the “total building and site” estimate for replacement cost (refer Sayani 2009).
Initially, the EAL estimate of 0.134 % for the isolated building suggests a continuation of the general trend of a traditional modern building giving results on the order of 0.5–1.5 % of replacement with the drastic reduction stemming from the intuitive “protection” that base isolation can provide. However, the traditional steel building (SMRF) gave EAL results (0.194 %) less than half of the lower bound (0.55 %) value reported from PEER studies which implies that the manner in which the replacement cost was calculated is inconsistent with previous studies conducted in the PEER benchmark study. Opposite of the suggestion to use the same costing reference for both replacement and repair costs set by Liel and Deierlein (2008), the work of Sayani (2009) used a professional cost estimator for the replacement and construction costs while repair costs were adjusted based on reported values within RS Means (Balboni 2007). Notably, the possible underestimation of up to $200/ft2 when using RS Means for replacement cost was not a terrible estimate in this case, where only by adding $200/ft2 to the 2 and 4 storey buildings (more than doubling the cost) examined in Liel and Deierlein (2008) are the replacement costs in agreement with the 3-storey estimates made by Sayani (2009), at least in terms of storey height and gross area. This raises much concern for the results of advanced loss estimates as neither study estimated the replacement cost improperly as no clear guidelines for performing this step are currently in available guidelines (ATC 2011a). Further, it could be argued that the replacement estimate by Sayani (2009) was performed at a very high level of competence, yet due to the repair costs not being treated to the same level the resulting estimates are not held to the same criteria as other studies and therefore can not be compared.
In addition to problems associated with the manner in which replacement cost is estimated, the numerous decisions that must be made in order to estimate EAL will be shown to drastically affect results. Although only the selection of damageable assemblies and variation in fragility selection will be the focus, it must also be noted that selection of initial (onset of damage) intensity, consideration of downtime or fatalities, and numerous economic factors (post-event demand surge for repairs, additional costs of tear down due to residual displacements) could also drastically affect EAL.
The Van Nuys Hotel study that was discussed when describing trends with non-ductile structures is recalled. Interestingly, there are two loss estimates for this building, the aforementioned study by Krawinkler (2005) and another conducted by Porter et al. (2004). The two estimates of EAL for the Van Nuys hotel are displayed in Table 11.4 showing the estimate of Porter et al. (2004) to be approximately one third (0.77 % vs. 2.2 %) of that reported by Krawinkler (2005).
Now how could such a discrepancy exist? Certainly the large difference is not rooted in the difference in replacement cost as the higher replacement cost (1 year of inflation is negligible) from Krawinkler (2005) would give a reduction in EAL by the same principles discussed in the previous section concerning the base isolated steel building. The large difference is most likely attributed to the number of damageable assemblies considered in the study and the manner in which their repair costs are distributed. Reportedly, the damageable assemblies (with subsequent fragilities and consequence functions) in Porter et al. (2004) consist of select structural and non-structural typologies from the collection of fragility and repair cost information within Beck et al. (2002). Conversely, the fragilities for the Krawinkler (2005) study consider a, comparatively, exhaustive list of non-structural components as identified by Taghavi and Miranda (2003) as well as numerous structural elements with distinct seismic fragility and consequences. Possibly the largest distinction is that the Krawinkler (2005) study adopts fragilities for numerous non-structural typologies and includes generic drift- and acceleration- sensitive fragilities in order to consider repair implications of numerous assemblies within the building in lieu of specific experimental data.
As a final point, loss estimates conducted within Welch et al. (2012) recreated previous assessments of a four-storey RC frame building using both the component-based model developed by Mitrani-Reiser (2007) and the storey-based model by Ramirez and Miranda (2009). Even with varying modelling assumptions and discrepancies within the many steps of the PEER PBEE framework, the resulting losses tended toward the parent study which highlights the reliability in the methodology. However, since the difference in the values between the two models varied by 30 % on average, the manner in which the loss model is developed should also be regulated in order to classify seismic risk. Finally, given the that the topic is relatively new, it is expected that rigorous loss assessments would be best for internal comparisons and cost benefit analysis, where regulations in order to reduce the interpretation required by the analyst may be defeating the purpose of having such a versatile loss framework.
11.3.4 Tentative Classification Framework
The previous sections have highlighted some important uncertainties in the definition of EAL as a performance parameter. In particular, (and leaving the performance issue of life-safety aside as a matter that could be addressed through code-requirements) the following two points were made:
-
EAL is currently very uncertain and the values obtained are greatly affected by the loss models adopted and the value placed on replacement.
-
The total EAL for a building, expressed as a fraction of the building replacement cost, will tend to decrease as the building height increases.
For what regards the first point, this would appear to be an issue with the current state of the art and could be dealt with by more research and some consensus on a standard procedure for estimating EAL. This uncertainty need not, however, prevent the creation of an EAL-based performance classification framework (which could actually help motivate the additional research that is required into EAL) and one should recognize that the engineering community already accepts large uncertainties and variations in performance checks. For example, the Eurocode 8 (CEN 2005) currently allows the use of four different types of structural analysis (equivalent-lateral force, modal-response spectrum analysis, pushover analysis, and non-linear dynamic analyses) in order to check specific engineering performance criteria and all four methods will generally provide different response estimates. Therefore, the current uncertainties inherent in EAL need not be seen as a large deterrent for the creation of an EAL-based performance classification scheme.
The second point raised above, which notes that EAL tends to decrease with building height, should also be given some attention. As the building height increases the total EAL may well tend to decrease because deformations and damage tend to be concentrated on specific floors, which make up a smaller fraction of the total building as the number of storeys increases. Nevertheless, it would appear inappropriate to tell the owner of the storey in which high losses are expected that the EAL for the whole building was very low, when in fact it is the EAL of their apartment that is of most interest and relevance to them. A logical solution to this is to define EAL not on a building level, but on a storey-by-storey basis, so that different storeys of a building might be given different performance classifications. To this extent, the proposal is not that the performance of one storey can be considered completely independent of another and clearly, if there is a soft-storey collapse at the ground floor of a building then all floors have a high loss as the building will have to be replaced. However, it is proposed that the whole building be assessed and performance ratings then assigned to different levels, recognizing that repairable damage from low to moderate intensity earthquake shaking may tend to concentrate in specific levels. Then, a given owner at a certain level of the building might recognize that by using well-detailed non-structural elements they could significantly reduce the EAL for their storey.
With the above points in mind, and considering the EAL results from the literature presented in Sect. 3.2, Table 11.5 proposes a tentative EAL-based seismic performance rating scheme. It is proposed that the EAL limits in Table 11.5 refer to storey-specific values of EAL (i.e. the expected annual loss of the storey divided by the replacement value of the storey) which is a slightly different definition of EAL than is traditionally used, but would assist in addressing bullet-point 2 made above. The next section of the paper will present some simplified tools for the estimation of the EAL which will be followed by a case-study example.
11.4 Tools for Simplified Performance Classification
For most practicing engineers the challenge of computing the EAL for a building is currently likely to appear a somewhat daunting and impractical task. As computing power improves, software develops and loss assessment concepts and procedures become more widely established, it is likely that this situation will change. However, in the interim (and to permit such change to happen), it is apparent that there is a need for simplified tools that will allow engineers to estimate losses in a relatively simplified manner, without departing too greatly from current engineering procedures. This section reviews a recent proposal by Sullivan and Calvi (2011) and Welch et al. (2014) for simplified loss assessment, which combines the Direct-displacement based assessment (Priestley et al. 2007) and SAC-FEMA (Cornell et al. 2002) methodologies together with an evaluation of losses at specific limit states.
11.4.1 Displacement-Based Seismic Assessment
Within a text proposing Direct displacement-based design, Priestley et al. (2007) also set out a procedure for the displacement-based seismic assessment (DBA) of structures. The procedure offers an estimate of the probability of exceeding a certain limit state, which could be the collapse prevention limit state, serviceability limit state or some other intermediate limit state. The first task in the Direct DBA procedure is to establish a force-displacement response curve, such as that shown in Fig. 11.10a, for an equivalent SDOF representation of the building. Priestley et al. (2007) explain that this can be done using hand-calculations in which the relative strengths of members are first compared in order to identify the expected lateral mechanism, which is then used together with (mechanism-dependent) approximations for the displaced shape and limit-state deformation capacity (which may be linked to resistance of brittle mechanisms). Alternatively to hand-calculations, one could undertake non-linear static analyses to obtain the force-displacement response curve.
Overview of displacement-based assessment approach (after Priestley et al. 2007). (a) Equivalent SDOF representation of structure at critical limit state. (b) Force-Displacement (pushover) curve for equivalent SDOF system. (c) Identification of seismic intensity expected to create limit state damage
With the force-displacement curve known, the effective stiffness, effective mass and ductility demand at the assessment limit are computed for the equivalent SDOF system. Equation 11.2 is then used to compute the system’s effective period:
where m e is the effective mass given, as a function of the assessed displaced shape Δ i , by:
The use of the effective period and mass stems from the substitute-structure concept of Shibata and Sozen (1976) and Gulkan and Sozen (1974) and permits the use of linear elastic spectrum analysis to gauge the impact of seismic demands, with the effect of non-linear response accounted for through the use of effective-period inelastic spectrum scaling factors. Traditionally, such spectral scaling factors are set in Direct displacement-based design as a function of an equivalent viscous damping value, which is in turn a function of the ductility demand and hysteretic properties of the building. Recent research (Pennucci et al. 2011) has indicated that there are advantages in computing the spectral scaling factor (referred to as the displacement reduction factor in Pennucci et al. 2011) directly as a function of the ductility demand, skipping the computation of the equivalent viscous damping. This lead to the proposal that the inelastic displacement demand, Δ in , can be related to an elastic spectral displacement demand, S d,el , using an empirical ductility-dependent expression. The resulting expression obtained for RC wall structures and bridge piers using equations proposed in Priestley et al. (2007) is:
Note that this expression can be related back to an equivalent viscous damping value from expressions in the literature, such as that proposed in Eurocode 8 (CEN 2005) (adapted here to give ξ as a function of η):
Proceeding with the displacement-based assessment, once the effective period and system ductility demand, μ, at the limit state have been identified, an empirical spectral displacement scaling factor is computed (11.6) and divided into limit state displacement capacity to provide an equivalent elastic spectral displacement capacity, S d,el,cap , as shown:
With knowledge of elastic spectral displacement demands at a site, for various hazard levels, the earthquake intensity required to push the structure to its limit state can then be identified using the effective period (T e ) and spectral displacement capacity (S d,el,cap ) as shown in Fig. 11.10c. Note that this relatively simple approach could also be done using a capacity-spectrum method or other non-linear static procedures.
The benefit of this type of assessment over a traditional assessment approach in which code-specified intensity levels are checked via a pass-fail type approach is that a better appreciation of the real risk can be obtained. Priestley et al. (2007) go as far as suggesting that the probability associated with the hazard level shown in Fig. 11.10c provides an indication of the probability that the assessed limit state will be exceeded. However, such a proposal does neglect the effect of dispersion in both demand and capacity which is should be accounted for in probabilistic assessment methods.
In order to extend the DBA procedure to provide a probabilistic assessment of the likelihood of exceeding a certain limit state, some consideration must be made of uncertainties in the assessment process, and more generally, for dispersion in the demand and capacity estimates. To permit a simplified probabilistic displacement-based assessment, Sullivan and Calvi (2011) and Welch et al. (2014) have recommended adaption of the SAC-FEMA approach (Cornell et al. 2002) simplified as per the suggestions of Fajfar and Dolsek (2010). According to the SAC-FEMA approach, the probability, PLS,x, of exceeding a certain limit state can be found for an x-confidence level according to:
Where C x , C H and Cf are coefficients account for C values are coefficients accounting for the desired confidence level, differences between mean and median hazard levels, and dispersion in the demand and capacity, respectively. \( \tilde{H} \)(S a,C ) is the median value of the hazard function at the seismic intensity S a,C , expected to cause a specific limit state to develop. Simplifying the approach according to the suggestions of Fajfar and Dolsek (2010) both the coefficients C H and C x are set to one, and a 50 % confidence level estimate using the mean hazard of the probability of exceedence is obtained as:
As shown in Fig. 11.10c, the DBA procedure as proposed by Priestley et al. (2007) provides the mean value of the hazard function, \( \overline{H}\left({S}_{a,\overline{C}}\right) \), expected to cause a selected limit state to develop. Subsequently, the adjustment required to arrive at a simplified estimate of the probability of exceeding a certain limit state only needs computation of the dispersion factor, Cf. According to Cornell et al. (2002), the Cf factor can be calculated, assuming log-normal distributions of demand and capacity, as:
where the constant k is set as a function of local hazard data using a power expression to relate hazard with probability of exceedence, the constant b relates engineering demand parameters to the intensity measure and could be approximated as 1.0 (as per equal-displacement rule even if in reality more accurate values could be obtained considering different structural typologies and hysteretic systems), and β CR and β DR are dispersion measures for randomness in capacity (modelling) and demand (record-to-record) respectively. Indicatively, one could expect a value of (β DR 2 + β CR 2) = 0.2025 as suggested by Fajfar and Dolsek (2010), who also report that reliable data on modelling dispersion is not yet available. More refined/reliable information on dispersion appears to emerging within the recent ATC-58 document (ATC 2011a) based on recent parametric studies as described in Sect. 11.2.1.
As discussed in the fib Bulletin 68 (fib 2012), the accuracy of the SAC-FEMA approach is limited but it is very simple and therefore is considered to provide engineers with a useful approach in the transition to more rigorous probabilistic methods. The approach will be used later in Sect. 11.5 as part of an example case-study to illustrate possible application of the performance-classification scheme.
One aspect of the DBA procedure not clarified above is that in addition to checking displacement demands, one should also take care to assess demands on acceleration-sensitive non-structural elements and secondary-structural elements, particularly when assessing the serviceability limit state. In work by Welch et al. (2014) acceleration demands up the height of a building were estimated using empirical expressions from ATC-58 (ATC 2011a) but existing empirical procedures are known to possess a number of limitations. Progress towards improved estimation of floor acceleration spectra has been made by Sullivan et al. (2013), Calvi and Sullivan (2014), who provide expressions for the estimation of floor acceleration spectrum demands as a function of the non-linear response of the underlying structure and the period and damping of the supported non-structural element. However, it is still an area of the DBA procedure that requires further development.
11.4.2 Approximation of the Expected-Annual Loss
The DBA procedure described in the previous section provides an estimate of the probability of exceeding a given limit state. This approach should appear within the grasp of most practicing engineers who have become used to exercise of assessing different limit states. However, the proposal in this paper is for the performance of a building to be classified according to the expected annual monetary loss (EAL). As such, the next step in the assessment process is to convert the probability of exceeding different limit states into values of EAL. In order to do this, Welch et al. (2014) have shown that by estimating losses associated with four key limit states, and assuming that losses vary linearly with intensity between the key limit states, simple integration can be used to arrive at an estimate of EAL. This process is illustrated in Fig. 11.11 and will be explained in more detail subsequently.
Overview of the simplified EAL estimation using displacement-based assessment as proposed by Welch et al. (2014)
Referring to Fig. 11.11, it is shown that the smooth curve, representing a series of intensity-based assessments using refined methods (e.g. PEER PBEE), has a distinct transition region between intensities of large annual frequency (lower expected losses) and rarer events with smaller annual frequency (higher expected losses). The main concept behind the simplified method using DBA is that a refined loss curve is reasonably approximated using only four key limit states; two bounding limit states to represent the onset of damage (zero loss) and the point of total loss (near collapse), as well as two intermediate limit states (operational and damage control) that represent the transition region in the loss curve.
As discussed previously, a single DBA assessment is capable of estimating the probability of exceeding a limit state defined by a peak displacement demand (e.g. peak IDR). Therefore only limit state definition is required in order to obtain the vertical ordinates (mean annual frequency) shown in Fig. 11.11, yet the loss values associated with each of the four limit states are conditioned on a few simplifying assumptions. The zero loss limit state is assigned a mean damage factor (MDF, % of replacement cost) of zero; a similar assumption to assigning an initial intensity to begin analysis within the PEER PBEE approach. The near collapse limit state is assumed to represent the total loss threshold and is attributed a MDF of 1.0. This leaves only direct loss estimates to be calculated at the intermediate operational and damage control limit states.
In order to estimate losses at intermediate limit states, the work within Welch et al. (2014) adopted the engineering demand parameter to decision variable functions (EDP-DV) formulated by Ramirez and Miranda (2009). These functions are constructed for frame buildings based on number of stories, ductility capacity, structural system (space or perimeter frame) and occupancy (e.g. office). As part of a storey-based loss framework, EDP-DV functions directly relate the EDP’s of peak inter-storey drift ratio (IDR) and peak floor acceleration (PFA) to the expected direct losses associated with structural and non-structural damage. The functions assume three performance groups considering structural (drift-sensitive), non-structural drift-sensitive and non-structural acceleration-sensitive components. The functions consider the variation in expected assembly inventory between ground floor, typical floors, and roof level. Notably, the EDP-DV functions consider many interactions between components in order to avoid attributing the same repair cost twice to a component that may need repair in order to access additional elements for repair. A summary of how EDP-DV functions are developed and implemented is shown in Fig. 11.12.
Summary of the development of EDP-DV functions (Ramirez and Miranda 2009) used to estimate repair costs at intermediate damage states using the four-point EAL model
With the assumptions in place, the last important aspect of the simplified EAL calculation using DBA is the definition of limit states. Ideally, the zero loss limit state should represent the onset of damage of the most fragile non-structural components (e.g. partitions, infills) and this should transition to an operational limit state that would produce only light non-structural damage. Further, the damage control limit state should represent only minor structural damage and the near collapse limit state, appropriately, should consider the expected displacement demand at imminent collapse. Notably, the work within Welch et al. (2014) developed limit state criteria similar to that described in Vision 2000 (SEAOC 1995), yet a few modifications were made. Most importantly the near collapse limit state considered both the imminent collapse displacement as well as an approximation of the peak displacement corresponding to a target residual drift in order to include the possibility of a total loss due to residuals.
11.5 An Example Application
11.5.1 Assessment, Retrofit Options, Estimate of EAL
In order to illustrate how a performance classification scheme could be used in practice, the three storey office building shown in Fig. 11.13 is examined. This hypothetical case study building, assumed to be located in the city of L’Aquila, possesses features typical of construction practice in the 1980s with a ductile RC frame structure, an exterior glass façade, lightweight steel framed interior partitions and suspended ceilings. This example will consider how a performance classification scheme could be coupled with a government-funded incentive scheme to encourage retrofit and subsequently reduce likely monetary losses and disruption caused by earthquakes.
A non-linear static (pushover) seismic assessment of the building reveals that the building forms a ductile beam-sway mechanism and develops the bi-linearized force-displacement response shown in Fig. 11.14, with a (cracked) fundamental period of vibration of 1.15 s (similar responses are expected for both the E-W and N-S directions). The base shear resistance at yield of 2250kN is approximately 20 % of the full seismic weight of the building. The pushover curve is annotated to show the corresponding storey drift demands for different potentially critical response points.
As shown in Fig. 11.14, the lightweight steel framed partitions considered for this example structure are assessed as possessing a drift-capacity of 0.3 % before repairs are required (noting that 0.3 % drift capacity has been observed through experimental testing by Davies et al. (2011). The drift limit corresponds to an equivalent SDOF system displacement limit of 0.0231 m at period of 1.15 s (i.e. the cracked elastic period). The other non-structural elements in the case-study building are assessed as being less critical, with the glazing have a serviceability drift capacity of greater than 1.0 % and the ceilings expected to sustain the peak acceleration demands without damage. The frame has a yield drift of 1.0 %, which is quite typical of RC frame structures and a total drift capacity of 5.0 %
In the following paragraphs the EAL expected for the building under three different retrofit approaches will be reported:
-
OPTION 1: no retrofit such that the structure remains as it is;
-
OPTION 2: replacement of the lightweight steel partitions with well detailed partitions that increase the drift required to exceed zero-loss limit state from 0.3 to 0.7 %;
-
OPTION 3: replacement of the partitions (as per OPTION 2) and addition of viscous dampers to reduce the seismic demands at all limit states.
The retrofit options listed above will allow this study to highlight how the improvement of non-structural elements (OPTION 2) could lead to significant reductions in EAL that could represent a more feasible option for building owners to consider than the costlier OPTION 3 that would improve the performance at all limit states. Clearly other retrofit options could also be considered and the options listed above should not necessarily be considered the most effective retrofit solutions. Another retrofit possibility could have been to add a RC wall or other structural elements that increase the stiffness and strength of the system. This would have the benefit of reducing the displacement demands but would have the negative effect of increasing acceleration demands, which in the present scenario are considered to be below limit state values for the ceilings. Note therefore that in all cases the structure remains as it is, coherently with a satisfactory predicted drift capacity of 5 % at collapse.
Proceeding with the displacement-based assessment approach described in Sect. 11.4, Table 11.6 summarizes the characteristics (effective period, displacement capacity and equivalent viscous damping) for the three different retrofit scenarios at both the zero-loss and replacement limit states. Note that the replacement limit state was defined as being the point at which the peak storey drift reached 2.0 %, making the relatively conservative assumption that residual drifts would become unrepairable at this level (exceeding a residual drift limit of 0.5 %). It can be seen that the effective period for the zero-loss limit state for all three retrofit options is 1.15 s (the fundamental period of the building), whereas the effective period for the replacement limit state is 1.59 s (obtained using the effective stiffness of the building at a peak drift of 2 %).
Spectral displacement demands at each value of effective period and for each value of equivalent viscous damping were then obtained from seismic hazard data for L’Aquila (NTC 2008). Subsequently, the hazard level expected to cause the limit state displacement values indicated in Table 11.6 were identified, as per the procedure described in Sect. 11.4.1. To account for dispersion, Eq. (11.8) was applied, with the constant k set to the local hazard data for the site (around the displacement response point of interest), the constant b set equal to 1.0 (which is approximate but should not affect dispersion estimates too greatly), and with estimated values of dispersion in demand and capacity equal to 0.35 respectively (as used for RC frames by Fajfar and Dolsek 2010). Table 11.7 presents values from the simplified SAC-FEMA approach used to identify the probability of exceeding different limit states. The limit states include the zero-loss limit state which (as the name suggests) corresponds to a mean damage factor (MDF) of 0.0, and the replacement which corresponds to an MDF of 1.0 (i.e. the full replacement cost). In order to be able to apply the four-point loss model described in Sect. 11.4.2, the probability of exceeding another two intermediate limit states corresponding to mean damage factors (MDFs) of 0.2 and 0.5 were also computed, making simplifying assumptions about EDP-loss values for the purpose of this example.
At this stage of the assessment one can already begin to get a feel for the impact of the different retrofit measures on the likely losses. Figure 11.15 compares the probability of exceedence of each value of MDF reported in Table 11.7 for the three different retrofit options. The increased deformation capacity offered by the new partitions in retrofit OPTION 2 leads to a considerable reduction in the probability of exceedence of the zero-loss limit state and the overall losses, which can be gauged from the area under the curves. This reduction occurs even if retrofit OPTION 1 and OPTION 2 have the same probability of exceeding the replacement limit state. By adding viscous dampers in retrofit OPTION 3, it can be seen that probability of exceeding all limit states are reduced, but considering the areas under the curves, the difference in losses between retrofit OPTION 2 to OPTION 3 do not appear as significant as those between retrofit OPTION 1 to OPTION 2.
The next step in the assessment is to compute the EAL for each retrofit strategy and this is done here using the approximate 4-point approach described in Sect. 11.4.2. Figure 11.16 presents the results obtained, together with the performance classification that would be assigned to the building according to the proposal made in Sect. 11.3.4. It can be seen that the existing building would be a class C building, bordering on class B (and if required, more refined loss estimates could be undertaken to confirm the final class). If the non-structural partitions are replaced, as per retrofit strategy 2, the building would become class A. If, in addition to this, viscous dampers are provided then it can be seen that a seismic performance Class A+ can be achieved.
In order to highlight the possible implications of these retrofit options, Table 11.8 presents possible costs of the different retrofit scenarios, considering also a possible tax incentive scheme that a government might provide (clearly there is no fundament on the values provided, assumed for the sake of discussion only).
11.5.2 Breakeven Times
In order to further illustrate the potential benefits of the retrofit options, as well as the influence of subsidiary measures, the EAL values are presented in terms of break-even times. The break-even time, t Break-Even , represents, probabilistically, the time necessary for the upfront cost of the retrofitting intervention to be balanced by the expected annual reduction in seismic losses as shown in (11.10):
where the total cost of the intervention, Cost Retrofit , could include a reduction to due subsidiary measures depending on the situation. The results of break-even times are shown in Fig. 11.17 for the example case study. Notably, the replacement cost of the structure is taken as €2,000,000 for the sake of simplicity. Actual values could vary significantly yet this cost corresponds to the more comprehensive retrofit (e.g. added damping) to be 10 % of the replacement cost. The values used for calculation of t Break-Even are shown in Table 11.9.
Reflecting on the numbers shown, one can see that a significant capital outlay is required to increase the performance class to A+. Even though the government incentive for this option is assumed to be greater than for retrofit option 2, it might be deemed too expensive by the building owner to pursue. Retrofit option 2 still results in a significant retrofit cost, but is likely to be more acceptable to the building owner, particularly considering that the replacement of partitions might be undertaken as part of a refurbishment scheme. Another instance in which option 2 might be considered more attractive is the situation in which the building is owned by several different parties, as is the case for the majority of residential buildings in Italy. In such occasions it may be very difficult to obtain agreement from all building owners to proceed with retrofit option 3, owing to the costs. On the other hand, retrofit option 2 could actually be implemented only on specific floors of a building (or part of it), by owners interested in improving the seismic performance rating of their apartment. Clearly, the same cannot be said for retrofit option 3 (addition of structural dampers) which should be implemented for the entire building system.
As a closing comment to this example, note that by motivating people to make some form of retrofit, even if only to non-structural elements as for option 2, the negative impacts of earthquakes should be reduced, with reduced disruption, monetary losses and downtime in the event of an earthquake. This is considered to provide good justification for the development and implementation of a seismic performance rating system, ideally coupled with some form of incentive scheme, in the years ahead.
11.6 Conclusions
This paper has reviewed a range of performance measures that are being adopted in modern seismic engineering applications and has then proposed a seismic performance classification framework based on expected annual losses. The motivation for an EAL-based performance framework stems from the observation that, in addition to limiting lives lost during earthquakes, changes are needed to improve the resilience of our societies, and it is proposed that increased resilience could be achieved by limiting monetary losses. Typical values of EAL reported in the literature have been reviewed, uncertainties in such EAL estimates have been discussed and then a EAL-based seismic performance classification framework has been proposed. The proposal has been made that the EAL should be computed on a storey-by-storey basis in recognition that EAL for different storeys of a building could vary significantly and also recognizing that a single building may have multiple owners.
A number of tools for the estimation of EAL exist in the literature and both the PEER PBEE framework and a simplified displacement-based loss assessment (DBLA) procedure have been reviewed in this paper. It has also been argued that there is a need for simplified methods for the prediction of EAL as engineers make a transition into this new performance parameter. In order to illustrate the potential value of an EAL-based classification scheme, a three storey RC frame building is assessed using the simplified DBLA procedure and performance classifications are made for three different retrofit solutions. The results show that even if only limited non-structural interventions are made to the case study building, the EAL could be significantly reduced. As the less-expensive non-structural retrofit could be more within the grasp of building owners, it is argued that overall, such a performance classification, coupled with some form of government or insurance-driven incentive scheme, may provide an effective means of motivating (even if limited) retrofit, thereby reducing the risk and increasing the resilience of our societies.
References
Anderson JC, Fillipou FC (1995) Dynamic response analysis of the 17-story canoga building, SAC technical report 95-04, pp 12-1–12-53
Altoonash A (2004) Simulation and damage models for performance assessment of reinforced beam-column joints. PhD dissertation, Stanford University
Aslani H, Miranda E (2005) Probability-based seismic response analysis. Eng Struct 27(8):1151–1163
ATC (2005) Procedures for postearthquake safety evaluation of buildings. ATC-20. Applied Technology Council, Redwood City, Published 1989, Revised 2005
ATC (2011a) Guidelines for seismic performance assessment of buildings: vol 1 – methodology. ATC 58-1. Applied Technology Council, Redwood City
ATC (2011b) Guidelines for seismic performance assessment of buildings: vol 2 – implementation guide. ATC 58-1. Applied Technology Council, Redwood City
Baker JW, Cornell CA (2006a) Which spectral acceleration are you using? Earthq Spectra 22(2):293–312
Baker JW, Cornell CA (2006b) Spectral shape, epsilon and record selection. Earthq Eng Struct Dyn 34(10):1193–1217
Balboni B (ed) (2007) Means square foot costs. R.S. Means Co., Inc., Kingston
Beck JL, Kiremidjian A, Wilkie S et al (1999) Decision support tools for earthquake recovery of business, final report for CUREe-Kajima phase III project, Consortium of Universities for Research in Earthquake Engineering, Richmond
Beck JL, Porter KA, Shaikhutdinov R, Au SK, Moroi T, Tsukada Y, Masuda M (2002) Impact of seismic risk on lifetime property values. Final report for CUREE-Kajima phase IV project, Consortium of Universities for Research in Earthquake Engineering, Richmond
Berry M, Parrish M, Eberhard M (2004) PEER structural performance database user’s manual. Pacific Earthquake Engineering Research Center, University of California, Berkeley. http://nisee.berkeley.edu.spd
Calvi PM, Sullivan TJ (2014) Improved estimation of floor spectra in RC wall buildings. In: Proceedings of the 10th US national conference on earthquake engineering, Anchorage, paper 1113
CEN (2005) Eurocode 8: design of structures for earthquake resistance. EN 1998-1, Brussels
Chang SE, Falit-Baiamonte A (2002) Disaster vulnerability of businesses in the 2001 Nisqually earthquake. Environ Hazards 4(2/3):59–71
Charleson A (2007) Architectural design for earthquakes – a guide to the design of non-structural elements. New Zealand Society for Earthquake Engineering, Wellington
Coburn A, Spence R, Pomonos A (1992) Factors determining human casualty levels in earthquakes: mortality prediction in building collapse. 10th world conference on earthquake engineering, Madrid, Spain
Comerio MC, Stallmeyer JC, Holmes W, Morris P, Lau S (2001) Nonstructural loss estimation: The UC Berkeley case study, PEER report 2002/01, Pacific Earthquake Engineering Research Center, Dec 2001
Comerio MC (2006) Estimating downtime in loss modeling. Earthq Spectra 22(2):349–365
Comerio MC (2012) Resilience, recovery and community renewal, Keynote paper. In: 15th world conference of earthquake engineering, Lisbon, Portugal
Cornell CA, Jalayer F, Hamburger RO, Foutch DA (2002) Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J Struct Eng 128(4):526–533
Davies RD, Retamales R, Mosqueda G, Filiatrault A (2011) Experimental seismic evaluation, model parameterization, and effects of cold-formed steel-framed gypsum partition walls on the seismic performance of an essential facility, MCEER-NEES nonstructural, technical report MCEER-11-0005, Buffalo, New York
Durkin ME, Thiel CC (1992) Improving measures to reduce earthquake casualties. Earthq Spectra 8(1):95–113
Fajfar P, Dolsek M (2010) A practice-oriented approach for probabilistic seismic assessment, In: Fardis MN (ed) Advances in performance-based earthquake engineering. Springer, Dordrecht, Netherlands pp 225–333
Federal Highway Administration (FHWA) (1994) Technical advisory: motor vehicle accident costs. Technical advisory #7570.2. U.S. Department of Transportation, Washington, DC
FEMA (2009) Quantification of building seismic performance factors. FEMA P695. Prepared by the Applied Technology Council for the Federal Emergency Management Agency, Washington, DC
FEMA (2011) Reducing the risks of nonstructural earthquake damage – a practical guide. FEMA E-74. Prepared by the ATC for FEMA, Washington, DC, 2011
fib (2012) Probabilistic performance-based seismic design, fib Bulletin 68. International Federation of Structural Concrete, Lausanne, Switzerland
Filiatrault A, Uang CM, Folz B, Christopoulos C, Gatto K (2001) Reconnaissance report of the 28 Feb 2001 Nisqually (Seattle-Olympia) Earthquake, report no. SSRP-2001/02. University of California, San Diego
Gulkan P, Sozen M (1974) Inelastic response of reinforced concrete structures to earthquake motions. ACI J 71(12):604–610
Haselton CB, Deierlein GG (2007) Assessing seismic collapse safety of modern reinforced concrete moment frame buildings, Technical report no. 156, John A. Blume Earthquake Engineering Research Center, Stanford University
Haselton CB, Goulet CA, Mitrani-Reiser J et al (2008) An assessment to benchmark the seismic performance of a code-conforming reinforced concrete moment frame building, Report no. PEER 2007/12, Pacific Earthquake Engineering Research Center, Aug 2008
Haselton CB, Baker JW, Liel AB, Deierlein GG (2011) Accounting for expected spectral shape (epsilon) in collapse performance assessment. ASCE J Struct Eng, Special Issue on Earthquake Ground-Motion Selection and Modification for Nonlinear Dynamic Analysis, 137(3):332–344
Hengjiam L, Kohiyama M, Horie K, Maki N, Hayashi H, Tanaka S (2003) Building damage and casualties an earthquake. Nat Hazards 29:387–403
Ibarra LF, Medina RA, Krawinkler H (2005) Hysteretic models that incorporate strength and stiffness deterioration. Earthqu Eng Struct Dyn 34:1489–1511
Iervolino I, Manfredi G, Cosenza E (2006) Ground-motion duration effects on nonlinear seismic response. Earthq Eng Struct Dyn 35:21–38
International Code Council Evaluation Services (ICC-ES) (2010) Acceptance criteria for certification by shake-table testing of nonstructural components, ICC-ES AC 156, Subsidiary of the International Code Council
Kalkan E, Kunnath SK (2006) Effects of fling step and forward directivity effects on seismic response of buildings. Earthq Spectra 22(2):367–390
Krawinkler H (2005) Van Nuys hotel building testbed report: exercising seismic performance assessment. Report PEER 2005/11. Pacific Earthquake Engineering Research Center, Richmond
Liel AB, Deierlein GG (2008) Assessing the collapse risk of California’s existing reinforced concrete frame structures: metrics for seismic safety decisions. Technical report no. 166, John A. Blume Earthquake Engineering Research Center, Stanford University
Lignos D (2013) Web-based interactive tools for performance-based earthquake engineering, http://dimitrios-lignos.research.mcgill.ca/databases/index.php. Accessed 26 Jan 2014
Lignos D, Krawinkler H (2011) Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading. J Struct Eng 137(11):1291–1302
Mahin SA, Bertero VV (1981) An evaluation of inelastic seismic design spectra. J Struct Eng 107(ST9):1777–1795
Miranda E, Mosqueda G, Retamales R, Pekcan G (2012) Performance of nonstructural components during the 27 February 2010 Chile earthquake. Earthq Spectra 28(S1):S453–S471
Mitrani-Reiser J (2007) An ounce of prevention: probabilistic loss estimation for performance-based earthquake engineering. PhD dissertation, CalTech, Passadena
Mohammadjavad H, Filiatrault A, Aref A (2013) Simplified sidesway collapse analysis of frame buildings. Earthq Eng Struct Dyn. doi:10.1002/eqe.2353
Mrozek JR, Taylor LO (2002) What determines the value of life? A meta-analysis. J Policy Anal Manage 21(2):253–270
NTC (2008) Norme techniche per le costruzioni, Decreto Ministrale (in Italian)
Pampanin S, Magenes G, Carr A (2003) Modelling of shear hinge mechanism in poorly detailed RC beam-column joints. In: Proceedings of the FIB 2003 symposium, Athens, Greece
Pennucci D, Sullivan TJ, Calvi GM (2011) Displacement reduction factors for the design of medium and long-period structures. J Earthq Eng 15(S1):1–29
Perus I, Klinc R, Dolenc M, Dolsek M (2013) A web-based methodology for the prediction of approximate IDA curves. Earthq Eng Struct Dyn 42(1):43–60
Porter KA (2003) An overview of PEER’s performance-based earthquake engineering methodology. In: Proceedings of 9th international conference on applications of probability and statistics in engineering, San Francisco, CA
Porter KA, Kiremidjian AS, LeGrue JS (2001) Assembly-based vulnerability of buildings and its use in performance evaluation. Earthq Spectra 12(2):291–312
Porter KA, Beck JL, Shaikhutdinov R (2004) Simplified estimation of economic seismic risk for buildings. Earthq Spectra 20(4):1239–1263
Porter KA, Shoaf K, Seligson H (2006) Value of injuries in the northridge earthquake, technical note. Earthq Spectra 22(2):553–563
Priestley MJN, Calvi GM, Kowalsky MJ (2007) Displacement-based seismic design of structures. IUSS Press, Pavia
Rackwitz R (2004) Optimal and acceptable technical facilities involving risk. Risk Anal 24(3):675–695
Ramirez CM, Miranda E (2009) Building specific loss estimation methods & tools for simplified performance-based earthquake engineering. Technical report no. 171, John A. Blume Earthquake Engineering Center, Stanford University
Ramirez CM, Miranda E (2012) Significance of residual drifts in building earthquake loss estimation. Earthq Eng Struct 41(11):1477–1493
Ramirez CM, Liel AB, Mitrani-Reiser J, Haselton CB, Spear AD, Steiner J, Deierlein GG, Miranda E (2012) Expected earthquake damage and repair costs in reinforced concrete buildings. Earthq Eng Struct Dyn 41:1455–1475
Reitherman R, Sabol T (1995) Nonstructural damage. In: Hall J (ed) Northridge earthquake of 17 Jan 1994 Reconnaissance report. Earthq Spectra 11(C):453–514
Rosenbluth E, Meli R (1986) The 1985 Mexico earthquake: causes and effects in Mexico City. Concr Int 8(5):23–34
Sayani PJ (2009) Relative performance comparison and loss estimation of seismically isolated and fixed-based buildings using PBEE approach. All Graduate Theses and Dissertations, Paper 482, http://digitalcommons.usu.edu/etd/482
SEAOC (1995) Vision 2000, a framework for performance-based engineering. Structural Engineers Association of California, Sacramento
Shibata A, Sozen M (1976) Substitute structure method for seismic design in reinforced concrete. J Struct Div, ASCE 102(ST1):1–18
Stojanovski P, Dong W (1994) Simulation model for earthquake casualty estimation. In: 5th national conference on earthquake engineering, Chicago, IL
Sullivan TJ, Calvi GM (2011) Considerations for the seismic assessment of buildings using the direct displacement-based assessment approach. In: Proceedings of the 2011 ANIDIS conference, Bari, Italy
Sullivan TJ, Calvi PM, Nascimbene R (2013) Towards improved floor spectra estimates for seismic design. Earthq Struct 4(1):109–132
Taghavi S, Miranda E (2003) Response assessment of nonstructural building elements. Report PEER 2003/05. Pacific Earthquake Engineering Research Center, Richmond
Trifunac MD, Hao TY (2001) 7-storey reinforced concrete building in Van Nuys, California: photographs of the damage from the 1994 northridge earthquake. Report CE01-05, University of Southern California Department of Civil Engineering, Los Angeles, CA
Vamvatsikos D, Cornell CA (2002) Incremental dynamic analysis. Earthq Eng Struct Dyn 31(3):491–514
Vamvatsikos D, Cornell CA (2006) Direct estimation of seismic demand and capacity of oscillators with multilinear static pushovers through incremental dynamic analysis. Earthq Eng Struct Dyn 35(9):1097–1117
Welch DP, Sullivan TJ, Calvi GM (2012) Developing direct displacement-based design and assessment procedures for performance-based earthquake engineering. ROSE report 2012/03. IUSS Press, Pavia
Welch DP, Sullivan TJ, Calvi GM (2014) Developing direct displacement-based procedures for simplified loss assessment in performance-based earthquake engineering. J Earthq Eng 18(2):290–322
Yeo G, Cornell C (2003) Building-specific seismic fatality estimation methodology. In: 9th international conference on applications of statistics and probability in civil engineering, San Francisco, CA
Acknowledgements
The authors would like to acknowledge that this work is a product of Research Line 7 of the 2014 RELUIS Project.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
This chapter is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
Copyright information
© 2014 The Author(s)
About this chapter
Cite this chapter
Calvi, G.M., Sullivan, T.J., Welch, D.P. (2014). A Seismic Performance Classification Framework to Provide Increased Seismic Resilience. In: Ansal, A. (eds) Perspectives on European Earthquake Engineering and Seismology. Geotechnical, Geological and Earthquake Engineering, vol 34. Springer, Cham. https://doi.org/10.1007/978-3-319-07118-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-07118-3_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-07117-6
Online ISBN: 978-3-319-07118-3
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)