Abstract
Among optimality criteria adopted to select best experimental designs to discriminate between different models, the KL-optimality criterion is very general. A KL-optimum design is obtained from a minimax optimization problem on an infinite-dimensional space. In this paper some important properties of the KL-optimality criterion function are highlighted and an algorithm to construct a KL-optimum design is proposed. It is analytically proved that a sequence of designs obtained by iteratively applying this algorithm converges to the set of KL-optimum designs, provided that the designs are regular. Furthermore a regularization procedure is discussed.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
When Ω 2(ξ) is empty, replace it with
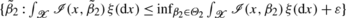 , for an arbitrary ε>0.
, for an arbitrary ε>0.
References
Aletti, G., May, C., Tommasi, C.: Properties of the KL-optimality criterion. arXiv:1212.3556 (2012)
Atkinson, A.C., Fedorov, V.V.: The design of experiments for discriminating between two rival models. Biometrika 62, 57–70 (1975a)
Atkinson, A.C., Fedorov, V.V.: Optimal design: experiments for discriminating between several models. Biometrika 62, 289–303 (1975b)
Fedorov, V.V., Hackl, P.: Model-Oriented Design of Experiments. Springer, New York (1997)
López-Fidalgo, J., Tommasi, C., Trandafir, P.C.: An optimal experimental design criterion for discriminating between non-normal models. J. R. Stat. Soc. B 69, 231–242 (2007)
Luenberger, D.G., Ye, Y.: Linear and Nonlinear Programming, 3rd edn. Springer, New York (2008)
May, C., Tommasi, C.: Model selection and parameter estimation in non-linear nested models: A sequential generalized DKL-optimum design. Stat. Sin. (2012). doi:10.5705/ss.2012.258
Polak, E.: Optimization; Algorithms and Consistent Approximations. Springer, New York (1997). doi:10.1007/978-1-4612-0663-7
Tommasi, C.: Optimal designs for discriminating among several non-normal models. In: López-Fidalgo, J., Rodríguez-Díaz, J.M., Torsney, B. (eds.) mODa 8—Advances in Model-Oriented Design and Analysis, pp. 213–220. Physica-Verlag, Heidelberg (2007). doi:10.1007/978-3-7908-1952-6_27
Tommasi, C.: Optimal designs for both model discrimination and parameter estimation. J. Stat. Plan. Inference 139, 4123–4132 (2009). doi:10.1016/j.jspi.2009.05.042
Uciński, D., Bogacka, B.: T-optimum designs for multiresponse dynamic heteroscedastic models. In: Di Bucchianico, A., Läuter, H., Wynn, H.P. (eds.) mODa 8—Advances in Model-Oriented Design and Analysis, pp. 191–199. Physica-Verlag, Heidelberg (2004)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
The convergence of the algorithm is studied by means of the property of closeness of point-to-set maps (Luenberger and Ye 2008), which is a generalization of the classical concept of continuity.
Lemma 1
 is continuous in (ξ,β
2).
is continuous in (ξ,β
2).
Proof
Take (ξ n ,β n )→(ξ,β). We have

From the definition of weak convergence, it follows that A→0 as ξ
n
→ξ, since  is continuous in x and
is continuous in x and  is compact. To prove that
is compact. To prove that  as ξ
n
→ξ, take a converging sequence β
n
→β and define the function
as ξ
n
→ξ, take a converging sequence β
n
→β and define the function  . Let \(\hat{x}_{n}\) be a maximum point:
. Let \(\hat{x}_{n}\) be a maximum point:  . Since
. Since  is compact, from any subsequence of \((\hat{x}_{n} )_{n}\), we can extract a converging subsequence \(\hat{x}_{n_{k}}\to\hat{x}\). Hence
is compact, from any subsequence of \((\hat{x}_{n} )_{n}\), we can extract a converging subsequence \(\hat{x}_{n_{k}}\to\hat{x}\). Hence

The continuity of  with respect to both the variables concludes the proof. □
with respect to both the variables concludes the proof. □
Corollary 1
The map Map 1 is closed.
Proof
Let ξ n →ξ, β n ∈Ω 2(ξ n ) and β n →β. We must prove that β∈Ω 2(ξ). By Lemma 1, we have that, for n sufficiently large,

Moreover, since I
2,1 is a continuous function, then I
2,1(ξ)≤ε+I
2,1(ξ
n
) (again for n sufficiently large). Therefore, since  , we get
, we get

The arbitrary choice of ε ensures that  . □
. □
Lemma 2
The map
 is closed.
is closed.
Proof
First note that  for any β, since
for any β, since  is compact and
is compact and  is continuous. Now, let β
n
→β,
is continuous. Now, let β
n
→β,  and x
n
→x. By definition,
and x
n
→x. By definition,  for any n and s. The desired result is a consequence of the continuity of
for any n and s. The desired result is a consequence of the continuity of  . □
. □
The following lemma extends the closedness of line search algorithms in an infinite-dimensional space.
Lemma 3
The map Map ξ is closed.
Proof
Let (ξ n ,x n )→(ξ,x), \(\xi'_{n}\in\mathbf{Map}_{\boldsymbol{\xi}}(\xi_{n},x_{n})\) and \(\xi'_{n}\to\xi '\). We need to prove that ξ′∈Map ξ (ξ,x). For any n, define
Since
we have that d(K n ,K)→0, where K={(1−α)ξ+αδ x for some 0≤α≤1}.
Since \(\xi'_{n}\in K_{n}\), it follows that
which implies ξ′∈K, that is, ξ′=(1−α′)ξ+α′δ x for some α′∈[0,1].
By the definition of \(\xi_{n}'\), we have that \({I_{2,1}}(\xi_{n}') \geq{I_{2,1}} [(1-\alpha) \xi_{n} + \alpha\delta_{x_{n}}] \) for any α∈[0,1]. Letting n→∞, we get
Thus I 2,1(ξ′)≥max α∈[0,1] I 2,1[(1−α)ξ+αδ x ], and hence ξ′∈Map ξ (ξ,x). □
Corollary 2
The map Map 2 is closed.
Proof
By Lemmas 2 and 3, the maps  and
and  are closed. Since
are closed. Since  is compact, the composition of the closed point-to-set mappings
is compact, the composition of the closed point-to-set mappings

is closed (see Luenberger and Ye 2008, p. 205, Cor. 1). □
Proof of Theorem 1
From Lemma 1, Lemma 2 and Luenberger and Ye (2008, Cor. 2, p. 205), it follows that Alg KL is closed. Moreover, as a consequence of Theorem 1 of López-Fidalgo et al. (2007), it is simple to prove that I 2,1(ξ) is an ascent function for the set of KL-optimal designs and Alg KL . Finally, it is sufficient to apply the Global Convergence Theorem for ascendant algorithms in Luenberger and Ye (2008, p. 206). □
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this paper
Cite this paper
Aletti, G., May, C., Tommasi, C. (2013). A Convergent Algorithm for Finding KL-Optimum Designs and Related Properties. In: Ucinski, D., Atkinson, A., Patan, M. (eds) mODa 10 – Advances in Model-Oriented Design and Analysis. Contributions to Statistics. Springer, Heidelberg. https://doi.org/10.1007/978-3-319-00218-7_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-00218-7_1
Publisher Name: Springer, Heidelberg
Print ISBN: 978-3-319-00217-0
Online ISBN: 978-3-319-00218-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


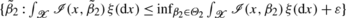 , for an arbitrary ε>0.
, for an arbitrary ε>0.