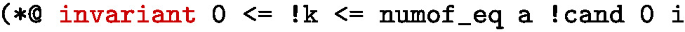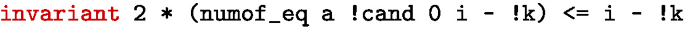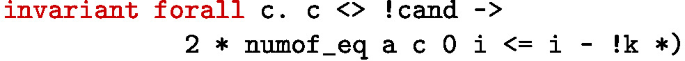Keywords

figure a
figure b

1 Introduction

Deductive software verification [11] is a subject within the larger field of formal methods [23]. One can define deductive software verification as the process of expressing the correctness of a program as a mathematical statement, then proving it. However, such a definition does not properly highlight the connection between the three main components in deductive verification: the logical specification, which mathematically captures what one wishes to compute; the code, which stands for how one materializes ideas as a piece of software; and, finally, a formal proof of why the code adheres to the given specification. This last component can be realized via a so-called Verification Conditions Generator, a mechanical tool that takes as input the code and the specification, producing the aforementioned correctness statement.

In this tutorial paper, we focus on the deductive verification of programs developed in the OCaml language. We use the Cameleer  [27] tool to verify, in a mostly-automated fashion, that an OCaml program adheres to its specification. One key aspect of our presentation is the use of GOSPEL  [8], the Generic OCaml SPEcification Language. This is a tool-agnostic language, which serves as a common ground for the different OCaml verification tools and techniques. One important feature of GOSPEL is that specifications are written in a subset of the OCaml language, plus quantifiers, making the adoption of formal methods even more appealing for the working OCaml programmer.

Throughout this tutorial, we harmoniously combine an algorithmic discovery journey with the art of deductive software verification. We believe verification tools and techniques are better presented through the lens of classical data structures and algorithms. We believe this hands-on, example-oriented approach is a more efficient and convincing way to justify the interest in using verification tools. In order to follow this tutorial, we only assume the reader to possess basic knowledge of functional programming (not necessarily in OCaml) and some knowledge of deductive verification, at least to the level of understanding function contracts, loop invariants, and proofs by induction.

This paper is organized as follows. Section 2 provides an overview of the GOSPEL language. Section 3 introduces the Cameleer tool, mainly using two examples of verified OCaml programs, the first being a pure implementation, the other featuring mutability. In Sect. 4, we take a more in-depth dive into the verification of functional programs. Section 5 extends our class of verified programs, incorporating some imperative traits of the OCaml language. We terminate with some related work (Sect. 6) and closing remarks and future perspectives (Sect. 7). All the software and proofs used in this paper are publicly available in a companion artifact [28], which also complements this paper with other case studies verified in Cameleer.

2 A Primer on GOSPEL

GOSPEL is a behavioral specification language for OCaml code. It is a contract-based, statically typed language, with a formal semantics defined by means of translation into Separation Logic [6, 30]. The term Generic comes from the fact that GOSPEL is not tied to any particular tool or analysis technique. In fact, nowadays, one can use GOSPEL to attach specifications to OCaml that are then analyzed using runtime assertion checking techniques [13], or formally verified using deductive verification tools [7, 27]. GOSPEL is inspired by other behavioral specification languages [15], such as JML [19] or Eiffel [22]. However, both JML and Eiffel require the specification to always be executable. This in not the case in GOSPEL. In this tutorial paper, we focus on the use of GOSPEL for deductive verification.

When compared to other specification languages based on Separation Logic, e.g., VeriFast [17], Viper [24], or Gillian [21], GOSPEL takes a different design choice: permission and separation conditions are implicitly associated with function arguments, which greatly improves conciseness over Separation Logic. We argue this is an important argument in favor of GOSPEL adoption by regular OCaml programmers, who are not necessarily proof experts. We believe it is of crucial importance to develop the languages and tools that bring practitioners into formal methods.

Fig. 1.
figure 1

GOSPEL-annotated Stack Interface.

Full size image

GOSPEL was initially designed as an interface behavioral specification language. The interface shown in Fig. 1 exemplifies the use of GOSPEL to specify an OCaml interface for a polymorphic stack data structure, independent of the underlying implementation (it could be, e.g., a linked-list, a ring buffer, etc.). GOSPEL specification is given within comments of the form (*@ ... *). We start by specifying that type t of stacks is described, at the logical level, via a model field named view. This field is of type ’a list (here, we use OCaml ’s immutable lists) and describes the sequence of elements contained in the data structure. There is, however, one important aspect about the use of view: it is declared as a field, which means one should expect in-place modifications to the stack. In other words, t represents an imperative data structure.

When it comes to attaching specification to functions, the first line in the GOSPEL comments names function arguments and its return value. To describe the behavior of a function, we mainly use three clauses: , to introduce a precondition; , to introduce a postcondition; and , which enumerates all the mutable fields changed during the call to a function. For instance, functions create and is_empty are simply annotated with postcondition s stating, respectively, that a fresh stack is created with no elements and, conversely, a stack is empty if it does not contain any element. Finally, functions push, pop, and transfer modify the contents of a stack via side-effects. The former inserts a new element to the top of the view model; the latter removes the top element, assuming as a precondition that the stack is not empty. The term represents the pre-state of model view, i.e., the value of this field at the moment the function is called.

Throughout this tutorial, we will use and discover GOSPEL features via OCaml examples formally verified using the Cameleer tool. However, we are not able to cover here all the relevant aspects of the language in full detail. For a more in-depth presentation of GOSPEL, we refer the reader to the original paper [8] and the user manualFootnote 1.

3 The Cameleer Verification Tool

Up until recently, programmers would face a difficult choice if they wished to produce verified OCaml code: either conduct automated proof, but entirely re-implement their code-bases in a proof-aware language, and then rely on code extraction; or verify actual OCaml code, but using an interactive proof assistant, with the burden of manual proofs. Cameleer offers a compromise between the two approaches: it is a tool for the deductive verification of OCaml-written programs, with a clear focus on proof automation. It aims to provide an easy to use framework for the specification and verification of OCaml code.

Fig. 2.
figure 2

Cameleer Architecture and verification pipeline, taken from [27].

Full size image

Figure 2 presents the verification pipeline of the tool. It takes as input an OCaml implementation file, annotated using GOSPEL, and translates it into an equivalent WhyML program, the programming and specification language of the Why3 framework [14]. Why3 is a tool-set for the deductive verification of software, oriented towards automated proof. A distinctive feature of Why3 is that it can interface with different off-the-shelf SMT solvers, which greatly increases proof automation.

With Cameleer, we put forward the vision of the specifying programmer: those who write the code, should also be able to specify it. But, we want to push this vision even further: those who write the code, should be able to specify it and formally verify it. Leveraging on the proof automation and tool-set offered by Why3, we believe Cameleer is a good candidate to fill this need in the working OCaml programmers community.

In this section, we introduce Cameleer via two examples of mechanically verified algorithms implemented in OCaml and specified in GOSPEL. The first one is a traditional merge operation over sorted lists. The second one is a linear-search operation on arrays, hence an imperative implementation, featuring some interesting constructions from the OCaml language. The two examples have a common point: both are written using functors, showing how Cameleer proofs can scale up to the level of modular algorithms and data structures.

Fig. 3.
figure 3

Type Equipped With a Total Preorder Relation.

Full size image

3.1 A Simple Functional Program the Merge Routine

Modular Definitions, Using Functors. The OCaml module system, in particular functors, offers flexible mechanisms to derive implementations that are agnostic to the actual representation of manipulated data types. Functors stand for modules that take other modules as parameters, similar to Scala traits. As an introductory example on the use of functors, consider the following implementation of a max function within functor Max:

figure h

The signature type PRE_ORD is given in Fig. 3. It introduces a type t together with a function leq, which establishes a total preorder on values of type t. The GOSPEL specification in this module type introduces a predicate le, which we assume it respects the three laws of a preorder: reflexivity, totality, and transitivity. Such laws are encoded as axioms, which stand for logical assumptions upon which one relies without actually providing them correct. Finally, the postcondition of program function leq states this is a decidable implementation of predicate le.

For the above implementation of max, we use the leq function provided in the functor argument E, to check whether function argument x is less or equal to y. This comparison is made with respect to the preorder relation induced by E. We can provide this implementation with suitable GOSPEL specification. This is as followsFootnote 2:

figure i

The first clause in the postcondition states that both x and y must be smaller than or equal to the returned value r, with respect to the preorder induced by predicate E.le. The second clause states that r must be either equal x or y, where (=) stands for polymorphic, potentially undecidable, logical equality.

OCaml Implementation. The merge sort algorithm gets its name from its main step: merging the elements of two sorted lists, producing a third sorted list. Here, our goal is to provide a merge implementation independently of the type of list elements. To do so, we introduce the following functor Merge:

figure j

The above merge definition is an efficient implementation of a merge routine, since it makes use of the tail-recursive, auxiliary function merge_aux. This function merges lists l1 and l2 into the accumulator acc. Since every new element is inserted to the head of acc, then in the base cases one must first reverse it and then concatenate the result with l, the suffix list of elements (either from l1 or l2) that remains to be enumerated. The OCaml standard library function rev_append efficiently implements this “reverse then concatenate” process. Finally, the main merge function calls merge_aux with the empty list as the initial value for the accumulator.

GOSPEL Specification.Let us now describe the specification of the merge_aux and merge functions. In order to specify that merge always returns a sorted list, we must first introduce what it means for a list to be sorted. We introduce the following GOSPEL predicate:

figure k

The empty or singleton lists of integers are always sorted. If the list has at least two elements, then the first must less than or equal to the second one and the suffix list y : : r must also be a sorted list. Since sorted_list is to be used within specifications, it must be a total (i.e., terminating) function. We supply the variant l, which represents a termination measure for every recursive call to the sorted_list predicate. A variant represents a quantity that always strictly decreases at every recursive call. In this case, we state that the argument of every recursive call is structurally smaller than the value of l at the entry point.

Note that the elements of the argument l are of type integer, the GOSPEL type for mathematical integers. When applying this function to a list of values of OCaml int type (63-bit machine integers), the GOSPEL and Cameleer tool-chains will apply a conversion mechanism from machine integers into their equivalent mathematical representation.

Using sorted_list predicate, we attach the following GOSPEL specification to the merge_aux function:

figure l

The precondition reads as follows: the acc list is sorted in reverse order, while l1 and l2 are sorted in natural order; every element from acc must be less or equal to any element from either l1 or l2. Finally, the postcondition simply asserts the returned list r is sorted and we prove termination using the lexicographic order on the pair l1, l2. In other words, if in a recursive call l1 structurally decreases, then the whole variant decreases; otherwise, when l1 does not decrease, then it must be the case that l2 decreases. Cameleer ships with a subset of the OCaml standard library specified using GOSPEL, hence one is able to use and reason about functions such as List.mem or List.rev.

Finally, the specification of merge is as follows:

figure m

If both l1 and l2 are sorted lists, then the call merge l1 l2 always produces a sorted list.

Fig. 4.
figure 4

Why3 Proof Session for the Merge Sort Routine.

Full size image

Cameleer Proof.Assuming the OCaml implementation and GOSPEL specification of the merge routine are contained in file merge.ml, one can start the verification process by typing the command cameleer merge.ml. This launches the interactive Why3 graphical user interface [10], as depicted in Fig. 4. On left-hand side, the Why3 IDE features a node for the generated verification conditions (VCs) of each top-level definition, together with any proof attempt on such VCs. Calling a SMT solver to prove a generated VC can be done by right-clicking a node and selecting the desired solver. A green button on the left of a node means that a solver was able to discharge the corresponding VC. This is the case of the sorted_list predicate and the merge function, for which Alt-Ergo is able to prove that both adhere to their specification, in less than a second. The proof time is shown on the right of the solver name, together with the number of conducted proof steps. One can also apply proof transformations on nodes, for instance to split a larger VC into its conjunctive clauses. This is done for the merge_aux definition. After split, one can focus on a specific part of the verification, such as proving a precondition, variant decrease, or postcondition. Moreover, each of these individual formulae is smaller and less involved than the original VC, hence more likely to be automatically discharged by an SMT solver.

On the right-hand side of the Why3 IDE, one can inspect the code under verification. On one hand, the green labels stand for the assumptions (flow of the execution and parts of the specification) made at some point of the verification process. On the other hand, the yellow labels mark what one is actually trying to verify. In this case, we are trying to discharge the first precondition of the merge_aux function, at the recursive call merge_aux (x : : acc) xs l2. We shall explain the Task tab in Sect. 3.2.

As shown in Fig. 4, we fail to prove that function merge_aux adheres to its GOSPEL specification. We are not able to verify every individual VC for this function, after split. The three used solvers, Alt-Ergo, CVC5, and Z3, all time-out after 1 s for every condition except that the supplied variant measure decreases. One could attempt to provide more time to each solver, to allow these tools to conduct more proof steps, hopefully leading to more VCS being discharged. However, in this case, we are actually missing some auxiliary lemmas about the sorted_list predicate. A lemma in GOSPEL represents a property that, once stated, can be explored by SMTs to discharge other VCs. However, contrarily to axioms, lemmas are not assumed: these must be proved correct at definition time.

To close the verification of the merge_aux function, we need two auxiliary lemmas: first, one that states we can insert a new value x as the head of a sorted list l if and only if x is less than or equal to every element in l. We introduce such a lemma in GOSPEL as follows:

figure n

Second, the concatenation l1 @ l2 of sorted lists l1 and l2 is a sorted list if and only if all the elements in l1 are less or equal than all the elements of l2. We provide the following GOSPEL lemma:

figure o

Using the given lemmas, the correctness proof for merge_aux now succeeds. Alt-Ergo is able to explore these auxiliary definitions to discharge all the remaining VCs. As for the proofs of the lemmas themselves, both require proofs by induction. We can conduct such proofs inside the Why3 IDE, using a dedicated transformation for induction over algebraic types (in this case lists). For a more complete presentation on how to use the Why3 IDE, including on how to apply different interactive proof transformations, we refer the reader to the framework user’s manual [2].

Fig. 5.
figure 5

Type Equipped With an Equality Relation.

Full size image

3.2 Searching an Element Within an Array

OCaml Implementation. We now make a shift from the purely functional world to present some OCaml imperative features, and showcase how one can use Cameleer to reason about such features. Consider the following modular implementation of a function that performs a linear search in an array:

figure p

Fig. 5 presents the definition of the signature type EQUAL. It declares a function eq that decides whether two values of type t are logically equal. This is exactly what is stated in the postcondition clause.

The definition of the find function presents some interesting OCaml imperative traits. On one hand, the use of a for loop to scan the array a; on the other hand, the declaration and use of the local exception Found. The latter is used to signal that the search succeeded, carrying the index of x within a. The use of local exceptions in OCaml is a convenient way to simulate the behavior of a return statement, commonly found in other languages. In fact, the whole loop is surrounded with a try..with block that ensures exception Found is always caught. Finally, to signal that x does not occur in a, we use the Not_found exception from the OCaml standard library. It is worth noting that we purposely let such an exception escape the scope of find.

Cameleer Proof. In order to prove the correctness of function find, one must supply a loop invariant. This is done in Cameleer as follows:

figure q

This invariant simply asserts that while in the loop, we know for sure x does not occur in the prefix of a that we have already scanned. The infix operator (<>) stands for logical inequality. As for the equality operator, (=), inequality is expressed using the same syntax in OCaml and in GOSPEL and both are built-in symbols of the GOSPEL language. We recall that, except for quantifiers and logical connectives, GOSPEL terms are a written in a subset of the OCaml language.

Now, we focus on providing a specification contract for function find. But first, it is crucial to distinguish the possible outcome behaviors of this function. On one hand, it returns normally whenever exception Found is raised; on the other hand, it raises the Not_found exception to abort execution. For the former, we shall establish a regular postcondition. For the latter, we shall introduce what is called an exceptional postcondition. We attach the following GOSPEL annotations to find:

figure r

The ensures clause is checked when find indeed returns an integer i, representing the (first) index of x in a. The raises clause states the logical property that holds when Not_found is raised. This stands for the case when we have scanned all the array a, finding no occurrence of x. We restrict the range of values that the universally quantified variable i can take, since GOSPEL establishes that undefined array indices are arbitrary values, not necessarily different from x.

For this program, Cameleer generates 6 VCs, after splitting the formula generated for the find function. All are immediately discharged by Alt-Ergo.

Fig. 6.
figure 6

Proof Task for an Incorrect Loop Invariant Initialization.

Full size image

Providing an Incorrect Loop Invariant. Let us take a step back in the verification process of the find implementation. Imagine a scenario where one would have, incorrectly, supplied the following loop invariant:

figure s

The only difference, when compared with the previously presented invariant, is that now the value of the universally quantified variable j can be equal to i, the loop index. Figure 6 shows that by feeding the new invariant to the Cameleer-Why3 pipeline, one is still able to prove the postcondition of find holds, but not the invariant initialization (i.e., the invariant holds before the first iteration), neither invariant preservation (i.e., assuming the invariant holds before an arbitrary iteration, it still holds after that iterations completes). To debug a failed proof attempt, the Why3 IDE allows the user to inspect the task [3], a representation of the formula that is sent to solvers. Under tab Task, such formula is displayed as a (i.e., what one is actually trying to prove) and the proof context (i.e., the hypotheses) above the dashed line.

Figure 6 depicts the task for the loop invariant initialization. After reading the task, we can conclude that hypotheses H1 and H2 imply that j is equal to 0. Hence, we are trying to prove a goal that asserts the actual first element in the array a is not x. There is nothing in our proof context that allows us to prove such a statement. This is an indication that either our context is not enough to discharge the goal (e.g., the specification is incomplete), or rather there is an actual bug in the specification or implementation. In this case, however, we already know the answer: changing the loop invariant to j < i would generate a task, for loop invariant initialization, with hypotheses 0 <= j and j < 0, hence the goal would hold vacuously. It is worth noting that tasks are written in the logical fragment of the WhyML language. This is the only point in the verification process that a Cameleer user must read a formula that is not written in GOSPEL. However, since GOSPEL and WhyML are syntactically very similar, we believe someone familiar with GOSPEL is able to read and understand a Why3 task.

4 Purely Functional Programming

We define purely functional programming as the approach to write a program where no mutable state is involved. Such a program is normally a collection of (recursive) functions that are composed with each other to perform some computation. The program also only employs data structures that do not require any memory manipulation, such as lists or trees. This style of programming is at the very essence of the OCaml language.

In this section, we use the Cameleer tool to conduct formal verification of a purely functional program that operates on trees. We present the OCaml implementation of such a program, annotated with suitable GOSPEL specifications. We interleave the presentation of code listings with explanations of the given implementation and specification. Hence, to ease readability, the example chunks that belong together are given running line numbers.

4.1 Same Fringe Comparing Two Binary Trees

Let us consider the following, very classic, programming challenge:

Write a function that, given two binary trees, decides whether the two trees present the same sequence of elements when traversed inorder.

This is known as the same fringe problem. One possible solution to this problem is as follows:

  1. 1.

    perform an inorder traversal on both trees, building the list of elements enumerated during such traversals;

  2. 2.

    compare, recursively, whether the two lists contain the same elements.

This is, however, a very naive approach, since it always builds the auxiliary lists for all the elements of both trees. Imagine the following scenario:

figure u

The two trees differ in the leftmost element, as we have x for the left-hand side tree, and y for the right-hand side tree. Following the solution proposed above, we would unnecessarily build two (huge) sequences. Note, however, that this implementation is easier to check for correctness than more efficient ones. Hence, this list-based approach can be used as a good specification for the solution we describe in the remaining of the section.

We propose to explore an approach that allows one to enumerate the elements of each tree, step-by-step. In such a way, we can stop as soon as two distinct elements are enumerated. If we complete the iteration process on both trees, then it must be the case the trees contain the same elements. This algorithm is implemented in OCaml and specified using GOSPEL as follows. First, we use the EQUAL signature from Fig. 5 to build a functor that implements same fringe. We start by defining the type of binary trees with elements of type E.t, as follows:

figure v

A tree is either Empty or a Node formed of two sub-trees and a root of type E.t.

Now, we define a logical function that implements an inorder traversal on a binary tree, returning the list of enumerated elements:

figure w

The traversal is implemented by: (i) traversing the whole left sub-tree; (ii) concatenating the resulting sequence of elements (the (@) operator represents list concatenation in OCaml) to x (the root) and the sequence of elements issued from the right sub-tree traversal. This is exactly the naive approach previously described. We shall only use the function elements for specification purposes.

In order to implement the step-by-step enumeration of elements in a tree, we use an explicit data representation of the call stack of the program that would construct the inoder list, so we can interrupt the traversal as soon as required. Such a representation is inspired by the zipper [16] structure.A zipper can be used as an efficient cursor into data structures, allowing one to arbitrarily traverse the structure, as well as to perform efficient local modifications (e.g., insertions or deletions) without the overhead of rebuilding the whole structure for each modification. In the case of the same fringe problem, we always traverse a tree towards its leftmost element, without performing any modifications to the structure. Hence, we specialize the zipper data type as follows:

figure x

A value of type zipper is a list, where each element is a pair composed of a tree element and the corresponding right sub-tree. We build such a list bottom-up, which represents the left spine of the tree that is still to be traversed. Together with the zipper data type, we introduce the following logical function to convert from a zipper to a list:

figure y

From a specification point of view, we have everything we need to tackle our verified implementation of the same fringe problem. We start by defining how to create a zipper from a tree. This is done as follows:

figure z

The specification of mk_zipper states that this is a terminating function, with argument t structurally decreasing at each recursive call. The functional behavior of this function is captured in the postcondition, where we state the sequence of elements of the resulting zipper is the same as the inorder sequence of elements from tree t, plus the elements of the accumulator e.

We now provide the actual, step-by-step, iteration on two zippers, as follows:

figure aa

This implementation distinguishes three cases:

  1. 1.

    If both zippers are empty, then we are sure to have enumerated the same sequence of elements.

  2. 2.

    If both zippers still have elements, then the next elements in the enumeration are the heads of both lists. We compare these and proceed recursively, only if the E.eq x1 x2 comparison holds.

  3. 3.

    Otherwise, if one of the zipper terminates before the other, then we are sure the enumerated sequences differ.

Very simply put, the postcondition of eq_zipper states that this function logically decides whether two zippers enumerate the same sequence of elements.

Finally, we provide the definition of the same_fringe function, which decides whether two binary trees present the same elements. This is as simple as

figure ab

From the postcondition of eq_zipper one can deduce that same_fringe will return the Boolean if and only if the two zippers passed as arguments represent the same sequence of elements. Since we use the empty list as the initial accumulator value for the creation of both zippers, then the postcondition of mk_zipper states the created zippers enumerate the exact same sequence of elements as those of trees t1 and t2, respectively. Hence, the postcondition of eq_zipper always holds.

Feeding our same fringe implementation to Cameleer generates 11 VCs, after splitting each top-level definition. These are discharged in roughly 1 s using a combination of the Alt-Ergo, Z3, and CVC5 SMT solvers. For reference, the complete OCaml implementation and GOSPEL specification for same fringe is given in the appendix of the extended version [29].

4.2 Summary

In this section, we used the same fringe example to motivate and showcase the use of Cameleer for the deductive verification of purely functional algorithms. Such functional implementations are closer to mathematical definitions, hence are normally easier to reason about. Other than the example presented in this section, Cameleer has been successfully used to prove the correctness of real-world functional OCaml data structures. We highlight the Set module from the OCaml standard library, and the Leftist Heap implementation issued from the widely used ocaml-containers libraryFootnote 3. Even if not presented in the body of this document, all such case studies are included in the companion artifact.

5 Imperative Programs

One important aspect of the OCaml language is the fact that it is a multi-paradigm language, combining functional with imperative and object-oriented programming. In this section, we use Cameleer to conduct the formal verification of an OCaml program that implements an historical algorithm using imperative features, namely loops, mutable references, and exceptions. As in Sect. 4, the main example code listings are presented using running line numbers.

5.1 Boyer-Moore MJRTY Algorithm

Let us, once again, use an algorithmic problem as the vehicle to showcase how to specify an OCaml program using GOSPEL, and how to prove it in Cameleer. Consider the following challenge:

Write a function that, given an array of votes, determines the candidate with the absolute majority, if any.

The more direct solution would take the following steps:

  1. 1.

    For a total of N candidates, we first allocate an array of integer values of length N that serves as an histogram.

  2. 2.

    We do a first pass over the array of votes, summing up in the histogram the number of votes for each candidate.

  3. 3.

    Finally, we iterate over the histogram to check if any of the candidates achieves majority.

This approach could certainly be implemented in OCaml and proved correct in Cameleer. It runs in \(\mathcal {O}(M + N)\) time (build the histogram, then iterate over it), where M is the number of votes . However, this approach allocates an extra memory space of N cells, i.e., the histogram. Here, we adopt a different solution, due to R. Boyer and J. Moore [4]. Such a solution uses at most 2M comparisons and constant extra space (other than the array of votes itself).

First, we build a functor parameterized with module type EQUAL from Fig. 5, so that we are able to compare candidates:

figure ad

We begin by declaring local exception Found, which we use to terminate the search and signal if some candidates reaches majority. We now introduce the only extra auxiliary references we need:

figure ae

The use of references cand and k is the actual core of the Boyer-Moore’s method.

We do a first traversal on the array of votes, updating cand and k accordingly:

figure af

Very briefly, the loop body does the following:

  • If the value stored in k is zero, then we change the candidate stored in cand to the i-th element of a and update k to one (lines 11 to 13);

  • If the i-th candidate in a is equal to the value stored in cand, then we increment reference k (line 14);

  • Otherwise, we decrement k (line 15).

So now, a crucial question arises: what are the invariants for this loop that allow verification to succeed? One crucial part of the process is to reason about “the number of votes for a certain candidate in a slice of the array”. To be able to express such notion in the specification, we declare the following GOSPEL function:

figure ag

This function represents the number of elements from a, within range \([\texttt{l}; \texttt{u})\), that are equal to value v. For now, we focus on using numof_eq to establish the loop invariants. Later in this section, we provide a proper definition for this function.

Let us a conduct a step-by-step analysis on how references cand and k are used together within the loop, as to derive the loop invariants. In fact, the invariants we present here are already given in Boyer and Moore’s original work [4], and we adapt those into GOSPEL:

  1. 1.

    The number of votes for candidate cand, within the array prefix already scanned, is at least k. We write this down in GOSPEL as follows:

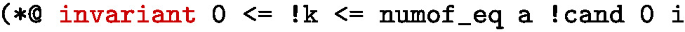
    figure ah

    This invariant is maintained by the case analysis implemented from line 11 to 15 in the code snippet above: we update the value of cand whenever !k reaches zero, hence !k never stores a negative number; we update the value stored in k, without changing the candidate, hence k is kept as a lower bound for the actual number of occurrences of !cand in the scanned part of the array. In other words, we are sure we only decrement k after a sufficient number of increments occurred (except if we decrement after reference cand is updated, but in this case k is update to one, hence an implicit increment has also occurred).

  2. 2.

    The actual number of votes for cand minus the value of k cannot exceed (i - !k)/2:

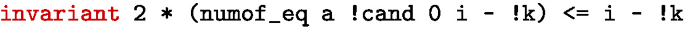
    figure ai

    Instead of a division, we write such an invariant using an equivalent multiplication. The reason is somehow low-level and tied to the upcoming verification effort: SMT solvers are known to handle multiplication better than division.

  3. 3.

    For every candidate c other than cand, the number of votes for c, within the scanned prefix of the array, cannot exceed (i - !k)/2:

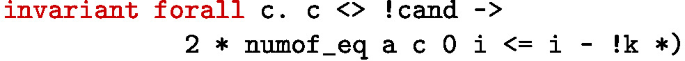
    figure aj

    This invariant implies that no other candidate, other than the one stored in cand, can have the majority of votes in the slice of the array already processed by the algorithm. Once again, we use a multiplication by two to avoid the division.

The last invariant actually allows one to deduce a crucial property: after scanning all the array, cand is the only candidate that can effectively reach majority.

After the loop, we immediately check whether we are in position to provide a final answer:

figure ak

If k stores zero, we are sure no candidate has reached majority. We use the OCaml standard library Not_found exception to signal such behavior. If the value stored in k is more than half of n, the size of the array, we are sure cand has reached majority. We use locally-defined exception Found to signal this behavior. If none of the above conditions is met, then we cannot give yet a definitive answer; we need an extra traversal over the array to check whether cand has the majority.

The final step of the implementation is a simple loop that counts the actual number of votes for cand. If, at some point in the traversal, the accumulated votes for cand are greater then half of n, we terminate signaling the majority of this candidate. We can then reuse reference k for the purpose of counting votes:

figure al

This loop invariant states that reference k stores the actual number of occurrences of cand and that, if we keep iterating, then it must be the case that the k does not yet represent the majority of votes. If we reach past the loop, then cand does not have the majority, neither does any other candidate. Once again, we use Not_found to signal such an outcome.

The final piece in our verified OCaml implementation of the Boyer-Moore algorithm is the actual specification for function mjrty. This is as follows:

figure am

As a precondition, we assume that the input array has at least one element. For the regular postcondition, i.e., the one reached by catching exception Found, we prove that the returned candidate indeed has the absolute majority of votes. Finally, in the exceptional postcondition (i.e., the one reached by raising exception Not_found), we prove that no candidate has enough votes to reach majority.

Definition of numof_eq Function. To conclude our proof of mjrty implementation, we must provide an actual definition for function numof_eq. We do so by means of an auxiliary function numof. This is defined, in GOSPEL, as follows:

figure an

The call numof p a b returns the number of integer values, within a certain range \([\texttt{a}; \texttt{b})\), that satisfy a given predicate p. We attach the variant b - a to the above definition, which allows us to prove this is a total function.

To define numof_eq, we specialize numof for arrays and an equality predicate:

figure ao

The use of the higher-order function numof leads to a concise and elegant definition for numof_eq. This is in an interesting application of functional programming concepts to derive sound, expressive, and yet intuitive specifications even in the presence of mutable data structures.

The right-to-left definition of numof is useful when it comes to proving the preservation of loop invariants where one is scanning an array from left to right. At the beginning of the i-th iteration, one assumes that numof p 0 i represents the number of elements, in the slice \([0; \texttt{i})\) of some array, that respect predicate p. At the end of the iteration, we must re-establish the invariant for the range \([0; \texttt{i}+1)\), i.e., numof p 0 (i + 1). If the i-th element respects predicate p, then we take the branch in the definition of numof; otherwise, we take the branch. In either cases, the invariant is re-established simply following the definition of numof, since the recursive call numof p 0 i is exactly what we assumed at the beginning of the iteration. This applies to the proof of invariant preservation for the loops in the mjrty function, where numof_eq a !cand 0 i is mapped into a call to .

Finally, we provide auxiliary lemmas about the behavior of the numof function that allows us to close the proof of the MJRTY algorithm. First, we establish the lower and upper bound for the result of numof. A call numof a b p, for any given integer values a and b and a predicate p, always returns a non-negative value and cannot exceed b - a. This is captured by the following lemma:

figure as

This lemma is proved interactively by induction on b, starting from a.

The next lemma states that a call to numof p a c can be written as the sum of calling numof in the range \([\texttt{a}; \texttt{b}[\) and calling numof in the range \([\texttt{b}; \texttt{c}[\), provided that \(\texttt{a} \le \texttt{b} \le \texttt{c}\). This is expressed as follows:

figure at

This lemma is proved by induction on c, starting from a.

The last two lemmas capture what happens in a single computation step of a call numof p l u, when l < u. On one hand, if value l respects predicate p, then we add 1 to the result of the recursive call numof p (l + 1) b:

figure au

On the other hand, if l does not respect p, then numof p a b is simply the result of the recursive call:

figure av

One can also think of these lemmas as establishing the equivalence between either counting the number of elements that satisfy a given predicate from left-to-right, or from right-to-left. Both lemmas are proved by instantiating lemma numof_append, where a is instantiated with l, b with l + 1, and c with u.

The Cameleer-Why3 pipeline generates a total of 25 VCs for function mjrty. These are discharged using a combination of the Alt-Ergo, Z3, and CVC5 solvers. The proof of the auxiliary lemmas is also carried in the Why3 IDE, using dedicated transformations for induction over integer numbers and instantiating other lemmas. For reference, the complete OCaml implementation, GOSPEL specification, and auxiliary definitions for the MJRTY algorithm are given in appendix [29].

5.2 Summary

In this section, we showed how to use the imperative traits of OCaml to write elegant and efficient code. Moreover, with Cameleer, we are still able to prove the correctness of such implementations. The gallery of Cameleer verified programs includes several examples of verified imperative implementations. From those, we highlight the verification of a Union Find data structure, encoded in an array of integer values. An important feature of this case study is the use of the decentralized invariants technique [12] to achieve a fully-automated proof.

6 Related Work

Deductive software verification is now a mature discipline that is taught, worldwide, in the vast majority of Computer Science curricula. However, a large corpus of pedagogical, practical, hands-on oriented bibliography is still missing. One can cite the recent book on Dafny [20] as valuable contribution to fill this gap. On the other end of the spectrum of verification tools, the book by Nipkow et al. [26] and the Software Foundations volumes 3 [1] and 6 [9] provide comprehensive collections of data structures and algorithms formally verified in proof assistants. The first is completely developed in Isabelle, the other two in Coq.

When it comes to deductive verification of programs written in functional languages, one can cite frameworks like Iris [18] and Hoare Type Theory [25]. These are built on Coq, on top of very rich reasoning logics based on Separation Logic. These can scale up to the verification of complex imperative and concurrent programs. However, proofs in such frameworks are conducted manually, requiring a high degree of human interaction and proof expertise. In the particular case of verification of OCaml programs, the CFML  [5] tool takes as input an OCaml program and translates it into a Coq term that captures the semantics of the program. The proof is then conducted using Separation Logic. CFML proofs are laborious and, in particular when compared with Cameleer, require extensive human interaction.

7 Conclusions and Future Perspectives

In this tutorial paper, we presented the deductive verification of different OCaml programs, ranging from purely functional implementations to code combining imperative features, such as mutable state and local exceptions. We use the Cameleer tool to conduct our practical experiments. This tool takes as input an actual OCaml implementation and translates it into an equivalent WhyML program, the language of the Why3 verification framework. Cameleer avoids the need to re-write entire OCaml code bases, just for sake of verification, as it would be the case with a direct use of Why3: one would have first to write a WhyML implementation and specification, then rely on an extraction mechanism to get an executable equivalent OCaml program. On the other hand, Cameleer is conceived with a clear focus towards proof automation, improving on the experience of entirely conducting manual proofs in an interactive proof assistant.

Throughout the paper, we use GOSPEL to attach formal specification to OCaml programs. Our experience suggests that this language is a good compromise when it comes to conciseness and readability of specifications, without sacrificing rigor. This is a major argument to bring even more OCaml programmers to adopt formal methods techniques in their daily routines. Finally, GOSPEL can be used not only for deductive verification but also for dynamically analyze OCaml code. As future work, it would be interesting to collaboratively use static and dynamic analysis techniques to tackle the verification of different parts of a big piece of OCaml software, resorting to GOSPEL as the aggregation entity.