Abstract
Switching controllers play a pivotal role in directing hybrid systems (HSs) towards the desired objective, embodying a “correct-by-construction” approach to HS design. Identifying these objectives is thus crucial for the synthesis of effective switching controllers. While most of existing works focus on safety and liveness, few of them consider timing constraints. In this paper, we delves into the synthesis of switching controllers for HSs that meet system objectives given by a fragment of STL, which essentially corresponds to a reach-avoid problem with timing constraints. Our approach involves iteratively computing the state sets that can be driven to satisfy the reach-avoid specification with timing constraints. This technique supports to create switching controllers for both constant and non-constant HSs. We validate our method’s soundness, and confirm its relative completeness for a certain subclass of HSs. Experiment results affirms the efficacy of our approach.
This work has been partially funded by the NSFC under grant No. 62192732 and 62032024, by the National Key R&D Program of China under grant No. 2022YFA1005101, by the CAS Project for Young Scientists in Basic Research under grant No. YSBR-040.
You have full access to this open access chapter, Download conference paper PDF
Keywords

1 Introduction
Hybrid systems (HSs) provide a robust mathematical specification in modeling cyber-physical systems (CPS) with their unique fusion of continuous physical dynamics and discrete switching behaviors. Many CPSs are often complex and safety-critical which necessitates intricate control specifications. Switching controller synthesis offers a formal guarantee of the given specification of HS. Its applications include attitude control in aerospace [3], aircraft collision-avoidance protocols in avionics [43], and pacemakers for treating bradycardia [53], etc.
With the escalating complexity of CPSs [44, 45, 54], the specifications required to ensure their proper functionality grow increasingly intricate. Among these, the importance of timing constraints becomes paramount [48, 49]. This is evident in various scenarios, from orchestrating synchronized reactions in chemical processing [12] to ensuring seamless operations in multi-robot systems [24]. In this context, Signal Temporal Logic (STL), a rigorous formalism for defining linear-time properties of continuous signals [27], is exceptionally well-suited for specifying intricate timing constraints and qualitative properties of CPSs.
However, switching controller synthesis for HSs against STL specifications is not well addressed in the literature. The primary challenge arises from the complex interactions between continuous behaviors and discrete transitions. A common technique to synthesize switching controllers for HSs with complex specifications is the abstraction-based method [26, 28]. This technique involves abstracting the continuous state space of each mode into a finite set of states, which often results in the loss of precise timing information for each mode. Consequently, the abstraction-based technique struggles with timing constraint analysis in the abstracted state space. In contrast, Mixed Integer Linear Programming (MILP) based technique [34] for switching controller synthesis against STL specification can provide precise timing information, but this method faces challenges in handling the intricate interactions of diverse discrete transitions between modes.
In this paper, we considered the switching controller synthesis problem for HSs against a fragment of STL specification, which essentially corresponds to a reach-avoid problem with timing constraints. To the best of our knowledge, this is the first work that uses STL to specify HSs with both discrete transitions and continuous dynamics. Similar work in [39] focused only on HSs with discrete time dynamics in each mode, significantly simplifying the problem. The key idea behind our approach involves iteratively computing a sequence of state-time sets (x, t), state x and time t. These sets ensure that an HS, starting from state x at time t, adheres to the STL specification within a certain number (i.e., the number of iterations) of switches. The state-time sets are computed explicitly when the dynamics of the HSs are constant, and are inner-approximated when the dynamics are non-constant. Based on the state-time sets, we propose a sound and relatively complete method to synthesize a switching controller that satisfies the STL specification. Our experimental results demonstrate the efficacy of this approach.
The main contributions can be summarized as follows: (i) We conceptualize state-time set for HSs. (ii) We propose a methodology to synthesize switching controllers for HSs against a fragment of STL specification. (iii) We develop a prototype to demonstrate the efficiency and practical applicability of our methodology.
Organization. Section 2 gives an overview of our approach, Sect. 3 provides a recap of important preliminaries and formally defines the problem. We illustrate the calculation of the state-time sets in Sect. 4. Based on the state-time sets, Sect. 5 shows how to derive switching systems against a STL specification. In Sect. 6, we demonstrate the efficacy of our method through several examples. We discuss related work in Sect. 7 and draw conclusion in Sect. 8.
Due to space restrictions, proofs and benchmark details have been omitted, which can be found in an extended version of this paper [40]. Source code and examples of this paper can be found at Figshare: https://doi.org/10.6084/m9.figshare.26057410.v1.
2 An Illustrative Prelude
Example 1
In the reactor system depicted in Fig. 2, liquid is continuously consumed by the reaction and is replenished through pipe P. The system alternates
between modes of adding liquid (\(\boldsymbol{q_1}\)) and exclusively consuming it (\(\boldsymbol{q_2}\)). The objectives are to keep the liquid level, h, between 0 and 4 meters, and to ensure that h remains between 3 and 5 meters at a certain point during a critical reaction phase - time interval 3 to 4, for proper interaction with the reactor rod R. These objectives can be given as an STL formula
 . \(\lhd \)
. \(\lhd \)
We present the core idea behind our approach in Fig. 1. Initially, we compute the state-time set \(X_q^i\) iteratively. As shown in the upper block of Fig. 1, the set \(X_q^i\) encompasses states in mode q from which \(\varphi \) can be satisfied within i switches (as detailed in Sect. 5). Once these state-time sets are determined, the switching controllers can be synthesized using the methods outlined in Alg. 1 and Alg. 2.
3 Notations and Problem Formulation
Notations. Let \(\mathbb {N},\mathbb {R},\) and \(\mathbb {R}_{\ge 0} \) denote the set of natural, real, and non-negative real numbers, respectively. Given vector \(x \in \mathbb {R}^n \), \(x_i\) refers to its i-th component, and \(p\,[x\!=\!u ]\) denotes the replacement of x by u for any predicate p where x serves as a variable.
Differential Dynamics. We consider a class of dynamical systems featuring differential dynamics governed by ordinary differential equations (ODEs) of the form \(\dot{\boldsymbol{x}} = f(\boldsymbol{x})\), where f is a continuous differentiable function. Given an initial state \(x_0\in \mathbb {R}^n \), there exist a unique solution \(\boldsymbol{x}:\mathbb {R} _{\ge 0} \rightarrow \mathbb {R}^n \) in the sense that \(\dot{\boldsymbol{x}}(t) = f(\boldsymbol{x} (t))\) for \(t\ge 0\) and \(\boldsymbol{x} (0) = x_0\).
Switched Systems. A switched system is defined as a tuple \(\varPhi = (Q, F, \texttt{Init}, \pi )\), where
-
\(Q \triangleq \{\,q_1, q_2,\dots , q_m\,\}\) is a finite set of discrete modes.
-
\(F \triangleq \{\, f_q\mid q\in Q\,\}\) is a set of vector fields, and each mode \(q\in Q\) endows with a unique vector field \(f_q\) which specifies how system evolves in mode q.
-
\(\texttt{Init} \subseteq \mathbb {R}^n \) is a set of initial states.
-
\(\pi :\texttt{Init} \rightarrow (\mathbb {R} _{\ge 0} \rightarrow Q)\) is a switching controller. The controller maps each initial state \(x_0\in \texttt{Init} \) to a piecewise constant function \(\pi (x_0)\), which in turn maps a time t to the corresponding control mode \(\pi (x_0)(t)\).
Given any initial state \(x_0\), the dynamics of the switched system \(\varPhi \) is governed by equation \( \dot{\boldsymbol{x}} (t) = f_{\pi (x_0)(t)}(\boldsymbol{x} (t))\) with initial condition \(\boldsymbol{x} (0) = x_0\).
Signal Temporal Reach-Avoid. We consider a fragment of signal temporal logic, namely signal temporal reach-avoid formula (ST-RA for short). The syntax of ST-RA is defined by
where \(\phi \) is a Boolean combination of predicates over x and time t, \(I \triangleq [l,u]\) is a closed time interval for some \(0\le l\le u\). Intuitively, an ST-RA formula \(\varphi \) expresses the requirement that the system should reach \(\phi _2\) while avoid leaving \(\phi _1\) within time frame I. The semantics of ST-RA formula, in alignment with STL, is defined as the satisfaction of a formula \(\varphi \) with respect to a signal \(\boldsymbol{x} \) and a time instant t.
Remark 1
Compared with the standard signal temporal logic (STL) [27], ST-RA formula does not allow nested “until” operator, this makes ST-RA formula a fragment of STL.
Formally, given function \(\boldsymbol{x} :\mathbb {R} _{\ge 0}\rightarrow \mathbb {R}^n \) (termed signal) and time \(\tau \), the satisfaction of \(\varphi \) at \((\boldsymbol{x}, \tau )\), denoted by \((\boldsymbol{x},\tau ) \models \varphi \), is inductively defined as follows:

Intuitively, the subscript I in the until operator \(\mathcal {U}_I\) defines the timing constraints under which a signal must reach \(\phi _2\) while avoid leaving \(\phi _1\).
Given a ST-RA formula \(\phi \), we say a switched system \(\varPhi = (Q,F, \texttt{Init}, \pi )\) models \(\varphi \), denoted by \(\varPhi \models \varphi \), if \((\boldsymbol{x}, 0) \models \varphi \) for any trajectory \(\boldsymbol{x} \) starting from initial set \(\texttt{Init} \). We now formulate the problem addressed in this paper.
Problem Formulation. Suppose there exists a finite set of control modes \(Q = \{\, q_1, q_2, \dots , q_m\,\}\) and associated vector fields \(F = \{\, f_{q_1}, f_{q_2}, \dots , f_{q_m}\,\}\). Each mode \(q\in Q\) is associated with a vector field \(f_q\) that governs the system’s behavior in mode q. Let \(\varphi = \phi _1 \,\mathcal {U}_I\,\phi _2\) be an ST-RA formula, a natural question is how to design a system that incorporates mode \(q\in Q\) as subsystems, while ensuring any trajectory of the system satisfies \(\varphi \). To address this, we formulate the problem as follows.

Remark 2
The solutions to the above synthesis problem is inherently non-unique and may encompass trivialities, such as the one only with an empty initial set. Therefore, our goal is to identify a system with a nontrivial initial set \(\texttt{Init} \).
4 State-Time Set and Its Calculation
This section dedicates to synthesize a switched system \(\varPhi \) that satisfies the given ST-RA formula \(\varphi = \phi _1\, \mathcal {U}_I\, \phi _2\). The key idea behind our approach is to compute a sequence of state-time sets \(\{X_q^i\}_{q\in Q}\) for \(i\in \mathbb {N}\), where \(X_q^i\) denotes the set of all \((x,\tau )\) such that starting from x at time \(\tau \) in mode q, the system can be driven to reach \(\phi _2\) while satisfying \(\phi _1\) within i times of switches. In what follows, we first formally propose the concept of state-time sets and show how to calculate it explicitly. Subsequently, leveraging these state-time sets, we demonstrate the synthesis of a switched system that satisfies \(\varphi \) in Sect. 5.
4.1 State-Time Sets
The concept of state-time set is formally summarised by the following definition.
Definition 1
(State-time Sets). For any \(i\in \mathbb {N} \) and any \(q\in Q\), let \(X_q^i\) denote the set of all state-time pairs \((x,\tau )\) such that there exists a controller \(\pi (x) :[\tau ,\infty )\rightarrow Q\), satisfying
-
(i)
\(\pi (x)(\tau ) = q\), and the piecewise constant function \(\pi (x)\) contains at most i discontinuous points;
-
(ii)
 , where \(\boldsymbol{x} \) is the solution of ODE \(\dot{\boldsymbol{x}}(t) = f_{\pi (x)(t) } (\boldsymbol{x} (t), t) \) over \([\tau ,\infty )\) with \(\boldsymbol{x} (\tau ) = x\), and
, where \(\boldsymbol{x} \) is the solution of ODE \(\dot{\boldsymbol{x}}(t) = f_{\pi (x)(t) } (\boldsymbol{x} (t), t) \) over \([\tau ,\infty )\) with \(\boldsymbol{x} (\tau ) = x\), and
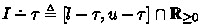 for any interval \(I = [l,u]\).
for any interval \(I = [l,u]\).
Intuitively, condition (ii) suggests that the system can be driven to reach \(\phi _2\) while satisfying \(\phi _1\) from x at time \(\tau \), and condition (i) indicates that the system initially remains in mode q, and the switching controller undergoes no more than i switches. From the above definition of state-time sets, the following results can be derived:
Corollary 1
The following properties hold for the state-time sets \(\{X_q^i\}_{q\in Q}\):
-
1.
For any \(q\in Q\), \(\{X_q^i\}\) is monotonically increasing, i.e. \(X_q^0 \subseteq X_q^1 \subseteq X_q^2 \subseteq \cdots \).
-
2.
For any \(i\in \mathbb {N} \) and any \(x \in X_q^i [t \!=\!0]\), x can be driven to satisfy
 , i.e. there exists a switching controller \(\pi \), such that
, i.e. there exists a switching controller \(\pi \), such that
 , where \(\boldsymbol{x} \) is the trajectory starting from x at time 0 under controller \(\pi \), and \(X_i^q [t \!=\!0] \triangleq \{x \mid (x,0)\in X_i^q\}\) is the projection of \(X_i^q\) into \(t = 0\).
, where \(\boldsymbol{x} \) is the trajectory starting from x at time 0 under controller \(\pi \), and \(X_i^q [t \!=\!0] \triangleq \{x \mid (x,0)\in X_i^q\}\) is the projection of \(X_i^q\) into \(t = 0\). -
3.
\(\displaystyle \cup _{i\in \mathbb {N}} \cup _{q\in Q} X_q^i[t\!=\!0]\) is the set of all states that can be driven to satisfy
 .
.
According to Cor. 1, the state-time sets encompass the initial set of the switched system that we intend to synthesize. However, the state-time set and controller defined in Def. 1 are not given explicitly. To address this, we first elucidate the process of calculating the state-time sets.
The subsequent result establishes a relationship between the sets \(\{X_q^i\}_{q\in Q}\) and \(\{X_{q}^{i-1}\}_{q\in Q}\), forming the foundation for the inductive computation of state-time sets.
Theorem 1
Follow the notations as before, we haveFootnote 1
-
1.
Given any \(q\in Q\), \((x,\tau )\in X_q^0\) if and only if
$$\begin{aligned} (\boldsymbol{x}, \tau ) \models \phi _1\, \mathcal {U}\, (\phi _2\wedge (t\in I)) \end{aligned}$$(1)where \(\boldsymbol{x} \) is the solution of ODE \(\dot{\boldsymbol{x}}(t) = f_{q } (\boldsymbol{x} (t), t) \) over \([\tau ,\infty )\) with \(\boldsymbol{x} (\tau ) = x\).
-
2.
Given any \(q\in Q\), for any \(i\ge 1\), \((x,\tau )\in X_{q}^i\) if and only if
$$\begin{aligned} \exists q'\ne q\in Q, \;(\boldsymbol{x},\tau ) \models \phi _1\, \mathcal {U}\, X_{q'}^{i-1} \end{aligned}$$(2)where \(\boldsymbol{x} \) is the solution of ODE \(\dot{\boldsymbol{x}}(t) = f_{q } (\boldsymbol{x} (t), t) \) over \([\tau ,\infty )\) with \(\boldsymbol{x} (\tau ) = x\).
For any formula \(\psi (u,v)\), let \(\texttt{QE} \left( \exists u,\, \psi (u,v)\right) \triangleq \{ v\mid \exists u,\, \text {s.t. } \psi (u, v)\text { holds} \} \) denote the set of all v for which \(\exists u,\, \psi (u,v)\) is true. Utilizing this notation, the state-time sets can be represented inductively.
Theorem 2
For any \(q\in Q\), suppose the solution of ODE \( \dot{\boldsymbol{x}}(t) = f_q (\boldsymbol{x} (t)) \) with initial x at time \(\tau \) is denoted by \(\varPsi (\,\cdot \, ; x, \tau , q)\), then the state-time sets can be inductively represented by
for any \(q\in Q\) and any \(i\in \mathbb {N} \).
Remark 3
When \(\psi (u,v)\) consists of a Boolean combination of polynomial inequalities, a decidable procedure, such as cylindrical algebraic decomposition [2], exists for computing \(\texttt{QE} \left( \exists u,\, \psi (u,v)\right) \). This procedure exhibits a complexity that is double exponential with respect to the number of variables involved.
Remark 4
Our methodology essentially shares the idea of backward induction in controller synthesis for timed games [9]. However, our approach diverges in two key aspects: (1) the safety/target sets and timing constraints are intricately interwoven in ST-RA formula, necessitating their concurrent consideration at each step of the induction process; (2) our method operates within an infinite-dimensional space due to the continuous nature of the state space, in contrast to the backward induction for timed games, which is confined to a finite set of k-polyhedra.
4.2 Computing/Approximating State-Time Sets
Although Thm. 2 offers an inductive representation of \(X_q^i\), the explicit computation of Eqs. (3) and (4) are challenging. This difficulty arises from two main factors: (i) the necessity to explicitly solve the ordinary differential equation in each mode, and (ii) the high complexity of \(\texttt{QE} \), and the potential inclusion of non-elementary functions (such as exponential functions) in Eqs. (3) and (4), for which a generally decidable procedure to solve \(\texttt{QE} \) may not exist.
To address the difficulties outlined above, we categorize the dynamics into constant and non-constant systems. For the constant dynamics, its solution can be directly computed, and there exists a decidable procedure to solve \(\texttt{QE} \) with a complexity polynomially dependent on the formula length. For the non-constant dynamics, due to their high complexity, we forego an explicit solution for the state-time set and instead demonstrate a method to approximate this set.
Constant Dynamics. Suppose the dynamics within each mode \(q \in Q\) is constant, and both \(\phi _1\) and \(\phi _2\) are Boolean combinations of linear inequalities, Eqs. (3) and (4) can be effectively solved using readily available solvers, such as Z3 [10]. Thm. 2 directly implies the following result.
Corollary 2
Following the notations as before, suppose the dynamics within each mode is constant, i.e. \(f_q = a_q\) for any \(q\in Q\), and both \(\phi _1\) and \(\phi _2\) are Boolean combinations of linear inequalities, then \(\{X_q^i\}_{q\in Q}\) can be inductively solved by Eqs. (3) and (4) with \( \varPsi (t; x, \tau , q) = x + (t-\tau )\cdot a_q\).
Remark 5
Although \(\texttt{QE} \) on polynomial constraints is double-exponential in general [2], constant dynamics facilitate a relatively efficient (polynomial in formula length) solving procedure. This comes from the following observation: (1) the \(\texttt{QE} \) procedure in Eqs. (3) and (4) operates in polynomial time when the constraints are linear and involve only a single existential and a single universal variable [46, Thm 6.2]. (2) if \(X_{q}^{i-1}\) is linear for all \(q\in Q\), then \(X_{q}^i\) is also linear.
We now illustrate the computation process of \(X_q^i\) via the following example.
Example 2
Let’s reconsider the reactor system in Exmp. 1. The reactor system consists of two modes \(q_1\) and \(q_2\) with \(f_{q_1} = 1\), \(f_{q_2} = -1\), and the liquid level requirement is
 .
.
The state-time sets calculation of the reactor system in Exmp. 1. The state-time sets reach a fixpoint after 2 iteration.
Based on Eqs. (3) and (4), the state-time sets we calculate are illustrated in Fig. 3. The procedure reaches a fixpoint within 2 iterations for any \(q\in Q\). \(\lhd \)
Non-constant Dynamics. Assuming that the dynamics are non-constant, the exact computation of Eqs. (3) and (4) may prove to be overly complex or potentially undecidable. We thus seek to inner-approximate the state-time sets. According to Thm. 1,
-
\(X_q^0\) is the set from which the system in mode q will satisfy \(\phi _1\, \mathcal {U}\, (\phi _2\wedge (t\in I))\);
-
\(X_q^i\) is the set from which the system in mode q will satisfy \(\phi _1\, \mathcal {U}\, X_{q'}^{i-1}\) for some \(q'\in Q\).
We identify that the crucial element for inner-approximating the state-time sets lies in employing a method that finds sets from which the system will satisfy a classical ‘until’ or ‘reach-avoid’ formulaFootnote 2. Numerous studies have explored this issue; in this paper, we employ the approach proposed in [52].
Theorem 3
(Inner-approximation of Reach-avoid Set [52]). Given dynamic system
 , safety set \(\psi _1 \subseteq \mathbb {R}^n \) and target set \( \psi _2 \subseteq \mathbb {R}^n \). If there exists continuously differentiable function \(v(x):\overline{\psi _1}\rightarrow \mathbb {R} \) and \(w(x):\overline{\psi _1} \rightarrow \mathbb {R} \), satisfyingFootnote 3
, safety set \(\psi _1 \subseteq \mathbb {R}^n \) and target set \( \psi _2 \subseteq \mathbb {R}^n \). If there exists continuously differentiable function \(v(x):\overline{\psi _1}\rightarrow \mathbb {R} \) and \(w(x):\overline{\psi _1} \rightarrow \mathbb {R} \), satisfyingFootnote 3
then any trajectory starting from \(\{x\mid v(x)\ge 0\}\) satisfies formula \(\psi _1\, \mathcal {U}\,\psi _2\).
Remark 6
The synthesis of function v(x) and w(x) can be reduce to a SDP problem. For a detailed formulation, we refer the reader to [52].
Since the state-time sets \(X_q^{i}\) depend on both the state x and time t, we first lift the dynamics of each mode to a higher dimension that incorporates time t. Specifically, the dynamics in mode q are transformed into \(\left( \dot{x}, \dot{t}\right) = (f_q,1)\). Subsequently, employing Thms. 3 and 1, we can inductively inner-approximate the state-time set \(X_q^i\). The resulting approximation is denoted by \(\widetilde{X_q^i}\).
Example 3
Consider a temperature control system featuring two modes, \(q_1\) and \(q_2\), with dynamics given by \(f_{q_1} = 20 - 0.2x - 0.001x^2\) and \(f_{q_2} = -0.2x - 0.001x^2\),
where x represents the temperature. The control objective is defined by the ST-RA formula
 .
.
Figure 4 presents the result obtained by inner-approximatingFootnote 4 \(X_{q_1}^0\), \(X_{q_2}^0\), \(X_{q_1}^1\), and \(X_{q_2}^0\). Based on the results, we observe that when x is within the range of [20, 80] in mode \(q_1\), the system can satisfy \(\varphi \) without any switching. However, for \(x\in [20, 80]\) in mode \(q_2\), at least one switch is necessary for \(\varphi \) to be satisfied. \(\lhd \)
5 Synthesizing Switched Systems
In this section, we demonstrate the synthesis of a switched system \(\varPhi \) that conforms to the formula \(\varphi = \phi _1, \mathcal {U}_I, \phi _2\). This synthesis builds on the state-time sets introduced in Sect. 4. We initially outline the synthesis procedure for the switched system in Alg. 1 and subsequently describe the extraction of a switching controller in Alg. 2.
Switched System Synthesis. We now summary the synthesis algorithm in Alg. 1. Given any \(k\in \mathbb {N} \) that serves as a prescribed upper bound of switching time, Alg. 1 inductively calculates/inner-approximatesFootnote 5 state-time sets \(\{X_q^i\}_{q\in Q}\) (line 3, 8), and partition \(X_q^k[t\!=\!0]\) into \(\texttt{Init} (q)^i \triangleq (X_q^i \setminus X_q^{i-1})[t\!=\!0]\) (line 3, 8) for \(i = 0,1, \dots , k\). \(\texttt{Init} (q)^i\) denote the set of states (in mode q) that can be driven to satisfy \(\varphi \) with at least i times of switching (cf. Cor. 1). The initial set is defined by
which contains states that can be driven to satisfy \(\varphi \) within k times of switching, and the switching controller \(\pi \) is synthesized by Alg. 2 (line 12).
Switching Controller Synthesis. For any \(x_0\in \texttt{Init} \), Alg. 2 computes the controller that drives \(x_0\) to satisfy \(\varphi \). Alg. 2 first finds \(\texttt{Init}(q_0) ^l\) that contains \(x_0\) with l be the smallest index (line 1). l is the smallest switching time that can drive \(x_0\) to satisfy \(\varphi \), and the subscript \(q_0\) indicates \(x_0\) first lies in mode \(q_0\).
Line 4–10 find the next switching time and switching mode. Let \(\texttt{Reach} (t; x_0, t_0, q)\) denote the over-approximation of the reachable set starting from \((x_0, t_0)\) in mode q at time t. Next switching time \(\widetilde{t}\) and switching mode \(\widetilde{q}\) are chosen to ensure that the system enters \(X_{\widetilde{q}}^{l-j}\) at time \(\widetilde{t}\) in mode \(q_{j-1}\), this is formally encoded by
In line 12, the controller \(\pi \) maps \(x_0\) to a piecewise constant function \(\pi (x_0) = (q_0,t_0)(q_1,t_1)\cdots (q_l,t_l) \), which represents a function that maps t to \(q_i\) if \(t_{i} \le t < t_{i+1}\).
Remark 7
Numerous methods are available to estimate the reachable set of a dynamic system [6, 50, 51]. In this paper, we employ Flow* [7], a method based on Taylor model, to over-approximate the reachable set.
Remark 8
Assuming that the dynamics (i.e. \(f_q\)) within each mode remain constant, the reachable set can be explicitly calculated. This, in conjunction with the explicit calculation of state-time sets, is crucial for demonstrating relative completeness in the context of constant dynamics (c.f. Thm. 4).
Remark 9
For non-constant dynamics, since the state-time sets and reachable sets are inner- and over-approximated, there may exist an initial state \(x_0\) that can be driven to satisfy the ST-RA formula, while our method fails to identify a controller.
We now illustrate our approach through two examples.
Example 4
In Exmp. 2, we have obtained the state-time sets \(\{X_{q_1}^i,X_{q_2}^i\}\) for \(i \le 2\), thus, according to Alg. 1 (with \(k=2\)), we have
Based on these sets, we can synthesize a switched system \(\varPhi \) with \(\texttt{Init} = \{h \mid 0\le h\le 4\}\). The corresponding switching controller \(\pi \) is defined by
\(\lhd \)
Switching controller synthesis of Exmp. 3
Example 5. Let’s reconsider Exmp. 3, we demonstrate our approach by synthesizing the switching controller for initial state \(x_0=80\) in mode \(q_2\). The reachable set \(\texttt{Reach} (t;x_0,t_0,q_2)\) is represented by green boxes in Fig. 5. We observe the reachable set will enter \(X_{q_1}^0\) for any \(t\in [0,2]\), this implies initial state \(x_0=80\) in mode \(q_2\) can be driven to satisfy \(\varphi \) if the system switches into mode \(q_1\) within time interval [0, 2], i.e. \(\pi (80) = (q_2,0) (q_1,\widetilde{t})\) for any \(\widetilde{t} \in [0,2]\). \(\lhd \)
The following result states the advantages of our approach.
Theorem 4
(Soundness, Relative Completeness, Minimal Switching Property). Given modes Q, vector fields F, and formula \(\varphi =\phi _1\,\mathcal {U}_I\, \phi _2\), the following results hold:
-
1.
Alg. 1 is sound, that is \(\varPhi \models \varphi \);
-
2.
Alg. 1 is relatively complete for constant dynamics: for any \(x\in \mathbb {R}^n \), if x can be driven to satisfy \(\varphi \) with some controller \(\pi \), then there exists \(k \in \mathbb {N} \)Footnote 6, such that the initial set of the synthesized switched system contains x.
-
3.
The controller synthesized in Alg. 2 features minimal switching property for constant dynamics: for any \(x_0\in \texttt{Init} \), there does not exists any controller \(\pi '\), that can drive \(x_0\) to satisfy \(\varphi \) with switching time (equivalently, number of discontinuous points of \(\pi '(x_0)\)) less than \(\pi (x_0)\).
Remark 10
Suppose the dynamic in each mode can be explicitly solved and there exists a decidable procedure for solving \(\texttt{QE} (\cdot )\) in Eqs. (3) and (4), then Alg. 1 is also relatively complete and the corresponding controller also features minimal switching property.
6 Experimental Evaluation
We develop a prototype of our synthesis method in Python, employing the Z3 solver [10] to explicitly compute the state-time sets for HSs with constant dynamicsFootnote 7. For HSs with linear or polynomial dynamics, we use the semidefinite programming solver MOSEK [30] to approximate the state-time set. The prototype is evaluated on various benchmark examples using a laptop with a 3.49 GHz Apple M2 processor, 8 GB RAM, and macOS 14.3.
As shown in Table 1, our experiments involve five distinct models, with three exhibiting constant dynamics and two exhibiting non-constant dynamics. We adjust the model scale or the ST-RA formula for each model to assess the efficacy of our method under varying conditions. And there are 15 different benchmarks in total included in our study. Table 2 details the empirical results of the benchmarks. In each case, the synthesis process continues iterating until either a fixpoint is achieved or the maximum calculation time of 5 min is met.
Our empirical results illustrate that our method is capable of effectively synthesizing controllers for models with both constant and non-constant dynamics. Notably, for models with constant dynamics, the iterative process tends to converge to a fixpoint, meaning that a complete controller is achieved. Moreover, the synthesis time for these controllers is significantly influenced by both the scale of the model and the complexity of ST-RA formulas. Specially, our analysis reveals: (i) an increased number of modes (Reactor) or a higher state dimension (CarSeq) both lead to prolonged synthesis times, (ii) more intricate predicates or larger future-reach timeFootnote 8 (WaterTank) results in increased synthesis times. For the third benchmark within CarSeq, the model does not reach a fixpoint, primarily because the large model scale rapidly increase the formula size, posing substantial challenges for the Z3 solver.
When dealing with non-constant dynamics, an approximation method is applied, thereby a fixpoint might not be achievable. The influence of model scale on synthesis time remains consistent with that observed in constant ODE models, as evidenced in Oscillator. Interestingly, the synthesis time for controllers using approximation methods is less affected by the complexity of the ST-RA formula. For example, in Temperature, despite \(\varphi _3\) being more complex than \(\varphi _2\), it requires less synthesis time, primarily because the complexity of SDP is influenced more by state space dimensions than by constraints.
Overall, our method exhibits a high capability in synthesizing switching controller for HSs with various dynamics. It can achieve sound and complete results for constant dynamics within a reasonable time. For more general dynamics, our method can still synthesize a sound result in a reasonable time.
7 Related Work
HSs have been a key research focus in the academic community [47]. The autonomous verification and synthesis of HSs began from timed automata [1]. Subsequently, various mathematical models, including hybrid automata [18, 19], delay differential systems [14, 56], stochastic systems [13, 31], have been employed to reason about HSs. For a survey of these methods, we refer to [11].
In the realm of formal synthesis of HSs, different methods [21, 42] can be classified along several dimensions. (i) Along the designable part of the system, the synthesis problem can be categorized into feedback controller synthesis [38], switching controller synthesis [20, 22], and reset controller synthesis [8, 25, 41]. (ii) Along the properties of interest, the problem can be classified into safety controller synthesis, liveness controller synthesis, etc.
Switching controller synthesis [22], shaping HSs by strategically constraining their discrete behavior, can be categorized into two fundamentally approaches. The first is based on constraint solving [42, 55]. This approach highly dependents on finding suitable certificate templates, which is challenging to generate manually. The other approach is abstraction-based method. Given its capability to easily handle complex temporal specifications, this method has been increasingly adopted in recent research [4, 16, 26].
The synthesis of HSs against reach-avoid type specifications, similar to those discussed in this paper, predominantly focuses on feedback controllers. Notable methods include Counterexample-Guided Inductive Synthesis (CEGIS) [36, 37], optimization-based methods [52], and others [15, 32].
When considering STL as the specification, most works focus solely on the continuous dynamics of HSs. Raman et al. proposed a method to encode the STL specification of a hybrid system into MILP [34]. This method was further employed to synthesize robust controllers [35]. The Control Barrier Function-based method can also extends to synthesize feedback controllers with respect to STL specification [23]. Recently, [29] utilizes reinforcement learning technique to synthesize robust controllers for essential discrete-time systems. To the best of our knowledge, [39] is the only work that considers controller synthesis problem of switched systems against STL specification. However, [39] focuses on synthesizing switch input for the hybrid automata with discrete dynamics, while our work aims at synthesizing switching controllers that determine the switch time for the system.
8 Conclusion
We proposed a novel method to synthesize switching controllers for HSs against a fragment of the STL. Our method iteratively calculates the state-time set for each mode, which services as foundation of the synthesize algorithm. The distinctive feature of our approach lies in its soundness and relative completeness. Our preliminary experiments, leveraging a range of notable examples from existing literature, have effectively demonstrated the method’s efficiency and efficacy.
For future work, we plan to continue to explore in two directions. (i) Enlarge the range of specifications under consideration to encompass general STL formulas featuring nested temporal operators. The primary challenge here is devising a unified, recursive formula reasoning approach for general STL specifications. (ii) Broaden the types of controllers that can be synthesized from the calculated state-time sets.
Data Availability Statement
The experimental results of this paper may be reproduced using the artifact on Figshare [17].
Notes
- 1.
For any \(a, b \in \mathbb {R}_{> 0} \) such that \(a \le b\), the constraint \(a \le t \le b\) is concisely denoted as \(t \in [a, b]\).
- 2.
This problem is also referred to as the inner approximation of the reach-avoid problem.
- 3.
\(\nabla _x v(x)\) represents the gradient of v(x) with respect to x, \(\overline{\psi _1}\) denotes the closure of set \(\psi _1\) and \(\partial \psi _1\) refers to the boundary of \(\psi _1\).
- 4.
The approximation of \(X_{q_2}^0\) and \(X_{q_1}^1\) is an empty set, hence it is not depicted.
- 5.
To clarify, we continue to use \(X_q^i\) to represent the inner approximation of the state-time sets, rather than using \(\widetilde{X_q^i}\).
- 6.
In fact, k can be chosen to the number of discontinuous points of \(\pi (x)\).
- 7.
The results and the scripts to reproduce them are available at Figshare [17] or Github https://github.com/Han-SU/BenchMark_STLControlSyn4HS.
- 8.
Future-reach time represents the maximum time horizon required to verify the correctness of an STL formula [5], in WaterTank, the future-reach times of \(\varphi _1\), \(\varphi _2\), and \(\varphi _3\) are 60, 40, and 40 respectively.
References
Alur, R., Dill, D.L.: A theory of timed automata. Theoret. Comput. Sci. 126(2), 183–235 (1994)
Arnon, D.S., Collins, G.E., McCallum, S.: Cylindrical algebraic decomposition i: the basic algorithm. SIAM J. Comput. 13(4), 865–877 (1984)
Atkins, E.M., Bradley, J.M.: Aerospace cyber-physical systems education. In: AIAA Infotech@ Aerospace (I@ A) Conference, p. 4809 (2013)
Aydin Gol, E., Lazar, M., Belta, C.: Language-guided controller synthesis for discrete-time linear systems. In: Proceedings of the 15th ACM international conference on Hybrid Systems: Computation and Control, pp. 95–104 (2012)
Bae, K., Lee, J.: Bounded model checking of signal temporal logic properties using syntactic separation. Proc. ACM Program. Lang. 3(POPL), 1–30 (2019)
Chen, X., Abraham, E., Sankaranarayanan, S.: Taylor model flowpipe construction for non-linear hybrid systems. In: 2012 IEEE 33rd Real-Time Systems Symposium, pp. 183–192. IEEE (2012)
Chen, X., Ábrahám, E., Sankaranarayanan, S.: Flow*: an analyzer for non-linear hybrid systems. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 258–263. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_18
Clegg, J.C.: A nonlinear integrator for servomechanisms. Trans. Am. Inst. Electr. Eng. Part II Appl. Ind. 77(1), 41–42 (1958)
de Alfaro, L., Faella, M., Henzinger, T.A., Majumdar, R., Stoelinga, M.: The element of surprise in timed games. In: Amadio, R., Lugiez, D. (eds.) CONCUR 2003. LNCS, vol. 2761, pp. 144–158. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45187-7_9
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Deshmukh, J.V., Sankaranarayanan, S.: Formal techniques for verification and testing of cyber-physical systems. In: Al Faruque, M.A., Canedo, A. (eds.) Design Automation of Cyber-Physical Systems, pp. 69–105. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-13050-3_4
Engell, S., Kowalewski, S., Schulz, C., Stursberg, O.: Continuous-discrete interactions in chemical processing plants. Proc. IEEE 88(7), 1050–1068 (2000)
Feng, S., Chen, M., Xue, B., Sankaranarayanan, S., Zhan, N.: Unbounded-time safety verification of stochastic differential dynamics. In: Lahiri, S.K., Wang, C. (eds.) CAV 2020. LNCS, vol. 12225, pp. 327–348. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-53291-8_18
Feng, S., Chen, M., Zhan, N., Fränzle, M., Xue, B.: Taming delays in dynamical systems. In: Dillig, I., Tasiran, S. (eds.) CAV 2019. LNCS, vol. 11561, pp. 650–669. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-25540-4_37
Fränzle, M., Chen, M., Kröger, P.: In memory of oded maler: automatic reachability analysis of hybrid-state automata. ACM SIGLOG News 6(1), 19–39 (2019)
Girard, A.: Controller synthesis for safety and reachability via approximate bisimulation. Automatica 48(5), 947–953 (2012)
Han, S., Shenghua, F., Sinong, Z., Naijun, Z.: Benckmark examples of paper “switching controller synthesis for hybrid systems against STL formulas.” Figshare. Software (2024). https://doi.org/10.6084/m9.figshare.26057410.v1
Henzinger, T.A.: The theory of hybrid automata. In: Proceedings 11th Annual IEEE Symposium on Logic in Computer Science, pp. 278–292. IEEE (1996)
Henzinger, T.A., Majumdar, R.: Symbolic model checking for rectangular hybrid systems. In: Graf, S., Schwartzbach, M. (eds.) TACAS 2000. LNCS, vol. 1785, pp. 142–156. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46419-0_11
Jha, S., Seshia, S.A., Tiwari, A.: Synthesis of optimal switching logic for hybrid systems. In: Proceedings of the Ninth ACM International Conference on Embedded Software, pp. 107–116 (2011)
Jin, X., An, J., Zhan, B., Zhan, N., Zhang, M.: Inferring switched nonlinear dynamical systems. Formal Aspects Comput. 33(3), 385–406 (2021)
Liberzon, D.: Switching in Systems and Control, vol. 190. Springer (2003). https://doi.org/10.1007/978-1-4612-0017-8
Lindemann, L., Dimarogonas, D.V.: Control barrier functions for signal temporal logic tasks. IEEE Control Syst. Lett. 3(1), 96–101 (2018)
Lindemann, L., Nowak, J., Schönbächler, L., Guo, M., Tumova, J., Dimarogonas, D.V.: Coupled multi-robot systems under linear temporal logic and signal temporal logic tasks. IEEE Trans. Control Syst. Technol. 29(2), 858–865 (2019)
Liu, J., et al.: Correct-by-construction for hybrid systems by synthesizing reset controller. arXiv preprint arXiv:2309.05906 (2023)
Liu, J., Ozay, N., Topcu, U., Murray, R.M.: Synthesis of reactive switching protocols from temporal logic specifications. IEEE Trans. Autom. Control 58(7), 1771–1785 (2013)
Maler, O., Nickovic, D.: Monitoring temporal properties of continuous signals. In: Lakhnech, Y., Yovine, S. (eds.) FORMATS/FTRTFT -2004. LNCS, vol. 3253, pp. 152–166. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30206-3_12
Mazo, M., Davitian, A., Tabuada, P.: PESSOA: a tool for embedded controller synthesis. In: Touili, T., Cook, B., Jackson, P. (eds.) CAV 2010. LNCS, vol. 6174, pp. 566–569. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14295-6_49
Meng, Y., Fan, C.: Signal temporal logic neural predictive control. IEEE Robot. Autom. Lett. 8(11), 7719–7726 (2023). https://doi.org/10.1109/LRA.2023.3315536
Mosek, A.: The MOSEK optimization toolbox for MATLAB manual. Version 7.1 (revision 28) (2015). http://mosek.com. Accessed 20 Mar 2015
Prajna, S., Jadbabaie, A., Pappas, G.J.: A framework for worst-case and stochastic safety verification using barrier certificates. IEEE Trans. Autom. Control 52(8), 1415–1428 (2007)
Prajna, S., Rantzer, A.: Convex programs for temporal verification of nonlinear dynamical systems. SIAM J. Control. Optim. 46(3), 999–1021 (2007)
Raisch, J., Klein, E., Meder, C., Itigin, A., O’Young, S.: Approximating automata and discrete control for continuous systems — two examples from process control. In: Antsaklis, P., Lemmon, M., Kohn, W., Nerode, A., Sastry, S. (eds.) HS 1997. LNCS, vol. 1567, pp. 279–303. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-49163-5_16
Raman, V., Donzé, A., Maasoumy, M., Murray, R.M., Sangiovanni-Vincentelli, A., Seshia, S.A.: Model predictive control with signal temporal logic specifications. In: 53rd IEEE Conference on Decision and Control, pp. 81–87. IEEE (2014)
Raman, V., Donzé, A., Sadigh, D., Murray, R.M., Seshia, S.A.: Reactive synthesis from signal temporal logic specifications. In: Proceedings of the 18th International Conference on Hybrid Systems: Computation and Control, pp. 239–248 (2015)
Ravanbakhsh, H., Sankaranarayanan, S.: Counterexample-guided stabilization of switched systems using control lyapunov functions. In: Proceedings of the 18th International Conference on Hybrid Systems: Computation and Control, pp. 297–298 (2015)
Ravanbakhsh, H., Sankaranarayanan, S.: Robust controller synthesis of switched systems using counterexample guided framework. In: Proceedings of the 13th International Conference on Embedded Software, pp. 1–10 (2016)
Sanfelice, R.G.: Hybrid Feedback Control. Princeton University Press (2021)
da Silva, R.R., Kurtz, V., Lin, H.: Symbolic control of hybrid systems from signal temporal logic specifications. Guidance Navig. Control 1(02), 2150008 (2021)
Su, H., Feng, S., Zhan, S., Zhan, N.: Switching controller synthesis for hybrid systems against STL formulas. arXiv preprint arXiv:2406.16588 (2024)
Su, H., et al.: Reset controller synthesis by reach-avoid analysis for delay hybrid systems. arXiv preprint arXiv:2309.05908 (2023)
Taly, A., Gulwani, S., Tiwari, A.: Synthesizing switching logic using constraint solving. Int. J. Softw. Tools Technol. Transfer 13(6), 519–535 (2011)
Tomlin, C.J., Lygeros, J., Sastry, S.S.: A game theoretic approach to controller design for hybrid systems. Proc. IEEE 88(7), 949–970 (2000)
Wang, Y., et al.: Joint differentiable optimization and verification for certified reinforcement learning. In: Proceedings of the ACM/IEEE 14th International Conference on Cyber-Physical Systems (with CPS-IoT Week 2023), pp. 132–141 (2023)
Wang, Y., et al.: Enforcing hard constraints with soft barriers: safe reinforcement learning in unknown stochastic environments. In: International Conference on Machine Learning, pp. 36593–36604. PMLR (2023)
Weispfenning, V.: The complexity of linear problems in fields. J. Symb. Comput. 5(1–2), 3–27 (1988)
Witsenhausen, H.: A class of hybrid-state continuous-time dynamic systems. IEEE Trans. Autom. Control 11(2), 161–167 (1966)
Wu, Q., et al.: Boosting long-delayed reinforcement learning with auxiliary short-delayed task. arXiv preprint arXiv:2402.03141 (2024)
Wu, Q., et al.: Variational delayed policy optimization. arXiv preprint arXiv:2405.14226 (2024)
Xue, B., Fränzle, M., Zhan, N.: Inner-approximating reachable sets for polynomial systems with time-varying uncertainties. IEEE Trans. Autom. Control 65(4), 1468–1483 (2019)
Xue, B., She, Z., Easwaran, A.: Under-approximating backward reachable sets by polytopes. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 457–476. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_25
Xue, B., Zhan, N., Fränzle, M., Wang, J., Liu, W.: Reach-avoid verification based on convex optimization. IEEE Trans. Autom. Control 69, 598–605 (2023)
Ye, P., Entcheva, E., Smolka, S.A., Grosu, R.: Modelling excitable cells using cycle-linear hybrid automata. IET Syst. Biol. 2(1), 24–32 (2008)
Zhan, S.S., Wang, Y., Wu, Q., Jiao, R., Huang, C., Zhu, Q.: State-wise safe reinforcement learning with pixel observations. arXiv preprint arXiv:2311.02227 (2023)
Zhao, H., Zhan, N., Kapur, D.: Synthesizing switching controllers for hybrid systems by generating invariants. In: Liu, Z., Woodcock, J., Zhu, H. (eds.) Theories of Programming and Formal Methods. LNCS, vol. 8051, pp. 354–373. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39698-4_22
Zou, L., Fränzle, M., Zhan, N., Mosaad, P.N.: Automatic verification of stability and safety for delay differential equations. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9207, pp. 338–355. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21668-3_20
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2025 The Author(s)
About this paper
Cite this paper
Su, H., Feng, S., Zhan, S., Zhan, N. (2025). Switching Controller Synthesis for Hybrid Systems Against STL Formulas. In: Platzer, A., Rozier, K.Y., Pradella, M., Rossi, M. (eds) Formal Methods. FM 2024. Lecture Notes in Computer Science, vol 14934. Springer, Cham. https://doi.org/10.1007/978-3-031-71177-0_15
Download citation
DOI: https://doi.org/10.1007/978-3-031-71177-0_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-71176-3
Online ISBN: 978-3-031-71177-0
eBook Packages: Computer ScienceComputer Science (R0)




 , where
, where 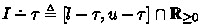 for any interval
for any interval  , i.e. there exists a switching controller
, i.e. there exists a switching controller  , where
, where  .
.



