Abstract
Autonomous hybrid systems are systems that combine discrete and continuous behavior with autonomous decision-making, e.g., using reinforcement learning. Such systems are increasingly used in safety-critical applications such as self-driving cars, autonomous robots or water supply systems. Thus, it is crucial to ensure their safety and resilience, i.e., that they function correctly even in the presence of dynamic changes and disruptions. In this paper, we present an approach to obtain formal resilience guarantees for autonomous hybrid systems using the interactive theorem prover KeYmaera X. Our key ideas are threefold: First, we derive a formalization of resilience that is tailored to autonomous hybrid systems. Second, we present reusable patterns for modeling stressors, detecting disruptions, and specifying resilience as a service level response in the differential dynamic logic (d\(\mathcal {L}\)). Third, we combine these concepts with an existing approach for the safe integration of learning components using hybrid contracts, and extend it towards dynamic adaptations to stressors. By combining reusable patterns for stressors, observers, and adaptation contracts for learning components, we provide a systematic approach for the deductive verification of resilience of autonomous hybrid systems with reduced specification effort. We demonstrate the applicability of our approach with two case studies, an autonomous robot and an intelligent water distribution system.
You have full access to this open access chapter, Download conference paper PDF
Keywords
1 Introduction
Autonomous hybrid systems (AHS), such as self-driving vehicles, robots, and intelligent water supply systems, combine autonomous decision-making with both discrete and continuous behavior. They often act autonomously in dynamic, safety-critical environments, where failures can cause damage or even endanger human lives. As a consequence it is essential to ensure their resilience, i.e., the system’s capability to adapt and maintain its correct functioning amidst changes and disruptions. However, the formal verification of AHS poses distinct challenges because of their hybrid nature and the inclusion of learning components like reinforcement learning (RL), which are hard to capture formally. Approaches to overcome this problem using model checking or statistical model checking are impeded by the state-space explosion problem and often only consider resilience up to a certain time bound. Deductive verification, on the other hand, is a powerful approach for scalable mathematical reasoning even for complex unbounded systems, but demands high expertise and manual effort to provide the necessary specifications and invariants. In particular, there is a lack of reusable formal definitions of resilience in the context of AHS and the few existing definitions are not directly applicable for the deductive verification of qualitative resilience guarantees. This is because they are either not formally specified (e.g., [34]), defined for time-bounded quantitative analysis (e.g., [16, 17, 40]) or tailored to specific classes of systems (e.g., [8]). In this paper, we present a systematic approach for defining, modeling, and verifying resilience of AHS within d\(\mathcal {L}\) [55,56,57] using the interactive theorem prover KeYmaera X [22].
Our approach is based on three key ideas. First, to address the lack of formal qualitative resilience definitions for AHS, we formalize resilience for the deductive verification of AHS based on the informal definition by Laprie [34] by introducing the concept of service levels for AHS which are provided under varying stress conditions. We identify stressors as the key factors causing failures and disruptions, and define service levels to capture dynamic adaptations to stress, such as graceful degradation. Second, to enable systematic deductive verification of resilience properties for AHS, we introduce stressor patterns for modeling stressors and observer patterns for observing the induced stress. Our stressor patterns facilitate integrating various kinds of stressors in formal AHS models, for example noise, component failures, or unexpected delays. Our observer patterns enable formally capturing the stress induced on a system, and thus to verify the system response as service levels, such as a maximum supply or minimum speed, under varying stress levels. Third, we combine our reusable specification patterns with our own previous approach for deductive verification of Simulink models using d\(\mathcal {L}\) [36, 37], and for the safe integration of learning into AHS [1, 4]. In [1, 4], we have specified reusable contract patterns for verifying AHS with RL components with reduced specification and verification effort. In this paper, we extend this approach to reusable resilience contract patterns, which link service levels to the stress intensity experienced by the system and ensure that an RL agent dynamically adapts to stressors. By combining reusable patterns for stressors, observers, and dynamic adaptations using service levels, we provide a systematic approach for the deductive verification of resilience of AHS with reduced specification effort.
We demonstrate the applicability of our approach with two case studies: an intelligent water distribution system and an autonomous robot. The former is based on a model used by MathWorks [42] to demonstrate the RL Toolbox [43], the latter to demonstrate the Robotics System Toolbox [44].
The rest of this paper is structured as follows: we introduce preliminaries in Sect. 2 and our approach in Sect. 3. We present verification results in Sect. 4, discuss related work in Sect. 5, and conclude in Sect. 6.
2 Preliminaries and Case Studies
In this section, we use our two case studies to introduce Simulink and the RL Toolbox, d\(\mathcal {L}\), Simulink2d\(\mathcal {L}\), and our approach for safe RL using contracts.
2.1 Case Studies in Simulink
Simulink [45] is an industrially well established graphical modeling language for AHS. Simulink is block based and provides a large selection of predefined blocks with discrete or continuous behavior, which can be connected via signals. The semantics of Simulink is informally defined in [45]. The RL Toolbox enables directly integrating and simulating RL agents in Simulink models via an RL agent block, which executes an RL algorithm at discrete time steps.
The upper part of Fig. 1a shows a Simulink model of a reservoir of an intelligent water distribution system (IWDS) based on [47]. In [3], we have presented an approach to safely optimize a similar system using a combination of deductive verification and a statistical model checking based learning approach. Using this approach, an RL agent successfully optimizes the supply provided by the system with a given energy budget by decreasing the inflow (e.g., by switching off pumps) whenever the demand is low and by reducing the maximum available supply if necessary due to pump failures. The Simulink model has a constant maximum inflow rate \(\textit{i}_{\texttt{max}}\). The RL agent (\(\texttt{RL}_\texttt{w}\)) can choose a reduced inflow
 and a maximum supply
and a maximum supply
 , which sets a limit on the actual demand d. The reservoir water level h evolves by integrating the difference of the inflow
, which sets a limit on the actual demand d. The reservoir water level h evolves by integrating the difference of the inflow
 and demand
and demand
 , which are computed in the \(\texttt{Flw}_\texttt{w} \) subsystem.
, which are computed in the \(\texttt{Flw}_\texttt{w} \) subsystem.
The upper part of Fig. 1b shows a Simulink model of an autonomous robot in a factory inspired by [41]. The autonomous robot is dynamically assigned goals within a factory, and its RL controller tries to get the robot there as fast as possible without colliding with moving opponents. We have demonstrated that the robot reaches goals safely for a similar system in [4]. The Simulink model consists of an RL controller (\(\texttt{RL}_\texttt{r}\)), which receives distance data from a sensor (\(\texttt{Sns}_\texttt{r}\)), and a second controller for the opponent (\(\texttt{Opp}_\texttt{r}\)). The RL agent can choose the velocity and direction of the RL robot (
 ). The positions of \(\vec {p}_\texttt{r}\) and \(\vec {p}_\texttt{a}\) evolve continuously with axial velocities (
). The positions of \(\vec {p}_\texttt{r}\) and \(\vec {p}_\texttt{a}\) evolve continuously with axial velocities (
 and \(\vec {v}_\texttt{a}\)) respectively.
and \(\vec {v}_\texttt{a}\)) respectively.
2.2 Differential Dynamic Logic d\(\mathcal {L}\) and Simulink2d\(\mathcal {L}\)
Differential dynamic logic (d\(\mathcal {L}\)) [55,56,57] is a logic for formally specifying and reasoning about properties of hybrid systems, which are modeled as hybrid programs (HP). Hybrid Programs are build from the following syntax: \(\alpha ;\beta \) is a sequential composition of two HP \(\alpha \) and \(\beta \). \(\alpha ^*\) is a non-deterministic repetition. \(x:=e\) is a discrete assignment of term e to variable x. \(x:=*\) assigns a non-deterministically chosen value to x. \(\alpha ++\beta \) is a non-deterministic choice. \(?\mathcal {Q}\) is a test formula. \(if(\mathcal {Q})\{\alpha \}else\{\beta \}\) is syntactic sugar for \(\{?\mathcal {Q};\alpha ++?\lnot \mathcal {Q};\beta \}\). {\(x_1' = \eta _1\), ... , \(x_n' = \eta _n\) & \(\mathcal {Q}\)} is a continuous evolution, where variables \(x_i\) evolve with differential equations \(x_i'=\eta _i\) while an evolution domain \(\mathcal {Q}\) is satisfied. Furthermore, in this paper we use \(x \in [l,u]\) as syntactic sugar for \(l \le x \wedge x \le u\). d\(\mathcal {L}\) provides modalities [\(\alpha \)]\(\phi \) and \(\langle \alpha \rangle \phi \) for reasoning about reachable states. Safety specifications are expressed as \(pre\rightarrow [\alpha ]post\) and can be verified using KeYmaera X [22]. Proofs in KeYmaera X are based on the d\(\mathcal {L}\) sequent calculus.
In [36], we have presented an automated transformation from Simulink into d\(\mathcal {L}\), called Simulink2d\(\mathcal {L}\). This provides us with a formal representation of a given Simulink model, and thus enables formal verification of Simulink models using KeYmaera X. Furthermore, we have defined the concept of hybrid contracts (HC) for compositional verification of Simulink models in [37]. HC can be defined for components of Simulink models as d\(\mathcal {L}\) formulas with \(hc = (\phi _{in},\phi _{out})\), where \(\phi _{in}\) are input assumptions and \(\phi _{out}\) are output and trajectory guarantees. HC can be verified for components individually and replace these components during transformation. To integrate RL agents safely into the transformation, the safe behavior of RL agents can also be defined using HC [4]. HC can be used as shields [23] during simulation to enforce safe behavior of RL agents.
The lower part of Fig. 1a shows a d\(\mathcal {L}\) model of the IWDS. The RL agent (\(\texttt{RL}_\texttt{w}\)) is captured by a conditional hybrid program. If the sample time elapses \(c\ge T_S\) the agent selects safe actions
 and
and
 non-deterministically but in compliance to \(HC_\texttt{w} \). \(\texttt{Flw}_\texttt{w}\) computes the current inflow \(\textit{i}\) and demand \(d\). Continuous behavior is captured in the continuous evolution (\(\texttt{Plnt}_\texttt{w}\)). The water level \(h\) evolves with \(h'=\textit{i}-d\), the clock \(c\) and simulation time \(t\) evolve with constant rate 1. The evolution domain \(c\le T_S\) ensures that no sample times of the RL agent are missed. The global simulation loop is modeled by a nondeterministic repetition.
non-deterministically but in compliance to \(HC_\texttt{w} \). \(\texttt{Flw}_\texttt{w}\) computes the current inflow \(\textit{i}\) and demand \(d\). Continuous behavior is captured in the continuous evolution (\(\texttt{Plnt}_\texttt{w}\)). The water level \(h\) evolves with \(h'=\textit{i}-d\), the clock \(c\) and simulation time \(t\) evolve with constant rate 1. The evolution domain \(c\le T_S\) ensures that no sample times of the RL agent are missed. The global simulation loop is modeled by a nondeterministic repetition.
The lower part of Fig. 1b shows a d\(\mathcal {L}\) model of the autonomous robot. The sensor (\(\texttt{Sns}_\texttt{r}\)) assigns the distance \(d(\vec {p}_\texttt{r},\vec {p}_\texttt{a},\)) to a variable \(d_{sens}\). The RL controller (\(\texttt{RL}_\texttt{r}\)) chooses new velocities \(\vec {v}_\texttt{r}\) according to its hybrid contract \(HC_\texttt{r} \). The opponent \(\texttt{Opp}_\texttt{r} \) chooses velocities \(\vec {v}_\texttt{a}\) limited by \(?|\vec {v}_\texttt{a}|\le v_{\texttt{max},\texttt{a}};\). In the continuous evolution, the positions \(\vec {p}_\texttt{a}\), \(\vec {p}_\texttt{r}\), the sampling time clock \(c\) and simulation time \(t\) evolve within the domain constraint \(c\le T_S\). We use \(\vec {v}\) as an abbreviation for axial velocities \((\vec {v_x},\vec {v_y})\) and \(\vec {p}\) for coordinates \((\vec {x},\vec {y})\).
2.3 Reusable Contracts for Safe Integration of Learning
In [1], we have introduced reusable HC patterns for addressing common verification challenges in AHS. These patterns are derived from recurring elements in AHS verification problems and provide templates for the specification of contracts and invariants for learning components. As an example, Table 1 shows the threshold pattern and its application to our two case studies. The pattern specifies the contract that is needed to ensure that the variable \(var_{sc}\) stays within a given threshold \(\theta \) (\(pre\rightarrow [\alpha ]\,var_{sc}\sim \theta \) with \(\sim \,\in \{<, \le , =, \ge , >\}\)). To ensure this property on system level, the RL agent has to maintain the threshold within the next sample time while accounting for the systems worst case reaction (\(wcr\)) to the current state,
 and the sample time (\(T_S\)) of the RL agent.
and the sample time (\(T_S\)) of the RL agent.
In the IWDS, the RL agent has to keep the water level above a minimum \(h\ge h_{min}\). As an action, the agent may choose an inflow
 and limit the outflow to a maximum supply
and limit the outflow to a maximum supply
 . The worst case reaction of the environment is a demand that fully exploits the supply limit (
. The worst case reaction of the environment is a demand that fully exploits the supply limit (
 ). For the robot, a crucial safety requirement is to maintain a minimum distance \(d(\vec {p}_\texttt{r},\vec {p}_\texttt{a})>\theta _{\texttt{evd}}\) to the opponent or to stop if the opponent further decreases the distance. The RL agents threshold contract ensures that the chosen velocity
). For the robot, a crucial safety requirement is to maintain a minimum distance \(d(\vec {p}_\texttt{r},\vec {p}_\texttt{a})>\theta _{\texttt{evd}}\) to the opponent or to stop if the opponent further decreases the distance. The RL agents threshold contract ensures that the chosen velocity
 maintains the distance \(\theta _{\texttt{evd}}\) from the opponents current position. To stop if \(\theta _{\texttt{evd}}\) can no longer be maintained, we add a disjunction to the contract (
maintains the distance \(\theta _{\texttt{evd}}\) from the opponents current position. To stop if \(\theta _{\texttt{evd}}\) can no longer be maintained, we add a disjunction to the contract (
 ) (not shown in the table).
) (not shown in the table).
3 Reusable Patterns for Deductive Verification of Resilience in Autonomous Hybrid Systems
Autonomous hybrid systems (AHS) may face various stressors, for example, sensor noise, component failures, or unexpected delays. It is highly desirable to ensure that AHS are resilient, i.e., that they still function correctly in the presence of such stressors. There exist various definitions of resilience [8, 16, 17, 34, 40]. However, there is a lack of reusable formal definitions of resilience for AHS specifically, especially for the deductive verification of qualitative resilience guarantees.
In this paper, we follow the informal definition provided by Laprie in [34]: “The persistence of service delivery that can justifiably be trusted, when facing changes”. From this definition, we derive a formalization of resilience for the deductive verification of AHS via reusable specification patterns using stressors to describe (safety-critical) changes, and service levels to describe service delivery.
Our overall approach is shown in Fig. 2. Our process starts with an Autonomous Hybrid System (AHS) modeled in Simulink, which includes a reinforcement learning (RL) agent for autonomous decision-making, and Informal Requirements, including resilience. The AHS is transformed into a \(d\mathcal {L}\) Model using the Simulink2d\(\mathcal {L}\) transformation [4, 36]. To establish a structured approach for formalizing and verifying resilience properties, we introduce Service Levels to formalize the system’s adaptive response to stressors. This means, for example, that we describe graceful degradation using a degraded service level together with safety thresholds that are still maintained under stress.
For verifying resilience in AHS, we need to formally model stressors. However, this typically requires high expertise. In particular, it is often unclear how to specify changes in behavior and the intensity of stress induced by given stressors in a formally modeled system. To tackle this, we introduce reusable Stressor Patterns. They are designed to capture various disturbances and changes, ranging from discrete or continuous noise over timed delays to complete failures. In our definition, stressors strictly extend the possible behavior of components with non-determinism. This facilitates easy integration of stressors into existing d\(\mathcal {L}\) models. Furthermore we avoid the need to provide probability distributions, which are often not available or hard to obtain.
To deductively verify and safely integrate learning in AHS modeled in Simulink, we have proposed an approach to replace RL components by hybrid contracts that describe safe actions in [4]. These contracts can be used as shields via automatically generated runtime monitors [23, 49]. In [1] we have proposed reusable contract patterns for common verification problems in AHS. In this paper, to ensure Resilient RL for AHS, we extend this approach with reusable Resilience Contract Patterns, which link appropriate service levels to the stress intensity experienced by the system. With such Resilience Contracts, we can enforce that the RL agent dynamically adapts to stressors and disruptions using service levels.
To be able to verify an overall AHS under different stress levels, capturing the stress intensity induced by stressors formally is desirable. To address this, we propose reusable Observer Patterns. In our definition, observers may never change the system’s behavior but are used to passively capture the dynamic effects of stressors and stress intensity on the system.
With our reusable stressor, resilience contracts, and observer patterns, we enable formal specifications of resilient systems in d\(\mathcal {L}\), and their deductive verification using KeYmaera X [22].
In the following subsections, we introduce the concept of service levels as means for dynamic adaptation, our reusable patterns for stressors and observers, as well as resilience contracts, in more detail.
3.1 Formalization of Resilience Using Service Levels
In AHS, learning components dynamically adapt to changes in the environment. To ensure safety and resilience, we have to make sure that the system remains operational in the presence of stressors. To achieve this, we want to verify that the system satisfies requirements under varying stress levels for all possible adaptations. However, the number of possible adaptations is potentially infinite.
To overcome this problem, we introduce the idea of (a finite number of) service levels (e.g., full, degraded, and no service) to define resilience properties. For each service level, we define ranges of actions (e.g., inflow and supply or speed in our case studies) together with safety thresholds, which can be guaranteed at each service level under varying stress conditions. We can use this to describe high service levels in the absence of stress, and graceful degradation under stress by defining thresholds where we degrade to lower service. Note that within each service level, the system may still choose arbitrary actions from the given range, which enables, for example, learning components or RL agents to safely optimize w.r.t performance properties while resilience guarantees are maintained.
Table 2 shows service levels together with the enabled actions
 and corresponding safety thresholds under high or low stress for the IWDS and the robot. For the IWDS, at full service
and corresponding safety thresholds under high or low stress for the IWDS and the robot. For the IWDS, at full service
 , the highest possible supply \(sup_{\texttt{max}}\) is enabled. In the absence of high stress, a water level \(h\ge h_{\texttt{max}}\) can be maintained. If high stress occurs, \(h\ge h_{\texttt{dgr}}\) with \(h_{\texttt{dgr}}< h_{\texttt{max}}\) must still be maintained to ensure that we can gracefully degrade to the lower service level
, the highest possible supply \(sup_{\texttt{max}}\) is enabled. In the absence of high stress, a water level \(h\ge h_{\texttt{max}}\) can be maintained. If high stress occurs, \(h\ge h_{\texttt{dgr}}\) with \(h_{\texttt{dgr}}< h_{\texttt{max}}\) must still be maintained to ensure that we can gracefully degrade to the lower service level
 . If stressors persist, the system degrades to
. If stressors persist, the system degrades to
 , where only a degraded water level \(h\ge h_{\texttt{dgr}}\) is maintained even in the absence of high stress. Under high stress, the minimum water level \(h_{min}< h_{\texttt{dgr}}\) has to be maintained. If these thresholds can be no longer maintained, the system degrades even further to
, where only a degraded water level \(h\ge h_{\texttt{dgr}}\) is maintained even in the absence of high stress. Under high stress, the minimum water level \(h_{min}< h_{\texttt{dgr}}\) has to be maintained. If these thresholds can be no longer maintained, the system degrades even further to
 , where no supply is provided and only \(h_{min}\) is guaranteed at all stress levels.
, where no supply is provided and only \(h_{min}\) is guaranteed at all stress levels.
For the robot, at full service level
 , the robot is moving and any speed within
, the robot is moving and any speed within
 may be chosen. In the absence of high stress, the robot maintains an evasion distance \(\theta _{\texttt{evd}}\), where opponents have room to safely evade. If stress occurs, the robot at least maintains a stopping distance \(\theta _{\texttt{stp}}\), where it can still safely stop before a potential collision. If these thresholds can not be maintained, the robot stops, i.e., degrades to
may be chosen. In the absence of high stress, the robot maintains an evasion distance \(\theta _{\texttt{evd}}\), where opponents have room to safely evade. If stress occurs, the robot at least maintains a stopping distance \(\theta _{\texttt{stp}}\), where it can still safely stop before a potential collision. If these thresholds can not be maintained, the robot stops, i.e., degrades to
 .
.
3.2 Reusable Stressor Patterns
The inherent uncertainties and dynamic nature of stressors present a significant challenge and their formal specification requires high expertise and manual effort. To address this problem, we introduce reusable stressor patterns. These patterns can be used to formally define the effect of changes and disturbances such as noisy sensors, component failures, or unexpected delays. In our reusable stressor patterns, we over-approximate possible changes with non-determinism. With that, we deliberately avoid the need to provide probability distributions, which are often not available or hard to obtain due to the unpredictable nature of stress factors. Our stressor patterns strictly extend the possible behavior of HPs, thus all behavior of the original HS without stressors is still part of the reachable states. We propose four types of stressor patterns for modeling typical stressors in AHS: discrete and continuous noise, execution delays, and failures. The patterns and their application to our case studies are illustrated in Table 3.
The Discrete Noise pattern models random or unwanted signals. It broadens the range of possible assignments to the variable of a discrete signal x by adding a non-deterministically chosen noise value
 can be limited using a Test
can be limited using a Test
 .
.
 illustrates the application of this pattern with the robot sensor. To ensure that an added stressor variable does not exclude runs of the original HP, the range of possible values must contain the identity element for the operator \(\circ \), i.e., 0 for additive \((\circ =\pm )\) and 1 for multiplicative noise \((\circ =\cdot )\).
illustrates the application of this pattern with the robot sensor. To ensure that an added stressor variable does not exclude runs of the original HP, the range of possible values must contain the identity element for the operator \(\circ \), i.e., 0 for additive \((\circ =\pm )\) and 1 for multiplicative noise \((\circ =\cdot )\).
Continuous Noise can influence the continuous behavior of components. For example, we can have a motion drift, where a robot’s actual trajectory deviates from its intended path over time, caused by factors such as wheel slippage or actuator inaccuracies. To model continuous noise, our pattern adds a disturbance value
 to the derivative of x. We illustrate this pattern with a continuous leakage of the plant of the IWDS (
to the derivative of x. We illustrate this pattern with a continuous leakage of the plant of the IWDS (
 ) and a motion drift of the robot (
) and a motion drift of the robot (
 ).
).
The Failure pattern models failures using a non-deterministic choice between an original HP \(\alpha \) and a failure HP
 , which models the behavior of \(\alpha \) under failure. By retaining the original HP \(\alpha \) as one of the choices, the original runs of the model are preserved and we can reason over arbitrary alternations \(\alpha \) and \(\alpha _{\text {fail}}\). We illustrate this pattern with the IWDS (
, which models the behavior of \(\alpha \) under failure. By retaining the original HP \(\alpha \) as one of the choices, the original runs of the model are preserved and we can reason over arbitrary alternations \(\alpha \) and \(\alpha _{\text {fail}}\). We illustrate this pattern with the IWDS (
 ). The failure model introduces pump failures by setting the inflow rate to zero (\(\textit{i}:=0;\)).
). The failure model introduces pump failures by setting the inflow rate to zero (\(\textit{i}:=0;\)).
The Delay pattern introduces variability to the execution time of discrete components, such as an RL agent, by adding a non-deterministic delay (
 ) into their periodicity. The sampling clock (\(c\)) is then permitted to exceed its normal cycle (\(T_S\)) by
) into their periodicity. The sampling clock (\(c\)) is then permitted to exceed its normal cycle (\(T_S\)) by
 in all tests and evolution domains. We illustrate this pattern with the RL agent of the IWDS (
in all tests and evolution domains. We illustrate this pattern with the RL agent of the IWDS (
 ) and robot (
) and robot (
 ). Note that we omit the evolution domain in the delay examples for brevity.
). Note that we omit the evolution domain in the delay examples for brevity.
3.3 Safe Integration of Learning Using Resilience Contract Patterns
To ensure that a learning component adapts correctly and safely switches between service levels as defined above, we adopt our approach for the safe integration of learning presented in [1, 4]. There, we have defined safe actions for learning components using reusable contract patterns to address recurring verification problems in AHS. To exploit this concept for the formal verification of resilience and dynamic adaptations using service levels, we introduce reusable hybrid contract patterns for resilience via dynamic adaptation to stressors.
Resilience Contract Patterns. The top row of Table 4 presents the pattern we use to define resilience contracts for learning components within a given AHS. A primary challenge in defining contracts for learning components in AHS is that these components typically select actions at discrete sample times, while thresholds must be maintained throughout all continuous evolutions. As detailed in Sect. 2.3, an RL agent, for example, must maintain safety thresholds within the next sample time while accounting for the system’s worst-case reaction (\(wcr\)) relative to the current state (s), action (
 ), and the sample time (\(T_S\)) of the RL agent. To ensure resilience, we utilize a conjunction of two threshold patterns: one for maintaining the threshold under low stress \(\theta _\texttt{ls}\) with a worst-case reaction in the absence of high stress \(wcr_\texttt{ls}\), and another for maintaining the threshold under high stress \(\theta _\texttt{ls}\) with a worst-case reaction in the presence of high stress \(wcr_\texttt{hs}\). This ensures that while providing a service level, the system can respond to both low stress scenarios and high stress conditions by maintaining the corresponding thresholds. The contracts for the IWDS (
), and the sample time (\(T_S\)) of the RL agent. To ensure resilience, we utilize a conjunction of two threshold patterns: one for maintaining the threshold under low stress \(\theta _\texttt{ls}\) with a worst-case reaction in the absence of high stress \(wcr_\texttt{ls}\), and another for maintaining the threshold under high stress \(\theta _\texttt{ls}\) with a worst-case reaction in the presence of high stress \(wcr_\texttt{hs}\). This ensures that while providing a service level, the system can respond to both low stress scenarios and high stress conditions by maintaining the corresponding thresholds. The contracts for the IWDS (
 ) and autonomous robot (
) and autonomous robot (
 ) in Table 4 utilize this pattern with the action ranges and corresponding thresholds from Table 2. In all of these definitions, the worst case reaction of the environment depends on the stress level.
) in Table 4 utilize this pattern with the action ranges and corresponding thresholds from Table 2. In all of these definitions, the worst case reaction of the environment depends on the stress level.
Worst Case Reactions Under Stress. Table 5 shows the definitions of the worst case reactions \(wcr_\texttt{ls}\) and \(wcr_\texttt{hs}\) for our case studies for various stressors under low (ls) and high stress (hs). For pump failures in the IWDS case study (stressor fail), low stress means that no pump fails. The worst case reaction of the environment is then that the current water level is increased by the inflow chosen by the RL agent
 , while it is decreased by the full maximum supply
, while it is decreased by the full maximum supply
 as the demand fully exploits the available supply within the next sample time \(T_S\). In case of high stress, i.e., if the pump fails, the inflow becomes
as the demand fully exploits the available supply within the next sample time \(T_S\). In case of high stress, i.e., if the pump fails, the inflow becomes
 , and the current water level is decreased by
, and the current water level is decreased by
 only within the next sample time. If the execution of the learning agent is delayed (stressor delay), the time for which the worst case reaction is considered is increased by
only within the next sample time. If the execution of the learning agent is delayed (stressor delay), the time for which the worst case reaction is considered is increased by
 under low stress resp.
under low stress resp.
 under high stress. If the water tank is leaking (stressor leak), the IWDS looses water at rate
under high stress. If the water tank is leaking (stressor leak), the IWDS looses water at rate
 under low stress and at rate
under low stress and at rate
 under high stress. For the robot case study with added sensor noise (stressor noise), the worst case reaction of the environment is that the distance to the opponents is reduced by the chosen speed of the robot
under high stress. For the robot case study with added sensor noise (stressor noise), the worst case reaction of the environment is that the distance to the opponents is reduced by the chosen speed of the robot
 , the maximum speed of the opponent \(v_{\texttt{max},\texttt{a}}\), and the real distance is additionally reduced by the measurement error
, the maximum speed of the opponent \(v_{\texttt{max},\texttt{a}}\), and the real distance is additionally reduced by the measurement error
 under low stress resp.
under low stress resp.
 under high stress. If the execution of the learning agent is delayed (stressor delay) in the robot case study, the time for which the worst case reaction is considered is again increased by
under high stress. If the execution of the learning agent is delayed (stressor delay) in the robot case study, the time for which the worst case reaction is considered is again increased by
 resp.
resp.
 . If the robot is drifting (stressor drift), the axial velocity chosen by the RL agent is in the worst case increased by a factor
. If the robot is drifting (stressor drift), the axial velocity chosen by the RL agent is in the worst case increased by a factor
 under low stress resp.
under low stress resp.
 under high stress.
under high stress.
Safe Recovery to higher Service Levels. Our resilience contracts ensure graceful degradation, i.e., that appropriate service levels are chosen and associated thresholds are maintained. However, these contracts do not guarantee that the system will automatically recover to a higher service level during periods of reduced stress. Our service recovery pattern in the last two rows of Table 4 captures this by ensuring that, under low stress (\(wcr_\texttt{ls}\)), the safety critical variable increases by at least the recovery rate \(\texttt{rr}\) at each sampling step. With \(\texttt{rr}> 0\), the system reaches a higher service level eventually.
 applies this pattern to the IWDS. Note that we can’t ensure recovery for the robot, as even under low stress, the robot might be forced to stop infinitely by the opponent.
applies this pattern to the IWDS. Note that we can’t ensure recovery for the robot, as even under low stress, the robot might be forced to stop infinitely by the opponent.
Dynamic Adaptation Using Resilience Contracts. Our resilience contracts shown in Table 4 and 5 ensure that RL agents may only choose actions that are resilient in the sense that stress-dependent safety thresholds are maintained on each service level. To integrate these contracts into a d\(\mathcal {L}\) model of the overall AHS, we use a compositional embedding as shown in Table 6, which can be used for an arbitrary but fixed number of service levels. As described in Sect. 2.2, we embed RL agents into a given d\(\mathcal {L}\) model via a conditional discrete HP [4], where a new action that satisfies the HC is non-deterministically chosen at each sample time (\(c\ge T_S\)). To facilitate dynamic adaptation using resilience contracts, we additionally propose a hierarchical if-else contract composition that enforces the highest possible service level. This structure sequentially evaluates the applicability of service levels from higher to lower, starting at service level i. If an action exists that fulfills the service level, the non-deterministically chosen action of the RL agent is constrained to the respective service level contract by a test. Otherwise, we check the next lower service level for applicability. The second and third columns of Table 6 show the actions and the hierarchy of service levels for both the IWDS and for the autonomous robot. The highest service level for the IWDS is
 and
and
 for the robot. In case of the IWDS,
for the robot. In case of the IWDS,
 additionally ensures service recovery in case of degraded or no service.
additionally ensures service recovery in case of degraded or no service.
3.4 Reusable Observer Patterns
So far, we have introduced stressors patterns that introduce stress into a given AHS and resilience contracts with a compositional embedding to dynamically adapt to stress by switching between service levels. We now introduce observer patterns to systematically track the current stress and the system state when disruptions occur. This enables us to observe the stress imposed on a given AHS and to relate it to appropriate service levels as a system response. With this, we define resilience specifications which can then be verified using KeYmaera X.
Table 7 shows our observer patterns and applications to the IWDS and robot case studies. The upper part of Table 7 shows our observer pattern for failures. We introduce two observer variables, \({\texttt{f}}\) and \({\texttt{f}_{\texttt{old}}}\). If a failure occurs, i.e., \(\alpha _{\texttt{f}}\) is executed, \({\texttt{f}}\) is set to 1 (otherwise \({\texttt{f}}:=0;\)). \({\texttt{f}_{\texttt{old}}}\) stores the previous failure state. If changes in the failure state occur (\( cond ({\texttt{f}},{\texttt{f}_{\texttt{old}}})\)) relevant system state variables, e.g., the time of failure and the current service level, are stored.
 in Table 7 demonstrates this observer pattern for the IWDS flow component with possible pump failures. \({\texttt{f}}\) is set to 1 in the event of pump failures. Upon a failure (
in Table 7 demonstrates this observer pattern for the IWDS flow component with possible pump failures. \({\texttt{f}}\) is set to 1 in the event of pump failures. Upon a failure (
 ), we record the time (
), we record the time (
 ), water level (
), water level (
 ), and current supply (
), and current supply (
 ). We also observe recovery by checking if
). We also observe recovery by checking if
 , and store the repair time (
, and store the repair time (
 ).
).
The observer pattern for discrete noise, delay, and continuous noise shown in the lower part of Table 7 is similar to the observer pattern for failures. For these stressors we observe the variable s that introduces stress (
 in case of noise and
in case of noise and
 in case of delay). We introduce an observer variable \(s_{old}\) to store the previous stress level. Then, we execute the discrete part of the HP of the stressed component (\(S(\alpha _{discr})\)). We check for possible disruptions via checking \(cond(s,s_{old})\), e.g., whether one of the thresholds defined for high stress or low stress was just exceeded. In this case, we store relevant state variables and then execute continuous evolutions under stress (\(S(\alpha _{cont})\)).
in case of delay). We introduce an observer variable \(s_{old}\) to store the previous stress level. Then, we execute the discrete part of the HP of the stressed component (\(S(\alpha _{discr})\)). We check for possible disruptions via checking \(cond(s,s_{old})\), e.g., whether one of the thresholds defined for high stress or low stress was just exceeded. In this case, we store relevant state variables and then execute continuous evolutions under stress (\(S(\alpha _{cont})\)).
 in Table 7 shows the application to the RL agent of the robot in the presence of delay. First, the previous delay
in Table 7 shows the application to the RL agent of the robot in the presence of delay. First, the previous delay
 is stored in
is stored in
 . Then, the RL agent is executed with a newly chosen delay. We check whether the delay level has switched from low to high stress (
. Then, the RL agent is executed with a newly chosen delay. We check whether the delay level has switched from low to high stress (
 ). If so, we store the current time in
). If so, we store the current time in
 and the distance in
and the distance in
 . We also check whether the delay has switched back from high to low and store the time in
. We also check whether the delay has switched back from high to low and store the time in
 and the distance in
and the distance in
 .
.
 and
and
 in Table 7 show the application for sensor noise and drift respectively. There we observe switching from low to high stress only.
in Table 7 show the application for sensor noise and drift respectively. There we observe switching from low to high stress only.
4 Evaluation
To evaluate our approach, we have defined resilience properties for our two case studies, which ensure that the system reacts to different stress conditions with an appropriate service level. Table 8 shows the specifications for both the IWDS and the robot. The RL components use the embeddings defined in Table 6.
For the IWDS, we have specified the following resilience properties in the presence of pump failures (IWDS fail):
-
(a)
If the pump has failed for less than
 time and the system was at full service level when the pump failed, degraded service is still provided.
time and the system was at full service level when the pump failed, degraded service is still provided. -
(b)
If the pump is functioning for
 , at least degraded service is provided.
, at least degraded service is provided. -
(c)
If the pump is functioning for
 time, full service is provided.
time, full service is provided. -
(d)
A minimum water level \(h_{min}\) is always maintained, even with no supply.
For the autonomous robot, we have specified the following resilience properties in the presence of delay (e-g), discrete noise (h-i), and drift (j).
-
(e)
If high delay has never occurred (
 ) the robot either maintains \(\theta _{\texttt{evd}}\) while moving or stops (if the opponent gets too close).
) the robot either maintains \(\theta _{\texttt{evd}}\) while moving or stops (if the opponent gets too close). -
(f)
If high delay occurred at some point (
 ) the robot stops before \(\theta _{\texttt{stp}}\).
) the robot stops before \(\theta _{\texttt{stp}}\). -
(g)
If high delay occurred (
 ) and the delay returned to low delay (
) and the delay returned to low delay (
 ) at a distance greater than the evasion distance (
) at a distance greater than the evasion distance (
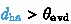 ), the robot either maintains \(\theta _{\texttt{evd}}\) while moving or stops (if the opponent gets too close).
), the robot either maintains \(\theta _{\texttt{evd}}\) while moving or stops (if the opponent gets too close). -
(h)
If high sensor noise has never occurred (
 ), the robot either maintains \(\theta _{\texttt{evd}}\) while moving or stops (if the opponent gets too close).
), the robot either maintains \(\theta _{\texttt{evd}}\) while moving or stops (if the opponent gets too close). -
(i)
If high sensor noise was experienced (
 ), the robot stops before \(\theta _{\texttt{stp}}\).
), the robot stops before \(\theta _{\texttt{stp}}\). -
(j)
If severe drift was experienced (
 ), the robot stops before reaching \(\theta _{\texttt{stp}}\).
), the robot stops before reaching \(\theta _{\texttt{stp}}\).
We have verified all of the resilience properties defined above for the IWDS and the autonomous robot using KeYmaera X. The models and proof files are available at https://www.uni-muenster.de/EmbSys/research/Simulink2dL.htmlhttps://www.uni-muenster.de/EmbSys/research/Simulink2dL.html. The last column of Table 8 shows the number of manual proof steps used for each system specification, providing a rough comparison of verification effort. More proof steps generally indicate higher effort, but shorter proofs may also result from better rule application or clever invariant choices. The proofs for properties (b) with 169 steps and (c) with 259 steps were the most challenging and took roughly two and three person-days respectively. All other proofs were completed in less than one person-day each.
5 Related Work
Many approaches for formal verification of hybrid systems are based on model checking and leverage symbolic reachability, e.g., with polyhedra [13], zonotopes [25], or support functions [35] to over-approximate continuous state spaces. However, these approaches are usually limited to linear dynamics or only consider time-bounded properties. Probabilistic methods [20, 26, 27, 39] face similar limitations. Approaches for deductive verification of hybrid systems, such as differential dynamic logic [55, 56], differential Hoare logic [21], and hybrid Hoare logic for HCSP [38] exploit inductive reasoning to overcome the state space explosion problem. However, they typically require high manual effort and expertise.
Many approaches for formal verification of systems modeled in Simulink, e.g., [7, 30, 58], including the Simulink Design Verifier [46], only support discrete models. Methods that support models of hybrid systems are, e.g., proposed in [12, 14, 48, 66]. However, none of these methods supports learning or resilience.
There also exists a broad variety of approaches to formally ensure safety of learning components using shielding or runtime monitoring [5, 19, 33, 54]. KeYmaera X also enables synthesis of verified runtime monitors for learning components [23, 49,50,51]. However, these methods do not cover the integration of stressors through reusable patterns or dynamic adaptations via service levels.
A wide range of research exists on proof reusability, e.g., within KeY [9] and KeYmaera X [22]. There exist various approaches for automated invariant generation [31, 59, 63]. However, these approaches focus on proof construction rather than domain-specific patterns [28]. [24, 61] provide application-specific patterns to address complex verification issues, like structured arrays [24] and parallel prefix sums [61]. A contract-based approach for system analysis across application domains is introduced in [15], and techniques for structured proof reuse in software variations are proposed in [64], while [6, 32, 65] focus on easing verification through reusable patterns. [53] introduces a contract-based verification in d\(\mathcal {L}\) and provides specifications for output and communication reliability.
There exists work on definitions and formal verification of resilience for CPS, e.g., using temporal logics [11, 60, 62] but these often only consider time discrete systems. [29, 52] consider resilience and robustness for timed (I/O) systems. [10, 18, 40] use Markov decision processes or discrete time Markov chains. However, none of these approaches support deductive verification of hybrid systems.
To the best of our knowledge, none of the existing works specifically address resilience in AHS. In our own previous work [1,2,3], we have presented some initial concepts for reusable resilience contracts. However, we only provided a rudimentary service level concept and we have not considered reusable resilience specifications using stressor and observer patterns.
6 Conclusion and Outlook
In this paper, we have presented an approach for the formal specification and verification of resilience in AHS using d\(\mathcal {L}\) and the interactive theorem prover KeYmaera X. We have presented a structured approach and reusable patterns for modeling stressors and observers, and for specifying resilience as a service level response. Our specifications are more dynamic than traditional safety properties, and thus better capture the adaptive aspects of resilience, as we define service levels relative to the intensity of stress an autonomous hybrid system experiences. By providing resilience contract patterns for learning components, we enable safe and resilient learning with a shielding-based approach, where the shields can automatically be generated from our resilience contracts.
We have demonstrated the applicability of our approach with designs inspired by MathWorks, namely an intelligent water distribution system and an autonomous robot. Our patterns can help reduce the specification effort for deductive verification of resilience properties. By defining coarse- or fine-granular service levels, the designer can choose a trade-off between the specification and verification effort and the strengths of the resulting resilience guarantees.
In future work, we plan to fully integrate our reusable patterns and specifications for resilience with our existing Simulink2d\(\mathcal {L}\) transformation to enable the automatic transformation of Simulink models into resilient AHS models in d\(\mathcal {L}\). We plan to use our approach on larger case studies and to investigate the trade-off between fine- and coarse-granular service levels, and their effect on the precision and permissiveness of contracts. We plan to derive guidelines for the specification of service levels together with safety thresholds for various system classes. Furthermore, we plan to exploit symbolic AI and explainability techniques to generate such specifications automatically.
References
Adelt, J., Brettschneider, D., Herber, P.: Reusable contracts for safe integration of reinforcement learning in hybrid systems. In: Bouajjani, A., Holík, L., Wu, Z. (eds.) Automated Technology for Verification and Analysis. ATVA 2022. LNCS, vol. 13505. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-19992-9_4
Adelt, J., Bruch, S., Herber, P., Niehage, M., Remke, A.: Shielded Learning for Resilience and Performance Based on Statistical Model Checking in Simulink. In: Steffen, B. (eds.) Bridging the Gap Between AI and Reality, vol. 14380, pp. 94–118. Springer Nature Switzerland, Cham (2024). https://doi.org/10.1007/978-3-031-46002-9_6
Adelt, J., Herber, P., Niehage, M., Remke, A.: Towards safe and resilient hybrid systems in the presence of learning and uncertainty. In: Margaria, T., Steffen, B. (eds.) Leveraging Applications of Formal Methods, Verification and Validation. Verification Principles. ISoLA 2022. LNCS, vol. 13701, pp. 299–319. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-19849-6_18
Adelt, J., Liebrenz, T., Herber, P.: Formal verification of intelligent hybrid systems that are modeled with Simulink and the reinforcement learning toolbox. In: Huisman, M., Păsăreanu, C., Zhan, N. (eds.) FM 2021. LNCS, vol. 13047, pp. 349–366. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90870-6_19
Alshiekh, M., Bloem, R., Ehlers, R., Könighofer, B., Niekum, S., Topcu, U.: Safe reinforcement learning via shielding. In: AAAI Conference on Artificial Intelligence 32 (2018). https://doi.org/10.1609/aaai.v32i1.11797
André, É.: Observer patterns for real-time systems. In: 2013 18th International Conference on Engineering of Complex Computer Systems, pp. 125–134. IEEE Computer Society (2013). https://doi.org/10.1109/ICECCS.2013.26
Araiza-Illan, D., Eder, K., Richards, A.: Formal verification of control systems properties with theorem proving. In: International Conference on Control (CONTROL), pp. 244–249. IEEE (2014). https://doi.org/10.1109/CONTROL.2014.6915147
Arghandeh, R., Von Meier, A., Mehrmanesh, L., Mili, L.: On the definition of cyber-physical resilience in power systems. Renew. Sustain. Energy Rev. 58, 1060–1069 (2016). https://doi.org/10.1016/j.rser.2015.12.193
Beckert, B., Klebanov, V.: Proof reuse for deductive program verification. In: International Conference on Software Engineering and Formal Methods (SEFM), pp. 77–86. IEEE (2004). https://doi.org/10.1109/SEFM.2004.1347505
Camilli, M., Mirandola, R., Scandurra, P.: Runtime equilibrium verification for resilient cyber-physical systems. In: 2021 IEEE International Conference on Autonomic Computing and Self-Organizing Systems (ACSOS), pp. 71–80. IEEE (2021). https://doi.org/10.1109/ACSOS52086.2021.00025
Chen, H., Lin, S., Smolka, S.A., Paoletti, N.: An STL-based formulation of resilience in cyber-physical systems. In: Formal Modeling and Analysis of Timed Systems: 20th International Conference, FORMATS 2022, Warsaw, Poland, 13–15 September 2022, Proceedings, pp. 117–135. Springer-Verlag, Heidelberg (2022). https://doi.org/10.1007/978-3-031-15839-1_7
Chen, M., et al.: MARS: a toolchain for modelling, analysis and verification of hybrid systems. In: Hinchey, M.G., Bowen, J.P., Olderog, E.-R. (eds.) Provably Correct Systems. NMSSE, pp. 39–58. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-48628-4_3
Chutinan, A., Krogh, B.H.: Computing polyhedral approximations to flow pipes for dynamic systems. In: Proceedings of the 37th IEEE Conference on Decision and Control (Cat. No. 98CH36171), vol. 2, pp. 2089–2094. IEEE (1998). https://doi.org/10.1109/CDC.1998.758642
Chutinan, A., Krogh, B.H.: Computational techniques for hybrid system verification. IEEE Trans. Autom. Control 48(1), 64–75 (2003). https://doi.org/10.1109/TAC.2002.806655
Cimatti, A., Dorigatti, M., Tonetta, S.: OCRA: a tool for checking the refinement of temporal contracts. In: International Conference on Automated Software Engineering, pp. 702–705. IEEE (2013). https://doi.org/10.1109/ASE.2013.6693137
Clark, A., Zonouz, S.: Cyber-physical resilience: definition and assessment metric. IEEE Trans. Smart Grid 10(2), 1671–1684 (2017). https://doi.org/10.1109/TSG.2017.2776279
Cloth, L., Haverkort, B.R.: Model checking for survivability! In: International Conference on the Quantitative Evaluation of Systems (QEST), pp. 145–154. IEEE (2005). https://doi.org/10.1109/QEST.2005.21
Cámara, J., de Lemos, R.: Evaluation of resilience in self-adaptive systems using probabilistic model-checking. In: 2012 7th International Symposium on Software Engineering for Adaptive and Self-Managing Systems (SEAMS), pp. 53–62 (2012). https://doi.org/10.1109/SEAMS.2012.6224391
David, A., Jensen, P.G., Larsen, K.G., Mikučionis, M., Taankvist, J.H.: Uppaal Stratego. In: Baier, C., Tinelli, C. (eds.) TACAS 2015. LNCS, vol. 9035, pp. 206–211. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46681-0_16
David, A., Larsen, K.G., Legay, A., Mikučionis, M., Wang, Z.: Time for statistical model checking of real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 349–355. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_27
Foster, S., Huerta y Munive, J.J., Struth, G.: Differential Hoare logics and refinement calculi for hybrid systems with Isabelle/HOL. In: Fahrenberg, U., Jipsen, P., Winter, M. (eds.) RAMiCS 2020. LNCS, vol. 12062, pp. 169–186. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-43520-2_11
Fulton, N., Mitsch, S., Quesel, J.-D., Völp, M., Platzer, A.: KeYmaera X: an axiomatic tactical theorem prover for hybrid systems. In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 527–538. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21401-6_36
Fulton, N., Platzer, A.: Safe reinforcement learning via formal methods: toward safe control through proof and learning. AAAI Conf. on Artif. Intellig. 32 (2018). https://doi.org/10.1609/aaai.v32i1.12107
Genestier, R., Giorgetti, A., Petiot, G.: Sequential generation of structured arrays and its deductive verification. In: Blanchette, J.C., Kosmatov, N. (eds.) TAP 2015. LNCS, vol. 9154, pp. 109–128. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21215-9_7
Girard, A.: Reachability of uncertain linear systems using zonotopes. In: Morari, M., Thiele, L. (eds.) HSCC 2005. LNCS, vol. 3414, pp. 291–305. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31954-2_19
Gribaudo, M., Remke, A.: Hybrid petri nets with general one-shot transitions. Perform. Eval. 105, 22–50 (2016). https://doi.org/10.1016/J.PEVA.2016.09.002
Hahn, E.M., Hartmanns, A., Hermanns, H., Katoen, J.P.: A compositional modelling and analysis framework for stochastic hybrid systems. Formal Methods Syst. Des. 43(2), 191–232 (2013). https://doi.org/10.1007/S10703-012-0167-Z
Hähnle, R., Huisman, M.: Deductive software verification: from pen-and-paper proofs to industrial tools. In: Steffen, B., Woeginger, G. (eds.) Computing and Software Science. LNCS, vol. 10000, pp. 345–373. Springer, Cham (2019). https://doi.org/10.1007/978-3-319-91908-9_18
Henzinger, T.A., Otop, J., Samanta, R.: Lipschitz robustness of timed I/O systems. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 250–267. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49122-5_12
Herber, P., Reicherdt, R., Bittner, P.: Bit-precise formal verification of discrete-time MATLAB/Simulink models using SMT solving. In 2013 Proceedings of the International Conference on Embedded Software, pp. 1–10. IEEE (2013). https://doi.org/10.1109/EMSOFT.2013.6658586
Hoder, K., Kovács, L., Voronkov, A.: Invariant generation in vampire. In: Abdulla, P.A., Leino, K.R.M. (eds.) TACAS 2011. LNCS, vol. 6605, pp. 60–64. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19835-9_7
Jonker, C.M., Treur, J., de Vries, W.: Reuse and abstraction in verification: agents acting in dynamic environments. In: Ciancarini, P., Wooldridge, M.J. (eds.) AOSE 2000. LNCS, vol. 1957, pp. 253–267. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44564-1_17
Könighofer, B., Lorber, F., Jansen, N., Bloem, R.: Shield synthesis for reinforcement learning. In: Margaria, T., Steffen, B. (eds.) ISoLA 2020. LNCS, vol. 12476, pp. 290–306. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-61362-4_16
Laprie, J.C.: From dependability to resilience. In: 38th IEEE/IFIP International Conference On dependable systems and networks, pp. G8–G9 (2008)
Le Guernic, C., Girard, A.: Reachability analysis of hybrid systems using support functions. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 540–554. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02658-4_40
Liebrenz, T., Herber, P., Glesner, S.: Deductive verification of hybrid control systems modeled in simulink with KeYmaera X. In: Sun, J., Sun, M. (eds.) ICFEM 2018. LNCS, vol. 11232, pp. 89–105. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-02450-5_6
Liebrenz, T., Herber, P., Glesner, S.: A service-oriented approach for decomposing and verifying hybrid system models. In: Arbab, F., Jongmans, S.-S. (eds.) FACS 2019. LNCS, vol. 12018, pp. 127–146. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-40914-2_7
Liu, J., et al.: A calculus for hybrid CSP. In: Ueda, K. (ed.) APLAS 2010. LNCS, vol. 6461, pp. 1–15. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17164-2_1
Lygeros, J., Prandini, M.: Stochastic hybrid systems: a powerful framework for complex, large scale applications. Eur. J. Control. 16(6), 583–594 (2010). https://doi.org/10.3166/EJC.16.583-594
Madni, A.M., Erwin, D., Sievers, M.: Constructing models for systems resilience: challenges, concepts, and formal methods. MDPI Syst. 8(1), 3 (2020). https://doi.org/10.3390/systems8010003
MathWorks: control and simulate multiple warehouse robots. https://www.mathworks.com/help/robotics/ug/control-and-simulate-multiple-warehouse-robots.html
MathWorks: MATLAB simulink. www.mathworks.com/products/simulink.html
MathWorks: reinforcement learning toolbox. https://www.mathworks.com/products/reinforcement-learning.html
MathWorks: robotics systems toolbox. https://www.mathworks.com/products/robotics.html
MathWorks: simulink. https://www.mathworks.com/products/simulink.html
MathWorks: simulink design verifier. https://www.mathworks.com/products/simulink-design-verifier.html
MathWorks: Water distribution system scheduling using reinforcement learning. https://www.mathworks.com/help/reinforcement-learning/ug/water-tank-simulink-reinforcement-learning-environment.html
Minopoli, S., Frehse, G.: SL2SX Translator: from Simulink to SpaceEx models. In: International Conference on Hybrid Systems: Computation and Control, pp. 93–98. ACM (2016). https://doi.org/10.1145/2883817.2883826
Mitsch, S., Platzer, A.: ModelPlex: verified runtime validation of verified cyber-physical system models. Formal Methods Syst. Des. 49(1), 33–74 (2016). https://doi.org/10.1007/s10703-016-0241-z
Mitsch, S., Platzer, A.: Verified runtime validation for partially observable hybrid systems. CoRR (2018). https://doi.org/10.48550/arXiv.1811.06502
Mitsch, S., Platzer, A.: The KeYmaera X Proof IDE - concepts on usability in hybrid systems theorem proving. Electron. Proc. Theoret. Comput. Sci. 240 (2017). https://doi.org/10.4204/EPTCS.240.5
Mouelhi, S., Laarouchi, M.E., Cancila, D., Chaouchi, H.: Predictive formal analysis of resilience in cyber-physical systems. IEEE Access 7, 33741–33758 (2019). https://doi.org/10.1109/ACCESS.2019.2903153
Müller, A., Mitsch, S., Retschitzegger, W., Schwinger, W., Platzer, A.: Tactical contract composition for hybrid system component verification. Int. J. Softw. Tools Technol. Transfer 20(6), 615–643 (2018). https://doi.org/10.1007/s10009-018-0502-9
Phan, D., et al.: A component-based simplex architecture for high-assurance cyber-physical systems. In: International Conference on Application of Concurrency to System Design, pp. 49–58. IEEE (2017). https://doi.org/10.1109/ACSD.2017.23
Platzer, A.: Differential dynamic logic for hybrid systems. J. Autom. Reason. 41(2), 143–189 (2008). https://doi.org/10.1007/s10817-008-9103-8
Platzer, A.: A complete uniform substitution calculus for differential dynamic logic. J. Autom. Reason. 59(2), 219–265 (2017). https://doi.org/10.1007/s10817-016-9385-1
Platzer, A.: The complete proof theory of hybrid systems. In: 2012 27th Annual IEEE Symposium on Logic in Computer Science, pp. 541–550 (2012). https://doi.org/10.1109/LICS.2012.64
Reicherdt, R., Glesner, S.: Formal verification of discrete-time MATLAB/Simulink models using boogie. In: Giannakopoulou, D., Salaün, G. (eds.) SEFM 2014. LNCS, vol. 8702, pp. 190–204. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10431-7_14
Rodríguez-Carbonell, E., Kapur, D.: Automatic generation of polynomial invariants of bounded degree using abstract interpretation. Sci. of Comp. Progr. 64(1), 54–75 (2007). https://doi.org/10.1016/j.scico.2006.03.003
Rungger, M., Tabuada, P.: A notion of robustness for cyber-physical systems. IEEE Trans. Autom. Control 61(8), 2108–2123 (2015). https://doi.org/10.1109/TAC.2015.2492438
Safari, M., Oortwijn, W., Joosten, S., Huisman, M.: Formal verification of parallel prefix sum. In: Lee, R., Jha, S., Mavridou, A., Giannakopoulou, D. (eds.) NFM 2020. LNCS, vol. 12229, pp. 170–186. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-55754-6_10
Saoud, A., Jagtap, P., Soudjani, S.: Temporal logic resilience for cyber-physical systems. In: 2023 62nd IEEE Conference on Decision and Control (CDC), pp. 2066–2071 (2023). https://doi.org/10.1109/CDC49753.2023.10384033, https://api.semanticscholar.org/CorpusID:267046171
Sogokon, A., Mitsch, S., Tan, Y.K., Cordwell, K., Platzer, A.: Pegasus: a framework for sound continuous invariant generation. In: ter Beek, M.H., McIver, A., Oliveira, J.N. (eds.) FM 2019. LNCS, vol. 11800, pp. 138–157. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-30942-8_10
Thüm, T., Schaefer, I., Apel, S., Hentschel, M.: Family-based deductive verification of software product lines. In: International Conference on Generative Programming and Component Engineering, pp. 11–20. ACM (2012). https://doi.org/10.1145/2371401.2371404
Vogel, T., Carwehl, M., Rodrigues, G.N., Grunske, L.: A property specification pattern catalog for real-time system verification with UPPAAL. Inf. Softw. Technol. 154, 107100 (2023). https://doi.org/10.1016/j.infsof.2022.107100
Zou, L., Zhan, N., Wang, S., Fränzle, M.: Formal verification of Simulink/Stateflow diagrams. In: Finkbeiner, B., Pu, G., Zhang, L. (eds.) ATVA 2015. LNCS, vol. 9364, pp. 464–481. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24953-7_33
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2025 The Author(s)
About this paper
Cite this paper
Adelt, J., Mensing, R., Herber, P. (2025). Reusable Specification Patterns for Verification of Resilience in Autonomous Hybrid Systems. In: Platzer, A., Rozier, K.Y., Pradella, M., Rossi, M. (eds) Formal Methods. FM 2024. Lecture Notes in Computer Science, vol 14934. Springer, Cham. https://doi.org/10.1007/978-3-031-71177-0_14
Download citation
DOI: https://doi.org/10.1007/978-3-031-71177-0_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-71176-3
Online ISBN: 978-3-031-71177-0
eBook Packages: Computer ScienceComputer Science (R0)




 time and the system was at full service level when the pump failed, degraded service is still provided.
time and the system was at full service level when the pump failed, degraded service is still provided. , at least degraded service is provided.
, at least degraded service is provided. time, full service is provided.
time, full service is provided. ) the robot either maintains
) the robot either maintains  ) the robot stops before
) the robot stops before  ) and the delay returned to low delay (
) and the delay returned to low delay (
 ) at a distance greater than the evasion distance (
) at a distance greater than the evasion distance (
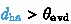 ), the robot either maintains
), the robot either maintains  ), the robot either maintains
), the robot either maintains  ), the robot stops before
), the robot stops before  ), the robot stops before reaching
), the robot stops before reaching